悬臂结构允许挠度
均布荷载悬臂梁挠度计算公式

为保证承重结构的承载能力和防止在一定条件下出现脆性破坏,应根据结构的重要性、荷载特征、结构形式、应力状态、连接方法、钢材厚度和工作环境等因素综合考虑,选用合适的钢材牌号和材性。
承重结构的钢材宜采用Q235钢、Q345钢、Q390钢和Q420钢,其质量应分别符合现行国家标准《碳素结构钢》GB/T700和《低合金高强度结构钢》GB/T 1591的规定。
当采用其他牌号的钢材时,尚应符合相应有关标准的规定和要求。
对Q235钢宜选用镇静钢或半镇静钢。
承重结构的钢材应具有抗拉强度、伸长率、屈服强度和硫、磷含量的合格保证,对焊接结构尚应具有碳含量的合格保证。
焊接承重结构以及重要的非焊接承重结构的钢材还应具有冷弯试验的合格保证。
对于需要验算疲劳的焊接结构的钢材,应具有常温冲击韧性的合格保证。
当结构工作温度等于或低于0℃但高于-20℃时,Q235钢和Q345钢应具有0℃C冲击韧性的合格保证;对Q390钢和Q420钢应具有-20℃冲击韧性的合格保证。
当结构工作温度等于或低于-20℃时,对Q235钢和Q345钢应具有-20℃冲击韧性的合格保证;对Q390钢和Q420钢应具有-40℃冲击韧性的合格保证。
对于需要验算疲劳的非焊接结构的钢材亦应具有常温冲击韧性的合格保证,当结构工作温度等于或低于-20℃时,对Q235钢和Q345钢应具有0℃冲击韧性的合格保证;对Q390钢和Q420钢应具有-20℃冲击韧性的合格保证。
当焊接承重结构为防止钢材的层状撕裂而采用Z向钢时,其材质应符合现行国家标准《厚度方向性能钢板》GB/T 5313的规定。
钢材的强度设计值(材料强度的标准值除以抗力分项系数),应根据钢材厚度或直径按表1采用。
钢铸件的强度设计值应按表2采用。
连接的强度设计值应按表3~5采用。
1钢材的强度设计值(N/mm2)表1注:表中厚度系指计算点的钢材厚度,对轴心受力构件系指截面中较厚板件的厚度。
2钢铸件的强度设计值(N/mm2)表23焊缝的强度设计值(N/mm2)表3注:1.自动焊和半自动焊所采用的焊丝和焊剂,应保证其熔敷金属的力学性能不低于现行国家标准《碳素钢埋弧焊用焊剂》GB/T 5293和《低合金钢埋弧焊用焊剂》GB/T 12470中相关的规定;2.焊缝质量等级应符合现行国家标准《钢结构工程施工质量验收规范》GB 50205的规定。
悬臂梁挠度试验.ppt

V
M EI
dx
(4.5)
M
M EI
dxdx
(4.6)
比較(4.1)與(4.5)式、(4.2)與(4.6)式,可得到以下 之結論:
1. 受實際載重作用之樑上某斷面之斜率=受彈性載重作 用之共軛樑上同一斷面之剪力。
2. 受實際載重作用之樑上某斷面之撓度=受彈性載重作 用之共軛樑上同一斷面之彎矩。
3. 真實樑之邊界束制情形與共軛樑之邊界束制情形具有 如下之對應關係:
曲率、彎矩與斜率之關係-
撓曲曲線之曲率,其定義為,若考慮樑之變形單純由彎 矩所造成,則曲率與彎矩具有之關係。此外,撓曲曲線 之斜率則為。今假設樑之變形非常微小,亦即、(之單位 為弳),則可得,或可寫為,積分之,可得
M EI
dx
(4.1)
再將以代入,則關係式可改寫為,再積分之,則可得
y
M EI
撓度測定裝置(含20mm測微錶)。
試驗原理
符號系統之定義-
x軸向右為正。 y軸向下為正。
載重向下作用為正。 剪力造成樑之右半部相對於左半部向下移動而變形,則
此剪力為正。 彎矩造成樑之上半部受壓縮,則此彎矩為正。 撓度向下為正。
撓曲曲線上某特定點之切線與x軸間之夾角為,與x軸成
順時針轉動者為正。 樑彎曲成凹向下時,曲率為正。
真實樑之內接點(
L
,
R
y
0)
共軛樑之內支承(V L , V R M 0 )
本試驗單元擬採用共軛樑法,進行懸臂樑撓度之分析
a
b
P
x max L
y
首先,將相等於真實樑之圖之彈性載重作用於共軛樑, 如下圖所示
Pa EI
其中
F1
F1
MECHANICA计算悬臂梁受力后产生的挠度教程
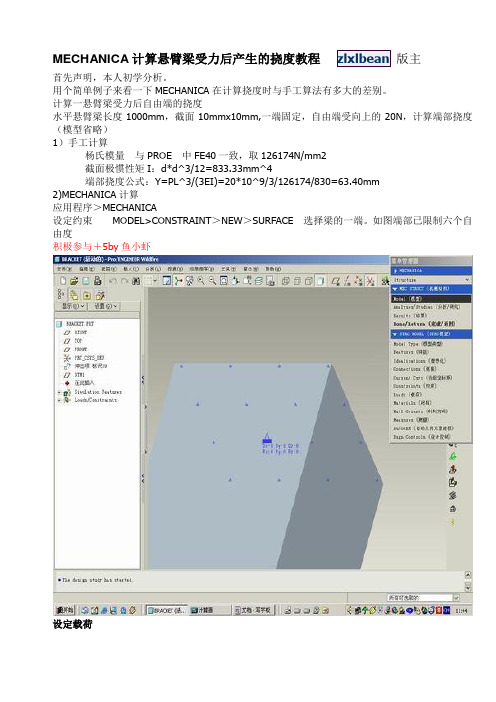
MECHANICA计算悬臂梁受力后产生的挠度教程版主首先声明,本人初学分析。
用个简单例子来看一下MECHANICA在计算挠度时与手工算法有多大的差别。
计算一悬臂梁受力后自由端的挠度水平悬臂梁长度1000mm,截面10mmx10mm,一端固定,自由端受向上的20N,计算端部挠度(模型省略)1)手工计算杨氏模量与PROE中FE40一致,取126174N/mm2截面极惯性矩I:d*d^3/12=833.33mm^4端部挠度公式:Y=PL^3/(3EI)=20*10^9/3/126174/830=63.40mm2)MECHANICA计算应用程序>MECHANICA设定约束MODEL>CONSTRAINT>NEW>SURFACE选择梁的一端。
如图端部已限制六个自由度积极参与+5by鱼小虾设定载荷设定材料MODEL>MATERIALS 在材料库中选择FE40,>>>,选择右侧模型材料清单中的FE40,EDIT查看材料特性:可以看见FE40的泊松比已预设为0.25,杨氏模量已预设为126174N/mm2,ASSIGN >MODEL,选择模型,将材料赋于模型,ANALYSES/STUDIES>START RUNSTUDY STATUS 中的计算结果MAX_DISP_Y即为Y方向挠度62.988......Measures:max_beam_bending: 0.000000e+00max_beam_tensile: 0.000000e+00max_beam_torsion: 0.000000e+00max_beam_total: 0.000000e+00max_disp_mag: 6.301795e+01max_disp_x: 3.586717e-03max_disp_y: 6.298895e+01max_disp_z: -2.855637e+00max_prin_mag: -1.367307e+02max_rot_mag: 0.000000e+00max_rot_x: 0.000000e+00max_rot_y: 0.000000e+00max_rot_z: 0.000000e+00max_stress_prin: 1.336835e+02max_stress_vm: 1.208697e+02max_stress_xx: -4.803162e+01max_stress_xy: 8.678658e+00max_stress_xz: -1.299264e+01max_stress_yy: -4.804984e+01max_stress_yz: -8.408328e+00max_stress_zz: -1.366642e+02min_stress_prin: -1.367307e+02strain_energy: 6.279311e+02最后还可图形表示挠度RESULTQUANTITY选DISPLACEMENT、COMPONENT YDISPLAY OPTIONS勾选DEFORMED、TRANSPARENT OVERLAY结果基本一致PROE:6.2989E+1mm公式计算:63.40mm本想在题目前加上“菜鸟”二字的没想到没加上去,惭愧的很:rose超级斑竹这种小问题都被怀疑那这个mechanica就完蛋了!我算的肯定比你更快更准,是用理想化的BEAM算出来的。
结构力学中的杆件挠度分析

结构力学中的杆件挠度分析在结构力学中,杆件是指用来承载和传递载荷的构件,它们通常是细长的,而挠度是衡量杆件变形程度的参数。
挠度分析是结构力学中的重要内容之一,它可以帮助工程师评估结构的强度和稳定性,并设计出更加安全可靠的结构。
一、杆件挠度的定义和分类在进行挠度分析之前,我们首先需要了解挠度的定义。
挠度是指杆件在受力作用下发生的形变,是杆件纵向偏移的量。
根据杆件的简化模型,挠度可以分为两类:横向挠度和纵向挠度。
1. 横向挠度:横向挠度是指杆件端部在垂直于杆件轴线方向上的位移。
它受到弯矩作用的影响,通常发生在杆件的中间或两端。
2. 纵向挠度:纵向挠度是指杆件在沿着轴线方向上的位移,也称为轴向压缩或拉伸变形。
纵向挠度主要受到轴向力的影响,比如拉力或压力。
二、杆件挠度的计算方法杆件挠度的计算方法可以根据杆件的受力情况和边界条件进行选择。
以下是常见的几种计算方法:1. 静力法:静力法适用于较为简单的杆件结构,通过受力平衡和力矩平衡等基本原理,将受力杆件简化为悬臂梁、梁或柱等模型,然后采用梁或柱的挠度计算方法进行分析。
2. 叠加法:叠加法适用于复杂的受力情况,如多个载荷作用在杆件上。
它将不同载荷下的挠度分别计算,再将其叠加求和得到最终结果。
3. 差分法:差分法是一种基于微积分的计算方法,通过将杆件划分为多个小段,利用微分、积分等数学工具,进行近似计算。
差分法适用于复杂的非均匀截面和载荷分布情况。
三、杆件挠度分析的应用杆件挠度分析在工程设计和结构优化中具有重要的应用价值,主要体现在以下几个方面:1. 结构安全性评估:通过对杆件挠度的计算和分析,可以评估结构在受力过程中的安全性。
当挠度超过一定限制时,可能会导致结构的破坏或失稳,因此需要对挠度进行合理的限制和控制。
2. 结构优化设计:挠度分析可以帮助工程师找出结构中可能存在的弱点或疲劳区域,并提供改进的方案。
通过对挠度进行分析和比较,可以选择合适的材料、改变结构形状或调整支承方式,从而提高结构的强度和稳定性。
悬臂梁挠度方程的伽辽金法

悬臂梁挠度方程的伽辽金法
悬臂梁挠度方程是一个二阶微分方程,常常使用伽辽金法求解。
伽辽
金法是一种基于离散化的数值解法,利用有限元方法将连续问题转化为离
散问题,然后通过求解离散问题得到连续问题的近似解。
具体步骤如下:
1.将悬臂梁分成n个小段,在每个小段内选择一个节点,称为节点i。
2. 假设悬臂梁在每个小段上的挠度分别为wi,则可以得到如下形式
的微分方程:
EIw''(xi)=Mi,其中EI为弯曲刚度,Mi为单位长度内的力矩。
3.将w(x)在节点i处展开为一次函数:
w(x)≈wi+ai(x-xi)+bi(x-xi)2。
其中ai和bi为待求系数。
4.将上述近似式代入微分方程中,得到:
EI(ai+2bi(x-xi))=Mi。
5.将上述方程写成矩阵形式:
[EI/h2 -EI/h2] [ai] = [Mi]。
其中h为小段长度。
6. 重复上述步骤,在每个小段上求解ai和bi的值。
7.最后将所有小段的近似式组合起来,得到整个悬臂梁的挠度分布。
需要注意的是,伽辽金法求解的是近似解,随着离散节点数的增加,
解的精度也会增加。
因此,在实际应用中需要根据需要选择合适的节点数。
结构挠度的规定

起重机梁的最大允许相对挠度设计为L/1000(L为跨距),最大不得超过L/700。
绝对挠度前面的数值还要加上梁的上拱度。
承重的钢结构梁可参考前面数据,并根据结构重要性增减《钢结构设计规范》8.3.1 吊车梁和吊车衍架不应下挠。
10.3.4 单层钢结构主体结构的整体垂直度和整体平面弯曲的允许偏差应符合表10.3.4的规定。
整体垂直度和整体平面弯曲的允许偏差(mm)表10.3.411.3.5 多层及高层钢结构主体结构的整体垂直度和整体平面弯曲的允许偏差应符合表11.3.5的规定。
整体垂直度和整体平面弯曲的允许偏差(mm)表11.3.512.3.4 钢网架结构总拼完成后及屋面工程完成后应分别测量其挠度值,且所测的挠度值不应超过相应设计值的1.15倍。
受弯构件的容许挠度表3.3.2《城市人行天桥与人行地道技术规范》 CJJ 69--952.5.1天桥与地道的结构应符合以下要求:2.5.1.1结构在制造、运输、安装和使用过程中,应具有规定的强度、刚度、稳定性和耐久性。
2.5.2天桥上部结构,由人群荷载计算的最大竖向挠度,不应超过下列允许值:梁板式主梁跨中L/600;梁板式主梁悬臂端L1/300;桁架、拱L/800。
注:I为计算跨径;L1为悬臂长度。
2.5.4为避免共振,减少行人不安全感,天桥上部结构竖向自振频率不应小于3Hz。
2.5.7地道结构,以汽车荷载(不计冲击力)计算的最大挠度不应超过L/600。
注:用平板挂车或履带车荷载验算时,上述允许挠度可增加20%。
名句赏析!!!!!不限主题不限抒情四季山水天气人物人生生活节日动物植物食物山有木兮木有枝,心悦君兮君不知。
____佚名《越人歌》人生若只如初见,何事秋风悲画扇。
____纳兰性德《木兰词·拟古决绝词柬友》十年生死两茫茫,不思量,自难忘。
____苏轼《江城子·乙卯正月二十日夜记梦》只愿君心似我心,定不负相思意。
____李之仪《卜算子·我住长江头》玲珑骰子安红豆,入骨相思知不知。
悬臂梁受三角形荷载时的挠度和弯矩公式

悬臂梁受三角形荷载时的挠度和弯矩公式一、概述悬臂梁是一种常见的结构工程中使用的梁形式,其受力情况复杂多样。
本文将讨论悬臂梁在受到三角形分布荷载时的挠度和弯矩计算公式,为工程设计和分析提供参考。
二、三角形分布荷载的数学表达1. 三角形分布荷载可用数学函数表达,通常采用线性函数。
其一般形式为:\[ q(x) = kx + b \]式中,q(x)为位置x处的荷载大小,k为斜率,b为截距。
2. 一般情况下,三角形分布荷载的斜率k可表示为:\[ k = \frac{q_b - q_a}{c} \]其中,q_a和q_b分别为荷载作用起始和终止位置的荷载大小,c为荷载作用的距离。
三、悬臂梁受三角形分布荷载的挠度计算1. 悬臂梁在受到三角形分布荷载作用时,其挠度可根据悬臂梁的弯曲方程和边界条件进行计算。
一般情况下,悬臂梁的挠度计算需要考虑均匀荷载的影响,而在受到三角形分布荷载时,需要针对荷载分布进行积分求解。
2. 三角形分布荷载的挠度计算公式可表示为:\[ \delta(x) = \frac{1}{EI} \int_{0}^{x} q(x)(L-x)^2 dx \]式中,δ(x)为位置x处的挠度,E为梁的弹性模量,I为梁的截面惯性矩,L为悬臂梁的长度。
3. 根据上述公式,可以通过对三角形分布荷载进行积分,得到悬臂梁在任意位置的挠度大小。
这为工程设计和分析提供了重要的理论支持。
四、悬臂梁受三角形分布荷载的弯矩计算1. 悬臂梁在受到三角形分布荷载作用时,其弯矩分布可以通过梁的受力分析和力学平衡方程求解。
2. 三角形分布荷载在悬臂梁上的弯矩计算公式可表示为:\[ M(x) = \frac{1}{2} q(x)(L-x)x \]式中,M(x)为位置x处的弯矩大小。
3. 通过对三角形分布荷载进行弯矩计算,可以得到悬臂梁在各个位置上的弯矩大小。
这对于梁的抗弯设计和受力分析具有重要的意义。
五、结论本文对悬臂梁受三角形分布荷载的挠度和弯矩进行了详细的讨论和推导,给出了相应的数学计算公式。
简支梁和悬臂梁的弯矩挠度计算

0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
注明:1.在使用此表格计算弯矩和挠度时,要结合实际情况选择正确的图示模型。相
臂长/mm
l=a+b或 l=a1+a2
剪力/N
Vb 0 0 0 0 0 0 0 0 0 0 0 0
弯矩/N.m
Mx 0 0 0 0 0 0 0 0 0 0 0 0
弯矩/N.m
Mmax 0 0 0 0 0 0 0 0 0 0 0 0
选型计算 设计允许 挠度差值
挠度/mm 挠度/mm /△mm
W=Wsmax-
Wsmax Wmax
Wmax
0
0
图示载荷
载荷等 单位载 单位载荷 C型槽钢 载荷/N 分数 荷/N/mm 长度/mm
F=q*l
n
q
c
ACS-21
0
0
ACS-31
0
0
ACS-41
0
0
ACS-52
0
0
ACS-62
0
0
ACS-72
0
0
ACS-82
0
0
ACS-21D
0
0
ACS-41D
0
0
ACS-52D
0
0
ACS-52-72D 0
0
ACS-72D
