悬臂梁挠度计算公式
挠度计算
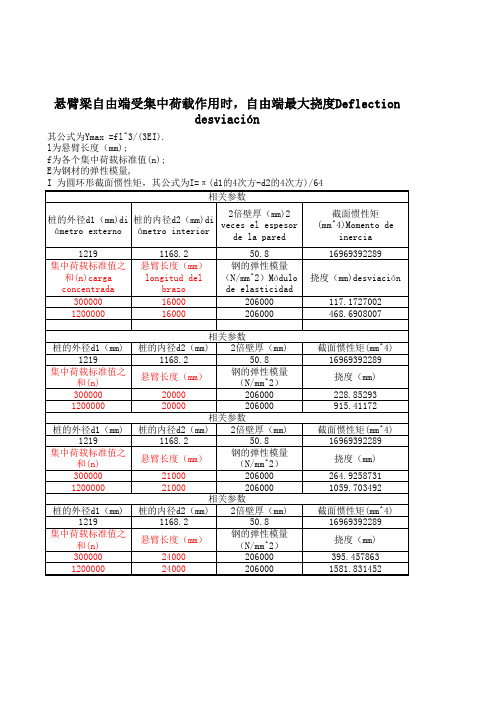
其公式为Ymax =fl^3/(3EI). l为悬臂长度(mm); f为各个集中荷载标准值(n); E为钢材的弹性模量, I 为圆环形截面惯性矩,其公式为I=π (d1的4次方-d2的4次方)/64 相关参数 2倍壁厚(mm)2 桩的外径d1(mm)di 桩的内径d2(mm)di veces el espesor ámetro externo ámetro interior de la pared 1219 集中荷载标准值之 和(n)carga concentrada 300000 1200000 1168.2 悬臂长度(mm) longitud del brazo 16000 16000 50.8 钢的弹性模量 (N/mm^2)Módulo de elasticidad 206000 206000 截面惯性矩 (mm^4)Momento de inercia 16969392289 挠度(mm)desviación 117.1727002 468.6908007
桩的外径d1(mm) 1219 集中荷载标准值之 和(n) 300000 1200000 桩的外径d1(mm) 1219 集中荷载标准值之 和(n) 300000 1200000 桩的外径d1(mm) 1219 集中荷载标准值之 和(n) 300000 1200000
相关参数 桩的内径d2(mm) 2倍壁厚(mm) 1168.2 50.8 钢的弹性模量 悬臂长度(mm) (N/mm^2) 20000 206000 20000 206000 相关参数 桩的内径d2(mm) 2倍壁厚(mm) 1168.2 50.8 钢的弹性模量 悬臂长度(mm) (N/mm^2) 21000 206000 21000 206000 相关参数 桩的内径d2(mm) 2倍壁厚(mm) 1168.2 50.8 钢的弹性模量 悬臂长度(mm) (N/mm^2) 24000 206000 24000 206000
均布荷载悬臂梁挠度计算公式

为保证承重结构的承载能力和防止在一定条件下出现脆性破坏,应根据结构的重要性、荷载特征、结构形式、应力状态、连接方法、钢材厚度和工作环境等因素综合考虑,选用合适的钢材牌号和材性。
承重结构的钢材宜采用Q235钢、Q345钢、Q390钢和Q420钢,其质量应分别符合现行国家标准《碳素结构钢》GB/T700和《低合金高强度结构钢》GB/T 1591的规定。
当采用其他牌号的钢材时,尚应符合相应有关标准的规定和要求。
对Q235钢宜选用镇静钢或半镇静钢。
承重结构的钢材应具有抗拉强度、伸长率、屈服强度和硫、磷含量的合格保证,对焊接结构尚应具有碳含量的合格保证。
焊接承重结构以及重要的非焊接承重结构的钢材还应具有冷弯试验的合格保证。
对于需要验算疲劳的焊接结构的钢材,应具有常温冲击韧性的合格保证。
当结构工作温度等于或低于0℃但高于-20℃时,Q235钢和Q345钢应具有0℃C冲击韧性的合格保证;对Q390钢和Q420钢应具有-20℃冲击韧性的合格保证。
当结构工作温度等于或低于-20℃时,对Q235钢和Q345钢应具有-20℃冲击韧性的合格保证;对Q390钢和Q420钢应具有-40℃冲击韧性的合格保证。
对于需要验算疲劳的非焊接结构的钢材亦应具有常温冲击韧性的合格保证,当结构工作温度等于或低于-20℃时,对Q235钢和Q345钢应具有0℃冲击韧性的合格保证;对Q390钢和Q420钢应具有-20℃冲击韧性的合格保证。
当焊接承重结构为防止钢材的层状撕裂而采用Z向钢时,其材质应符合现行国家标准《厚度方向性能钢板》GB/T 5313的规定。
钢材的强度设计值(材料强度的标准值除以抗力分项系数),应根据钢材厚度或直径按表1采用。
钢铸件的强度设计值应按表2采用。
连接的强度设计值应按表3~5采用。
1钢材的强度设计值(N/mm2)表1注:表中厚度系指计算点的钢材厚度,对轴心受力构件系指截面中较厚板件的厚度。
2钢铸件的强度设计值(N/mm2)表23焊缝的强度设计值(N/mm2)表3注:1.自动焊和半自动焊所采用的焊丝和焊剂,应保证其熔敷金属的力学性能不低于现行国家标准《碳素钢埋弧焊用焊剂》GB/T 5293和《低合金钢埋弧焊用焊剂》GB/T 12470中相关的规定;2.焊缝质量等级应符合现行国家标准《钢结构工程施工质量验收规范》GB 50205的规定。
材料力学中挠度的单位

材料力学挠度计算公式:
1、在跨中单个荷载F作用下的挠度是:F*L^3/(48EI)
2、在均不荷载q作用下的挠度是:5*q*L^4/(384EI)
3、在各种荷载作用下,利用跨中弯矩M可以近似得到统一的跨中挠度计算公式:0。
1*M*L^2/(EI)。
其中:p=kN=1000N,L=8。
16m=8 160mm,E=2。
1x10^5N/mm^2=210000N/mm^ 2,Ix=5280cm^4=52800000mm^4,计算结果单位= mm。
悬臂梁受均布荷载或自由端受集中荷载作用时,自由端最大挠度分别为的,其计算公式:
Ymax=1ql^4/(8EI)。
;Ymax=1pl^3/(3EI)。
q为均布线荷载标准值(kn/m)。
;p为各个集中荷载标准值之和(kn)。
你可以根据最大挠度控制1/400,荷载条件25kn/m以及一些其他荷载条件。
扩展资料
挠度是在受力或非均匀温度变化时,杆件轴线在垂直于轴线方向的线位移或板壳中面在垂直于中面方向的线位移。
细长物体(如梁或柱)的挠度是指在变形时其轴线上各点在该点处轴线法平面内的位移量。
薄板或薄壳的挠度是指中面上各点在该点处中面法线上的位移量。
物体上各点挠度随位置和时间变化的规律称为挠度函数或位移函数。
通过求挠度函数来计算应变和应力是固体力学的研究方法之一。
工字钢挠度计算公式

工字钢挠度计算公式工字钢是一种常见的结构钢材,广泛应用于建筑、桥梁、机械制造等领域。
在使用过程中,我们常常需要了解工字钢的挠度情况,以便评估其承载能力和结构稳定性。
工字钢的挠度计算是基于悬臂梁的理论基础上进行的。
悬臂梁是指梁的一端固定,另一端自由悬挂。
工字钢在实际应用中常常处于悬臂状态,因此可以采用相应的悬臂梁挠度计算公式进行计算。
工字钢的挠度计算公式如下:δ = (5 * q * L^4) / (384 * E * I)其中,δ表示工字钢的挠度,q表示悬臂梁上的集中载荷,L表示悬臂梁的长度,E表示工字钢的弹性模量,I表示工字钢截面的惯性矩。
在实际应用中,我们需要根据具体的工字钢尺寸和载荷情况来计算挠度。
首先,我们需要测量工字钢的长度L,并计算出截面的惯性矩I。
惯性矩是描述截面形状对于承载能力的影响的重要参数,可以通过工字钢的几何尺寸计算得出。
接下来,我们需要确定悬臂梁上的集中载荷q。
集中载荷是指作用在悬臂梁上的单点力或集中力,可以通过实际测量或结构设计参数得出。
我们需要知道工字钢的弹性模量E。
弹性模量是描述材料对外力作用下变形程度的物理量,可以通过实验测量或查阅资料得到。
根据上述计算公式,我们可以将具体数值代入进行计算,从而得出工字钢的挠度。
挠度的数值可以帮助我们评估工字钢的承载能力,如果挠度过大,则可能存在结构安全隐患,需要采取相应的加固措施。
工字钢挠度的计算也对工字钢的设计和选型具有重要意义。
通过计算不同尺寸和材质的工字钢的挠度,可以比较不同方案的承载能力和结构稳定性,从而选择合适的工字钢材料和尺寸。
工字钢的挠度计算是工程设计和结构评估中重要的一环。
通过合理计算工字钢的挠度,可以评估其承载能力和结构稳定性,为工程安全提供重要参考。
同时,工字钢挠度的计算也对工字钢的设计和选型具有指导意义,帮助选择合适的工字钢材料和尺寸。
梁的刚度计算范文

梁的刚度计算范文梁的刚度是指材料在受到外力作用时的抵抗变形的能力。
在工程中,刚度是一个非常重要的参数,它决定了梁的强度和稳定性。
梁的刚度计算可以通过不同的方法进行,下面将介绍两种常用的计算方法:简支梁的刚度计算和悬臂梁的刚度计算。
一、简支梁的刚度计算简支梁是指两个端点都可以转动的梁,它的刚度可以通过弯曲刚度来计算。
弯曲刚度是指单位长度下的梁的抵抗弯曲变形的能力。
1.简支梁的弯曲刚度公式简支梁的弯曲刚度可以通过以下公式进行计算:EI=(WL^3)/(48D)其中,EI为弯曲刚度,W为作用在梁上的力或负荷,L为梁的长度,D为梁的挠度。
2.弯曲刚度的单位和性质弯曲刚度的单位是N.m^2,它的数值越大,梁的刚度越高。
弯曲刚度与梁的材料属性有关,即与材料的弹性模量E和惯性矩I有关。
E表示材料的刚度,单位为N/m^2,I表示梁的惯性矩,单位为m^4、弯曲刚度EI 的数值越大,表示材料的刚度越高。
二、悬臂梁的刚度计算悬臂梁是指只有一个端点可以转动的梁,它的刚度可以通过挠度和力矩进行计算。
1.悬臂梁的挠度计算悬臂梁的挠度是指梁在受到外力作用时的弯曲变形。
悬臂梁的挠度可以通过以下公式进行计算:δ=(FL^3)/(3EI)其中,δ为悬臂梁的挠度,F为作用在梁上的力或负荷,L为梁的长度,E为梁的弹性模量,I为梁的惯性矩。
2.悬臂梁的刚度计算悬臂梁的刚度可以通过力矩和挠度的比值来计算:K=M/δ其中,K为悬臂梁的刚度,M为悬臂梁上的力矩,δ为悬臂梁的挠度。
总结:梁的刚度是指梁在受到外力作用时的抵抗变形的能力。
梁的刚度可以通过弯曲刚度和挠度进行计算。
简支梁的刚度可以通过弯曲刚度进行计算,悬臂梁的刚度可以通过力矩和挠度的比值进行计算。
两种方法都可以用来计算梁的刚度,根据具体的梁结构和受力情况选择适当的计算方法。
工程力学挠度计算公式

工程力学挠度计算公式在工程力学领域中,挠度是一个重要的参数,用来描述结构在受力作用下的变形情况。
挠度计算公式是工程师在设计和分析结构时必须掌握的基本知识之一。
通过挠度计算公式,可以帮助工程师预测结构在实际工作中的变形情况,从而确保结构的安全性和稳定性。
挠度计算公式的推导通常是基于梁的弹性理论。
在弹性理论中,假设结构受到的载荷是小幅度的,且结构材料具有线弹性特性。
根据这些假设,可以得到梁的挠度计算公式,其基本形式为:δ = (F * L^3) / (3 * E * I)其中,δ表示梁的挠度,F表示作用在梁上的外力,L表示梁的长度,E表示梁的弹性模量,I表示梁的惯性矩。
这个公式是工程力学中常用的简化形式,适用于许多工程实际问题的分析。
在实际工程中,为了更准确地计算结构的挠度,有时还需要考虑结构的边界条件、截面形状等因素。
对于不同形状和受力条件的结构,挠度计算公式可能会有所差异。
例如,对于悬臂梁、简支梁、悬臂梁等不同类型的梁,其挠度计算公式会有所不同。
除了梁的挠度计算公式外,对于其他类型的结构如板、壳、柱等,也有相应的挠度计算公式。
这些公式通常是基于结构的几何形状、材料性质和受力条件等因素推导而来的。
工程师在实际工作中需要根据具体情况选择合适的挠度计算公式,并结合有限元分析等方法进行结构的挠度分析。
总的来说,挠度计算公式是工程力学中的重要概念,对于工程师设计和分析结构具有重要意义。
掌握挠度计算公式可以帮助工程师更好地理解结构的变形特性,从而设计出更安全、稳定的工程结构。
在工程实践中,工程师需要灵活应用挠度计算公式,结合实际情况进行分析,确保结构的安全性和可靠性。
常用挠度公式

常用挠度公式常用的挠度公式指的是用于计算结构物挠度的公式,挠度是指结构物在受力作用下发生的形变。
挠度公式的应用十分广泛,涉及到工程、建筑、力学等领域。
在工程中,我们经常需要计算结构物的挠度,以评估其受力性能和安全性。
挠度公式是用来描述结构物在受力作用下发生的弯曲变形的数学公式。
常用的挠度公式有梁的挠度公式和杆的挠度公式。
我们来看梁的挠度公式。
梁是一种常见的结构物,在很多工程中起着承载和支撑作用。
梁的挠度是指梁在受力作用下发生的弯曲形变程度。
梁的挠度公式可以根据梁的几何形状、材料性质和受力情况进行推导。
常用的梁的挠度公式有三种,分别是简支梁的挠度公式、悬臂梁的挠度公式和悬臂梁的挠度公式。
简支梁的挠度公式是根据梁的几何形状和受力情况推导出来的。
简支梁的挠度公式可以用来计算在梁两端施加集中力或均布力时梁的挠度。
简支梁的挠度公式是根据梁的受力平衡方程和弯矩-挠度关系推导出来的。
简支梁的挠度公式可以表述为:挠度=(集中力或均布力乘以梁的长度的平方)/(48倍的弹性模量和惯性矩的乘积)。
悬臂梁的挠度公式是用来计算在梁一端施加集中力或均布力时梁的挠度的公式。
悬臂梁的挠度公式可以根据悬臂梁的受力平衡方程和弯矩-挠度关系推导出来。
悬臂梁的挠度公式可以表述为:挠度=(集中力或均布力乘以梁的长度的平方)/(3倍的弹性模量和惯性矩的乘积)。
杆的挠度公式是用来计算杆在受力作用下发生的挠度的公式。
杆的挠度公式可以根据杆的几何形状、材料性质和受力情况进行推导。
常用的杆的挠度公式有两种,分别是短杆的挠度公式和长杆的挠度公式。
短杆的挠度公式是用来计算短杆在受力作用下发生的挠度的公式。
短杆的挠度公式可以根据短杆的受力平衡方程和弯矩-挠度关系推导出来。
短杆的挠度公式可以表述为:挠度=(集中力或均布力乘以杆的长度的平方)/(2倍的弹性模量和截面面积的乘积)。
长杆的挠度公式是用来计算长杆在受力作用下发生的挠度的公式。
长杆的挠度公式可以根据长杆的受力平衡方程和弯矩-挠度关系推导出来。
三跨连续梁 内力计算公式(一)

三跨连续梁 内力计算公式(一)三跨连续梁 内力计算公式1. 弯矩计算公式•综合法:根据对称轴原理,可以得到弯矩计算公式为:M =qL 28,其中q 为荷载值,L 为跨度。
• 悬臂法:对于三跨连续梁中两个悬臂梁的弯矩计算,可以使用悬臂法,其公式为:M =qL 212,其中q 为荷载值,L 为悬臂梁的长度。
2. 剪力计算公式• 剪力平衡法:根据剪力平衡原理,可以得到剪力计算公式为:V =qL 2,其中q 为荷载值,L 为跨度。
• 弯矩法:根据弯矩和剪力的关系,可以得到剪力计算公式为:V =−dM dx ,其中M 为弯矩,x 为跨度上的任意位置。
3. 梁的挠度计算公式• 三跨连续梁的挠度计算可以使用弹性力学理论,其中常用的公式是梁的挠度计算公式为:δ=5qL 4384EI ,其中q 为荷载值,L 为跨度,E 为梁的弹性模量,I 为梁的惯性矩。
• 对于三跨连续梁中两个悬臂梁的挠度计算,可以使用悬臂梁挠度计算公式为:δ=qL 4192EI ,其中q 为荷载值,L 为悬臂梁的长度,E 为梁的弹性模量,I 为梁的惯性矩。
举例解释假设有一根三跨连续梁,其总跨度为10米,其中两个悬臂梁的长度为2米,受到均匀分布荷载为10kN/m 的作用。
根据上述计算公式,可以得到以下结果:1. 弯矩计算:• 综合法:M =10×1028=125 kNm • 悬臂法:M =10×2212=103 kNm ,对应两个悬臂梁 2. 剪力计算:• 剪力平衡法:V =10×102=50 kN• 弯矩法:根据弯矩和剪力的关系,可以在弯矩计算的基础上求得剪力分布。
例如,在距离支座2米处的剪力为V =−dM dx =−1255=−25 kN 。
3. 梁的挠度计算:• 综合法:δ=5×10×104384×E×I ,需要进一步提供梁的弹性模量E 和惯性矩I 来计算。
• 悬臂法:δ=10×24192×E×I ,同样需要提供梁的弹性模量E 和惯性矩I 。
