材料力学第9章_梁的挠度和刚度计算
合集下载
材料力学简明教程(景荣春)课后答案第九章
解 设各杆与铅垂线夹角为 θ ，则由平衡的各杆的受力
130
3FN cosθ = F ， FN =
设钢管材料为 Q235，则
F F 2 .5 5 F = ⋅ = = 0.417 F 3 cos θ 3 2 12
= 269 > λp D2 + d 2 30 2 + 22 2 × 10 −3 π 2 EI π 3 E (D 4 − d 4 ) π 3 × 210 × 10 9 × (30 2 − 22 2 )× 10 −12 Fcr = = = = 9.37 kN 2 64 × 2.5 2 (μl )2 64(μl ) Fcr F 1 1 9.37 × 10 3 [F ] = = × = × = 7.49 kN 0.417 0.417 [n]st 0.417 3 i = =
2
127
比值差不多时较有利。 9-8 从稳定性的角度考虑，一般压杆截面的周边取圆形较为合理，但可以是空心或实 心的。如规定压杆横截面面积相同，则： (1) 从强度方面看，它们有无区别？为什么？ (2) 从稳定性方面看，哪一种截面形式较为合理？为什么？ (3) 如果空心圆形截面较合理的话，是否其内、外半径越大越好？ 答 (1) 从强度方面看，它们无区别。因为 σ = F / A 。 (2) 从稳定性方面看，空心截面形式较为合理，因空心截面惯性矩较大。 (3) 如果空心圆形截面较合理的话，其内、外半径不是越大越好，因为在面积一定的情 况下，内、外半径太大了会造成薄壁失稳。 9-9 如何进行压杆的合理设计？ 答 （1） 选择合理的截面形状； （2） 改变压杆的约束条件； （3）合理选择材料。 9-10 满足强度条件的等截面压杆是否满足稳定性条件？满足稳定性条件的压杆是否 满足强度条件？为什么？ 答 （1） 因为强度条件是 σ < [σ ] =
材料力学第9章 压杆稳定
第9章 压杆稳定 图9－6
第9章 压杆稳定
9.2.3 两端非铰支细长压杆的临界载荷 1.一端固定一端自由的细长压杆的临界载荷 图9－7所示为一端固定、一端自由的长为l的细长压杆。
当轴向压力F=Fcr时，该杆的挠曲轴与长为2l的两端铰支细 长压杆的挠曲轴的一半完全相同。因此，如果二杆各截面的 弯曲刚度相同，则临界载荷也相同。所以，一端固定一端自 由、长为l的细长压杆的临界载荷为
第9章 压杆稳定
9.2.2 大挠度理论与实际压杆 式（9－1）与式（9－2）是对于理想压杆根据小挠度挠
曲轴近似微分方程得到的。如果采用大挠度挠曲轴的微分方
程 ddx1xM ExI进行理论分析，则轴向压力F与压杆最
大挠度wmax之间存在着如图9－6中的曲线AB所示的确定关 系，其中A点为曲线的极值点，相应之载荷Fcr即为上述欧拉 临界载荷。
Fcr
2 EI
2l 2
（9－3）
第9章 压杆稳定
图9－7
第9章 压杆稳定
2.两端固定的细长压杆的临界载荷 图9－8所示为两端固定的长为l的细长压杆，当轴向压 力F=Fcr时，该杆的挠曲轴如图9－8(a)所示，在离两固定端 各l/4处的截面A、B存在拐点，A、B截面的弯矩均为零。因 此，长为l/2的AB段的两端仅承受轴向压力Fcr（见图9－8 (b)），受力情况与长为l/2的两端铰支压杆相同。所以，两 端固定的压杆的临界载荷为
Fcr
2EI
0.5l 2
（9－4）
第9章 压杆稳定
图9－8
第9章 压杆稳定
3.一端固定一端铰支的细长压杆的临界载荷 图9－9所示为一端固定一端铰支的长为l的细长压杆， 在微弯临界状态，其拐点与铰支端之间的正弦半波曲线长为
工程力学---材料力学(第七章- 梁弯曲时位移计算与刚度设计)经典例题及详解
得： D 0
Pl 2 得： C 16
AC段梁的转角方程和挠曲线方程分别为：
P 2 2 (4 x l ) 16 EI Px y (4 x 2 3 l 2 ) 48 EI
y
P
B
A
x
l 2
C
l 2
x
最大转角和最大挠度分别为：
max A B
ymax y
q 7qa 8k 384 EI
3
q/2
B C
q/2
A B C
顺时针
q/2
例16：图示梁Ｂ处为弹性支座，弹簧刚 度
EI k 求C端挠度fC。 2a 3
q
A
EI k
B
C
2a
a
解：(1)梁不变形，仅弹簧变形引起的C点挠度为 4 3 qa 3qa B处反力=qa fC 1 2 k EI
q
B
x
l
由边界条件： x 0时，y 0
x l时，y 0
得：
ql 3 C , D0 24
梁的转角方程和挠曲线方程分别为：
y
q 2 3 3 (6lx 4 x l ) 24 EI
q
x
A qx y (2lx 2 x 3 l 3 ) 24 EI
ql 3 24 EI
A a a
q
B C
a
qa 12 EI
顺时针
3 3
P=qa
A B
P=qa
m=qɑ²/2
qa qa C B 6 EI 4 EI
4
顺时针
B
q
C
qa 5qa fC B a 8EI 24 EI
整理材料力学梁的挠度对照表
材料力学梁的挠度对照表整理表姓名:职业工种:申请级别:受理机构:填报日期:A4打印/ 修订/ 内容可编辑材料力学一、考试目标与要求《材料力学》课程考试旨在考核学生对本课程知识的掌握和运用能力，包括必要的材料力学的基础知识，一定的分析问题解决问题能力以及用力学知识解决工程实际问题的能力等。
参照教材《材料力学》第3版，沈养中、李桐栋编，科学出版社，2015，确定该科目专升本招生考试的考核目标与要求。
二、考试范围与要求1.绪论考核知识点：材料力学的研究对象及主要任务；杆件变形的基本形式及各自的受力特征和变形特征；变形固体的基本假设。
2. 轴向拉伸与压缩本模块主要研究杆件在轴向拉伸和压缩时的内力、应力、变形和强度计算以及材料的力学性质。
考核知识点：轴向拉压杆件的内力计算，内力图的绘制；轴向拉压杆件横截面上任一点应力的计算，强度条件的应用；轴向拉压杆件伸长量的计算，纵向线应变的计算。
3.扭转本模块主要研究圆杆扭转时的内力、应力、变形及强度和刚度计算。
考核知识点：扭转变形的概念，外力偶的计算；扭转杆件横截面内力的计算，内力图的绘制；扭转杆件横截面上任一点应力的计算，强度条件的应用；圆轴扭转杆件扭转的刚度条件。
4.截面的几何性质本模块主要研究静矩和惯性矩的计算。
静矩、惯性矩等都属平面图形的几何性质。
在研究梁的应力、变形等问题时，将用到静矩、惯性矩等几何性质。
考核知识点：截面静矩、形心、惯性矩、极惯性矩、惯性积的概念；圆形截面、矩形截面对其形心轴的惯性矩的计算。
5.弯曲梁是以弯曲变形为主的杆件，它在工程中应用极为广泛。
本模块将研究梁的内力力和内力图，梁弯曲时横截面上的正应力、切应力、梁的强度计算以及梁弯曲时的位移计算。
考核知识点：梁的平面弯曲的概念；梁横截面内力（剪力、弯矩）的计算，剪力图和弯矩图的绘制；梁横截面正应力的计算，正应力强度条件的应用；梁横截面剪应力的计算；度量梁变形后横截面位移的基本量，梁的挠曲线近似微分方程及其积分。
材料力学梁的弯曲变形第3节 用叠加法求梁的变形
挠曲轴线 近似微分方程
y M (x) EI
• 叠加原理：当梁为小变形时，梁的挠度和转角均是 载荷的线性函数，可以使用叠加法计算梁的转角和 挠度，即梁在几个载荷同时作用下产生的挠度和转 角等于各个载荷单独作用下梁的挠度和转角的叠加 和，这就是计算梁弯曲变形的叠加原理。
• 叠加原理的步骤： ①分解载荷；②分别计算各载荷 单独作用时梁的变形；③叠加得最后结果。
a
x
5ql 4 384 EI
例6-5 悬臂梁AB上作用有均布载荷q，自由端作 用有集中力F = ql，梁的跨度为l，抗弯刚度为EI，如 图所示。试求截面B的挠度和转角。
解：（1）分解载荷
梁上载荷可分解成均布载 荷 q 与集中力 F 的叠加。
（2）查表得这两钟情况下
截面 B 的挠度和转角
yBq
ql3 2EI
2ql
3
（顺时针）
3EI
例6-6 如图所示，外伸梁在外伸段作用有均布 载荷q，梁的抗弯刚度为EI。求C截面的挠度。
解： 1）简化、分解载荷
2）分别计算 B 截面挠度：
悬臂梁因 B 截面产生转角引
起的挠度 yC1和悬臂梁在均布 载荷作用下产生的挠度 yC2
0.5qa2
qa
+
B
yA3
ql4 8EI
7ql 4 384EI
5Fl3 48EI
41ql4 5Fl3 384EI 48EI
代入数值得：
yA 3.89 103 m 3.89mm（）
ql 4 8EI
+
Bq
ql3 6EI
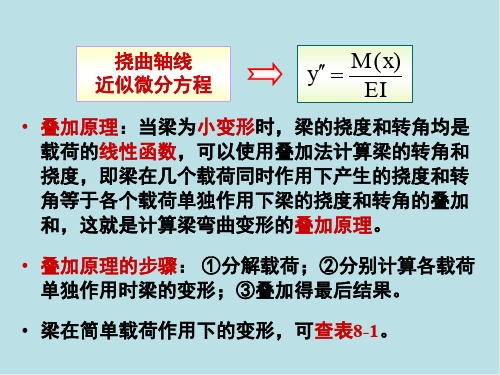
y M (x) EI
• 叠加原理：当梁为小变形时，梁的挠度和转角均是 载荷的线性函数，可以使用叠加法计算梁的转角和 挠度，即梁在几个载荷同时作用下产生的挠度和转 角等于各个载荷单独作用下梁的挠度和转角的叠加 和，这就是计算梁弯曲变形的叠加原理。
• 叠加原理的步骤： ①分解载荷；②分别计算各载荷 单独作用时梁的变形；③叠加得最后结果。
a
x
5ql 4 384 EI
例6-5 悬臂梁AB上作用有均布载荷q，自由端作 用有集中力F = ql，梁的跨度为l，抗弯刚度为EI，如 图所示。试求截面B的挠度和转角。
解：（1）分解载荷
梁上载荷可分解成均布载 荷 q 与集中力 F 的叠加。
（2）查表得这两钟情况下
截面 B 的挠度和转角
yBq
ql3 2EI
2ql
3
（顺时针）
3EI
例6-6 如图所示，外伸梁在外伸段作用有均布 载荷q，梁的抗弯刚度为EI。求C截面的挠度。
解： 1）简化、分解载荷
2）分别计算 B 截面挠度：
悬臂梁因 B 截面产生转角引
起的挠度 yC1和悬臂梁在均布 载荷作用下产生的挠度 yC2
0.5qa2
qa
+
B
yA3
ql4 8EI
7ql 4 384EI
5Fl3 48EI
41ql4 5Fl3 384EI 48EI
代入数值得：
yA 3.89 103 m 3.89mm（）
ql 4 8EI
+
Bq
ql3 6EI
附录3简单荷载作用下梁的挠度和转角
2EI
w = Fx2 (3l − x) 6EI
w = Fx2 (3a − x) 6EI
(0 ≤ x ≤ a) w = Fa2 (3x − a)
6EI (a ≤ x ≤ l)
w = qx2 (x2 + 6l2 − 4lx) 24EI
转角和挠度
θB
=
Mel EI
wB
=
Mel 2 2EI
θB
=
Fl 2 3EI
附录 3 简单荷载作用下梁的挠度和转角
序号
梁上荷载及弯矩图
1
2
3
4
w=沿 y 方向的挠度
wB=w(l)=梁右端处的挠度 θB = w′(l) =梁右端处的转角
w=沿 y 的方向挠度
wc=w(
l 2
)=梁的中点挠度
θa = w′(0) =梁左端处的转角
θa = w′(l) =梁右端处的转角
挠曲线方程 w =Mex2
⎡⎢⎢⎢⎣2
x3 b3
−
x b
⎛⎜⎜⎜⎝2
l2 b2
−1⎞⎠⎟⎟⎟⎟⎤⎥⎥⎥⎦
(0 ≤ x ≤ a)
θB
=
−
qb2 (2l − b)2 24EIl
wc
=
qb5 24EIl
⎜⎜⎝⎛⎜
3 4
l3 b3
−
1 2
l b
⎠⎞⎟⎟⎟⎟
13
w
=
−
q 24EI
⎡⎢⎢⎣2
b2x3 l
−
b2x l
(2l 2
− b2 )
wB
=
Fl 3 3EI
θB
=
Fa2 2EI
wB
=
Fa2 6EI
w = Fx2 (3l − x) 6EI
w = Fx2 (3a − x) 6EI
(0 ≤ x ≤ a) w = Fa2 (3x − a)
6EI (a ≤ x ≤ l)
w = qx2 (x2 + 6l2 − 4lx) 24EI
转角和挠度
θB
=
Mel EI
wB
=
Mel 2 2EI
θB
=
Fl 2 3EI
附录 3 简单荷载作用下梁的挠度和转角
序号
梁上荷载及弯矩图
1
2
3
4
w=沿 y 方向的挠度
wB=w(l)=梁右端处的挠度 θB = w′(l) =梁右端处的转角
w=沿 y 的方向挠度
wc=w(
l 2
)=梁的中点挠度
θa = w′(0) =梁左端处的转角
θa = w′(l) =梁右端处的转角
挠曲线方程 w =Mex2
⎡⎢⎢⎢⎣2
x3 b3
−
x b
⎛⎜⎜⎜⎝2
l2 b2
−1⎞⎠⎟⎟⎟⎟⎤⎥⎥⎥⎦
(0 ≤ x ≤ a)
θB
=
−
qb2 (2l − b)2 24EIl
wc
=
qb5 24EIl
⎜⎜⎝⎛⎜
3 4
l3 b3
−
1 2
l b
⎠⎞⎟⎟⎟⎟
13
w
=
−
q 24EI
⎡⎢⎢⎣2
b2x3 l
−
b2x l
(2l 2
− b2 )
wB
=
Fl 3 3EI
θB
=
Fa2 2EI
wB
=
Fa2 6EI
挠度计算
? te为以有效受拉混凝土截面面积
计算的受拉钢筋配筋率。
Ate为有效受拉混凝土截面面积，对
受弯构件取
Ate ? 0.5b ?h (bf ? b)hf
A
14
10.3 受弯构件的挠度验算
第十章 变形和裂缝宽度的计算
Bs
?
Es Ash02
? ? ? E?
??
Bs
?
Es Ash02
1.15?
? 6? E ? 1? 3.5??f
对钢筋混凝土梁
f
?
S
Mk B
l02
短期弯矩Mk一般处于第Ⅱ阶段，刚度计算需要研究构件带裂缝 时的工作情况。该阶段裂缝基本等间距分布，钢筋和混凝土的
应变分布具有以下特征：
A
6
10.3 受弯构件的挠度验算
第十章 变形和裂缝宽度的计算
?
c
?
ec ec
f ? es ? ec
h0
? ? es es
A
Bs
?
Ms
验值。在短期弯矩Msk=（0.5~0.7）Mu范围，系数? 的变化很小， 仅与配筋率有关。《规范》根据试验结果分析给出，
?E? ?
?
0.2 ?
6? E ? 1? 3.5??f
? ?f
?
(b?f ? b)h?f bh0
受压翼缘加强系数
A
12
10.3 受弯构件的挠度验算
第十章 变形和裂缝宽度的计算
A
13
10.3 受弯构件的挠度验算
第十章 变形和裂缝宽度的计算
3、钢筋应变不均匀系数?
?
?
1.1 ?
0.65 s
ftk
? sk te
《材料力学》第五版_刘鸿文第9_10章习题答案
0
−P
0
P
− 2P P
0
0
2P
0
−P
P
− 2P 0
0
解： a、c 桁架 b 桁架
Pcr =
Pb ≥ Pc = Pa
π 2 EI ( 2l ) 2 π 2 EI Pcr = (l ) 2
HAII MAXUN
N ≤ Pcr = 2 P N ≤ Pcr = P
π 2 EI 2 2l 2 π 2 EI P= (l ) 2 P=
8.5 ×1.43 (14 − 8.5) × 9.63 4 4 Iy = + cm = 407cm 12 12
9.6 × 143 (9.6 − 1.4) × 8.53 4 4 Iz = + cm = 1780cm 12 12
iy =
λP =
Iy A
=
407 cm = 2.51cm iz = 64.7
湖北汽车工业学院
材料力学
主讲教师：马迅
10.14 材料相同、长度相等的变截面杆和等截面杆,若两 杆的最大横截面面积相同，问哪一根杆件承受冲击的能 力强？设变截面杆直径为d的部分长为2/5l。假设H较 大，近似把动载系数取为 2H 2H 解：
Kd = 1+ 1+ ∆ st ≈ ∆ st
3 2 lW lW Nl 4Wl ∆st = ∑ = 5 + 5 = π π EA 5Eπ E D2 E d 2 4 4
湖北汽车工业学院
材料力学
主讲教师：马迅
第9+10章习题
教材：9.13、9.16、10.14 附加习题： 9-1、9-2、9-3、9-4、10-2、10-4
附加习题9-2: 1、2杆均为圆截面，直径相同，d=8mm， 材料的E=120GPa，适用欧拉公式的临界柔度为90，规定 稳定性安全系数nst=1.8，求结构的许可载荷P。 解： 应用平衡条件有
−P
0
P
− 2P P
0
0
2P
0
−P
P
− 2P 0
0
解： a、c 桁架 b 桁架
Pcr =
Pb ≥ Pc = Pa
π 2 EI ( 2l ) 2 π 2 EI Pcr = (l ) 2
HAII MAXUN
N ≤ Pcr = 2 P N ≤ Pcr = P
π 2 EI 2 2l 2 π 2 EI P= (l ) 2 P=
8.5 ×1.43 (14 − 8.5) × 9.63 4 4 Iy = + cm = 407cm 12 12
9.6 × 143 (9.6 − 1.4) × 8.53 4 4 Iz = + cm = 1780cm 12 12
iy =
λP =
Iy A
=
407 cm = 2.51cm iz = 64.7
湖北汽车工业学院
材料力学
主讲教师：马迅
10.14 材料相同、长度相等的变截面杆和等截面杆,若两 杆的最大横截面面积相同，问哪一根杆件承受冲击的能 力强？设变截面杆直径为d的部分长为2/5l。假设H较 大，近似把动载系数取为 2H 2H 解：
Kd = 1+ 1+ ∆ st ≈ ∆ st
3 2 lW lW Nl 4Wl ∆st = ∑ = 5 + 5 = π π EA 5Eπ E D2 E d 2 4 4
湖北汽车工业学院
材料力学
主讲教师：马迅
第9+10章习题
教材：9.13、9.16、10.14 附加习题： 9-1、9-2、9-3、9-4、10-2、10-4
附加习题9-2: 1、2杆均为圆截面，直径相同，d=8mm， 材料的E=120GPa，适用欧拉公式的临界柔度为90，规定 稳定性安全系数nst=1.8，求结构的许可载荷P。 解： 应用平衡条件有