化学计算方法与技巧----差值法
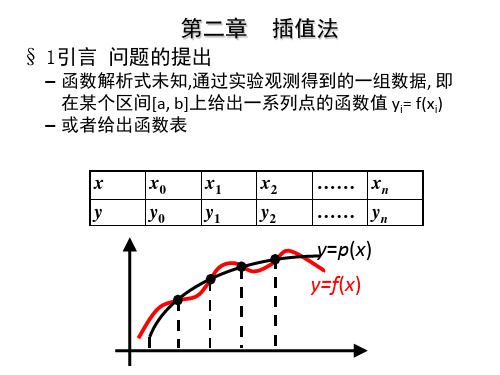
计算方法插值法.ppt

拉格朗日插值余项
设节点a x0 x1 xn b ,且 f 满足条件 f C n[a,b] , f (n1)在[a , b]内存在, 考察截断误差
Rn( x) f ( x) - Ln( x)
n
Rn(x) 至少有 n+1 个根
Rn( x) K(x) ( x - xi )
Pn ( xi ) yi , i 0, ... , n
条件:无重合节点,即 i j xi x j
n=1
已知 x0 , x1 ; y0 , y1 ,求 P1( x) a0 a1 x 使得
P1( x0 ) y0 , P1( x1 ) y1
可见 P1(x) 是过 ( x0 , y0 ) 和 ( x1, y1 ) 两点的直线。
li ( x )
i0
y i
,则显然有Pn(xi) = yi 。
每个 li 有 n 个根 x0 … xi-1, xi+1 … xn
li (x) Ci
(x-
ji
xj )
li (xi ) 1
Ci
ji
( xi
1 - xj)
li ( x)
n ji
(x- xj) (xi - x j )
3!
(x
-
6
)(
x
-
4
)(
x
-
3
)
;
1 2
cos x
3 2
0.00044
R2
5
18
0.00077
sin 50 = 0.7660444…
2次插值的实际误差 0.00061
第六章 插值计算与插值多项式模型

ω 3 ( x) =
( x − x1 )( x − x 2 ) 1 = ( x − 1)( x − 3) ( x3 − x1 )( x3 − x 2 ) 8
Ln-1(x)模型为 当X=4℃时
拉格朗日多项式形式简单、对称,便于计算机编程计算;但计算工作量较大,而且 当全部点作插值时,舍人误差也大,多项式次数较高,曲线的波动较大,一般计算时,取 距插值点j较近的几个点进行插值计算。
拉氏插值模型的余项估计
用拉氏插值多项式模型表示函数f(x)时,引起的误差由 Rn-1(x) = f(x) - Ln-1(x)给出。 或写成如下形式
线 性 插 值
线性插值是最简单的插值方法,设已知函数y=f(x),在x0、x1处的值分别 为y0,y1,则过点(x0,y0),(xl,y1)的连线方程为
y1 − y0 y = y0 + ( x1 − x0 ) x1 − x0
[x。,x1]内任一点的插值为
y1 − y0 y = y0 + ( x − x0 ) x1 − x0
∆f 0 ∆2 f 0 y = y0 + ( x − x0 ) + ( x − x0 )( x − x1 ) h 2h 2
例:6.2某流体实测温度与粘度的关系如下表所示;试求出t=25℃时的粘度值。 解:用牛顿插值计算首先求一阶差分,二阶差分…并列入表中:
T℃ 20 22 24 26 28 30 μ 1.0051 0.9579 0.91442 0.8737 0.8360 0.8007 △ -0.0472 -0.0437 -0.0405 -0.0337 -0.0353 △2 0.0035 0.0032 0.0028 0.0024 △3 -0.0003 -0.0004 -0.004
化学方程式计算的技巧与方法

•. 化学方程式计算的技巧与方法:(1)差量法(差值法)化学反应都必须遵循质量守恒定律,此定律是根据化学方程式进行计算的依据。
但有的化学反应在遵循质量守恒定律的州时,会出现固体、液体、气体质量在化学反应前后有所改变的现象,根据该变化的差值与化学方程式中反应物、生成物的质量成正比,可求出化学反应中反应物或生成物的质量,这一方法叫差量法。
此法解题的关键是分析物质变化的原因及规律,建立差量与所求量之间的对应关系。
如:①2KMnO4K2MnO4+MnO2+O2反应后固体质量减小,其差值为生成氧气的质量②H2+金属氧化物金属+水,该变化中固体质量减少量为生成水中氧元素的质量(或金属氧化物中氧元素的质量)③CO+金属氧化物金属+CO2,该变化中固体质量减少量为气体质量的增加量。
④C+金属氧化物金属+CO2,反应后固体质量减小,其差值为生成的二氧化碳的质量。
⑤2H2+O22H2O,反应后气体质量减小,其减小值为生成水的质量。
⑥金属+酸→盐+H2,该变化中金属质量减小,溶液质量增加,其增加值等于参加反应的金属质量与生成氢气质量的差值。
⑦金属+盐→盐+金属,该变化中金属质量若增加,溶液的质量则减小,否则相反。
其差值等于参加反应的金属质量与生成的金属质量的差值。
⑧难溶性碱金属氧化物+水,该变化中固体质量减小,其差值为生成的水的质量例:为了测定某些磁铁矿中四氧化三铁的质量,甲、乙两组同学根据磁铁矿与一氧化碳反应的原理,分别利用两种方法测定了磁铁矿中四氧化三铁的质量分数,已知磁铁矿与一氧化碳反应的化学方程式如下:Fe3O4+4CO3Fe+4CO2(1)甲组同学取该磁铁矿10g与足量的一氧化碳充分反应,并将产生的气体通入足量的氢氧化钠溶液中,溶液的质量增加了5.5g,请你根据甲组同学的实验数据,计算出磁铁矿样品中四氧化三铁的质量分数。
(2)乙组同学取该磁铁矿样品10g与足量的一氧化碳充分反应,测得反应后固体物质的质量为8g,请你根据乙组同学的实验数据,计算出磁铁矿样品中四氧化三铁的质量分数。
插值法技巧

插值法技巧《巧用插值法技巧,做个数学小机灵鬼》嘿,朋友们!今天咱就来聊聊这个插值法技巧,这可真是个神奇的玩意儿啊!说到插值法,可能有些朋友会觉得这是啥高深莫测的东西,一听就头大。
但其实啊,它就像是生活中的小窍门,一旦你掌握了,那可就好玩啦!咱就拿平时买东西讲吧。
比如说你去买水果,知道了苹果一斤5 块钱,香蕉一斤3 块钱,那要是有人问你4 块钱一斤能买个啥,这时候插值法就派上用场啦!你可以像个小机灵鬼一样,根据价格的比例,大概估摸出4 块钱能买到的水果种类和数量。
这是不是有点像在数学的世界里玩“猜猜猜”的游戏呀?插值法还特别像一个贴心的小伙伴,能在关键时刻帮你一把呢!比如你在做一道数学题,给了你几个数据点,但是就缺中间那个,这时候插值法闪亮登场,一下子就帮你把那个缺失的数据给找出来了。
就好像是拼图里的那块关键拼图,一旦放上,整个画面就完整啦!我记得有一次,老师在课堂上出了一道题,看着挺难的。
大家都抓耳挠腮,不知道该咋办。
我就试着用了下插值法,嘿,还真就把那答案给算出来了。
当时我那个得意呀,感觉自己就像是个数学小天才!而且我发现,用了插值法之后,那些看起来很复杂的问题瞬间就变得简单多啦,就像是给大象穿上了轮滑鞋,一下子就轻松跑起来了呢!其实啊,插值法技巧不仅仅在数学上有用,在生活的其他方面也能派上用场哦!比如说你想估计一下自己做一件事需要多长时间,你可以根据以前类似事情的经验,用插值法来大概估摸一下,这样就能更好地安排自己的时间啦。
总之呢,插值法技巧就像是一把神奇的钥匙,能打开很多难题的大门。
我们要做的就是好好掌握它,把它变成我们的秘密武器,在数学的世界里尽情地玩耍,做个快乐的数学小机灵鬼!所以呀,朋友们,别再害怕插值法啦,大胆地去尝试,去发现它的乐趣吧!说不定你会爱上这个有趣又实用的小技巧哦!。
数值计算方法-插值法
定理2 设f(x)在a, b有n+1阶导数, x0, x1,…, xn 为 a, b上n+1个互异的节点, p(x)为满足 p(xi) = f(xi) (i=1,2, …, n) 的n 次插值多项式,那么对于任何x a, b有
插值余项
f ( n 1) ( ) R( x) f ( x) p ( x) ( x) (n 1)!
P( x) l0 ( x) y0 l1 ( x) y1 l n ( x) y n
l k ( x)( k 0,1,, n)
P( x)
l
k 0
n
k
( x) y k
(2.8)
是次数不超过n次的多项式 , 称形如(2.8)式的插 值多项式为n次拉格朗日插值多项式。并记为
Ln (x)
li (x)
xi
l k ( x0 ) 0,, l k ( xk 1 ) 0, l k ( xk ) 1, l k ( xk 1 ) 0,, l k ( xn ) 0
即
1 (i k ) l k ( xi ) ki 0 (i k )
由条件
l k ( xi )( 0 )知,i k
在插值区间a, b上用插值多项式p(x)近似代替f(x), 除了在插值节点xi上没有误差外, 在其它点上一般是存在误差的。
y=f(x)
y=p(x)
a x0 x1
b xixi+1 xn-1 xn
若记 R (x) = f(x) - p(x) 则 R(x) 就是用 p(x) 近似代替 f(x) 时的截断误差, 或称 插值余项我们可根据后面的定理来估计它的大小。
f[x1,x2]- f[x0,x1]
高中化学题型之溶解度曲线的计算

高中化学题型之溶解度曲线的计算溶解度曲线是化学中常见的一种重要图像,它描述了在一定温度下溶质在溶剂中的溶解度随溶质的浓度变化的关系。
在化学学习中,我们经常需要计算溶解度曲线上的各个点的数值,以便更好地理解和应用溶解度曲线。
本文将以具体题目为例,说明溶解度曲线的计算方法和相关考点。
首先,让我们来看一个典型的题目:题目:某溶质在水中的溶解度随温度的变化如下表所示:温度(℃)溶解度(g/100 mL)20 1030 2040 3050 4060 50请根据上述数据绘制溶解度曲线,并回答以下问题:1. 温度为35℃时,溶解度为多少?2. 溶解度为25g/100 mL时,温度为多少?解析:首先,我们需要将给定的数据绘制成溶解度曲线图。
横轴表示温度(℃),纵轴表示溶解度(g/100 mL)。
根据表中的数据,我们可以得到以下溶解度曲线图:(插入溶解度曲线图)接下来,我们来解答第一个问题:温度为35℃时,溶解度为多少?根据溶解度曲线图,我们可以看到35℃对应的溶解度应该在20和30之间。
为了更精确地计算出溶解度,我们可以使用线性插值法。
线性插值法的基本原理是根据已知数据点的坐标,通过直线的斜率来估算未知点的坐标。
首先,我们找到温度为30℃和40℃时的溶解度,分别为20g/100 mL和30g/100 mL。
然后,我们可以根据这两个点的坐标计算出直线的斜率:斜率 = (30 - 20) / (40 - 30) = 1接下来,我们计算35℃对应的溶解度。
根据线性插值法的公式:溶解度 = 20 + (35 - 30) * 1 = 25g/100 mL因此,温度为35℃时,溶解度为25g/100 mL。
接下来,我们来解答第二个问题:溶解度为25g/100 mL时,温度为多少?根据溶解度曲线图,我们可以看到溶解度为25g/100 mL对应的温度应该在30℃和40℃之间。
同样地,我们可以使用线性插值法来计算温度。
首先,我们找到溶解度为20g/100 mL和30g/100 mL时的温度,分别为30℃和40℃。
插值的概念和各种基本方法
k o o b n c . w ww( xi ) = yi ( i = 0, 1, 2, L , n ) 。 证明:
要证明 P( x) 存在惟一,就是要证明存在惟一的一个 P( x) = a0 + a1 x + L an x n 满足:
n ⎧a0 + a1 x0 + L an x0 = y0 ⎪ n ⎪a0 + a1 x1 + L an x1 = y1 ⎨ ⎪L ⎪a + a x + L a x n = y n n n ⎩ 0 1 n
点
函
l0 ( x) l1 ( x)
k o o b n c . w ww
x0 x1
1 0 0 0 0 1
t e .n
x2
0 1
t e n . k o o b n c .
l2 ( x )
由上表知 l0 ( x) 有 x1 和 x2 两个零点,故 l0 ( x) 有因子 ( x − x1 ) ⋅ ( x − x2 ) ,又因为它的次数不超过 3 ,故
t e n . t k e o n o . b k n o c o . b w n w c w . w ww t k e o n o . b k n o c o . b w n w c w . w ww t e n . k o c o . b w n w c w . w w w t e n . k o o
函 数 值
k o o b n c . w ww
x0 x1
0 1
l0 ( x)
1
l1 ( x)
0
由表 2 和图 3 可以看出两个基函数的性质。插值函数 P 1 ( x ) 实质上是插值基函数 l0 ( x ) 和 l1 ( x ) 的线
插值法 PPT课件
y1 y0 P1(x)=y0+ ( x- x0 ) x1 x0
第6章 插值法
整理得
x x1 x x0 P1(x)= y0 y1 l0 ( x) y0 l1 ( x) y1 x0 x1 x1 x0 x x0 x x1 式中l0(x)= ,l1(x)= 。 显然l0(x),l1(x)具 x x x0 x1 1 0 有以下性质。
定理的存在性说明插值问题总是有解的,唯一性说明插 值多项式的构造与所用的方法无关。
第6章 插值法
6.2 拉格朗日插值
根据插值条件(6.1)通过求解线性方程组(6.3)来确定插值 多项式的系数,其计算量较大,因此常用其它方法来构造插
值多项式,而插值多项式的唯一性保证了用这些方法构造的
函数P(x)与解方程组(6.3)得到的函数是一致的。
第6章 插值法
图 6.1
第6章 插值法
插值方法源于科学研究的实践。17世纪的西欧科学家探
索活动空前活跃,出现了诸如哥伦布发现“新大陆”、麦哲 伦环球航行等一系列重大事件,科学活动的客观需要强烈地 刺激了插值方法的深入研究。其实,插值方法是一类古老的 数学方法,早在一千多年前的隋唐时期,中华先贤在制定历
法的过程中就已经广泛地应用了插值技术。公元6世纪,隋
唐时期的刘焯已将等距节点的二次插值应用于天文计算,而 直到17世纪Newton才建立起等距节点上一般的插值公式,插 值的基本理论和结果也随之得以逐步完善,其应用日益增多。
第6章 插值法
电子计算机广泛使用以后,由于航空、造船、精密机械
加工等实际问题的需要,使插值法在实践或理论上显得更为 重要,并得到进一步发展,尤其是近几十年发展起来的样条 (Spline)插值更获得了广泛的应用。 函数插值的基本问题有: 存在唯一性, 构造方法, 截断误 差和收敛性,以及数值计算的稳定性等。 定理6.1(插值多项式的存在唯一性) 在n+1个互异节点
插值计算公式
题目:对n+1个节点xi及yi=f(xi)(i=0,…,n)编制通用程序(1)n次lagrange插值计算公式Ln(x)(2)n次Newton插值计算公式并利用上述两种方法对f(x)=ln(x),[a,b]=[1,2],取h=0.1,xi=1+ih,i=0,1,…,10.计算ln(1.54)及ln(1.98)的近似值。
grange 插值法的function文件function yy=lagrange(x,y,xx)n=length(y);m=length(x);if m~=nerror('向量长度不一致');ends=0;for i=1:1:nt=ones(1,length(xx));for j=1:nif j~=it=t.*(xx-x(j))/(x(i)-x(j));endends=s+t*y(i);endyy=s;end2 Netwon 插值法的function文件function yi=cnewton(x,y,xi)n=length(x);m=length(y);if m~=nerror('向量长度不一致');endY=zeros(n);Y(:,1)=y';for k=1:n-1for i=1:n-kif abs(x(i+k)-x(i))<1e-10error(‘数据错误’);endY(i,k+1)=(Y(i+1,k)-Y(i,k))/(x(i+k)-x(i));endendyi=0;for i=i:nz=1;for k=1:i-1z=z*(xi-x(k));endyi=yi+Y(1,i)*z;endend对题目进行输入,结果运行如下:format long;>> x=[1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2]';y=log(x)y =0.0953101798043250.1823215567939550.2623642644674910.3364722366212130.4054651081081640.4700036292457360.5306282510621700.5877866649021190.6418538861723950.693147180559945Lagrange插值结果>> yy=lagrange(x,y,1.54)yy =0.431782416482614>> yy=lagrange(x,y,1.98)yy =0.683096848636761Newton 插值结果yi=cnewton(x,y,1.54)yi =0.431782416482615>> yi=cnewton(x,y,1.98)yi =0.683096848636760通过结果显示,两种方法对不同的插值点进行近似计算,差别只在显示数值结果的最后一位上,表明结果已经非常接近精确解。
插值计算的原理及应用方法
插值计算的原理及应用方法概述插值计算是基于已知一些数据点,通过建立一个合理的数学函数来估计未知位置的值的一种方法。
它广泛应用于数据分析、数值计算、图像处理等领域。
本文将介绍插值计算的原理以及常见的应用方法。
原理插值计算的原理是基于一个假设:在已知的数据点之间的未知位置上的值可以由数据点之间的函数关系来表示。
通过建立一个合适的插值函数,我们可以预测未知位置上的值。
插值方法可以分为两种类型:多项式插值和非多项式插值。
多项式插值使用多项式函数来逼近数据点之间的关系;非多项式插值使用其他函数形式,如三角函数、指数函数等。
以下是常见的插值方法:1.线性插值–原理:通过连接两个相邻数据点之间的直线来估计未知点的值。
–公式:假设已知数据点为(x0,y0)和(x1,y1),则未知位置(x,y)的值可以通过公式$y = y_0 + \\frac{(x - x_0)(y_1 - y_0)}{(x_1 - x_0)}$来计算。
–适用场景:适用于数据点之间的变化趋势比较平滑的情况。
2.拉格朗日插值–原理:通过一个多项式函数的线性组合来逼近数据点之间的关系。
–公式:假设已知数据点为(x i,y i),则未知位置(x,y)的值可以通过公式$y = \\sum_{i=0}^n y_i \\cdot L_i(x)$来计算,其中L i(x)为拉格朗日基函数。
–适用场景:适用于不等间隔的数据点。
3.牛顿插值–原理:通过一个n次多项式来逼近数据点之间的关系。
–公式:假设已知数据点为(x i,y i),则未知位置(x,y)的值可以通过公式$y = f[x_0] + f[x_0, x_1](x-x_0) + f[x_0, x_1, x_2](x-x_0)(x-x_1) +\\ldots$来计算,其中$f[x_0], f[x_0, x_1], f[x_0, x_1, x_2], \\ldots$为差商。
–适用场景:适用于等间隔的数据点。
应用方法插值计算在许多领域中都有广泛应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题28 差值法
差值法就是根据化学方程式,利用反应物与生成物之间的质量差与反应物或生成物之间的比例关系进行计算的一
种简捷而快速的解题方法。
利用差量解题的关键在于寻求差量与某些量之间的比例关系,以差量做为解题的突破口。
如果能找出造成差量的原因,并掌握其运算范围,既使题目形式多变,也能迅速作出答案。
差量法所用的数学知识是等比定理,主要运用它的两种衍生形式。
等比定理,可表过为:a:b=c:d=(a-c):(b-d) a:b=c:d=e:f=(a+c-e):(b+d-f)……………
一、解题方法指导
例题1 取一定量的CuO粉末,与足量的稀硫酸充分反应后,再将一根50g的铁棒插入上述溶液中,至铁棒质量
不再变化时,铁棒增重0.24g,并收集到0.02g气体。
由此推算CuO粉末的质量为( )
A、 1.92g
B、 2.4g
C、 6.4g
D、 0.8g
思考:此题若将0.24g的增量认为是Fe和CuSO4反应产生的差量,折算成CuO的质量为2.4g,故选出发答案B,
你认为正确否?若不正确,0.24g与哪两个量有关?如何找到关系?本题的正确答案是什么?还有其它解法吗?
例题2 在94.6g稀硫酸中放入一小块铁块,待铁块完全反应后,称得溶液的质量为100g,问反应前放入的铁块
质量为多少克?产生氢气多少克?
思考:稀硫酸和铁块发生化学反应吗?方程式如何写?怎样理解题目中的“完全反应”?溶液增加质量:100g-94.6
g=5.4g是否就是放入的铁块的质量?若不是,哪么5.4g质量差是怎么产生的?又怎么求放入的铁块的质量?
例题3 已知NaHCO3煅烧按下式分解:2NaHCO3 = Na2CO3+H2O↑+CO2↑,Na2CO3煅烧不分解。
现有Na2CO3和NaHCO3的
混合物95g,经充分煅烧后质量减少了31g,求原混合物中Na2CO3的质量。
思考:减少的31g不单纯是CO2的质量,还有水蒸气的质量。
此题用“和量”法较为简单,原理同“差量”法。
解:设原混合物中Na2CO3的质量为x。
2NaHCO3 == Na2CO3 + H2O↑ + CO2↑
2×84 18 44
95g-x 31g
2×84 : 62 = (95g-x) : 31g 解得:x=11g
答:原混合物中有碳酸钠11g。
二、知识能力训练
1、实验室用8gKMnO4分解制氧气,反应后称得固体物质的质量为7.2g,则剩余固体物质的成分是( )
A、K2MnO4和MnO2
B、KMnO4和K2MnO4
C、KMnO4
D、KMnO4、K2MnO4和MnO2
2、将一定量的CaCO3和Cu粉置于一敞口容器中,加热煅烧,使其充分反应,反应前后容器内固体质量未变,则容
器中Cu和CaCO3的质量比是( )
A、11 : 4
B、20 : 4
C、44 : 25
D、16 : 25
3、在试管中有ag氧化铜,通入氢气并加热,反应一段时间停止加热,冷却后,停止通氢气,并称量试管中的固
体物质为bg,则参加反应的氢气质量为( )
A、a-bg
B、b-ag
C、(a-b)/8g
D、(b-a)/8g
4、现有干燥的氯酸钾与二氧化锰的混合物30g,加热充分反应后,得到固体物质20.4g,求原混合物中含氯酸钾
多少克?(24.5g)
5、现有干燥的氯酸钾与二氧化锰的混合物30g,加热反应一段时间后,得到固体物质26g,若求氯酸钾的分解
率还需要知道什么条件?请补充条件后,再计算氯酸钾的分解率。
6、某氯酸钾与二氧化锰的混合物中,二氧化锰的质量分数为20%,取一定量的此混合物加热制取氧气,反应一段
时间后停止加热,测得反应后混合物中,二氧化锰的质量分数为25%,计算氯酸钾的分解率。
(63.8%)
7、由CuO和木炭混合而成的黑色粉末100g,将其放入试管内加热一段时间,停止加热并冷却,称得剩余固体混合物的质量为78g,求:(1)生成铜多少克? (2)参加反应的CuO的质量是多少? (3)据此你能否计算出原混合物中CuO 的质量分数?请说明理由。
(碳与试管中少量氧气的反应忽略不计)
8、12.4gFe2O3和CuO的混合物与CO充分反应后,固体减少3.1g,则原混合物中的Fe2O3和CuO的质量比是多少?(1 : 1)
9、用足量CO充分还原氧化铁和铁的混合物26g,得到铁21.2g,求原混合物中氧化铁的质量。
(16g)
10、将16gCuO加强热,部分分解成Cu2O,称得所得固体为15.2g,则剩余固体中,CuO和Cu2O的质量之比为多少? 提示:4CuO == 2Cu2O + O2↑ (10:9)
△
11、取含有少量杂质(杂质不与氢气反应)的氧化铜样品12.5g,在加热的条件下通入足量的氢气,充分反应后,冷却,称得剩余固体物质的质量为10.1g。
求(1)样品中的CuO的质量分数。
(2)参加反应的氢气的质量。
附:天平平衡问题
例题: 在托盘天平两盘的烧杯中分别盛有足量的稀硫酸,此时天平平衡。
若向左盘烧杯中加入11.2g铁粉,若要使天平最终仍保持平衡,应向右盘的烧杯中加入多少克锌粉?
思考:(1) 若向右盘的烧杯中加入11.2g锌粉,天平能否平衡? 与产生氢气的量是否有关? (2)若要使产生的氢气质量相同,天平能平衡吗? 与加入铁粉和锌粉的质量是否有关?满足天平平衡的条件是什么 ?
练习:
1、在两个质量相同的烧杯中分别加入100g质量分数为3.65%的稀盐酸,然后分别加入mg石灰及ngNa2CO3,欲使反应后两烧杯质量仍相等,则m与n的关系为( )
A、m = n>5g
B、m = n≥10g
C、m = n≥10.6g
D、m : n = 775 : 742且n≤9.57g
2、天平两盘分别放一只质量相等的烧杯,内盛同质量、同溶质质量分数的盐酸,在左盘的烧杯中放入36gMg粉,在右盘的烧杯中放入36gAl粉,等反应完合后,怎样才能使天平重新平衡。
( )
A、右边再加1gAl粉
B、左边再加1gMg粉
C、右边再加1.125gAl粉
D、右边再加1gCu粉
3、在托盘天平的左右两盘上分别放两只烧杯,调至平衡,再向两烧杯中加入同质量、同溶质质量分数的硫酸,再向左烧杯中加入2g锌,右两烧杯中加入2g镁,待锌镁全部溶解后,天平指针()
A、偏右
B、偏左
C、在分度盘中间
D、左右摇摆不定
4、在托盘天平的左右两盘上的两只烧杯中,分别盛有足量的稀硫酸,调平后,若向两烧杯中加入等质量的镁和铜铝合金,完全反应后,天平仍平衡,则合金中铜和铝的质量比是()
A、1 : 1
B、1 : 2
C、1 : 3
D、3 : 1
5、在天平两边分别放有盛足量稀硫酸的烧杯,天平平衡,当向两烧杯中分别加入下列各组物质后,天平仍平衡的是()
A、5.0gMgO和5.0gMgCO3
B、6.3gCu和6.5gZn
C、1.0gAgNO3和1.0gNaOH
D、2.4gFe和2.4gAl
6、在天平两边分别放有盛足量稀硫酸的烧杯,天平平衡,若左烧杯中放入0.22gCaO,要使天平平衡,应向右烧杯中加入( )
A、0.36gAl
B、0.462gMgCO3
C、5.6gNa2CO3
D、0.44g铜锌合金
7、将质量为wg的稀硫酸分成二等份,分别放入两小烧杯中,放在托盘上,调节平衡。
然后向左烧杯中加入ngZn,向右烧杯中加入ngFe。
(1)若天平仍平衡,则反应物中一定无剩余的物质是,一定有剩余的是,可能有剩余的是。
(2)若天平失去平衡,则指针向偏转。
