2018年八年级数学下册 小专题(八)一次函数与方程、不等式的综合应用练习 (新版)新人教版
人教版-数学-八年级下册《一次函数与方程、不等式》习题

人教版数学八年级下册- 打印版
一次函数与方程、不等式
1.根据下列条件写出相应的函数关系式.
(1)直线y=kx+5经过点(-2,-1);
(2)一次函数中,当x=1时,y=3;当x=-1时,y=7.
2.写出两个一次函数,使它们的图象都经过点(-2,3).
3.如图是某长途汽车站旅客携带行李费用示意图.试说明收费方法,并写出行李费y(元)与行李重量x(千克)之间的函数关系.
4.一次函数y=kx+b(k≠0)的图象经过点(3,3)和(1,-1).求它的函数关系式,并画出图象.
5.陈华暑假去某地旅游,导游要大家上山时多带一件衣服,并介绍当地山区海拔每增加100米,气温下降0.6℃.陈华在山脚下看了一下随带的温度计,气温为34℃,乘缆车到山顶发现温度为32.2℃.求山高.。
人教版八年级数学下册同步练习题一次函数与方程、不等式

k 1 k 2 x m n 的解是()《一次函数与方程不等式》同步练习◆ ◆ 基础题一、单选题1. 如图所示,已知此一次函数 y =kx +b (k ,b 是常数, k ≠0)的图象,求不等式 kx +b >0 的解集是( )集应为(A .x >-2.x <02. 如图,直线 y =kx +b 经过点 A ( -1 , -2 )和点 B ( -2 , 0),直线 y =2x 过点 A ,则不等式2x < kx +b <0 的解集为( A .x <-2.-2 <x <-1 .-2 <x <0 D . -1<x < 03. 一次函数 y =ax + b A .x ≤m.x ≤-m .x ≥mD.x ≥-m4.如图,已知直线 y 1 k 1x m 和直线 y 2 k 2x n 交于点 P 1, 2 ,则关于 x 的不等式a >0)元一次不等式 ax +b ≤0的解解为 ( )是(二、填空题7. 一次函数 y =-2 x +4,当函数值为正时, x 的取值范围是 =8. 已知一次函数 y =ax +b ( a 、b 为常数), x 与 y 的部分对应值如右表:A. x 2B. x 1C. 1 x 2D. x 15.如图,两个一次函数图象的交点坐标为( y k 1x b 12,4),则关于 x ,y 的方程组 { 1 1 的 y k 2x b 2x2 A. {x y 24D.x3{x y 306. 如图,直线 y=kx+b 经过 A ( 2, 1),B ( -1 , -2)两点,则不等式 kx b 2 的解集A. x < 2B. x > - 1C. x< 1 或 x > 2 D. -1 < x <2C.B.{y 2{y 0那么方程ax+b=0 的解是,不等式ax+b> 0 的解是9. 已知一次函数的图象过点3,5 与4,9 ,那么这个函数的解析式是____________ ,则该函数的图象与y 轴交点的坐标为_____________ .10. 一次函数y1=kx+b 与y 2=x+a 的图象如图,则下列结论:① k< 0;②a>0;③当x<3 时,y1<y2;④方程kx+b=x+a 的解是x-3 ,其中正确的是__________ . (填写序号)◆ 能力题11. 在平面直角坐标系中有两条直线l1:y3x9和l2: y3x 6,它们的交点为P,直1 5 5 22线l1与x 轴交于点A,直线l2与x轴交于B点.(1) 求A、 B 两点的坐标;(2) 用图象法解方程组:3x 5y 9, 3x 2y 12;(3) 求△ PAB的面积.12.画出函数y=2x- 4 的图象,并回答下列问题:(1) 当x 取何值时,y> 0?(2) 若函数值满足-6≤y≤6,求相应的x 的取值范围.13.在平面直角坐标系xoy 中,已知一次函数y1 mx m 0 与y2 kx b k 0 相交于点A 1,2 ,且y2 kx b k 0 与y 轴交于点B 0,3 .(1)求一次函数y1 和y2 的解析式;2)当y1 y2 0时,求出x 的取值范围.◆ 提升题14. 如图,直线l 是一次函数y=kx+b的图象,点A、B在直线l 上.根据图象回答下列问题:(1)写出方程kx+b=0 的解;(2)写出不等式kx+b> 1 的解集;(3)若直线l 上的点P(m,n)在线段AB上移动,则m、n 应如何取值.15. 已知:如图,已知直线AB的函数解析式为y=-2 x+8,与x 轴交于点A,与y 轴交于点B.(1)求A、B 两点的坐标;(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥ x轴于点E,PF⊥y 轴于点F,连接EF,问:①若△ PAO的面积为S,求S 关于m的函数关系式,并写出m的取值范围;②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.答案与解析◆ 基础题1.A【解析】从图象得知一次函数y=kx+b(k,b 是常数,k≠0)的图象经过点(-2,0),并且函数值y 随x 的增大而增大,因而则不等式kx+b>0的解集是x>-2 .2.B【解析】不等式2x< kx +b< 0 体现的几何意义就是直线y=kx+b 上,位于直线y=2x 上方,x 轴下方的那部分点,显然,这些点在点 A 与点 B 的横坐标之间.3.A【解析】∵一次函数y=ax+b(a>0)与x 轴的交点坐标为(m,0),∴一元一次不等式ax+b≤0的解集是x≤m.4.B【解析】根据图形,找出直线y1在直线y2上方部分的x 的取值范围即可.解:由图形可,当x>-1 时,k1x+m>k2x+n,即(k1-k2)x>- m+n,所以,关于x 的不等式(k1- k2)x>- m+n的解集是x>- 1.y k 1x b 1x 2 5.A 【解析】因为两函数的图象的交点坐标是 ( 2,4),所以方程组 { 1 1 的解为 { .y k 2x b 2y 4本题考查了一次函数与二元一次方程组: 满足函数解析式的点就在函数的图象上, 在函数的 图象上的点, 就一定满足函数解析式 .函数图象交点坐标为两函数解析式组成的方程组的解 .116.D 【解析】画出函数 y=kx+b 及 y x 的图象如图,根据题意可知,函数 y x 过点 A221 (2,1).结合函数的图象可知,x kx b 2 所对应的自变量的取值范围是 -1<x<2.27.x <28.x =1, x < 1. 【解析】方程 ax +b =0的解为 y =0时函数 y =ax +b 的 x 的值,根据图表即可得出此方程的解. 不等式 ax +b >0的解集为函数 y =ax +b 中y >0时自变量 x 的取值范围, 由图 表可知, y 随 x 的增大而减小, 因此 x <1 时,函数值 y >0;即不等式 ax +b >0 的解为 x < 1. 9.y=2x-1 (0,-1)10. ①④ 【解析】 根据图象及数据可知: ①k<0 ,②a<0;③当 x<3 时,y 1>y 2;④方程 kx+b=x+a 的解是 x-3. 故说法正确的是①④ .◆ 能力题3911. 【解析】 (1) 由 y x知,当 y=0 时, x=-3 ,55当 y=0 时, x=4,∴ B(4 , 0) .∴A (-3,0 ).由 y3x 6知,239 (2) 由 3x-5y= -9 可得 y x , 55由 3x+2y=12 可得 y3x 6 .在同一直角坐标系 2中作出一次函数 y 3x 9和 y553x 6的图象 2图略) ,观察图象可得 l 1、 l 2的交点为 P (2 ,3) ,∴方程组3x 5y 9,的解是3x 2y 12x 2, y 3.(3)S△PAB = OA OB 3 10.5 .12.(1) x >2 (2) -1≤ x ≤5 【解析】 试题分析求出函数图象与两坐标轴的交点,利用两 点法作出图象即可; ( 1)求出直线与 x 轴的交点,再根据 y >0 确定 x 的取值范围; (2)分别求出 y=6 和 y=-6 时 x 的值,根据- 6≤ y ≤6,求相应的 x 的取值范围.13. (1) y 2 x 3 (2) 1<x<3 【解析】 (1) ∵一次函数 y 1 mx m 0 过点 A 1,2 ∴2 m∴y 1 2x ;又∵一次函数 y 2 kx b k 0 经过点A 1,2 , B 0,3(2) 1<x<3 . ◆ 提升题14. x =-2 ;x > 0; - 2≤ m ≤2时, 0≤ n ≤2. 【解析】 函数与 x 轴的交点 A 坐标为( -2, 0),与 y 轴的交点的坐标为( 0, 1),且 y 随 x 的增大而增大.(1)函数经过点( -2 , 0),则方程 kx +b =0 的根是 x =-2; (2)函数经过点( 0, 1),则当 x > 0 时,有 kx +b > 1, 即不等式 kx +b > 1 的解集是 x > 0;(3)线段 AB 的自变量的取值范围是: -2≤x ≤2,当- 2≤ m ≤2时,函数值 y 的范围是 0≤y ≤2, 则 0≤ n ≤2.15. 【解析】( 1)令 x =0,则 y =8, ∴ B ( 0,8),令 y =0,则 -2 x +8=0, ∴x =4, ∴A ( 4,0),(2)∵点 P (m ,n )为线段 AB 上的一个动点, ∴-2 m +8=n ,∵ A (4,0), ∴OA =4, ∴0<m <4 ∴ S △PAO = OA × PE = ×4× n =2( -2 m +8) =-4 m +16,( 0< m <4); (3)存在,理由如下:∵ PE ⊥x 轴于点 E , PF ⊥y 轴于点 F , OA ⊥OB , ∴四边形 OEPF 是矩形, ∴EF =OP ,当 OP ⊥AB 时,此时 EF 最小, ∵ A ( 4, 0), B (0,8), ∴AB =4∴EF 最小 =OP = .k1解得:{∴y 2x 3 ;b3∵S △ AOB = OA × OB = AB ×OP ,。
人教版数学八年级下册19.2《一次函数与方程、不等式》综合测试题

?一次函数与方程、不等式?测试题一、 填空题〔每题3分,共24分〕1、假设32k -有意义,那么函数1y kx =-的图象不经过第 象限。
2、一次函数22+=x y 的图象如下图,那么由图象可知,方程022=+x 的解为 。
3、一次函数b kx y +=的图象如下图,由图象可知,当x 时,y 值为正数,当x 时,y 为负数。
4、方程组⎩⎨⎧=+=-82237y x y x 的解为⎩⎨⎧==42y x ,那么一次函数____=y 与一次函数____=y 的交点为〔2,4〕。
5、一次函数12+-=x y 与一次函数93--=x y 两图象有一个公共点,那么这个公共点的坐标为 。
6、一次函数b ax y +=的图象过点〔0,-2〕和〔3,0〕两点,那么方程0=+b ax 的解为 。
7、直线a x y +=21与直线1-=bx y 相交于点〔1,-2〕,那么a = ,b= 。
二、选择题〔每题3分,共24分〕1、如图,一次函数b kx y +=与x 轴的交点为〔-4,0〕,当y >0时,x 的取值范围是〔 〕A 、4->xB 、0>xC 、4-<xD 、0<x2、一次函数1y kx b =+与2y x a =+的图象如图,那么以下结论①0k <;②0a >;③当3x <时,12y y <中,正确的个数是〔 〕A 、0B 、1C 、2D 、33、根据函数1036521+=+=x y x y 和的图象,当2>x 时,1y 与2y 的大小关系是〔 〕A 、21y y <B 、21y y >C 、21y y =D 、不能确定 4、一次函数b ax y +=,当32>x 时,0>y ,那么不等式0≥+b ax 的解集为〔 〕 A 、32>x B 、32<x C 、32≥x D 、32≤x 5、假设直线3+=kx y 与b x y 23-=的交点在x 轴上,当k =2时,b 等于〔 〕A 、9B 、-3C 、23-D 、49- 6、假设直线221-=x y 与直线a x y +-=41相交于x 轴上,那么直线ax y +-=41不经过〔 〕A 、第一象限B 、第二象限C 、第三象限D 、第四象限 7、一次函数b kx y +=的图象经过点〔0,2〕和〔-3,0〕,那么0<+b kx 的解集为〔 〕A 、3->xB 、3-<xC 、2>xD 、23<<-x8、两个一次函数212-=x y 与32+-=x y 的图象交点坐标为〔 〕 A 、)185,187( B 、)32,21( C 、)21,32(- D 、)65,67(三、解答题〔9+9+12+12=42分〕1、函数12,5421+=-=x y x y ,请答复以下问题: 〔1〕求当x 取什么值时,函数1y 的值等于0? 〔2〕当x 取什么值时,函数2y 的值恒小于0? 〔3〕当x 取何值时函数2y 的值不小于1y 的值。
八年级数学下册 小专题(八)一次函数与方程、不等式的综合应用练习 (新版)新人教版

小专题(八) 一次函数与方程、不等式的综合应用1.(2017·绍兴)某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.(1)若每月用水量为18立方米,则应交水费多少元?(2)求当x>18时,y 关于x 的函数解析式.若小敏家某月交水费81元,则这个月用水量为多少立方米?解:(1)45元.(2)当x >18时,设直线函数解析式为y =kx +b ,将(18,45),(28,75)代入y =kx +b ,得⎩⎪⎨⎪⎧18k +b =45,28k +b =75, 解得⎩⎪⎨⎪⎧k =3,b =-9.∴y =3x -9.当y =81时,3x -9=81,解得x =30. 答:这个月的用水量为30立方米.2.(2017·陕西)在精准扶贫中,某村的李师傅在县政府的扶持下,去年下半年,他对家里的3个温室大棚进行整修改造,1个大棚种植香瓜,2个大棚种植甜瓜.今年上半年喜获丰收,现在他家的甜瓜和香瓜已全部售完,他高兴地说:“我的日子终于好了”.最近,李师傅在扶贫工作者的指导下,计划在农业合作社承包5个大棚,以后就用8个大棚继续种植香瓜和甜瓜.他根据种植经验及今年上半年的市场情况,打算下半年种植时,两个品种同时种,一个大棚只种一个品种的瓜,并预测明年两种瓜的产量、销售价格及成本如下:现假设李师傅今年下半年香瓜种植的大棚数为x 个,明年上半年8个大棚中所产的瓜全售完后,获得的利润为y 元.根据以上提供的信息,请你解答下列问题: (1)求出y 与x 之间的函数关系式;(2)求出李师傅种植的8个大棚中,香瓜至少种植几个大棚?才能使获得的利润不低于10万元. 解:(1) y =(2 000×12-8 000)x +(4 500×3-5 000)(8-x)=7 500x +68 000. (2)由题意,得7 500x +68 000≥100 000. ∴x ≥4415∵x 为整数,∴x 最小为5.∴李师傅种植的8个大棚中至少有5个大棚种植香瓜.3.现正是闽北特产杨梅热销的季节,某水果零售商店分两批次从批发市场共购进杨梅40箱,已知第一、二次进货分别为每箱50元、40元,且第二次比第一次多付款700元.(1)设第一、二次购进杨梅的箱数分别为a 箱、b 箱,求a ,b 的值;(2)若商店对这40箱杨梅先按每箱60元销售了x 箱,其余的按每箱35元全部售完. ①求商店销售完全部杨梅所获利润y(元)与x(箱)之间的函数关系式; ②当x 的值至少为多少时,商店才不会亏本. (注:按整箱出售,利润=销售总收入-进货总成本)解:(1)依题意,得⎩⎪⎨⎪⎧a +b =40,40b -50a =700,解得⎩⎪⎨⎪⎧a =10,b =30.(2)①y=60x +35(40-x)-(10×50+30×40) =25x -300.②由题意,得25x -300≥0.解得x≥12. 答:当x 的值至少为12时,商店才不会亏本.4.A 城有肥料300吨,B 城有肥料200吨,现要把这些肥料全部运往C ,D 两乡,从A 城往C ,D 两乡运肥料的费用分别为每吨20元和25元;从B 城往C ,D 两乡运肥料的费用分别为每吨15元和24元,现C 乡需要肥料240吨,D 乡需要肥料260吨,怎样调运总费用最少?解:设总运费为y 元,A 城运往C 乡的肥料量为x 吨,则运往D 乡的肥料量为(300—x)吨;B 城运往C ,D 两乡的肥料量分别为(240—x)吨与(x -40)吨.由题意,得y =20x +25(300-x)+15(240-x)+24(x -40) =4x +10 140(40≤x≤240).∵k =4>0,∴当x 取最小值40时,y 有最小值10 300. ∴300-x =260,240-x =200,x -40=0.答:从A 城运往C 乡40吨,运往D 乡260吨;从B 城运往C 乡200吨,运往D 乡0吨,此时总费用最少,总运费最少为10 300元.5.(2017·连云港)某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤,设安排x 名工人采摘蓝莓,剩下的工人加工蓝莓.(1)若基地一天的总销售收入为y 元,求y 与x 的函数关系式; (2)试求如何分配工人,才能使一天的销售收入最大?并求出最大值. 解:(1)根据题意得:y =70x×40+(20-x)×35×130 =-1 750x +91 000.(2)∵70x≥35(20-x),∴x ≥203.又∵x 为正整数,且x≤20, ∴7≤x ≤20,且x 为正整数.∵-1 750<0,∴y 的值随着x 的值增大而减小,∴当x =7时,y 取最大值,最大值为-1 750×7+91 000=78 750.答:安排7名工人进行采摘,13名工人进行加工,才能使一天的收入最大,最大收入为78 750元.6.(2016·天津)公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台,租车费用为400元,每辆乙种货车一次最多运送机器30台,租车费用为280元.(1)设租用甲种货车x辆(x为非负整数),试填写表格:表一运送机器的数量50表二40租用乙种货(2)若租用甲种货车x辆时,设两种货车的总费用为y元,试确定能完成此项运送任务的最节省费用的租车方案.解:y=400x+(-280x+2 240)=120x+2 240.又∵45x+(-30x+240)≥330,解得x≥6.∵120>0,∴在函数y=120x+2 240中,y随x的增大而增大,∴当x=6时,y取得最小值,y最小=2 960.∴完成此项运送任务的最节省费用的租车方案是租用甲种货车6辆,乙种货车2辆.7.小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:服装店准备购进甲、乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.(1)若购进这100件服装的费用不得超过7 500元,则甲种服装最多购进多少件?(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行优惠促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?解:(1)设购进甲种服装x件,由题意,得80x+60(100-x)≤7 500,解得x≤75.答:甲种服装最多购进75件.(2)设总利润为W元,∵甲种服装不少于65件,∴65≤x≤75.W=(120-80-a)x+(90-60)(100-x)=(10-a)x+3 000.方案1:当0<a<10时,10-a>0,W随x的增大而增大,∴当x=75时,W有最大值,则购进甲种服装75件,乙种服装25件;方案2:当a=10时,所有方案获利相同,∴按哪种方案进货都可以;方案3:当10<a<20时,10-a<0,W随x的增大而减小,∴当x=65时,W有最大值,则购进甲种服装65件,乙种服装35件.。
专题08 一次函数与方程、不等式的综合问题-2023年初中数学8年级下册同步压轴题(学生版)

专题08 一次函数与方程、不等式的综合问题 类型一、一次函数与方程综合例.如图,一次函数y kx b =+的图像与x 轴的交点坐标为()2,0-,则下列说法正确的有( ).A .y 随x 的增大而减小B .0k >,0b <C .当2x >-时,0y <D .关于x 的方程0kx b +=的解为2x =-【变式训练1】直线y =ax +b (a ≠0)过点A (0,2),B (1,0),则关于x 的方程ax +b =0的解为( ) A .x =0B .x =2C .x =1D .x =3【变式训练2】如图,直线y =kx +b (k ≠0)与x 轴交于点(﹣5,0),下列说法正确的是( )A .k >0,b <0B .直线y =bx +k 经过第四象限C .关于x 的方程kx +b =0的解为x =﹣5D .若(x 1,y 1),(x 2,y 2)是直线y =kx +b 上的两点,若x 1<x 2,则y 1>y 2【变式训练3】如图,一次函数y kx b =+的图象经过点()0,4,则下列结论正确的是( )A .图像经过一、二、三象限B .关于x 方程0kx b +=的解是4x =C .0b <D .y 随x 的增大而减小【变式训练4】一次函数(0)y kx b k =+≠的图象如图所示,则关于x 的不等式20kx b +>的解集是( )A .2x >-B .2x <-C .2x <D .2x >类型二、一次函数与不等式综合例.如图,已知函数y =3x +b 和y =ax ﹣3的图象交于点P (﹣2,﹣5),则根据图象可得不等式3x +b >ax ﹣3的解集是( )A .x >﹣2B .x <﹣2C .﹣2<x <0D .x >0【变式训练1】如图,一次函数y =kx +b (k >0)的图像过点()1,0-,则不等式()20k x b -+>的解集是( )A .x >-3B .x >-2C .x >1D .x >2【变式训练2】如图,一次函数y =kx +b 的图象经过点(4,0),(0,4),那么关于x 的不等式0<kx +b <4的解集是______.【变式训练3】如图,一次函数y =kx +b 与y =x +2的图象交于点P (m ,5),则关于x 的不等式kx +b >x +2的解集是______.【变式训练4】如图,直线y 1=x +b 与y 2=kx ﹣1相交于点P ,点P 的横坐标为﹣1,则关于x 的不等式kx ﹣1<x +b 的解集为______.课后训练1.已知不等式0ax b +<的解是2x >-,下列有可能是函数y ax b =+的图像的是( )A .B .C .D .2.如图所示为两个一次函数的图象,则关于x ,y 的方程1122y k x b y k x b =+⎧⎨=+⎩的解为________.3.函数y ax =和y kx b =+的图象相交于点()2,1A -,则方程ax kx b =+的解为______.4.已知一次函数y kx b =-(k 、b 为常数,且0k ≠,0b ≠)与13y x =的图象相交于点1(,)2M a ,则关于x 的方程1()3k x b -=的解为x =____________. 5.如图,直线1:1l y x =+与直线2:l y mx n =+相交于点()1,2P ,则关于x 的不等式1x mx n +≥+的解集为______.6.如图,直线1y kx =+与直线2y x b =-+交于点()1,2A ,由图象可知,不等式12kx x b +≥-+的解为______.7.数形结合是解决数学问题常用的思想方法.如图,直线21y x =-与直线()0y kx b k =+≠相交于点()2,3P .根据图象可知,关于x 的不等式21x kx b ->+的解集是______8.如图,直线l 1:y 1=ax +b 经过(﹣3,0),(0,1)两点,直线l 2:y 2=kx ﹣2;①若l 1∥l 2,则k 的值为 _____;②当x <1时,总有y 1>y 2,则k 的取值范围是 ________.9.如图,一次函数y kx b =+的图象与x 轴交于点A (3,0),与y 轴交于点B (0,4),与正比例函数y ax =的图象交于点C ,且点C 的横坐标为2,则不等式ax kx b <+的解集为______.10.直线y=kx+b与直线y=5﹣4x平行,且与直线y=﹣3(x﹣6)相交,交点在y轴上,求直线y=kx+b对应的函数解析式.。
八年级数学 一次函数与方程和不等式练习题
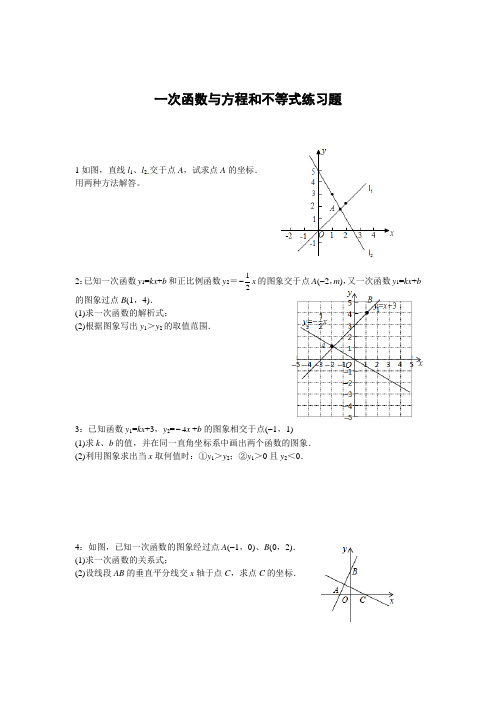
一次函数与方程和不等式练习题1如图,直线l1、l2交于点A,试求点A的坐标.用两种方法解答。
2:已知一次函数y1=kx+b和正比例函数y2=12-x的图象交于点A(-2,m),又一次函数y1=kx+b的图象过点B(1,4).(1)求一次函数的解析式;(2)根据图象写出y1>y2的取值范围.3:已知函数y1=kx+3,y2=4x-+b的图象相交于点(-1,1)(1)求k、b的值,并在同一直角坐标系中画出两个函数的图象.(2)利用图象求出当x取何值时:①y1>y2;②y1>0且y2<0.4:如图,已知一次函数的图象经过点A(-1,0)、B(0,2).(1)求一次函数的关系式;(2)设线段AB的垂直平分线交x轴于点C,求点C的坐标.5 某单位要印刷产品说明书,甲印刷厂提出:每份说明书收1元印刷费,另收1500元制版费;乙印刷厂提出:每份说明书收2.5元印刷费,不收制版费。
(1)分别写出两个印刷厂的收费y 甲、y 乙(元)与印刷数量x (份)之间的函数关系式; (2)在同一坐标系中作出它们的图像; (3)根据图像回答问题:①印刷800份说明书时,选择哪家印刷厂比较合算?②该单位准备拿出3000元用于印刷说明书,找哪家印刷厂印制的说明书多一些?6为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a 元收费,超过6立方米时,不超过的部分每立方米仍按a 元收费,超过的部分每立方米按c 元收费,该市某户今年9、10月份的用水量和所交水费如下表所示:设某户每月用水量x(立方米),应交水费y(元) (1) 求a,c 的值(2) 当x ≤6,x ≥6时,分别写出y 于x 的函数关系式(3) 若该户11月份用水量为8立方米,求该户11月份水费是多少元?月份用水量(m 3) 收费(元)9 5 7.5 10 927。
八年级数学(下)第十九章《一次函数与方程、不等式》同步练习题(含答案)

八年级数学(下)第十九章《一次函数与方程、不等式》同步练习题(含答案)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.一次函数y =ax +b (a >0)与x 轴的交点坐标为(m ,0),则一元一次不等式ax +b ≤0的解集应为 A .x ≤m B .x ≤-m C .x ≥mD .x ≥-m【答案】A【解析】∵一次函数y =ax +b (a >0)与x 轴的交点坐标为(m ,0),∴一元一次不等式ax +b ≤0的解集是x ≤m ,故选A .2.如图,直线y =kx +b 交坐标轴于A (-3,0)、B (0,5)两点,则不等式-kx -b <0的解集为A .x >-3B .x <-3C .x >3D .x <3【答案】A【解析】观察图象可知,当x >-3时,直线y =kx +b 落在x 轴的上方,即不等式kx +b >0的解集为x >-3, ∵-kx -b <0,∴kx +b >0,∴-kx -b <0解集为x >-3.故选A .3.如图,经过点(20)B -,的直线y kx b =+与直线42y x =+相交于点(12)A --,,则不等式42x +>kx b +的解集为A .2x <-B .1x >-C .1x <-D .2x >-【答案】B【解析】观察函数图象可知:已知相交于点(12)A --,,当x >-1时,直线y =4x +2在直线y =kx +b 的上方,∴不等式4x +2>kx +b 的解集为x >-1.故选B . 4.如果直线y =3x +6与y =2x -4交点坐标为(a ,b ),则x ay b =⎧⎨=⎩是方程组__________的解. A .3624x y y x -=⎧⎨+=-⎩B .3624x y y x -=⎧⎨-=⎩C .3634x y x y -=⎧⎨-=⎩D .3624x y x y -=-⎧⎨-=⎩【答案】D【解析】直线y =3x +6与y =2x -4交点坐标为(a ,b ),则x ay b=⎧⎨=⎩是方程组3624y x y x =+⎧⎨=-⎩的解,即x a y b =⎧⎨=⎩是方程组3624x y x y -=-⎧⎨-=⎩的解,故选D . 5.如图,直线y 1=k 1x +b 和直线y 2=k 2x +b 分别与x 轴交于A (-1,0)和B (3,0)两点,则不等式组1200k x b k x b +>⎧⎨+>⎩的解集为A .13x -<<B .03x <<C .10x -<<D .3x >或1x <-【答案】A 【解析】120k x b k x b +>⎧⎨+>⎩,即10y >,20y >同时大于0时,自变量x 的取值范围,通过看图可知10y >时,x >-1,20y >时,x <3,两个解联立,得到解集13x -<<,故选A . 二、填空题:请将答案填在题中横线上.6.如图,一次函数y =kx +b (k <0)的图象经过点A .当y <3时,x 的取值范围是__________.【答案】x >2【解析】由函数图象可知,此函数中的y 随x 的增大而减小,当y =3时,x =2,故当y <3时,x >2. 故答案为:x >2.7.一次函数y =kx +b (k ≠0)中,x 与y 的部分对应值如下表:那么,一元一次方程kx +b =0在这里的解为__________. 【答案】x =1【解析】根据上表中的数据值,当y =0时,x =1,即一元一次方程kx +b =0的解是x =1.故答案为:x =1. 8.如图,直线y =kx +b 经过点A (-1,-2)和点B (-2,0),直线y =2x 过点A ,则不等式2x <kx +b <0的解集为__________.【答案】-2<x <-1【解析】由题意知,当kx +b <0时,x >-2;当kx +b >2x 时,直线y =kx +b 在直线y =2x 上方,所以x <-1.所以不等式2x <kx +b <0的解集为-2<x <-1.故答案为:-2<x <-1.9.如图,一次函数y =kx +b 的图象与x 轴的交点坐标为(2,0),则下列说法: ①y 随x 的增大而减小; ②b >0;③关于x的方程kx+b=0的解为x=2;④不等式kx+b>0的解集是x>2.其中说法正确的有__________(把你认为说法正确的序号都填上).【答案】①②③【解析】①因为一次函数的图象经过二、四象限,所以y随x的增大而减小,故本项正确;②因为一次函数的图象与y轴的交点在正半轴上,所以b>0,故本项正确;③因为一次函数的图象与x轴的交点为(2,0),所以当y=0时,x=2,即关于x的方程kx+b=0的解为x=2,故本项正确;④由图象可得不等式kx+b>0的解集是x<2,故本项是错误的,故正确的有①②③,故答案为:①②③.10.已知关于x的一元一次不等式组232x bx b>+⎧⎨<-⎩有解,则直线y=-x+b不经过第__________象限.【答案】三【解析】根据题意得:b+2<3b-2,解得:b>2.当b>2时,直线经过第一、二、四象限,不过第三象限.故答案为:三.三、解答题:解答应写出文字说明、证明过程或演算步骤.11.如图,函数y=2x和y=-23x+4的图象相交于点A.(1)求点A的坐标;(2)根据图象,直接写出不等式2x≥-32x+4的解集.【解析】(1)由2243y xy x=⎧⎪⎨=-+⎪⎩,解得323xy⎧=⎪⎨⎪=⎩,∴点A的坐标为(32,3).(2)由图象,得不等式2x≥-23x+4的解集为:x≥32.12.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:(1)方程kx+b=0的解;(2)式子k+b的值;(3)方程kx+b=-3的解.【解析】(1)如图所示,当y=0时,x=2.故方程kx+b=0的解是x=2.(2)根据图示知,该直线经过点(2,0)和点(0,-2),则202k bb+=⎧⎨=-⎩,解得12 kb=⎧⎨=-⎩,故k+b=1-2=-1,即k+b=-1.(3)根据图示知,当y=-3时,x=-1.故方程kx+b=-3的解是x=-1.13.如图,根据图中信息解答下列问题:(1)关于x的不等式ax+b>0的解集是__________;(2)关于x的不等式mx+n<1的解集是__________;(3)当x为何值时,y1≤y2?(4)当x<0时,比较y2与y1的大小关系.【解析】(1)∵直线y2=ax+b与x轴的交点是(4,0),∴当x<4时,y2>0,即不等式ax+b>0的解集是x<4.故答案为:x<4.(2)∵直线y1=mx+n与y轴的交点是(0,1),∴当x<0时,y1<1,即不等式mx+n<1的解集是x<0.故答案为:x<0.(3)由一次函数的图象知,两条直线的交点坐标是(2,18),当函数y1的图象在y2的下面时,有x≤2,所以当x≤2时,y1≤y2.(4)如图所示,当x<0时,y2>y1.。
八年级下册数学 一次函数与不等式练习题

一次函数与不等式练习题【1.一次函数与一元一次方程、一元一次不等式】A. B. C. D.例2:直线3+=kx y 经过点A (2,1),则不等式03≥+kx 的解集是 ( ) A.3≤x B.3≥x C.3-≥x D.0≤x针对训练1、一次函数b kx y +=的图象如图所示,则方程0=+b kx 的解为 ( ) A.=x 2 B.=y 2 C.=x -3 D.=y -1第1题图 第2题图 第3题图2、如图,一次函数b kx y +=的图象经过A 、B 两点, 则不等式0<+b kx 的解集是 ( ) A.0<x B.10<<x C.1<x D.1>x3、如图,已知一次函数3+=kx y 和b x y +-=的图象交于点P (2,4),则关于x 的方程b x kx +-=+3的解是_____.4、如图,直线b x y +=与直线6+=kx y 交于点P (3,5),则关于x 的不等式6+>+kx b x 的解集是_____.5、画出函数62+=x y 的图象,利用图象: (1)求方程062=+x 的解; (2)求不等式062>+x 的解; (3)若22≤≤-y ,求x 的取值范围.强化训练1.已知点(2,1y ) 和(4,2y ) 都在直线4)5(+-=x k y 上,若1y <2y ,则k 的取值范围是() A.k >0 B.k <0 C.k >5 D.k <52.若0<ab ,0=bc ,则0=++c by ax 直线通过 ( ) A.第一、三象限 B.第二、四象限 C.第一、二、三象限 D.第一、二、四象限3.关于x 的一次函数12++=k kx y 的图象可能正确的是 ( )4.若k ≠0,b<0,则b kx y +=的图象可能是 ( )5.下列图形中,表示一次函数n mx y +=与正比例函数mnx y =(m 、n 为常数,且mn ≠0)的图象的是 ( )6.直线1l :b x k y +=11与直线2l :x k y 22=在同一平面直角坐标系中的图象如图所示,则关于x 的不等式x k b x k 21>+的解集为 ( ) A.x >-1 B.x <-1 C.x <-2 D.无法确定第6题图 第8题图 第9题图7.设点A (a ,b )是正比例函数x y 23-=图像上的任意一点,则下列等式一定成立的是( )A.2a +3b=0B.2a -3b=0C.3a -2b=0D.3a +2b=08.如图,直线b ax y +=过点A (0,2)和点B (-3,0),则方程0=+b ax 的解是 ( ) A.=x 2 B.=x 0 C.=x -1 D.=x -3 9.如图,若一次函数b x y +-=2的图象交y 轴于点A(0,3),则不等式02>+-b x 的解集为( ) A.23>x B.3>x C.23<x D.3<x 10.一次函数42-=x y 的图像与x 轴、y 轴分别交于A 、B 两点,O 为原点,则三角形AOB 的面积是 ( ) A.2 B.4 C.6 D.811.已知,一次函数b kx y +=的图象经过点(0,2),且y 随x 的增大而减小,请你写出一个符合上述条件的函数关系式:_________ . 12.若函数2)3(-+=k xk y 是一次函数,则函数解析式是.13.已知一次函数2+=kx y ,当1-=x 时,1=y ,求此函数的解析式,并在平面直角坐标系中画出此函数图象.14.如图,正比例函数与一次函数交于点A(3,4),且一次函数与x轴交于点C,与y轴交于点B.(1)求两个函数解析式;(2)求△AOC的面积.15.在“母亲节”期间,某校部分团员准备购进一批“康乃馨”进行销售,并将所得利润捐给贫困同学的母亲.根据市场调查,这种“康乃馨”的销售量y(枝)与销售单价x(元/枝)之间成一次函数关系,它的部分图象如图.(1)试求y与x之间的函数关系式;(2)若“康乃馨”的进价为5元/枝,且要求每枝的销售盈利不少于1元,问:在此次活动中,他们最多可购进多少数量的康乃馨?16.现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克20元收费;超过1千克,超过的部分按每千克10元收费.乙公司表示:按每千克15元收费,另收包装费3元.设小明快递物品x千克.(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;(2)小明选择哪家快递公司更省钱?能力提升1.直线y=k x+b如图所示,则下列结论:①k>0,②b>0,③k+b>0,④2k+b=0,⑤不等式.其中正确的结论是(填序号).k x+b0第1题图第2题图2.如图,小明购买一种笔记本所付款金额y(元)与购买量x(本)之间的函数图象由线段OB 和BE射线组成,则一次购买8个笔记本比分次购买每次购买1个可节省_____元.3.为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第_____秒.4.一次函数y=k x+b(k≠0)的自变量x的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,求这个函数的解析式.5.某工厂用一种自动控制加工机制作一批工件,该机器运行过程分为加油过程和加工过程.加工过程中,当油箱中油量为10L时,机器自动停止加工进入加油过程,将油箱加满后继续加工,如此往复.已知机器需运行185min才能将这批工件加工完.下图是油箱中油量y(L)与机器运行时间x(min)之间的函数关系图象.根据图象回答下列问题:(1)函数图像中描述机器加油过程的是(填“OA”或“OB”);(2)求在第一个加工过程中,油箱中油量y(L)与机器运行时间x(min)之间的函数关系式(不必写出自变量x的取值范围);并求出机器运行多少分钟时,第一个加工过程停止;*(3)加工完这批工件,机器耗油多少升?6.公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆.已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元.(1)设租用甲种货车x辆(x为非负整数),试填写表格.表一:表二:(2)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.7.在一条笔直的公路上有A、B两地,甲乙两人同时出发,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(s)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:(1)写出A、B两地的距离;(2)求出点M的坐标,并解释该点坐标所表示的意义.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小专题(八) 一次函数与方程、不等式的综合应用
1.(2017·绍兴)某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
(1)若每月用水量为18立方米,则应交水费多少元?
(2)求当x>18时,y 关于x 的函数解析式.若小敏家某月交水费81元,则这个月用水量为多少立方米?
解:(1)45元.
(2)当x >18时,设直线函数解析式为y =kx +b ,将(18,45),(28,75)代入y =kx +b ,得
⎩⎪⎨⎪⎧18k +b =45,28k +b =75, 解得⎩
⎪⎨⎪⎧k =3,b =-9. ∴y =3x -9.
当y =81时,3x -9=81,解得x =30. 答:这个月的用水量为30立方米.
2.(2017·陕西)在精准扶贫中,某村的李师傅在县政府的扶持下,去年下半年,他对家里的3个温室大棚进行整修改造,1个大棚种植香瓜,2个大棚种植甜瓜.今年上半年喜获丰收,现在他家的甜瓜和香瓜已全部售完,他高兴地说:“我的日子终于好了”.
最近,李师傅在扶贫工作者的指导下,计划在农业合作社承包5个大棚,以后就用8个大棚继续种植香瓜和甜瓜.他根据种植经验及今年上半年的市场情况,打算下半年种植时,两个品种同时种,一个大棚只种一个品种的瓜,并预测明年两种瓜的产量、销售价格及成本如下:
项目 品种 产量 (斤/每棚) 销售价 (元/每斤)
成本 (元/每棚) 香瓜 2 000 12 8 000 甜瓜
4 500
3
5 000
现假设李师傅今年下半年香瓜种植的大棚数为x 个,明年上半年8个大棚中所产的瓜全售完后,获得的利润为y 元.
根据以上提供的信息,请你解答下列问题: (1)求出y 与x 之间的函数关系式;
(2)求出李师傅种植的8个大棚中,香瓜至少种植几个大棚?才能使获得的利润不低于10万元. 解:(1) y =(2 000×12-8 000)x +(4 500×3-5 000)(8-x)=7 500x +68 000. (2)由题意,得7 500x +68 000≥100 000. ∴x ≥44
15
∵x 为整数,∴x 最小为5.
∴李师傅种植的8个大棚中至少有5个大棚种植香瓜.
3.现正是闽北特产杨梅热销的季节,某水果零售商店分两批次从批发市场共购进杨梅40箱,已知第一、二次进货分别为每箱50元、40元,且第二次比第一次多付款700元.
(1)设第一、二次购进杨梅的箱数分别为a 箱、b 箱,求a ,b 的值;
(2)若商店对这40箱杨梅先按每箱60元销售了x 箱,其余的按每箱35元全部售完. ①求商店销售完全部杨梅所获利润y(元)与x(箱)之间的函数关系式; ②当x 的值至少为多少时,商店才不会亏本. (注:按整箱出售,利润=销售总收入-进货总成本)
解:(1)依题意,得⎩⎪⎨⎪⎧a +b =40,40b -50a =700,解得⎩
⎪⎨⎪⎧a =10,b =30. (2)①y=60x +35(40-x)-(10×50+30×40) =25x -300.
②由题意,得25x -300≥0.解得x≥12. 答:当x 的值至少为12时,商店才不会亏本.
4.A 城有肥料300吨,B 城有肥料200吨,现要把这些肥料全部运往C ,D 两乡,从A 城往C ,D 两乡运肥料的费用分别为每吨20元和25元;从B 城往C ,D 两乡运肥料的费用分别为每吨15元和24元,现C 乡需要肥料240吨,D 乡需要肥料260吨,怎样调运总费用最少?
解:设总运费为y 元,A 城运往C 乡的肥料量为x 吨,则运往D 乡的肥料量为(300—x)吨;B 城运往C ,D 两乡的肥料量分别为(240—x)吨与(x -40)吨.由题意,得
y =20x +25(300-x)+15(240-x)+24(x -40) =4x +10 140(40≤x≤240).
∵k =4>0,∴当x 取最小值40时,y 有最小值10 300. ∴300-x =260,240-x =200,x -40=0.
答:从A 城运往C 乡40吨,运往D 乡260吨;从B 城运往C 乡200吨,运往D 乡0吨,此时总费用最少,总运费最少为10 300元.
5.(2017·连云港)某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤,设安排x 名工人采摘蓝莓,剩下的工人加工蓝莓.
(1)若基地一天的总销售收入为y 元,求y 与x 的函数关系式; (2)试求如何分配工人,才能使一天的销售收入最大?并求出最大值. 解:(1)根据题意得:
y =70x×40+(20-x)×35×130 =-1 750x +91 000.
(2)∵70x≥35(20-x),∴x ≥20
3.
又∵x 为正整数,且x≤20, ∴7≤x ≤20,且x 为正整数.
∵-1 750<0,∴y 的值随着x 的值增大而减小,
∴当x=7时,y取最大值,最大值为-1 750×7+91 000=78 750.
答:安排7名工人进行采摘,13名工人进行加工,才能使一天的收入最大,最大收入为78 750元.
6.(2016·天津)公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台,租车费用为400元,每辆乙种货车一次最多运送机器30台,租车费用为280元.
(1)设租用甲种货车x辆(x为非负整数),试填写表格:
表一
租用甲种货车的数量/辆 3 7 x
租用的甲种货车最多
135 315 45x 运送机器的数量/台
租用的乙种货车最多
150 30 -30x+240 运送机器的数量/台
表二
租用甲种货
3 7 x
车的数量/辆
租用甲种货
1 200
2 800 400x
车的费用/元
租用乙种货
1 400 280 -280x+
2 240
车的费用/元
(2)若租用甲种货车x辆时,设两种货车的总费用为y元,试确定能完成此项运送任务的最节省费用的租车方案.
解:y=400x+(-280x+2 240)=120x+2 240.
又∵45x+(-30x+240)≥330,解得x≥6.
∵120>0,
∴在函数y=120x+2 240中,y随x的增大而增大,
∴当x=6时,y取得最小值,y最小=2 960.
∴完成此项运送任务的最节省费用的租车方案是租用甲种货车6辆,乙种货车2辆.
7.小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲、乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7 500元,则甲种服装最多购进多少件?
(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行优惠促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
解:(1)设购进甲种服装x件,由题意,得
80x+60(100-x)≤7 500,解得x≤75.
答:甲种服装最多购进75件.
(2)设总利润为W元,
∵甲种服装不少于65件,∴65≤x≤75.
W=(120-80-a)x+(90-60)(100-x)
=(10-a)x+3 000.
方案1:当0<a<10时,10-a>0,W随x的增大而增大,
∴当x=75时,W有最大值,则购进甲种服装75件,乙种服装25件;
方案2:当a=10时,所有方案获利相同,∴按哪种方案进货都可以;
方案3:当10<a<20时,10-a<0,W随x的增大而减小,
∴当x=65时,W有最大值,则购进甲种服装65件,乙种服装35件.。
