专题十五函数与方程(组)、不等式
函数与方程不等式之间的关系

函数与方程不等式之间的关系
函数、方程和不等式是数学中的基本概念,它们之间存在密切的联系。
函数是描述两个变量之间关系的数学模型,通常表示为 y = f(x),其中 x 和
y 是变量,f 是函数关系。
函数有多种类型,其中一次函数是最简单的一种,表示为 y = ax + b,其中 a 和 b 是常数,a ≠ 0。
方程是含有未知数的等式,用来表示未知数和已知数之间的关系。
一元一次方程是最简单的一类方程,形如 ax + b = 0,其中 a 和 b 是已知数,a ≠ 0。
解这个方程可以得到未知数的值。
不等式是用不等号连结的两个解析式,表示两个量之间的大小关系。
一元一次不等式是最简单的一类不等式,形如 ax + b > 0 或 ax + b < 0,其中 a 和 b 是已知数,a ≠ 0。
解这个不等式可以得到满足不等式的值的范围。
函数、方程和不等式之间存在密切的联系。
一次函数和一元一次方程、一元一次不等式之间的关系特别重要。
对于一次函数 y = ax + b,当函数的值等于 0 时,自变量 x 的值就是一元一次方程 ax + b = 0 的解。
如果一次函数的值大于 0,则自变量 x 的值满足一元一次不等式 ax + b > 0;如果一次函数的值小于 0,则自变量 x 的值满足一元一次不等式 ax + b < 0。
因此,函数、方程和不等式是相互联系的,可以通过它们之间的关系来理解和解决数学问题。
知识总结,关于不等式的性质,以及函数方程不等式之间的联系

知识总结,关于不等式的性质,以及函数方程不等式之间的联系本文分析了不等式的定义、性质及函数方程不等式之间的联系。
首先,我们讨论了不等式概念的基本概念,包括不等式的类型和不等式组;其次,我们探讨了不等式的性质,比如非负性、可加性和对称性等;最后,我们研究了不等式方程与函数不等式之间的联系。
一、不等式的定义不等式是数学中最基本的概念之一,它表示两个数的大小关系。
它的具体定义可以表达为:如果a、b是数,且a≠b,那么根据其大小关系,存在如下不等式:a>b(a大于b)、a≥b(a大于等于b)、a<b(a小于b)、a≤b(a小于等于b)。
不等式组指的是由多个不等式组成的集合,它是一种非常有用的数学工具,可以被用来描述更多有趣且复杂的结果。
不等式组可以根据其形式来分类,常见的不等式组有:单不等式、多个不等式连续构成的多个不等式组、范围不等式组等。
二、不等式的性质不等式性质指的是不等式具有的一系列普遍性质,它们可以帮助我们协助理解不等式的表达和运用。
常见的不等式性质有:1.负性:我们知道大于号的符号表示结果大于零,而小于号的符号表示结果小于零,这就限定了不等式的结果一定是大于或小于零。
2.加性:任何两个不等式可以加在一起,等价于将两个不等式结合起来,例如a<b 与 c<d,把它们加在一起可以得到a+c < b+d。
3.称性:一个不等式的符号可以和相反的符号交换形成新的不等式,例如a<b 与 b>a,它们是等价的。
4.合性:一个不等式可以和多个不等式结合,并可以生成更大的不等式,例如a<b 与 c<d以构成a+c<b+d。
三、函数方程与不等式之间的联系在很多数学问题中,不等式和函数方程经常会被混合使用,因为它们之间有一定的联系。
函数方程与不等式之间的联系可以表示为:函数方程是一个数学表达式,它可以定义函数的输入和输出值之间的关系,例如 y=f(x),表示y是x的函数;而不等式可以表示两个值之间的大小关系,例如y>f(x),表示y大于x的函数。
中考数学复习:函数与方程、不等式的关系

中考数学复习:函数与方程、不等式的关系1.函数与方程的关系(1)关于x的一元二次方程ax2+bx+c=0(a≠0)的解⇔抛物线y=ax2+bx+c(a≠0)与x轴交点的横坐标的值;(2)关于x的一元二次方程ax2+bx+c=mx+n(am≠0)的解⇔抛物线y=ax2+bx+c (a≠0)与直线y=mx+n(m≠0)交点的横坐标的值.2.函数与不等式的关系(1)关于x的不等式ax2+bx+c>0(a≠0)的解集⇔抛物线y=ax2+bx+c(a≠0)位于x轴上方的所有点的横坐标的值;(2)关于x的不等式ax2+bx+c<0(a≠0)的解集⇔抛物线y=ax2+bx+c(a≠0)位于x轴下方的所有点的横坐标的值;(3)关于x的不等式ax2+bx+c>mx+n(ma≠0)的解集⇔抛物线y=ax2+bx+c(a≠0)位于直线y=mx+n(m≠0)上方的所有点的横坐标的值;(4)关于x的不等式ax2+bx+c<mx+n(ma≠0)的解集⇔抛物线y=ax2+bx+c(a≠0)位于直线y=mx+n(m≠0)下方的所有点的横坐标的值.例题讲解例1在平面直角坐标系xOy中,抛物线y=mx2-2mx-2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.若该抛物线在-2<x<-1这一段位于直线l:y=-2x+2的上方,并且在2<x<3这一段位于直线AB的下方,求该抛物线的表达式.解:如图,因为抛物线的对称轴是x=1,且直线l与直线AB关于对称轴对称.所以抛物线在-1<x<0这一段位于直线l的下方.又因为抛物线在-2<x<-1这一段位于直线l的上方,所以抛物线与直线l的一个交点的横坐标为-1.当x=-1时,y=-2×(-1)+2=4,则抛物线过点(-1,4),将(-1,4)代入y=mx2-2mx-2,得m+2m-2=4,则m=2.所以抛物线的表达式为y=2x2-4x-2.例2已知y=ax²+bx+c(a≠0)的自变量x与函数值y满足:当-1≤x≤1时,-1≤y≤1,且抛物线经过点A(1,-1)和点B(-1,1).求a的取值范围.解:因为抛物线y=ax²+bx+c经过A(1,-1)和点B(-1,1),代入得a+b+c=-1,a-b+c=1,所以a+c=0,b=-1,则抛物线y=ax²-x-a,对称轴为x=12a.①当a<0时,抛物线开口向下,且x=12a<0,如图可知,当12a≤-1时符合题意,所以-12≤a<0.当-1<12a<0时,图像不符合-1≤y≤1的要求,舍去.②当a>0时,抛物线开口向上,且x=12a>0.如图可知,当12a≥1时符合题意,所以0<a≤12.当0<12a<1时,图像不符合-1≤y≤1的要求,舍去.综上所述,a的取值范围是-12≤a<0或0<a≤12.例3在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,'b)给出如下定义:1 '1b abb a ≥⎧=⎨-<⎩,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(﹣2,5)的限变点的坐标是(﹣2,﹣5).(1)若点P在函数y=﹣x+3(﹣2≤x≤k,k>﹣2)的图象上,其限变点Q的纵坐标b′的取值范围是﹣5≤b′≤2,求k的取值范围;(2)若点P在关于x的二次函数y=x2﹣2tx+t2+t的图象上,其限变点Q的纵坐标b′的取值范围是b′≥m或b′<n,其中m>n.令s=m﹣n,求s关于t的函数解析式及s的取值范围.解:(1)依题意,y=﹣x+3(x≥﹣2)图象上的点P的限变点必在函数y=313-21x xx x-+≥⎧⎨-≤<⎩的图象上.∴b′≤2,即当x=1时,b′取最大值2.当b′=﹣2时,﹣2=﹣x+3.∴x=5.当b′=﹣5时,﹣5=x﹣3或﹣5=﹣x+3.∴x=﹣2或x=8.∵﹣5≤b′≤2,由图象可知,k的取值范围是5≤k≤8.(2)∵y=x2﹣2tx+t2+t=(x﹣t)2+t,∴顶点坐标为(t,t).若t<1,b′的取值范围是b′≥m或b′<n,与题意不符.若t≥1,当x≥1时,y的最小值为t,即m=t;当x<1时,y的值小于﹣[(1﹣t)2+t],即n=﹣[(1﹣t)2+t].∴s=m﹣n=t+(1﹣t)2+t=t2+1.∴s关于t的函数解析式为s=t2+1(t≥1),当t=1时,s取最小值2,∴s的取值范围是s≥2.1);点B;5≤k≤8;s≥2.进阶训练1.若关于x 的一元二次方程x 2+ax +b =0有两个不同的实数根m ,n (m <n ),方程x 2+ax+b =1有两个不同的实数根p ,q (p <q ),则m ,n ,p ,q 的大小关系为( )A .m <p <q <nB .p <m <n <qC .m <p <n <qD .p <m <q <nB【提示】 函数y =x 2+ax +b 和函数y =x 2+ax +b -1的图像如图所示,从而得到p <m <n<q解:函数y =x 2+ax +b 如图所示: xq n m p O2.在平面直角坐标系xOy 中,p (n ,0)是x 轴上一个动点,过点P 作垂直于x 轴的直线,交一次函数y =kx +b 的图像于点M ,交二次函数y =x ²-2x -3的图像于点N ,若只有当-2<n <2时,点M 位于点N 的上方,求这个一次函数的表达式.y =-2x +1【提示】 依据题意并结合图像可知,一次函数的图像与二次函数的图像的交点的横坐标分别为-2和2,由此可得交点坐标分别为-2和2,由此可得交点坐标为(-2,5)和(2,-3)将交点坐标分别代入一次函数表达式即可3.在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-5的图像与x轴有两个公共点,若m取满足条件的最小整数,当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n,求n的值n的值为-2【提示】根据已知可得m=1.图像的对称轴为直线x=32.当n≤x≤1<32时,函数值y随自变量x的增大而减小,所以当x=1时,函数的值为-6,当x=n时,函数值为4-n.所以n2-3n-4=4-n,解得n=-2或n=4(不符合题意,舍去),则n的值为-2。
从函数的观点看方程及不等式

从函数的观点看方程及不等式新疆布尔津县初级中学 刘海燕关键词:函数,方程(组),不等式(组),关系。
摘要:研究目的:加深对函数与方程(组),函数与不等式(组)的理解。
研究内容:函数与方程(组),函数与不等式(组)之间的关系。
基本结论:它们可以相互转化。
数学是研究现实世界量的关系的学科———恩格斯。
由于数学概念﹑理论和方法都源于实际,是从现实世界的材料中抽象出来的。
数学内容之间相互联系,充满运动变化和对立统一的辨证关系。
函数和方程(方程组)及不等式的这种对应关系正是这种辨证关系的真实写照。
一、函数与方程的关系。
(一)、从关系式上看:一次函数的关系式为:y=ax+b(a ≠0),一元一次方程的一般形式为:ax+b=0(a ≠0) 从形式上可以看出,当把一次函数关系式中的因变量y 改写为整数0就可将函数式转化为方程式;反之,把一元一次方程一般式等号右边的0改写为一个变量y 就可将方程式转化为函数式。
同理,二次函数的关系式为y=ax 2+bx+c(a ≠0),一元二次方程的一般形式为ax 2+bx+c=0(a ≠0),当把二次函数关系式中的因变量y 改写为整数0就可将函数式转化为方程式;将方程式右边的0换成一个变量y 则方程式变为函数式。
(二)、从函数的图象与方程的解来看。
一次函数的图象是一条直线,这条直线必与x 轴相交,其交点坐标为(-ab ,0),也就是当因变量y=0时其自变量x=-ab ,这个x 的值就是方程ax+b=0(a ≠0)的解,换句话说方程ax+b=0(a ≠0)的解就是相对应函数的图象,直线y=ax+b 上无数个点中的与x 轴相交的那一点的横坐标;二次函数的图象是一条抛物线,这条抛物线与x 轴的位置关系有三种情况:当抛物线与x 轴有一个交点时,相对应的方程ax 2+bx+c=0(a ≠0)就有两个相等的实数根x 1=x 2=-ab 2,当抛物线与x 轴有两个交点时,相对应的方程ax 2+bx+c=0(a≠0)就有两个不相等的实数根x1=a acb b24 2-+-,x2=a acb b24 2---,当抛物线与x轴没有交点时,相对应的方程ax2+bx+c=0(a≠0)就没有实数根。
函数方程不等式以及它们的图像

k 2m
k (2m 1) m Z
由①②可知,实数k的取值范围是
{k k m, m Z}
例题5、函数 f ( x ) 在 (1,1) 上有定义,
1 f ( ) 1 且满足 x, y (1,1) 时,有 2 xy f ( x ) f ( y) f 1 xy 。(1)证明:
x轴有两个交点且都在 (c,) 内,
又图像开口向上
解:
y
o
c
x
解:
(c 1) 2 4(c 2 c) 0 1 c c 2 2 f ( c ) 3 c 2 c 0
解:
1 c0 3
4 8 1 1 c , 1 c2 1 3 9 4 8 2 2 a b (1, ) , a b ( ,1) 3 9
x 3 。 例题7、已知函数 f (x) logm x 3 (1)若 f ( x ) 的定义域为 [, ] (0 ) ,
判断 f ( x ) 在定义域上的增减性,并用定 义证明;(2)当 0 m 1 时,使 f ( x )
的值域为 [logm m( 1), logm m( 1)]
解: 又f(x)是R上的偶函数 f ( x ) f (x )
f [2 (x )] f (x ) f (2 x) f (x)
f (2 x ) f ( x )
即f(x)是以2为周期的周期函数
解:(3)
由(2)知2n也是f(x)的周期
1 1 f (2n ) f ( ) 2n 2n 1 1 1 1 2n f (1) f ( ) [f ( )] 2n 2n 2n 2n 1 (把1分为2n个 的和) 2n
35函数与方程(组)不等式PPT课件

中考热点1:一次函数与一元一次方 程、一元一次不等式的综合应用.
• 例1(2008河南)某校八年级举行英语演讲比赛, 派了两位老师去学校附近的超市购买笔记本 作为奖品,经过了解得知,该超市的A、B两种 笔记本的价格分别是12元和8元,他们准备购 买这两种笔记本共30本.
• (1)如果他们计划用300元购买奖品,那么能买 这两种笔记本各多少本?
课堂小结
• 说说本节课我们学了什么,还有什么不太 清楚的地方吗?
自主训练
•1.(1)y1=12x+50;(2)y2=18x; • (3)当x=6时y2=108,而y1=122,y2<y1,没有超过小 明;
• (4)由18x>12x+50,得x>25/3,所以至少要9个月
后小丽存款数超过小明
•2.(1) •3.y=-
• 1.小明准备将平时的零用钱节约一些储存起 来,他已存有50元,从现在起每个月存12元.
• (3)半年以后小丽的存款数是多少?是否超过 了小明?
自主训练1(4)
• 1.小明准备将平时的零用钱节约一些储存起 来,他已存有50元,从现在起每个月存12元.
• (4)至少几个月后小丽的存款数超过小明?
自主训练2(1)
中考热点4: 二次函数与方程、不等 式的综合应用(1)
• 例4抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
(1)求出m的值 并画出这条抛 物线;
中考热点4: 二次函数与方程、不等 式的综合应用(2)
• 例4抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
(2)求它与x轴的 交点和抛物线顶 点的坐标;
• 1. 一次函数与一元一次方程、一元一次不等 式的关系,一次函数与二元一次方程(组)的关 系,二次函数与一元二次方程、不等式的关系, 题型以解答题为主.
函数,方程,不等式之间关系
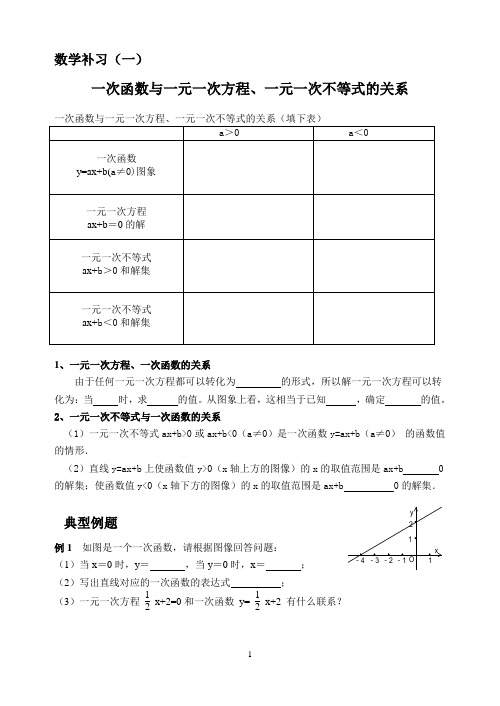
数学补习(一)一次函数与一元一次方程、一元一次不等式的关系1、一元一次方程、一次函数的关系由于任何一元一次方程都可以转化为 的形式,所以解一元一次方程可以转化为:当 时,求 的值。
从图象上看,这相当于已知 ,确定 的值。
2、一元一次不等式与一次函数的关系 (1)一元一次不等式ax+b>0或ax+b<0(a ≠0)是一次函数y=ax+b (a ≠0)•的函数值的情形.(2)直线y=ax+b 上使函数值y>0(x 轴上方的图像)的x 的取值范围是ax+b 0 的解集;使函数值y<0(x 轴下方的图像)的x 的取值范围是ax+b 0的解集.典型例题例1 如图是一个一次函数,请根据图像回答问题: (1)当x =0时,y = ,当y =0时,x = ; (2)写出直线对应的一次函数的表达式 ;(3)一元一次方程 12 x+2=0和一次函数 y= 12x+2 有什么联系?一元二次不等式与二次函数、一元二次方程的关系一元二次不等式与二次函数、一元二次方程的关系(填写下表)1.二次函数与一元二次方程的关系:(1)一元二次方程c bx ax y ++=2就是二次函数c bx ax y ++=2当函数y 的值为0时的情况. (2)二次函数c bx ax y ++=2的图象与x 轴的交点有三种情况:有两个交点、有一个交点、没有交点;当二次函数c bx ax y ++=2的图象与x 轴有交点时,交点的横坐标就是当0=y 时自变量x 的值,即一元二次方程02=++c bx ax 的根.(3)当二次函数c bx ax y ++=2的图象与x 轴有两个交点时,则一元二次方程c bx ax y ++=2有两个不相等的实数根;当二次函数c bx ax y ++=2的图象与x 轴有一个交点时,则一元二次方程02=++c bx ax 有两个相等的实数根;当二次函数c bx ax y ++=2的图象与x 轴没有交点时,则一元二次方程02=++c bx ax 没有实数根 2.一元二次不等式与二次函数的关系一元二次不等式()00022≠<++>++a c bx ax c bx ax 或的解集:设相应的一元二次方程()002≠=++a c bx ax 的两根为2121x x x x ≤且、,ac b 42-=∆,则不等式的解的各种情况填上表。
函数不等式知识点归纳总结

函数不等式知识点归纳总结函数不等式是解决数学问题中常见的一种形式,它涉及到函数的不等关系及其解集。
本文将对函数不等式的概念、解法和应用进行归纳总结,以帮助读者更好地理解和应用函数不等式。
一、函数不等式的概念函数不等式是指含有函数的不等式关系,其中函数可以是一元函数或多元函数。
函数不等式可以包含一个或多个变量,并且其解集通常是一个或多个实数区间。
解函数不等式的主要目标是确定变量的取值范围,以满足不等式关系。
二、一元函数不等式的解法解一元函数不等式的方法主要包括图像法、代数法和符号法。
图像法借助函数的图像找到不等式的解集;代数法借助代数运算和推导解出不等式的解集;符号法则通过符号变换和符号性质推导解出不等式的解集。
2.1 图像法图像法是通过函数的图像来解不等式的方法。
首先,绘制函数的图像,并观察函数图像的凹凸性、单调性和零点等信息。
然后,根据函数图像的性质确定不等式的解集。
2.2 代数法代数法是通过代数运算和推导来解不等式的方法。
利用一元函数的性质,将不等式进行化简、移项和分式分解等操作,最终得到不等式的解集。
2.3 符号法符号法是通过符号变换和符号性质来解不等式的方法。
不等式中的符号可根据不等式的性质进行变换,并利用符号性质推导出不等式的解集。
常见的符号性质包括非负性、相反性、单调性和倍数性等。
三、多元函数不等式的解法解多元函数不等式的方法主要包括图像法和代数法。
其中,图像法借助多元函数的图像确定不等式的解集;代数法则通过代数运算和推导解出不等式的解集。
3.1 图像法图像法是通过多元函数的图像来解不等式的方法。
首先,绘制多元函数的图像,并观察函数图像的变化趋势。
然后,根据函数图像的性质确定不等式的解集。
3.2 代数法代数法是通过代数运算和推导来解不等式的方法。
利用多元函数的性质,将不等式进行化简、移项和分式分解等操作,最终得到不等式的解集。
四、函数不等式的应用函数不等式在数学和实际问题中有着广泛的应用。
