必修四第一章1.5三角函数图像变换
人教版必修四三角函数图像性质变换
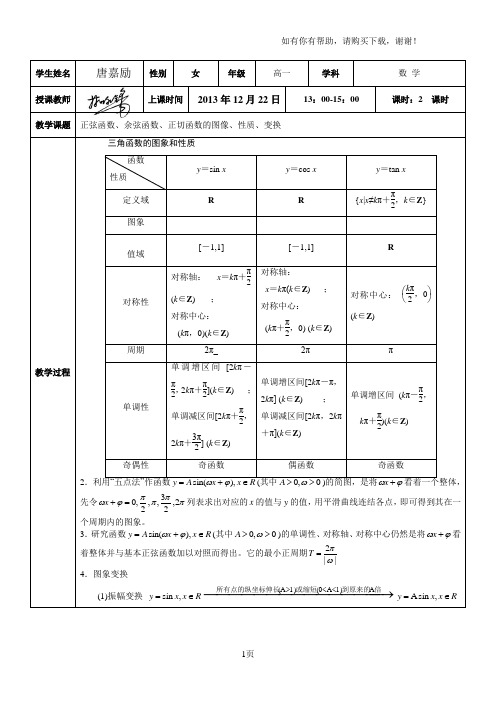
学生姓名唐嘉励性别女年级高一学科数学授课教师上课时间2013年12月22日13：00-15：00 课时：2 课时教学课题正弦函数、余弦函数、正切函数的图像、性质、变换教学过程三角函数的图象和性质函数性质y＝sin x y＝cos x y＝tan x定义域R R{x|x≠kπ＋π2，k∈Z} 图象值域[－1,1][－1,1]R对称性对称轴：__ x＝kπ＋π2(k∈Z)__ _；对称中心：_ (kπ，0)(k∈Z)__ _对称轴：x＝kπ(k∈Z)___；对称中心：_(kπ＋π2，0) (k∈Z)__对称中心：_⎝⎛⎭⎫kπ2，0(k∈Z) __周期2π_2ππ单调性单调增区间_[2kπ－π2，2kπ＋π2](k∈Z)___；单调减区间[2kπ＋π2，2kπ＋3π2] (k∈Z) __单调增区间[2kπ－π，2kπ] (k∈Z) ____；单调减区间[2kπ，2kπ＋π](k∈Z)______单调增区间_(kπ－π2，kπ＋π2)(k∈Z)___奇偶性奇函数偶函数奇函数2．利用“五点法”作函数RxxAy∈+=),sin(ϕω(其中0,0>>ωA)的简图，是将ϕω+x看着一个整体，先令ππππϕω2,23,,2,0=+x列表求出对应的x的值与y的值，用平滑曲线连结各点，即可得到其在一个周期内的图象。
3．研究函数RxxAy∈+=),sin(ϕω(其中0,0>>ωA)的单调性、对称轴、对称中心仍然是将ϕω+x看着整体并与基本正弦函数加以对照而得出。
它的最小正周期||2ωπ=T4．图象变换(1)振幅变换Rxxy∈=,sin−−−−−−−−−−−−−−→−<<>倍到原来的或缩短所有点的纵坐标伸长A1)A(01)(ARxxy∈=,sinA(2)周期变换 R x x y ∈=,sin −−−−−−−−−−−−−−→−<<>倍到原来的或伸长所有点的横坐标缩短ωωω11)(01)(R x x y ∈=,sin ω(3)相位变换 R x x y ∈=,sin −−−−−−−−−−−−→−<>个单位长度平移或向右所有点向左||0)(0)(ϕϕϕR x x y ∈+=,)(sin ϕ (4)复合变换 Rx x y ∈=,sin −−−−−−−−−−−−→−<>个单位长度平移或向右所有点向左||0)(0)(ϕϕϕR x x y ∈+=,)(sin ϕ5．主要题型：求三角函数的定义域、值域、周期，判断奇偶性，求单调区间，利用单调性比较大小，图象的平移和伸缩，图象的对称轴和对称中心，利用图象解题，根据图象求解析式，已知三角函数值求角。
人教A高中数学必修4第一章 1.5 第1课时 y=Asin(ωx+φ)图象的变换
[答案]
D
人教A版数学·必修4
返回导航
上页
下页
[错因与防范]
1.在解答过程中，若不能正确理解平移的实质，则会出现
π π π y＝sin(3x＋ － )，得到 y＝sin(3x＋ )．从而误选 A. 3 4 12 2．在解答过程中，若对伸缩变换理解不到位，对横坐标扩大或缩小为原来的倍 数把握不准，则易出现对 x 的系数缩小或扩大的倍数造成失误，会出现 3π y＝sin(6x＋ )等类似的错误答案． 4
重
难 突 破
重点：函数 y＝Asin(ωx＋φ) 的图象的画法及应用． 难点：y＝Asin(ωx＋φ)的图象 变换的理解及应用.
人教A版数学·必修4
返回导航
上页
下页
01 课前 自主梳理
02 课堂 合作探究
03 课后 巩固提升
课时作业
人教A版数学·必修4
返回导航
上页
下页
[自主梳理] 一、A、ω、φ 对函数 y＝Asin(ωx＋φ)图象的影响 1．φ 对函数 y＝Asin(x＋φ)图象的影响
π π π 移 个 单 位 长 度 后 ， 得 到 函 数 图 象 对 应 的 解 析 式 为 y ＝ 2sin 2x－ ＋ ＝ 4 6 4 π 2sin2x－ .故选 3
D.
答案：D
人教A版数学·必修4
返回导航
上页
下页
人教A版数学·必修4
[双基自测]
返回导航
上页
下页
π 1．把 y＝sin x 的图象向左平移 个单位，得到的图象的解析式为( 2 A．y＝－cos x π C．y＝sin x－ 2 π B．y＝sin x＋ 2 D．y＝cos x
数学北师大版高中必修4三角函数的图象变换
课题：三角函数的图象变换教学目标：1、知识目标：掌握函数Bx y x y x y x A y +=+===sin ),sin(,sin ,sin ϕϖ的图象变化规律，明确常数B A ,,,ϕϖ对图象变化的影响，进而使学生掌握函数B x A y ++=)sin(ϕϖ的图象；2、能力目标：培养学生发现问题、研究问题、解决问题的能力及创新能力；教学重、难点：介绍函数y=Asix （ωx+ψ）的图象的简图的作法，分层次、逐步讨论字母A 、ω、ψ变化时对函数图象的形状和位置的影响。
教学过程：一、引入课题1、引入：后面的同学听得到我说话吗？知道我在前面说，后面为什么能听到？声音靠什么传播？有没有见过弹簧震子，它运动的规律能画出图象来吗？2、在物理和工程技术的许多问题中，都要遇到形如y=Asix （ωx+ψ）的函数，下面我们来讨论这类函数的简图的作法。
3、[板书]函数y=Asix （ωx+ψ）的图象；二、新课教学1、作三角函数的图象的方法一般有两种：（1）描点法；（2）几何法；2、复习如何作三角函数的简图：主要先找出在确定图象性质时起关键作用的五个点（最大值点，最小值点，与x 轴的交点）3、[例题1]作函数x y x y sin 21)2(,sin 2)1(== 的简图。
问题1：函数 x y sin 2=的图象由正弦曲线经过怎样的变化得出？ 问题2：图象变换的实质是什么？（图象上每个点的变换）问题3：二函数图象上任意相关点的坐标之间有什么关系？问题4：不看图象猜想x y sin = 图象经过怎样的变化能够得到x y sin 21=的图象？计算机演示验证；对于同一个x 的值，（1）的图象上的点的纵坐标等于（2）的图象上的的纵坐标的2倍，因此（1）的图象可以看作是把x y sin = 的图象上所有点的纵坐标伸长到原来的2倍（横坐标不变）而得到。
（1）的值域是[-2，2]。
同样考虑（2）的图象变化。
（要求学生跟说一遍：函数x y sin 21= 的图象可以看作把图象上的所有点的纵坐标缩短到原来的21（横坐标不变）而得来；） 问题5：x A y sin = 图象是如何由 x y sin =变化得到的？问题6：在变化中A 起了什么作用？图象什么没变，什么变了？4、作函数：x y x y 21sin )2(,2sin )1(== 的简图。
高中数学 第一章 三角函数 1.5.1-2 从单位圆看正弦函数的性质 正弦函数的图像课件 北师大版
[变式训练]
3．(1)函数 y＝2sin x 与函数 y＝x 的图像的交点有( )
A．2 个
B．3 个
C．4 个
D．5 个
(2)研究方程 10sin x＝x(x∈R)根的个数．
解析： (1)在同一直角坐标系中作出函数 y＝2sin x
பைடு நூலகம்
与 y＝x 的图像，由图像可以看出有 3 个交点．
(2)如图所示，当 x≥4π 时，1x0≥41π0＞1≥sin x；当 x＝52π 时，sin x＝sin 52π＝1， 1x0＝52π0，1＞52π0，从而 x＞0 时，有 3 个交点，由对称性知 x＜0 时，有 3 个交点， 加上 x＝0 时的交点为原点，共有 7 个交点．即方程有 7 个根．
[名师指津]
用“五点法”作正弦曲线应注意的问题
(1)弄清五个关键点的意义．
平衡点 最高点 平衡点 最低点
平衡点
0，0 ―→ π2，1 ―→ π，0 ―→ 32π，－1 ―→ 2π，0
其中，平衡点是正弦曲线凹凸方向改变的位置．
最高点和最低点是正弦曲线上升或下降变化趋势改变的位置．
(2)明确正弦曲线的结构特征．
【规律方法】 作形如函数 y＝asin x＋b，x∈[0,2π]的图像的步骤
[变式训练]
1．试用“五点法”画出 y＝1＋2sin x，x∈[0,2π]的简图．
解析： 按五个关键点列表：
x
0
π 2
π
3 2π
2π
sin x 0 1 0 －1 0
描点连线：
1＋2sin x 1 3 1 －1 1
题型二 利用正弦函数的图像求函数的定义域 求函数 f(x)＝lg(sin x)＋ 16－x2的定义域． 【思路探究】 画出函数 y＝sin x 的图像，由 sin x＞0 的 x 的范围与 16－x2≥0 的 x 的范围取 交集，即为定义域．
1.5三角函数的应用(教案)(教案)
3.增强学生的直观想象与数据分析能力：通过对三角函数图像的观察与分析，让学生在实际问题中运用三角函数知识，培养他们的直观想象与数据分析素养。
三、教学难点与重点
-理解三角函数图像与性质的关系：学生在理解三角函数图像与性质之间的关系时可能会感到困惑。
-突破方法：利用动态图像、互动软件等教学工具，帮助学生直观地理解函数图像与性质之间的关系。
-建立和求解三角函数模型：学生在建立模型和求解过程中可能会遇到各种问题，如参数的选择、公式的应用等。
-突破方法：通过小组合作、讨论交流等方式，让学生在尝试解决问题的过程中，逐步掌握建立和求解三角函数模型的方法。
4.教学过程中，我发现有些学生对三角函数的应用仍然局限于课堂上的例子，缺乏将知识拓展到其他领域的能力。为了提高学生的知识迁移能力，我计划在后续的教学中加入更多不同领域的实际问题，让他们学会运用三角函数知识解决问题。
5.总结回顾环节，学生对今天所学内容的掌握程度较高，但仍有个别学生在某些知识点上存在疑惑。在课后，我会及时关注这些学生的疑问，并给予个别辅导，确保他们能够跟上教学进度。
3.三角函数模型的建立：结合实际问题，建立三角函数模型，如气温变化、物体振动等，并运用所学的三角函数知识进行求解。
本节课旨在让学生掌握三角函数在实际问题中的应用，提高他们解决实际问题的能力，同时深化对三角函数图像与性质的理解。
二、核心素养目标
本节课的核心素养目标主要包括以下三个方面：
1.培养学生的数学抽象能力：通过三角函数在实际问题中的应用，让学生学会从实际问题中抽象出数学模型，提高数学抽象素养。
高中数学必修四 三角函数的图像变换
y sin( x ) 3x
5
y 3sin x
3
6
1
o
3
-1
-3
5
6
y sin(2x )
3
y sin( x ) 3x
5
y 3sin x
3
6
1
o
3
-1
-3
y 3sin(2x )
3
5
6
y sin(2x )
3
y sin( x ) 3x
5
y 3sin x
先平移后伸缩
y 3sin(2x )
3
3
y 3sin 2x
1 o
6-1
5
6 y sin 2x
x
y sin x
-3 先伸缩后平移
练习1. 作下列函数在一个周期的闭区间上的简图，并指 出它的图象是如何由函数 y＝sinx 的图象而得到的.
练习2. 完成下列填空 ⑴ 函数y=sin2x图象向右平移
高中数学 必修四
1.5 三角函数的图像变换
学霸兔 微信：xuebatwo
三角函数的图像变换
y sin x
沿x轴平移：左加右减 y sin( x （) ＞0）
沿y轴平移：上加下减 y sin x （c c＞0）
？
y A sin x( A＞0 )
？
y sin( x（) ＞0）
y sin 2x
y
1
任意一个
y，每个
x
值乘以������
������
O －1
2
人教版高中数学必修四第一章1.5 三角函数的图象变换(第二课时)公开课教学课件共13张PPT含视频及歌曲
2
2
y 0 2 0 2 0
2
(2)描点:
O 2
7
-2 2
2
( ,0),(2 ,2),(7 ,0),(5 ,2),(13 ,0)
2
2
2
(3)连线 :
练习： 画出函数 y 3sin(2x ) 的简图.
3
5 13 x 2
例2：如图是某简谐运动的图象，试根据图象 （2）从O点起，到曲线上的哪一点，表示完成了一次
时间只是过客，自己才是主人，人生的路无需苛求，只要你迈步，路就在你的脚下延伸，只要你扬帆，便会有八面来风，启程了，人的生命 才真正开始。 一份信心，一份努力，一份成功；十分信心，十分努力，十分成功。 现代的婚姻并不是情感的产物，更多的是竞争的结晶，选配偶其实就是变相的竞争上岗，而小三就是原配最大的竞争对手。 哪怕是最没有希望的事情，只要有一个勇敢者去坚持做，到最后就会拥有希望。 你要结交敢于指责你缺点，当面批评你的人，远离恭维你缺点，一直对你嘻嘻哈哈的人！ 自然界没有风风雨雨，大地就不会春华秋实。 征服自己，就能征服一切。
3
2
K∈Z
=2K -
11 6
K∈Z
2×2 + =2K + 3
3
2
=2K +
6
K∈Z K∈Z
小结：
y sin x
y sin(x )
y sin(wx)
y sin(wx )
振幅 变换
y Asin(wx )
平衡位置
y Asin(wx ) k
在茫茫沙漠，唯有前时进的脚步才是希望的象征。 愚痴的人，一直想要别人了解他。有智慧的人，却努力的了解自己。 为了向别人、向世界证明自己而努力拼搏，而一旦你真的取得了成绩，才会明白：人无须向别人证明什么，只要你能超越自己。 你的选择是做或不做，做不一定会成功，但不做就永远不会有机会。 太阳虽有黑点，却在奋力燃烧中树立了光辉的形象。 要铭记在心：每天都是一年中最美好的日子。 失败的定义：什么都要做，什么都在做，却从未做完过，也未做好过。 青春一经“典当”，永不再赎。 生活就像海洋，只有意志将强的人才能到达彼岸。 觉得自己做得到和做不到，只在一念之间。 缺乏明确的目标，一生将庸庸碌碌。 过去不等于未来。 如果惧怕前面跌宕的山岩，生命就永远只能是死水一潭。
人教版高中数学必修四第一章三角函数图像变换
人教版高中数学必修四第一章三角函 数图像 变换
总结: y=sinx
y=Asin(x+)
方法1:(按 ,ω, A 顺序变换)
y=sinx
向左>0 (向右<0) 平移||个单位
y=sin(x+)
横坐标缩短>1 (伸长0<<1)到原来的1/倍
纵坐标不变
y=sin(x+)
横坐标不变
y=Asin(x+)
纵坐标伸长A>1 (缩短0<A<1)到原来的A倍
课后作业
1、指出函数y=2/5sin3x的振幅、周期，并画出其图象。 2、作出y=2sin1/2x的简图。
人教版高中数学必修四第一章三角函 数图像 变换
人教版高中数学必修四第一章三角函 数图像 变换
谢谢莅临指导！ 再见！
人教版高中数学必修四第一章三角函 数图像 变换
人教版高中数学必修四第一章三角函 数图像 变换
教学重点： “用五点法”作函数y=Asinx和y=sinωx的简图及振 幅、周期对正弦函数图象的影响。
教学难点：在直角坐标中会寻找“五点”的位置及由y=sinx的 图象变为y=Asinωx的图象规律。
人教版高中数学必修四第一章三角函 数图像 变换
人教版高中数学必修四第一章三角函 数图像 变换
导入课题：
解：∵函数y=sin4x的周期T=/2 ∴在[0, /2]上作图
令Z=4x 则x=Z/4 从而sinZ=sin4x
x
0
8
4
3
8
2
4x 0
2
3 2
2
sin 4 x 0 1 0 -1 0
y
1
y sin 4 x
(2021年整理)人教版高数必修四第5讲：三角函数图像变换(教师版)
（完整）人教版高数必修四第5讲：三角函数图像变换(教师版)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）人教版高数必修四第5讲：三角函数图像变换(教师版)）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）人教版高数必修四第5讲：三角函数图像变换(教师版)的全部内容。
三角函数y A x =+sin()ωϕ的图像变换____________________________________________________________________________________________________________________________________________________________________1结合具体实例，理解y=Asin ）（ϕω+x 的实际意义，会用“五点法”画出函数y=Asin ）（ϕω+x 的简图。
会用计算机画图，观察并研究参数ϕω,,A ,进一步明确ϕω,,A 对函数图象的影响。
2能由正弦曲线通过平移、伸缩变换得到y=Asin ）（ϕω+x 的图象。
3教学过程中体现由简单到复杂、特殊到一般的化归的数学思想。
1、函数图象的左右平移变换如在同一坐标系下，作出函数)3sin(π+=x y 和)4sin(π-=x y 的简图，并指出它们与y x=sin 图象之间的关系。
解析:函数)3sin(π+=x y 的周期为2π，我们来作这个函数在长度为一个周期的闭区间上的简图。
设Z x =+3π，那么Z x sin )3sin(=+π,3π-=Z x当Z 取0、ππππ2232，，，时,x 取-πππππ36237653、、、、。
高中数学必修四1.5.1三角函数图像的变化
)的图象
方法1：(按 , , A顺序变换)
y
3
2 1
y=3sin(2x+ 3 )
y=sinx
o
3
6-１
6 3
7 2 5 12 3 6
7 6
5 3
2
x
-2
-3
y=sin(x+ ) 3 y=sin(2x+ ) 3
函数, y A sin( x )
y=sin(2x+ 3
y=sin(2x+ 3 )
y=sin2x
)
y=3sin(2x&( x )
纵坐标保持不变，横坐标 1 缩短或伸长到原来的 倍
y sin( x )
y sin( x )
向左或向右平移
y sin( x )
巩固练习 作出下面函数在一个周期的闭区间上 的简图，并指出它的图像是如何由 函数y = sinx的图像而得到的。
1.5 函数 y A sin( x )图象 的探究
复习回顾：
y sin x, x [0, 2 ] 的图象
2 2 注意:五点是指使函数值为0及达到最大值和最小值 的点.
3 关键点： (0,0), ( ,1), (,0), ( ,-1), (2,0) .
y
1
. . . 3/2 2 .
的图象是由函数 y sin x 的图象经过怎样的变换而得到的？
y sin( x )的图象，可以看作是把正 弦曲线 y sin x 上所有的点向左（当
＞0时）或向右（当 ＜0时）平行 移动| |个单位长度而得到.
(完整版)人教高中数学必修四第一章三角函数知识点归纳
三角函数一、随意角、弧度制及随意角的三角函数1．随意角(1)角的观点的推行①按旋转方向不一样分为正角、负角、零角．正角 : 按逆时针方向旋转形成的角随意角 负角: 按顺时针方向旋转形成的角零角 : 不作任何旋转形成的角②按终边地点不一样分为象限角和轴线角．角 的极点与原点重合，角的始边与 x 轴的非负半轴重合，终边落在第几象限，则称 为第几象限角．第一象限角的会合为 k 360ok 360o 90o , k第二象限角的会合为 k 360o 90o k 360o 180o , k第三象限角的会合为 k 360o 180o k 360o 270o , k第四象限角的会合为k 360o 270ok 360o360o , k终边在 x 轴上的角的会合为 k 180o , k终边在 y 轴上的角的会合为 k 180o 90o , k终边在座标轴上的角的会合为k 90o ,k(2)终边与角 α同样的角可写成 α＋ k ·360 °(k ∈ Z)．终边与角 同样的角的会合为k 360o, k(3)弧度制① 1 弧度的角：把长度等于半径长的弧所对的圆心角叫做1 弧度的角．②弧度与角度的换算： 360°＝ 2π弧度； 180°＝ π弧度．③ 半径为 r 的圆的圆心角所对弧的长为 l ，则角的弧度数的绝对值是lr④ 若扇形的圆心角为 为弧度制 ，半径为 r ，弧长为 l ，周长为 C ，面积为 S ，则 lr，C2r l ，S1 lr 1 r2 ． 222 ．随意角的三角函数定义设 α是一个随意角，角 α的终边上随意一点P(x ， y)，它与原点的距离为 r rx 2 y 2 ，那么角 α的正弦、余弦、rrx（三角函数值在各象限的符号规律归纳为：一全正、二正弦、三正切分别是： sin α＝ y ， cos α＝ x ， tan α＝ y．正切、四余弦）3．特别角的三角函数值角度030456090120135150180270360函数角 a 的弧度0π /6π/4π /3π /22π /33π /45π/6π3π /22πsina01/2√ 2/2√ 3/21√ 3/2√ 2/21/20-10 cosa1√ 3/2√ 2/21/20-1/2-√ 2/2-√ 3/2-101 tana0√ 3/31√ 3-√ 3-1-√ 3/300二、同角三角函数的基本关系与引诱公式A.基础梳理1．同角三角函数的基本关系(1)平方关系： sin2α＋ cos2α＝ 1；（在利用同角三角函数的平方关系时，若开方，要特别注意判断符号）sin α(2)商数关系：＝tanα.（3）倒数关系：tan cot 1cos α2．引诱公式公式一： sin( α＋ 2kπ)＝sin α， cos(α＋ 2kπ)＝cos_α，tan(2k )tan此中 k∈Z .公式二： sin( π＋α)＝－ sin_α， cos( π＋α)＝－ cos_α， tan( π＋α)＝ tan α.公式三： sin( π－α)＝ sin α， cos( π－α)＝－ cos_α，tan tan．公式四： sin( －α)＝－ sin_α， cos(－α)＝ cos_α，tan tan .ππ公式五： sin －α＝ cos_α， cos－α＝ sin α.22ππ公式六： sin 2＋α＝ cos_α， cos2＋α＝－ sin_α.π口诀：奇变偶不变，符号看象限．此中的奇、偶是指π引诱公式可归纳为 k· ±α的各三角函数值的化简公式．的奇数22倍和偶数倍，变与不变是指函数名称的变化．假如奇数倍，则函数名称要变( 正弦变余弦，余弦变正弦 ) ；假如偶数倍，则函数名称不变，符号看象限是指：把πα当作锐角时，依据 k· ±α在哪个象限判断原三角函数值的符号，最后作为结．．．．2．．．果符号．B. 方法与重点一个口诀1、引诱公式的记忆口诀为：奇变偶不变，符号看象限．2、四种方法在求值与化简时，常用方法有：sin α(1)弦切互化法：主要利用公式tan α＝化成正、余弦．cos α(2)和积变换法：利用 (sin θ±cos θ)2＝1 ±2sin θcos θ的关系进行变形、转变．（ sin cos、sin cos、sin cos三个式子知一可求二）(3)巧用 “1”的变换： 1＝ sin 2θ＋ cos 2θ= sinπ＝tan 42（4）齐次式化切法：已知 tank ，则 a sinbcos a tan b ak bm sinn cos m tan n mk n三、三角函数的图像与性质学习目标：1 会求三角函数的定义域、值域2 会求三角函数的周期 ：定义法，公式法，图像法（如y sin x 与 y cosx 的周期是）。
人教版高中数学必修四课件：1.5 三角函数图像平移伸缩变换(共22张PPT)
x
sin x 2sin x 1 sin x 2
y
2
1
o
-1 -2
0
2
3
2
2
0
1
0
-1 0
0
2
0
-2 0
0
1
2
0
1 2
0
y=2sinx y=sinx
y= 12sinx
2
3
2
2
x
小结1 函数 y Asin x, x R 的图象
（其中A 0且 A 1）
可以看作把正弦曲线上所有点的
纵坐标伸长（当A>1时）或缩短（当
0<A<1时）到原来的A倍（横坐标不变）
而得到． A的作用
引起值域 改变
纵向伸缩
函数 y Asin x, x R 的值域是 A, A
问题2
在同一坐标系中作出函数y=sin2x 及图y象=间sin的12关x的系简。图，并指出它们y=sinx
x
0
4
• 再把所有点的纵坐标伸长（当A>1时）或缩短（当
0<A<1时）到原来的A倍（横坐标不变）, 得到
y=Asin( x+ )。
变换2:
函数y=Asin(x+ )(其中A>0, >0)的
图象，可看作由下面方法得到：
• 把y=sinx图象上所有点的横坐标缩短(当
>1时)或伸长(当0< <1时)到原来的 1 倍
函数y Asin(x )的图像
复习：
2．用五点法作函数 y sin x, x 0,2
高中数学必修4三角函数图像变化1.5图像变换
y=2sinx
3 2 2
2 1
1
2
o1 -1 2 -2
2
x
2
1 y= sinx 2
---振幅变换
y=Asinx
振幅变换
y sin x y A sin x
y f ( x) y Af ( x)
正弦曲线上所有的点横坐标不变，纵坐标伸
长（A>1)或缩短（A<1)为原来的A倍。
★图像的位置向x轴负半轴移动了，图像 发生了“平移” ★图像一个周期的宽窄发生了变化，也就 是图像的“周期”改变了
新图像与y=sinx图像 函数的哪个性质改变 有什么区别？ 了，变成了什么样？
图像
★图像的最高点与最低点之间的距离 改变了，我们将这个距离称之为 “振幅”
从这几个方面 回答！
性质
★图像的位置变化了，相应的对称轴、单 调区间的数值也变化了 ★周期变化了，按照公式计算可得周期为π ★ “振幅”的改变使得函数的最值发生了 变化，最大值变为3，最小值变为-3
★图像的位置向x轴负半轴移动了，图像 发生了“平移” ★图像一个周期的宽窄发生了变化，也就 是图像的“周期”改变了
新图像与y=sinx图像 有什么区别？
图像
★图像的最高点与最低点之间的距离 改变了，我们将这个距离称之为 “振幅”
从这几个方面 回答！
性质
坐标
y=sinx
3
(0,0)
( ,1) 2 (
（0< <1) 或缩短（ >1)为原来的 1/ 倍。
实践应用
练习：考虑下列函数是由函数y=sinx通过 何种办法变化而来？
1、y sin(5 x)
三角函数图像三种变换
C •3. 要得到函数 y=sin（x + π/3）的图象，只需将 y=sinx 图象（ ）
A. 向左平移π/6个单位 B. 向右平移π/6个单位
C. 向左平移π/3个单位 D. 向右平移π/3个单位
D •4. 要得到函数 y=sin（2x－π/3）的图象,只需将y=sin2x图象（ ） A. 向左平移π/3 个单位 B. 向右平移π/3个单位
(1)A
振幅
(2)T = 2π ω
周期
(3)f = 1 = ω T 2π
频率
(4)ωx +
相位
(5)
初相
二）尝试练习题
二、学习过程：
1、为了得到函数y cos(x 1)的图象，只需把函数? 3
y cos x图象上所有的点( D )(1月4题)
A. 向左平行移动 1 个单位 B. 向左平行移动 1 个单位
D •1. 要得到函数 y= 2 sin x 的图象，只需将 y= sinx 图象（ ）
A.横坐标扩大原来的两倍 B. 纵坐标扩大原来的两倍
C.横坐标扩大到原来的两倍 D. 纵坐标扩大到原来的两倍
D •2. 要得到函数 y=sin3x 的图象，只需将 y=sinx 图象（ ）
A. 横坐标扩大原来的3倍 B.横坐标扩大到原来的3倍
π 6
)
（四）总结归纳：
y=sinx
y=Asin(x+)
方法1:按先平移后变周期的顺序变换
y=sinx
向左>0 (向右<0) 平移||个单位
y=sin(x+)
横坐标缩短>1 (伸长0<<1)到原来的1/倍 y=sin(x+) 纵坐标不变
第13讲 必修4第一章三角函数的图像与性质(教师版)
11．α是第一象限角，tan α＝34，则sin α＝()A.45 B.35C．－45D．－35解析：选B tan α＝sin αcos α＝34，sin2α＋cos2α＝1，且α是第一象限角，所以sin α＝35.2．(2013·安徽名校模拟)已知tan x＝2，则sin2x＋1＝()A．0 B.95 C.43 D.53解析：选B sin2x＋1＝2sin2x＋cos2xsin2x＋cos2x＝2tan2x＋1tan2x＋1＝95.3．(2013·西安模拟)已知2tan α·sin α＝3，－π2＜α＜0，则sin α＝()A.32B．－32 C.12D．－12解析：选B由2tan α·sin α＝3得，2sin2αcos α＝3，即2cos2α＋3cos α－2＝0，又－π2＜α＜0，解得cos α＝12(cos α＝－2舍去)，故sin α＝－3 2.4．若cos α＋2sin α＝－5，则tan α＝()A.12B．2 C．－12D．－2解析：选B∵cos α＋2sin α＝－5，结合sin2α＋cos2α＝1得(5sin α＋2)2＝0，∵sin α＝－255，cos α＝－55，∵tan α＝2.5．化简sin ⎝ ⎛⎭⎪⎫π2＋α·cos ⎝ ⎛⎭⎪⎫π2－αcos π＋α＋sin π－α·cos ⎝ ⎛⎭⎪⎫π2＋αsin π＋α＝________.解析：原式＝cos α·sin α－cos α＋sin α－sin α－sin α＝－sin α＋sin α＝0.答案：01．(教材改编)函数y ＝12sin x ，x ∵[－π，π]的单调性是( )A ．在[－π，0]上是增函数，在[0，π]上是减函数B ．在⎣⎡⎦⎤－π2，π2上是增函数，在⎣⎡⎦⎤－π，－π2和⎣⎡⎦⎤π2，π上都是减函数 C ．在[0，π]上是增函数，在[－π，0]上是减函数D ．在⎣⎡⎦⎤π2，π和⎣⎡⎦⎤－π，－π2上是增函数，在⎣⎡⎦⎤－π2，π2上是减函数 答案 B2．函数y ＝tan 2x 的定义域是( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π＋π4，k ∵Z B.⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2＋π8，k ∵Z C.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π＋π8，k ∵Z D.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π2＋π4，k ∵Z 答案 D解析 由2x ≠k π＋π2，k ∵Z ，得x ≠k π2＋π4，k ∵Z ，∵y ＝tan 2x 的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2＋π4，k ∵Z . 3．若函数f (x )＝sin ωx (ω＞0)在区间[0，π3]上单调递增，在区间[π3，π2]上单调递减，则ω等于( )A.23B.32 C ．2 D ．3 答案 B解析 ∵f (x )＝sin ωx (ω＞0)过原点，∵当0≤ωx ≤π2，即0≤x ≤π2ω时，y ＝sin ωx 是增函数； 当π2≤ωx ≤3π2，即π2ω≤x ≤3π2ω时， y ＝sin ωx 是减函数．由f (x )＝sin ωx (ω＞0)在⎣⎡⎦⎤0，π3上单调递增，在⎣⎡⎦⎤π3，π2上单调递减知，π2ω＝π3，∵ω＝32. 4．(2015·安徽)已知函数f (x )＝A sin(ωx ＋φ)(A ，ω，φ均为正的常数)的最小正周期为π，当x ＝2π3时，函数f (x )取得最小值，则下列结论正确的是( ) A ．f (2)<f (－2)<f (0) B ．f (0)<f (2)<f (－2)C ．f (－2)<f (0)<f (2)D ．f (2)<f (0)<f (－2) 答案 A解析 由于f (x )的最小正周期为π， ∵ω＝2，即f (x )＝A sin(2x ＋φ)，又当x ＝2π3时，2x ＋φ＝4π3＋φ＝2k π－π2(k ∵Z )，∵φ＝2k π－11π6(k ∵Z )，又φ>0，∵φmin ＝π6，故f (x )＝A sin(2x ＋π6)．于是f (0)＝A sin π6，f (2)＝A sin ⎝⎛⎭⎫4＋π6＝A sin ⎣⎡⎦⎤π－⎝⎛⎭⎫4＋π6＝A sin ⎝⎛⎭⎫5π6－4， f (－2)＝A sin ⎝⎛⎭⎫－4＋π6＝A sin ⎝⎛⎭⎫13π6－4＝A sin ⎣⎡⎦⎤π－⎝⎛⎭⎫13π6－4＝A sin ⎝⎛⎭⎫4－7π6. 又∵－π2<5π6－4<4－7π6<π6<π2，又f (x )在⎝⎛⎭⎫－π2，π2上单调递增， ∵f (2)<f (－2)<f (0)，故选A.5．函数y ＝3－2cos ⎝⎛⎭⎫x ＋π4的最大值为________，此时x ＝________. 答案 5 3π4＋2k π(k ∵Z )解析 函数y ＝3－2cos ⎝⎛⎭⎫x ＋π4的最大值为3＋2＝5， 此时x ＋π4＝π＋2k π(k ∵Z )，即x ＝3π4＋2k π(k ∵Z )．1．用五点法作正弦函数和余弦函数的简图跟踪练习1 (1)函数y ＝lg(sin x )＋cos x －12的定义域为__________________________．(2)函数y ＝sin x －cos x ＋sin x cos x 的值域为______________________________________．答案 (1)⎩⎨⎧⎭⎬⎫x |2k π＜x ≤π3＋2k π，k ∵Z(2)⎣⎡⎦⎤－12－2，1 解析 (1)要使函数有意义必须有⎩⎪⎨⎪⎧sin x ＞0，cos x －12≥0， 即⎩⎪⎨⎪⎧ sin x ＞0，cos x ≥12，解得⎩⎪⎨⎪⎧2k π＜x ＜π＋2k πk ∵Z ，－π3＋2k π≤x ≤π3＋2k πk ∵Z ， ∵2k π＜x ≤π3＋2k π(k ∵Z )，∵函数的定义域为⎩⎨⎧⎭⎬⎫x |2k π＜x ≤π3＋2k π，k ∵Z .(2)设t ＝sin x －cos x ，则t 2＝sin 2x ＋cos 2x －2sin x cos x ，sin x cos x ＝1－t 22，且－2≤t ≤ 2.∵y ＝－t 22＋t ＋12＝－12(t －1)2＋1.当t ＝1时，y max ＝1；当t ＝－2时，y min ＝－12－ 2.∵函数的值域为⎣⎡⎦⎤－12－2，1.题型二 三角函数的单调性例2 (1)函数f (x )＝tan ⎝⎛⎭⎫2x －π3的单调递增区间是( ) A.⎣⎡⎦⎤k π2－π12，k π2＋5π12(k ∵Z ) B.⎝⎛⎭⎫k π2－π12，k π2＋5π12(k ∵Z ) C.⎝⎛⎭⎫k π＋π6，k π＋2π3(k ∵Z ) D.⎣⎡⎦⎤k π－π12，k π＋5π12(k ∵Z ) (2)已知ω＞0，函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π4在⎝⎛⎭⎫π2，π上单调递减，则ω的取值范围是________． 答案 (1)B (2)⎣⎡⎦⎤12，54解析 (1)由k π－π2＜2x －π3＜k π＋π2(k ∵Z )得，踪练习3 (1)已知函数f (x )＝2sin(ωx ＋φ)，对于任意x 都有f ⎝⎛⎭⎫π6＋x ＝f ⎝⎛⎭⎫π6－x ，则f ⎝⎛⎭⎫π6的值为________． (2)已知函数f (x )＝sin x ＋a cos x 的图象关于直线x ＝5π3对称，则实数a 的值为( )A ．－ 3B ．－33 C. 2 D.22答案 (1)2或－2 (2)B解析 (1)∵f ⎝⎛⎭⎫π6＋x ＝f ⎝⎛⎭⎫π6－x ，∵x ＝π6是函数f (x )＝2sin(ωx ＋φ)的一条对称轴．∵f ⎝⎛⎭⎫π6＝±2.(2)由x ＝5π3是f (x )图象的对称轴，可得f (0)＝f ⎝⎛⎭⎫10π3， 解得a ＝－33.1、 (2014陕西,2,5分,∵∵∵)函数f(x)=cos 的最小正周期是( )A. B.π C.2π D.4π 思路点拨 根据公式T=计算.[答案] B [解析] T===π.故选B.2、(2013江苏,1,5分,∵∵∵)函数y=3sin的最小正周期为________.[答案]π[解析]由题意知ω=2,所以T==π.3、(2015山东烟台模拟,∵∵∵)求下列函数的最小正周期:(1)y=sin;(2)y=|sin x|.思路点拨(1)利用公式求最小正周期;(2)可利用图象法求最小正周期.[答案]答案见解析[解析](1)y=sin,其中ω=2,∵T==π.(2)函数y=|sin x|的图象如下图所示,可知其最小正周期为π.4、(2015四川,5,5分,∵∵∵)下列函数中,最小正周期为π的奇函数是()A.y=sinB.y=cosC.y=sin 2x+cos 2xD.y=sin x+cos x思路点拨利用函数的奇偶性逐项验证.[答案]B[解析]A中,y=cos 2x,最小正周期为π,为偶函数,不符合题意;B中,y=-sin 2x,最小正周期为π,且为奇函数,符合.C,D为非奇非偶的函数.5、(2014陕西西安模拟,∵∵∵)下列函数中是奇函数的是()A.y=-|sin x|B.y=sin(-|x|)C.y=sin |x|D.y=x·sin |x|思路点拨利用f(-x)=-f(x)进行判断.[答案]D[解析]四个函数的定义域都是R,设f(x)=x·sin|x|,则f(-x)=(-x)·sin|-x|=-x·sin|x|=-f(x),∵y=x·sin|x|是奇函数,故选D.6、(2014广东,5,5分,∵∵∵)下列函数为奇函数的是()A.y=2x-B.y=x3sin xC.y=2cos x+1D.y=x2+2x思路点拨根据奇函数的定义判断.[答案]A[解析]由函数奇偶性的定义知,B、C中的函数为偶函数,D中的函数为非奇非偶函数,只有A中的函数为奇函数,故选A.7、(2012天津,6,5分,∵∵∵)下列函数中,既是偶函数,又在区间(1,2)内是增函数的为()A.y=cos 2x,x∵RB.y=log2|x|,x∵R且x≠0C.y=,x∵RD.y=x3+1,x∵R思路点拨根据选项中各个函数的性质判断,有一定的综合性.[答案]B[解析]函数y=cos 2x在区间上单调递减,在区间上单调递增,不合题意,排除A;函数y=是奇函数,排除C;y=x3+1是非奇非偶函数,排除D;y=log2|x|=是偶函数,且在(0,+∞)上是增函数,故选B.8、(2012大纲全国,3,5分,∵∵∵)若函数f(x)=sin (φ∵[0,2π])是偶函数,则φ=()A. B. C. D.思路点拨根据特例来求解.[答案]C[解析]∵f(x)是偶函数,∵=+kπ(k∵Z).∵φ=π+3kπ(k∵Z),又φ∵[0,2π],∵φ=π.9、(2014安徽,14,5分,∵∵∵)若函数f(x)(x∵R)是周期为4的奇函数,且在[0,2]上的解析式为f(x)=则f+f=________.思路点拨根据函数的周期性将待求函数值的自变量值转化到分段函数中的定义域范围内,结合奇函数性质求解.[答案][解析]∵f(x)是以4为周期的奇函数,∵f=f=f,f=f=f.∵当0≤x≤1时, f(x)=x(1-x),∵f=×=.∵当1<x≤2时, f(x)=sin(πx),∵f=sin=-.又∵f(x)是奇函数,∵f=-f=-,f=-f=.∵f+f=-+=.10、(2012课标全国,9,5分,∵∵∵)已知ω>0,函数f(x)=sin在单调递减,则ω的取值范围是()A. B. C. D.(0,2]思路点拨利用正弦函数的单调性及单调区间求解.[答案]A[解析]由<x<π得+<ωx+<ωπ+,又y=sin α在(k∵Z)上递减,∵解得由ω>0知+2k>0,∵k>-.若要不等式组有解,则+4k≤+2k,解得k≤,又k∵Z,∵k=0,∵≤ω≤,故选A.11、(2011安徽,9,5分,∵∵∵)已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤对x∵R恒成立,且f>f(π),则f(x)的单调递增区间是()A. (k∵Z)B. (k∵Z)C. (k∵Z)D. (k∵Z)思路点拨恒成立问题可转化为最值问题,然后根据单调区间等知识求解.[答案]C[解析]∵f(x)≤恒成立,∵=1.∵+φ=+kπ,k∵Z.∵φ=+kπ,k∵Z.又∵f>f(π),即sin(π+φ)>sin(2π+φ),∵-sin φ>sin φ,∵2sin φ<0,∵sin φ<0.∵当k=1时,φ=+π=,满足sin φ<0,∵f(x)=sin=-sin.∵要求f(x)的单调递增区间,只需2kπ+≤2x+≤2kπ+,k∵Z,即kπ+≤x≤kπ+,k∵Z.∵f(x)的单调递增区间是(k∵Z).12、(2015上海长宁区一模,∵∵∵)设ω>0,若函数f(x)=2sin ωx在上单调递增,则ω的取值范围是________.思路点拨∵ω>0,先求出f(x)=2sin ωx的单调递增区间,而是其中的一个子集,由集合关系,求出ω的取值范围.[答案][解析]三角函数f(x)=2sin ωx的图象如图.由图知f(x)在上是单调增函数,结合题意得解得0<ω≤.13、(2014福建,7,5分,∵∵∵)已知函数f(x)=则下列结论正确的是()A.f(x)是偶函数B.f(x)是增函数C.f(x)是周期函数D.f(x)的值域为[-1,+∞)思路点拨分段函数问题可以考察各段函数的性质,或结合图象判断.[答案]D[解析]作出f(x)的图象如图所示,可排除A,B,C,故D正确.14、(2014课标∵,6,5分,∵∵∵)如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,垂足为M,将点M到直线OP的距离表示成x的函数f(x),则y=f(x)在[0,π]上的图象大致为()思路点拨列出函数y=f(x)的表达式后判断函数的图象,或取x的几个特殊值来验证.[答案]C[解析]由题图可知:当x=时,OP∵OA,此时f(x)=0,排除A、D;当x∵时,OM=cos x,设点M到直线OP 的距离为d,则=sin x,即d=OMsin x=sin xcos x,∵f(x)=sin xcos x=sin 2x≤,排除B,故选C.15、(2013江西改编,∵∵∵)设f(x)=2sin,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是________.思路点拨对已知条件“对任意实数x都有|f(x)|≤a”的理解是解答关键,把此条件转化为函数f(x)的最大值问题.[答案] [2,+∞) [解析] ∵≤1,∵≤2,即对任意实数x,有|f(x)|≤2,要使|f(x)|≤a 恒成立,只要a 不小于|f(x)|的最大值即可,∵a≥2.[方法与技巧]1．讨论三角函数性质，应先把函数式化成y ＝A sin(ωx ＋φ)(ω>0)的形式．2．函数y ＝A sin(ωx ＋φ)和y ＝A cos(ωx ＋φ)的最小正周期为2π|ω|，y ＝tan(ωx ＋φ)的最小正周期为π|ω|.3．对于函数的性质(定义域、值域、单调性、对称性、最值等)可以通过换元的方法令t ＝ωx ＋φ，将其转化为研究y ＝sin t 的性质．4．对于已知函数的单调区间的某一部分确定参数ω的范围的问题：首先，明确已知的单调区间应为函数的单调区间的子集；其次，要确定已知函数的单调区间，从而利用它们之间的关系可求解． [失误与防范]1．闭区间上最值或值域问题，首先要在定义域基础上分析单调性，含参数的最值问题，要讨论参数对最值的影响．2．要注意求函数y ＝A sin(ωx ＋φ)的单调区间时ω的符号，若ω<0，那么一定先借助诱导公式将ω化为正数．3．三角函数的最值可能不在自变量区间的端点处取得，直接将两个端点处的函数值作为最值是错误的．A 组 专项基础训练 (时间：35分钟)1．对于函数f (x )＝sin ⎝⎛⎭⎫πx ＋π2，下列说法正确的是( ) A ．f (x )的周期为π，且在[0,1]上单调递增B ．f (x )的周期为2，且在[0,1]上单调递减C ．f (x )的周期为π，且在[－1,0]上单调递增D ．f (x )的周期为2，且在[－1,0]上单调递减 答案 B解析 因为f (x )＝sin ⎝⎛⎭⎫πx ＋π2＝cos πx ，则周期T ＝2，在[0,1]上单调递减，故选B. 2．函数y ＝2sin ⎝⎛⎭⎫πx 6－π3(0≤x ≤9)的最大值与最小值之和为( ) A ．2－ 3B ．0C ．－1D ．－1－3 答案 A解析 利用三角函数的性质先求出函数的最值．∵0≤x ≤9，∵－π3≤π6x －π3≤7π6，∵sin ⎝⎛⎭⎫π6x －π3∵⎣⎡⎦⎤－32，1.由2k π－π2≤2x ＋π4≤2k π＋π2，k ∵Z ，解得k π－3π8≤x ≤k π＋π8，k ∵Z .当k ＝0时，－3π8≤x ≤π8，故选C.12．已知函数f (x )＝2sin ωx (ω＞0)在区间⎣⎡⎦⎤－π3，π4上的最小值是－2，则ω的最小值等于( ) A.23 B.32 C ．2 D ．3答案 B解析 ∵ω＞0，－π3≤x ≤π4，∵－ωπ3≤ωx ≤ωπ4.由已知条件知－ωπ3≤－π2，∵ω≥32.13．(2014·北京)设函数f (x )＝A sin(ωx ＋φ)(A ，ω，φ是常数，A >0，ω>0)．若f (x )在区间⎣⎡⎦⎤π6，π2上具有单调性，且f ⎝⎛⎭⎫π2＝f ⎝⎛⎭⎫2π3＝－f ⎝⎛⎭⎫π6，则f (x )的最小正周期为________． 答案 π解析 ∵f (x )在⎣⎡⎦⎤π6，π2上具有单调性， ∵T 2≥π2－π6， ∵T ≥2π3.∵f ⎝⎛⎭⎫π2＝f ⎝⎛⎭⎫2π3，∵f (x )的一条对称轴为x ＝π2＋2π32＝7π12.又∵f ⎝⎛⎭⎫π2＝－f ⎝⎛⎭⎫π6， ∵f (x )的一个对称中心的横坐标为π2＋π62＝π3.∵14T ＝7π12－π3＝π4，∵T ＝π. 14.已知函数f (x )＝A tan(ωx ＋φ)(ω>0，|φ|<π2)，y ＝f (x )的部分图象如图，则f (π24)＝________. 答案 3解析 由题中图象可知，此正切函数的半周期等于3π8－π8＝π4，即最小正周期为π2，所以ω＝2.∵g (x )的单调减区间为⎝⎛⎭⎫k π＋π6，k π＋π3，k ∵Z .。
人版高数必修四第5讲_三角函数图像变换[教师版]
![人版高数必修四第5讲_三角函数图像变换[教师版]](https://img.taocdn.com/s3/m/f1e02619b4daa58da0114afc.png)
三角函数y A x =+sin()ωϕ的图像变换__________________________________________________________________________________ __________________________________________________________________________________1结合具体实例，理解y=Asin ）（ϕω+x 的实际意义，会用“五点法”画出函数y=Asin ）（ϕω+x 的简图。
会用计算机画图，观察并研究参数ϕω,,A ，进一步明确ϕω,,A 对函数图象的影响。
2能由正弦曲线通过平移、伸缩变换得到y=Asin ）（ϕω+x 的图象。
3教学过程中体现由简单到复杂、特殊到一般的化归的数学思想。
1、函数图象的左右平移变换如在同一坐标系下，作出函数)3sin(π+=x y 和)4sin(π-=x y 的简图，并指出它们与y x =sin 图象之间的关系。
解析：函数)3sin(π+=x y 的周期为2π，我们来作这个函数在长度为一个周期的闭区间上的简图。
设Z x =+3π，那么Z x sin )3sin(=+π，3π-=Z x当Z 取0、ππππ2232，，，时，x 取-πππππ36237653、、、、。
所对应的五点是函数)3sin(π+=x y ，⎥⎦⎤⎢⎣⎡-∈35,3ππx 图象上起关键作用的点。
列表：x-π3π623π76π53π x +π3π2π32π2πsin()x +π31－1类似地，对于函数)4sin(π-=x y ，可列出下表：xπ434π54π74π94π x -π4π2π32π2πsin()x -π41－1描点作图（如下）利用这类函数的周期性，可把所得到的简图向左、右扩展，得出)3sin(π+=x y ，x R ∈及)4sin(π-=x y ，x R ∈的简图（图略）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
8
O
8
3 8
5 8
x
-2
变式题 : 画出函数y 2 sin 2( x )在长度为一个周期的 4 闭区间上的简图 .
当堂练习：
1.选择题 :已知函数y 3sin( x )的图象为C. 5
(1)为了得到函数 y 3 sin( x )的图象, 只要 5 把C上所有的点 C ( A)向右平行移动 ( B )向左平行移动
y
3
2
1
y=sin(x- )① 6
y=sinx
1 y 2 sin( x ) ③ 3 6
1 y sin( x ) ② 3 6
2
7 2
o
-１
6
2
13 2
x
-2
-3
1 令X x , 则x 3( X ). 3 6 6 3 当X取0, , , ,2时, 可求得相对应的x和y 2 2 . 然 . 后 将 简 图 的值, 得到"五点", 再描点作图 .
X x y
0
2
1 (画法二)利用 "五点法"画函数y 2 sin( x )在 3 6 2 一个周期(T 6 )内的图象 . 1 3
再 , "描 点
2
7 2
3 2
2
13 2
2
5
0
2
0
2
0
(1)列表 :
X x y
0
2
2
7 2
3 2
y
2
13 2
1.选择题 :已知函数y 3sin( x )的图象为C. 5 (3)为了得到函数 y 4 sin( x )的图象, 只要 5 把C上所有的点 C 4 ( A)横坐标伸长到原来的 倍, 纵坐标不变 3 3 ( B )横坐标缩短到原来的 倍, 纵坐标不变 4 4 (C )纵坐标伸长到原来的 倍, 横坐标不变 3 3 ( D)纵坐标缩短到原来的 倍, 横坐标不变 4
（3）横坐标不变
纵坐标伸长到原来的3倍
方法2：(按 , , A顺序变换 )
y
3
2
y=3sin(2x+ ) 3
1
y=sinx
3
5 6
6
o
-１
3
5 3
2
x
-2
y=sin2x y=sin(2x+ ) 3
-3
例2
1 画出函数y 2 sin( x )的简图. 3 6
o
3
6 -１
6 3
7 2 5 12 3 6
7 6
5 3
2
x
-2
-3
y=sin(x+ ) 3 y=sin(2x+ ) 3
1
y o
2
步骤1
-1
3 2
2
x
(沿x轴平行移动)
y
步骤2
1
o
-1
3 2
2
2
x (横坐标伸长或缩短)
1
y o
2
步骤3
-1
作是把y=sinx的图象上所有的点向左（当 ＞ 0时 ）或向右（当 ＜0时 ）平行移动 个单位而得到的。
平移变换
练习：函数y = 3cos(x+ 4 )图象向左平移 3个单位所得图象的函数表达式为 _____ 7 答案：y 3cos( x ) 12 5
思考：函数y = sin2x图象向右平移 12 个 单位所得图象的函数表达式为______ 5
1 (纵坐标 倍
>1时)或伸长(当0<<1时) 到原来的
不变) 而得到的。
周期变换
3.探索A( A 0)对y A sin( x )的图象的影响
1
y
o
-1
2
3 2
2
x
三、函数y=Asin(x+ )
函数y=Asin(x+
(A>0)图象
) （A＞0且A≠1）的图象可 以看作是把y=sin(x+ )的图象上所有点的纵坐标
引入思考：
• 活动： 学生阅读教科书开头一段，并思考、 回答问题。 • 问题： 你认为可怎样讨论参数φ、ω、A对y＝ Asin(ωx+φ)的图象的影响？
1.探索y=sin(x+ )与y=sinx的图象关系
1
o
-1
2
3 2
2
x
一、函数y=sin(x+ ) 图象
函数y=sin(x+ )（ ≠0）的图象可以看
答案：y sin(2 x 6 )
2.探索( 0)对y sin(x )的图象的影响
1
o
-1
2
3 2
2
x
二、函数y=sin(x+ )
是把 y=sin(x+
函数y=sin(x+ ) ( >0且≠1)的图象可以看作
(>0)图象
) 的图象上所有点的横坐标缩短(当
伸长（当A＞1时 ）或缩短（当0＜A＜1时 ）到原
来的A倍（横坐标不变）而得到的。 y=Asin(x+ ) ， x∈R的值域是［-A，A］，最大 值是A，最小值是-A。
振幅变换
y sinx 变换得 y 3 sin( 2 x )的图象？ 3 方法1：
例1、如何由
（1）向左平移 3 函数 y=sinx
函数y A sin(x )的图象
高一数学组
学习目标：
• ①理解三个参数A、ω、φ对函数 y=Asin(ωx+φ)，（A>0、ω>0）图象的影 响； • ②揭示函数y=Asin(ωx+φ),（A>0、ω>0） 的图象与正弦曲线的变换关系。 • ③结合具体实例，了解y=Asin(ωx+φ)的 实际意义
5
个单位长度. 个单位长度.
5 2 (C )向右平行移动 个单位长度. 5 2 ( D )向左平行移动 个单位长度. 5
1.选择题 :已知函数y 3sin( x )的图象为C. 5
(2)为了得到函数 y 3 sin(2 x )的图象, 只要 5 把C上所有的点 B ( A)横坐标伸长到原来的 2倍, 纵坐标不变 1 ( B)横坐标缩短到原来的 倍, 纵坐标不变 2 (C )纵坐标伸长到原来的 2倍, 横坐标不变 1 ( D)纵坐标缩短到原来的 倍, 横坐标不变 2
3 2
2
x
(纵坐标伸长或缩短)
1
y o
思 考: 有 否 别 的 变 换
2
步骤4
-1
3 2
2
x
方法2(选讲)：
（1）横坐标缩短到原来的 函数 y=Sinx 纵坐标不变
1 2
倍
y=Sin2x的图象
（2）向左平移 6
y=Sin(2x+ ) 的图象 3 y=3Sin(2x+ )的图象 3
2.把y sin( 2 x )的图象向右平移 个单位, 3 6 这时图象所表示的函数 为 D A. y sin( 2 x ) 2 B. y sin( 2 x ) 6 3 C. y sin( 2 x ) 2 D. y sin 2 x
x x 3.要得到函数 y sin( )的图象, 可由y sin 2 6 2 的图象 C A. 向右平移 B. 向左平移 C. 向右平移 D. 向左平移
解 : (画法一 )先把正弦曲线上所有点 向右平移 个 6 单位长度, 得到y sin( x )的图象; 再把后者所有 6 点的横坐标伸长到原来 的3倍(纵坐标不变 ), 得到 1 y sin( x )的图象; 再把所得图象上所有的 纵坐标 3 6 1 伸长到原来的 2倍(横坐标不变 )而得到函数 y 2 sin( x ) 3 6 的图象.
1 2
y=sin(x+ ) 的图象 3 y=sin(2x+ ) 的图象 3
（2）横坐标缩短到原来的 纵坐标不变 （3）横坐标不变
倍
纵坐标伸长到原来的3倍
y=3sin(2x+ )的图象 3
) 方法1：(按 , , A顺序变换
y
3
2 1
y=3sin(2x+ 3 )
y=sinx
重点与难点：
• 重点：将考察参数A、ω、φ对函数图象 y=Asin(ωx+φ) ,（A>0、ω>0）的影响的 问题进行分解，从而学习如何将一个复 杂问题分解为若干个简单问题的方法。 • 难点：ω对函数y=Asin(ωx+φ) ,（A>0、 ω>0）图象的影响规律的概括。 • 关键：理解三个参数A、ω、φ对函数 y=Asin(ωx+φ)图象的影响。
2
5
0
2
0
2
0
2
O
2
2
(2)描点 :
-2
7 2
5
13 2
x
7 13 ( ,0), (2 ,2), ( ,0), (5 ,2), ( ,0) 2 2 2
(3)连线 :
用两种方法画出函数y 2 sin(2 x )在长度 4 为一个周期的闭区间上 的简图.
y
2
3 8