气液相平衡
气液平衡的相平衡条件

气液平衡的相平衡条件
气液平衡的相平衡条件是指在闭合系统中,气体与液体达到相平衡的必要条件。
相平衡意味着系统中气体和液体之间的物质交换达到了平衡状态,即两者之间的反应速率相等。
首先,气液相平衡条件之一是液体中溶解的气体分子的逸出速率等于气体中溶
解的气体分子的溶解速率。
这意味着当气体分子从液体中逸出的速率等于气体分子溶解进液体中的速率时,系统达到气液相平衡。
这个平衡条件可以通过亨利定律来描述,该定律指出气体与液体之间的溶解度与气体的分压成正比。
其次,气液相平衡条件还要求气体和液体之间存在均匀的分配。
这意味着在相
平衡状态下,气体和液体之间的分子自由移动并且均匀分布,没有净流动的趋势。
这种均匀分配的态势是通过扩散和浓度均化过程实现的。
最后,气液相平衡还要求液体和气体之间的压力相等。
当气体溶解进液体中时,气体分子对液体施加一定的压力,这被称为溶解气体的蒸气压。
在相平衡状态下,液体的蒸气压与气体的分压相等,从而实现了压力的平衡。
总结来说,气液平衡的相平衡条件包括气体和液体之间溶解速率的平衡、分子
的均匀分配以及压力的平衡。
这些条件是系统达到气液相平衡的前提,同时也是液体和气体之间物质交换达到稳定状态的保证。
气液相平衡关系

二、气液相平衡关系 平衡状态:在一定压力和温度下,当吸收和解吸速率相等时,气液两相达到平衡。
相平衡关系:吸收过程中气液两相达到平衡时,吸收质在气相和液相中的浓度关系1.气体在液体中的溶解度 (图8-1)平衡时溶质在气相中的分压称为平衡分压,用符号*A p 表示;溶质在液相中的浓度称为平衡溶解度,简称溶解度;它们之间的关系称为相平衡关系。
结论:①在相同的吸收剂、温度和分压下,不同溶质的溶解度不同;②分压一定时,温度越低,则溶解度越大。
较低的温度有利于吸收操作;③温度T 一定时,分压P 越大,溶解度越大。
较高的分压有利于吸收操作;④加压和降温对吸收操作有利。
2.亨利定律(1)亨利定律亨利定律内容:在总压不太高,温度一定的条件下,稀溶液上方溶剂的平衡分压*A p 与溶质在液相中的摩尔分数A x 成正比,比例系数为亨利系数E 。
即: A A Ex p =* 形式一E ——亨利系数, Pa讨论:①E 的来源:实验测得,查手册②E 的影响因素:溶质、溶剂、T 。
物系一定时, ③亨利系数表示气体溶解的难易程度。
E 大的,溶解度小,难溶气体;E 小的,溶解度大,易溶气体。
(2)亨利定律的其它形式① 溶质在液相中的浓度用量浓度A c 表示,气相用分压*A p 表示,则: Hc p A A =* 形式二 ↑↑⇒E TH ——溶解度系数,实验测定。
溶解度↓溶解度系数表示气体溶解的难易程度。
易溶气体,H ↑;难溶气体,H ↓。
溶解度系数H 和亨利系数E 的关系:剂剂EM H ρ=②溶质在气液相中的浓度均用摩尔浓度表示, 则:A A A mx x PE P p y ===** 形式三 m ——相平衡常数。
P E m = 是温度和压强的函数。
讨论:1)P 一定时, 溶解度↓。
升温不利于吸收;2)t 一定时, 溶解度↑。
加压有利于吸收。
③溶质在气液相中的浓度均用比摩尔分数表示时,AA A A X X m Y Y +=+**11 整理得: A A A X m mX Y )1(1-+=* 形式四 比摩尔分数表示的气液相平衡关系。
化工原理8.2 相平衡关系8.2 吸收过程的相平衡关系

溶解度/[g(SO2)/1000g(H2O)]
250
200 150
0 oC 10 oC
100 50
20 oC 30 oC 40 oC
50 oC
0
20 40 60 80 100 120
pSO2/kPa
SO2在水中的溶解度
(1)总压、y一定,温度下降,在同一溶剂中,溶 质的溶解度x随之增加,有利于吸收。
101.3kPa
y
202.6kPa
x
20℃下SO2在水中的溶解度
(2)温度、y一定,总压增加,在同一溶剂中,溶 质的溶解度x随之增加,有利于吸收。
4
溶解度/[g(SO2)/1000g(H2O)]
溶解度/[g(O2)/1000g(H2O)]
0.10 0.08 0.06 0.04 0.02
0 oC
10 oC 20 oC 30 oC 40 oC 50 oC
p*=E·x
亨利系数,kPa
E值大,溶解度小,难溶气体 E值小,溶解度大,易溶气体 E影响因素:溶质、溶剂、T
T,E
p*=c/H
H 越大,溶解度越大 H :T,H
溶解度系数,kmol/(m3·kPa)
y*=m·x
m越大,溶解度越小; m:T,m;p,m
相平衡常数,无因次
Y*=mX
X:液相摩尔比 Y:气相摩尔比
在低浓度气体吸收计算中,通常采用基准不变的摩尔 比 Y( 或 X )表示组成
Y
气相中溶质A的摩尔数 气相中惰气B的摩尔数
y 1 y
X
液相中溶质A的摩尔数 液相中溶剂S的摩尔数
x 1 x
以摩尔比表示组成 的相平衡关系
3、气液相平衡

第三节
气液相平衡
一、气液相平衡关系
二、亨利定律
三、相平衡关系在吸收过程中的应用
返回
滁州职业技术学院化工原理电子课件
一、 气液相平衡关系
平衡状态:一定压力和温度,一定量的吸收剂与 混合气体充分接触,气相中的溶质向
溶剂中转移,长期充分接 触后,液相
中溶质组分的浓度不再增加,此时, 气液两相达到平衡。 饱和浓度:平衡时溶质在液相中的浓度。 平衡分压:平衡时气相中溶质的分压。 返回
pA 5.94 E 287.0kPa x 0.0207
E 287.0 m 2.83 p 101.3
c 55.6 H 0.194 Kmol/(m3.kPa) E 287 .0
返回
滁州职业技术学院化工原理电子课件
【例6-9】上述例题中,若加入惰性气体使总 压增至202.6kPa,系统温度仍为20℃,求
解:取100g水为基准,含氨为2g,
w A /M A 2 / 17 x 0.0207 w A /M A w B /M B w N /M N 2 / 17 100/ 18
* 由pA Ex, 可得
pA 1.60 E 77.3kPa x 0.0207
返回
滁州职业技术学院化工原理电子课件
E小的,溶解度大,易溶气体 3)E的来源:实验测得;查手册
返回
滁州职业技术学院化工原理电子课件
2、亨利定律其它形式
cA 1)p H
* A
H——溶解度系数, kmol/(m3· kPa)
cA——摩尔浓度,kmol/m3;
H与E的关系:
cA c c p x H c H
化工原理第五章气液相平衡

亨利简介
威廉·亨利于1774年12月12日出生在英国的曼彻斯特市。 他们祖孙三代都是医师兼有名的化学家。发明亨利定律的亨利的名字 是威廉·亨利(William Henry),他的父亲名托马斯·亨利( Thomas Henry ),他的儿子名威廉·查尔斯·亨利(William Charles Henry)。他们三代 是十八世纪到十九世纪的著名学者。 威廉·亨利在1795年进爱丁堡大学,一年之后。因为他父亲医务工作 上需要助手,他离开了大学,在家里做实医师。到1805年他又回到爱丁 堡大学,继续学业。1807年化完成了医学博士学位。 亨利定律是在1803年由威廉·亨利在英国皇家学会上宣读的一篇论文 里,加以详细说明的。从此以后,这个定律就被命名为亨利定律了。 1888年,在亨利发表他的定律八十多年后,法国化学家拉乌尔( Francois-Marie Raoult,1830-1901)发表了他在溶液蒸气压方面的发 现,这就是我们现在所称的拉乌尔定律。 亨利晚年因为严重的头痛和失眠,几乎无法工作,于1836年9月2日离 开人世,终年62岁。
2021/7/31
2、相平衡的理论依据 对单组分物理吸收的物系,根据相律:
F=K-Φ+2=3-2+2=3
(K=3,溶质A,惰性组分B,溶剂S,Φ=2,气、
液两相)
【结论】在温度T、总压P和气、液相组成共4个变量
中,有3个自变量(独立变量),另1个是它们的函
数。即:
yfT 、 P 、 x
2021/7/31
mE485023.94 p 20.26
从气相分析 y*=mx=23.94×0.01=0.24<y=0.3
故SO2必然从气相转移到液相,进行吸收过程。 【结论】增大压力(30℃,101.3kPa→202.6kPa)有 利于吸收。
气液相平衡方程

气液相平衡方程
气液相平衡方程是描述气体和液体之间物质传递的数学关系。
它是化学工程、环境科学、生物工程等领域中重要的理论工具。
气液相平衡方程的基本形式是亨利定律,即气体在液体中的溶解度与气体的分压成正比。
这个方程可以用以下数学表达式表示:
C = kH * P
其中,C是气体在液体中的溶解度,kH是亨利常数,P是气体的分压。
亨利常数是气体溶解度与分压的比例常数,它依赖于具体的气体和溶剂系统。
除了亨利定律,还有其他描述气液相平衡的方程,比如罗特定律和拉乌尔定律。
罗特定律是描述溶剂中溶质的逸度与溶液中溶质的摩尔分数之间的关系。
拉乌尔定律是描述理想混合溶液的蒸气压与组成之间的关系。
在工程实践中,气液相平衡方程经常用于设计和优化化工装置。
例如,在气体吸附过程中,通过气液相平衡方程可以计算出吸附剂中溶质的负荷量。
在化学反应工程中,气液相平衡方程可以帮助确定反应器中气体和液体的相互作用,从而优化反应条件。
此外,气液相平衡方程还可以应用于环境科学研究中。
例如,在水体中溶解氧的研究中,可以利用亨利定律来计算氧气在水中的溶解度,从而评估水体的氧化能力。
在大气污染研究中,可以利用拉乌尔定律来估算不同气体在大气中的浓度。
总之,气液相平衡方程是描述气体和液体之间物质传递的重要工具。
通过这些方程,可以深入理解气体和液体的相互作用,为工程设计和科学研究提供有力的支持。
8.2气液相平衡
8.2气液相平衡吸收(传质)与传热两个过程的相似处:传热与吸收过程均由三步构成(解释三步相似),但两个过程也有不同处:传热的推动力是两流体的温度差,过程的极限是两流体的温度相等;吸收的推动力不是两相的浓度差,过程的极限也不是两相的浓度相等。
这是由于气液之间的相平衡不同于冷热流体之间的热平衡,气液相平衡关系是吸收过程的重要基础,我们将详细讨论它。
8.2.1平衡溶解度在一定的温度t 与总压p 下,使一定量的溶剂与溶质接触,溶质便由气相向液相转移,随着溶液浓度的逐渐增高,传质速率将逐渐减慢,最后降为零,此时液相中溶质达到饱和,浓度达到一最大限度e x (x 为液相中溶质A 的摩尔分数,下标e 代表平衡),这时称气液两相达到相平衡,e x 称为平衡溶解度,简称为溶解度(溶解度可以用不同的方式表示,相平衡关系亦可用不同的方式表示,如e p ~x 、e p ~e x 、e y ~x 、e y ~e x 等)。
注意:此时并非没有溶质分子继续进入液相,只是任何瞬间进入液相的溶质分子数与从液相逸出的溶质分子数恰好相等,在宏观上过程就象是停止了。
这种状态称为相际动平衡,简称相平衡。
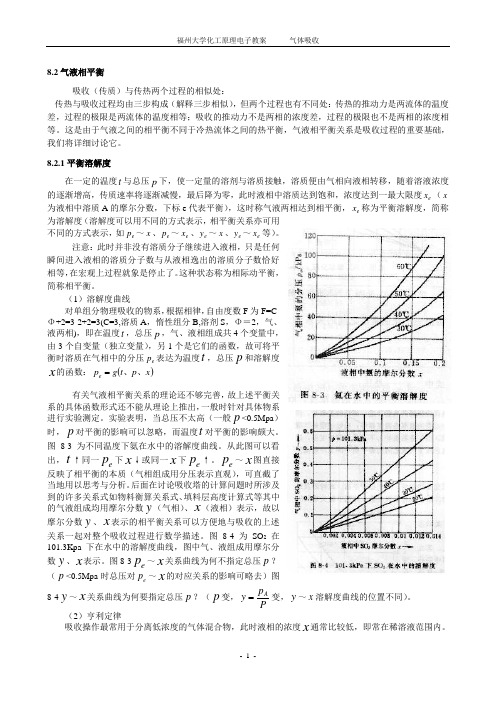
(1)溶解度曲线对单组分物理吸收的物系,根据相律,自由度数F 为F=C-Φ+2=3-2+2=3(C=3,溶质A ,惰性组分B,溶剂S ,Φ=2,气、液两相),即在温度t ,总压p ,气、液相组成共4个变量中,由3个自变量(独立变量),另1个是它们的函数,故可将平衡时溶质在气相中的分压e p 表达为温度t ,总压p 和溶解度x 的函数:()x p t g p e 、、=有关气液相平衡关系的理论还不够完善,故上述平衡关系的具体函数形式还不能从理论上推出,一般时针对具体物系进行实验测定。
实验表明,当总压不太高(一般p <0.5Mpa )时,p 对平衡的影响可以忽略,而温度t 对平衡的影响颇大。
图8-3为不同温度下氨在水中的溶解度曲线。
从此图可以看出,t ↑同一e p 下x ↓或同一x 下e p ↑。
分离工程--02 汽液相平衡-1

由逸度定义可以推出气液相平衡的条件是:
TV TL PV PL
fiV fiL, (i 1, 2,...,C)
(2-6)
其中,fi 为组分i在混合物中的逸度。
逸度系数 ; ;
f i
iP
f iV
iV y P
i
f iL
iL x P
i
活度及活度系数
也与温度有关。甚至与拟合导出的算法有关。
但是,范德华仅仅多引入两个参数,就对计算精度 作出了很大改进,这应该说,范德华方程是成功的。
(2) 范德华常数与临界参数的关系
在临界点Tc时有:
p Vm
Tc
0
,
2 p Vm2
Tc
0
将 Tc 温度时的 p - Vm关系以范德华方程表示:
p
RTc Vm b
a Vm2
对其进行一阶、二阶求导,并令其导数为 0,有:
p Vm
Tc
RTc
Vm b2
2a Vm3
0
2 p Vm2
Tc
2RTc
Vm b3
6a Vm4
0
联立求解,可得:
Vm,c 3b ,
Tc
则:
Ki
pi0 p
Pi0:为系统温度下,纯i组分的饱和 蒸汽压。
相平衡常数Ki仅与体系的温度、压力有关,与溶液组
成无关。 饱和蒸汽压:
ln
Pi 0
Ai
Bi Ci T
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ΔX=X*-X
Δc A
=
c
* A
−
cA
18
2)在x~y图
y
A·
y*
C
x
19
B AC = y − y * AB = x * − x
x*
例5-2-3 在一填料塔内用清水逆流吸收某二元混合 气体中的溶质A。已知进塔气体中溶质的浓度为0.03 (摩尔比,下同),出塔液体浓度为0.0003,总压为 101kPa,温度为 40℃,问: (1)压力不变,温度降为20℃时,塔底推动力
m
=
E p
=
7.6 × 104 200 × 103
= 0.38 ⇒
m
↓, x不变 ⇒
y* ↓
(2)T ↑, x不变,pA* ↑⇒ E = pA * / x = 9.1× 104 Pa ↑
H = 6.1×10−4 kmol /(m 3 .Pa) ↓ m = 0.9 ↑
讨论: (1)亨利定律是压力不太高,一定温度下,稀溶液
吸收过程:y > y* x* >x或 c*A > cA
15
y
y1
·A
y* = mx
y2*
y1* y2
·B
x2* x1 x2 x1* x
A点:平衡线上方,吸收 y1 > y1 * 或x1* > x1
B点:平衡线下方,解吸 y2* > y2或x2 > x2 *
16
二、指明过程进行的极限——相平衡
1)逆流,塔高无限
⇒ Y* =m X 1+Y * 1+ X
⇒ Y * = mX 1 + (1 − m)X
⎯稀⎯溶⎯液 X⎯⎯小→ Y * ≈ mX
9
例5-2-1 在常压及20ºC下测得氨在水中的平衡数 据为:浓度为0.5gNH3/100gH2O的稀氨水上方的平 衡分压为400Pa,在该浓度范围下相平衡关系可用 亨利定律表示。试求:E、H、m?
p
1.013 ×105
例5-2-2 (1)氨水的温度与浓度同例5-2-1, 氨水上方总压强
变为200kPa ,试求:E,H,m (2) 总压与氨水浓度同例5-2-1, 若氨水温度升高到
50ºC, 已知此时氨水上方的平衡分压为500Pa, E,H,m 为多少?
12
(1)E和H不变,x不变 ⇒ pA *不变 ⇒ p ↑ y* ↓
2
二、溶解度曲线
20℃
氨在水中的溶解度曲线
3
SO2在水中的溶解度曲线
几种气体在水中的溶解度曲线
4
讨论: (1)在同一溶剂中,pA (或 p,y)一定,T↓ x↑ (2)在同一溶剂中,T、y一定,p↑(pA↑) x ↑
低温高压利于吸收,高温低压利于解吸。 (3)相同pA (或 p,y)
cO2 < cCO2 < cSO2 < cNH3 O2、CO2等为难溶气体,NH3等为易溶气体
H——溶解度系数, kmol/(m3·kPa)
H与E的关系:
p*A
=
cA H
⋅
c c
=cx H
⇒E= c H
c = ρL =
ρL
⎯稀⎯溶⎯液→ c ≈ ρS
ML MS (1 − x) + M A x
MS
⇒ E = ρS HM S
7
H的讨论: • H=f(物系、T ) 物系一定,T ↑⇒ H ↓,同pA*下 ⇒ c A ↓ • H大,溶解度大,易溶气体
2) y* = mx m——相平衡常数,无因次
m与E的关系 : p*A = py*
⇒ py* = Ex
⇒m= E p
8
m的讨论: • m=f(物系、T 、p ) T ↑⇒ E ↑ m ↑,同y *下x ↓ p ↑⇒ E不变m ↓,同y *下x ↑
• m小,溶解度大,易溶气体
3)用X, Y表示
y* = mx
24
作业:p245 2 (上方气相:水汽加CO2) 3 6
25
10
(1)x =
0.5 / 17
= 0.00527
0.5 / 17 + 100 / 18
pA* = Ex ⇒ E = 400 / 0.00527 = 7.6 × 104 Pa
(2)H
=
ρS EM S
⇒
H
=
1000 18 × 7.6 × 104
= 7.3 × 10−4 kmol /(m 3 .Pa)
(3)m = E ⇒ m = 7.6× 104 = 0.75
(2) 压力达到202 kPa,温度为 40°C
m'' = p1 m = 1 × 50 = 25 ⇒ Y ∗ = m'' X = 25× 3×10−4 = 0.0075
p2
2
( ) (( )) Y − Y ∗ 2 = 0.03 − 0.0075 = 0.0225
⇒
Y Y
−Y∗ −Y∗
2 1
=0Leabharlann 0225 0.0155三.亨利定律
平衡分压
p*A = Ex
E ——亨利常数,单位同压强。
E的讨论:1)E=f(物系、T ) 物系一定,T ↑⇒ E ↑,同pA*下 ⇒ x ↓
2)E小,溶解度大,易溶气体 3)E的来源:实验测得;查手册 适用条件:一定T下、 p<5atm,稀溶液。
6
(2)亨利定律其它形式
1)
p*A
=
cA H
V, y2 L,x2
L ↑⇒ y2 ↓
y2,min = y2* = mx2
2)逆流,塔高无限
V,y1
L ↓⇒ x1 ↑
x1,max
=
x1* =
y1 m
L,x1
17
三、确定过程的推动力 1) 表达式 推动力 = 实际组成 −平衡组成
气相: Δy=y - y* 液相: Δx=x* -x
ΔY=Y -Y* ΔpA = pA − p*A
= 1.5倍
21
小结: (1) 低温高压,溶解度增加,有利于吸收;
高温低压,溶解度降低,有利于解吸。 (2)根据气液平衡关系,可判断溶质的传递方向 (即吸收或解吸),并计算过程极限及推动 力,但不能说明过程原理与传质过程的快慢?
22
2节小结
(1)亨利定律:稀溶液,一定T和p (p<5atm) 下
pA* = Ex
pA*
=
cA H
y* = mx
H = c ≈ ρs
• E, H, m之间的换算:
E EM s
m= E p
• p↑⇒ E 和 H不变, m ↓;溶解度↑ ,利于吸收
• t ↓ ⇒ E↓, H↑, m↓; 溶解度↑ ,利于吸收
23
(2)相平衡关系应用 • 吸收或解吸——y与y*,x*与x • 难溶气体或易溶气体——E和m,H
( ) Y − Y ∗ 1 = 0.03 − 0.015 = 0.015
(1)压力不变,温度降为20°C时
Y ∗ = m' X = 20× 3× 10−4 = 0.006
( ) (( )) Y − Y ∗ 2 = 0.03 − 0.006 = 0.024
⇒
Y −Y∗ Y −Y∗
2 1
= 0.024 = 1.6倍 0.015
5.2 气液相平衡关系及应用
5.2.1 气液相平衡关系 5.2.2 相平衡关系在吸收过程中的应用
1
5.2.1 气液相平衡关系
一、相平衡关系 • 气液平衡状态 • 饱和浓度或溶解度 ——用cA或x表示 • 平衡分压 ——用pA或y表示 • 相律 F=C-ϕ+2 = 3-2+2 = 3
当T、p一定(p<5atm)时: pA* =f1( x ) y*= f2( x ) pA * =f3( cA)
时,气相分压与液相浓度之间的关系; (2) E, H只取决于物系和T,而m还与总p有关; (3) T ↑, E ↑ 及m ↑但 H↓,对吸收不利; (4) y一定,总p ↑( pA↑ ),m↓,对吸收有利。
14
5.2.2 相平衡关系在吸收过程中的应用
一、判断过程进行的方向 pA > p*A A由气⇒液传质,吸收 pA = p*A 平衡状态 pA < p*A A由液⇒气传质,解吸
(Y-Y*)变为原来的多少倍?
(2)温度不变,压力达到202 kPa,塔底推动力 (Y-Y*)变为原来的多少倍?
已知:总压为101kPa,温度为 40℃时,物系气液 相平衡关系为Y*=50X。总压为101kPa,温度为 20℃时,物系气液相平衡关系为Y*=20X。
20
总压为101kPa,温度为 40℃时 Y ∗ = mX = 50× 3 ×10−4 = 0.015
