湖南省益阳市箴言中学2014-2015学年高二上学期12月月考试题数学(理)含答案
湖南省益阳市箴言中学高二上学期12月月考试题 数学(

益阳市箴言中学2014—2015学年高二12月月考理科数学试题〖命题范围:选修2—1,2—2〗 时量 120分钟 总分 150分一、选择题(10×5=50分)1. 命题“∃x ∈Z ,使x 2+2x +m <0”的否定是( )A .∃x ∈Z ,使x 2+2x +m ≥0B .不存在x ∈Z ,使x 2+2x +m ≥0C .∀x ∈Z ,使x 2+2x +m >0D .∀x ∈Z ,使x 2+2x +m ≥0 2. 复数ii i i -++1432(i 为虚数单位)的共轭复数....是( ) A .-21-21i B .-21+21i C .21-21i D .21+21i3. 用数学归纳法证明不等式11+n +21+n +···+n 21>2413(n >1,n ∈N*),在证明n =k +1这一步时,需要证明的不等式是( ) A .11+k +21+k +···+k 21>2413B .11+k +31+k +···+k 21+121+k >2413 C .21+k +31+k +···+k 21+121+k >2413D .21+k +31+k +···+k 21+121+k +221+k >2413 4. 若抛物线y 2=2px 的焦点与椭圆2622y x +=1的右焦点重合,则p 的值为( )A .-2B .2C .-4D .45. 过椭圆22ax +22b y =1(a >b >0)的左焦点F 1作x 轴的垂线交椭圆于点P ,F 2为右焦点,若∠F 1PF 2=60°,则椭圆的离心率为( ) A .22 B .33 C .21 D .316. 双曲线223y x -=1的一个焦点到它的渐近线的距离为( ) A .1 B .2 C .3 D .27. 已知定点A (2014,2),F 是抛物线y 2=2x 的焦点,点P 是抛物线上的动点,当|PA|+|PF|最小时,点P 的坐标为( )A .(0,0)B .(1,2)C .(2,2)D .(21,1)8. 观察)(2'x =2x ,)(4'x =4x 3,)('cosx =-sinx ,由此可得,若定义在R 上的函数)(x f 满足)(x f -=)(x f ,记)(x g 为)(x f 的导函数,则)(x g -=( ) A .)(x f B .-)(x f C .)(x g D .-)(x g 9. 如图,棱长为1的正方体ABCD -A 1B 1C 1D 1中,点P 在侧面BCC 1B 1及其边界上运动,并且总保持向量在1BD 上的投影为0,则线段AP 扫过的区域的面积为( ) A .21 B.22C.23 D.4510. “若存在一条与函数y =)(x f 的图象有两个不同交点P(x 1,y 1),Q(x 2,y 2)的直线,使y =)(x f 在x =221x x +处的切线与此直线平行”,则称这样的函数y =)(x f 为“hold 函数”;下列函数:①y =x1;②y =2x (x >0);③y =21x -;④y =lnx ;其中为“hold 函数”的是( )A .①②④B .②③C .③④D .①③④二、填空题(5×5=25分) 11. 若dx k x )2(10+⎰=2,则实数k = .12. 设平面α的法向量1n =(1,2,-2),平面β的法向量2n =(-2,-4,k ),若α∥β,则k = .13. 设条件p :a >0;条件q :a 2+a ≥0,那么p 是q 的 条件(填“充分不必要,必要不充分,充要”). 14. 先阅读下面的文字:“求 +++111的值时,采用了如下的方法:令+++111=x ,则有x +1=x ,从而解得x =251+(负值已舍去)”;运用类比的方法,计算:++++2111211= .15. 将全体正奇数排成一个三角形数阵;接照图中的排列规律,第n 行(n ≥3)从左向右的第3个数为 .C A三、解答题(本大题共有6道小题,75分)16. (本小题满分12分)已知复数z =yi x +-)2((x ,y ∈R ,i 为虚数单位)的模为3,求xy的最大值.17. (本小题满分12分)已知p :函数y =12++mx x 在(-1,+∞)上单调递增;q :函数y =42x +4(m -2)x +1大于零恒成立。
【名师解析】湖南省益阳市箴言中学2014届高三第一次模拟考试数学(理)试题 Word版含解析

第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若i 为虚数单位,则i i -+11等于 ( ) A 、i B 、i - C 、1 D 、-12.已知集合{}97<-=x x M ,{}29x y x N -==,且N M ,都是全集U 的子集,则右图中阴影部分表示的集合是 ( )3.按照如图的程序框图执行,若输出结果为15,则M 处条件为 ( ) A .16k ≥ B .8k < C .16k < D .8k ≥4.给出下列命题:○1向量a ,b 满足b a b a -==,则a ,b 的夹角为030;○2a ∙b 0> 是〈a ,b 〉为锐角的充要条件;○3将函数1-=x y 的图象按向量)0,1(-=a 平移,得到函数x y =的图象;○4若)(AC AB +∙0)(=-AC AB ,则ABC ∆为等腰三角形。
以上命题正确的个数是 ( )A 、1个B 、2个C 、3个D 、4个)(AC AB +∙0)(=-AC AB ,则220AB AC -=,即AB AC =,故○4正确,因此选B. 考点:1.向量的运算;2.图像的平移.5.已知某几何体的正视图和侧视图均是边长为1的正方形,则这个几何体的体积不可能是A 、21B 、4πC 、1D 、3π ( )6.有下列四种说法:①命题:“R x ∈∃0,使得02>-x x ”的否定是“R x ∈∀,都有02≤-x x ”;○2已知随机变量x 服从正态分布),1(2σN ,79.0)4(=≤x P ,则21.0)2(=-≤x P ;○3函数)(,1cos sin 2)(R x x x x f ∈-=图像关于直线43π=x 对称,且在区间⎥⎦⎤⎢⎣⎡-4,4ππ上是增函数;○4设实数[]1,0,∈y x ,则满足:122<+y x 的概率为4π。
湖南省益阳市箴言中学2013-2014学年高二下学期第一次月考试题 数学(理) 含答案

时量:120分钟 满分:150分 命题:高二理科数学备课组第(Ⅰ)卷一、选择题:(本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.因指数函数x a y =是增函数(大前提),而x y )31(=是指数函数(小前提),所以x y )31(=是增函数(结论)”,上面推理的错误是 ( )A .大前提错导致结论错B .小前提错导致结论错C .推理形式错导致结论错D .大前提和小前提都错导致结论错2.对“a 、b 、c 至少有一个是正数”的反设是 ( ) A .a 、b 、c 至少有一个是负数 B. a 、b 、c 至少有一个是非正数C .a 、b 、c 都是非正数 D. a 、b 、c 都是正数3.已知复数Z=2)1(24i i++(i 为虚数单位)在复平面内对应的点在直线x-2y+m=0上,则m= ( )A.-5B.-3C.3D.54.用数学归纳法证明等式(3)(4)123(3)()2n n n n *+++++++=∈N 时,第一步验证1n =时,左边应取的项是 ( )A .1B .12+C .123++D .1234+++5.若1010991010)1()1()1(+++++++=x a x a x a a x ,则=9a( ) A .9B .10C .9-D .10-6.某地区气象台统计,该地区下雨的概率是415,刮风的概率为215,既刮风又下箴言中学2012级高二月考理科数学试题(含答案)雨的概率为110,则在下雨天里,刮风的概率为( )A.8225B.12C.38D.347.)(x f 是定义在(0,+∞)上的非负可导函数,且满足x )(x f '≤)(x f ,对任意的正数a.b 若a<b,则必有 ( ) A.af(a) ≤ bf(b) B. af(a) ≥bf(b)C.af(b) ≤ bf(a)D. af(b) ≥bf(a)8.某人射击一发子弹的命中率为0.8,现在他射击19发子弹,理论和实践都表明,在这19发子弹中命中目标的子弹数X 的概率满足P (X =k )=C k 19·0.8k ·0.219-k (k =0,1,2,…,19),则他射完19发子弹后,击中目标的子弹最可能是( )A .14发B .15发C .16发D .15发或16发二、填空题 (本大题共7小题,每小题5分,满分35分.)9.设O 是原点,向量,OA OB 对应的复数分别为23,32,i i --+那么向量BA 对应的 复数是_______10.在251(2)x x-的二项展开式中,第4项的系数为.11.一物体在力5, 02,()34, 2x F x x x ≤≤⎧=⎨+>⎩(单位:N )的作用下沿与力F 相同的方向,从0x =处运动到4x = (单位:m )处,则力()F x 做的功为 焦. 12. 某外商计划在四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有 (用数字作答)13. 在某次数字测验中,记座位号为n (n =1,2,3,4)的同学的考试成绩为f (n ).若f (n )∈{70,85,88,90,98,100},且满足f (1)<f (2)≤f (3)<f (4),则这4位同学考试成绩的所有可能有________种.14.已知函数f(x)=x 3-3x -1,若直线y=m 与y=f(x)的图像有三个不同的交点,则m 的取值范围是 .15.如下图所示,对大于或等于2的自然数M 的n 次幂进行如下方式的“分裂”: 依次类推,20143“分裂”中最大的数是 .33第(II )卷 (答 卷) 一、选择题答题表:(每小题有且只有一个正确答案,每小题5分,共40分)二、填空题答案:(每小题5分,共35分)9、 10、 11、 12、 13、14 、 15、三、解答题:(6道大题,共75分) 16.(本小题满分12分)已知∆ABC 的三个内角A 、B 、C 成等差数列,a 、b 、c 分别为∆ABC 所对的边。
湖南省益阳市箴言中学2015届高三上学期第三次模拟考试 数学(理) Word版含答案

益阳市箴言中学2015届高三第三次模拟考试数学(理科)时量:120分钟 总分:150分一、选择题:(本大题共10小题,每小题5分,共50分.)1.设集合}02|{},01|{<-=>+=x x N x x M ,,则=N M ( ) A .),1(+∞- B .)2,1[- C .)2,1(- D .]2,1[- 2. 复数iiz 21-=的虚部是( ) A .1 B .-1 C .i D .i -3.已知βα,角的终边均在第一象限,则“βα>”是“βαsin sin >”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.函数周期为π,其图像的一条对称轴是3π=x ,则此函数的解析式可以是( )A .sin 26y x π⎛⎫=- ⎪⎝⎭ B .sin 26y x π⎛⎫=+ ⎪⎝⎭ C .sin 23y x π⎛⎫=- ⎪⎝⎭ D .sin 26x y π⎛⎫=+ ⎪⎝⎭ 5.设a 、b 都是非零向量,下列四个条件中,一定能使0||||a b a b +=成立的是( )A .2a b =B .//a bC .13a b=- D .a b ⊥ 6.方程()()2ln 10,0x x x +-=>的根存在的大致区间是( )A .)1,0(B .)2,1(C .),2(eD .)4,3(7.已知向量,a b 的夹角为45︒,且1a =,210a b -=b=( )A..2 C..8.已知函数()()21,f x x g x kx=-+=,若方程()()f xg x =有两个不相等的实根,则实数k 的取值范围是( )A .10,2⎛⎫ ⎪⎝⎭B .1,12⎛⎫⎪⎝⎭ C .()1,2 D .()2,+∞9.对于非零向量βα,,定义一种向量积:βββα=)4,0(,πθ∈的夹角b a ,且 ,都在集合}|2{Z n n∈中。
则 = ( )A .23,25B .23,21C .21,25 D .2110.函数x ax x x f +-=221ln )(有极值且极值大于0,则a 的取值范围是 ( )A .)1,0(B .)2,1(C .)2,0(D .)4,3( 4二、填空题:(本大题共5小题,每小题5分,共30分.)11.函数()f x =的定义域为 。
湖南省益阳市箴言中学2015届高三第一次模拟考试 数学(理)

益阳市箴言中学2015届高三第一次模拟考试理科数学(考试时间120分钟 满分150分) 命题:第I 卷 (选择题 共50分)一、选择题(本大题共10小题,每小题5分,共50分. 在每小题列出的的四个选项中,选出符合题目要求的一项)1.已知集合{}2230A x x x =--≥,{}22B x x =-≤<,则AB =( )(A )[]2,1-- (B )[)1,2- (C ) []1,1- (D )[)1,2 2.设,a b R ∈,则“a b >”是“a a b b >”成立的( )(A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件 (D )既不充分也不必要条件3.已知函数()()()210cos 0x x f x x x ⎧+>⎪=⎨≤⎪⎩ ,则下列结论正确的是( ) (A )()f x 是偶函数 (B )()f x 在(),-∞+∞上是增函数 (C )()f x 是周期函数 (D )()f x 的值域为[]1,-+∞4.已知函数()21f x x =-+,()g x kx =. 若方程()()f x g x =有两个不相等的实根, 则实数k 的取值范围是( ) (A )10,2⎛⎫ ⎪⎝⎭ (B )1,12⎛⎫⎪⎝⎭(C ) ()1,2 (D )()2,+∞ 5.已知向量,a b 的夹角为45︒,且1a =,210a b -=,则b =( )(A (B )2 (C ) (D )6.已知数列}{n a 为等比数列,n S 是它的前n 项和。
若1322a a a =⋅,且4a 与72a 的等差中项为,45则=5S ( )A .35 B.33 C.31 D.297.已知a b >,椭圆1C 的方程为22221x y a b +=,双曲线2C 的方程为22221x y a b-=,1C 与2C 的离心率,则2C 的渐近线方程为( )A . 0x = B. 0y ±= C.20x y ±= D.20x y ±=8.已知()f x 是定义在(-∞,+∞)上的偶函数,且在(-∞,0]上是增函数,设4(log 7)a f =,12(log 3)b f =, 1.6(2)c f =,则,,a b c 的大小关系是( )A.c a b <<B. c b a <<C. b c a <<D. a b c <<9.下列四个图中,函数( )10. 某同学在研究函数()f x()f x 变形为()f x ()f x 表示PA PB +(如图),①()f x 的图象是中心对称图形; ②()f x 的图象是轴对称图形;③函数()f x 的值域为,+∞);④方程(())1f f x =有两个解.上述关于函数()f x 的描述正确的是( ) A. ①③ B. ③④ C. ②③ D. ②④第II 卷 (非选择题 共100分)二、填空题(本大题共5小题,每小题5分,共25分)11.下列结论:①若命题;1tan ,:=∈∃x R x P 命题,01,:2>+-∈∀x x R x q 则命题""q p ⌝且是假命题; ②已知直线,01:,013:21=++=-+by x l y ax l 则21l l ⊥的充要条件是3-=ba; ③命题“若,0232=+-x x 则1=x ”的逆否命题为:“若1≠x 则.0232≠+-x x ”其中正确结论的序号是.____________(把你认为正确结论的序号都填上)12.已知函数()()()11330log 0x x f x x x +⎧≤⎪=⎨>⎪⎩ ,则不等式()1f x >的解集为 .13.在ABC ∆中,内角,,A B C 所对的边分别是,,a b c . 已知14b c a -=,2sin 3sin B C =,则co s A 的值为 .14.已知菱形ABCD 的边长为2,120BAD ︒∠=,点,E F 分别在边,BC DC 上,3BC BE =,DC DF λ=. 若1AE AF ⋅=,则λ的值为 .15.若集合{}{},,,2,0,1,5a b c d =,且下列四个关系:① 2a =; ② 2b ≠; ③ 0c =; ④ 5d ≠.有且只有一个是正确的,则符合条件的有序数组(),,,a b c d 的个数是 .三、解答题 (本大题共6小题,共75分. 解答应写出文字说明、演算步骤或证明过程)16. (本小题满分12分)已知函数f (x )=2cos ⎝ ⎛⎭⎪⎫x +π3⎣⎢⎡⎦⎥⎤sin ⎝ ⎛⎭⎪⎫x +π3-3cos ⎝⎛⎭⎪⎫x +π3.(1)求f (x )的值域和最小正周期;(2)若对任意x ∈⎣⎢⎡⎦⎥⎤0,π6,使得m [f (x )+3]+2=0恒成立,求实数m 的取值范围.17.(本小题满分12分)如图,A B C ∆中,90,1,B B C D E∠==、两点分别是线段A B A C 、 的中点,现将A B C ∆沿DE 折成直二面角AD EB --。
湖南省益阳市箴言中学2014-2015学年高二上学期期中考试数学(理科)Word版含答案
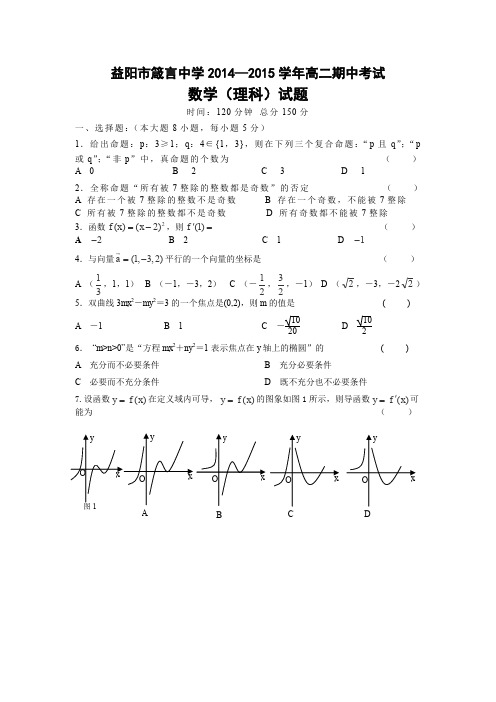
益阳市箴言中学2014—2015学年高二期中考试数学(理科)试题时间:120分钟 总分150分一、选择题:(本大题8小题,每小题5分)1.给出命题:p :3≥1;q :4∈{1,3},则在下列三个复合命题:“p 且q ”;“p 或q ”;“非p ”中,真命题的个数为 ( ) A 0 B 2 C 3 D 12.全称命题“所有被7整除的整数都是奇数”的否定 ( ) A 存在一个被7整除的整数不是奇数 B 存在一个奇数,不能被7整除 C 所有被7整除的整数都不是奇数 D 所有奇数都不能被7整除 3.函数2(x)(2)f x =-,则(1)f '= ( ) A 2- B 2 C 1 D 1-4.与向量(1,3,2)a =-平行的一个向量的坐标是 ( ) A (31,1,1) B (-1,-3,2) C (-21,23,-1) D (2,-3,-22) 5.双曲线3mx 2-my 2=3的一个焦点是(0,2),则m 的值是 ( ) A -1 B 1 C -1020D1026. “m >n >0”是“方程mx 2+ny 2=1表示焦点在y 轴上的椭圆”的 ( ) A 充分而不必要条件 B 充分必要条件C 必要而不充分条件D 既不充分也不必要条件7.设函数()y f x =在定义域内可导,()y f x =的图象如图1所示,则导函数()y f x '=可能为 ( )ABCD8.如图正方体A 1B 1C 1D 1-ABCD 的侧面AB 1内有动点P 到直线AB 与到直线B 1C 1的距离相等,则动点P 所在的曲线的形状为 ( )二、填空题:(本大题共7小题,每小题5分)9.已知向量)1,5,3(=a ,)3,2,2(=b ,)3,1,4(--=c,则向量c b a 432+-的坐标为 .10.平面向量a 、b 都是非零向量,a ·b <0是a 与b 夹角为钝角的________条件. 11.抛物线y 2=8x 的焦点坐标是________.12.已知A 、B 、C 三点的坐标分别为A (1,2,3),B(2,1-,1),C(3,λ,λ)AB AC ⊥ ,则λ13.函数)0(ln )(>=x x x x f 的单调递增区间是 .14.若曲线21y x =-与31y x =-在0x x =处的切线互相垂直,则0x 等于 . 15.过抛物线y 2=4x 的焦点,作倾斜角为3π4的直线交抛物线于P ,Q 两点,O 为坐标原点,则△POQ 的面积等于__________.三、解答题:(本大题共6小题,共70分)16.(本小题满分12分)已知命题p :x 2-5x +6≥0;命题q :0<x <4.若p 是真命题,q 是假命题,求实数x 的取值范围.17.(本小题满分12分).已知直线x +y -1=0与椭圆x 2+by 2=34相交于两个不同点,求实数b 的取值范围.18.(本小题满分12分)一艘轮船在航行中每小时的燃料费和它的速度的立方成正比,已知在速度为每小时10千米时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每千米的费用总和最小? 19、(本小题满分12分)如图,正方体1111ABCD A B C D -的棱长 为2,E 为棱1CC 的中点. (1)求1AD 与DB 所成角的大小; (2)求证DB ⊥平面1AEA .A 1B 1C 1D 1E20、(本小题满分13分)设函数323()(1)1,32a f x x x a x a =-+++其中为实数。
湖南省益阳市箴言中学高二数学上学期12月月考试题 文

益阳市箴言中学2014—2015学年高二12月月考文科数学试题总分:150分 时量:120分钟一、选择题:本题共10小题,每小题5分,满分50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、设a ,b 为实数,若复数i bi a i +=++121,则( )A 、a =23,b =21B 、a =3,b =1C 、a =21,b =23D 、a =1,b =32、设p :m >6;q :362>m ,则是⌝p 是⌝q 的( )A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分又不必要条件3、命题“)(x f >0(R x ∈)恒成立”的否定是( )A 、0)(,<∈∀x f R xB 、0)(,≤∈∀x f R xC 、0)(,<∈∃x f R xD 、0)(,≤∈∃x f R x4、用反证法证明命题“若,b a >则33b a >”时,假设的内容是( ) A 、b a > B 、b a ≤ C 、33b a > D 、33b a ≤5、椭圆:12222=+b y ax )0(>>b a 上存在点P 使21PF ∙<0则离心率e ∈( ) A 、(0,22) B 、(0,22] C 、(22,1) D 、(22,1]6、点P 在双曲线C :1422=-y x 上,1F 、2F 是双曲线的焦点,∠1F P 2F =60°,则P 到x 轴的距离为( )A 、55B 、515C 、5152D 、20157、正实数a ,b 满足:3=++ab b a ,则b a +有( )A 、最大值2B 、最小值2C 、最大值23D 、最小值23与销售额y 的统计数据如下表:根据上表利用最小二乘法可得回归方程a x b y ˆˆˆ+=,据此模型预报广告费用为7万元时销售额为74.9万元,则据此模型预报,广告费每增加1万元,销售额大约增加( )A 、9.1万元B 、9.4万元C 、9.7万元D 、10万元9、设△ABC 三边长为a ,b ,c ;△ABC 的面积为S ,内切圆半径为r ,则c b a S r ++=2,类比这个结论可知,四面体S-ABC 的四个面的面积分别为4321,,,S S S S ,内切球半径为r ,体积为V ,则r =( ) A 、4321S S S S V +++ B 、43212S S S S V+++ C 、43213S S S S V +++ D 、43214S S S S V+++ 10、为考察高中生的性别与是否喜欢数学课程之间的关系,在湖南某所示范性高中的学生中 )参考公式:))()()(()(22d b c a d c b a bc ad n K ++++-=,其中d c b a n +++=;B 、约有99%的把握认为“性别与喜欢数学课程之间有关系”C 、在犯错误的概率不超过0.050的前提下认为“性别与喜欢数学课程之间有关系”D 、在犯错误的概率不超过0.010的前提下认为“性别与喜欢数学课程之间有关系”二、填空题:本大题共5小题,每小题5分,共25分。
湖南省益阳市箴言中学—学年高二3月月考数学理试题

益阳市箴言中学2014—2015学年高二3月月考理科数学试题(本试卷满分150分,考试时间120分钟)第Ⅰ卷(选择题50分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个选项是正确的)1、如图,D 、E 分别是AB 、AC 上两点,CD 与BE 相交于点O ,下列条件中不能使ΔABE 和ΔACD 相似的是( )A. ∠B=∠CB. ∠ADC=∠AEBC .BE=CD ,AB=AC D. AD ∶AC=AE ∶AB2.如右图,A 、B 是⊙O 上的两点,AC 是⊙O 的切线,∠B=70°,则∠BAC 等于( )A. 70°B. 20°C. 35°D. 10°3.若点在以点为焦点的抛物线上,则等于( )A .B .C .D .4.极坐标方程表示的曲线为( )A .一条射线和一个圆B .两条直线C .一条直线和一个圆D .一个圆5.在⊙O 中,直径AB 、CD 互相垂直,BE 切⊙O 于B ,且BE=BC ,CE 交AB 于F ,交⊙O 于M ,连结MO 并延长,交⊙O 于N ,则下列结论中,正确的是( )A. CF=FMB. OF=FBC. BM ⌒的度数是22.5°D. BC ∥MN6.在△ABC 中,∠A ∶∠B ∶∠C =1∶2∶3,CD ⊥AB 于D ,AB =,则DB =( ) A . B . C . D . 7.若且满足,则的最小值是( ) A . B . C . D . 8.不等式的解集为( )A .B .C .D .9.直线被圆截得的弦长为( )A .B .C .D . 10.如图,平行四边形ABCD 中,,若的面积等于,则 的面积等于( ).A .B .C .D .ABD CEF第Ⅱ卷(非选择题 共100分)二、填空题(本大题共5小题,每小题5分,共25分。
把答案填在题中的横线上) 11.点是椭圆上的一个动点,则的最大值为___________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
益阳市箴言中学2014—2015学年高二12月月考理科数学试题〖命题范围:选修2—1,2—2〗 时量 120分钟 总分 150分一、选择题(10×5=50分)1. 命题“∃x ∈Z ,使x 2+2x +m <0”的否定是( )A .∃x ∈Z ,使x 2+2x +m ≥0B .不存在x ∈Z ,使x 2+2x +m ≥0C .∀x ∈Z ,使x 2+2x +m >0D .∀x ∈Z ,使x 2+2x +m ≥0 2. 复数ii i i -++1432(i 为虚数单位)的共轭复数....是( ) A .-21-21i B .-21+21i C .21-21i D .21+21i3. 用数学归纳法证明不等式11+n +21+n +···+n 21>2413(n >1,n ∈N*),在证明n =k +1这一步时,需要证明的不等式是( ) A .11+k +1+···+1>2413B .11+k +31+k +···+k 21+121+k >2413 C .21+k +31+k +···+k 21+121+k >2413D .21+k +31+k +···+k 21+121+k +221+k >2413 4. 若抛物线y 2=2px 的焦点与椭圆2622y x +=1的右焦点重合,则p 的值为( )A .-2B .2C .-4D .45. 过椭圆22a x +22by =1(a >b >0)的左焦点F 1作x 轴的垂线交椭圆于点P ,F 2为右焦点,若∠F 1PF 2=60°,则椭圆的离心率为( ) A .2B .3C .21D .316. 双曲线223y x -=1的一个焦点到它的渐近线的距离为( ) A .1 B .2 C .3 D .27. 已知定点A (2014,2),F 是抛物线y 2=2x 的焦点,点P 是抛物线上的动点,当|PA|+|PF|最小时,点P 的坐标为( )A .(0,0)B .(1,2)C .(2,2)D .(21,1)8. 观察)(2'x =2x ,)(4'x =4x 3,)('cosx =-sinx ,由此可得,若定义在R 上的函数)(x f 满足)(x f -=)(x f ,记)(x g 为)(x f 的导函数,则)(x g -=( ) A .)(x f B .-)(x f C .)(x g D .-)(x g 9. 如图,棱长为1的正方体ABCD -A 1B 1C 1D 1中,点P 在侧面BCC 1B 1及其边界上运动,并且总保持向量在1BD 上的投影为0,则线段AP 扫过的区域的面积为( ) A .21 B.22C.23 D.4510. “若存在一条与函数y =)(x f 的图象有两个不同交点P(x 1,y 1),Q(x 2,y 2)的直线,使y =)(x f 在x =221x x +处的切线与此直线平行”,则称这样的函数y =)(x f 为“hold 函数”;下列函数:①y =x1;②y =2x (x >0);③y =21x -;④y =lnx ;其中为“hold 函数”的是( )A .①②④B .②③C .③④D .①③④二、填空题(5×5=25分) 11. 若dx k x )2(10+⎰=2,则实数k = .12. 设平面α的法向量1n =(1,2,-2),平面β的法向量2n =(-2,-4,k ),若α∥β,则k = .13. 设条件p :a >0;条件q :a 2+a ≥0,那么p 是q 的 条件(填“充分不必要,必要不充分,充要”). 14. 先阅读下面的文字:“求 +++111的值时,采用了如下的方法:令+++111=x ,则有x +1=x ,从而解得x =251+(负值已舍去)”;运用类比的方法,计算:++++2111211= .15. 将全体正奇数排成一个三角形数阵;接照图中的排列规律,第n 行(n ≥3)从左向右的第3个数为 .C A三、解答题(本大题共有6道小题,75分)16. (本小题满分12分)已知复数z =yi x +-)2((x ,y ∈R ,i 为虚数单位)的模为3,求xy的最大值.17. (本小题满分12分)已知p :函数y =12++mx x 在(-1,+∞)上单调递增;q :函数y =42x +4(m -2)x +1大于零恒成立。
若“p ∨q ”为真,“p ∧q ”为假,求实数m 的取值范围.18. (本小题满分12分)如图,已知四棱锥P —ABCD 的底面为直角梯形,AB ∥DC ,∠DAB =90°,PA ⊥底面ABCD ,且PA =AD =DC =1,AB =2,M 是PB 的中点. (1)证明:平面PAD ⊥平面PCD ;(2)求AC 与PB 所成的角的余弦值.AD C B M P19. (本小题满分13分)已知某公司的品牌服装的年固定成本为10万元,每生产1千件,需要另外投入1.9万元,设R(x )(单位:万元)为销售收入,根据市场调查,知R(x )=⎪⎩⎪⎨⎧>≤≤-)10(,3200)100(,301103x x x x ,其中x 是年产量(单位:千件). (1)写出年利润W 关于年产量x 的函数解析式;(2)当年产量为多少时,该公司在这一品牌服装的生产中所获年利润最大?20. (本小题满分13分)已知椭圆22a x +22by =1(a >b >0)的右焦点为)0,3(2F ,离心率为e .(1)若e =23,求椭圆的方程;(2)设直线y =kx 与椭圆相交于A ,B 两点,M ,N 分别为线段2AF ,2BF 的中点,若坐标原点O 在以MN 为直径的圆上,且22<e ≤3,求k 的取值范围.21. (本小题满分13分) 已知函数)(x f =1)(+x ax ln ,曲线y =)(x f 在x =1处的切线与直线x -2y =0平行. (1)求a 的值;(2)若)(x f ≤b -12+x 恒成立,求实数b 的最小值.理科数学试卷 参考答案一、选择题:(每小题5分,共50分)DDDDB ACDCB 二、填空题:(每小题5分,共25分)11、【1】;12、【4】;13、【充分不必要】;14、【231+】;15、【n 2-n +5】. 三、解答题:(本大题共75分) 16、(本小题满分12分) 解:由3)2(=+-yi x 得:3)2(22=+-y x ,由几何意义易得:xy的最大值为3. 17、(本小题满分12分)解:若p 为真,则m ≥2;若q 为真,则1<m <3,∵“p ∨q ”为真,“p ∧q ”为假,∴p 与q 是“一真一假”,∴⎩⎨⎧≤≥≥132m m m 或,或⎩⎨⎧<<<312m m ,解得:m ≥3或1<m <2,∴m ∈(1,2)∪[3,+∞).18、(本小题满分12分)证明:(1)∵AB ∥DC ,∠DAB =90°,∴DC ⊥AD ,又PA ⊥面ABCD ,∴PA ⊥DC , ∴DC ⊥面PAD ,又DC ⊂面PDC ,∴平面PAD ⊥平面PCD ; 解:(2)以A 为原点,AD ,AB ,AP 分别为x ,y ,z 轴, 建立空间直角坐标系, 则A (0,0,0),P (0,0,1),D (1,0,0),C (1,1,0),B (0,2,0), ∴AC =(1,1,0),=(0,2,-1),设AC 与PB 所成的角为θ(0<θ<90°) ∴cos θ=|cos <,>|=522⋅=510. 19、(本小题满分13分)解:(1)W =⎪⎩⎪⎨⎧>-≤≤--)10(,9.13170)100(,103011.83x x x x x .(2)当0<x <10时,W '=8.1-0.1x 2,令W '=0,解得:x =9或x =-9(舍去),比较W (0),W (9),W (10)得W (9)最大;当x >10时,函数是减函数, ∴当年产量为9千件时,该公司所获年利润最大,最大利润为38.6万元.AD C BM P20、(本小题满分13分)解:(1)由题意得:⎪⎩⎪⎨⎧==233ac c ,解得a =23,∴2b =3,∴椭圆的方程为31222y x +=1.(2)由⎪⎩⎪⎨⎧==+kxy b y a x 12222,得0)(222222=-+b a x k a b ,设A(1x ,1y ),B(2x ,2y ),∴1x +2x =0,1x ·2x =22222ka b b a +-,依题意,OM ⊥ON ,∴·=0,又M(231+x ,21y ),N(232+x ,22y ),∴OM ·ON =4)(392121x x x x ++++421y y =0,代入整理得:212)1(x x k ++9=0,即)9()1)(9(222222-++--a k a k a a +9=0,将其整理为:24242188118a a a a k +-+-==-1-2421881a a k -=,∵22<e ≤23,∴23≤a <32,∴12≤2a <18,∴2k ≥81,即k ∈(-∞,-2]∪[2,+∞).21、(本小题满分13分)解:(1)∵)(x f '=2)1()1(1+-+x lnax x x =2)1(11+-+x lnaxx ,由)1(f '=42lna -=21, 解得a =1.(2)∵a =1,∴)(x f =1+x lnx ,∴由题得:b ≥12++x lnx (x >0)恒成立,设)(x g =2+lnx ,则)(x g '=2)1(11+--x lnx x ,再设)(x h =11--lnx ,则)(x h '=21xx +-<0,∴)(x h 在(0,+∞)上递减,又)1(h =0,∴当x ∈(0,1)时,)(x h >0,即)(x g '>0,∴)(x g 在(0,1)上为增函数;当x ∈(1,+∞)时,)(x h <0,即)(x g '<0,∴)(x g 在(1,+∞)上为减函数;∴max x g )(=)1(g =1,∴只需b ≥max x g )(=1, 即b ≥1,∴b 的最小值min b =1.。
