2008年数学解题能力六年级集训
小学六年级数学下册计算能力训练

小学六年级数学下册计算能力训练(一)一、直接写得数 3+3%=18÷6%=1-26.4%= 0.625+81= 0.25×7.6×4= 1-0.01=6151-=21512153⨯÷⨯= 二、填空:1.()()=1:4=2:( )=6÷( )=( )=( )% 2. ( )的54是20千克 41比51多( )% 10千克比( )千克多25% 30千克比40千克少( )%3.如果y=3x ,x 和y 成( )比例,y=x 3,x 和y 成( )比例。
4.如果32a=b(a.b ≠0),那么a:b =( ):( )5.在比例尺为4:1的图上,8厘米的线段表示实际长度( )厘米。
6.用1,2,6和x 四个数组成比例,x 最小是( ),最大是( )。
7.一种糖水,糖占10%,糖与水的重量比是( )。
三、求未知数xx -20%x =4 2x ÷31=43 x: 41=12: 61四、怎样算简便就怎样算。
65755672⨯+÷5123232+÷-9.0%908.171092.81+⨯+⨯131)163939(⨯+一、直接写得数3274÷=057⨯=8327553⨯⨯= 9032⨯=2154+=9104532÷⨯=二、填空 1.52时=( )分403公顷=( )平方米5.07立方米=( )升3.5升=( )毫升3÷( )=7.5%=()16=15:( )=( ):242.一件衣服原价160元,打七折出售,现价是( )元。
3.女生占全班人数的40%,男生比女生多( )%,女生比男生少( )%。
4.甲数是乙数的54,甲数比乙数少( )%,乙数比甲数多( )%。
5.已知甲数的52等于乙数的21,那么乙数是甲数的)() (。
6.小明买一本书,八折后是16元,他买这本书便宜了( )元。
三、求x12:41:61x = x =631+x218385=-x四、怎样算简便,就怎样算9441495⨯+÷ 306-(206+7827434373÷-⨯ 0.25×32×1.25一、直接写得数3274÷=057⨯=8327553⨯⨯= 9032⨯=2154+=9104532÷⨯=二、填空 1.52时=( )分403公顷=( )平方米5.07立方米=( )升3.5升=( )毫升3÷( )=7.5%=()16=15:( )=( ):242.一件衣服原价160元,打七折出售,现价是( )元。
2008年数学解题能力六年级集训习题[1]
![2008年数学解题能力六年级集训习题[1]](https://img.taocdn.com/s3/m/1bb1bfea31126edb6e1a1094.png)
2008年数学解题能力六年级集训习题[1]2008年数学解题能力六年级集训一:计算篇【例1】141516413750455667⨯+⨯+⨯=_______________【例2】111111212312341232008++++++++++++++=_______________【例3】123246369200400600135261039152006001000⨯⨯+⨯⨯+⨯⨯++⨯⨯⨯⨯+⨯⨯+⨯⨯++⨯⨯=_____________【例4】321345432345432123321345432123345432()()()()123234543234543321123234543321234543++⨯++-+++⨯+【例5】200720062008200720081+⨯⨯-=___________【例6】1236_______1212312341234567++++=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯【例7】0.1234562+0.8765442+0.123456×0.876544×2=__________【例11】(迎春杯考题)计算:11+______112+1113+1114+311+4+12006+2006=+++ 【例12】() 19927a迎春杯考题化成小数后,小数点后第一位到若干位数字和为,问a= 。
【例13】计算:0.16+0.1+0.125+0.142857=______()精确到小数后第三位二:几何篇-几何之常考几大模型【例1】如图,有四个长方形的面积分别是1平方厘米、2平方厘米、3平方厘米和4平方厘米,组合成一个大的长方形,求图中阴影部分的面积。
【例2】如下图,D、E、F、G均为各边的三等分点,线段EG和DF把三角形ABC分成四部分,如果四边形FOGC的面积是24平方厘米,求三角形ABC的面积。
【例3】在边长是8的正方形ABCE中,E是AD的中点,F是CE的中点,G是BF的中点,H是AG的中点,求四边形HGFI比三角形EID大__ ___.【补充】园林小路,曲径通幽.如右上图所示,小路由白色正方形石板和内外两种三角形石板铺成.问:内圈三角形石板的总面积大,还是外圈三角形的总面积大?说项说明原因?【例4】如图:已知在梯形ABCD中,上底是下底的2,其3中F是BC边上任意一点,三角形AME、三角形BMF、三角形NFC的面积分别为14、20、12。
2008年“数学解题能力展示”读者评选活动三年级组初赛试卷及详解答案

2008“数学解题能力展示”读者评选活动(三年级)三年级组初赛试题(测评时间:2007年12月2日11:00—12:00;满分150)一、填空题Ⅰ(每题10分,共60分)1. 计算:24+63+52+17+49+81+74+38+95=________。
2.计算:53×57-47×43=_____________。
3. 星期天小明、小强和小佳一起去采摘。
小强说:“我摘的苹果最多了,比你们俩摘的苹果总和还多1个。
”小明回答说:“是啊。
你比我多摘了10个,但我比小佳多摘了10个。
”那么他们三人共摘了_____________个苹果。
4. 用火柴棍拼成的数字和符号如下图所示,那么用火柴棍拼成一个减法等式最少要用_____________根火柴。
5. 将1~9这9个数字分别填入下图的方框中,每个数字恰好用一次,使等式成立;现已将8填入,则最左边的两个方框中所填的两位数是________。
6. 一个文具店中橡皮的售价为每块5角,圆珠笔的售价为每支1元,签字笔的售价为每支2元5角。
小明要在该店花5元5角购买其中两种文具,他有___________种不同的选择。
二、填空题Ⅱ(每题15分,共90分)1. 一个书架上有数学、语文、英语、历史4种书共27本,且每种书的数量互不相同。
其中数学书和英语书共有12本,语文书和英语书共有13本。
有一种书恰好有7本,是_____________书。
2. 下面两个算式中,相同的字母代表相同的数字,不同的字母代表不同的数字,那么A+B+C+D +E+F+G=_____________。
3. 小名、小亮两人玩扑克牌,他们手里各有点数为1、2、3、4、5、6、7、8、9、10的纸牌各一张,两人每轮各出一张牌,点数大的为胜,并将两张牌的点数差(大减小),做为获胜一方的分数,另一方不得分,10轮牌出完之后,两人总分之和最大是_____________。
4. 有125个同样大小的正方体木块,木块的每个面的面积均为1平方厘米,其中63个表面涂上白色,还有62个表面涂上蓝色。
广东省江门鹤山市2008年六年级数学综合练习题及答案(九)

广东省江门鹤山市2008年六年级数学综合练习题(九)班级____________姓名____________分数____________一、 直接写出得数。
(9分)①7.2-4.98= ②(32-72)×21= ③3.9÷0.13= ④0.25×32= ⑤43×15-7×43= ⑥21×5÷21×5= ⑦17.85-(7.85-3.9)= ⑧1÷7+76= ⑨1÷0.1%=二、 简便计算。
(9分)⑴7÷125 ⑵ 41×37+63÷4 ⑶74-0.65+73-0.35三、 递等式计算。
(12分)⑴18÷1.5-0.2×0.5 ⑵(21+31)×52-72⑶51÷[(32+51)×131 ] ⑷98×[43-(167-41)]四、 求未知数x 。
(9分)⑴2.8x -4.3=9.7 ⑵x -0.6x =12 ⑶43︰x =52︰51五、 列式计算。
(9分)⑴210的31比125除以85的商少多少?⑵一个数的53比24的41多3,求这个数。
(列方程解)⑶ 40减去35的71,所得的差被0.5除,商是多少?六、 判断题。
(5分)⑴所有质数都是奇数。
( )⑵任意一个三角形至少有两个锐角。
( )⑶有一个角是直角的平行四边形就是长方形或正方形。
() ⑷体积相等的两个正方体,它们的表面积一定相等。
()⑸圆的半径与面积成正比例。
( )七、 选择题。
(5分)⑴一种瓶装矿泉水,在瓶的侧面写有净含量600毫升,是指这个水瓶的( )。
A. 侧面积B. 表面积C. 体积D. 容积⑵一个三角形的内角度数的比是2︰3︰5,这个三角形是( )三角形。
A. 锐角B. 直角C. 钝角 ⑶125的分子扩大3倍,要使分数的大小不变,分母应加上( )。
2008学年六年级数学第二学期综合检测题

2008学年第二学期六年级数学综合能力检测题班别: 姓名-----------一、直接写出得数。
(16分)53×21= 21÷3= 43 ×32 = 10÷75= 92 ×3 75÷2110= 51+43= 31-41= 36÷76= 21 ÷31= 7+ 95 = 5-31= 0÷121×10= 54-0.8= 6- 53-52 = 43÷6= 二、填空题:(12分) 1、3.4平方米=( )平方分米 1吨 = ( )千克 2、2.55立方米=( )立方分米( )升3、5立方米40立方分米=( )立方米4、一个圆柱的底面直径是4分米,高是5分米,它的侧面积是( )平方分米,体积是( )立方分米。
5、一个底直径和高都是6分米的圆锥体,它的体积是( )立方分米。
6、等底等高的圆柱和圆锥,圆柱的体积是圆锥体积( )倍。
7、一个圆柱的底面周长是18.84厘米,高是10厘米,它的侧面积是( )平方厘米。
8、一个圆柱的底面积是12.56平方分米,这个圆柱的体积是( )立方分米。
9、把一根长2分米的圆木锯成两段后,表面积增加了12.56平方分米,这根圆木的体积是( )立方分米。
10、一个圆柱形水桶体积是62.8立方分米,底面积是2分米,高是( )米三、判断题:(10分)1、圆柱的体积一定比圆锥体积大。
( )2、一个圆柱的底面周长和高都是相等,那么它的侧面展开一定是正方形。
( )3、圆柱的底面半径扩大3倍,它的体积就扩大6倍。
( )4、长方体、正方体和圆柱的体积都可以统一用“底面积×高”来计算。
( )5、侧面积相等的两个圆柱体,它们的底面周长一定相等。
( )。
四、选择题(4分)1、一个圆柱的底面直径和高都是4厘米,圆柱的侧面积的( )平方厘米A 、50.24B 、12.56C 、94.22、圆的半径扩大3倍,它的面积就扩大( )A 、3倍B 、9倍C 、6倍3、棱长2分米的正方体,它的体积是( )立方分米。
小学数学解题能力训练及答案详解六

小学数学解题能力训练六一填空题1、2006×2007200720072007-2007×2006200620062006=_________________解:原式=2006×2007×1000100010001-2007×2006×1000100010001=0.2、一次考试,参加的学生中有1/7得优,1/3得良,1/2得中,其余的得差,已知参加考试的学生不满50人,那么得差的学生有人。
解:提示:7,2,3的最小公倍数为42(小于50人),所以参加的学生总数为42人。
答案为1人3、有一城镇共5000户居民,每户的子女不超过2人,一部分家庭有1个孩子,余下的家庭中一半每家有2个孩子,那么此城镇共有孩子人。
解:设有1个孩子家庭X个,则孩子共有X+(5000-X)/2×2=50004、1992年爷爷年龄是孙子的10倍,再过12年,爷爷年龄是孙子子的4倍,那么1993年孙子是岁。
解:设1992年爷爷年龄时10X,孙子为X. 则:4×(X+12)=10X+12,则X=6所以1993年孙子是7岁。
5、有一块麦地和一块菜地,菜地的一半和麦地的1/3合起来是13亩。
麦地的一半和菜地的1/3合起来是12亩,那么菜地有亩。
解:设二元方程求解即可,菜地X,麦地Y.则:X/2+Y/3=13,X/3+Y/2=12解得:X=18,Y=126、科学家进行一次实验,每隔5小时作一次记录,他做第12次记录时,时钟正好九点正,问第一次作记录时,时钟是点。
解:这是一个等差数列的问题,很简单。
2点7、甲数是36,甲、乙两数最大公约数是4,最小公倍数是288,那么乙数是。
解:甲数×乙数=4×288,所以288×4÷36=328、一名学生在计算一道除数是两位数的没有余数的除法时,错把被除数百位上的3看成了8,结果得商383,余17,这商比正确的商大21,那么这道题的被除数是,除数是。
2008年“数学解题能力展示”复试读者评选活动中年级组题(B版)
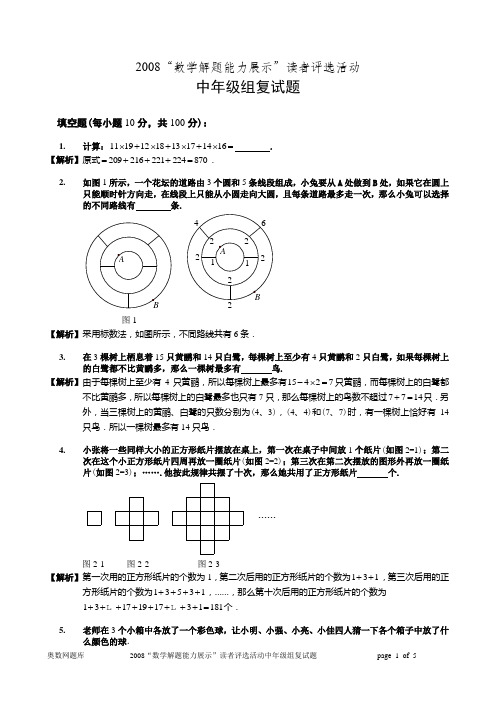
2008“数学解题能力展示”读者评选活动中年级组复试题填空题(每小题10分,共100分):1. 计算:1119121813171416⨯+⨯+⨯+⨯= .【解析】 原式209216221224870=+++=.2. 如图1所示,一个花坛的道路由3个圆和5条线段组成,小兔要从A 处做到B 处,如果它在圆上只能顺时针方向走,在线段上只能从小圆走向大圆,且每条道路最多走一次,那么小兔可以选择的不同路线有 条.图1【解析】 采用标数法,如图所示,不同路线共有6条.3. 在3棵树上栖息着15只黄鹂和14只白鹭,每棵树上至少有4只黄鹂和2只白鹭,如果每棵树上的白鹭都不比黄鹂多,那么一棵树最多有 鸟.【解析】 由于每棵树上至少有4只黄鹂,所以每棵树上最多有15427-⨯=只黄鹂,而每棵树上的白鹭都不比黄鹂多,所以每棵树上的白鹭最多也只有7只,那么每棵树上的鸟数不超过7714+=只.另外,当三棵树上的黄鹂、白鹭的只数分别为(4、3),(4、4)和(7、7)时,有一棵树上恰好有14只鸟.所以一棵树最多有14只鸟.4. 小张将一些同样大小的正方形纸片摆放在桌上,第一次在桌子中间放1个纸片(如图2-1);第二次在这个小正方形纸片四周再放一圈纸片(如图2-2);第三次在第二次摆放的图形外再放一圈纸片(如图2-3);…….他按此规律共摆了十次,那么她共用了正方形纸片个. ……图2-1 图2-2 图2-3【解析】 第一次用的正方形纸片的个数为1,第二次后用的正方形纸片的个数为131++,第三次后用的正方形纸片的个数为13531++++,……,那么第十次后用的正方形纸片的个数为1317191731181++++++++= 个.5. 老师在3个小箱中各放了一个彩色球,让小明、小强、小亮、小佳四人猜一下各个箱子中放了什么颜色的球.小明说:“1号箱子中放的是黄色的,2号箱子中放的是黑色的,3号箱子中放的是红色的.” 小亮说:“1号箱子中放的是橙色的,2号箱子中放的是黑色的,3号箱子中放的是绿色的.” 小强说:“1号箱子中放的是紫色的,2号箱子中放的是黄色的,3号箱子中放的是蓝色的.”小佳说:“1号箱子中放的是橙色的,2号箱子中放的是绿色的,3号箱子中放的是紫色的.” 老师说:“你们中有一个人恰好猜对了两个,其余三人都只猜对了一个.”那么3号箱子中放的是 色的球.【解析】 观察可知,小明、小强、小佳三人所猜的每一个箱中的颜色都各不相同,如果他们三人中有一个人猜中了两个,那么另外两个人猜中的都是这个人猜错的那个箱子的颜色,但是这另外的两个人猜的颜色也不相同,矛盾.所以他们三人中没有人猜中两个,而是各猜中一个,猜中两个的是小亮.由于小亮猜的1号箱子颜色与小佳猜的相同,2号箱子颜色与小明相同,所以小亮猜中了1、2号箱子,小佳猜中1号箱子,小明猜中2号箱子,那么小强猜中3号箱子,故3号箱子中放的是蓝色的球.6. 在下面两个算式中,相同的字母代表相同的数字,不同的字母代表不同的数字,那么四位数ABCD为 .2008A B C DE F G H- 2424A E F G E F G H -【解析】 如果8D H -=,那么将有0C G -=,即C G =,与题意不符,所以108D H +-=,即2D H +=.类似分析可知1100C G -+-=,即9C G +=,故0C =,9G =.由9G =知4G H -=,故5H =,3D =.由102F G +-=得1F =,由10B F --=得2B =,由14E F --=得6E =,由2A E -=得8A =,故四位数ABCD 为8203.7. 如图3所示,一个长方形广场的正中央有一个长方形的水池,水池长8米、宽3米,水池周围用边长为1米的方砖一圈一圈的向外铺.恰好铺了若干圈,共用了152块方砖,那么共铺了 圈.图3【解析】 由于水池的四周均铺上方砖,那么铺上方砖后得到的大长方形的长与宽之差等于水池的长与宽之差,为835-=.如果水池中也铺上方砖,需要8324⨯=块,那么整个大长方形需要15224176+=块,而1761611=⨯,16与11的差恰好为5,所以大长方形的长为16米,共铺了(168)24-÷=圈.8. 现有5段铁链,每段上有4个封闭的铁环.现在要打开一些铁环,把这20个铁环焊接成一个一环套一环的圆圈.如果每打开一个铁环要2分钟,焊接上一个铁环要3分钟,那么焊成这个圆圈,最少需要 分钟.图4【解析】 要焊成这个圆圈必须得打开若干个铁环,每打开一个铁环最后就得将它焊上,每一个铁环上花的时间为235+=分钟,为使用的时间最少,应打开最少的铁环.如果只打开3个铁环,那么还剩下5段铁链(尽管有可能有1段铁链只剩1个圈),用3个铁环无法将5段铁链连起来,所以只打开3个铁环无法焊成圆圈.如果打开4个铁环,可以将原来的某段铁链的4个铁环全打开,这样还剩下4段铁链,用打开的4个铁环可以将它们连成一个圆圈,所以最少需打开4个铁环,那么用的时间最少为5420⨯=分钟.9.在下面的表1中,一条直线穿过其中若干个方格,穿过的方格中各数之和为1513105649++++=。
6年级数学集训1-15(全)经典

强化训练(1)1、计算:=+⨯+⨯25033337571432、比较大小:54321542( )654321654323、有一串数2,5,10,17,26,37,50,…它们按照一定的规律排列,其中第100个数 与第101个数相差( )。
4、魔盒里现有5只弹珠,若从中取出一只弹珠,魔盒中就会增加5只,若从中取出2只,魔盒中就会增加10只,若某人从中取10次,分别取出1只、2只、3只……10只,那么现在魔盒中共有( )只弹珠。
5、从1、2、3、4、5、6这6个数中任取3个组成三位数,其中能被6整除的有多少个?6、20个左右的小朋友围成一圈,从1开始报数,其中报5的小朋友恰好也报195,这里共有()个小朋友。
7、自然数N有多少个约数,把它的这些约数两两求和得到一组新数,其中最小的是4,最大的是196,N有()个约数。
8、八张纸片上分别写着8个不同的自然数,按从小到大的顺序从左到右依次排成一行(正面朝下),已知他们的排列规律是从第三张开始每一张卡片上的数都恰是它前面两张卡片上的数的和,现在翻开了第四张和第七张,问,第八张上的数字是()。
9、数学兴趣班有学生36人,某次测试结果全班平均分为93分,而男生平均分为95分,女生平均分为87分,这班有女生()人。
10、一项工程,甲、乙两人合作8天可以完成,甲单独做需要12天完成,现在两人合作几天后,余下的工程由乙独自完成,乙前后两段时间比为1:3,这个工程实际工期为多少天。
11、计算:200410011003200310012004⨯+⨯+12、2004年7月26日我们可以用8位数记为20040726,这个数有两大特点:(1)个位数字为6;(2)能被3整除,在2004年的366个数中,符合以上两大特点的数共有( )个。
13、这里共有2004个苹果,如果不能一个一个地拿,也不能一次全拿完,并且要求每次拿出的苹果数一样多,而且正好可以拿完,共有( )种不同的拿法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008年数学解题能力六年级集训一:计算篇【例1】141516413750455667⨯+⨯+⨯=_______________【例2】111111212312341232008++++++++++++++=_______________【例3】123246369200400600 135261039152006001000⨯⨯+⨯⨯+⨯⨯++⨯⨯⨯⨯+⨯⨯+⨯⨯++⨯⨯=_____________【例4】321345432345432123321345432123345432 ()()()() 123234543234543321123234543321234543 ++⨯++-+++⨯+【例5】200720062008200720081+⨯⨯-=___________【例6】1236_______ 1212312341234567 ++++=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯【例7】0.1234562+0.8765442+0.123456×0.876544×2=__________【例8】求满足条件:198********641n n <<的最简分数之总和(n 是自然数)【例9】18=1111+12+14x +已知,那么x=______【例10】繁分数1111111111++++共有10条分数线,把它化成最简分数是多少?【例11】(迎春杯考题)计算:11+______112+1113+1114+311+4+12006+2006=+++【例12】() 19927a 迎春杯考题化成小数后,小数点后第一位到若干位数字和为,问a= 。
【例13】计算:0.16+0.1+0.125+0.142857=______() 精确到小数后第三位【例14】计算:2000200020002001200020002000200020002000=_______200120012001200120012001++++++个个二:几何篇-几何之常考几大模型思路提示:在求边长之比时常转化为面积之比,求面积之比常转化为边长之比。
模型一:等积变化原理:两个三角形高相等,面积之比等于对应底边之比。
bS 1︰S 2 =a ︰b ;模型一的拓展: 等分点结论(“鸟头定理”):如下图,三角形AED 占三角形ABC 面积的23×14=16模型二:等积变化原理之四边形应用S 4S 3s 2s 1O DC BA141423213S S =S S S S D O O BS S +==+模型三:梯形中比例关系(“梯形蝴蝶定理”)(1)相似图形,面积比等于对应边长比的平方S 1︰S 3=a 2︰b 2(2)S 1︰S 3︰S 2︰S 4= a 2︰b 2︰ab ︰ab (3)S 2=S 4 ; (4)141423213S S =S S S S D O O BS S +==+ :模型四:相似三角形性质①a b c h A B C H=== ; ②相似三角形面积之比等于对应连长之比的平方S 1︰S 2=a 2︰A 2hh H cb aCB Aac b H CBA模型五:燕尾定理F D CBAS △ABG :S △AGC =S △BGE :S △GEC =BE :EC ; S △BGA :S △BGC =S △AGF :S △GFC =AF :FC ; S △AGC :S △BCG =S △ADG :S △DGB =AD :DB ;【例1】如图,有四个长方形的面积分别是1平方厘米、2平方厘米、3平方厘米和4平方厘米,组合成一个大的长方形,求图中阴影部分的面积。
B【例2】如下图,D 、E 、F 、G 均为各边的三等分点,线段EG 和DF 把三角形ABC 分成四部分,如果四边形FOGC 的面积是24平方厘米,求三角形ABC 的面积。
O GA BC E FD【例3】在边长是8的正方形ABCE 中,E 是AD 的中点,F 是CE 的中点,G 是BF的中点,H 是AG 的中点,求四边形HGFI 比三角形EID 大__ ___.B【补充】园林小路,曲径通幽.如右上图所示,小路由白色正方形石板和内外两种三角形石板铺成.问:内圈三角形石板的总面积大,还是外圈三角形的总面积大?说项说明原因?【例6】如图,在梯形ABCD 中,已知AB ︰CD=1︰2,E 、F 分别是AD 与BC 边上的三等分点。
已知梯形ABCD 的面积是297平方厘米,那么,四边形EMFN 的面积 平方厘米,DECBA【例8】(06年北京五中实验班选拔)一只装有水的圆柱形玻璃杯,底面积是80平方厘米,水深8厘米。
现将一个底面积是16平方厘米的长方体铁块竖放在水中后,仍有一部分铁块露在外面。
现在水深多少厘米?【例9】如图,长方形水槽,内部有一个30厘米高的隔板,同时打开A 、B 两个水龙头,4分钟后左侧水面与隔板一样高,右侧水面高5厘米,9分钟后右侧水面和隔板一样高,18分钟后将整个水槽注满水。
如果隔板的体积忽略不计,A 、B 每分钟的注水量各是多少升?(本题哪一个条件是多余的?并说明理由)120cm60三:行程与工程篇【例1】A 、B 两地相距22.4千米。
有一支游行队伍从A 出发,向B 匀速前进;当游行队伍队尾离开A 时,甲,乙两人分别从A ,B 两地同时出发。
乙向A 步行;甲骑车先追向队头,追上队头后又立即骑向队尾,到达队尾后再立即追向队头,追上队头后又立即骑向队尾……当甲第5次追上队头时恰与乙相遇在距B 地5.6千米处;当甲第7次追上队头时,甲恰好第一次到达B 地,那么此时乙距A 地还有多少千米。
队伍长度是多少?(保留一位小数)【例2】一列火车通过长320米的隧道,用了52秒。
当它通过长864米的大桥时,速度比通过隧道时提高41,结果用了1分36秒。
求火车通过大桥时的速度。
火车车长是多少?【例3】AB 两地相距4千米,在从A 地到B 地的公交路线上,只有两辆BUS ,一辆平均每小时行驶30千米,另一辆因为服役时间太长,所以跑不动了,平均每小时行20千米(乘客上下车时间忽略不计)。
早上5:00都从A 地发车, 到晚上6:00共相遇了多少次?(两车在同一地视为一次相遇,包括出发时为第一次)【例4】A ,B 两地相距1100米,甲、乙两人同时从A 地出发,在A 、B 间往返锻炼。
甲步行每分钟行60米,乙跑步每分钟行160米,40分钟后停止运动。
甲、乙两人第几次相遇时距B 地最近?最近距离是多少米?【例5】有一种机器人玩具装置,配备长、短不同的两条跑道,其中长跑道长400厘米,短跑道长300厘米,且有200厘米的公用跑道(如下图)。
机器人甲按逆时针方向以每秒6厘米的速度在长跑道上跑动,机器人乙按顺时针方向以每秒4厘米的速度在短跑道上跑动。
如果甲、乙两个机器人同时从点A 出发,那么当两个机器人在跑道上第3次迎面相遇时,机器人甲距离出发点A 点多少厘米?【例6】 乌龟和蜗牛赛跑,跑道是周长300厘米的等边三角形。
它们从三角形的同一顶点同时出发,乌龟每分钟行50厘米,蜗牛每分钟行46厘米,它们每到三角形的一个顶点都要休息1分钟。
出发后多长时间乌龟追上蜗牛? (请学生重点研究这类题如何求解是万能的)【拓展】在例题中,将“它们每到三角形的一个顶点都要休息1分钟”中的1分钟改为8秒钟,其余不变。
【例7】正方形ABCD(如图),边长80米,甲从A点、乙从B点同时沿逆时针方向运动,每分钟甲行135米,乙行120米,每过一个顶点时要多用5秒。
出发后,甲与乙相会需多长时间?在何处相会?【例8】A、B、C三辆汽车以相同的速度同时从甲市开往乙市.开车后1小时A车出了事故,B和C车照常前进.A车停车修理半小时后以原速度的45继续前进.B、C两车行至距离甲市200千米处B车出了事故,C车照常前进.B车停了半小时后也以原速度的45继续前进.结果到达乙市的时间C车比B车早1小时,B车比A车早1小时,求甲、乙两市的距离为多少千米?三:工程篇【例1】(北京市第六届“迎春杯”决赛试题)一项工程,甲单独做要12小时完成,乙单独做要18小时完成.若甲先做1小时,然后乙接替甲做1小时,再由甲接替乙做1小时,……,两人如此交替工作,请问:完成任务时,共用了多少小时?【例2】有一个敞口的立方体水箱,在其侧高线的三等分处开两个排水孔A和B,已知两孔的排水速度相同且孔,打开B孔,则需要16分钟,才能将水箱注满,如果将两孔都打开,经过分钟才能将水箱注满.【例3】(2007年迎春杯)公园水池每周需换一次水。
水池有甲、乙、丙三根进水管。
第一周小李按甲、乙、丙、甲、乙、丙、……的顺序轮流打开 1 小时,恰好在打开水管整数小时后灌满空水池。
第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开 1 小时,灌满一池水比第一周少用了15 分钟;第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开 1 小时,比第一周多用了 15 分钟。
第四周他三个管同时打开,灌满一池水用了 2 小时20 分,第五周他只打开甲管,那么灌满一池水需用________小时。
四:时间问题篇【例1】(迎春杯试题)从时钟指向4点开始,在经过几分钟,时针正好与分针重合?【例2】(迎春杯初赛试题)从3点钟开始,分针与时针第二次形成30度角的时间是3点几分?【例3】(迎春杯试题)在8点到9点之间,钟表的长针与短针在同一直线上,这时是8点几分?【例4】(迎春杯决赛试题)王叔叔有一只手表,他发现手表比家里的闹钟每小时快30秒,而闹钟却比标准时间每小时慢30秒,问王叔叔的手表是标准时间吗?如果是,请说明理由?如果不是,那么王叔叔的手表一昼夜比标准时间差几秒?【例5】如图,假设某星球的一天只有6小时,每小时36分钟,那么3点18分时,时针与分针所形成的锐角是________度?【例6】如图,假设某星球的一天只有10小时,每小时100分钟,那么6点75分时,时针与分针所形成的锐角是________度?五:数字迷与数阵图篇【例1】右边算式中,A 表示同一个数字,填入适当的数字在各个□中,使算式完整。
那么两个乘数的差(大数减小数)是 。
【例2】(1)将九个数填入下图(1)的九个空格中,使得任一行、任一列以及两条对角线上的三个数之和都等于定数k ,则中心方格中的数必为3k .请你说明理由!(2)将九个数填入下图(2)的空格中,使得每行、每列、每条对角线上的三个数之和都相等,则一定有:2a b e +=.请你说明理由!(3)将九个数填入下图(3)的空格中,使得每行、每列、每条对角线上的三个数之和都相等,则一定有:2a b c +=.请你说明理由!(这就是“黄金三角”)【例3】将3,5,7,11,13,17,19,23,29这9个数分别填人右图的9个○中,使3条边上的○中的数之和都相等。
