初中几何模型全等三角形专题手拉手模型--定稿版
完整版)全等三角形之手拉手模型

完整版)全等三角形之手拉手模型
本文将介绍手拉手模型中的全等三角形。
所谓手拉手模型,是指有公共顶点的两个等腰三角形,顶角相等。
因为顶点相连的四条边,形象的可以看作两双手,所以通常称为手拉手模型。
基本模型如下:已知,△ABB'和△ACC'都是等腰三角形,AB=AB',AC=AC',且∠BAB'=∠CAC'。
可以得出三个结论:结论1:△ABC≌△AB'C'(SAS),BC=B'C';结论2:
∠BOB'=∠BAB';结论3:AO平分∠BOC'。
在共顶点的等腰直角三角形中,也可以应用手拉手模型。
例如,如下图所示,△ABC和△ADE是等腰直角三角形,且
∠BAC=∠DAE=90°。
可以证明:⑴BD=CE⑵BD⊥CE。
另外,在共顶点的等边三角形中,也可以使用手拉手模型。
如下图,点A为线段BD上一点,△ABC和△ADE均是等边
三角形。
可以求出:(1)CD=BE;(2)∠DAE+
∠BFD=180°;(3)∠BFA=∠DFA=60°。
总之,手拉手模型在全等三角形的证明中是一个非常有用的工具,能够帮助我们更好地理解和应用三角形的性质。
全等三角形——手拉手模型(完整资料).doc

【最新整理,下载后即可编辑】手拉手模型要点一:手拉手模型特点:由两个等顶角的等腰三角形所组成,并且顶角的顶点为公共顶点结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180°(3)OA平分∠BOC变形:例1.如图在直线ABC的同一侧作两个等边三角形ABD∆,∆与BCE 连结AE与CD,证明(1)DBC∆ABE∆≅(2)DCAE=(3)AE与DC之间的夹角为︒60(4)DFB≅∆AGB∆(5)CFB≅∆EGB∆(6)BH平分AHC∠(7)ACGF//变式精练1:如图两个等边三角形ABD∆与∆,连结AE与CD,BCE证明(1)DBC∆≅ABE∆(2)DCAE=(3)AE与DC之间的夹角为︒60(4)AE与DC的交点设为H,BH平分AHC∠变式精练2:如图两个等边三角形ABD∆与∆,连结AE与CD,BCE证明(1)DBC∆≅ABE∆(2)DCAE=(3)AE与DC之间的夹角为︒60(4)AE与DC的交点设为H,BH平分AHC∠例2:如图,两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立?(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?例3:如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立?(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?例4:两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD , 问:(1)DBC ABE ∆≅∆是否成立?(2)AE 是否与CD 相等?(3)AE 与CD 之间的夹角为多少度?(4)HB 是否平分AHC ∠?。
专题12.19 三角形全等几何模型-“手拉手”模型(知识讲解)
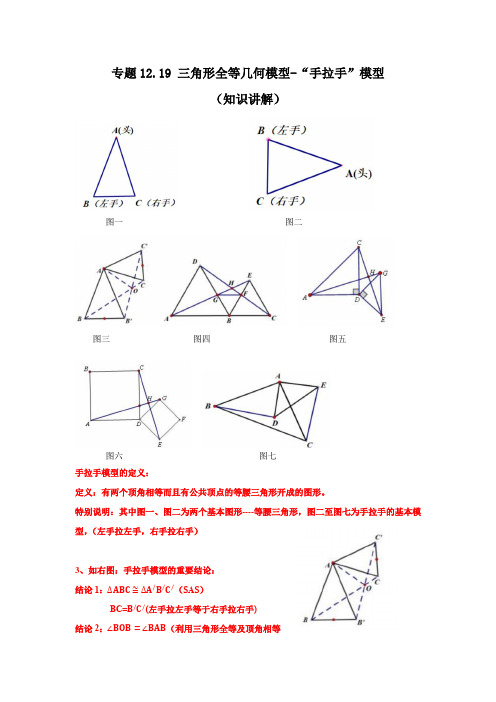
专题12.19 三角形全等几何模型-“手拉手”模型(知识讲解)图一图二图三图四图五图六图七手拉手模型的定义:定义:有两个顶角相等而且有公共顶点的等腰三角形开成的图形。
特别说明:其中图一、图二为两个基本图形----等腰三角形,图二至图七为手拉手的基本模型,(左手拉左手,右手拉右手)3、如右图:手拉手模型的重要结论:结论1:∆ABC≅∆A/B/C/(SAS)BC=B/C/(左手拉左手等于右手拉右手)结论2:∠BOB=∠BAB(利用三角形全等及顶角相等的等腰三角形底角相等)结论3:AO平分∠B O C/(利用三角形全等面积相等,再利用角平分线性质定理证明)典型例题讲练:在学习全等三角形知识时、教学兴趣小组发现这样一个模型:它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.通过资料查询,他们得知这种模型称为“手拉手模型” 兴趣小组进行了如下操究:(1)如图1、两个等腰三角形△ABC和△ADE中,AB=AC,AE=AD,△BAC=△DAE,连接BD、CE、如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,这个就是“手拉手模型”,在这个模型中,和△ADB 全等的三角形是,此线BD和CE的数量关系是(2)如图2、两个等腰直角三角形△ABC和△ADE中,AB=AC,AE=AD,△BAC=△DAE=90°,连接BD,CE,两线交于点P,请判断线段BD和CE的数量关系和位置关系,并说明理由:(3)如图3,已知△ABC、请完成作图:以AB、AC为边分别向△ABC外作等边△ABD和等边△ACE(等边三角形三条边相等,三个角都等于60°),连接BE,CD,两线交于点P,并直接写出线段BE和CD的数量关系及△PBC+△PCB的度数、【答案】(1)△AEC,BD=CE;(2)BD=CE且BD△CE,理由见解析;(3)作图见解析,BE=CD,△PBC+△PCB=60°.【分析】(1)根据SAS证明两个三角形全等即可证明;(2)通过条件证明△DAB△△EAC(SAS),得到△DBC+△ECB=90°,即可证明BD△CE,从而得到结果;≅即可得到证明;(3)根据已知条件证明DAC BAE解:(1)△AB=AC,AE=AD,△BAC=△DAE,∠+∠=∠+∠,△DAE EAB BAC EAB即DAB EAC ∠=∠,△()△△ADB AEC SAS ≅,△BD=CE ;(2)BD=CE 且BD△CE ;理由如下:因为△DAE=△BAC=90°,如图2.所以△DAE+△BAE=△BAC+△BAE .所以△DAB=△EAC .在△DAB 和△EAC 中,,,.AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩所以△DAB△△EAC (SAS ).所以BD=CE ,△DBA=△ECA .因为△ECA+△ECB+△ABC=90°,所以△DBA+△ECB+△ABC=90°.即△DBC+△ECB=90°.所以△BPC=180°-(△DBC+△ECB )=90°.所以BD△CE .综上所述:BD=CE 且BD△CE .(3)如图3所示,BE=CD ,△PBC+△PCB=60°.由图可知60DAB EAC ∠=∠=︒,AD=AB ,AE=AC ,△+DAB BAC EAC BAC ∠∠=∠+∠,即DAC BAE ∠=∠,△()△DAE △BAE SAS ≅,△BE=CD ,ABE ADC ∠=∠,又△60BDA ∠=︒,△60ADC BDC ABE BDC ∠+∠=∠+∠=︒,△120BPC ABP BDC BDA ∠=∠+∠+∠=︒,△△PBC+△PCB=60°.【点拨】本题主要考查了全等三角形的知识点应用,准确分析图形是解题的关键. 举一反三变式1:如图,AC △BC ,DC △EC ,AC =BC ,DC =EC ,AE 与BD 交于点F .(1)求证:AE =BD ;(2)求△AFD 的度数.【答案】(1)详情见解析;(2)90AFD ∠=︒【分析】(1)利用角的等量代换求出ACE BCD ∠=∠,再判断ACE ≌BCD △即可求解; (2)利用全等三角形的性质得到E D ∠=∠,再通过角的等量代换求解即可.解:(1)△AC BC ⊥,DC EC ⊥△90ACB ECD ∠=∠=︒△ACB BCE ECD BCE ∠+∠=∠+∠△ACE BCD ∠=∠在ACE 和BCD △中AC BC ACE BCD DC EC =⎧⎪∠=∠⎨⎪=⎩△ACE ≌BCD △(SAS)△AE BD =(2)设BD 与CE 的交点为G ,如图所示:△ACE ≌BCD △△E D ∠=∠△180EFG FGE E ++=︒∠∠∠,180GCD CGD D ++=︒∠∠∠,且BGE CGD ∠=∠△90EFG GCD ==︒∠∠△90AFD ∠=︒【点拨】本题主要考查了全等三角形的性质和判定,灵活运用角的等量代换是解题的关键.例题2.已如:如图1,B ,C ,D 三点在一条直线上,△ABC 和△ECD 均为等边三角形,连接BE ,AD 交于点F ,BE 交AC 于点M ,AD 交CE 于点N .(1)以下结论正确的有 ;△AD =BE △△EFD =60° △MC =NC △△AMB =△END(2)探究:将图1中的△ECD 绕点C 顺时针旋转一个角度(旋转角小于60°),如图2所示. △问:(1)中的正确结论哪些还成立?若成立,请说明理由;△连接FC ,如图3所示,求证:FC 平分△BFD【答案】(1)△△△;(2)△ △△;△见解析.【分析】(1)△根据等边三角形的性质得CA =CB ,CD =CE ,△ACB =60°,△DCE =60°,则△ACE =60°,利用“SAS ”可判断△ACD △△BCE ,则AD =BE ;△根据三角形外角关系得△EFD =△EBC +△ADC =△DAC +△ADC =△ACB =60°,从而可得结论; △连接MN ,证明△MCN 是等边三角形即可得出结论;△60,60AMB EBC END NDC ∠=︒+∠∠=︒+∠,而AC ≠CD 得CAD CDA ∠≠∠,从而可得出结论;(2)△方法同(1),逐个结论进行证明即可;△作,CG BE CH AD ⊥⊥于点G ,H ,证明△BGC △△AHC ,△CGF △△CHF 可得△CFG CFH =∠,从而可得结论.解:(1)△△ABC ,△ECD 是等边三角形,△AC=BC ,CE=CD ,△ACB=△ECD=60°△△ACD=△BCE=△120°△△ACD△△BCE△AD=BE ,故△正确;△△FEN=△NDC又△△ENF=△CND△△EFD=△ECD=60°,故△正确;又△△ACE=△NCD=60°△MEC=△NDCEC=CD△△EMC△△DNC△MC=NC ,故△正确;又△△AMB=△ACB+△ECB=60°+△ECB ,△END=△ECD+△NDC=60°+△NDC而AC CD ≠△CAD CDA ∠≠∠△MBC NDC ∠≠∠△MBC END ∠≠∠,故△错误;故答案为:△△△;(2)△△ACB=△ECD=60°△△BCE=△ACD又AC=BC ,CE=CD△△ACD△△BCE△AD=BE,故△正确;△△ADC=△BEC又△ENF=△CND△△EFD=△ECD=60°,故△正确△△ACE≠60°=△ECD△△EMC 不全等于△DNC ,△MC≠NC ,故△错误(3),CG BE CH AD ⊥⊥于点G ,H ,如图,由(2)△知,△CBG=△CAHAC=BC△BGC=△AHC=90°△△BGC△△AHC△CG=CH又CF=CF ,△CGF=△CHF=90°△△CGF△△CHF△△CFG=△CFH△FC 平分△BFD【点拨】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS ”、“SAS ”、“ASA ”、“AAS ”;全等三角形的对应边相等.也考查了等边三角形的判定与性质.举一反三变式:如图,在ABC∆中,分别以AC,BC为边作等边三角形ACD和等边三角形BCE,连接AE,BD交于点O,则AOB∠的度数为()A.100︒B.120︒C.130︒D.150︒【答案】B【分析】先证明△DCB△△ACE,求出△CAE=△CDB,再利用“8字型”证明△AOH=△DCH =60°即可解决问题.解:如图:AC与BD交于点H,△△ACD,△BCE都是等边三角形,△CD=CA,CB=CE,△ACD=△BCE=60°,△△DCB=△ACE,在△DCB和△ACE中,CD CADCB ACECB CE⎧⎪∠∠⎨⎪⎩===,△△DCB△△ACE,△△CAE=△CDB,△△DCH+△CHD+△BDC=180°,△AOH+△AHO+△CAE=180°,△DHC=△OHA,△△AOH=△DCH=60°,△△AOB=180°−△AOH=120°.故选:B.【点拨】本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形,学会利用“8字型”证明角相等,属于中考常考题型.例题3.(阅读材料)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若△BAC=△DAE,AB=AC,AD=AE,则△ABD△△ACE.(材料理解)(1)在图1中证明小明的发现.(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:△BD=EC;△△BOC=60°;△△AOE=60°;△EO=CO,其中正确的有.(将所有正确的序号填在横线上).(延伸应用)(3)如图3,AB=BC,△ABC=△BDC=60°,试探究△A与△C的数量关系.【答案】(1)证明见解析;(2)△△△;(3)△A+△C=180°.【分析】(1)利用等式的性质得出△BAD=△CAE,即可得出结论;(2)同(1)的方法判断出△ABD△△ACE,得出BD=CE,再利用对顶角和三角形的内角和定理判断出△BOC=60°,再判断出△BCF△△ACO,得出△AOC=120°,进而得出△AOE=60°,再判断出BF<CF,进而判断出△OBC>30°,即可得出结论;(3)先判断出△BDP是等边三角形,得出BD=BP,△DBP=60°,进而判断出△ABD△△CBP(SAS ),即可得出结论.(1)证明:△△BAC=△DAE ,△△BAC+△CAD=△DAE+△CAD , △△BAD=△CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== ,△△ABD△△ACE ;(2)如图2,△△ABC 和△ADE 是等边三角形, △AB=AC ,AD=AE ,△BAC=△DAE=60°, △△BAD=△CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== ,△△ABD△△ACE ,△BD=CE ,△正确,△ADB=△AEC , 记AD 与CE 的交点为G ,△△AGE=△DGO ,△180°-△ADB -△DGO=180°-△AEC -△AGE , △△DOE=△DAE=60°,△△BOC=60°,△正确,在OB上取一点F,使OF=OC,△△OCF是等边三角形,△CF=OC,△OFC=△OCF=60°=△ACB,△△BCF=△ACO,△AB=AC,△△BCF△△ACO(SAS),△△AOC=△BFC=180°-△OFC=120°,△△AOE=180°-△AOC=60°,△正确,连接AF,要使OC=OE,则有OC=12 CE,△BD=CE,△CF=OF=12 BD,△OF=BF+OD,△BF<CF,△△OBC>△BCF,△△OBC+△BCF=△OFC=60°,△△OBC>30°,而没办法判断△OBC大于30度,所以,△不一定正确,即:正确的有△△△,故答案为△△△;(3)如图3,延长DC至P,使DP=DB,△△BDC=60°,△△BDP 是等边三角形,△BD=BP ,△DBP=60°,△△BAC=60°=△DBP ,△△ABD=△CBP ,△AB=CB ,△△ABD△△CBP (SAS ),△△BCP=△A ,△△BCD+△BCP=180°,△△A+△BCD=180°.【点拨】此题考查三角形综合题,等腰三角形的性质,等边三角形的性质,全等三角形的判定和性质,构造等边三角形是解题的关键.举一反三变式:如图,C 为线段AE 上一动点(不与点,A E 重合),在AE 同侧分别作等边三角形ABC 和等边三角形,CDE AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下结论:①AD BE =;①//PQ AE ;①60AOB ∠=︒;①CPQ 是等边三角形,恒成立的是______.【答案】△△△△【分析】△由△ABC 和△CDE 都是等边三角形,可知AC=BC ,CD=CE ,△ACB=△DCE=60°,所以△ACD=△BCE=120°,所以△ACD△△BCE (SAS ),从而AD=BE ,故△正确;△△由△ACD△△BCE 得△CBE=△DAC ,加之AC=BC ,易得△ACB=△BCQ=60°,可证△CQB△△CPA (ASA ),从而CP=CQ ,再加之△PCQ=60°,可推出△PCQ 为等边三角形,易得△PQC=60°=△DCE ,根据内错角相等,两直线平行,可知△△正确;△结合△ACD△△BCE 和三角形的外角的性质,可得△AOB=60°,故△正确.解:△△等边△ABC 和等边△CDE ,△AC=BC ,CD=CE ,△ACB=△DCE=60°,△△ACB+△BCD=△DCE+△BCD ,即△ACD=△BCE ,△在△ACD 与△BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===△△ACD△△BCE (SAS ),△AD=BE ,故△正确;△△△△ACD△△BCE ,△△CBE=△DAC ,△由△ACB=△DCE=60°得△BCD=60°,△△ACP=△BCQ ,又△AC=BC ,△△CQB△△CPA (ASA ),△CP=CQ ,又△△PCQ=60°△△PCQ 为等边三角形,△△PQC=60°,△△PQC=60°=△DCE△PQ△AE故△△正确;△△△ACD△△BCE (SAS ),△△CAD=△CBE ,△△AOB=△CAD+△CEB=△CBE+△CEB ,又△△ACB=△CBE+△CEB=60°,△△AOB=△ACB=60°,故△正确.故答案为:△△△△.【点拨】本题考查了等边三角形的性质、全等三角形的判定与性质、三角形外角的性质,熟练应用三角形全等的判定是解题的关键.。
全等三角形——手拉手模型

手拉手模型要点一:手拉手模型 特点:由两个等顶角的等腰三角形所组成,并且顶角的顶点为公共顶点 结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180°(3)OA 平分∠BOC变形:三角形ABD∆例1.如图在直线ABC 的同一侧作两个等边与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆(2)AE 与DC 之间的夹角为︒60(3)BH 平分AHC ∠变式精练1:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD , 证明(1)DBC ABE ∆≅∆(2)AE 与DC 之间的夹角为︒60(3)AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD , 证明(1)DBC ABE ∆≅∆(2)AE 与DC 之间的夹角为︒60(3)AE 与DC 的交点设为H ,BH 平分AHC ∠CE AG ,,二例2:如图,两个正方形ABCD 与DEFG ,连结者相交于点H问:(1)CDE ADG ∆≅∆是否成立?(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?结CE AG ,,二者相例3:如图两个等腰直角三角形ADC 与EDG ,连交于点H问:(1)CDE ADG ∆≅∆是否成立?(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?BD AB =,例4:两个等腰三角形ABD ∆与BCE ∆,其中,EB CB =α=∠=∠CBE ABD ,连结AE 与CD , 问:(1)DBC ABE ∆≅∆是否成立?(2)AE 是否与CD 相等?(3)AE 与CD 之间的夹角为多少度?(4)HB 是否平分AHC ∠?。
初中数学全等三角形手拉手模型

∵ቐ∠ABE = ∠EBC
= BC
∴△ABE≌△DBC(SAS)
过B点分别向AE和DC作垂线,垂足为点M,N
∵BM,BN分别为△ABE和△DBC对应边上的高
∴BM=BN
在Rt△BMF和Rt△BNF中
BF =
∵ቊ
BM =
∴Rt△BMF≌Rt△BNF(HL)
手拉手模型-等边三角形
为右手顶点。
B(左手)
(头 )
(头)
B(左手
)
C(右手 )
C(右手)
手拉手模型基于
“ASA全等判定”
2、手拉手模型-模型分析
二、“手拉手模型”的基本构图:
常见变形:
手拉手模型-等边三角形
例1、如图在直线ABC的同一侧作两个等边三角形△ABD与△BCE,连结AE与CD.
证明:(1)△ ≌△ (2) = (3)与之间的夹角为60°(4)△ ≌△ (5)△ ≌△ (6)
∴AE=DC
(3)延长AE分别交BD于点N,CD于H
由(1)可知,∠BDC=∠BAE
又∵∠ANB=∠HND(对顶角相等)
∴180°-( ∠BDC + ∠HND )=
180°-(∠BAE + ∠ANB )
即∠DHN=∠ABD=60°
∴ 与的夹角为60°
(4)过点B分别向AE和DC所在直
变式1-4.
D
如果两个等边三角形△ABD和△BCE,连接AE与CD,证明:
1. △ABE≌△DBC
2. AE=DC
3. AE与DC的夹角为60°
4. AE与DC的交点设为H,BH平分∠AHC
【解析】①利用角度的和差关系证明∠ABE=∠DBC,且AB=DB,BC=BE
三角形全等中的手拉手模型

DAEBECECB CDCC AC A B 手拉手模型模块一:“手来手”模型 知识导航手拉手的一般形式:两个顶角相等并且共顶角顶点的等腰三角形已知:△ABC ,△DBE 均为等腰三角形,BA =BC ,BD =BE ,∠ABC =∠DBE . 结论:△ABD ≌△CBE 二、手拉手的特殊形式:1.两个共直角顶点的等腰直角三角形已知:△ABC ,△DBE 均为等腰直角三角形,BA =BC ,BD =BE ,∠ABC =∠DBE =90° 结论:△ABD ≌△CBE2.两个共顶点的等边三角形C已知:△ABC ,△DBE 均为等边三角形 结论:△ABD ≌△CBE例1:已知点C 为线段AB 上一点,分别以AC 、BC 为边在AB 同侧作等边△ACD 与等边△BCE ,AE 交BD 于F ,连接CF ,求证: (1)BD =AE ;(2)∠BFE =60°;(3)CF 平分∠AFB .练习:若【例1】中A 、C 、B 三点不在一条直线上,如下图所示,其它条件不变,问上述三个结论是否成立?证明你的结论.BA例2:(2016年武珞路八上其中第23题改编)如图:△ABD 、△AEC 中,∠BAD =∠CAE =90°,AB =AD ,AC =AE ,DC 、BE 相交于点M . (1)求证:BE =CD (2)求证:CD ⊥BE ; (3)求∠AMD 的度数.练习:(2015年洪山区八上期中第2问)如图,已知直线AB 交x 轴于点A (a ,0),交y 轴于点B (0,b ),且a ,b 满足|a +b|+(a +4)2=0,若点C 在第一象限,且BE ⊥AC 于点E ,延长BE 到D ,使BD =AC ,连OC ,OD ,CD ,试判断△COD 的形状,并说明理由.A B EA E拓展:如图,△ACD 与△BCE 为等腰三角形,其中CA =CD ,CB =CE ,∠ACD =∠BCE = ,BD 、AE 交于F .(1)求证:AE =BD (2)求∠BFE =∠AFC 的度数.模块二 “手拉手”模型的应用 题型一:“手拉手”与中点的结合例3 已知如图△ACB 与△CEF 为等腰直角三角形,∠ACB =∠ECF =90°,AE ,BF 交于点O ,M 是AE 中点,N 是BF 的中点,试判断△CMN 的形状.练习:已知△ABC ,分别以AB ,AC 为边作△ABD 和△ACD ,且AD =AB ,AC =AE ,∠DAB =∠CAE ,连接DC 与BE ,G ,F 分别是DC 与BE 的中点. (1) 如图,若∠DAB =60°,则∠AFG =_________.DED ECEC BC AB(2)如图,若∠DAB =90°,则∠AFG =_________.(3) 如图,若∠DAB =α,则试探究∠AFG 与α之间的关系.模型三“手拉手”背景下的综合应用例4 (2016年武路八上其中第23题)如图,设△ADC 和△CBE 都是等边三角形,连接AE 、AB 、BD ,∠ABD =80°,求∠EAB 的度数.练习(2015年洪山区八上期中)如图,设△ABC 和△CDE 都是等边三角形,且∠EBD =65°,求∠AEB 的度数.例5(2014年江岸区八上期中第24题第(1)(2)问)如图,△AOB 是等边三角形,以直线OA 为x 轴建立平面直角坐标系,B(a ,b)且a ,b 满足,D 为y 轴上移动点,以AD 为边做等边△ADC ,直线CB 交y 轴于点E .(1)如图1,求A 点的坐标(2)如图2,D 在y 轴正半轴上,C 在第二象限,CE 的延长线交x 轴于点M ,当D 点在y 轴正半轴上运动时,M 点的坐标是否发生变化,若不变,求M 点的坐标,若变化,说明理由.xy xy图1 图2EAOAOBBCD例6 (2016年武昌区八上期中)△AOB 和△ACD 是等边三角形,其中AB ⊥x 轴于E 点, (1)如图,若OC =5,求BD 的长度(2)设BD 交x 轴于点F ,求证:∠OF A =∠DF A . (3)如图,若正△AOB 的边长为4,点C 为x 轴上一动点,以AC 为边在直线AC 下方作正△ACD ,连接DE ,求DE 的最小值.ECA B B DAA B D DB 练习:如图△ABC 是直角三角形,记BC =a ,分别以直角三角形的三边向外作正方形ABDE ,正方形ACFG ,正方形BCMN ,过点C 作BA 边上的高CH 并延长交正方形ABDE 的边DE 于点K ,则四边形BDKH 的面积为_________。
中考数学常见几何模型手拉手模型(从全等到相似)

专题03 手拉手模型(从全等到相似)全等三角形与相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就手拉手模型进行梳理及对应试题分析,方便掌握。
模型1.手拉手模型(全等模型)【模型解读】将两个三角形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
【常见模型及证法】(等腰)(等边)(等腰直角)公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
对应操作:左手拉左手(即连结BD),右手拉右手(即连结CE),得ABD ACE 1.(2022·青海·中考真题)两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若ABC 和ADE 是顶角相等的等腰三角形,BC ,DE 分别是底边.求证:BD CE =;(2)解决问题:如图2,若ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,点A ,D ,E 在同一条直线上,CM 为DCE 中DE 边上的高,连接BE ,请判断∠AEB 的度数及线段CM ,AE ,BE 之间的数量关系并说明理由.图1 图2【答案】(1)见解析 (2)90DCE ∠=︒;2AE AD DE BE CM =+=+【分析】(1)先判断出∠BAD =∠CAE ,进而利用SAS 判断出△BAD ∠∠CAE ,即可得出结论; (2)同(1)的方法判断出△BAD ∠∠CAE ,得出AD =BE ,∠ADC =∠BEC ,最后用角的差,即可得出结论.【解析】(1)证明:∠ABC 和ADE 是顶角相等的等腰三角形,∠AB AC =,AD AE =,BAC DAE ∠=∠,∠BAC CAD DAE CAD ∠-∠=∠-∠,∠BAD CAE ∠=∠. 在BAD 和CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∠()BAD CAE SAS ≌△△,∠BD CE =.(2)解:90AEB =︒∠,2AE BE CM =+,理由如下:由(1)的方法得,≌ACD BCE ,∠AD BE =,ADC BEC ∠∠=,∠CDE △是等腰直角三角形,∠45CDE CED ∠=∠=︒,∠180135ADC CDE ∠=︒-∠=︒,∠135BEC ADC ∠=∠=︒,∠1354590AEB BEC CED ∠=∠-∠=︒-︒=︒.∠CD CE =,CM DE ⊥,∠DM ME =.∠90DCE ∠=︒,∠DM ME CM ==,∠2DE CM =.∠2AE AD DE BE CM =+=+.【点睛】此题是三角形综合题,主要考查了全等三角形的判定和性质,等腰三角形,等边三角形,等腰直角三角形的性质,判断出△ACD ∠∠BCE 是解本题的关键.2.(2022·黑龙江·中考真题)ABC 和ADE 都是等边三角形.(1)将ADE 绕点A 旋转到图①的位置时,连接BD ,CE 并延长相交于点P (点P 与点A 重合),有PA PB PC +=(或PA PC PB +=)成立;请证明.(2)将ADE 绕点A 旋转到图②的位置时,连接BD ,CE 相交于点P ,连接P A ,猜想线段P A 、PB 、PC 之间有怎样的数量关系?并加以证明;(3)将ADE 绕点A 旋转到图③的位置时,连接BD ,CE 相交于点P ,连接P A ,猜想线段P A 、PB 、PC 之间有怎样的数量关系?直接写出结论,不需要证明.【答案】(1)证明见解析 (2)图②结论:PB PA PC =+,证明见解析 (3)图③结论:PA PB PC +=【分析】(1)由△ABC 是等边三角形,得AB =AC ,再因为点P 与点A 重合,所以PB =AB ,PC =AC ,P A =0,即可得出结论;(2)在BP 上截取BF CP =,连接AF ,证明BAD CAE ≌(SAS ),得ABD ACE ∠=∠,再证明CAP BAF ≌△△(SAS ),得CAP BAF ∠=∠,AF AP =,然后证明AFP 是等边三角形,得PF AP =,即可得出结论;(3)在CP 上截取CF BP =,连接AF ,证明BAD CAE ≌(SAS ),得ABD ACE ∠=∠,再证明BAP CAF ≌△△(SAS ),得出CAF BAP ∠=∠,AP AF =,然后证明AFP 是等边三角形,得PF AP =,即可得出结论:PA PB PF CF PC +=+=.(1)证明:∠∠ABC 是等边三角形,∠AB =AC ,∠点P 与点A 重合,∠PB =AB ,PC =AC ,P A =0,∠PA PB PC +=或PA PC PB +=;(2)解:图②结论:PB PA PC =+证明:在BP 上截取BF CP =,连接AF ,∠ABC 和ADE 都是等边三角形,∠AB AC =,AD AE =,60BAC DAE ∠=∠=︒∠BAC CAD DAE CAD ∠+∠=∠+∠,∠BAD CAE ∠=∠,∠BAD CAE ≌(SAS ),∠ABD ACE ∠=∠,∠AC =AB ,CP =BF , ∠CAP BAF ≌△△(SAS ),∠CAP BAF ∠=∠,AF AP =,∠CAP CAF BAF CAF ∠+∠=∠+∠,∠60FAP BAC ∠=∠=︒,∠AFP 是等边三角形,∠PF AP =,∠PA PC PF BF PB +=+=;(3)解:图③结论:PA PB PC +=,理由:在CP 上截取CF BP =,连接AF ,∠ABC 和ADE 都是等边三角形,∠AB AC =,AD AE =,60BAC DAE ∠=∠=︒∠BAC BAE DAE BAE ∠+∠=∠+∠,∠BAD CAE ∠=∠,∠BAD CAE ≌(SAS ),∠ABD ACE ∠=∠,∠AB =AC ,BP =CF ,∠BAP CAF ≌△△(SAS ),∠CAF BAP ∠=∠,AP AF =,∠BAF BAP BAF CAF ∠+∠=∠+∠,∠60FAP BAC ∠=∠=︒,∠AFP 是等边三角形,∠PF AP =,∠PA PB PF CF PC +=+=,即PA PB PC +=.【点睛】本题考查等边三角形的判定与性质,全等三角形的判定与性质,熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键.3.(2022·吉林·九年级期末)如图①,在ABC 中,90C ∠=︒,6AC BC ==,点D ,E 分别在边AC ,BC 上,且2CD CE ==,此时AD BE =,AD BE ⊥成立.(1)将CDE △绕点C 逆时针旋转90︒时,在图②中补充图形,并直接写出BE 的长度;(2)当CDE △绕点C 逆时针旋转一周的过程中,AD 与BE 的数量关系和位置关系是否仍然成立?若成立,请你利用图③证明,若不成立请说明理由;(3)将CDE △绕点C 逆时针旋转一周的过程中,当A ,D ,E 三点在同一条直线上时,请直接写出AD 的长度.【答案】(1)补充图形见解析;22BE =;(2)AD BE =,AD BE ⊥仍然成立,证明见解析;(3)51AD =-或51=+AD .【分析】(1)根据旋转作图的方法作图,再根据勾股定理求出BE 的长即可;(2)根据SAS 证明E ACD BC ≅∆∆得AD =BE ,∠1=∠2,再根据∠1+∠3+∠4=90°得∠2∠3+∠4=90°,从而可得出结论;(3)分两种情况,运用勾股定理求解即可.【详解】解:(1)如图所示,根据题意得,点D 在BC 上,∠BCE ∆是直角三角形,且BC =6,CE =2由勾股定理得,2222(2)(6)22BE CE BC =+=+=;(2)AD BE =,AD BE ⊥仍然成立. 证明:延长AD 交BE 于点H ,∠90ACB DCE ∠=∠=︒,ACD ACB BCD ∠=∠-∠,BCE DCE BCD ∠=∠-∠,∠ACD BCE ∠=∠,又∠CD CE =,AC BC =,∠ACD BCE ≅△△,∠AD BE =,12∠=∠,在Rt ABC 中,13490∠+∠+∠=︒,∠23490∠+∠+∠=︒,∠90AHB ∠=︒,∠AD BE ⊥.(3)①当点D 在AC 上方时,如图1所示,同(2)可得ACD BCE ≅△△∠AD =BE同理可证BE AE ⊥在Rt △CDE 中,2CD CE ==∠DE =222CD CE +=在Rt △ACB 中,6AC BC ==∠2223AB AC BC =+=设AD =BE =x ,在Rt △ABE 中,222BE AE AB +=∠222(2)(23)x x ++=解得,51x =-∠ 51AD =-②当点D 在AC 下方时,如图2所示,同(2)可得ACD BCE ≅△△∠AD =BE同理可证BE AE ⊥在Rt △CDE 中,2CD CE ==∠DE =222CD CE +=在Rt △ACB 中,6AC BC ==∠2223AB AC BC =+=设AD =BE =x ,在Rt △ABE 中,222BE AE AB +=∠222(2)(23)x x +-=解得,5+1x =∠ 51=+AD .所以,AD 的值为51-或5+1【点睛】本题考查了旋转的性质,全等三角形的判定与性质,勾股定理等知识,熟练解答本题的关键.模型2.手拉手模型(旋转相似模型)【模型解读与图示】旋转放缩变换,图中必有两对相似三角形.1.(2022·四川达州·中考真题)某校一数学兴趣小组在一次合作探究活动中,将两块大小不同的等腰直角三角形ABC 和等腰直角三角形CDE ,按如图1的方式摆放,90ACB ECD ∠=∠=︒,随后保持ABC 不动,将CDE △绕点C 按逆时针方向旋转α(090α︒<<︒),连接AE ,BD ,延长BD 交AE 于点F ,连接CF .该数学兴趣小组进行如下探究,请你帮忙解答:(1)【初步探究】如图2,当ED BC ∥时,则α=_____;(2)【初步探究】如图3,当点E ,F 重合时,请直接写出AF ,BF ,CF 之间的数量关系:_________; (3)【深入探究】如图4,当点E ,F 不重合时,(2)中的结论是否仍然成立?若成立,请给出推理过程;若不成立,请说明理由.(4)【拓展延伸】如图5,在ABC 与CDE △中,90ACB DCE ∠=∠=︒,若BC mAC =,CD mCE =(m 为常数).保持ABC 不动,将CDE △绕点C 按逆时针方向旋转α(090α︒<<︒),连接AE ,BD ,延长BD 交AE 于点F ,连接CF ,如图6.试探究AF ,BF ,CF 之间的数量关系,并说明理由.【答案】(1)45︒(2)2BF AF CF =+(3)2BF AF CF =+仍然成立,理由见解析(4)21BF m FC mAF =++【分析】(1)根据等腰直角三角形的性质,可得AC BC ⊥,根据题意可得AC ED ⊥,根据等原三角形的性质可得AC 平分ECD ∠,即可得45ACE ∠=︒,根据旋转的性质可知ECA α∠=;(2)证明ACE ≌BCD △,可得AE DB =,根据等腰直角三角形可得2ED CE =,由BE BD ED =+,即可即可得出2BF AF CF =+;(3)同(2)可得ACE ≌BCD △,过点C ,作CH FC ⊥,交BF 于点H ,证明FEC HDC ≌,AFC △≌BHC △,可得BH AF =,即可得出2BF AF CF =+;(4)过点C 作CG CF ⊥,交BF 于点G ,证明ACE BCD △∽△,可得BG mAF =,GC mFC =,在Rt FCG 中,勾股定理可得21FG m FC =+,即可得出21BF m FC mAF =++.(1)等腰直角三角形ABC 和等腰直角三角形CDE ,90ECD ∴∠=︒,AC BC ⊥ED BC ∥ED AC ∴⊥45ACE α∴∠==︒故答案为:45︒(2)90∠=∠=︒ACB ECD ACE ACD ACD BCD ∴∠+∠=∠+∠ACE BCD ∴∠=∠ 在ACE 与BCD △中,AC BC ACE BCD EC DC =⎧⎪∠=∠⎨⎪=⎩ ACE ≌BCD △∴AE DB =BE BD ED ∴=+ 又2ED CE =2BE AE CE ∴=+,E F 重合,2BF AF CF ∴=+故答案为:2BF AF CF =+ (3)同(2)可得ACE ≌BCD △AE DB ∴=,EAC DBC ∠=∠过点C ,作CH FC ⊥,交BF 于点H ,则90ECF FCD FCD DCH ∠+∠=∠+∠=︒,∴ECF DCH ∠=∠, 在FEC 与HDC △中,FEC HDC EC CD ECF DCH ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴FEC HDC ≌, FC CH ∴=,CFH ∴是等腰直角三角形,2FH FC ∴=,CH FC =,90,90FCH ACF ACH ACB BCH ACH ∴∠=∠+∠=︒∠=∠+∠=︒,ACF BCH ∴∠=∠,在AFC △与BHC △中,FC HC ACF BCH AC BC =⎧⎪∠=∠⎨⎪=⎩,∴AFC △≌BHC △,BH AF ∴=,2BF FH BH CF AF ∴=+=+,即2BF AF CF =+,(4)过点C 作CG CF ⊥,交BF 于点G ,BC mAC =,CD mCE =,BC CDAC CE ∴=,AC BC EC DC∴=, ACE BCD α∠=∠=,ACE BCD ∴△△∽,CBG CAF ∴∠=∠,FCA ACG GCB ACG ∠+∠=∠+∠,∴FCA GCB ∠=∠,AFC BGC ∴∽,BG GC BC AF FC AC∴==m =, BG mAF ∴=,GC mFC =, Rt FCG 中,2221FG FC CG m FC =+=+,∴21BF FG GB m FC mAF =+=++,即21BF m FC mAF =++.【点睛】本题考查了等腰直角三角形的性质,旋转的性质,全等三角形的性质与判定,相似三角形的性质与判定,掌握全等三角形的性质与判定,相似三角形的性质与判定是解题的关键.2.(2022·山东烟台·中考真题)(1)【问题呈现】如图1,∠ABC 和∠ADE 都是等边三角形,连接BD ,CE .求证:BD =CE .(2)【类比探究】如图2,∠ABC 和∠ADE 都是等腰直角三角形,∠ABC =∠ADE =90°.连接BD ,CE .请直接写出BD CE的值.(3)【拓展提升】如图3,∠ABC 和∠ADE 都是直角三角形,∠ABC =∠ADE =90°,且AB BC =AD DE =34.连接BD ,CE .①求BD CE的值;②延长CE 交BD 于点F ,交AB 于点G .求sin∠BFC 的值.【答案】(1)见解析(2)22(3)①35;②45 【分析】(1)证明△BAD ∠∠CAE ,从而得出结论; (2)证明△BAD ∠∠CAE ,进而得出结果;(3)①先证明△ABC ∠∠ADE ,再证得△CAE ∠∠BAD ,进而得出结果; ②在①的基础上得出∠ACE =∠ABD ,进而∠BFC =∠BAC ,进一步得出结果. (1)证明:∠∠ABC 和△ADE 都是等边三角形, ∠AD =AE ,AB =AC ,∠DAE =∠BAC =60°, ∠∠DAE ﹣∠BAE =∠BAC ﹣∠BAE ,∠∠BAD =∠CAE ,∠∠BAD ∠∠CAE (S A S ),∠BD =CE ; (2)解:∠∠ABC 和∠ADE 都是等腰直角三角形,12AB AB AE AC ∴==,∠DAE =∠BAC =45°,∠∠DAE ﹣∠BAE =∠BAC ﹣∠BAE , ∠∠BAD =∠CAE ,∠∠BAD ∠∠CAE ,1222BD AB CE AC ∴===; (3)解:①34AB AD AC DE ==,∠ABC =∠ADE =90°, ∠∠ABC ∠∠ADE ,∠∠BAC =∠DAE ,35AB AD AC AE ==, ∠∠CAE =∠BAD ,∠∠CAE ∠∠BAD ,35BD AD CE AE ∴== ; ②由①得:∠CAE ∠∠BAD ,∠∠ACE =∠ABD ,∠∠AGC =∠BGF ,∠∠BFC =∠BAC ,∠sin∠BFC 45BC AC ==. 【点睛】本题考查了等腰三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解决问题的关键是熟练掌握“手拉手”模型及其变形. 3.(2022·山东·东营市一模)【提出问题】(1)如图1,在等边∠ABC 中,点M 是BC 上的任意一点(不含端点B 、C ),连结AM ,以AM 为边作等边∠AMN ,连结CN .求证:∠ABC =∠ACN .【类比探究】(2)如图2,在等边∠ABC 中,点M 是BC 延长线上的任意一点(不含端点C ),其它条件不变,(1)中结论∠ABC =∠ACN 还成立吗?请说明理由.【拓展延伸】(3)如图3,在等腰∠ABC 中,BA =BC ,点M 是BC 上的任意一点(不含端点B 、C ),连结AM ,以AM 为边作等腰∠AMN ,使顶角∠AMN =∠ABC .连结CN .试探究∠ABC 与∠ACN 的数量关系,并说明理由.【答案】(1)证明见解析;(2)成立,理由见解析;(3)∠ABC=∠CAN,理由见解析.【分析】(1)利用SAS可证明∠BAM∠∠CAN,继而得出结论.(2)也可以通过证明∠BAM∠∠CAN,得出结论,和(1)的思路完全一样.(3)首先得出∠BAC=∠MAN,从而判定∠ABC∠∠AMN,得到AB ACAM AN=,根据∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,得到∠BAM=∠CAN,从而判定∠BAM∠∠CAN,得出结论.【详解】解:(1)证明:∠∠ABC、∠AMN是等边三角形,∠AB=AC,AM=AN,∠BAC=∠MAN=60°.∠∠BAM=∠CAN.∠在∠BAM和∠CAN中,AB ACBAM CANAM AN=⎧⎪∠=∠⎨⎪=⎩,∠∠BAM∠∠CAN(SAS).∠∠ABC=∠ACN.(2)结论∠ABC=∠ACN仍成立.理由如下:∠∠ABC、∠AMN是等边三角形,∠AB=AC,AM=AN,∠BAC=∠MAN=60°.∠∠BAM=∠CAN.∠在∠BAM和∠CAN中,AB ACBAM CANAM AN=⎧⎪∠=∠⎨⎪=⎩,∠∠BAM∠∠CAN(SAS),∠∠ABC=∠ACN.(3)∠ABC=∠ACN.理由如下:∠BA=BC,MA=MN,顶角∠ABC=∠AMN,∠底角∠BAC=∠MAN,∠∠ABC∠∠AMN,∠AB ACAM AN=,又∠∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,∠∠BAM=∠CAN,∠∠BAM∠∠CAN,∠∠ABC=∠ACN.4.(2022·山西长治·九年级期末)问题情境:如图1,在∠ABC中,AB=6,AC=5,点D,E 分别在边AB,AC上,且∥DE BC.数学思考:(1)在图1中,BDCE的值为 ;(2)图1中∠ABC 保持不动,将∠ADE 绕点A 按逆时针方向旋转到图2的位置,其它条件不变,连接BD ,CE ,则(1)中的结论是否仍然成立?并说明理由;(3)拓展探究:在图2中,延长BD ,分别交AC ,CE 于点F ,P ,连接AP ,得到图3,探究∠APE 与∠ABC 之间有何数量关系,并说明理由;(4)若将∠ADE 绕点A 按逆时针方向旋转到图4的位置,连接BD ,CE ,延长BD 交CE 的延长线于点P ,BP 交AC 于点F ,则(3)中的结论是否仍然成立,若成立,请说明理由;若不成立,请直接写出∠APE 与∠ABC 之间的数量关系.【答案】(1)65(2)(1)中结论仍然成立,理由见解析(3)∠APE =∠ABC ,理由见解析(4)结论不成立,∠APE +∠ABC =180°,理由见解析 【分析】(1)根据平行线分线段成比例定理求解即可;(2)根据旋转的性质得到∠BAD =∠CAE ,由(1)可证明∠BAD ∠∠CAE ,从而可证∠APE +∠ABC得到65BD AB CE AC ==;(3)由(2)可证∠ABD =∠ACE ,证明∠AFB ∠∠PFC 和∠AFP ∠∠BFC 即可得到结论;(4)证明∠ABD =∠ACE ,推出A 、B 、C 、P 四点共圆即可得到结论;(1)解:∠∥DE BC ,∠BD CE AB AC=,∠65BD AB CE AC ==;(2)解:中结论仍然成立,理由如下: ∠旋转的性质,∠∠ADE =∠ABC ,∠AED =∠ACB , ∠∠ADE ∠∠ABC ,∠AD AE AB AC=,在图2中,由旋转的性质可知,∠BAC =∠DAE ,∠∠BAD =∠CAE ,∠∠BAD ∠∠CAE ,∠65BD AB CE AC ==; (3)解:∠APE =∠ABC ,理由如下: 由(2)得∠BAD ∠∠CAE ,∠∠ABD =∠ACE , 又∠∠AFB =∠PFC ,∠∠AFB ∠∠PFC ,∠AF BFBAC BPC PF CF ==,∠∠,∠AF PF BF CF=,又∠∠AFP =∠BFC ,∠∠AFP ∠∠BFC ,∠∠CBF =∠P AF ,∠∠APE =∠ACE +∠P AF ,∠ABC =∠ABF +∠CBF ,∠∠APE =∠ABC ; (4)解:(3)结论不成立,∠APE +∠ABC =180°,理由如下: 由(2)知,∠BAD ∠∠CAE ,∠∠ABD =∠ACE , ∠A 、B 、C 、P 四点共圆,∠∠APE +∠ABC =180°.【点睛】本题主要考查了平行线分线段成比例,旋转的性质,相似三角形的性质与判定,圆内接四边形的性质等等,熟练掌握相关三角形的性质与判定是解题的关键.课后专项训练:1.(2022·湖南·中考真题)如图,点O 是等边三角形ABC 内一点,2OA =,1OB =,3OC =,则AOB ∆与BOC ∆的面积之和为( )A .34B .32C .334D .3【答案】C【分析】将AOB ∆绕点B 顺时针旋转60︒得BCD ∆,连接OD ,得到BOD 是等边三角形,再利用勾股定理的逆定理可得90COD ∠=︒,从而求解.【详解】解:将AOB ∆绕点B 顺时针旋转60︒得BCD ∆,连接OD ,OB OD ∴=,60BOD ∠=︒,2CD OA ==,BOD ∴∆是等边三角形, 1OD OB ∴==,∵()2222134OD OC +=+=,2224CD==,222OD OC CD ∴+=,90DOC ∴∠=︒, AOB ∴∆与BOC ∆的面积之和为23133113424BOC BCD BOD CODSSSS+=+=⨯+⨯⨯=.故选:C .【点睛】本题主要考查了等边三角形的判定与性质,勾股定理的逆定理,旋转的性质等知识,利用旋转将AOB ∆与BOC ∆的面积之和转化为BOCBCDSS+,是解题的关键.2.(2022·四川宜宾·中考真题)如图,ABC 和ADE 都是等腰直角三角形,90BAC DAE ∠=∠=︒,点D 是BC 边上的动点(不与点B 、C 重合),DE 与AC 交于点F ,连结CE .下列结论:①BD CE =;②DAC CED ∠=∠;③若2BD CD =,则45CF AF =;④在ABC 内存在唯一一点P ,使得PA PB PC ++的值最小,若点D 在AP 的延长线上,且AP 的长为2,则23CE =+.其中含所有正确结论的选项是( )A .①②④B .①②③C .①③④D .①②③④【答案】B【分析】证明BAD CAE ≌,即可判断①,根据①可得ADB AEC ∠=∠,由180ADC AEC ∠+∠=︒可得,,,A D C E四点共圆,进而可得DAC DEC ∠=∠,即可判断②,过点A 作AG BC ⊥于G ,交ED 的延长线于点H ,证明FAH FCE ∽,根据相似三角形的性质可得45CF AF =,即可判断③,将APC △绕A 点逆时针旋转60度,得到AB P ''△,则APP '是等边三角形,根据当,,,B P P C ''共线时,PA PB PC ++取得最小值,可得四边形ADCE 是正方形,勾股定理求得DP , 根据CE AD AP PD ==+即可判断④. 【详解】解:ABC 和ADE 都是等腰直角三角形,90BAC DAE ∠=∠=︒,,,AB AC AD AE BAD CAE ∴==∠=∠BAD CAE ∴△≌△BD CE ∴=故①正确;BAD CAE ≌ADB AEC ∴∠=∠180ADC AEC ∴∠+∠=︒,,,A D C E ∴四点共圆, CD CD =DAC DEC ∴∠=∠故②正确;如图,过点A 作AG BC ⊥于G ,交ED 的延长线于点H ,BAD CAE ≌,45,45ACE ABD ACB ∴∠=∠=︒∠=︒ 90DCE ∴∠=︒FC AH ∴∥2BD CD =,BD CE =1tan 2DC DEC CE ∴∠==,13CD BC = 设6BC a =,则2DC a =,132AG BC a ==,24EC DC a ==则32GD GC DC a a a =-=-= FC AH ∥1tan 2GD H GH ∴==22GH GD a ∴==325AH AG GH a a a ∴=+=+= AH ∠CE ,FAH FCE ∴∽CF CE AF AH ∴=4455CF a AF a ∴==则45CF AF =;故③正确 如图,将ABP 绕A 点逆时针旋转60度,得到AB P ''△,则APP '是等边三角形,PA PB PC PP P B PC B C '''+++∴'+=≥,当,,,B P P C ''共线时,PA PB PC ++取得最小值, 此时180********CPA APP '∠=-∠=︒-=︒︒︒,180********APB AP B AP P ∠=∠=︒-∠=︒-︒='''︒, 360360*********BPC BPA APC ∠=︒-∠-∠=︒-︒-︒=︒,此时120APB BPC APC ∠=∠=∠=︒,AC AB AB '==,AP AP '=,APC AP B ''∠=∠, AP B APC ''∴≌, PC P B PB ''∴==, 60APP DPC '∠=∠=︒,DP ∴平分BPC ∠, PD BC ∴⊥,,,,A D C E 四点共圆,90AEC ADC ∴∠=∠=︒,又AD DC BD ==,BAD CAE ≌, AE EC AD DC ∴===,则四边形ADCE 是菱形, 又90ADC ∠=︒,∴四边形ADCE 是正方形,9060150B AC B AP PAC P AP ''''∠=∠+∠+∠=︒+︒=︒,则'B A BA AC ==,()1180152B ACB B AC '''∠=∠=︒-∠=︒,30PCD ∠=︒,3DC PD ∴=,DC AD =,2AP =,则()312AP AD DP DP =-=-=,23131DP ∴==+-, 2AP =,33CE AD AP PD ∴==+=+,故④不正确,故选B .【点睛】本题考查了旋转的性质,费马点,圆内接四边形的性质,相似三角形的性质与判定,全等三角形的性质与判定,勾股定理,解直角三角形,正方形的性质与判定,掌握以上知识是解题的关键. 3.(2022·湖北·襄阳市樊城区青泥湾中学九年级阶段练习)如图,已知AOB 和MON 都是等腰直角三角形(22OA <OM =ON ),∠AOB =∠MON =90°.(1)如图①,连接AM,BN,求证:AOM∠BON;(2)若将MON绕点O顺时针旋转,①如图②,当点N恰好在AB边上时,求证:22220BN AN N+=;②当点A,M,N在同一条直线上时,若OB=4,ON =3,请直接写出线段BN的长.【答案】(1)见解析;(2)①见解析;②46322+或46322-.【分析】(1)利用SAS定理证明AOM BON≌即可;(2)①连接AM,证明AOM BON≌,即可证2222BN AN ON=+;②当点N在线段AM上时,连接BN,在Rt ANB中构造勾股定理的等量关系;当点M在线段AN上时,同理即可求得.(1)证明:90AOB MON︒∠=∠=,MON AON AOB AON∴∠+∠=∠+∠,即AOM BON∠=∠.MON和AOB是等腰直角三角形,,OM ON OA OB∴==,AOM BON∴≌(SAS) .(2)解:①证明:如图,连接AM.90AOB MON︒∠=∠=,MON AON AOB AON∴∠-∠=∠-∠,即AOM BON∠=∠.MON和AOB是等腰直角三角形,,,45OM ON OA OB OAB OBA︒∴==∠=∠=,.()AOM BON SAS∴≌45,MAO OBA AM BN︒∴∠=∠==,90MAN︒∴∠=,222AM AN MN∴+=.MON是等腰直角三角形,222MN ON∴=,2222BN AN ON=∴+.②46322+或46322-.∠△AOB和△MON都是等腰直角三角形,OB=4,ON =3,∠42,32AB MN==.当点N在线段AM上时,如图,连接BN,设BN x=,由(1)可知AOM BON≌.∠OAM OBN∠=∠,AM BN x==.∠NAB ABN OAM OAB ABN OBN ABN OAB∠+∠=∠+∠+∠=∠+∠+∠18090OBA OAB AOB =∠+∠=︒-∠=︒,∠()18090ANB NAB ABN ∠=︒-∠+∠=︒,∠ANB 是直角三角形,222+=AN BN AB . 又∠32AN AM MN BN MN x =-=-=-,∠222(32)(42)x x -+=, 解得:1246324632,22x x +-+==(舍去)∠46322BN +=;当点M 在线段AN 上时,如图,连接BN ,设BN x =,由(2)①可知AOM BON ≌. ∠OAM OBN ∠=∠,AM BN x ==.∠NAB ABN OAM OAB ABN OBN ABN OAB ∠+∠=∠+∠+∠=∠+∠+∠18090OBA OAB AOB =∠+∠=︒-∠=︒,∠()18090ANB NAB ABN ∠=︒-∠+∠=︒,∠ANB 是直角三角形,222+=AN BN AB . 又∠32AN AM MN BN MN x =+=+=+,∠222(32)(42)x x ++=, 解得: 1246324632,22x x ---==(舍去)∠46322BN -=综上所述:BN 的长为46322+或46322-.【点睛】本题主要考查全等三角形的判定与性质、等腰直角三角形的性质,三点共线分类讨论,对几何题目的综合把握是解题关键. 4.(2022·山西朔州·九年级期末)综合与实践问题情境:在数学课上老师出了这样一道题:如图1,在ABC 中6AB AC ==,30BAC ∠=︒,求BC 的长.(1)探究发现:如图2,勤奋小组经过思考后,发现:把ABC 绕点A 顺时针旋转90︒得到ADE ,连接BD ,BE ,利用直角三角形的性质即可求解,请你根据勤奋小组的思路,求BC 的长; (2)探究拓展:如图3,缜密小组的同学在勤奋小组的启发下,把ABC 绕点A 顺时针旋转120︒后得到ADE ,连接BD ,CE 交于点F ,交AB 于点G ,请你判断四边形ADFC 的形状并证明;(3)奇异小组的同学把图3中的BGF 绕点B 顺时针旋转,在旋转过程中,连接AF ,发现AF 的长度在不断变化,直接写出AF 的最大值和最小值.【答案】(1)BC 的长是3632-,见解析;(2)四边形ADFC 是菱形,见解析; (3)AF 的最大值是63,AF 的最小值是1263-,见解析.【分析】(1)过点B 作BH DE ⊥交DE 的延长线于点H .由旋转性质进一步得AEB △是等边三角形, EBH △是等腰直角三角形,ABD △是等腰直角三角形,45BDA ∠=︒,在Rt EBH △中由勾股定理,1832HE HB ===,在Rt BDH 中,62BD =.在Rt BDH 中,求得36=DH ,进而得解;(2)利用旋转的性质得到相关结论,进一步证明四边形ADFC 是平行四边形.又有AD AC =,得证四边形ADFC 是菱形;(3)作AH ∠BD 于点H ,则90AHB ∠=︒,利用解直角三角形求得BF 的长,分两种情况进行分析,即可得解. (1)解:如图4,延长CB 、DE 交于点H .∠ABC 绕点A 顺时针旋转90︒得到ADE ∠ABC ADE △≌△,90CAE BAD ∠=∠=︒,∠H =90°, ∠AB AD ==6,AC AE ==6,DAE BAC ∠=∠,DE BC =∠6AB AC ==,30BAC ∠=︒∠∠ABC 是等腰三角形,60∠=∠-∠=︒BAE CAE BAC ∠180752-=︒∠∠=︒BAC ABC , ∠=6AE AB = ∠AEB △是等边三角形∠6BE AB ==,60ABE ∠=︒∠18045∠=︒-∠-∠=︒EBH ABE ABC ∠EBH △是等腰直角三角形∠HE HB =.∠AD AB =,90DAB ∠=︒.∠ABD △是等腰直角三角形,45BDA ∠=︒.在Rt EBH △中,由勾股定理,得222+=HE HB BE .∠2226+=HE HB =36.∠HE 2=HB 2=18∠1832HE HB ===.在BDH 中,90H ∠=︒,30∠=∠-∠=∠=︒-∠BDH EDA BDA ABC BDA .在Rt BDH 中,1322==BH BD .∠62BD =. 在Rt BDH 中,tan ∠=BH BDH DH ,∠3233=DH , ∠36=DH .∠3632=-=-DE DH EH .∠DE BC =,∠BC 的长是3632-.(2)解:四边形ADFC 是菱形.理由如下:∠ABC 绕点A 顺时针旋转120︒得到ADE ,AB AC =,30BAC ∠=︒,∠ABC ADE △≌△,120∠=∠=︒BAD CAE .∠AC AE =,AB AD =,30BAC DAE ∠=∠=︒.∠AC AE AB AD ===.∠∠ACE 是等腰三角形∠180302︒-∠=︒∠=∠=CAE ACE AEC .同理可得:30ABD ADB ∠=∠=︒.∠180752-=︒∠∠=︒BAC ACB .∠45∠=∠-∠=︒BCG ACB ACE ,105∠=∠+∠=︒FBC ABC ABF .∠在BFC △中,18030∠=︒-∠-∠=︒BFG FBC BCG .∠∠=∠BFG ACF ,∠=∠BFG ADB .∠∥DB AC ,∥FC AD .∠四边形ADFC 是平行四边形.∠AD AC =,∠四边形ADFC 是菱形.(3)如图5,作AH ∠BD 于点H ,则90AHB ∠=︒∠ABC 绕点A 顺时针旋转120︒得到ADE , ∠ABC ADE △≌△,120BAD ∠=︒∠AB AD ==6∠∠ABD 是等腰三角形∠BH =DH =12BD ∠180302BAD ABD ADB ︒-∠∠=∠==︒ .在Rt △ABH 中,∠AHB =90°,∠ABH =30°, AB =6∠cos cos30BH ABH AB==︒∠∠BH =33∠BD =2 BH =63 由(2)知四边形ADFC 是菱形∠DF =AD =6 ∠BF =BD -DF =63-6当BGF 绕点B 顺时针旋转,在旋转过程中,当旋转到A 、B 、F 第一次三点共线时,如图6,∠=BF ''BF此时AF 有最小值,此时AF =AF ''=AB -BF ''=AB -BF =6-(63-6)=12-63 当旋转到A 、B 、F 第二次三点共线时,如图7,BGF ''△≌△BGF ,∠=BF 'BF 此时AF 有最大值,此时AF =AB +BF '=AB +BF =6+63-6=63故AF 的最大值是63,AF 的最小值是1263-【点睛】本题以图形的变换——旋转为载体考查了全等三角形的性质和判定,菱形的判定,线段长度的最值问题等知识点,综合性较强,准确作出辅助线是解题的关键.5.(2022·湖北武汉·八年级期末)已知ABC中,∠BAC=60°,以AB和BC为边向外作等边ABD和等边BCE.(1)连接AE、CD,如图1,求证:AE=CD;(2)若N为CD中点,连接AN,如图2,求证:CE=2AN(3)若AB∠BC,延长AB交DE于M,DB=2,如图3,则BM=_______(直接写出结果)【答案】(1)见解析(2)见解析(3)22【分析】(1)先判断出∠DBC=∠ABE,进而判断出∠DBC∠∠ABE,即可得出结论;(2)先判断出∠ADN∠∠FCN,得出CF=AD,∠NCF=∠AND,进而判断出∠BAC=∠ACF,即可判断出∠ABC∠∠CF A,即可得出结论;(3)先判断出∠ABC∠∠HEB(ASA),得出22=,再判断出∠ADM∠∠HEMBH AC==,AB EH(AAS),得出AM=HM,即可得出结论.(1)解:∠∠ABD和∠BCE是等边三角形,∠BD=AB,BC=BE,∠ABD=∠CBE=60°,∠∠ABD+∠ABC=∠CBE+∠ABC,∠∠DBC=∠ABE,∠∠ABE∠∠DBC(SAS),∠AE=CD;(2)解:如图,延长AN使NF=AN,连接FC,∠N为CD中点,∠DN=CN,∠∠AND=∠FNC,∠∠ADN∠∠FCN(SAS),∠CF=AD,∠NCF=∠AND,∠∠DAB=∠BAC=60°∠∠ACD +∠ADN=60°∠∠ACF=∠ACD+∠NCF=60°,∠∠BAC=∠ACF,∠∠ABD 是等边三角形,∠AB =AD ,∠AB =CF ,∠AC =CA ,∠∠ABC ∠∠CF A (SAS ),∠BC =AF ,∠∠BCE 是等边三角形,∠CE =BC =AF =2AN ;(3)解: ∠∠ABD 是等边三角形,∠2AB AD DB ===,∠BAD =60°,在Rt ∠ABC 中,∠ACB =90°-∠BAC =30°,∠222AC AB ==,如图,过点E 作EH // AD 交AM 的延长线于H ,∠∠H =∠BAD =60°,∠∠BCE 是等边三角形,∠BC =BE ,∠CBE =60°,∠∠ABC =90°,∠∠EBH =90°-∠CBE =30°=∠ACB ,∠∠BEH =180°-∠EBH -∠H =90°=∠ABC ,∠∠ABC ∠∠HEB (ASA ),∠22BH AC ==,AB EH =,∠AD =EH ,∠∠AMD =∠HME ,∠∠ADM ∠∠HEM (AAS ),∠AM =HM ,∠()()1111122222BM AM AB AH AB AB BH AB BH AB BH AB =-=-=+-=-=- ∠22BH =,2AB =,∠22BM =.故答案为:22. 【点睛】此题是三角形综合题,主要考查了等边三角形的性质,含30°角的直角三角形的性质,全等三角形的判定和性质,构造出全等三角形是解本题的关键.6.(2022·湖南·长沙市湘郡培粹实验中学八年级阶段练习)如图1,在Rt ∠ABC 中,∠B =90°,AB =BC =4,点D ,E 分别为边AB ,BC 上的中点,且BD =BE =2.(1)如图2,将∠BDE 绕点B 逆时针旋转任意角度α,连接AD ,EC ,则线段EC 与AD 的关系是;(2)如图3,DE∠BC,连接AE,判断∠EAC的形状,并求出EC的长;(3)继续旋转∠BDE,当∠AEC=90°时,请直接写出EC的长.【答案】(1)EC=AD,EC∠AD(2)等腰三角形,10(3)151【分析】(1)延长CE交AD于F,交AB于O,证明∠ABD∠∠CBE(SAS),得∠BCE=∠BAD,CE=AD,再由∠AOF=∠BOC,可得∠AFC=∠ABC=90°,即可得到结论;(2)设DE与AB的交点为H,可得AB是DE的垂直平分线,利用勾股定理可求出AE的长,由(1)知CE=AD,从而得出答案;(3)分当点E在BC上方时和当点E在BC下方时,分别画图,利用勾股定理计算即可.(1)EC与AD垂直且相等,理由如下:延长CE交AD于F,交AB于O,∠∠BDE和△ABC都是等腰直角三角形,∠BD=BE,AB=BC,∠DBE=∠ABC=90°,∠∠ABD=∠CBE,∠∠ABD∠∠CBE(SAS),∠∠BCE=∠BAD,CE=AD,∠∠AOF=∠BOC,∠∠AFE=∠ABC=90°,∠AD∠CE,∠故答案为:EC=AD,EC∠AD;(2)设DE与AB的交点为H,∠DE∠BC,∠∠AHE=∠ABC=90°,∠BD=BE,∠AB是DE的垂直平分线,∠AD =AE ,由(1)知AD =CE ,∠AE =CE ,∠∠ACE 是等腰三角形, ∠BE =2,∠BH =HE =1,∠AH =AB ﹣BH =4﹣1=3,在Rt △AHE 中,由勾股定理得:AE =2210AH HE +=,∠CE =AE =10;(3)如图4,当点E 在BC 上方时,过点B 作BG ∠DE 于G ,∠∠AEC =90°,CE ∠AD ,∠A 、E 、D 三点共线,∠AG =2215AB BG -=,∠AD =AG +DG =151+,∠CE =AD =15+1;如图,当点E 在BC 下方时,同理可得CE =CG ﹣GE =15﹣1.综上:CE =15+1或15﹣1.【点睛】本题主要考查了等腰直角三角形的判定与性质,全等三角形的判定与性质,旋转的性质,勾股定理等知识,根据前面探索的结论解决新的问题是解题的关键.7.(2022·广东·惠州一中八年级期中)ABC 为等边三角形,4AB =,AD BC ⊥于点D .E 为线段AD 上一点,3AE =.以AE 为边在直线AD 右侧构造等边AEF .连结CE ,N 为CE 的中点.(1)如图1,EF 与AC 交于点G ,①连结NG ,求线段NG 的长;②连结ND ,求DNG ∠的大小.(2)如图2,将AEF 绕点A 逆时针旋转,旋转角为α.M 为线段EF 的中点.连结DN 、MN .当30120α︒<<︒时,猜想DNM ∠的大小是否为定值,并证明你的结论.【答案】(1)①72;②120︒;(2)120DNM ∠=︒,证明见解析 【分析】(1)①根据等边三角形的性质,AD BC ⊥,可得60,30AEF EAG ∠=︒∠=︒,NG 是Rt EGC △斜边EC 上的中线,勾股定理在Rt EDC 中可求得EC 的长,进而求得NG 的长;②根据①的结论可得NG NC ND ==,根据120NGC NCG NCD NDC ∠+∠+∠+∠=︒=GND ∠,即可求得GND ∠的度数; (2)连接,BE FC ,证明BAE CAF ≌,进而可得ABE ACF ∠=∠,则120EBC BCF ABC ABE ACB ACF ABC ACB ∠+∠=∠-∠+∠+∠=∠+∠=︒,进而根据D 为BC的中点,N 为EC 的中点,M 为EF 的中点,根据三角形中位线定理可得,DN BE MN CF ∥∥,进而可得MNE DNE ∠+∠=FCE DCE ∠+∠120=︒【详解】(1)①ABC 是等边三角形,4,AB AD BC =⊥222,23DB DC AD AC DC ∴===-=,60BAC ∠=︒3AE =3ED AD AE ∴=-=AEF 是等边三角形,60AEG ∴∠=︒1302DAG DAB CAB ∠=∠=∠=︒90EGC ∴∠=︒ N 为CE 的中点()22221117322222NG EC DE DC ∴==+=+= ②如图,连接DN ,11,22NG EC NC DN EC ===NG NC ND ∴== ==NGC NCG NCD NDC ∴∠∠∠∠,()2=2120NGC NCG NCD NDC NCD NCG BCA ∴∠+∠+∠+∠=∠+∠=︒NGC NCG NCD NDC GNE DNE GND ∠+∠+∠+∠=∠+∠=∠120GND ∴∠=︒;(2)120DNM ∠=︒,理由如下,如图,连接,BE FC ABC,AEF 为等边三角形,,AB AC AE AF ∴==,60BAE BAC CAE CAE ∠=∠+∠=︒+∠60CAF CAE EAF CAE ∠=∠+∠=︒+∠BAE CAF ∴∠=∠BAE CAF ∴△≌△∴ABE ACF ∠=∠则120EBC BCF ABC ABE ACB ACF ABC ACB ∠+∠=∠-∠+∠+∠=∠+∠=︒D 为BC 的中点,N 为EC 的中点,M 为EF 的中点,DN BE MN CF ∴∥∥,MNE FCE EBC NDC ∴∠=∠∠=∠END NDC NCD ∠=∠+∠∴DNM DNE MNE NDC ACB ACN ECF∠=∠+∠=∠+∠+∠+∠=∠+∠+∠=∠+∠=︒120EBC ACB ACF EBC BCFDNM∴∠=︒120【点睛】本题考查了等边三角形的性质,勾股定理,三线合一,直角三角形斜边上的中线等于斜边的,勾股定理,中位线定理,三角形全等的性质与判定,旋转的性质,综合运用以上知识是解题的关键.8.(2022•新乡中考模拟)在△ABC中,CA=CB=m,在△AED中,DA=DE=m,请探索解答下列问题.【问题发现】(1)如图1,若∠ACB=∠ADE=90°,点D,E分别在CA,AB上,则CD 与BE的数量关系是,直线CD与BE的夹角为;【类比探究】(2)如图2,若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图2所示的位置,则CD与BE之间是否满足(1)中的数量关系?说明理由.【拓展延伸】(3)在(1)的条件下,若m=2,将△AED绕点A旋转过程中,当B,E,D 三点共线.请直接写出CD的长.【分析】(1)根据等腰直角三角形的性质得到AB=AC=m,AE=AD=m,计算即可;(2)过点C作CH⊥AB于H,延长CD、BE交于点F,根据直角三角形的性质得到AB=AC,AE=AD,证明△CAD∽△BAE,根据相似三角形的性质解答即可;(3)分点E在线段BD上、点D在线段BE上两种情况,根据相似三角形的性质计算即可.【解答】解:(1)∵∠ACB=∠ADE=90°,CA=CB,DA=DE,∴∠A=∠B=∠DEA=45°,∴AB=AC=m,AE=AD=m,∴CD=AC﹣AD=m,BE=AB﹣AE=m,∴BE=CD,∵∠A=45°,∴直线CD与BE的夹角为45°,故答案为:BE=CD,45°;(2)不满足,BE=CD,直线CD与BE的夹角为30°,理由如下:如图2,过点C作CH⊥AB于H,延长CD、BE交于点F,∵CA=CB,∴AH=HB,∵∠ACB=∠ADE=120°,CA=CB,DA=DE,∴∠CAB=∠CBA=30°,∠DAE=∠DEA=30°,∴AC=2CH,∠CAD=∠BAE,由勾股定理得:AH=AC,∴AB=AC,同理可得:AE=AD,∴=,∵∠CAD=∠BAE,∴△CAD∽△BAE,∴==,∠ACD=ABE,∴BE=CD,∠F=∠CAB=30°,∴BE=CD,直线CD与BE的夹角为30°;(3)如图3,点E在线段BD上,∵m=2,∴AD=DE=1,AB=2,由勾股定理得:BD==,∴BE=BD﹣DE=﹣1,∴CD=BE=,如图4,点D在线段BE上,BE=BD+DE=+1,∴CD=BE=,综上所述:当B,E,D三点共线.CD的长为或.【点评】本题考查的是相似三角形的判定和性质、直角三角形的性质、等腰三角形的性质,掌握相似三角形的判定定理和性质定理是解题的关键.9.(2022•虹口区期中)如图,在△ABC和△ADE中,△BAD=△CAE,△ABC=△ADE.(1)求证:△ABC△△ADE;(2)判断△ABD与△ACE是否相似?并证明.【分析】(1)由△BAD=△CAE,可得△BAC=△DAE,又有△ABC=△ADE,即可得出相似;(2)有(1)中可得对应线段成比例,又有以对应角相等,即可判定其相似.【解答】证明:(1)△△BAD=△CAE,△△BAC=△DAE,。
几何模型之——“手拉手”及其经典考题

几何模型之——“手拉手”及其经典考题几何模型之——“手拉手”及其经典考题一、“手拉手”全等模型如图,△ABC与△ADE都是等腰三角形,AB=AC,AD=AE.∠BAC=∠DAE.结论:△BAD≌△CDE.二、模型分析手拉手模型常和旋转结合,在考试中作为几何综合题目出现。
三、模型实例例1.如图,△ABC与△EDC都为等腰直角三角形,连接AE、BD,相交于点F.问:(1)AE与BD是否相等?(2)AE与BD之间的夹角为多少度?例2.如图,直线AB的同一侧作△ABD和△BCE都为等边三角形,连接AE交DB于点G、连接CD交BE于点F,AE与CD交于点H.求证:(1)△ABE≌△DBC;(2)AE=DC;(3)∠DHA=60°;(4)△AGB≌△DFB;(5)△EGB≌△CFB;(6)连接GF,GF∥AC;(7)连接HB,HB平分∠AHC。
四、精选练习1.如图,在△ABC中,AC=CB,∠ACB=90°,D为AC延长线上一点,点E在BC上,且AE=BD.(1)求证:CD=CE;(2)若∠BAE=30°,求∠ABD度数.2.如图,△ABD与△BCE都为等边三角形,连接AE与CD,延长AE交CD于点F.求证:(1)AE=DC;(2)∠AFD=60°;(3)连接FB,FB平分∠AFC。
3.在线段AE同侧作等边△CDE(∠ACE<120°),点F,G分别是线段BE和AD的中点.求证:△CFG是等边三角形.4.将等腰Rt△ABC和等腰Rt△ADE按图①方式放置,∠A=90°,AD边与AB边重合,AB=2AD=4。
将△ADE绕点A逆时针方向旋转一个角度(0°<>180°),BD的延长线交CE于P.(1)如图②,证明:BD=CE,BD⊥CE;(2)如图③,在旋转的过程中,当AD⊥BD时,求出CP的长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形专题------手拉手模型不积跬步,无以至千里;不积小流,无以成江海。
荀子——《劝学》学习目标:1、认识并学会识别手拉手模型
2、掌握手拉手模型的证明
3、学会运用手拉手模型解题
手拉手:Ⅰ顶角相等的两个等腰三角形
Ⅱ顶点相同
手拉手模型:1、识别:顶角相等的等腰三角形,顶点相同
2、步骤:等边、等角、全等找(大手拉小手)
常见图形
【例1】如图在直线ABC的同一侧作两个等边三角形ABD
∆,连结AE与CD,
∆与BCE
证明以下常用结论:
1、DBC
∆
ABE∆
≅
2、DC
AE=
60(底边夹角等于顶角)
3、AE与DC之间的夹角为︒
4、DFB
AGB∆
∆
≅
5、CFB
≅
∆
EGB∆
6、连接GF,则B GF
∆为等边三角形
7、BH平分AHC
∠
8、AC
GF//
9、AH=DH+BH,CH=EH+BH(截长补短法)
【变式精练1】如图两个等边三角形ABD
∆,连结AE与CD,
∆与BCE
证明(1)DBC
∆
≅
ABE∆
(2)DC
AE=
(3)AE与DC之间的夹角为︒
60
(4)AE与DC的交点设为H,BH平分AHC
∠
【变式精练2】如图两个等边三角形ABD
∆,连结AE与CD,
∆与BCE
证明(1)DBC
≅
∆
ABE∆
(2)DC
AE=
60
(3)AE与DC之间的夹角为︒
(4)AE与DC的交点设为H,BH平分AHC
∠
【例2】如图,两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H
问:(1)CDE ADG ∆≅∆是否成立?
(2)AG 是否与CE 相等?
(3)AG 与CE 之间的夹角为多少度?
(4)HD 是否平分AHE ∠?
【例3】如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H
问:(1)CDE ADG ∆≅∆是否成立?
(2)AG 是否与CE 相等?
(3)AG 与CE 之间的夹角为多少度?
(4)HD 是否平分AHE ∠?
【例4】两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ,
问:(1)DBC ABE ∆≅∆是否成立?
(2)AE 是否与CD 相等?
(3)AE 与CD 之间的夹角为多少度?
(4)HB 是否平分AHC ∠?
综合练习
1、如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正∆ABC和正∆CDE,AD
与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,以下五个结论:
①AD=BE ②PQ∥AE ③AP=BQ
④DE=DP ⑤∠AOB=60°
恒成立的结论有 __________________ (填序号)
2、如图,在线段A E 同侧作两个等边三角形△ABC 和△CDE(∠ACE<120°),点P与点M
分别是线段 BE 和AD 的中点,则△CPM 是()
A.钝角三角形B.直角三角形
C.等边三角形D.非等腰三角形
3、如图,△DAC 和△EBC 均是等边三角形,AE、BD 分别与CD、CE 交于点 M、N,有如下结
论:①△ACE≌△DCB;②CM=CN;
③AC=DN.其中,正确结论的个数是()
A.3 个B.2 个
C.1 个D.0 个
4、如图,四边形ABCD、BEFG 均为正方形,连接AG、CE.
(1)求证:AG=CE;
(2)求证:AG⊥CE.
5、、(1)问题发现
如图 1,△ACB 和△DCE 均为等边三角形,点A,D,E 在同一直线上,连接BE.
填空:①∠AEB 的度数为___________;②线段 AD,BE 之间的数量关系为_________ (2)拓展探究
如图 2,△ACB 和△DCE 均为等腰直角三角形,∠ACB=∠DCE=90°,点 A,D,E 在同一直线上,CM 为△DCE 中DE 边上的高,连接 BE,请判断∠AEB 的度数及线段CM, AE,BE 之间的数量关系,并说明理由.。
