工程制图 轴测投影图
合集下载
07第7章轴测投影

O1 X1
Y1 X
Z
S O
Y
二、正等轴测投影的轴间角和轴向伸缩系数
Z
O
120º
120º
X
Y
轴间角:120° 轴向变形系数:p=q=r=0.82 简化轴向变形系数: p=q=r=1
5.4 平行于坐标面的圆的轴测投影
Z
椭圆
X
Y
注意椭圆长、短轴的方向!
画法:八点法(以水平圆为例)
画法:四心法(以水平圆为例)
轴间角:120° 轴向变形系数:p=q=r=o.82 简化轴向变形系数: p=q=r=1
x'
a' b'
xa
s
o' o"
y"
c' a"(c") b"
oc
b
y
画坐标轴
按各点坐标沿轴度量
连线并加深X1 AZ1 NhomakorabeaSCO130° Y1
B
例:画出圆柱体的正等测 o'
x'
z'
x
o
y
外切正方形
X1
Y1
Z1
四心椭圆法(菱形法) 注意:椭圆长、短轴方向
土木工程制图
Civil Engineering Drawing
第7章 轴测投影
西北工业大学出版社
Press of Northwestern Polytechnical University
目录
• 7.1 基本知识 • 7.2 斜轴测投影 • 7.3 正等轴测投影 • 7.4 平行于坐标面的圆的轴测投影 • 7.5 轴测投影的画法
G2● O1 G●
1
E2 ●
Y1 X
Z
S O
Y
二、正等轴测投影的轴间角和轴向伸缩系数
Z
O
120º
120º
X
Y
轴间角:120° 轴向变形系数:p=q=r=0.82 简化轴向变形系数: p=q=r=1
5.4 平行于坐标面的圆的轴测投影
Z
椭圆
X
Y
注意椭圆长、短轴的方向!
画法:八点法(以水平圆为例)
画法:四心法(以水平圆为例)
轴间角:120° 轴向变形系数:p=q=r=o.82 简化轴向变形系数: p=q=r=1
x'
a' b'
xa
s
o' o"
y"
c' a"(c") b"
oc
b
y
画坐标轴
按各点坐标沿轴度量
连线并加深X1 AZ1 NhomakorabeaSCO130° Y1
B
例:画出圆柱体的正等测 o'
x'
z'
x
o
y
外切正方形
X1
Y1
Z1
四心椭圆法(菱形法) 注意:椭圆长、短轴方向
土木工程制图
Civil Engineering Drawing
第7章 轴测投影
西北工业大学出版社
Press of Northwestern Polytechnical University
目录
• 7.1 基本知识 • 7.2 斜轴测投影 • 7.3 正等轴测投影 • 7.4 平行于坐标面的圆的轴测投影 • 7.5 轴测投影的画法
G2● O1 G●
1
E2 ●
轴测投影—轴测投影的基本知识(工程制图课件)

Y1
P
Z1 Z
X1
O1
O
X
图3 正轴测投影
02 轴测投影的分类
轴测图
正轴测图 斜轴测图
正等轴测图 p = q = r 正二等轴测图 p = q r 或 p q=r 或 p= r q 正三轴测图 p q r
斜等轴测图 p = q = r 斜二等轴测图 p = q r 或 p q=r 或 p= r q 斜三轴测图 p q r
测投影图,简称轴测图。
Y1
P
Z1 Z
Y
X1
O1
S
O
X
图2 轴测投影的形成
01 轴测投影的形成
Y1
P
Z1 Z
Y
X1
O1
S
O
X
轴测轴:形体上的直角坐标轴OX、OY、OZ 在轴测投影面上的投影O1X1、 O1Y1、 O1Z1 称为轴测轴。
轴间角:相邻两根轴测轴之间的夹角 ∠X1O1Y1、 ∠X1O1Z1 、 ∠Y1O1Z1称为轴间 角。
《工程制图》
轴测投影的基本知识
(a)
(b)
图1
三面正投影图与轴测投影图
(a)三面正投影图 (b)轴测投影图
轴测投影的基本知识
1 轴测投影的形成 2 轴测投影图的分类 3 轴测投影图的投影特性
01 轴测投影的形成
将空间形体连同确定其空间位置的直角坐标系,沿不平行于任一坐标面
的方向,用平行投影法将其投影到单一投影面上,所得到的投影称为轴
02
轴测投影的分类
Z
Y
O
S
Z1 X Y1
O1
P
X1
图4 斜轴测投影
第一种情况
当坐标系O-XYZ中的三个坐标轴 都与投影面P相倾斜,投影线S与
工程制图-第五章-轴测图详解

斜等轴测图 p = q = r 斜二轴测图 p = r q 斜三轴测图 p q r
正等轴测图
斜二轴测图
➢5.1.3 轴测图的投影特性
(1)平行性:物体上互相平行的线段,轴测图中仍然互 相平行。
(2)沿轴性:凡是与坐标轴平行的线段,就可以在轴测图上 沿轴向进行度量和作图。
注意:与坐标轴不平行的线段其伸缩系数与之不同,不能 直接度量与绘制,只能根据端点坐标,作出两端点后连线绘制 。
例5:作出如图所示带孔圆锥台的斜二轴测图。
x′
o′
o〞
a″ y〞
L
Z1
X1
O1
L2
A
O 1A
Y1
圆弧公切
线
➢5.3.3 轴承座的斜二轴测图
例6:已知两视图,画斜二轴测图。
x′
o′
z〞
L1
L o〞 y〞圆弧公切线
Z1
X1 L1/2 L/2
o1
Y1
本章结束
第五步:擦去作图 线,加深轮廓线, 完成轴测图。
⒉ 切割法
例2:已知三视图,画轴测图。
➢5.2.3 回转体的正等轴测图 ⒈ 平行于各个坐标面的椭圆的画法
平行于W面的椭 圆长轴⊥O1X1轴
Z1
平行于H面的椭 圆长轴⊥O1Z1轴
平行于V面 的椭圆长轴 ⊥O1Y1轴
X1
Y1
画法:
菱形四心椭圆法 (以平行于H面的圆为例)
O X
轴间角
正轴测图
斜轴测图
Y 物体上 OX, OY, OZ 坐标轴 投影面上 O1X1,O1Y1,O1Z1
轴测轴
X1O1Y1, X1O1Z1, Y1O1Z1
2. 轴向伸缩系数
物体上平行于坐标轴的线段在轴测图上的长度与实际长 度之比叫做轴向伸缩系数。
正等轴测图
斜二轴测图
➢5.1.3 轴测图的投影特性
(1)平行性:物体上互相平行的线段,轴测图中仍然互 相平行。
(2)沿轴性:凡是与坐标轴平行的线段,就可以在轴测图上 沿轴向进行度量和作图。
注意:与坐标轴不平行的线段其伸缩系数与之不同,不能 直接度量与绘制,只能根据端点坐标,作出两端点后连线绘制 。
例5:作出如图所示带孔圆锥台的斜二轴测图。
x′
o′
o〞
a″ y〞
L
Z1
X1
O1
L2
A
O 1A
Y1
圆弧公切
线
➢5.3.3 轴承座的斜二轴测图
例6:已知两视图,画斜二轴测图。
x′
o′
z〞
L1
L o〞 y〞圆弧公切线
Z1
X1 L1/2 L/2
o1
Y1
本章结束
第五步:擦去作图 线,加深轮廓线, 完成轴测图。
⒉ 切割法
例2:已知三视图,画轴测图。
➢5.2.3 回转体的正等轴测图 ⒈ 平行于各个坐标面的椭圆的画法
平行于W面的椭 圆长轴⊥O1X1轴
Z1
平行于H面的椭 圆长轴⊥O1Z1轴
平行于V面 的椭圆长轴 ⊥O1Y1轴
X1
Y1
画法:
菱形四心椭圆法 (以平行于H面的圆为例)
O X
轴间角
正轴测图
斜轴测图
Y 物体上 OX, OY, OZ 坐标轴 投影面上 O1X1,O1Y1,O1Z1
轴测轴
X1O1Y1, X1O1Z1, Y1O1Z1
2. 轴向伸缩系数
物体上平行于坐标轴的线段在轴测图上的长度与实际长 度之比叫做轴向伸缩系数。
土木工程制图第8章轴测投影

③过各顶点向下作O1Z1轴的平行线,并量取棱高h,得到下
④擦去多余的作图线并描深,完成正六棱柱的正等轴测图, 如图8-4(d)所示。 (2)切割法。该方法适用于以切割方式构成的平面立体,它以 坐标法为基础,先用坐标法画出未被切割的平面立体的轴测
8.2 正轴测图的画法
图8-4
8.2 正轴测图的画法
XOY面,街道中心为坐标原点O
(1)在投影图上定出坐标轴和原点。取街道中心为原点O,如图 8-16(a)
8.3 斜轴测图的画法
【例8-9】 (2)画轴测轴,使O1Z1轴为竖直方向,O1X1轴与水平方向成30°, O1X1轴与O1Y1轴成90°。根据水平投影作每个建筑物底面的轴 测投影(与水平投影图的形状、大小及位置均相同)。沿Z1轴方 向,过各个角点作建筑图可见棱线的轴测投影,并取每个建筑 物高度的一半,再画出每个建筑物顶面的轮廓线,如图8-16(b) 所示。(3)擦去多余的作图线并描深,完成总平面图的水平斜二 测,如图8-16(c)所示。
(1)直线的轴测投影一般为直线,特殊时为点。
(2)空间互相平行的直线,它们的轴测投影仍然互相平行。
(3)空间互相平行两线段的长度 之比等于其轴测投影的长度之比。
(4)曲线的轴测投影一般是曲线,曲线切 线的投影仍是该曲线轴测投影的切线。
8.2 正轴测图的画法
【例8-1】
作出图8-4(a) 【解】分析:由于作物体的轴测图时,习惯上是不画出虚线 的,因此作正六棱柱的轴测图时,为了减少不必要的作图线, 宜选择六棱柱的上底面作为XOY面,如图8-4(a)所示;又由 于正六棱柱前后、左右均对称,故选其上底面的中心为坐标 原点O,轴线为OZ
图8-9 正二测的画法
8.2 正轴测图的画法
【例8-6】 求作图8-10(a) 【解】分析:根据截头三棱锥的形状特点,宜选择其底面作 为XOY面,顶点C为坐标原点O,采用坐标法画出三棱锥及截 断面上各顶点的轴测投影,然后连接各顶点,这样作图较为
④擦去多余的作图线并描深,完成正六棱柱的正等轴测图, 如图8-4(d)所示。 (2)切割法。该方法适用于以切割方式构成的平面立体,它以 坐标法为基础,先用坐标法画出未被切割的平面立体的轴测
8.2 正轴测图的画法
图8-4
8.2 正轴测图的画法
XOY面,街道中心为坐标原点O
(1)在投影图上定出坐标轴和原点。取街道中心为原点O,如图 8-16(a)
8.3 斜轴测图的画法
【例8-9】 (2)画轴测轴,使O1Z1轴为竖直方向,O1X1轴与水平方向成30°, O1X1轴与O1Y1轴成90°。根据水平投影作每个建筑物底面的轴 测投影(与水平投影图的形状、大小及位置均相同)。沿Z1轴方 向,过各个角点作建筑图可见棱线的轴测投影,并取每个建筑 物高度的一半,再画出每个建筑物顶面的轮廓线,如图8-16(b) 所示。(3)擦去多余的作图线并描深,完成总平面图的水平斜二 测,如图8-16(c)所示。
(1)直线的轴测投影一般为直线,特殊时为点。
(2)空间互相平行的直线,它们的轴测投影仍然互相平行。
(3)空间互相平行两线段的长度 之比等于其轴测投影的长度之比。
(4)曲线的轴测投影一般是曲线,曲线切 线的投影仍是该曲线轴测投影的切线。
8.2 正轴测图的画法
【例8-1】
作出图8-4(a) 【解】分析:由于作物体的轴测图时,习惯上是不画出虚线 的,因此作正六棱柱的轴测图时,为了减少不必要的作图线, 宜选择六棱柱的上底面作为XOY面,如图8-4(a)所示;又由 于正六棱柱前后、左右均对称,故选其上底面的中心为坐标 原点O,轴线为OZ
图8-9 正二测的画法
8.2 正轴测图的画法
【例8-6】 求作图8-10(a) 【解】分析:根据截头三棱锥的形状特点,宜选择其底面作 为XOY面,顶点C为坐标原点O,采用坐标法画出三棱锥及截 断面上各顶点的轴测投影,然后连接各顶点,这样作图较为
名词解释正轴测投影

名词解释正轴测投影
正轴测投影图是一种特定的轴测投影图。
当投影方向垂直于轴测投影面时,所得的图形被称为正轴测投影图。
根据轴向变形系数的不同,正轴测投影图又可以进一步分为正等测轴测投影图,这是一种三个轴向变形系数都相等的类型(p=q=r) 。
在形成轴测投影图的过程中,需要将物体和确定其空间位置的直角坐标系,沿不平行于任一坐标面的方向,用平行投影法投射在单一投影面上,从而得到具有立体感的图形。
特别地,在画正等轴测图时,首先需要对物体进行形体分析,并在视图中选定直角坐标系,确定坐标轴,然后按照轴测轴方向和轴向伸缩系数作出形体上各点及主要轮廓线。
投影法和轴测图的介绍
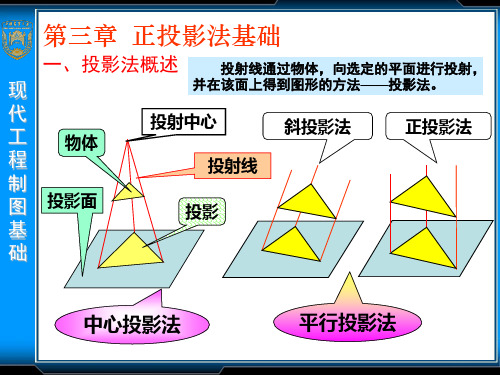
例1、已知轴测轴的轴间角和轴向伸缩系数p1、q1、r1,画
现 出点A(5,7,10)的轴测图,如图所示。
代 1、轴间角、轴测轴;
工 程
2、沿OX轴量取Oax=5 p1
制 3、过点ax作axa//OY,并使axa=7 q1
图 4、过点a作aA//OZ,并使aA =10 r1 基
础
轴测投影的种类
现 按投射方向和投影面是否垂直,分为两类: 代 正轴测投影:垂直 工 斜轴测投影:倾斜 程 制 图 基 础
复习
现 代 工 程 制
图 预习
基 础
投影法基础 三视图的投影规律 轴测图
点的投影规律 直线的投影规律
轴测投影的种类
根据各轴向伸缩系数之间关系,
现 代
正轴测投影分为:正等轴测图 p1=q1=r1=1
工
正二轴测图 p1=2q1=r1 =1(Y坐标减半)
程
正三轴测图:各不相等
制 斜轴测投影分为:
图
斜等测图
基
斜二测图 p1=2q1=r1
础
斜三测图
国家标准推荐使用三种(作图简便、兼具度量性)作为工 程图的辅助图样:正等测、正二测、斜二测。
程
制
图
基 础
两点透视
工程上常见的四种投影图
现 工程上常用的这四种图示方法,
代
多面正投影法:即正投影法,本课程重点
பைடு நூலகம்
工
轴测投影法: 本课程内容
程
标高投影法: 其他课程讲授
制
透视投影法: 其他课程讲授
图
基 因为正投影法在工程上应用最广,所以我们主要介绍正投
础 影法。以后在没有指明投影方法时,均指正投影法。
《工程制图》第六章轴测投影图

⒉ 斜二测
Z1 Z1
1 1
O1
1
1
X1
1 O1
0.5
X1
Y1
Y1
二、正等轴测图画法
⒈ 平面体的正等轴侧图画法 ⑴ 坐标法
例1:画三棱锥的正等轴测图
s
Z Z s
S Z1 ●
X a b a
X
s
b
c OOcOca
Y
b
Y
A●
X1
●CO1
Y1
●B
⑵ 切割法
例2:已知三视图,画轴测图。
⑶ 叠加法 例3:已知三视图,画轴正等测图。
⒉ 回转体的正等轴测图画法
⑴ 平行于各个坐标面的椭圆的画法
用正投影法形成的轴测图叫正轴测图。
用斜投影法形成的轴测图叫斜轴测图。
二、轴测轴、轴间角和轴向伸缩系数
1. 轴测轴和轴间角
建立在物体上的坐标轴在投影面上的投影
叫做轴测轴,轴测轴间的夹角叫做轴间角。
投影面
Z
Z1
X
O
Z1 投影面
X1
O1
Y1
Y
Z
O1 X1
Y1O正轴测Fra bibliotek斜轴测
X
Y
物体上
OX,
OY, OZ
坐标轴
平行于W面的椭
Z1
圆长轴⊥O1X1轴
平行于H面的椭 圆长轴⊥O1Z1轴
平行于V面 的椭圆长轴 ⊥O1Y1轴
X1
Y1
画法:四心椭圆法
(以平行于H面的圆为例)
e
E1
●
●
B● 1
a
b
●
●
A● 1 ●
F● 1
f
工程制图第五章轴测投影00

工程制图第五章轴测投影00
下一步 上一级
步骤四
工程制图第五章轴测投影00
下一步 上一级
完成
工程制图第五章例题2
工程制图第五章轴测投影00
[例题1] 基础的正等测图画 法
工程制图第五章轴测投影00
Z
6
6
28
20
8
Y
X
32
O
O
X
O
24
Y
工程制图第五章轴测投影00
例题3.
工程制图第五章轴测投影00
结果 上一级
工程制图第五章轴测投影00
上一级
例题4.
工程制图第五章轴测投影00
下一步 上一级
步骤一
工程制图第五章轴测投影00
下一步 上一级
步骤二
工程制图第五章轴测投影00
下一步 上一级
步骤三
工程制图第五章轴测投影00
轴测图有两种表示方法:线条图和具有真 实感的图形(图像)。
工程制图第五章轴测投影00
二、轴测图的形成
1.形成
投影面P
Z1
O1 X1 Z
O
X
Y
投射方向
将物体和确定其空 间位置的直角坐标 系沿不平行于任一 Y1 坐标面的方向,用 平行投影法将其投 射在单一投影面上 所得的具有立体感 的图形叫做轴测图。
工程制图第五章轴测投影00
六、 组合体的正等轴测图的画法
Z
Z
Z
18
10
例题1
25
16 8
8
X
36
O
O
O X
20
Y X
Y
步骤1
O Y
25
工程制图第五章轴测投影00
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
形。——实形性
5
三、轴测投影的分类
1.根据投射线和轴测投影面相对位置的不同,轴测投影可分为两 种:
(1)正轴测投影 投射线S垂直于轴测投影面P; (2)斜轴测投影 投射线S倾斜于轴测投影面P。
2.根据轴向变形系数的不同,轴测投影又可分为三种:
(1)正(或斜)等轴测投影: p=r=q; (2)正(或斜)二等轴测投影: p=r≠q或p=q≠r或 p≠q=r; (3)正(或斜)三测投影: p≠q≠r。
7
8
二、实例
例1 已知斜垫块的正投影图,画出其正等测图
z
z1
H1 xa
H2
o’ o
b
o1
x1
y
y1
9
例2 已知墩础的正投影图,画出其正等测图。zo’x来自oz1o1
x1
y1
y
10
11
三、圆的正等测 投影和画法
H面:短轴∥Z1轴 V面:短轴∥Y1轴 W面:短轴∥X1轴
12
四心椭圆法
(以平行于H面的圆为例 )
工程制图
2
基本知识
Z1
P
一、轴测投影图
的形成
O1
P-轴测投影面
S-投射方向
X1
Z Y1
轴测轴—O1X1、O1Y1、O1Z1
S
轴间角—∠X1O1Y1、∠X1O 1Z1、∠Y1O1Z1
O
X
Y
3
➢ 轴测轴上某线段长度
Z1
与它的实长之比,称
P
为轴向变形系数。 O1
O1X1/OX= p ——称为X轴
向变形系数
23
a
d
x
x1
b
c
y
y1
24
轴测投影总结
1.轴测图的选择(先正后斜,先等后二)
➢ 当形体上多个方向有圆或多个方向形状复杂时,应选用正等测。 ➢ 对于有一个方向复杂或圆弧较多的物体,应采用斜二测,使作
图简便。
25
2.轴测投影方向的选择
➢ 应针对物体的形状特征选择恰当的投影方向。使物体的主要平 面或棱线不与投影方向平行。
e
●
E1 ●
B● 1
a
b
●
●
●
A1
●
F ● 1
f
➢ 画圆的外切菱形
➢ 确定四个圆心和半径 ➢ 分别画出四段彼此相切的圆弧
13
➢钝角与大圆弧相对
➢锐角与小圆弧相对
r1
➢菱形相邻两边的中
垂线的交点就是该圆
弧的圆心。
14
如何快
速绘制
1/4圆
x
弧?
y
o x1 y1
r2 o1
x1
r1 o1
y1
15
§2-2 斜二等轴测投影
26
FIN.
27
Z
O1Y1/OY= r ——称为Y轴 X1
Y1
向变形系数
S
O1Z1/OZ= q ——称为Z轴
O
向变形系数
X
Y
4
二、轴测投影的基本性质
1.平行二直线,其轴测投影仍相互平行。——平行性 2.平行二线段长度之比,等于其轴测投影长度之比。——定比性 3.平行于轴测投影面的直线或平面,在轴测图上反映实长或实
其中,正等轴测投影、斜二等轴测投影在工程上常用,本章介绍正等 轴测投影和斜二等轴测投影。
6
§2-1 正等轴测投影
一、轴间角和轴向变 形系数
➢ 正等测的轴向变形系数p= q=r=0.82 (cos35.16°)
➢ 轴间角∠X1O1Z1=∠X1O1Y1 =∠Y1O1Z1=120°
➢ 画图时,规定把O1Z1轴画 成铅垂位置
一、 斜二测的轴间 角和轴向变形系 数
➢轴间角:∠X1O1Z1=90°,
O1Y1与水平线成45°。
➢轴向变形系数:q=0.5
16
正面斜二测图的四种形式
(a)右俯视图 (c)右仰视图
(b)左俯视图
(d)左仰视图
17
➢轴间角:∠X1O1Y1=90°,O1X1与
水平线成30°或60°。
➢轴向变形系数:p=q=r=1(绘制建
筑轴测图时候用)
18
二、斜二测投影图的画法
例1 画出下图回转体的斜二测。
b1 a1 o1
19
例2:已知两视图,画斜二轴测图。
20
例3 画出下图建筑形体的斜二测。
21
实例:
正面斜 二测:
用于画小 构件,不 适用于画 建筑外观
水平斜 二测:
能快速完 成建筑外 观轴测图
22
四、用八点法画斜二测椭圆
5
三、轴测投影的分类
1.根据投射线和轴测投影面相对位置的不同,轴测投影可分为两 种:
(1)正轴测投影 投射线S垂直于轴测投影面P; (2)斜轴测投影 投射线S倾斜于轴测投影面P。
2.根据轴向变形系数的不同,轴测投影又可分为三种:
(1)正(或斜)等轴测投影: p=r=q; (2)正(或斜)二等轴测投影: p=r≠q或p=q≠r或 p≠q=r; (3)正(或斜)三测投影: p≠q≠r。
7
8
二、实例
例1 已知斜垫块的正投影图,画出其正等测图
z
z1
H1 xa
H2
o’ o
b
o1
x1
y
y1
9
例2 已知墩础的正投影图,画出其正等测图。zo’x来自oz1o1
x1
y1
y
10
11
三、圆的正等测 投影和画法
H面:短轴∥Z1轴 V面:短轴∥Y1轴 W面:短轴∥X1轴
12
四心椭圆法
(以平行于H面的圆为例 )
工程制图
2
基本知识
Z1
P
一、轴测投影图
的形成
O1
P-轴测投影面
S-投射方向
X1
Z Y1
轴测轴—O1X1、O1Y1、O1Z1
S
轴间角—∠X1O1Y1、∠X1O 1Z1、∠Y1O1Z1
O
X
Y
3
➢ 轴测轴上某线段长度
Z1
与它的实长之比,称
P
为轴向变形系数。 O1
O1X1/OX= p ——称为X轴
向变形系数
23
a
d
x
x1
b
c
y
y1
24
轴测投影总结
1.轴测图的选择(先正后斜,先等后二)
➢ 当形体上多个方向有圆或多个方向形状复杂时,应选用正等测。 ➢ 对于有一个方向复杂或圆弧较多的物体,应采用斜二测,使作
图简便。
25
2.轴测投影方向的选择
➢ 应针对物体的形状特征选择恰当的投影方向。使物体的主要平 面或棱线不与投影方向平行。
e
●
E1 ●
B● 1
a
b
●
●
●
A1
●
F ● 1
f
➢ 画圆的外切菱形
➢ 确定四个圆心和半径 ➢ 分别画出四段彼此相切的圆弧
13
➢钝角与大圆弧相对
➢锐角与小圆弧相对
r1
➢菱形相邻两边的中
垂线的交点就是该圆
弧的圆心。
14
如何快
速绘制
1/4圆
x
弧?
y
o x1 y1
r2 o1
x1
r1 o1
y1
15
§2-2 斜二等轴测投影
26
FIN.
27
Z
O1Y1/OY= r ——称为Y轴 X1
Y1
向变形系数
S
O1Z1/OZ= q ——称为Z轴
O
向变形系数
X
Y
4
二、轴测投影的基本性质
1.平行二直线,其轴测投影仍相互平行。——平行性 2.平行二线段长度之比,等于其轴测投影长度之比。——定比性 3.平行于轴测投影面的直线或平面,在轴测图上反映实长或实
其中,正等轴测投影、斜二等轴测投影在工程上常用,本章介绍正等 轴测投影和斜二等轴测投影。
6
§2-1 正等轴测投影
一、轴间角和轴向变 形系数
➢ 正等测的轴向变形系数p= q=r=0.82 (cos35.16°)
➢ 轴间角∠X1O1Z1=∠X1O1Y1 =∠Y1O1Z1=120°
➢ 画图时,规定把O1Z1轴画 成铅垂位置
一、 斜二测的轴间 角和轴向变形系 数
➢轴间角:∠X1O1Z1=90°,
O1Y1与水平线成45°。
➢轴向变形系数:q=0.5
16
正面斜二测图的四种形式
(a)右俯视图 (c)右仰视图
(b)左俯视图
(d)左仰视图
17
➢轴间角:∠X1O1Y1=90°,O1X1与
水平线成30°或60°。
➢轴向变形系数:p=q=r=1(绘制建
筑轴测图时候用)
18
二、斜二测投影图的画法
例1 画出下图回转体的斜二测。
b1 a1 o1
19
例2:已知两视图,画斜二轴测图。
20
例3 画出下图建筑形体的斜二测。
21
实例:
正面斜 二测:
用于画小 构件,不 适用于画 建筑外观
水平斜 二测:
能快速完 成建筑外 观轴测图
22
四、用八点法画斜二测椭圆
