第七章 轴测投影
合集下载
07第7章轴测投影

O1 X1
Y1 X
Z
S O
Y
二、正等轴测投影的轴间角和轴向伸缩系数
Z
O
120º
120º
X
Y
轴间角:120° 轴向变形系数:p=q=r=0.82 简化轴向变形系数: p=q=r=1
5.4 平行于坐标面的圆的轴测投影
Z
椭圆
X
Y
注意椭圆长、短轴的方向!
画法:八点法(以水平圆为例)
画法:四心法(以水平圆为例)
轴间角:120° 轴向变形系数:p=q=r=o.82 简化轴向变形系数: p=q=r=1
x'
a' b'
xa
s
o' o"
y"
c' a"(c") b"
oc
b
y
画坐标轴
按各点坐标沿轴度量
连线并加深X1 AZ1 NhomakorabeaSCO130° Y1
B
例:画出圆柱体的正等测 o'
x'
z'
x
o
y
外切正方形
X1
Y1
Z1
四心椭圆法(菱形法) 注意:椭圆长、短轴方向
土木工程制图
Civil Engineering Drawing
第7章 轴测投影
西北工业大学出版社
Press of Northwestern Polytechnical University
目录
• 7.1 基本知识 • 7.2 斜轴测投影 • 7.3 正等轴测投影 • 7.4 平行于坐标面的圆的轴测投影 • 7.5 轴测投影的画法
G2● O1 G●
1
E2 ●
Y1 X
Z
S O
Y
二、正等轴测投影的轴间角和轴向伸缩系数
Z
O
120º
120º
X
Y
轴间角:120° 轴向变形系数:p=q=r=0.82 简化轴向变形系数: p=q=r=1
5.4 平行于坐标面的圆的轴测投影
Z
椭圆
X
Y
注意椭圆长、短轴的方向!
画法:八点法(以水平圆为例)
画法:四心法(以水平圆为例)
轴间角:120° 轴向变形系数:p=q=r=o.82 简化轴向变形系数: p=q=r=1
x'
a' b'
xa
s
o' o"
y"
c' a"(c") b"
oc
b
y
画坐标轴
按各点坐标沿轴度量
连线并加深X1 AZ1 NhomakorabeaSCO130° Y1
B
例:画出圆柱体的正等测 o'
x'
z'
x
o
y
外切正方形
X1
Y1
Z1
四心椭圆法(菱形法) 注意:椭圆长、短轴方向
土木工程制图
Civil Engineering Drawing
第7章 轴测投影
西北工业大学出版社
Press of Northwestern Polytechnical University
目录
• 7.1 基本知识 • 7.2 斜轴测投影 • 7.3 正等轴测投影 • 7.4 平行于坐标面的圆的轴测投影 • 7.5 轴测投影的画法
G2● O1 G●
1
E2 ●
轴测投影图同济大学
文档仅供参考,如有不当之处,请联系改正。
文档仅供参考,如有不当之处,请联系改正。
文档仅供参考,如有不当之处,请联系改正。
➢ 9.4 轴测剖视图 文档仅供参考,如有不当之处,请联系改正。
为了表达零件旳内部构造和形状,常用 两个剖切平面沿两个坐标面方向切掉零件旳 四分之一。
文档仅供参考,如有不当之处,请联系改正。
X1
Y1
文档仅供参考,如有不当之处,请联系改正。
画法: 四心椭圆法(菱形法)
(以平行于H面旳圆为例)
e
●
E1 ●
B● 1
a
b
●
●
A● 1 ●
F● 1
f
画圆旳外切菱形 拟定四个圆心和半径 分别画出四段彼此相切旳圆弧
画法:
文档仅供参考,如有不当之处,请联系改正。
四心扁圆法
O2 A
O1
O2 A
C O1
作图:用八点法作斜二测椭圆。
a
1
5
d
8
X2
O
4
a
f 45° 1
6
7
b
3Y
c
Z1
5
2
6
b
1:1
Y1
45° O1
1:1 X1
g
d
8
4
7
3
c
文档仅供参考,如有不当之处,请联系改正。
文档仅供参考,如有不当之处,请联系改正。
例:已知两视图,画斜二轴测图。
文档仅供参考,如有不当之处,请联系改正。
例 端盖旳斜二测作图环节 文档仅供参考,如有不当之处,请联系改正。
文档仅供参考,如有不当之处,请联系改正。
X'
工程制图-轴测投影

轴测投影的基本知识 二 轴测投影的投影特性
(1) 平行性 (2) 等比性
轴测图的投影特性
(1) 平行性 物体上相
互平行的线段,在轴测投影
图上仍相互平行。
z
z1
C D
S
C1
F
D1
F1 E1
E
A oB
x
G
x1
o1
y1
A1
B1
y
G1
续投影特性
(2) 定比性 平行线段的轴测投影,其变形系数相同。
(3)物体上平行于轴测投影面的直线和平面在轴测 投影面上分别反映实长和实形。
轴测投影图的形成
1 轴测投影的基本知识
一.概述
轴测图的形成
将物体和确定物体位 置的直角坐标系沿选 定的投影方向平行地 投影到某一投影面上, 所得到的能同时反映 物体三个方向形状的 投影图,称为轴测投影 图,简称轴测图。
正轴测图 斜轴测图
一 轴测投影图的形成
轴测投影面
z
z1
S(倾斜与三个坐标面)
o x
X
B
F
C
X1
Y1
C
E
Y
切出左上块
2.量取尺寸D,垂直向下切;量取G, 水平向后切
D
出3
左 前 角
量 取
、
, 切
. . EF
4
G
校 核 并 加 深
擦 除 多 余 作
图
线
例3 画出物体的正等测图 在视图上定坐标原点和坐标系
z' z"
x'
y"
o' o"
形体分析与作图相结合
形体分析与作图相结合
工程图学习题答案

a
b
Bb
A
aW
c
O
b
a C cc
Y
9
第二章 点、直线和平面
2-5 求点的投影。
(1) 已知A、B、C、D的两面投影图,求第三投影,并量出 (2) 已知点M、N、S分别属于H、V、W面,点K属于Z轴,试 各点到投影面的距离,填入表中(单位:mm,取整数)。 画出各点的三面投影图。
′
d
′
′b
a
′ ′
′ ′
28
第二章 点、直线和平面
2-36 完成下列各题。
AB为某平面对H面的最大斜度线,求作属于该平面且距V 面20mm的正平线。
2-37 已知△ABC 与V面的倾角为45度,补出其水平投影。
′
′
′
′
′
2021/6/16
29
第三章 直线与平面、平面与平面的相对位置
习题 3-1,2 习题 3-7,8 习题 3-13,14 习题 3-19,20 习题 3-25,26 习题 3-31,32
(6) 交叉
16
第二章 点、直线和平面
2-15 AB与CD相交,补出线段所缺的投影。
( 1)
′ ′
′
′
′
′
′
′
2-16 过点A作直线,与CD、EF相交。
( 1)
′
′
′
′
′
d ( 2)
c
d
′ ′
′
′
( 2)
′ ′′
′ ′
d
c
2021/6/16
17
第二章 点、直线和平面
2-17 完成下列个题。
(1) 作一直线KL,使其与AB平行,与CD相交,确定K。
轴测投影

3.作圆柱切口的轴测图,在椭圆上自1、2、3、4、5、6各点向上引垂线, 并截取相应高度即可作出;再根据圆柱的高度作圆柱的上顶圆;
1’(4’)
2’(5’)
3’(6’) 1 X
Z
Y 2 3
O
5 4 6
O 4 5 6 45°
45°
O
2
1
3
步骤: 1.画出轴测轴(为了看清切口,最好画成仰视的 轴测图); 2.用八点法作出下底圆的斜二测椭圆;
在工程中,轴测投影图一般作为工程辅助图样。
返回
2、轴间角和轴向伸缩系数
轴测轴——三个坐标轴X1、Y1、Z1的轴测投影X、Y、Z。 轴间角——轴测轴之间的夹角,∠XOY、∠YOZ、∠ZOX 。 轴倾角——轴测轴X、Y与水平线间的夹角。
Z 轴向伸缩系数——轴测轴上的 C 单位长度与对应坐标轴上的单 位长度之比。 O X轴轴向伸缩系数: p=OA/O1A1 X A Y轴轴向伸缩系数: q=OB/O1B1 Z轴轴向伸缩系数:r=OC/O1C1 推论: 与坐标轴平行的棱线,其轴测投影平 行于对应的轴测轴,其轴向伸缩系数 等于对应坐标轴的轴向伸缩系数。 P
高校建筑学与城市规划专业教材《画法几何与阴影透视》课件编制:北京建筑工程学院 中国建筑工业出版社出版
5
Z′
X′ O′ Y Z Y
O X
O
返回
倒圆角正等轴测图的画法
Z
返回
返回
综合法
Z′ Z
X′
O′ O
X
Y
返回
Z′
Z
X′O′ O X YY′Z′ZX′
O′ O X Y
Y′ 返回
Z′ Z
X′
O′ O
X
Y
画法几何:7轴测投影

平行性
空间平行的两直线,其轴测投影仍然平行;空间平行于坐标 轴的线,其轴测投影平行于相应的轴测轴。
定比性
互相平行的线段的长度之比,等于轴测投影长度之比;与坐 标轴平行的线段和该轴具有相同的伸缩系数。
7.2 正等轴测投影
➢ 7.2.1 轴间角和轴向伸缩系数 ➢ 7.2.2 正等轴测投影的画法 ➢ 7.2.3 平行于坐标面圆的正等轴测投影
90°
135°
135°
L 0.82L
L
边长为L的正 方体的轴测图
L
按简化轴向变形系数画
按理论轴向变形系数画
7.4 轴测投影的选择
要避免被遮挡
要避免转角处交线投影成一直线
要避免平面体投影成对称的图形
要避免有侧面的投影积聚为直线
合理选择轴测投射方向
X1
Z1
O1
Y1 X
Z
S O
Y
轴测 投影图
将物体连同确定其位置的直角坐标系按照不 平行于任一坐标面的方向S用平行投影法投影 到某一选定的投影面P上所得到的投影图称轴
测投影图。
7.1.2 轴测投影的形成
Z1
P
Z
轴测投影图
O1 X1
Y1 X
六个基本要素
S O
Y
空间坐标系 O-XYZ 空间形体 轴测投影方向 S 轴测投影面 P 轴测坐标系 O1-X1Y1Z1 轴测投影图
斜等测(p=q=r) 斜二测(p=r≠q)
斜三测(p ≠q ≠r)
7.1.4 轴测投影的分类 正轴测投影图
P
Z1
正轴测投影图
O1
X1
Y1 X
Z
S O
Y
7.1.4 轴测投影的分类 斜轴测投影图
空间平行的两直线,其轴测投影仍然平行;空间平行于坐标 轴的线,其轴测投影平行于相应的轴测轴。
定比性
互相平行的线段的长度之比,等于轴测投影长度之比;与坐 标轴平行的线段和该轴具有相同的伸缩系数。
7.2 正等轴测投影
➢ 7.2.1 轴间角和轴向伸缩系数 ➢ 7.2.2 正等轴测投影的画法 ➢ 7.2.3 平行于坐标面圆的正等轴测投影
90°
135°
135°
L 0.82L
L
边长为L的正 方体的轴测图
L
按简化轴向变形系数画
按理论轴向变形系数画
7.4 轴测投影的选择
要避免被遮挡
要避免转角处交线投影成一直线
要避免平面体投影成对称的图形
要避免有侧面的投影积聚为直线
合理选择轴测投射方向
X1
Z1
O1
Y1 X
Z
S O
Y
轴测 投影图
将物体连同确定其位置的直角坐标系按照不 平行于任一坐标面的方向S用平行投影法投影 到某一选定的投影面P上所得到的投影图称轴
测投影图。
7.1.2 轴测投影的形成
Z1
P
Z
轴测投影图
O1 X1
Y1 X
六个基本要素
S O
Y
空间坐标系 O-XYZ 空间形体 轴测投影方向 S 轴测投影面 P 轴测坐标系 O1-X1Y1Z1 轴测投影图
斜等测(p=q=r) 斜二测(p=r≠q)
斜三测(p ≠q ≠r)
7.1.4 轴测投影的分类 正轴测投影图
P
Z1
正轴测投影图
O1
X1
Y1 X
Z
S O
Y
7.1.4 轴测投影的分类 斜轴测投影图
第七章轴测图
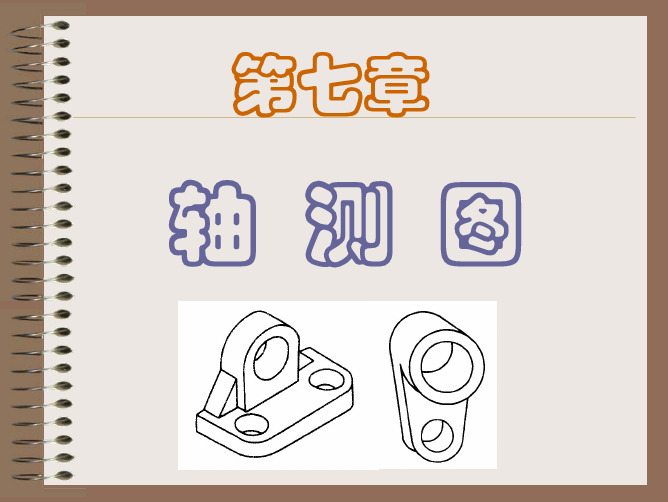
分析:由图可分析出,支架是 由底板、支承座及两个三角形 肋板叠加而成。底板为长方 体,有两个圆角并挖切两个圆 孔;支承座的U形是由半圆柱和 长方体叠加而成,其中间挖切 一通孔,支承座两边的三角形 肋为三棱柱。画轴测图时,按 叠加法作图,底板及支承先按 长方板画出,按其相对位置尺 寸叠加,然后典型示范画圆 孔、圆角等细节。支架左、右 对称,三部分的后表面共面, 三部分均以底板上面为结合 面,故坐标原点选在底板上面 与后端面的交线的中点处。
(续)
4、坐标法是画轴测图的基本方法。画立体的轴测图 时,应尽量利用立体各组成部分的相对位置尺寸定位,对能 分出层次的立体,还应该正确定出其各平面的位置。画有回 转结构的立体时,要注意轴测图上椭圆长短轴的方向,以免 出错。 5、具体画图时,一般应先画出立体的主要轮廓线;然 后再画出各部分的详细结构。要充分利用互相平行直线,在 轴测图中仍互相平行;平行于投影轴的直线,在轴测图中仍 平行于轴测轴的投影特性,采用从上到下、从前到后的顺序 作图,以便提高作图效率。
第三节 斜二等轴测图
一、斜二等轴测图的形成、轴间角和轴向变形系数
如图a所示,斜二等轴测图是由斜投影法得到的轴测图。当立体的两个坐标轴x和z 与轴测投影面P平行,而投影方向与轴测投影面倾斜时,所得到的轴测图称斜二等轴 测图,简称斜二测图。
第三节 斜二等轴测图
(续)
如图b所示,斜二等轴测图的轴间角分别为90°、135°、135°;x1和 z1轴的轴向变形系数p = r = 1,y1轴的轴向变形系数q = 0.5。
第一节 轴测图的基本知识
四、轴测图的分类
1)轴测图根据投影方向S与轴 测投影面P的相对位置不同。可分为 两大类: 2)正轴测图:轴测投影方向S垂 直于轴测投影面P。 3)斜轴测图:轴测投影方向S倾 斜于轴测投影面P。
(续)
4、坐标法是画轴测图的基本方法。画立体的轴测图 时,应尽量利用立体各组成部分的相对位置尺寸定位,对能 分出层次的立体,还应该正确定出其各平面的位置。画有回 转结构的立体时,要注意轴测图上椭圆长短轴的方向,以免 出错。 5、具体画图时,一般应先画出立体的主要轮廓线;然 后再画出各部分的详细结构。要充分利用互相平行直线,在 轴测图中仍互相平行;平行于投影轴的直线,在轴测图中仍 平行于轴测轴的投影特性,采用从上到下、从前到后的顺序 作图,以便提高作图效率。
第三节 斜二等轴测图
一、斜二等轴测图的形成、轴间角和轴向变形系数
如图a所示,斜二等轴测图是由斜投影法得到的轴测图。当立体的两个坐标轴x和z 与轴测投影面P平行,而投影方向与轴测投影面倾斜时,所得到的轴测图称斜二等轴 测图,简称斜二测图。
第三节 斜二等轴测图
(续)
如图b所示,斜二等轴测图的轴间角分别为90°、135°、135°;x1和 z1轴的轴向变形系数p = r = 1,y1轴的轴向变形系数q = 0.5。
第一节 轴测图的基本知识
四、轴测图的分类
1)轴测图根据投影方向S与轴 测投影面P的相对位置不同。可分为 两大类: 2)正轴测图:轴测投影方向S垂 直于轴测投影面P。 3)斜轴测图:轴测投影方向S倾 斜于轴测投影面P。
7-1 轴测投影的基本知识
木材科学与工程
16
第 七章轴测投影
1.轴测投影种类的选择 1) 轴测图都可根据正投影图来绘制,在 正投影图中,如果物体的表面有和水平方向成 45°的,就不应采用正等测图。因为这种方向 的平面在轴测图上积聚为一条直线,平面就显
示不出来,削弱了图形的立体感,故宜采用斜
二测较好。
木材科学与工程
17
第 七章轴测投影
木材科学与工程
2
第 七章轴测投影
一、轴测投影的形成 将物体连 同其参考直角 坐标系,沿不 平行于任一坐 标面的方向S, 用平行投影法 将其投射在单 一投影面P上所 得单面投影。
木材科学与工程
3
第 七章轴测投影
1、斜轴测投影图的形成
P
正投影图
Z S S0 Y
斜轴测投影图
Z1 X
O
O1 X1 Y1 木材科学与工程
p、q、r分别称为x轴、y轴、Z轴的变形系数
木材科学与工程
6
第 七章轴测投影
如果事先知道了轴测投影中的轴测轴的方 向和变形系数,则与每条坐标轴平行的直线, 其轴测投影必平行于轴测轴,其投影长度等于 原来长度乘以该轴的变形系数。 所谓 “ 轴测 ” ,就是说沿坐标轴的方 向,即平行于坐标轴的直线,可以测量长度。 它可以由空间长度乘以该轴的变形系数得出投 影长度,也可以由投影长度除以该轴的变形系 数,得出原来长度。轴测投影之名来源于此。
24 Z Z 6
6
20
28
Y
Z
X X
32
O O
O
8
O 24 Y
X
Y
步骤一
木材科学与工程
36
第 七章轴测投影
24 Z Z 6 Z 28
16
第 七章轴测投影
1.轴测投影种类的选择 1) 轴测图都可根据正投影图来绘制,在 正投影图中,如果物体的表面有和水平方向成 45°的,就不应采用正等测图。因为这种方向 的平面在轴测图上积聚为一条直线,平面就显
示不出来,削弱了图形的立体感,故宜采用斜
二测较好。
木材科学与工程
17
第 七章轴测投影
木材科学与工程
2
第 七章轴测投影
一、轴测投影的形成 将物体连 同其参考直角 坐标系,沿不 平行于任一坐 标面的方向S, 用平行投影法 将其投射在单 一投影面P上所 得单面投影。
木材科学与工程
3
第 七章轴测投影
1、斜轴测投影图的形成
P
正投影图
Z S S0 Y
斜轴测投影图
Z1 X
O
O1 X1 Y1 木材科学与工程
p、q、r分别称为x轴、y轴、Z轴的变形系数
木材科学与工程
6
第 七章轴测投影
如果事先知道了轴测投影中的轴测轴的方 向和变形系数,则与每条坐标轴平行的直线, 其轴测投影必平行于轴测轴,其投影长度等于 原来长度乘以该轴的变形系数。 所谓 “ 轴测 ” ,就是说沿坐标轴的方 向,即平行于坐标轴的直线,可以测量长度。 它可以由空间长度乘以该轴的变形系数得出投 影长度,也可以由投影长度除以该轴的变形系 数,得出原来长度。轴测投影之名来源于此。
24 Z Z 6
6
20
28
Y
Z
X X
32
O O
O
8
O 24 Y
X
Y
步骤一
木材科学与工程
36
第 七章轴测投影
24 Z Z 6 Z 28
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、坐标法
坐标法是轴测图作椭圆的真实画法
2、四心扁圆法
四心扁圆法简称四心法,是一种椭圆的近似画 法。画椭圆的关键有以下几点: ①分辨平行于哪个坐标面的圆; ②确定圆心的位置; ③画出与椭圆相切的菱形; ④确定椭圆长轴与短抽的方向; ⑤用四心法分别求四段圆弧。
例7-5 根据图所示水平圆的投影图,绘制 其正等测图。
第七章 轴测投影
7-1 轴测投影的基本知识 7-2 正轴测图 7-3 斜轴测图
轴测投影图
轴测投影图简称轴测图,有立体感是它的优点, 但它也存在着缺点。 首先是对形体表达不全面 其次,轴测图没有反映出形体各个侧面的实形 工程上仅用来作为辅助图样。在给排水和暖通 等专业图中,常用轴测投影图表达各种管道的 空间位置及其相互关系。
一、正面斜轴测;
⑴不管投射方向如何倾斜.平行于轴测投影面 的平面图形;它的斜轴测投影反映实形。 ⑵相互平行的直线,其正面斜轴测图仍相互平 行;平行于坐标轴的线段的止面斜轴测投影与 线段实长之比,等于相应的轴向伸缩系数。 (3)垂直于轴测投影面的直线,它的轴钡l投影 方向和长度,将随着投影方向S的不同而变化。
四、轴测投影图的分类
1.按投射方向与轴测投影面之间的关系分类 (1)正轴测投影。 (2)斜轴测投影。 2.按轴向伸缩系数的不同分类 (1)等测。 (2)二测。 (3)三测。
7-2 正轴测图
一、正等测 (一)轴间角和轴向伸缩系数
(二)轴测图的基本画法
1.坐标法
例7-1 下图所示为四坡顶房屋的投影图,作出 其正等测图。
7-1 轴测投影的基本知识 Nhomakorabea一、轴测投影图的形成 轴测投影属于平行投影的一种,它是用一组平 行投射线,采用与形体的三个向度都不一致的 投影方向。
二、轴间角及轴向伸缩系数
在轴测投影面P上,三 个轴测轴O1X1、O1Y1,、 O1Z1之间的夹角 ∠X1O1Y1、∠Y1O1Z1、 ∠X1O1Z1称为轴间角, 三个轴间角之和360o. p= O1X1/ OX q= O1Y1/ OY r= O1Z1/ OZ
四、曲面体的正等测图
例7-6 根据图所示圆 木木榫的投影图,绘 制其正等测图。
例7-7 根据图所示带圆角矩形板的投影图, 绘制其正等测图。
7-3 斜轴测图
投射方向s倾斜于轴测投影面时所得的投影, 称为斜轴测投影。以v面或V面平行面作为轴 测投影面,所得的斜轴测投影,称为正面斜轴 测投影。 若以H面或H面平行面作为轴测投影面,则得 水平斜轴测投影。 画斜轴测图与画正轴测图一样,也要先确定轴 间角,轴向伸缩系数以及选择轴测类型和投射 方向。
三、轴测投影的特性
(1)空间平行的两条直线在轴测投影中仍然平 行,所以凡与坐标轴平行的直线,其轴测投影 必然平行于相应的轴测轴. (2)空间与坐标轴平行的直线。其轴测投影具 有与该相应轴测轴相同的轴向伸缩系数与坐标 轴不平行的直线,其轴测投影具有不同的伸缩 系数,求这种直线的轴测投影,应该根据直线 端点的坐标,分别求得其轴测投影,再连接成 直线。
2.叠加法
例7-2 下图所示为某形体的投影图,作出 其正等测图。
3.切割法 例7-3 根据图所示某形体的投影图,用切 割法绘制其i正等测图。
二、正二测
例7-4 根据图所示某基础形体的投影图。 绘制其正二测图。
三、圆的正等测图
平行于坐标面的圆的 正等测投影都是椭圆。 绘制平行于坐标面 的圆的正等测图常见 的方法有两种:坐标 法和四心扁圆法。
例7-8 根据图所示某拱门的投影图,绘制 其正面斜二测图。
二、水平斜轴测
如果形体仍保持正投影的位置,而用倾 斜于H面的轴测投影方向S,向平行于H 面的轴测投影面P进行投影,如图所示, 则所得斜轴测图称为水平斜等测图.
例7-9 根据图所示某房屋的投影图,绘制 其水平斜等测图。
