运筹学清华第4版课后练习题答案解析
《管理运筹学》第四版课后习题答案

《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1.解:(1)可行域为OABC。
(2)等值线为图中虚线部分。
? (3)由图2-1可知,最优解为B 点,最优解 x =12 , x ??15 7 2 7 图2-1;最优目标函数值 69 。
72.解:(1)如图2-2所示,由图解法可知有唯一解?x 1 ??0.2 ,函数值为3.6。
?x 2 图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
? (5)无穷多解。
?x ? (6)有唯一解 ??1 ? 203 ,函数值为 92 。
8 3x ? ??2 3 3.解:(1)标准形式max f ??3x 1 ??2x 2 ??0s 1 ??0s 2 ??0s 39x 1 ??2x 2 ??s 1 ??303x 1 ??2x 2 ??s 2 ??132x 1 ??2x 2 ??s 3 ??9x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f ??4x 1 ??6x 2 ??0s 1 ??0s 23x 1 ??x 2 ??s 1 ??6x 1 ??2x 2 ??s 2??10 7x 1 ??6x 2??4x 1, x 2 , s 1, s 2 ≥ 0(3)标准形式min f ??x 1????2x 2????2x 2??????0s 1 ??0s 2?3x 1 ??5x 2????5x 2??????s 1 ??702x 1????5x 2????5x 2??????503x 1????2x 2????2x 2??????s 2 ??30x 1?, x 2??, x 2????, s 1, s 2 ≥ 0 4.解:标准形式max z ??10x 1 ??5x 2 ??0s 1 ??0s 23x 1 ??4x 2 ??s 1??95x 1 ??2x 2 ??s 2 ??8x 1, x 2 , s 1, s 2 ≥ 0≤ 松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
[运筹学第四版课后答案]课后答案
![[运筹学第四版课后答案]课后答案](https://img.taocdn.com/s3/m/24ea5b5d814d2b160b4e767f5acfa1c7aa008294.png)
[运筹学第四版课后答案]课后答案课后答案一:《蜀道难》课后题答案《蜀道难》课后题答案一、这是一首乐府诗,以七言为主,却有不少杂言句,节奏多变化,与散文句法相似。
试给下面的诗句划分节奏,朗读几遍,说说它们对本诗的风格起什么作用。
1.噫吁戏,危乎高哉!蜀道之难,难于上青天!2.上有六龙回日之高标,下有冲波逆折之回川。
3.其险也如此,嗟尔远道之人胡为乎来哉!4.剑阁峥嵘而崔嵬,一夫当关,万夫莫开。
解题指导这首诗较长,且内容有一定难度所以先设计此题,目的是使你初步适应这首诗节奏的变化。
在完成本题时你一定要朗读几遍,读出一点韵味来。
但要注意:不要把这些句子读成散文,这对领会诗人炽烈奔放的感情和飘逸的风格极为必要。
这是一首杂言体诗,但跟其他诗人的这类体裁作品和李白的另一些这类体裁作品(如《将进酒》《梁甫吟》《庐山谣寄卢待御虚舟》等)相比,都有显著的不同。
这不同就在于:其中的某些句子,如练习中所列举的,如果孤立地看,确属散文句。
但我们不这样称它们,因为它们毕竟是诗的整体中的一部分,只能说它们是散文化的诗句,或句法与散文近似。
这当然不能随意而为,没有李白那样的气概,那样的英才,是驾驭不了的。
参考答案这些诗句都仿佛是诗人在炽烈感情的驱动下,不能自已,脱口而出,生动地表现了诗人奔放豪迈的风格。
二、“蜀道之难,难于上青天”这句诗有什么含义它重复出现三次,有什么作用解题指导这道题是为鉴赏诗的内容设计的。
重点是前一问,后一问是对前一问的补充,意思是可以从形式入手鉴赏诗的内容。
因此在完成本题时,你可以先思考后一问,然后分析“蜀道之难”一句的含义。
此题有一定的难度,你最好先理清课文的结构层次并了解诗的大意,在此基础上完成本题。
李白善于从民歌中吸取养料。
这首诗中“一咏三叹”的写法,明显地是对《诗经》中复沓形式的继承,同时又有很大的发展。
这一特点同你已学过的《君子于役》《无衣》等相同。
参考答案诗人创造性地继承了古代民歌中常见的复沓形式(又称反复),主旨句凡三见:开头、中间、结尾各出现一次。
《管理运筹学》第四版课后习题解析(上)
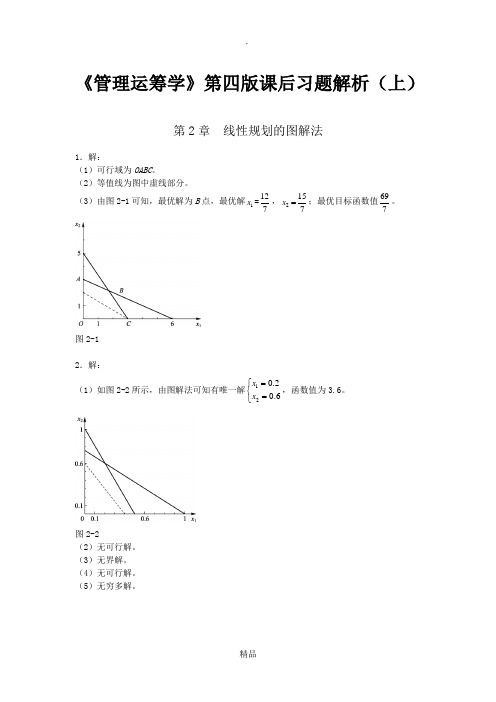
《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解1x =127,2157x =;最优目标函数值697。
图2-12.解:(1)如图2-2所示,由图解法可知有唯一解120.20.6x x =⎧⎨=⎩,函数值为3.6。
图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
(6)有唯一解 1220383x x ⎧=⎪⎪⎨⎪=⎪⎩,函数值为923。
3.解:(1)标准形式12123max 32000f x x s s s =++++1211221231212392303213229,,,,0x x s x x s x x s x x s s s ++=++=++=≥(2)标准形式1212min 4600f x x s s =+++12112212121236210764,,,0x x s x x s x x x x s s --=++=-=≥(3)标准形式12212min 2200f x x x s s ''''=-+++1221122122212212355702555032230,,,,0x x x s x x x x x x s x x x s s '''-+-+=''''-+=''''+--=''''≥4.解:标准形式1212max 10500z x x s s =+++1211221212349528,,,0x x s x x s x x s s ++=++=≥松弛变量(0,0)最优解为 1x =1,x 2=3/2。
5.解:标准形式12123min 118000f x x s s s =++++121122123121231022033184936,,,,0x x s x x s x x s x x s s s +-=+-=+-=≥剩余变量(0, 0, 13)最优解为 x 1=1,x 2=5。
管理运筹学第四版课后习题解析

管理运筹学第四版课后习题解析(总64页)本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解1x =127,2157x =;最优目标函数值697。
图2-12.解:(1)如图2-2所示,由图解法可知有唯一解120.20.6x x =⎧⎨=⎩,函数值为。
图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
(6)有唯一解 1220383x x ⎧=⎪⎪⎨⎪=⎪⎩,函数值为923。
3.解:(1)标准形式12123max 32000f x x s s s =++++1211221231212392303213229,,,,0x x s x x s x x s x x s s s ++=++=++=≥(2)标准形式1212min 4600f x x s s =+++12112212121236210764,,,0x x s x x s x x x x s s --=++=-=≥(3)标准形式12212min 2200f x x x s s ''''=-+++1221122122212212355702555032230,,,,0x x x s x x x x x x s x x x s s '''-+-+=''''-+=''''+--=''''≥4.解:标准形式1212max 10500z x x s s =+++1211221212349528,,,0x x s x x s x x s s ++=++=≥松弛变量(0,0)最优解为 1x =1,x 2=3/2。
管理运筹学第四版课后习题解析上定稿版

管理运筹学第四版课后习题解析上精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解1x =127,2157x =;最优目标函数值697。
图2-1 2.解:(1)如图2-2所示,由图解法可知有唯一解120.20.6x x =⎧⎨=⎩,函数值为3.6。
图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
(6)有唯一解 1220383x x ⎧=⎪⎪⎨⎪=⎪⎩,函数值为923。
3.解:(1)标准形式(2)标准形式(3)标准形式4.解:标准形式松弛变量(0,0)最优解为 1x =1,x 2=3/2。
5.解:标准形式剩余变量(0, 0, 13)最优解为 x 1=1,x 2=5。
6.解:(1)最优解为 x 1=3,x 2=7。
(2)113c <<。
(3)226c <<。
(4)1264x x ==。
(5)最优解为 x 1=8,x 2=0。
(6)不变化。
因为当斜率12113c c ---≤≤,最优解不变,变化后斜率为1,所以最优解不变。
7.解:设x ,y 分别为甲、乙两种柜的日产量,目标函数z=200x +240y , 线性约束条件:⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+006448120126y x y x y x 即 ⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+0162202y x y x y x 作出可行域.解⎩⎨⎧=+=+162202y x y x 得)8,4(Q 答:该公司安排甲、乙两种柜的日产量分别为4台和8台,可获最大利润2720元.8.解:设需截第一种钢板x 张,第二种钢板y 张,所用钢板面积zm2.目标函数z=x +2y , 线性约束条件:作出可行域,并做一组一组平行直线x +2y=t .解⎩⎨⎧=+=+12273y x y x 得)2/15,2/9(E .但E 不是可行域内的整点,在可行域的整点中,点)8,4(使z 取得最小值。
运筹学清华大学第四版答案

运筹学清华大学第四版答案【篇一:运筹学作业2(清华版第二章部分习题)答案】s=txt>2.1 题(p. 77)写出下列线性规划问题的对偶问题:????(1)?????maxz?2x1?2x2?4x3s.t.x1?3x2?4x3?22x1?x2?3x3?3x1?4x2? 3x3?5x1?0,x2?0,x3无约束;解:根据原—对偶关系表,可得原问题的对偶规划问题为:?maxw?2y1?3y2?5y3?s.t.y1?2y2?y3?2??3y1?y2?4y3?2 ? ?4y1?3y2?3y3?4?y1?0,y2?0,y3?0??mn?minz???cijxij?i?1j?1?n???cijxij?ai,i?1,?,m(2)? j?1?n??cijxij?bj,j?1,?,n?j?1???xij?0,i?1,?,m;j?1,?,n解:根据原—对偶关系表,可得原问题的对偶规划问题为:mn??maxw??aiui??bjvji?1j?1??ui?vj?cij ??i?1,?,m;j?1,?,n???ui无约束,vj无约束2.2判断下列说法是否正确,为什么?(1)如果线性规划的原问题存在可行解,则其对偶问题也一定存在可行解;答:错。
因为:若线性规划的原问题存在可行解,且其对偶问题有可行解,则原问题和可行问题都将有最优解。
但,现实中肯定有一些问题是无最优解的,故本题说法不对。
maxz?3x1?x2例如原问题s.t.?x1?x2?1?x2?3??x?0,x?02?1有可行解,但其对偶问题minw?y1?3y2s.t.?3?y1?y2?1?y1??y?0,y?02?1无可行解。
(2)如果线性规划的对偶问题无可行解,则原问题也一定无可行解;答:错,如(1)中的例子。
(3)在互为对偶的一对原问题与对偶问题中,不管原问题是求极大或求极小,原问题可行解的目标函数值一定不超过其对偶问题可行解的目标函数值。
答:错。
正确说法是:在互为对偶的一对原问题与对偶问题中,求极大的问题可行解的目标函数值一定不超过求极小的问题可行解的目标函数值。
管理运筹学》-第四版课后习题答案.docx
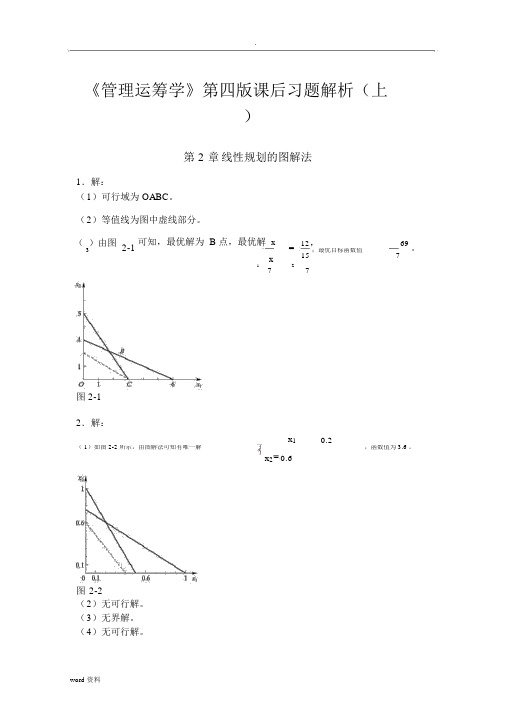
.《管理运筹学》第四版课后习题解析(上)第 2 章线性规划的图解法1.解:(1)可行域为 OABC。
(2)等值线为图中虚线部分。
()由图2-1可知,最优解为 B 点,最优解x=12,69。
315;最优目标函数值7x1277图 2-12.解:x10.2( 1)如图 2-2 所示,由图解法可知有唯一解,函数值为 3.6 。
x20.6图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
word 资料.( 5)无穷多解。
x2092( 6)有唯一解3,函数值为。
183x2 33.解:( 1)标准形式maxf 3 12x2010s20s3 x s9 x12x2s1303x12x2s2132 x12x2s39x1,x2, s1,s2,s3≥0( 2)标准形式min f4x16x20 s10s23x1x2s16x1 2 x2s2107 x16x24x1, x2, s1, s2≥0( 3)标准形式min f x12x22x20 s10s23x15x25x2s1702 x15x25x2503x1 2 x2 2 x2s230x1, x2, x2, s1 , s2≥ 04.解:标准形式max z10 x15x20 s10s2word 资料.3x14x2s195 x12x2s28x1, x2, s1, s2≥0word 资料.松弛变量( 0,0)最优解为 x 1 =1,x 2=3/2 。
5.解: 标准形式min f11x 18 x 20 s 10s 20s 310x 1 2x 2 s 1 20 3x 1 3x 2 s 2 18 4 x 19x 2s 336x 1, x 2 , s 1 , s 2 , s 3 ≥ 0剩余变量( 0, 0, 13 )最优解为 x 1=1,x 2=5。
6.解:( 1)最优解为 x 1=3,x 2=7。
( 2) 1 c 1 3 。
( 3) 2 c 26 。
( 4)x 16。
x 24。
( 5)最优解为 x 1=8,x 2=0。
管理运筹学》-第四版课后习题解析(上)
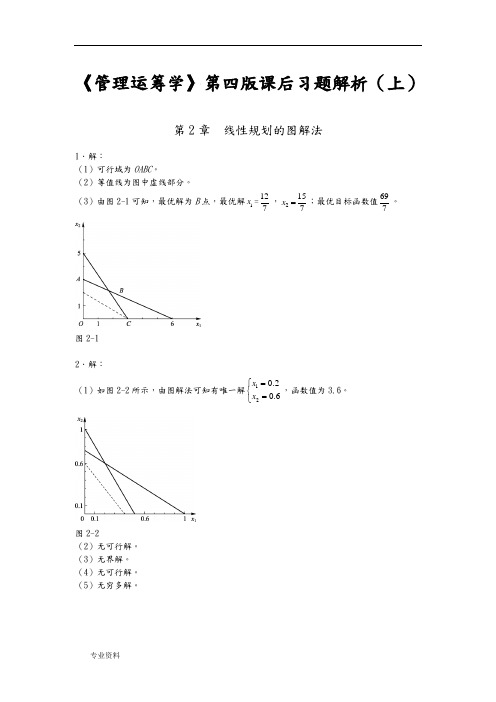
《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1.解:(1)可行域为OABC。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B点,最优解1x=127,2157x=;最优目标函数值697。
图2-12.解:(1)如图2-2所示,由图解法可知有唯一解120.20.6xx=⎧⎨=⎩,函数值为3.6。
图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
(6)有唯一解 1220383x x ⎧=⎪⎪⎨⎪=⎪⎩,函数值为923。
3.解:(1)标准形式12123max 32000f x x s s s =++++1211221231212392303213229,,,,0x x s x x s x x s x x s s s ++=++=++=≥(2)标准形式1212min 4600f x x s s =+++12112212121236210764,,,0x x s x x s x x x x s s --=++=-=≥(3)标准形式12212min 2200f x x x s s ''''=-+++ 1221122122212212355702555032230,,,,0x x x s x x x x x x s x x x s s '''-+-+=''''-+=''''+--=''''≥4.解: 标准形式1212max 10500z x x s s =+++1211221212349528,,,0x x s x x s x x s s ++=++=≥ 松弛变量(0,0) 最优解为 1x =1,x 2=3/2。
5.解:标准形式12123min 118000f x x s s s =++++121122123121231022033184936,,,,0x x s x x s x x s x x s s s +-=+-=+-=≥剩余变量(0, 0, 13) 最优解为 x 1=1,x 2=5。
