东北大学概率论与数理统计ppt第二章
第二章2《概率论与数理统计教程》PPT课件
联合概率函数的性质
1) p(xi , yj ) 0,
2) p(xi , yj )1;
ij
3) P(X,Y)D p(xi , yj ); (xi ,yj )D
若二维随机r.v.的联合概率函数 p(xi , yj )知道,则 联合概率分布函数为
F(xy, )p(i,xyj) xix yjy
4 -6
y
注:若将二维随机变量(X,Y) 看作是平面上的随机点的坐标,
(x,y)
则分布函数在点(x,y)处的函 数值,就是随机点(X,Y)落在 如图所示的以点(x,y)为顶点 而位于该点左下方的无穷矩形区 域4内- 3的概率
O
x
联合分布函数的性质
1) 0F(x,y)1
2)F(x,y)分别是变量x,y的单调不减函数; 3)对任意x,y,有
例1. 将一枚均匀的硬币抛掷4次, X表示正面向上的 次数, Y表示反面朝上次数, 求(X,Y)的联合概率分布.
例2. 设随机变量Y~U(0,1),令
0, |Y|1 0, |Y|2 X1 1, |Y|1,X2 1, |Y|2
求(X1,X2)的联合概率分布。 例3. 二维随机向量(X,Y)的联合概率分布为:
XY 0 1
-1 0.05 0.1
0
0.1 0.2
4-7 1
a 0.2
2
求:(1)常数a的取值;
0.1
(2)P(X≥0,Y≤1);
0.1
0.05 (3) P(X≤1,Y≤1)
二维连续随机变量的联合概率密度
定义:
P (xX x x ,y Y y y)
f(x ,y)lim
y x 0 0
x y
若此极限存在,则称此极限为二维连续随 机变量(X,Y)的联合概率密度。
概率论与数理统计课件第2章

2
2.2.1 随机变量 • 注意: 注意:
(1)随机变量定义于抽象的样本空间上,不是普 )随机变量定义于抽象的样本空间上, 通的实函数。 通的实函数。 (2)随机事件可以通过随机变量的各种取值状态 )随机事件可以通过随机变量的各种取值状态 取值范围来表示 来表示。 和取值范围来表示。
3
2.1.2 随机变量的分布函数 • 既然随机事件可以通过随机变量的各种取值状态和取值 范围来表示, 范围来表示,研究随机现象的统计规律性就转化为研究 随机变量取值的规律性,即取值的概率。 随机变量取值的规律性,即取值的概率。但概率是集合 函数,随机变量定义于抽象空间上,都不便于处理。 函数,随机变量定义于抽象空间上,都不便于处理。 • 能不能找到一种方法,使得我们研究随机变量取值的规 能不能找到一种方法, 律性可以转化为研究普通的实函数? 律性可以转化为研究普通的实函数?
2.1 随机变量及其分布函数 在前面的讨论中,只是孤立地考虑一些事件的概率, 在前面的讨论中,只是孤立地考虑一些事件的概率, 这种研究方法缺乏一般性, 这种研究方法缺乏一般性,而且不便于分析数学工具的引 为了这一目的,随机变量的引入具有非常重要的意义。 入,为了这一目的,随机变量的引入具有非常重要的意义。 随机变量的引入是概率论发展史上的重大事件。 随机变量的引入是概率论发展史上的重大事件。它使得研 究概率论的数学工具更丰富有力,从此, 究概率论的数学工具更丰富有力,从此,概率论的研究进 入一个崭新的天地。 . 入一个崭新的天地。
P{ X ≥ 1} = 5 / 9 ,求p =
x≤0 , 0 < x ≤1 x >1
,概率 P{0 ≤ X ≤ 0.25} =
,
;
X |< 0.5} ;2)分布函数 分布函数F(x) 分布函数
概率论与数理统计第2章ppt课件

1 3x
0
1
2
3X
处的离跳散跃型高随度机恰变为量P{的X=分x布i}.函数为跳跃函数,在xi
§4. 连续型随机变量的概率密度
1. 定义:对于随机变量X的分布函F(x), 如果存在非负函数f(x),使对于任意实数x有:
F(x)xf(t)dt
则称X为连续型随机变量;称f(x)为X的概率 密度函数。简称密度函数。
精选课件
21
例4. 3个人抓阄数。
解:X的概率分布: P{X=1}=1/3
P{X=2}=2/3×1/2=1/3
P{X=3}=2/3×1/2×1/1=1/3
X的分布函数:
Y
0 x <1
1
1/3 1 x <2
2/ 3
F(x)=
2/3 2 x <3 1/ 3
则:P{X=k} Cnk pnkqnnk 其中:qn=1-pn
(令=μV; pn=μ△V=μV/n= /n):
考虑当 n +时
P{X=k} =nl imCnkpnkqnnk
limn! ()k(1)nk
nl n i m k1 k !!n(nn (n n k1)) !n (n n kn 1)k((11 n))kn
k
k!
k=0、1、2、3、……
n
Poissn定理:n为正整数,pn=/n, >0。 则对任一非负整数k有:
nl im Cnkpnkqnnk
k
k!
其中:= npn.
例3. 某人打靶命中率为0.001, 重复射击 5000次,求至少命中2次的概率。
解:设X为至命中次数。
P(X2) =1-P(X<2) =1-P(X=0)-P(X=1)
概率论与数理统计--第二章PPT课件
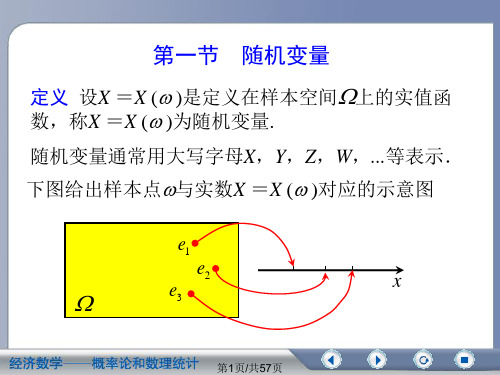
F(x) pk xk x
分布函数F(x)在x xk , 其跳跃值为pk P{X
对k 所1,有2,满足处x有k 跳 x跃的,k求和。
xk }
第26页/共57页
第四节 连续型随机变量及其概率密度
定义 对于随机变量X的分布函数F(x),如果存在非 负函数f (x),使对于任意实数有
售量服从参数为 10的泊松分布.为了以95%以上的
概率保证该商品不脱销,问商店在月底至少应进该商 品多少件? 解 设商店每月销售该种商品X件,月底的进货量为n件,
按题意要求为 PX n 0.95
由X服附从录的泊1松0的分泊布松表分知布k,140 1则k0!k有e1k0n01k00!k.9e1160 6
可以用泊松分布作近似,即
n
k
pk
1
p
nk
np k
k!
enp , k
0,1, 2,
.
例 4 为保证设备正常工作,需要配备一些维修工.如果各台设备
发生故障是相互独立的,且每台设备发生故障的概率都是 0.01.
试求在以下情况下,求设备发生故障而不能及时修理的概率.
(1) 一名维修工负责 20 台设备.
于是PX I P(B) Pw X (w) I.
随机变量的取值随试验的结果而定,而试验的各个 结果出现有一定的概率,因而随机变量的取值有一 定的概率.
按照随机变量可能取值的情况,可以把它们分为两 类:离散型随机变量和非离散型随机变量,而非离 散型随机变量中最重要的是连续型随机变量.因此, 本章主要研究离散型及连续型随机变量.
x
x
4. F(x 0) F(x) 即F(x)是右连续的
第23页/共57页
概率论与数理统计(完整版)(课堂PPT)

3
随机试验:
(1) 可在相同的条件下重复试验; (2) 每次试验的结果不止一个,且能事先明确所有可能的结 果; (3) 一次试验前不能确定会出现哪个结果.
4
§2. 样本空间与随机事件
(一) 样本空间:
定义 随机试验E的所有可能结果组成的集合称为 E的样 本空间, 记为S. 样本空间的元素称为样本点,用表示.
样本空间的分类:
1.离散样本空间:样本点为有限个或可列个. 例 E1,E2等. 2.无穷样本空间:样本点在区间或区域内取值. 例 灯泡的寿命{t|t≥0}.
5
(二) 随机事件
定义 样本空间S的子集称为随机事件, 简称事件. 在一 次试验中, 当且仅当这一子集中的一个样本点出现时, 称 这一事件发生.
基本事件: 由一个样本点组成的单点集. 如:{H},{T}.
复合事件: 由两个或两个以上的基本事件复合而成的事件 为复合事件. 如:E3中{出现正面次数为奇数}.
必然事件: 样本空间S是自身的子集,在每次试验中总是 发生的,称为必然事件。
为在事件A发生的条件下事件B发生的条件概率2.9
2. 性质: 条件概率符合概率定义中的三个条件, 即 10 对于每一 B有 个 , 1 事 P(件 |B A)0.
20 P (|SA) 1.
30 设B1,B2,两两互不,则 相容
P ( Bi |A)P(Bi |A.)
i1
i1
此外, 条件概率具有无条件概率类似性质.例如:
P(A 1)P(A 2)P(A n).(有限)可
性3质 . 若 AB,则有 P(BA)P(B)P(A);
概率论与数理统计课件第二章

P( X 1) 1 P( X 0) 1 C 0.1 0.9
0 n 0 n 0
1 0.9 0.9
n
n 22.
例4. 某车间有5台车床,由于种种原因(由
于装、卸工作等),时常需要停车.设各 台车床的停车或开车是相互独立的. 若车床在任一时刻处于停车状态的 概率是1/3,求车间中恰有一台车床处 于停车状态的概率。 解:X:处于停车状态的车床数 X~B(5,1/3)
当0 x 1时,F ( x) P( X x) P( X 0) 0.3
当1 x 2时,F ( x) P( X x) P( X 0) P( X 1) 0.9
当x 2时,F ( x) P( X 0) P( X 1) P( X 2) 1
k nk CM CN M P( X k ) , n CN
k 0,1,..., l ,
其中n≤N,M<N,l=min{n,M},n,N,M均为正 整数,则称X服从参数为N,M,n的超几何分 布,记作X~H(N,M,n).
例8. 某班有学生20名,其中有5名女生, 今从班上任选4名学生去参观展览, 求被选到的女同学人数X的分布律。 X~H(20,5,4)
Ω X R X(w)
w
随机变量的分类
离散型随机变量
有限个或可列个 可能值
随 机 多,而且还不能 一一列举,而是充满 一个区间.
许多随机事件都可以通过形如{X≤x}的 事件来表示:
1 { X x} X x k k 1
(5) F ( x)是连续函数, 若f ( x)在x0连续, 有 F ( x0 ) f ( x0 ) .
例1. 设连续型随机变量X的概率密度为
《概率论与数理统计》课件 概率学与数理统计 第二章
作为某一个离散型随机变量的分布律。
为了直观地表达分布律,我们还可以作类似图2-1的分布律图。
图2-1
图2-1中 xi 处垂直于 x 轴的线段高度为 pi,它表示 X 取 xi 的概 率值。
例2.1 一盒中装有编号为1,2,3,4,5的五个球,现从中任意取三 个球,求所抽出三个球的中间号码 X 的概率分布。
Pa X b PX b PX a Fb 0 Fa
Pa X b PX a Pa<X b
Fa Fa 0 Fb Fa
Fb Fa 0
随机变量的分类:
1. 离散型随机变量:随机变量只取数轴上的有限个或可列个点。 2. 连续型随机变量:随机变量的可能取值充满数轴上的一个或 若干区间。 3. 奇异型随机变量:既不是离散型随机变量,也不是连续型随 机变量。在理论上很有价值,而实际问题中很少有应用。
解 以 p 表示每盏灯禁止汽车通过的概率,显然 X 的可能取值
为0,1,2,3,4,易知 X 的分布律为
表2-3
或写成
P X k 1 pk p,k 0,1,2,3 P X 4 1 p4
将 p 0.4, p 0.6 代入上式,所得结果如表2-4所示。
表2-4
二、常用离散型随机变量的分布
1
PX 2 1 PX 2 1 PX k k 0
1 0.9995000 50.9994999
≈1 50 e5 5e5 0! 1!
查表可得 P X 2 1 0.00674 0.03369 0.95957
例2.6 某人进行射击,设每次射击的命中率为,独立射击400次, 试求至少击中两次的概率。
记作 X 0 -1 分布。写成分布律表形式见表2-5。
表2-5
对于一个随机试验,若它的样本空间只包含两个元素,
东北大学概率论课后习题答案PPT2-2
(1) pk 0, k=1,2, …
一个函数是否是
概率分布
(2) pk 1
k
分布律也可以用表格的形式来表示:
X
x1 x2 … xn …
pk
p1 p2 … pn …
称为随机变量X的概率分布表。
也可用矩阵表示
X
~
x1 p1
x2 p2
xi pi
也可用散点图表示。
有了分布列,可以计算任意时间的概率
几何分布的无记忆性
在贝努利试验中,等待首次成功的时间服从几何分布。 现在假定已知在前m次试验中没有出现成功,那么为了达到 首次成功所再需要的等待时间′也还是服从几何分布,与 前面的失败次数m无关,形象化地说,就是把过去的经历完 全忘记了。因此无记忆性是几何分布所具有的一个有趣的 性质。但是更加有趣的是,在离散型分布中,也只有几何 分布才具有这样一种特殊的性质。
件,第i个零件为不合格品的概率为 pi 1/ i 1,i 1,2,3 ,若
以X表示三个零件中合格品的个数,问X是二项变量吗?写出 X的分布律。
例5:某人进行射击,设每次射击的命中率为0.02,独立射击 400次,试求至少击中两次的概率。
解:将一次射击看成是一次试验.设击中的次数为X,则X~ B(400,0.02)。X的分布律为 P{ X k} 4k00(0.02)k (0.98)400k , k 0,1,,400. 于是所求概率为 P{X 2} 1 P{X 0} P{X 1} 1 (0.98)400 400(0.02)(0.98)399 0.9972.
P{Y
4} 1
k
3 0
8k0(0.01)k
(0.99)80k
0.0087.
我们发现,在后一种情况尽管任务重了(每人平均
概率论与数理统计PPT课件第二章随机向量及其分布(1)
用这两条性质判断 一个函数是否是 概率分布
ppt课件
25
例1 从1~10这10个数字中随机取出5个数字, X 表示取出的5个数字中的最大值. 试求X 的 分布列
解: X 的取值为5,6,7,8,9,10. 并且
PX kC C k 4 1 5 0 1 k5 , 6 ,, 1 0
即 X 的分布列为
的时候才将自变元 写出来
ppt课件
13
二.随机变量的意义
引入了随机变量, 随机试验中的各种事件, 就可以通过随机变量的关系式表达出来
可见,随机事件这个概念实际上是包容在 随机变量这个更广的概念内. 也可以说,随机 事件是从静态的观点来研究随机现象,而随机 变量则是一种动态的观点. 就象数学分析中常 量与变量的区别那样
其中每一个 i 只取 A 或 A ,共 有 2 n 个
现考虑事件
Bn,k {n 重贝努里试验中事件A 恰好发生k 次}
现求概率 P Bn,k :
ppt课件
44
在 n 次试验中,指定 k 次出现 A(成功),
其余 n – k 次出现 A (失败),这种指定的
方法有
C
k n
种
而对于每一种指定好的方法,有
第二章 随机变量及其分布
• 随机变量 • 离散型随机变量 • 连续型随机变量 • 概率分布函数 • 随机变量函数的分布
ppt课件
1
§1.1 随机变量
一.随机变量的概念
为了更深入地研究随机现象, 就要建立 数学模型,随机变量是随机现象的最基本的 数学模型. 引入了随机变量,我们就可以用 随机变量的值表示随机试验的结果
X 5 6 7 8 9 10
P1
5 15 35 70 126
概率论与数理统计第二章随机变量课件
第二章 随机变量第一节 随机变量及其分布函数上一章中我们讨论的随机事件中有些是直接用数量来标识的,例如,抽样检验灯泡质量试验中灯泡的寿命;而有些则不是直接用数量来标识的,如性别抽查试验中所抽到的性别.为了更深入地研究各种与随机现象有关的理论和应用问题,我们有必要将样本空间的元素与实数对应起来.即将随机试验的每个可能的结果e 都用一个实数X 来表示.例如,在性别抽查试验中用实数“1”表示“出现男性”,用“0”表示“出现女性”.显然,一般来讲此处的实数X 值将随e 的不同而变化,它的值因e 的随机性而具有随机性,我们称这种取值具有随机性的变量为随机变量.定义2.1 设随机试验的样本空间为Ω,如果对Ω中每一个元素e ,有一个实数X (e )与之对应,这样就得到一个定义在Ω上的实值单值函数(e ),称之为随机变量( ).随机变量的取值随试验结果而定,在试验之前不能预知它取什么值,只有在试验之后才知道它的确切值;而试验的各个结果出现有一定的概率,故随机变量取各值有一定的概率.这些性质显示了随机变量与普通函数之间有着本质的差异.再者,普通函数是定义在实数集或实数集的一个子集上的,而随机变量是定义在样本空间上的(样本空间的元素不一定是实数),这也是二者的差别.本书中,我们一般以大写字母如X ,Y ,Z ,W ,…表示随机变量,而以小写字母如,…表示实数.为了研究随机变量的概率规律,并由于随机变量X 的可能取值不一定能逐个列出,因此我们在一般情况下需研究随机变量落在某区间(x 1,x 2]中的概率,即求P {x 1<X ≤x 2},但由于P {x 1<X ≤x 2}{X ≤x 2}{X ≤x 1},由此可见要研究P {x 1<X ≤x 2}就归结为研究形如P {X ≤x }的概率问题了.不难看出,P {X ≤x }的值常随不同的x 而变化,它是x 的函数,我们称这函数为分布函数.定义2.2 设X 是随机变量,x 为任意实数,函数F (x ){X ≤x }称为X 的分布函数( ).对于任意实数x 12(x 1<x 2),有P {x 1<X ≤x 2}{X ≤x 2}{X ≤x 1}(x 2)(x 1), (2.1)因此,若已知X 的分布函数,我们就能知道X 落在任一区间(x 12]上的概率.在这个意义上说,分布函数完整地描述了随机变量的统计规律性.如果将X 看成是数轴上的随机点的坐标,那么,分布函数F (x )在x 处的函数值就表示X 落在区间(-∞]上的概率.分布函数具有如下基本性质: 1°F (x )为单调不减的函数.事实上,由(2.1)式,对于任意实数x 12(x 1<x 2),有F (x 2)(x 1){x 1<X ≤x 2}≥0.2°0≤F (x )≤1,且)(lim x F x +∞→=1,常记为F (+∞)=1.)(lim x F x -∞→=0,常记为F (-∞)=0.我们从几何上说明这两个式子.当区间端点x 沿数轴无限向左移动(x →-∞)时,则“X 落在x 左边”这一事件趋于不可能事件,故其概率P {X ≤x }(x )趋于0;又若x 无限向右移动(x →+∞)时,事件“X 落在x 左边”趋于必然事件,从而其概率P {X ≤x }(x )趋于1.3°F (0)(x ),即F (x )为右连续. 证略.反过来可以证明,任一满足这三个性质的函数,一定可以作为某个随机变量的分布函数. 概率论主要是利用随机变量来描述和研究随机现象,而利用分布函数就能很好地表示各事件的概率.例如,P {X >a }=1{X ≤a }=1(a ){X <a }(0){}(a )(0)等等.在引进了随机变量和分布函数后我们就能利用高等数学的许多结果和方法来研究各种随机现象了,它们是概率论的两个重要而基本的概念.下面我们从离散和连续两种类别来更深入地研究随机变量及其分布函数,另有一种奇异型随机变量超出本书范围,就不作介绍了.第二节离散型随机变量及其分布如果随机变量所有可能的取值为有限个或可列无穷多个,则称这种随机变量为离散型随机变量.容易知道,要掌握一个离散型随机变量X 的统计规律,必须且只须知道X 的所有可能取的值以及取每一个可能值的概率.设离散型随机变量X 所有可能的取值为(1,2,…)取各个可能值的概率,即事件{}的概率P {}, 1,2,… (2.2)我们称(2.2)式为离散型随机变量X 的概率分布或分布律.分布律也常用表格来表示(表2-1):表2-1 X x 1 x 2 x 3 … …p 1 p 2 p 3 … …由概率的性质容易推得,任一离散型随机变量的分布律{},都具有下述两个基本性质: 1°≥0,1,2,…; (2.3) 2°11=∑∞=k kp. (2.4)反过来,任意一个具有以上两个性质的数列{},一定可以作为某一个离散型随机变量的分布律.为了直观地表达分布律,我们还可以作类似图2-1的分布律图.图2-1图2-1中处垂直于x 轴的线段高度为,它表示X 取的概率值.例2.1 设一汽车在开往目的地的道路上需通过4盏信号灯,每盏灯以0.6的概率允许汽车通过,以0.4的概率禁止汽车通过(设各盏信号灯的工作相互独立).以X 表示汽车首次停下时已经通过的信号灯盏数,求X 的分布律.解 以p 表示每盏灯禁止汽车通过的概率,显然X 的可能取值为0,1,2,3,4,易知X 的分布律为或写成P {}=(1),0,1,2,3.P {4}=(1)4.将0.4,10.6代入上式,所得结果如表2-3所示.表2-3(1)两点分布若随机变量X 只可能取x 1与x 2两值,它的分布律是P {1}=1(0<p <1),P {2},则称X 服从参数为p 的两点分布.特别,当x 1=0,x 2=1时两点分布也叫(0-1)分布,记作(0-1)分布.写成分布律表形式见表2-4.表2-4对于一个随机试验,若它的样本空间只包含两个元素,即={e 1,e 2},我们总能在上定义一个服从(0-1)分布的随机变量,,,1,0)(21e e e e e X X ==⎩⎨⎧==当当用它来描述这个试验结果.因此,两点分布可以作为描述试验只包含两个基本事件的数学模型.如,在打靶中“命中”与“不中”的概率分布;产品抽验中“合格品”与“不合格品”的概率分布等等.总之,一个随机试验如果我们只关心某事件A 出现与否,则可用一个服从(0-1)分布的随机变量来描述.(2)二项分布若随机变量X 的分布律为P {}kn C (1), 0,1,…, (2.5)则称X 服从参数为n ,p 的二项分布( ),记作().易知(2.5)满足(2.3)、(2.4)两式.事实上,P ()≥0是显然的;再由二项展开式知n k n k nk k nnk p p p p k X P )]1([)1(C}{0-+=-==-==∑∑=1.我们知道,P {}=kn k k n p p --)1(C 恰好是[(1)]n 二项展开式中出现的那一项,这就是二项分布名称的由来.回忆n 重贝努里试验中事件A 出现k 次的概率计算公式(k )kn C (1), 0,1,…,可知,若(),X 就可以用来表示n 重贝努里试验中事件A 出现的次数.因此,二项分布可以作为描述n 重贝努里试验中事件A 出现次数的数学模型.比如,射手射击n 次中,“中的”次数的概率分布;随机抛掷硬币n 次,落地时出现“正面”次数的概率分布;从一批足够多的产品中任意抽取n 件,其中“废品”件数的概率分布等等.不难看出,(0-1)分布就是二项分布在1时的特殊情形,故(0-1)分布的分布律也可写成P {}1(0,1)(1).例2.2 某大学的校乒乓球队与数学系乒乓球队举行对抗赛.校队的实力较系队为强,当一个校队运动员与一个系队运动员比赛时,校队运动员获胜的概率为0.6.现在校、系双方商量对抗赛的方式,提了三种方案: (1)双方各出3人;(2)双方各出5人;(3)双方各出7人.三种方案中均以比赛中得胜人数多的一方为胜利.问:对系队来说,哪一种方案有利?解 设系队得胜人数为X ,则在上述三种方案中,系队胜利的概率为(1) P {X ≥2}=k kk k -=∑3323)6.0()4.0(C ≈0.352;(2) P {X ≥3}=k kk k -=∑5535)6.0()4.0(C ≈0.317;(3) P {X ≥4}=k kk k -=∑7747)6.0()4.0(C ≈0.290.因此第一种方案对系队最为有利.这在直觉上是容易理解的,因为参赛人数越少,系队侥幸获胜的可能性也就越大.例2.3 某一大批产品的合格品率为98%,现随机地从这批产品中抽样20次,每次抽一个产品,问抽得的20个产品中恰好有k 个(1,2,…,20)为合格品的概率是多少?解 这是不放回抽样.由于这批产品的总数很大,而抽出的产品的数量相对于产品总数来说又很小,那么取出少许几件可以认为并不影响剩下部分的合格品率,因而可以当作放回抽样来处理,这样做会有一些误差,但误差不大.我们将抽检一个产品看其是否为合格品看成一次试验,显然,抽检20个产品就相当于做20次贝努里试验,以X 记20个产品中合格品的个数,那么(20,0.98),即P {}=kk k -2020)02.0()98.0(C ,1,2, (20)若在上例中将参数20改为200或更大,显然此时直接计算该概率就显得相当麻烦.为此我们给出一个当n 很大而p (或1)很小时的近似计算公式.定理2.1(泊松()定理) 设λ(λ>0是一常数,n 是任意正整数),则对任意一固定的非负整数k ,有e lim (1)!k k k n knn n n C p p k λλ-→∞-=-.证 由λ,有().111121111!)1()(!)1()1(1C kn kkn k kn n kn k n n n n k n n k n n k k n n n p p ---⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⋅⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⋅=-+--=-λλλλλ对任意固定的k ,当n →∞时,11121111→⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⋅n k n n ,11,e 1→⎪⎭⎫ ⎝⎛-→⎪⎭⎫ ⎝⎛---kn n n λλλ故e lim (1).!k kk n knn n n C p p k λλ--→∞-=由于λ是常数,所以当n 很大时必定很小,因此,上述定理表明当n 很大p 很小时,有以下近似公式,!e )1(C k p p k kn k k nλλ--≈- (2.6)其中λ.从表2-5可以直观地看出(2.6)式两端的近似程度.表2-5由上表可以看出,两者的结果是很接近的.在实际计算中,当n ≥20≤0.05时近似效果颇佳,而当n ≥100≤10时效果更好.!e k k λλ-的值有表可查(见本书附表3)二项分布的泊松近似,常常被应用于研究稀有事件(即每次试验中事件A 出现的概率p 很小),当贝努里试验的次数n 很大时,事件A 发生的次数的分布.例2.4 某十字路口有大量汽车通过,假设每辆汽车在这里发生交通事故的概率为0.001,如果每天有5000辆汽车通过这个十字路口,求发生交通事故的汽车数不少于2的概率.解 设X 表示发生交通事故的汽车数,则(),此处5000,0.001,令λ5, P {X ≥2}=1{X <2}=1-{}∑==1k k X P=1-(0.999)5000-5(0.999)4999≈1!e 50!e 51550----. 查表可得P {X ≥2}=1-0.00674-0.03369=0.95957.例2.5 某人进行射击,设每次射击的命中率为0.02,独立射击400次,试求至少击中两次的概率.解 将一次射击看成是一次试验.设击中次数为X ,则(400,0.02),即X 的分布律为P {}=k400C (0.02)k (0.98)400, 0,1, (400)故所求概率为P {X ≥2}=1{0}{1}=1-(0.98)400-400(0.02)(0.98)399 =0.9972.这个概率很接近1,我们从两方面来讨论这一结果的实际意义.其一,虽然每次射击的命中率很小(为0.02),但如果射击400次,则击中目标至少两次是几乎可以肯定的.这一事实说明,一个事件尽管在一次试验中发生的概率很小,但只要试验次数很多,而且试验是独立地进行的,那么这一事件的发生几乎是肯定的.这也告诉人们决不能轻视小概率事件.其二,如果在400次射击中,击中目标的次数竟不到两次,由于P {X <2}≈0.003很小,根据实际推断原理,我们将怀疑“每次射击的命中率为0.02”这一假设,即认为该射手射击的命中率达不到0.02.(3)泊松分布若随机变量X 的分布律为P {} =e !k k λλ-,0,1,2,…, (2.7)其中λ>0是常数,则称X 服从参数为λ的泊松分布( ),记为(λ). 易知(2.7)满足(2.3)、(2.4)两式,事实上,P {}≥0显然;再由∑∞=-0!e k k k λλλ·e λ=1,可知∑∞==0}{k k X P =1.由泊松定理可知,泊松分布可以作为描述大量试验中稀有事件出现的次数0,1,…的概率分布情况的一个数学模型.比如:大量产品中抽样检查时得到的不合格品数;一个集团中生日是元旦的人数;一页中印刷错误出现的数目;数字通讯中传输数字时发生误码的个数等等,都近似服从泊松分布.除此之外,理论与实践都说明,一般说来它也可作为下列随机变量的概率分布的数学模型:在任给一段固定的时间间隔内,① 由某块放射性物质放射出的α质点,到达某个计数器的质点数;② 某地区发生交通事故的次数;③ 来到某公共设施要求给予服务的顾客数(这里的公共设施的意义可以是极为广泛的,诸如售货员、机场跑道、电话交换台、医院等,在机场跑道的例子中,顾客可以相应地想象为飞机).泊松分布是概率论中一种很重要的分布.例2.6 由某商店过去的销售记录知道,某种商品每月的销售数可以用参数λ=5的泊松分布来描述.为了以95%以上的把握保证不脱销,问商店在月底至少应进某种商品多少件?解 设该商店每月销售这种商品数为X ,月底进货为a 件,则当X ≤a 时不脱销,故有P {X ≤a }≥0.95.由于(5),上式即为∑=-ak kk 05!5e ≥0.95. 查表可知∑=-95!5e k kk ≈0.9319<0.95, ∑=-105!10e k kk ≈0.9682>0.95 于是,这家商店只要在月底进货这种商品10件(假定上个月没有存货),就可以95%以上的把握保证这种商品在下个月不会脱销.下面我们就一般的离散型随机变量讨论其分布函数.设离散型随机变量X 的分布律如表2-1所示.由分布函数的定义可知F (x ){X ≤x }=∑∑≤≤==xx kxx kk k px X P }{,此处的∑≤xx k 和式表示对所有满足≤x 的k 求和,形象地讲就是对那些满足≤x 所对应的的累加.例2.7 求例2.1中X 的分布函数F (x ). 解 由例2.1的分布律知 当x <0时,F (x ){X ≤x }=0;当0≤x <1时,F (x ){X ≤x }{0}=0.4;当1≤x <2时,F (x ){X ≤x }({0}∪{1}){0}{1}=0.4+0.24=0.64;当2≤x <3时F (x ){X ≤x }({0}∪{1}∪{2}) {0}{1}{2}=0.4+0.24+0.144 =0.784;当3≤x <4时F (x ){X ≤x }({0}∪{1}∪{2}∪{3}) =0.4+0.24+0.144+0.0864=0.8704;当x ≥4时F (x ){X ≤x }({0}∪{1}∪{2}∪{3}∪{4}) =0.4+0.24+0.144+0.0864+0.1296=1.综上所述F (x ){X ≤x }=⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<≤<≤<.4,1,43,8704.0,32,784.0,21,64.0,10,4.0,0,0x x x x x x F (x )的图形是一条阶梯状右连续曲线,在0,1,2,3,4处有跳跃,其跳跃高度分别为0.4,0.24,0.144,0.0864,0.1296,这条曲线从左至右依次从F (x )=0逐步升级到F (x )=1.对表2-1所示的一般的分布律,其分布函数F (x )表示一条阶梯状右连续曲线,在(1,2,…)处有跳跃,跳跃的高度恰为{},从左至右,由水平直线F (x )=0,分别按阶高p 1,p 2,…升至水平直线F (x )=1.以上是已知分布律求分布函数.反过来,若已知离散型随机变量X 的分布函数F (x ),则X 的分布律也可由分布函数所确定:{}()(0).第三节 连续型随机变量及其分布上一节我们研究了离散型随机变量,这类随机变量的特点是它的可能取值及其相对应的概率能被逐个地列出.这一节我们将要研究的连续型随机变量就不具有这样的性质了.连续型随机变量的特点是它的可能取值连续地充满某个区间甚至整个数轴.例如,测量一个工件长度,因为在理论上说这个长度的值X 可以取区间(0,+∞)上的任何一个值.此外,连续型随机变量取某特定值的概率总是零(关于这点将在以后说明).例如,抽检一个工件其长度X 丝毫不差刚好是其固定值(如 1.824)的事件{1.824}几乎是不可能的,应认为P{1.824}=0.因此讨论连续型随机变量在某点的概率是毫无意义的.于是,对于连续型随机变量就不能用对离散型随机变量那样的方法进行研究了.为了说明方便我们先来看一个例子.例2.8 一个半径为2米的圆盘靶,设击中靶上任一同心圆盘上的点的概率与该圆盘的面积成正比,并设射击都能中靶,以X 表示弹着点与圆心的距离,试求随机变量X 的分布函数.解 1°若x <0,因为事件{X ≤x }是不可能事件,所以F (x ){X ≤x }=0.2°若0≤x ≤2,由题意P {0≤X ≤x }2,k 是常数,为了确定k 的值,取2,有P {0≤X ≤2}=22k ,但事件{0≤X ≤2}是必然事件,故P {0≤X ≤2}=1,即221,所以1/4,即P {0≤X ≤x }2/4.于是F (x ){X ≤x }{X <0}{0≤X ≤x }= x 2/4.3°若x ≥2,由于{X ≤2}是必然事件,于是F (x ){X ≤x }=1.综上所述F (x )=⎪⎩⎪⎨⎧≥<≤<,2,1,20,41,0,02x x x x 它的图形是一条连续曲线如图2-2所示.图2-2另外,容易看到本例中X 的分布函数F (x )还可写成如下形式:F (x )=t t f xd )(⎰∞-,其中 f (t )=⎪⎩⎪⎨⎧<<.,0,20,21其他t t这就是说F (x )恰好是非负函数f (t )在区间(-∞,x ]上的积分,这种随机变量X 我们称为连续型随机变量.一般地有如下定义.定义2.3 若对随机变量X 的分布函数F (x ),存在非负函数f (x ),使对于任意实数x 有F (x )=⎰∞-xx t f d )(, (2.8)则称X 为连续型随机变量,其中f (x )称为X 的概率密度函数,简称概率密度或密度函数( ).由(2.8)式知道连续型随机变量X 的分布函数F (x )是连续函数.由分布函数的性质F (-∞)=0,F (+∞)=1及F (x )单调不减,知F (x )是一条位于直线0与1之间的单调不减的连续(但不一定光滑)曲线. 由定义2.3知道,f (x )具有以下性质:1°f (x )≥0;2°⎰+∞∞-x x f d )(=1;3°P {x 1<X ≤x 2}(x 2)-F (x 1)=⎰21d )(x x x x f (x 1≤x 2);4°若f (x )在x 点处连续,则有F ′(x )(x ).由2°知道,介于曲线(x )与0之间的面积为1.由3°知道,X 落在区间(x 1,x 2]的概率P {x 1<X ≤x 2}等于区间(x 1,x 2]上曲线(x )之下的曲边梯形面积.由4°知道,f (x )的连续点x 处有f (x )=.}{)()(lim lim 00x x x X x P x x F x x F x x ∆∆+≤<=∆-∆+++→∆→∆ 这种形式恰与物理学中线密度定义相类似,这也正是为什么称f (x )为概率密度的原因.同样我们也指出,反过来,任一满足以上1°、2°两个性质的函数f (x ),一定可以作为某个连续型随机变量的密度函数.前面我们曾指出对连续型随机变量X 而言它取任一特定值a 的概率为零,即P {}=0,事实上,令Δx >0,设X 的分布函数为F (x ),则由{}⊂{a -Δx <X ≤a },得 0≤P {}≤P {a -Δx <X ≤a }(a )-F (a -Δx ). 由于F (x )连续,所以)(lim 0x a F x ∆-→∆(a ).当Δx →0时,由夹逼定理得P {}=0,由此很容易推导出P {a ≤X <b }{a <X ≤b }{a ≤X ≤b }{a <X <b }.即在计算连续型随机变量落在某区间上的概率时,可不必区分该区间端点的情况.此外还要说明的是,事件{}“几乎不可能发生”,但并不保证绝不会发生,它是“零概率事件”而不是不可能事件.例2.9 设连续型随机变量X 的分布函数为F (x )=⎪⎩⎪⎨⎧≥<≤<.1,1,10,,0,02x x Ax x 试求:(1)系数A ;(2)X 落在区间(0.3,0.7)内的概率; (3)X 的密度函数.解 (1)由于X 为连续型随机变量,故F (x )是连续函数,因此有1(1)=2101lim lim )(Axx F x x -→-→= ,即1,于是有F (x )=⎪⎩⎪⎨⎧≥<≤<.1,1,10,,0,02x x x x (2) P {0.3<X <0.7}(0.7)-F (0.3)=(0.7)2-(0.3)2=0.4; (3) X 的密度函数为f (x )′(x )=⎩⎨⎧<≤.,0;10,2其他x x由定义2.3知,改变密度函数f (x )在个别点的函数值,不影响分布函数F (x )的取值,因此,并不在乎改变密度函数在个别点上的值(比如在0或1上f (x )的值).例2.10 设随机变量X 具有密度函数f (x )=⎪⎩⎪⎨⎧≤≤-<≤.,0,43,22,30,其他x x x kx (1) 确定常数k ;(2) 求X 的分布函数F (x );(3) 求P {1<X ≤72}. 解 (1)由⎰∞∞-x x f d )(=1,得x xx kx d )22(d 4330⎰⎰-+=1, 解得1/6,故X 的密度函数为f (x )=⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≤-<≤.,0,43,22,30,6其他x x x x(2) 当x <0时,F (x ){X ≤x }=⎰∞-xt t f d )( =0;当0≤x <3时,F (x ){X ≤x }⎰∞-xtt f d )(⎰⎰∞-+0d )(d )(xt t f t t f 12d 620x t t x =⎰;当3≤x <4时,F (x ){X ≤x }⎰∞-xtt f d )(033()()()x f t dt f t dt f t dt -∞++⎰⎰⎰=233(2)23;624x t t x dt dt x +-=-+-⎰⎰当x ≥4时,F (x ){X ≤x }⎰∞-xtt f d )(⎰⎰⎰⎰∞-+++030434d )(d )(d )(d )(xt t f t t f t t f t t f=t tt t d )22(d 64330⎰⎰-+ =1.即F (x )=⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤-+-<≤<.4,1,43,324,30,12,0,022x x x x x x x(3) P {1<X ≤7/2}(7/2)-F (1)=41/48.下面介绍三种常见的连续型随机变量. (1)均匀分布若连续型随机变量X 具有概率密度f (x )=⎪⎩⎪⎨⎧<<-.,0,,1其他b x a ab (2.9)则称X 在区间(a ,b )上服从均匀分布( ),记为().易知f (x )≥0且⎰⎰∞∞--=ba x ab x x f d 1d )(=1.由(2.9)可得 1°P {X ≥b }=⎰∞bx d 0 =0{X ≤a }⎰∞-ax d 00,即 P {a <X <b }=1-P {X ≥b }-P {X ≤a }=1;2°若a ≤c <d ≤b ,则P {c <X <d }=ab cd x a b dc--=-⎰d 1. 因此,在区间()上服从均匀分布的随机变量X 的物理意义是:X 以概率1在区间()内取值,而以概率0在区间()以外取值,并且X 值落入()中任一子区间()中的概率与子区间的长度成正比,而与子区间的位置无关. 由(2.8)易得X 的分布函数为F (x )=⎪⎩⎪⎨⎧≥<≤--<.,1,,,,0b x b x a a b ax a x (2.10) 密度函数f (x )和分布函数F (x )的图形分别如图2-3和图2-4所示.图2-3 图2-4在数值计算中,由于四舍五入,小数点后第一位小数所引起的误差X ,一般可以看作是一个服从在[-0.5,0.5]上的均匀分布的随机变量;又如在()中随机掷质点,则该质点的坐标X 一般也可看作是一个服从在()上的均匀分布的随机变量.例2.11 某公共汽车站从上午7时开始,每15分钟来一辆车,如某乘客到达此站的时间是7时到7时30分之间的均匀分布的随机变量,试求他等车少于5分钟的概率.解 设乘客于7时过X 分钟到达车站,由于X 在[0,30]上服从均匀分布,即有f (x )=⎪⎩⎪⎨⎧≤≤.,0,300,301其他x显然,只有乘客在7∶10到7∶15之间或7∶25到7∶30之间到达车站时,他(或她)等车的时间才少于5分钟,因此所求概率为P {10<X ≤15}{25<X ≤30}⎰⎰+15103025d 301d 301x x 1/3. (2)指数分布若随机变量X 的密度函数为f (x )=⎩⎨⎧≤>-.00,,0,e x x x λλ (2.11) 其中λ>0为常数,则称X 服从参数为λ的指数分布( ),记作(λ).显然f (x )≥0,且x x x f x d e d )(0⎰⎰∞∞-∞-=λλ=1.容易得到X 的分布函数为F (x )=⎩⎨⎧≤>--.00,,0,e 1x x x λ指数分布最常见的一个场合是寿命分布.指数分布具有“无记忆性”,即对于任意>0,有P {X >>s }{X >t }. (2.12)如果用X 表示某一元件的寿命,那么上式表明,在已知元件已使用了s 小时的条件下,它还能再使用至少t 小时的概率,与从开始使用时算起它至少能使用t 小时的概率相等.这就是说元件对它已使用过s 小时没有记忆.当然,指数分布描述的是无老化时的寿命分布,但“无老化”是不可能的,因而只是一种近似.对一些寿命长的元件,在初期阶段老化现象很小,在这一阶段,指数分布比较确切地描述了其寿命分布情况.(2.12)式是容易证明的.事实上,(){,}{}{}{}{}1()ee {}.1()es t t λsP X s X s t P X s t P X s t X s P X s P X s F s t P X t F s λλ-+->>+>+>+>==>>-+====>--(3)正态分布若连续型随机变量X 的概率密度为f (x )=222)(e π21σμσ--x , -∞<x <+∞, (2.13)其中μ,σ(σ>0)为常数,则称X 服从参数为μ,σ的正态分布( ),记为(μ,σ2).显然f (x )≥0,下面来证明⎰∞∞-x x f d )(=1.令σux -,得到.d eπ21d e π2122)(222t x t x ⎰⎰∞∞--∞∞---=σμσ记t t d e22⎰∞∞--,则有I 2=⎰⎰∞∞-∞∞-+-ds d e222t s t .作极坐标变换:θθ,得到I 2=22π22r redrd πθ∞--∞=⎰⎰,而I >0,,即有.π2d e22=⎰∞∞--t t于是.1π2π21d e 21222)(=⋅=--∞∞-⎰x x σμσπ 正态分布是概率论和数理统计中最重要的分布之一.在实际问题中大量的随机变量服从或近似服从正态分布.只要某一个随机变量受到许多相互独立随机因素的影响,而每个个别因素的影响都不能起决定性作用,那么就可以断定随机变量服从或近似服从正态分布.例如,因人的身高、体重受到种族、饮食习惯、地域、运动等等因素影响,但这些因素又不能对身高、体重起决定性作用,所以我们可以认为身高、体重服从或近似服从正态分布.参数μ,σ的意义将在第四章中说明(x )的图形如图2-5所示,它具有如下性质:图2-5 图2-61°曲线关于μ对称;2°曲线在μ处取到最大值,x 离μ越远,f (x )值越小.这表明对于同样长度的区间,当区间离μ越远,X 落在这个区间上的概率越小;3°曲线在μ±σ处有拐点; 4°曲线以x 轴为渐近线;5°若固定μ,当σ越小时图形越尖陡(图2-6),因而X 落在μ附近的概率越大;若固定σ,μ值改变,则图形沿x 轴平移,而不改变其形状.故称σ为精度参数,μ为位置参数. 由(2.13)式得X 的分布函数F (x )=t xt d eπ21-2)(22⎰∞--σμσ. (2.14)特别地,当μ=0,σ=1时,称X 服从标准正态分布N (0,1),其概率密度和分布函数分别用)(x ϕ,Φ(x )表示,即有22e π21)(x x -=ϕ, (2.15)Φ(x )=t xt d eπ2122⎰∞--. (2.16)易知,Φ(-x )=1-Φ(x ).人们已事先编制了Φ(x )的函数值表(见本书附录).一般地,若(μ,σ2),则有σμ-X (0,1).事实上,σμ-X 的分布函数为P {Z ≤x }=}{x X P ≤-σμ{X ≤μ+σx }=t t xd e π21222)(σμσμσ--+∞-⎰,令σμ-t ,得P {Z ≤x }=s xs d eπ2122⎰∞--=Φ(x ),由此知σμ-X (0,1).因此,若(μ,σ2),则可利用标准正态分布函数Φ(x ),通过查表求得X 落在任一区间(x 12]内的概率,即P {x 1<X ≤x 2}=⎭⎬⎫⎩⎨⎧-≤-<-σμσμσμ21x X x P =⎭⎬⎫⎩⎨⎧-≤--⎭⎬⎫⎩⎨⎧-≤-σμσμσμσμ12x X P x X P=⎪⎭⎫ ⎝⎛-Φ-⎪⎭⎫⎝⎛-Φσμσμ12x x . 例如,设(1.5,4),可得P {-1≤X ≤2}=⎭⎬⎫⎩⎨⎧-≤-≤--25.1225.125.11X P=Φ(0.25)-Φ(-1.25)=Φ(0.25)-[1-Φ(1.25)]=0.5987-1+0.8944=0.4931.设(μ,σ2),由Φ(x )函数表可得P {μ-σ<X <μ+σ}=Φ(1)-Φ(-1)=2Φ(1)-1=0.6826,P {μ-2σ<X <μ+2σ}=Φ(2)-Φ(-2)=0.9544, P {μ-3σ<X <μ+3σ}=Φ(3)-Φ(-3)=0.9974.我们看到,尽管正态变量的取值范围是(-∞,∞),但它的值落在(μ-3σ,μ+3σ)内几乎是肯定的事,因此在实际问题中,基本上可以认为有-μ|<3σ.这就是人们所说的“3σ原则”.例2.12 公共汽车车门的高度是按成年男子与车门顶碰头的机会在1%以下来设计的.设男子身高X 服从μ=170(),σ=6()的正态分布,即(170,62),问车门高度应如何确定?解 设车门高度为h (),按设计要求P {X ≥h }≤0.01或P {X <h }≥0.99,因为(170,62),故P {X <h }=⎪⎭⎫⎝⎛-Φ=⎭⎬⎫⎩⎨⎧-<-617061706170h h X P ≥0.99, 查表得 Φ(2.33)=0.9901>0.99.故取6170-h =2.33,即184.设计车门高度为184()时,可使成年男子与车门碰头的机会不超过1%.例2.13 测量到某一目标的距离时发生的随机误差X (单位:米)具有密度函数f (x )=3200)20(2eπ2401--x .试求在三次测量中至少有一次误差的绝对值不超过30米的概率.解 X 的密度函数为f (x )=222402)20(3200)20(e π2401eπ2401⨯----⨯=x x ,即(20,402),故一次测量中随机误差的绝对值不超过30米的概率为P {≤30}{-30≤X ≤30}=⎪⎭⎫⎝⎛--Φ-⎪⎭⎫⎝⎛-Φ402030402030 =Φ(0.25)-Φ(-1.25)=0.5981-(1-0.8944)=0.4931.设Y 为三次测量中误差的绝对值不超过30米的次数,则Y 服从二项分布b (3,0.4931),故P {Y ≥1}=1-P {0}=1-(0.5069)3=0.8698.为了便于今后应用,对于标准正态变量,我们引入了α分位点的定义. 设(0,1),若z α满足条件P {X >z α}=α,0<α<1, (2.17)则称点z α为标准正态分布的上α分位点,例如,由查表可得z 0.05=1.6450.001=3.16.故1.645与3.16分别是标准正态分布的上0.05分位点与上0.001分位点.第四节 随机变量函数的分布我们常常遇到一些随机变量,它们的分布往往难于直接得到(如测量轴承滚珠体积值Y 等),但是与它们有函数关系的另一些随机变量,其分布却是容易知道的(如滚珠直径测量值X ).因此,要研究随机变量之间的函数关系,从而通过这种关系由已知的随机变量的分布求出与其有函数关系的另一个随机变量的分布.例2.14 设随机变量X 具有表2-6所示的分布律,试求X 2的分布律.“X 2=9”等价,所以P {X 2=0}{0}=0.1, P {X 2=2.25}{1.5}=0.3, P {X 2=9}{3}=0.1.事件“X 2=1”是两个互斥事件“1”及“1”的和,其概率为这两事件概率和,即P {X 2=1}{1}{1}=0.2+0.3=0.5.于是得X 2的分布律如表2-7所示.解 先求Y 的分布函数(y ),由于(X )2≥0,故当y ≤0时事件“Y ≤y ”的概率为0,即(y ){Y ≤y }=0,当y >0时,有(y ){Y ≤y }{X 2≤y }{≤X ≤y }=x x f yyX d )(⎰-.将(y )关于y 求导,即得Y 的概率密度为(y )=()()[]⎪⎩⎪⎨⎧≤>-+.0,0,0,21y y y f y f y XX例如,当(0,1),其概率密度为(2.15)式,则2的概率密度为(y )=⎪⎩⎪⎨⎧≤>--.0,0,0,e π21221y y y y此时称Y 服从自由度为1的χ2分布.上例中关键的一步在于将事件“Y ≤y ”由其等价事件“≤X ≤y ”代替,即将事件“Y ≤y ”转换为有关X 的范围所表示的等价事件,下面我们仅对(X ),其中g (x )为严格单调函数,写出一般结论.定理2.2 设随机变量X 具有概率密度(x ),-∞<x <+∞,又设函数g (x )处处可导且g ′(x )>0(或g ′(x )<0),则(X )是连续型随机变量,其概率密度为(y )=⎩⎨⎧<<'.,0,)()]([其他βαx y h y h f X (2.18)其中α(g (-∞),g (+∞)),β(g (-∞),g (+∞)),h (y )是g (x )的反函数.我们只证g ′(x )>0的情况.由于g ′(x )>0,故g (x )在(-∞∞)上严格单调递增,它的反函数h (y )存在,且在(α,β)严格单调递增且可导.我们先求Y 的分布函数(y ),并通过对(y )求导求出(y ).由于(X )在(α,β)上取值,故 当y ≤α时,(y ){Y ≤y }=0; 当y ≥β时,(y ){Y ≤y }=1; 当α<y <β时,(y ){Y ≤y }{g (X )≤y }{X ≤h (y )}=⎰∞-)(d )(x h X x x f .于是得概率密度(y )=[()](),,0,X f h y h y x .αβ'<<⎧⎨⎩其他对于g ′(x )<0的情况可以同样证明,即(y )=[()][()],,0,fX h y h y x .αβ'<<⎧⎨⎩其他将上面两种情况合并得(y )=(())(),,0,fX h y h y x .αβ'⎧<<⎨⎩其他注:若f (x )在[a ,b ]之外为零,则只需假设在(a ,b )上恒有g ′(x )>0(或恒有g ′(x )<0),此时α{g (a ),g (b )},β{g (a ),g (b )}.例2.16 设随机变量(μ,σ2).试证明X 的线性函数(a ≠0)也服从正态分布. 证 设X 的概率密度(x )=,21222)(σμ--x e π-∞<x <+∞.再令(x ),得g (x )的反函数(y )=y ba-. 所以h ′(y )=1.由(2.18)式(X )的概率密度为(y )=⎪⎭⎫ ⎝⎛-a b y f a X 1, -∞<y <+∞, 即(y )=22)(2)]([21σμσa a b y a +--eπ,-∞<y <+∞,即有(a μ,(a σ)2).例2.17 由统计物理学知分子运动速度的绝对值X 服从麦克斯韦()分布,其概率密度为f (x )=⎪⎩⎪⎨⎧≤>-,0,0,0,42232x x a x a x e π其中a >0为常数,求分子动能221mX (m 为分子质量)的概率密度. 解 已知(x )=221mx (x )只在区间(0,+∞)上非零且g ′(x )在此区间恒单调递增,由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例2.1.5 某一时间段内,车站到来的乘客数, 或在某一个区域里,野生动物的数量 … ; 它所有可能的取值是一切非负整数。 例2.1.6 在一个区间中随机等可能取一个点 X ; X 可能取这个区间中任何一个数。 例2.1.7 在一批电子元件中随机抽取一只测试 它的寿命 X ; X 可取任意一个非负的实数。 例2.1.8 一个物体的测量值与真实值的 误差 X ; X 可以取任意一个实数。
(4) 密度函数是分布函数的一阶导数, 分布函数是密度函数的一个特殊原函数。 F (x) = –x∞ f(t) dt f(x) = F (x) / x 这个性质用来计算随机变量函数的分布 (5) 连续随机变量在任一常数取值概率是 0, 即对每一个常数 c ,P { X = c } = 0 。 但是 (X = c) 并不一定是不可能事件。 即,零概率事件≠不可能事件
2.2 离散随机变量及分布律
2.2.1 离散随机变量
只取有限多或者可数无穷多个值的随机变量
1. 分布律(或概率分布)
指离散随机变量所有可能的取值以及 相应的概率。分布律一般表示成: P { X = xk } = pk ,k ≥ 1 。
2. 分布律的表格形式
X pk x1 p1 x2 p2 x3 … xn … p3 … pn …
第2章 随机变量及其分布
2.1 2.2 2.3 2.4 2.5 随机变量 离散随机变量及分布律 随机变量分布函数 连续随机变量及概率密度 随机变量函数的概率分布
2.1 随机变量
2.1.1 随机变量的概念
随机变量是指取值随机会而定的变量, 它随着试验的不同结果而取不同的数值。 一个随机变量取值的规律称为它的 概率分布,简称 “分布”(distribution) 。 随机变量的分布包含两个部分: 取哪些值?取这些值相应的概率是多少?
3. 分布律的基本性质
pk ≥ 0 , k = 1, 2, 3, … ∑ k ≥ 1 pk = 1
例2.2.1 假设城市的某条街道有四个路口,汽车 在每个路口是否遇到红灯是独立的,并且概率 都是 p ,以 X 记汽车首次停下时通过路口数, 求 X 的概率分布。 解. X 的所有可能取值为:0,1,2,3,4。 ① ② ③ ④
离散随机变量分布函数的图形
1 p1+ p2 p1 ○ x1 ○ F (x) ... ○
阶梯型 跳跃线段
x
x2
x3
2.3.2 分布函数的主要性质
1. 非负有界 0 ≤ F (x) ≤ 1 ; ( 即概率定义中的非负与规范性 ) 2. 单调性 当 x1 < x2,则F (x1) ≤ F (x2) ; ( 即A B 则有 P (A) ≤ P (B) ) 3. 极限性质 F ( -∞) = lim x→ -∞ F (x) = 0 , F (+∞) = lim x→+∞ F (x) = 1 。
2.4.1 连续随机变量的定义
所有可能取值是连续区间的随机变量
1. 概率密度函数
非负函数 f (x),使得分布函数 能够表示成关于它的积分:F 来自 x) x
f ( t ) dt
例2.4.1 下面是三个分布函数 0,x<0, x/b,0≤x< b 1,x≥b 。 0,x≤0, F2 (x) = 1 - e – x,x > 0 f2 ( x ) = 1/b,0<x<b , f1 ( x ) = 0,其它 e - x,x > 0 , 0,其它
因此如果记 q = 1 – p ,则有: P { X = 0 } = p ;P { X = 1 } = pq ; P { X = 2 } = pq2 ;P { X = 3 } = pq3 ; P { X = 4 } = q4 。 验证:这 5 个概率的和应该等于 1。即 p + pq + pq2 + pq3 + q4 = p(1 + q + q2 + q3) + q4 1 – q4 = p + q4 = 1 。 1–q
2.3.3 利用分布函数计算概率
1. 对任意的实数 x1 < x2 , P { x1< X ≤ x2 } = F (x2) - F (x1) ; 2. P { X >x } = 1 - F (x) ;
Remark 这两个公式实际上来自概率的减法公式 以及对立事件的概率公式。
2.4 连续随机变量及概率密度
3. 概率密度函数的基本性质
f(x) (1)
(2)
f (x) ≥ 0 ;
f ( x ) dx 1
o
x
这也是概率密度函数的充分必要条件 比较离散分布律的两个性质: pk ≥ 0 ;∑k≥1 pk = 1
4. 连续随机变量概率的计算
对任意的 x1 < x2 ,有: P { x1 <X ≤ x2 } = F (x2) - F (x1)
2 3 k x x x ex=1+x+—+—+…+—+… 2! 3! k!
2.2.2 常见的离散分布
1. 两点分布 (也称0–1分布或Bernoulli 分布)
记为 X ~ B (1,p) , 0 <p<1 。 它只取 0 和1 两个可能值,分布律为: P { X = 1 } = p, P { X = 0 } = q = 1 – p 称随机变量X 服从参数 p 的两点分布。 两点分布用来描述所有 只有两个可能结果的随机试验
x2
f(x)
=
x1
f ( x ) dx
x1 o
x2
x
例2.4.2 确定常数 a 使得 f(x) 是密度函数。 ax, 0<x<1, f (x) = 2 - x , 1 ≤ x < 2 , 0, 其它 解. 要使 f (x) 成为一个密度函数,必须 而且只须满足两个条件:非负、积分为 1 。 因此首先有 a ≥ 0 ;其次计算积分:
定义 设E 是随机试验,S 是它的样本空间,
如果对于每一个样本点 都有一个实数 与它对应, 则称这个定义在样本空间上 的单值实函数 X = X () 是一个随机变量。
S
0
X ()
x
通过引进随机变量的概念能够把不同的 样本空间抽象化为一些定量的实数,由此就 可以利用更高深的数学方法来研究随机现象。 其次,在随机变量的概率分布中我们关注 的重点是这个随机变量取某些值的概率,而 不是它的取值。就象我们只关心样本空间里 一些样本点发生的概率,而这些样本点本身 并不是研究的目的。
□
3. Poisson (泊松) 分布,X ~ ()
这是最重要的离散分布 可能取值是所有非负整数 0,1,2,… ; 分布律为: k P { X = k } = — e – ,k ≥ 0 k! 这里泊松分布的参数 > 0 。
泊松分布的背景知识 在大量的重复试验中稀有事件出现的次数 近似服从泊松分布,如意外事故,非常见病, 大的自然灾害,害虫数量,动物种群等等; 另外,如果一个随机事件流满足“平稳性”、 “独立增量性”、“普通性”三个条件,它也近似 服从泊松分布,如通讯的呼叫次数,顾客数, 放射源衰变产生的粒子数等等。 在运筹学、管理科学、物理学中泊松 分布具有非常重要的应用。
例2.3.2 讨论如下的分布函数 F (x) = 1 - e - x , x > 0 (为简便总是省略分布函数等于 0 的部分)
F (x)
解. 0 ≤F (x)< 1,满足 非负有界;( - ∞,0 ] 上恒等于 0,[ 0,+ ∞] 单调递增,满足单调性; 极限性质显然满足。
1
o
x □
如何计算X 落在区间 (1,3 ]的概率?
2. 二项分布,X ~ B (n,p)
概率论中最重要的三种分布的第一种 X 全部可能取值是有限整数 0,1,…,n ; 分布律为: pk = Cnk pkqn – k ,0 ≤ k ≤ n 这里参数 0 < p < 1 , q = 1 – p 。 两点分布就是 n = 1 时的二项分布
二项分布的背景知识 它对应于随机抽样模型中的有放回抽样, 二项分布也与独立试验序列概型有关,即 在 n 重 Bernoulli 试验中,随机事件 A 发生 的次数服从参数为 n、p 的二项分布; 二项分布广泛应用于抽样调查的问题中, 以及在金融,保险,医学,生物遗传学等 都有重要的应用。
□
练习2.2.2 离散分布涉及的几个数列求和公式 (0 < x <1)
n +1 1 – x ① 1+x+ +…+ = ———— 1–x 1 2 ② 1 + x + x + …= —— 1–x 1 ③ 1 + 2x + 3x2 + 4x3 + … = ——— (1 – x)2
x2
xn
④ 对任意实数 x,有Taylor 展开:
1 2 e
x2 2
F1 (x) =
( x)
x
1 2
e
t2 2
dt
( x)
□
2. 概率密度函数的意义
(1) 它的作用类似于离散随机变量的分布律。 离散随机变量的分布函数是对分布律 “求和”, 得到的是一个阶梯形跳跃的间断函数; 连续随机变量分布函数是对密度函数 “积分”, 得到的是一个连续的函数。 (2) 连续随机变量只能在概率密度函数 不等于 0 的区间上取值。 (3) 分布函数、分布律、概率密度函数,都是 对随机变量的随机性质的完整刻划。
例2.3.1 参数 p 的两点分布的分布函数 解. 两点分布的分布律是: P (X = 0) = q, P (X = 1) = p ;q = 1 - p 由于 X 只可能取 0、1 两个值,因此 0,x<0, F (x) = q ,0 ≤ x < 1 , F (x) 1,x≥1 。
1 q ○ o ○ 1 x □
