第2章_桁架结构
高层建筑结构课件第2章(结构体系与结构布置)

六.截面尺寸初估(方案设计和初步设计时)
1.柱截面:
由轴压比控制
N c c f cbh
轴压比限值 P68表4.4
柱负荷面积 表4.4
单位面积荷载:框架、框-剪12~14kN/m2; 框架柱轴压比限值 剪力墙、筒体13~16
N Q S Qn
结1.1 构~ 体 系 系数 1.2
3.适用范围:适用于200m以下的超高层
代表作品及平面:
深圳国贸大厦
back
五.结构体系(抗侧力体系)的选择
•建筑使用功能 •建筑平面
•建筑高度
•抗震等级 •地质条件 •施工技术 ……
用 途 住 宅 旅 馆 公 共
≤50m 剪力墙、框架-剪力墙 剪力墙、框架-剪力墙、 框架 框架-剪力墙、框架
≥50m 剪力墙、框架-剪力墙 剪力墙、框架-剪力墙、 筒体 框架-剪力墙、筒体
竖向抗侧力构件不连 竖向抗侧力构件(柱、抗震墙、抗震支撑)的内力由水平 续 转换构件(梁、桁架等)向下传递 楼层承载力突变 抗侧力结构的层间受剪承载力小于相邻上一楼层的 80%
五.设置变形缝的原则
1.设置原则:
1)尽量不设缝,而调整平面形状、尺寸和结构布置, 采取构造和施工措施。 2)设缝时,应形成独立的结构单元,保证足够的缝宽。
框架结构 框架—剪力墙结构、筒体结构 部分框支剪力墙结构 0.7 0.75 0.6
抗震等级
计算截面以上层数 一级 二级
三级 0.9 0.95 ---
0.8 0.85 0.7
2.梁截面:
由高跨比控制:P18表2.9
注意:梁高有减小的趋势。
抵抗温度应力 3.板厚: 加强顶层约束 提高抗风抗震 一般楼层:80-140 顶层现浇板:≥120,宜双层双向配筋 地下室顶板:≥160
建筑结构第二版课后习题答案

建筑结构第二版课后习题答案建筑结构第二版课后习题答案建筑结构是建筑学中的重要课程,它涉及到建筑物的各个方面,包括结构设计、材料选择、力学分析等。
而课后习题是检验学生对所学知识理解程度的重要途径。
本文将为大家提供建筑结构第二版课后习题的答案,希望能够帮助大家更好地学习和掌握这门课程。
第一章:结构力学基础1. 问题:什么是静力学?答案:静力学是研究物体在平衡状态下受力和力的平衡关系的学科。
2. 问题:什么是结构?答案:结构是由构件和连接构件的节点组成的整体系统,用于承受和传递荷载。
3. 问题:什么是结构的稳定性?答案:结构的稳定性是指结构在受到外力作用时,不会发生失稳或破坏的能力。
第二章:杆件结构1. 问题:什么是杆件?答案:杆件是一种细长的构件,其长度远大于其横截面尺寸,主要受拉力、压力和弯矩作用。
2. 问题:杆件的受力分析方法有哪些?答案:杆件的受力分析方法包括静力学方法、力法和位移法。
3. 问题:什么是轴力?答案:轴力是杆件内部产生的沿轴线方向的拉力或压力。
第三章:梁结构1. 问题:什么是梁?答案:梁是一种承受弯曲力和剪切力的结构构件,主要用于支撑和传递荷载。
2. 问题:梁的受力分析方法有哪些?答案:梁的受力分析方法包括静力学方法、力法和位移法。
3. 问题:什么是弯矩?答案:弯矩是梁在受到外力作用时,横截面内部产生的力矩。
第四章:桁架结构1. 问题:什么是桁架?答案:桁架是由直杆构成的三角形网格结构,主要用于支撑和传递荷载。
2. 问题:桁架的受力分析方法有哪些?答案:桁架的受力分析方法包括静力学方法、力法和位移法。
3. 问题:桁架的应用领域有哪些?答案:桁架广泛应用于大跨度建筑、桥梁和塔楼等结构中。
第五章:板壳结构1. 问题:什么是板壳?答案:板壳是由薄板构成的扁平结构,主要用于承受和传递荷载。
2. 问题:板壳的受力分析方法有哪些?答案:板壳的受力分析方法包括静力学方法、力法和位移法。
3. 问题:板壳的应用领域有哪些?答案:板壳广泛应用于屋顶、地板和水箱等结构中。
第2章船体结构

第2章船体结构船体结构是指船舶的主要构造,在保证船舶强度和稳定性的基础上,承担船体的重量、保护船舶设备和货物等。
本章将介绍船体结构的主要组成部分和设计原则。
船体结构的主要组成部分包括船体底部、船体侧壁、船体甲板和船体纵横桁架。
船体底部是船体最底部的部分,承受船舶重量的主要部位,通常采用双底结构,即在船底板上增设一道底垫板,以增加船体的强度和耐磨性。
船体侧壁是船舶两侧的外壳,保护船舶内部设备和货物,同时也起到保护船体结构的作用。
船体甲板是船舶上层建筑的底板,分为主甲板和甲板下层。
主甲板是最上层的甲板,承载船舶上层建筑和装卸作业,甲板下层则起到加强船体结构的作用。
船体纵横桁架是连接船体各个部分的框架结构,提供船体的强度和刚度。
在船体结构的设计中,需要考虑以下几个原则。
首先是强度原则,即保证船体结构足够强度以承受各种外力的作用。
船舶在航行时会受到波浪、风力等力的作用,而在装卸货物时也会受到额外的压力,因此船体结构需要具备足够的强度以应对这些力的挑战。
其次是稳定性原则,即保证船体结构的稳定性和平衡性。
船体结构设计需要合理分布船舶的重心和重量,以确保船舶在航行和停泊时不会倾斜或发生危险。
此外,还需要考虑可靠性和经济性原则,即船体结构需要具备可靠性以应对各种恶劣环境和操作条件,同时也要尽可能降低造船成本和维护成本。
船体结构的设计和制造需要符合国际和国家的相关规范和标准。
船舶结构的设计和制造需要根据船舶类型、使用环境和载货量等因素来确定,以确保船体结构的适应性和可靠性。
船舶结构的制造通常采用焊接和拼装两种方式。
焊接是利用高温熔化金属材料来连接船体部件的技术,拼装则是将船体各个部件通过螺栓或铆钉等连接手段进行组装。
总之,船体结构是船舶的主要构造,保证船舶的强度和稳定性。
在设计和制造船体结构时需要考虑强度、稳定性、可靠性和经济性等原则,同时也需要符合相关的规范和标准。
只有具备良好的船体结构,船舶才能安全稳定地航行。
结构力学 第二章 结构的几何组成分析

第二章结构的几何组成分析李亚智航空学院·航空结构工程系2.1 概述结构要能承受各种可能的载荷,其几何组成要稳固。
即受力结构各元件之间不发生相对刚体移动,以维持原来的几何形状。
在任意载荷作用下,若不考虑元件变形,结构保持其原有几何形状不变的特性称为几何不变性。
在载荷作用下的系统可分为三类。
2.1.1 几何可变系统特点:不能承载,只能称作“机构”。
213 4P2’3’2.1.2 几何不变系统特点:能承载,元件变形引起几何形状的微小变化,可以称为结构。
2.1.3 瞬时几何可变系统特点:先发生明显的几何变形,而后几何不变。
P21342’3’2’3’P21345∞→=2321N N 123P内力巨大,不能作为结构。
N 21N 23P2由以上分析可见,只有几何不变的系统才能承力和传力,作为“结构”。
系统几何组成分析的目的:(1)判断系统是否几何不变,以决定是否能作为结构使用;(2)掌握几何不变结构的组成规律,便于设计出合理的结构;(3)区分静定结构和静不定结构,以确定不同的计算方法。
2.2 几何不变性的判断2.2.1 运动学方法将结构中的某些元件看成自由体,拥有一定数量的自由度;将结构中的另一些元件看成约束。
如果没有足够多的约束去消除自由度,系统就无法保持原有形状。
所谓运动学方法,就是指这种引用“约束”和“自由度”的概念来判断系统几何不变性的方法。
1、自由度与约束(1)自由度的定义决定一物体在某一坐标系中的位置所需要的独立变量的数目称为自由度,用n 表示。
平面一个点有2个独立坐标,故n =2空间一个点有3个独立坐标,故n =3xyy∆x∆AA 'xyAy Ax AzAz A 'O空间一根杆有5个自由度,一个平面刚体(刚片、刚盘)或一根杆有3个自由度,n =3xyAy A x AzA z A 'OBB 'αθxyy∆x∆AA 'OAx A y θ∆一个空间刚体有6个自由度,n =6θα,,,,A A A z y x ( ),n =5(2)约束的定义约束定义为减少自由度的装置,用c 来表示。
结构力学章节习题及参考答案
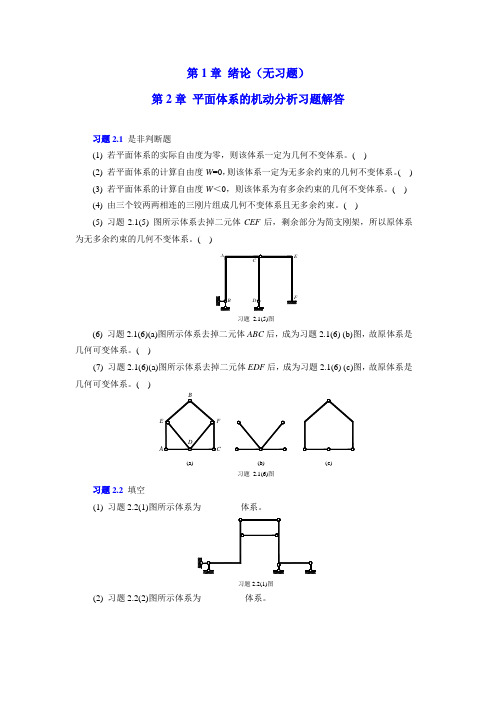
第1章绪论(无习题)第2章平面体系的机动分析习题解答习题2.1是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W=0,则该体系一定为无多余约束的几何不变体系。
( )(3) 若平面体系的计算自由度W<0,则该体系为有多余约束的几何不变体系。
( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )习题2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)习题2.1(6)图习题2.2填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
习题2.2(6)图(7) 习题2.2(7)图所示体系为_________体系,有_________个多余约束。
习题2.2(7)图习题2.3对习题2.3图所示各体系进行几何组成分析。
(a)(b)(c)(d)(e)(f)(h)(g)(i)(j)(k)(l)习题2.3图第3章 静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用内力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。
第2章轴向拉压--1

c d
F
根据静力平衡条件:
FN dA
A
dA A
FN A
A
拉压杆内最大的正应力:
FN FN max 等直杆: max 变直杆: max A A max 正应力的符号规定——同内力
拉伸——拉应力,为正值,方向背离所在截面。 压缩——压应力,为负值,方向指向所在截面。
A A cos
F
FN= F
(2)应力确定:
①应力分布——均布
F
FN
x
F p
n
②应力公式——
FN F F p cos cos A A A cos
FN
σα——斜截面上的正应力;τα——斜截面上的切应力
p cos cos2
FN1 FN2 FN2
以轴向拉压为主要变形的杆件,称为拉压杆或轴向承载杆。 7
轴向拉压主线:
杆件的内力分析 应力 变形
强度条件 内力图 (找到内力最大值)
刚度计算
§2.1 轴向拉伸与压缩的概念 §2.2 横截面上的内力与应力 §2.3 斜截面上的应力
1 内力的概念
外力引起的物体内部的作用力。
在外力作用下,构件内部各部分之间因相对位置改变而
各段的内力并画出杆的轴力图。 O A FA B FB C FC D FD
FN
2F
5F
3F
F
x
总
结
1、外力不能沿作用线 任意移动;
2、有集中力作用的截面处,轴力图有突变,突变值 等于集中力的大小。 3、简便画图法:自左向右,遇到向左的外力,轴力 增大;遇到向右的外力,轴力减小。 P16, 例题2-2
高层建筑结构设计第2章 高层建筑结构体系和布置原则
4 变形缝的设置
在未采取措施的情况下,伸缩缝的间距不宜超出 表1—8的限制。当有充分依据、采取有效措施时, 表中的数值可以放宽。
高层建筑结构伸缩缝的最大间距 表1—8
注: ①框架—剪力墙的伸缩缝间距可根据结构具体布置取表中框架结构与 剪力墙结构之间的数值; ②当屋面无保温或隔热层措施、混凝土的收缩较大或室内结构因施工 外露时间较长时,伸缩缝间距应适当减少; ③位于气候干燥地区、夏季炎热且暴雨频繁地区的结构,伸缩缝的间 距宜适当减少。
多年的高层建筑结构设计和施工经验表明:高层建 筑结构宜调整平面形状、尺寸和结构布置,采取构造 和施工措施,尽量不设变形缝;当需要设缝时,则应 将高层建筑结构划分为独立的结构单元,并设置必要 的变形缝。
4 变形缝的设置
温度缝:防止结构因温度变化和混凝土干缩变形 产生裂缝(基础以上上部结构断开) 不设温度缝的措施: 1. 温度影响较大部位提高配筋率; 2. 加厚屋面隔热保温层,或架空通风屋面; 3. 顶层局部设温度缝后浇带;即高强度等级的混凝 土;主体混凝土浇注后两个月;贯通结构的横截 面;位置应为结构受力影响最小,且曲折延伸避 免全部钢筋同截面搭接 ;一般每隔30~40m设一 道,后浇带宽800~1000mm。
适用30层以上 。
长/宽<2,截面尺寸接近正方形、圆形、正多边 形较好。
4、筒体结构体系
(1)框筒结构:内筒承受 竖向荷载,外筒承受水平 荷载,柱距一般在3m以内, 框筒梁比较高,开洞面积 在60%以下 1931年102层帝国大厦: 钢框架-剪力墙体系,用 钢量2.06kN/m2 1972年110层世界贸易中心:筒中筒结构体系,用 钢量1.81kN/m2
1974年110层西尔斯大楼:钢成束筒结构体系,用 钢量1.61kN/m2
桁架求解的几种方法
FA=40kN
a A G III 20kN II H III 20kN I 20kN
6x3m =18m F B= 20kN
C
隔离体,由ΣMF=0,得: F ×4-20×3-40×3 = 0,
图5-12
4m
B
(2) 取结点H为隔离体,由ΣFx = 0, 得:FNGH =FNHC = 45 kN (3) 作截面Ⅱ-Ⅱ,仍取左部分为隔离体,由ΣMF = 0,得 FNa×3/ 13 ×4+45×4-40×3 = 0, FNa = -513 = -18.0 kN 在该题中,若取截面Ⅲ-Ⅲ所截取的一部分为隔离体(图 5-12),由于ED杆为零,FNED = 0。 由平衡方程ΣMC = 0,可得 FNa×2/ 13 ×3+FNa×3/ ×2+20×3 = 0, 13 FNa = -513 = -18.0 kN 可见,按后一种方法计算更简单。
E
G
(a)
2m
A
D
2kN
C
4kN
F
2kN
B
解:该桁架为简单桁架, 由
于桁架及荷载都对称,故可计 算其中的一半杆件的内力,最 后由结点C的平衡条件进行校 核。 1.计算支座反力。 ΣFx = 0, FAx = 0
(d) (b)
4X 2m =8 m
F A Y = 4kN F B Y = 4kN
FNDE F NAE
60×3-10×3-FNa×3 = 0, FNa = 50 kN
(2) 求上弦杆c的内力时,以a、b两杆的交点D为矩心, 此时要计算FNc的力臂不太方便,为此将FNc分解为水平和
竖直方向的两个分力。则各分力的力臂均为已知。 10 10
空腹桁架钢框架论文
摘要空腹桁架钢框架是在钢框架的基础上,通过取消框架中间的柱子来增大结构的使用空间,同时为了不增大各个构件的截面尺寸,在框架的隔层增设腹板柱形成空腹桁架与钢框架组合的结构体系。
由于在钢框架中增设腹板柱形成空腹桁架结构,进一步增强了结构的水平刚度和竖向刚度,同时提高了结构的整体工作性能,进而实现了结构的大跨度。
空腹桁架钢框架结构可以应用于交错桁架结构体系和转换层结构,工程应用比较广泛。
对其受力性能、极限承载力以及结构的破坏模式进行深入的研究具有重要的理论意义和工程应用价值。
本文通过大量的算例分析,探讨空腹桁架层的节间数、节间间距、腹板柱的刚度以及结构的跨度对整体结构的受力性能、极限承载力及破坏模式的影响,分析表明:通过合理的桁架层设计,可以有效的提高结构的竖向刚度和水平刚度,以及结构的极限承载力,并可以使结构的塑性变形首先出现在腹板柱上,这有利于结构内力的重分布,增加结构的延性性能,充分发挥构件的极限承载能力。
在算例分析的基础上,设计合理的实验模型,对其进行极限承载力试验研究,分析结构的荷载-位移曲线以及最终破坏形式。
…………………关键词:Frame and Experiment Study(Structural Engineering )Vierendeel truss-steel frame has wide technical application that can be applied to the staggered truss structure and transfer structure. It has important theory significance and value of technical application to research the behavior,the ultimate load-carrying capacity and structural destroy mode.········· Key Words: vierendeel truss-steel frame, load bearing behavior, elastoplasticanalysis, ultimate load-carrying capacity, experimental research目录摘要·IABSTRACT·II1章绪论空腹桁架钢框架的特点及研究意义·1空腹桁架钢框架的研究现状·3现有研究的不足及本文的研究内容·5第2章空腹桁架钢框架有限元建模及验证2.1 引言·82.2 弹塑性分析方法简介·122.3 ANSYS在空腹桁架钢框架弹塑性分析中的应用·18 2.4 ANSYS分析模型正确性检验·202.5 小结·21第3章空腹桁架钢框架受力性能有限元分析3.1 引言·233.2 空腹桁架钢框架与普通钢框架力学性能对比·26 3.3 影响空腹桁架钢框架力学性能的因素·29第4章空腹桁架钢框架极限承载力试验研究4.1 试验目的·304.2 模型设计依据·324.3 试验概况·354.4 试验过程描述·384.5 试验结果·454.6 小结·55第5章全文总结5.1 主要结论·625.2 有待进一步解决的问题·64参考文献·65后记·68攻读硕士学位期间论文发表及科研情况·6911.1 空腹桁架钢框架的特点及研究意义用空间,同时为了不增大各个构件的截面尺寸,在框架的隔层增设腹板柱形成空腹桁架与钢框架组合的新型钢结构,结构形式如图1.1。
第二章-杆和梁结构的有限元法案例
第二章
杆和梁结构的有限元法
§2.1.2 弹簧系统分析
注意: 上述弹簧系统的分析求解原理和过程就是有限元 法求解连续体力学问题时对离散后系统的分析求 解原理和过程。
第二章
杆和梁结构的有限元法
§2.1.2 弹簧系统分析
例题1:弹簧系统
已知条件:
求:(a) 系统总刚度矩阵 (b) 节点2,3的位移
单元特性
系统平衡方程
第二章 杆和梁结构的有限元法
KD F
2)单元方程扩大相加法 单元特性
F1 f11
相加
F2 f 21 f12 F3 f 22
系统节点 平衡条件
引入系统节点平衡条件
KD F
系统节点平衡方程
第二章 杆和梁结构的有限元法
2.2 杆单元和平面桁架
杆单元
2.2.1 一维等截面 杆单元
fi k f j k
第二章
k ui k u j
f kd
杆和梁结构的有限元法
2、弹簧系统的集成 1)列节点平衡方程法
F1 f11 F2 f 21 f12 F3 f 22
系统节点 平衡条件
F1 k1u1 k1u2 F2 k1u1 ( k1 k2 )u2 k2u3 F3 k2u2 k2u3
第二章 杆和梁结构的有限元法
k k k
k k
fi k f j k
k ui k u j
kii k k ji
kij k jj
§2.1.2 弹簧系统分析
求解一个弹簧系统:
1)各单元的特性分别为:
第二章 杆和梁结构的有限元法
