衍射及成像原理_图文
电子衍射环分析 ppt课件

图8-3 单晶电子衍射成像原理
ppt课件
17
单晶电子衍射花样特征
单晶电子衍射花样就是(uvw)*0零层倒易平面(去除权重为零的倒 易点后)的放大像(入射线平行于晶带轴[uvw])。
ppt课件
18
五、单晶电子衍射花样的标定
主要指单晶电子衍射花样指数化,包括确定各衍射斑点相应衍射晶面 干涉指数(HKL)并以之命名(标识)各斑点和确定衍射花样所属 晶带轴指数[uvw]。对于未知晶体结构的样品,还包括确定晶体点阵 类型等内容。
第二十一章 电子衍射
ppt课件
1
电子衍射的类型
按入射电子能量的大小,电子衍射可分为 透射式高能电子衍射
高能电子衍射 反射式高能电子衍射
低能电子衍射
ppt课件
2
第一节 电子衍射原理
电子衍射与X射线衍射一样,遵从衍射产生的必要条件(布拉格方程+ 反射定律,衍射矢量方程或厄瓦尔德图解等)和系统消光规律。
单晶电子衍射花样标定时除应用衍射分析基本公式外还常涉及以下知 识:单晶衍射花样的周期性。
单晶电子衍射花样可视为某个(uvw)*0零层倒易平面的放大像 [(uvw)*0平面法线方向[uvw]近似平行于入射束方向(但反向)]。 因而,单晶电子衍射花样与二维(uvw)*0平面相似,具有周期性排 列的特征。
因此,由测量各衍射环R值获得R2顺序比,以之与N顺序比对照,即 可确定样品点阵结构类型并标出各衍射环相应指数。
因为N顺序比是整数比,因而R2顺序比也应整数化(取整)。
ppt课件
12
利用已知晶体(点阵常数a已知)多晶衍射花样指数化可标定相机 常数。
衍射花样指数化后,按源自计算衍射环相应晶面间ppt课件
物理PPT课件10.3单缝衍射

asin0
中央明纹中心
asin2kk
2
干涉相消(暗纹) 2k个半波带
asin(2k1)
干涉加强(明纹) 2k1
2
个半波带
asin k
2
(介于明暗之间) (k1 ,2 ,3 , )
精选课件ppt
6
10.3 光的衍射 单缝夫琅禾费衍射
第10章 波动光学
二 光强分布
asin2kk
2
干涉相消(暗纹)
asin(2k1)
1
arcsin
a
一定
a增大, a减小,
减小
1
增大
1
a
0,1
a,1
0
π 2
光直线传播 衍射最大
a一定,
越大,
越大,衍射效应越明显.
1
(2)中央明纹 ( k 1的两暗纹间)
角范围
sin
a
a
线范围
f x f
a
a
中央明纹的宽度
l0
2x1
2 a
f
精选课件ppt
10
10.3 光的衍射 单缝夫琅禾费衍射
第10章 波动光学
2
干涉加强(明纹)
I
3
2
a
a
a
o
2
3 sin
a
a
a
精选课件ppt
7
10.3 光的衍射 单缝夫琅禾费衍射
S
R
L1
L2
a
第10章 波动光学
Px
x
O
f
I 当较小时,sin
x f
3
2
a
a
a
o a
2 a
电子衍射

(1)由于电子波波长很短,一般只有千分之几nm, 按布拉格方程2dsin=可知,电子衍射的2角很小(一 般为几度),即入射电子束和衍射电子束都近乎平行 于衍射晶面。
由衍射矢量方程(s-s0)/=r*,设K=s/、K=s0/、 g=r*,则有
K-K=g
(8-1)
此即为电子衍射分析时(一般文献中)常用的衍射矢 量方程表达式。
H3=H1+H2、K3=K1+K2和L3=L1+L3。
单晶电子衍射花样的标定
立方晶系多晶体电子衍射标定时应用的关 系式:R21:R22:…:R2n=N1:N2:…:Nn 在立方晶 系单晶电子衍射标定时仍适用,此时R=R。 单晶电子衍射花样标定的主要方法为: 尝试核算法 标准花样对照法
“180不唯一性”或“偶合不唯一性”现象的产生,根 源在于一幅衍射花样仅仅提供了样品的“二维信息”。
通过样品倾斜(绕衍射斑点某点列转动),可获得另一晶带 电子衍射花样。而两个衍射花样组合可提供样品三维信息。
通过对两个花样的指数标定及两晶带夹角计算值与实测 (倾斜角)值的比较,即可有效消除上述之“不唯一性”。
(8-7)
式中:N——衍射晶面干涉指数平方和,即 N=H2+K2+L2。
多晶电子衍射花样的标定
对于同一物相、同一衍射花样各圆环而言,(C2/a2) 为常数,故按式(8-7),有
R12:R22:…:Rn2=N1:N2:…:Nn
(8-8)
此即指各衍射圆环半径平方(由小到大)顺序比等于
各圆环对应衍射晶面N值顺序比。
一、电子衍射基本公式
电子衍射基本公式的导出
设样品至感光平面的距离为L(可称为 相机长度),O与P的距离为R,
由图可知
X射线衍射方法详细讲解

tan
d d
对2L=R·4微分
L2R
因此
2Rtan
越大,则分辨率越大,故背反射衍射线条比前反射线条分辨率高。
19
3. 衍射花样指数标定
衍射花样指数标定:确定衍射花样中各线条(弧对)相应晶 面(即产生该衍射线条的晶面)的干涉指数,并以之标识衍 射线条。 又称衍射花样指数化 衍射花样指标化
不同晶系晶体的衍射花样(衍射图)的标定方法不同,下 面仅介绍最简介的立方晶系的标定。
按样品的化学成分选靶
当样品中含有多种元素时,一般按含量较多的几种元素中Z最小的元素选靶。 11
选靶时还需考虑其它因素:
•入射线波长对衍射线条多少的影响
布拉格方程: 2dHKsLin
K (nm)
Cr
0.228970
Fe
0.193604
Co
0.178897
Cu
0.154056
Cu(Ave) 0.154184
衍射花样、衍射图——diffraction patternΒιβλιοθήκη 2L1802L90 4R S
2L1802L90 4R S
2<90 =90-,2>90
17
测量
2倍于此长
因底片开口,无法直接测量的弧段
不对称装片法
在冲洗干燥后的底片上通过测量得到S。
一般将底片置于内有照明光源的底片测量箱毛玻璃上,通过 游标卡尺测量获得2L及S值。
若需精确测量时,则使用精密比长仪。
德拜(Debye)法:用其轴线与样品轴线重合的圆柱形底片 记录。
针孔法:用平板底片记录。
德拜法照相装置称为德拜相机
4
1.成像原理与衍射花样特征
成像原理: 厄瓦尔德图解
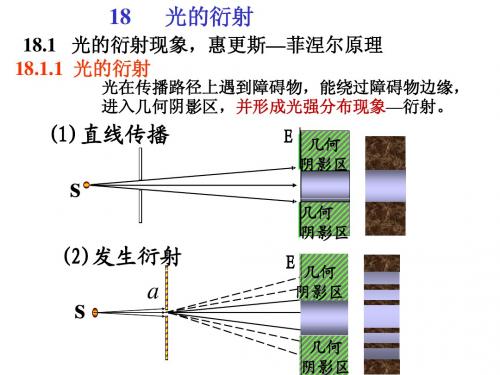
光的衍射
6 m 10 0.6m
在-900<sin<900范围内可观察到的明纹级数为 k=0,1, 2, 3, 5, 6, 7, 9,共15条明纹
例、一束平行光垂直入射到某个光栅上,该光束有 两种波长1=4400Å,2=6600Å。实验发现,两种波长 的谱线(不计中央明纹)第二次重合于衍射角=600的 方向上,求此光栅的光栅常数d。 解: d sin 1 k11 d sin 2 k22
3. 振幅矢量法(定量推导衍射 光强分布公式) 将缝分N个等宽的细窄条--子光源 每个子光源到P点的距离近似相等
引起的光振幅近似相等,
相邻面元的光程差 1 BC a sin 位相差
P点的合振幅AP:就是各子波的振幅矢量和的模, 这是多个同方向、同频率,同振幅、初相依次差一 个恒量的简谐振动的合成。
光栅分光原理
光栅分光镜
由 dsinθ=kλ,θ~λ关系
k 色散率 D d cos
光栅的色分辨本领
色分辨本领 R
由于光栅d很小,色散率很大, 色散本领强 .
恰能分辨的两条谱线的平均波长 与 这两条谱线的波长差 之比
R
波长为 的第 k 级主极大的角位置
例:以单色平行可见光垂直照射宽 a=0.6mm 的单缝,缝后凸透镜的 焦距f=40cm ,屏上离中心点O距离 x=1.4mm处P点恰为一明纹中 心,试求 (1)该入射光的波长; (2)P点条纹的级次; (3)从P点看来,对该光波而言,狭缝处被划分为多 少各半波带? (k 1,2,3,) 解:由单缝衍射明纹条件 a sin (2k 1) 2 又 f a,sin x/f,所以 a x (2k 1) (k 1,2,3,) f 2 3 2ax 4.2 10 nm f (2k 1) 2k 1 k=3时, = 600nm k=4时, = 466.7nm x 当 = 600nm时,级次为3 O 半波带数:2k+1=7 当 = 466.7nm 时,级次为4 半波带数:2k+1=9 10 f
光的衍射

决定衍射主极大明 纹的光栅方程
26
暗纹条件: N个缝在P点的N个振幅的矢量和为零
N 2k
2 d sin
Nd sin k
(k 1,2, , N 1, N 1, N 2, ,2 N 1, )
相邻主极大间有N-1个暗纹和N-2个次极大
干涉加强条件(布喇格公式)
称为掠射角
2d sin k k 0,1,2
符合上述条件时,各层晶面的反 射线干涉后将相互加强。
41
讨论
1. 如果晶格常数已知,可以用来测定X射线的 波长,进行伦琴射线的光谱分析。 2. 如果X 射线的波长已知,可以用来测定晶 体的晶格常数,进行晶体的结构分析。
3.把符合几何光学直线传播的光束的迭加称为干涉, 而把不符合直线传播的光束的迭加称为衍射。 4.从数学上,相干迭加的矢量图:干涉用折线, 衍射用 连续弧线,干涉用有限项求和, 衍射用积分。
15
例题1 (1)如果单缝夫琅禾费衍射的第一级暗条纹出现在衍射 角=30的方位上,若所用单色光的波长=500nm,求狭缝 宽度?(2)如果所用单缝的宽度b=0.5mm,在焦距f=1m的透镜 的焦平面上观测衍射条纹,问中央明纹及其它明纹宽度
S1 * S2 *
D
18
瑞利判据:如果一个点光源的衍射图象的中央最亮处刚 好与另一个点光源的衍射图象第一个最暗处相重合,认
为这两个点光源恰好能为这一光学仪器所分辨。
恰 能 分 辨 能 分 辨 不 能 分 辨
19
s1 * s2 *
D
0
在恰能分辨时,两个点光源在透镜前所张的角度, 称为最小分辨角0 ,等于爱里斑的半角宽度。
会发射一种穿透性很强的射线称x射线。 x 射线 冷却水
光的衍射
解: (1)由明纹条件
bsin (2k 1) / 2
x 1.5 明纹所在处 x 满足: tan 0.003 f 500
2bx / f 2 0.5 1.5 3 103 7 10 nm 2k 1 (2k 1) 500 2k 1
x sin tan f
d k k b
单
k — 光栅明纹缺级级次
I0 I单
-2 -1 0 2 1 I N I0 单 2 sin ( /a)
-8
-4
0
4
sin 8 ( /d )
斜入射时,明条纹的衍射角满足
d (sin sin ) k ,k 0,1, 2,
可以观看到的最高级次
kmax d (sin 900 sin )
b sin 2k
k 干涉相消(暗纹)
干涉加强(明纹)
其它明纹、暗纹宽度为中 央明纹的一半。
l0 x1
b
f
4. 单缝衍射的动态变化 单缝上下移动,根据透镜成像原理衍射图不变
R
f
o
单缝上移,中央明 纹仍在透镜光轴上.
5. 斜入射
光程差
入射光与衍射光在光轴同侧
Δ DB BC b(sin sin )
2 R
A
A1
C
L
P
Q
o
B
/2
AB 分为两个半波带 AA1 和 A1B ,其对应点发出的光的光程差为
/2,互相干涉抵消,因而在Q处出现暗条纹中心。
2. b sin 3 / 2
A
R
A1
C
L
P
13 光的衍射
o
B
C
d
A
晶格常数 d 掠射角
布拉格反射
入射波 散射波
o
B
C
Δ AC CB 2d sin 相邻两个晶面 反射的两X射线干 涉加强的条件
d
A
2d sin k k 0,1,2,
布拉格公式
S
观察屏 P ·
*
f
Aδ
f
0
▲ 光 程差为 a sin (a——缝宽) 0, 0 —— 中央明纹中心
▲
a sin
B 半波带 半波带 A θ
光屏上P处为暗纹中心
1 2 1′ 1 2′ 2 1′ 2′
a
半波带
半波带
λ /2
3 ▲当a sin 时,可将缝分成三个“半波带”。 2
kλf xk = ± ( k = 1,2) a
x (2) a (2k 1) f 2
明纹中心位置
xk (2k 1)
f
2a
(k 1,2)
明纹宽度——任意两相邻暗纹中心间的距离。 (1)中央明纹宽度l0
λ 对一级暗: x1 = ±f a l0 2 f
a
(2)其它明纹宽度△x
1 1 1 实验室常用: mm , mm , mm . 100 300 1000
二、光栅衍射谱线分析
衍射角
L
P
Q
o
f
光栅衍射的本质:衍射和干涉共同作用的结果。
1、只考虑单缝衍射的影响 ▲在单缝夫琅禾费衍射中,若单缝⊥光轴上下移 动,问衍射图样是否变化?
a
光的衍射现象
光的衍射现象光的衍射是一种光学现象,当光通过狭缝或者物体边缘时会发生弯曲和变化。
这种现象的发现对光学的发展产生了重要影响,并且在日常生活中也有着广泛的应用。
本文将对光的衍射现象进行探究,从衍射的原理、应用以及进一步研究的方向进行论述。
一、衍射的原理光的衍射现象是由光的波动性质所引起的。
根据赫兹的波动理论,光是一种电磁波,具有波长、频率和振幅等基本特征。
当光通过一个狭缝或者物体边缘时,波前会发生弯曲,从而导致光的方向发生变化。
光的衍射可以用惠更斯-菲涅尔原理来解释。
该原理认为,每个点上的波前可视为无限多个波源的球面波在该点的相干叠加。
当光通过一个小孔或者孔径较小的物体时,波前通过不同的路径到达屏幕上,形成交叠和干涉现象。
这种干涉使得光在屏幕上出现亮暗相间、彩色的衍射图案。
二、光的衍射应用1. 衍射光栅:光的衍射现象在光栅中得到了广泛应用。
光栅是一种带有周期性结构的物体,具有多个狭缝或者孔径。
当光通过光栅时,会发生衍射现象。
根据不同的衍射条件,光栅可以将入射光分散为不同的衍射线,这为光谱学研究和光学仪器的开发提供了基础。
2. 衍射成像:光的衍射也可以用于成像。
衍射成像利用光的衍射效应,通过特定的物体结构或者衍射光学元件,实现对物体的成像。
例如,透射光栅和反射光栅可以分别用于光谱成像和光学信息的编码与解码。
3. 衍射仪器:光的衍射现象在许多光学仪器中得到了应用,如干涉仪、衍射仪等。
这些仪器利用光的衍射特性,实现对光的操控、分析和测量。
通过衍射仪器,人们可以进一步研究光的波动性质以及物质的结构和性质。
三、光的衍射研究的发展方向随着科学技术的发展,人们对光的衍射现象的研究也在不断深入。
目前,有三个主要的研究方向:衍射理论的精确计算、新型衍射材料和器件的开发以及超分辨率成像技术的研究。
1. 衍射理论的精确计算:当前的衍射理论仍存在一些简化和近似,对于某些复杂系统的衍射计算精度还有待提高。
进一步的研究将致力于建立更加准确的衍射理论,为衍射现象的分析和应用提供更强的理论支持。
第十章 电子衍射 ppt课件
ppt课件
16
举例:
画出体心立方晶系[001]晶带轴的标准零 层倒易截面。
ppt课件
17
正、倒点阵对应关系
正空间 倒空间
简单立方 简单立方
四方
四方
面心立方 体心立方
体心立方 面心立方
六方
六方
菱形
菱形
ppt课件
18
FCC晶体标准电子衍射花样
ppt课件
19
fcc晶体的[001]电子衍射谱
ppt课件
ppt课件
35
已知相机常数和样品晶体结构
1)测量R1、R2、R3、R4… 2)根据R=λL/d,求出相应的晶面
间距d1、d2、d3、d4… 3)因晶体结构已知,故可根据d查
出相应的晶面族指数{hkl}
(八步校核法)
4)测定各衍射斑点之间的夹角φ
5)决定离中心斑点最近的衍射斑 点的指数
单晶
多晶
非晶
准晶(quasicrystals)
电子衍射的原理和X射线衍射相似,是以满足(或基本满足)
Bragg方程作为产生衍射的必要条件。两种衍射技术得到的衍
射花样在几何特征上也大致相似。
ppt课件
3
电子衍射花样特征
电子束照射 单晶体: 一般为斑点花样; 多晶体: 同心圆环状花样; 织构样品:弧状花样; 无定形试样(准晶、非晶):弥散环。
20
BCC晶体标准电子衍射花样
ppt课件
21
bcc晶体的[001]电子衍射谱
ppt课件
22
二、电子衍射基本公式
衍射花样:把倒易阵点的图像进行
空间转换并在正空间中记录下来, 记录下来的图像称为衍射花样。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4,衍射几何条件:厄瓦球面
S/l= k S0/l= k0
g
5,衍射仪原理
L=相机 长度
(hkl)
S/l= k
S0/l= k0 ghkl
000
(hkl)
Rhkl
6、 衍射和对称性:反射条件
F(q) = Sfj(q) exp[-2pi(k – k0).rj] = Sfj(q) exp[-2pi (h xj +k yj +l zj)], Ihkl ∝ Fhkl2, 即倒易阵点上才有强度。 However, not all reciprocal lattice points are associated with Bragg reflections. (1) inversion:(xj, yj, zj) –> (-xj, -yj, -zj),两个原子的散射 因子之和为实数,F(q) = Sfj(q) cos[2p (h xj + k yj + l zj)], Ihkl = Ihkl ,即 倒易点阵具有对称中心 –> 11种LAUE对称中心点群
衍射及成像原理_图文.ppt
2. 单原子散射
与时间无关的薛定谔方程
E1、 = Ekin + V总能量。解是粒子的状态。 对于平面波(点光源的波阵面(等相位面)为球面形,距离远,近 似为平面波,V = 常数)的单原子散射,其解为: = A exp(2pik.r) ,其中 r为wavefront上的一点,k是波矢(波矢空间或倒易空间,IkI = 1/l = (2m0e(E-V)/h2 ) 1/2 = (2m0eEkin/h2 ) 1/2 )
3.3 Bragg方程
所以S – S0垂直于晶面(hkl),如同镜面反射。 式a (S – S0) = h.l 两侧同乘a*,得(S – S0)/l = h a* = k – k0 = K,因 此K = h a* + k b* + l c*是倒易矢量, 波长的倍数为晶面指数,k 、k0 分别代表出射和入射波矢。 反射条件: I k– k0 I = 1/dhkl = 2 sinq,得Bragg方程l = 2 d sinq 当hkl有公因子时,nl = 2 d sinq,nh nk nl代表伪晶面。
Therefore, hkl are either all even or all odd Fhkl=4f, otherwise Fhkl=0.
衍射条件:(h+k) = 2n; (k+l) = 2n;(l+h) = 2n;只有 两个独立。同奇同偶
6、 衍射和对称性:反射条件
F(q) = Sfj(q) exp[-2pi(k – k0).rj] = Sfj(q) exp[-2pi (h xj +k yj +l zj)], Ihkl ∝ Fhkl2, 即倒易阵点上才有强度。
r Wave front
k wave vector
Phase difference =2p/l times the path difference
3、 多原子散射:
3.1 衍射现象:X光的电磁场使得被照射的原子的电子产生振 动,每个原子于是成为新的发射源,所发射X光波长与入射 波相同,方向以该原子为中心向外辐射;这些新的无数的散 射波与入射波相干,即振动方向、频率相同、位相(差)相 同,这样能够在某些方向产生相长干涉或相消干涉,X光强 度发生变化,这就是衍射。衍射是电磁波的固有特性。
(2) 点阵类型的影响: f is the scattering amplitude of the group of atoms associated with each lattice point. The points associated with Bragg reflections form a body centered cubic lattice in reciprocal space. When the crystal is monoatomic, I.e only one atom is associated with each lattice point, f is simply the scattering amplitude of that atom.
体心I:(xj, yj, zj) –> (1/2 + xj, 1/2 + yj, 1/2 + zj) exp (pi (h+k+l)) =-1时,–> Fhkl = 0。 exp (pi (h+k+l)) =1时,衍射–> 。 衍射条件:(h+k+l) = 2n
6、 衍射和对称性:反射条件
F(q) = Sfj(q) exp[-2pi(k – k0).rj] = Sfj(q) exp[-2pi (h xj +k yj +l zj)], Ihkl ∝ Fhkl2, 即倒易阵点上才有强度。 However, not all reciprocal lattice points are associated with Bragg reflections.
(3) 螺旋轴: 21: (xj, yj, zj) –> (-xj, -yj, 1/2 + zj),对于(00l),l = 2n
(4) 滑移面: b: (xj, yj, zj) –> (-xj, 1/2+yj, -zj),对于(hk0),k = 2n
S – S0
k q
k0
S0
k – k0 = K
q
S (hkl)
3.5 单胞散射
单胞内所有原子散射波的总和,振幅正比于
F(q) = Sfj(q) exp[-2pi(k – k0).rj],结构因子
k – k0 = K
k
k0
q
ra
3.6 完整晶体散射
fg=S Fn exp[-2piK.rn],其中Fn是第n个单胞的散射因子 ,rn =n1a+n2b+n3c是第n个单胞的位置,K是倒易矢量 当K.rn=m时产生衍射,即K 为倒易点阵结点位置 = g = h a* + k b* + l c*
圆锥面不易用要进一步简化。 S
A2
A1
a
a0
3.3 Bragg方程
考虑晶面(hkl),它与a, b, c轴截于a/h, b/k, c/l。
a (S – S0) = h.l b (S – S0) = k.l c (S – S0) = l.l 相减得
S – S0
S0
S
q (hkl)
S – S0 为法线倒易矢量?
6、 衍射和对称性:反射条件
F(q) = Sfj(q) exp[-2pi(k – k0).rj] = Sfj(q) exp[-2pi (h xj +k yj +l zj)], Ihkl ∝ Fhkl2, 即倒易阵点上才有强度。 However, not all reciprocal lattice points are associated with Bragg reflections. (2) 点阵类型的影响:
同理,三维情形:
a (cos a – cosa0) = h.l, 等效于: a (H2A1 – A2H1) = h.l
= a (S – S0),S、S0为单位矢量。 LAUE方程
b (cos b – cosb0) = k.l
S0
c (cos g – cosg0) = l.l
或变化角度(改变晶体取向),或变化波长(利用连续H1谱)H2 a
6、 衍射和对称性:反射条件
F(q) = Sfj(q) exp[-2pi(k – k0).rj] = Sfj(q) exp[-2pi (h xj +k yj +l zj)], Ihkl ∝ Fhkl2, 即倒易阵点上才有强度。 However, not all reciprocal lattice points are associated with Bragg reflections. (2) 点阵类型的影响:
S – S0
S0
S
q (hkl)
3.4波的合成
Consider a unit cell with atoms at rj. At distance IrI > IrjI, the amplitude scattered by the unit cell is A0= exp[2pikr]/r* Sfj exp[-2pi(k – k0).rj] F(q)= f =Sfj(q) exp[-2pi(k – k0).rj] , the structure factor. I k– k0 I = I K I = 2 I k I sinq = 2 I k0 I sinq = 2 sinq /l 当 (k – k0).rj = m时,I f I2最强,即 I (k – k0).rj I = m = I K I . I rj I . cosa = 2 sinq /l . d 因此2d sin q = ml
6、 衍射和对称性:反射条件
F(q) = Sfj(q) exp[-2pi(k – k0).rj] = Sfj(q) exp[-2pi (h xj +k yj +l zj)], Ihkl ∝ Fhkl2, 即倒易阵点上才有强度。
(2) 点阵类型的影响: NaCl, fcc, a pair of ions, Na+ and Cl-, is associated with each lattice point and f = f Na+ +f Cl-exp[-i2ph*0.5] = f Na+ f Cl-, depending on whether h is even or odd.
F:The 4 lattice points per unit cell are located at 000, 0.5 0.5 0, 0 0.5 0.5, 0.5 0 0.5. Then Fhkl= f {exp[-2pi (h 0 +k 0 +l 0)] + exp[-2pi (h 0 +k 1/2 +l 1/2)] + exp[-2pi (h 1/2 +k 1/2 +l 0)] + exp[-2pi (h 1/2 +k 0 +l 1/2)]}= f {1 + cosp(k+l) + cosp(l+h) + cosp(h+k)}.
