卷积码的译码算法研究
卷积码的一种译码方法的研究

卷积码的一种译码方法的研究摘要:卷积码是一种在深空通信和移动通信系统中使用较多的信道编码方案。
cdma is-95标准和wcdma 3gpp标准将卷积码作为实时要求较高业务的信道纠错编码。
本文是在现有卷积码译码方法较为复杂的情况下,对卷积码的译码方法进行了分析,对于五位以内突发错误的译码进行纠错的方法进行了探索性研究。
关键词:卷积码译码纠错中图分类号:tp3 文献标识码:a 文章编号:1672-3791(2012)10(b)-0002-011 卷积码基础1948年香农提出了噪声信道编码理论,其核心是通过适当的编码后,当信息传输率小于信道容量时,能够高效无误地传输。
卷积码是一个有限记忆系统,它是将信息序列分割成长度为k的一个个分组,然后将k个信息比特编成n个比特,但k和n通常很小,特别适合以串行形式进行传输,时延小。
与分组码不同的是,在某一分组编码时,不仅参看本时刻的分组而且参看本时刻以前的m+1个分组,编码过程中互相关联的码元个数为n(m+1)。
n=m+1称为约束长度。
n-1是卷积码的重要参数为了突出特征参数常把卷积码写成(n,k,m)卷积码[1]。
1.1 卷积码的原理卷积码的编码器的一般结构如图1所示。
它包括:一个由n段组成的输入移位寄存器,每段k个,共kn个寄存器;一组n个模2和相加器,一个由n级组成的输出移位寄存器。
对应于每段k个比特的输入序列,输出n个比特。
整个编码过程可以看成是输入信息序列与由移位寄存器和模2加法器之间连接所决定的另一个序列的卷积码,卷积码即由此得名。
在(n,k,m)卷积码中,n为码长,k为码组中信息码元的个数,它的编码效率为r=k/n[2]。
正因为卷积码在编码过程中,充分利用了各组之间的相关性,无论是从理论上还是实际上均已证明其性能要优于分组码,因此在通信领域应用得越来越多。
但目前尚未找到较为严密的数学手段,将码的构成与其纠/检错能力有规律的联系起来,另外,卷积码的译码算法也有待于进一步研究与完善。
LDPC码及级联LDPC卷积码编译码的性能研究

关键词:LDPC 码,BP 译码算法,生成矩阵,校验矩阵,LDPC/联 LDPC/卷积码编译码的性能研究
图、表清单
图 1.1 数字通信系统的基本模型 ................................................ 1 图 1.2 二进制对称信道(BSC)的转移概率 ......................................... 4 图 1.3 卷积码编码器 ......................................................... 10 图 1.4(2,1,2)卷积码编码器 ............................................... 11 图 1.5(2,1,2)卷积码编码器状态图 ......................................... 11 图 2.1 A(9,2,3)LDPC 码的二分图 .............................................. 17 图 2.2 A(9,2,3)LDPC 码经过列变换后的二分图................................... 18 图 3.1 BP 算法第二步中信息传播流程示意图..................................... 26 图 3.2 BP 算法第三步中信息传播流程示意图..................................... 27 图 3.3 AWGN 信道模型 ........................................................ 28 图 3.4 R=1/2 时,不同长度的 LDPC 码在迭代 3 次下的性能比较 ..................... 29 图 3.5 不同码率的 LDPC 码在迭代 3 次下的性能比较 .............................. 29 图 3.6 (8000,4,8)LDPC 码在不同迭代次数下的译码性能 ......................... 30 图 3.7 A(8,2,4)LDPC 校验矩阵对应的 TANNER 图 ................................... 31 图 3.8 TANNER 图中两个长度为 4 的环............................................ 31 图 3.9 长度为 4 的环在校验矩阵中的表示 ....................................... 31 图 3.10 长度为 8 的环在校验矩阵中的表示 ...................................... 32 图 3.11 BP 算法中信息在环中的传输示意图...................................... 33 图 4.1 例 4.1 中基于生成矩阵的非正规 LDPC 码的 TANNER 图 ........................ 37 图 4.2 基于生成矩阵的非正规 LDPC 码的性能曲线(不包含校验位) ................ 38 图 4.3 基于生成矩阵的非正规 LDPC 码和基于校验矩阵的 LDPC 码的性能比较 ......... 39 图 4.4 基于生成矩阵的 LDPC 码(包含校验位)和基于校验矩阵的 LDPC 码的性能比较 . 40 图 5.1 分块译码原理框图 ..................................................... 42 图 5.2 不同分块比例的译码性能比较 ........................................... 46 图 5.3 分块在不同迭代次数下的译码性能比较 ................................... 47 图 5.4 分块译码性能与正规 LDPC 码 BP 算法译码性能比较 ......................... 47 图 6.1 (2,1,2)码 L=5 时的篱笆图 .......................................... 50
实验二 卷积码编码及译码实验
实验二卷积码编码及译码实验一、实验目的通过本实验掌握卷积编码的特性、产生原理及方法,卷积码的译码方法,尤其是维特比译码的原理、过程、特性及其实现方法。
二、实验内容1、观察NRZ基带信号及其卷积编码信号。
2、观察帧同步信号的生成及巴克码的特性。
3、观察卷积编码信号打孔及码速率匹配方法。
4、观察接收端帧同步过程及帧同步信号。
5、观察译码结果并深入理解维特比译码的过程。
6、观察随机差错及突发差错对卷积译码的影响。
三、基本原理1、卷积码编码卷积码是一种纠错编码,它将输入的k个信息比特编成n个比特输出,特别适合以串行形式进行传输,时延小。
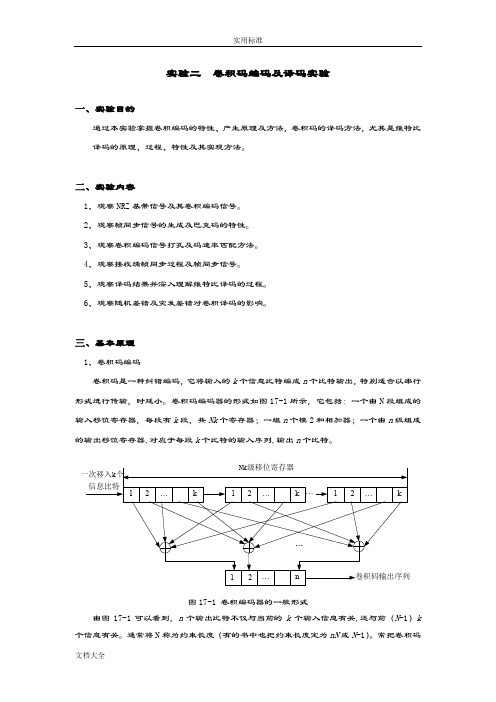
卷积码编码器的形式如图17-1所示,它包括:一个由N段组成的输入移位寄存器,每段有k段,共Nk个寄存器;一组n个模2和相加器;一个由n级组成的输出移位寄存器,对应于每段k个比特的输入序列,输出n个比特。
图17-1 卷积编码器的一般形式由图17-1可以看到,n个输出比特不仅与当前的k个输入信息有关,还与前(N-1)k 个信息有关。
通常将N称为约束长度(有的书中也把约束长度定为nN或N-1)。
常把卷积码记为:(n 、k 、N ),当k =1时,N -1就是寄存器的个数。
编码效率定义为:/c R k n =(17-1)卷积码的表示方法有图解表示法和解析表示法两种:解析法,它可以用数学公式直接表达,包括离散卷积法、生成矩阵法、码生成多项式法;图解表示法,包括树状图、网络图和状态图(最的图形表达形式)三种。
一般情况下,解析表示法比较适合于描述编码过程,而图形法比较适合于描述译码。
(1)图解表示法 (2)解析法下面以(2,1,3)卷积编码器为例详细讲述卷积码的产生原理和表示方法。
(2,1,3)卷积码的约束长度为3,编码速率为1/2,编码器的结构如图17-2所示。
jj图17-2 (2,1,3)卷积编码器这里我们主要介绍码多项式法。
我们可以用多项式来表示输入序列、输出序列、编码器中移位寄存器与模2和的连接关系。
请简述卷积码译码的维特比算法

请简述卷积码译码的维特比算法
卷积码译码的维特比算法是一种概率译码方法,通过计算接收序列的每个可能的发送序列的概率,然后选择具有最大概率的发送序列作为译码输出。
具体步骤如下:
1. 计算每个时刻每个状态下的分支度量。
2. 对于每个时刻,计算每个状态下的部分路径和。
3. 将部分路径和与该时刻的接收路径进行比较,计算汉明码距离。
4. 选择具有最小汉明码距离的状态作为幸存路径。
5. 将幸存路径的最后一个时刻作为输出,并删除所有其他路径。
6. 重复步骤3-5,直到所有接收序列都被译码。
该算法的核心思想是“加、比、选”,即先将每个时刻每个状态下的分支度量进行累积,然后比较每个时刻每个状态下的部分路径和,选择具有最小汉明码距离的状态作为幸存路径。
通过重复执行这些步骤,最终得到译码输出。
卷积码编码和维特比译码的原理、性能与仿真分析

卷积码编码和维特比译码的原理、性能与仿真分析1.引言卷积码的编码器是由一个有k位输入、n位输出,且具有m位移位寄存器构成的有限状态的有记忆系统,通常称它为时序网络。
编码器的整体约束长度为v,是所有k个移位寄存器的长度之和。
具有这样的编码器的卷积码称作[n,k,v]卷积码。
对于一个(n,1,v)编码器,约束长度v等于存储级数m.卷积码是由k个信息比特编码成n(n>k)比特的码组,编码出的n比特码组值不仅与当前码字中的k个信息比特值有关,而且与其前面v个码组中的v*k个信息比特值有关。
卷积码有三种译码方式:序列译码、门限译码和概率译码。
其中,概率译码根据最大似然译码原理在所有可能路径中求取与接收路径最相似的一条路径,具有最佳的纠错性能,维特比译码是概率译码中极重要的一种方式。
序列译码和门限译码则不一定能找出与接收路径最相似的一条路径。
不同于维特比译码,门限译码与序列译码所需的计算量是可变的且对于给定信息分组的最终判决仅仅基于(m+1)个接收分组,而不是基于整个接收序列。
与维特比译码所使用的对数似然量度不同,序列译码所使用的量度为Fano量度。
在接收序列受扰严重的情况下,序列译码的计算量大于维特比译码所需的固定计算量,虽然序列译码要求的平均计算次数通常小于维特比译码。
在采用并行处理的情况下,维特比译码的速度会优于序列译码。
在同样码率和存储级数的条件下,门限译码的性能比维特比译码低大约3dB.维特比译码的数据输出方式有硬判决及软判决两种方式,本文选取生成多项式为561,753的(2,1,8)卷积码对硬判决的性能进行分析,并依据维特比译码的原理以及卷积码的特性,对卷积码编码和维特比译码过程在加性高斯白噪声(AWGN)信道下进行仿真,并且根据仿真结果对维特比译码(硬判决)的结果进行分析。
由于卷积码的生成可以看做一个马尔科夫过程,因此,不同状态间的转移概率对描述这个过程有极关键的作用。
本文则基于MATLAB对不同状态间的转移概率进行求解,从而更准确地分析维特比译码的性能。
卷积码编码及译码实验 浅谈卷积编码下的FPGA实现

卷积码编码及译码实验浅谈卷积编码下的FPGA实现
卷积编码是现代数字通信系统中常见的一种前向纠错码,区别于常规的线性分组码,卷积编码的码字输出不仅与当前时刻的信息符号输入有关,还与之前输入的信息符号有关。
本文主要是关于卷积码编码及译码实验的相关介绍,并着重分析阐述了基于卷积编码下的FPGA实现。
卷积编码卷积码的编码分为两类:前馈和反馈,在每类中又可分为系统和非系统形式。
我们这里只考虑非系统形式的前馈编码器。
‘
上图是WLAN 802.11a协议中采用的卷积编码器结构,输入比特k=1,输出n=2,存储器长度m=6,编码输出不仅与当前输入有关,还与存储器存储的之前的输入数据有关,具体由之前的哪些数据得到编码输出呢,由生成多项式确定其连接关系。
这里,生成多项式为g0=133(八进制)和g1=171(八进制)(右边是最高位),输出数据A的生成多项式为:
输出数据B的生成多项式为:
生成多项式确定了卷积编码器输出的连接关系。
根据多项式的系数,在相应项进行连接。
生成多项式写成二进制序列的形式分别为:g0 = [1 0 1 1 0 1 1]和g1 = [1 1 1 1 0 0 1](右边是最高位)。
我们假设信息序列u,两个编码器输出序列分别为v(0)和v(1),编码器可以看成一个线性系统,系统的信道响应脉冲最多持续m+1个时间单元,编码输出可以写成编码输入与信道脉冲响应的卷积(即生成多项式),即
其中需要注意的是,所有的加法都是模2加运算。
卷积码编码及译码实验基本原理
1、卷积码编码
卷积码是一种纠错编码,它将输入的k个信息比特编成n个比特输出,特别适合以串行形。
Turbo译码算法综述
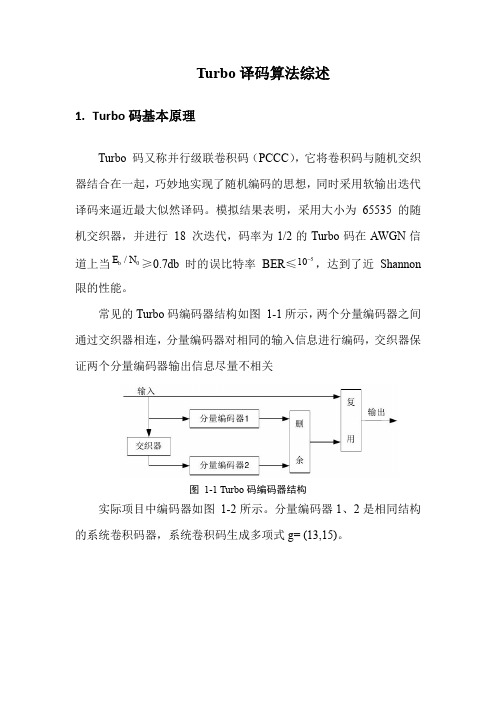
图 1-1 Turbo 码编码器结构
实际项目中编码器如图 1-2 所示。分量编码器 1、2 是相同结构 的系统卷积码器,系统卷积码生成多项式 g= (13,15)。
)
|
(|
r(q) n
|
4
/
42) | 2 /
42
n
(a6
)
|
(|
r(q) n
|
4
/
42) | 2 /
42
4) 自己的想法(以 64-QAM 为例说明)
I、Q 两路信号分别解调自己的比特,即 a1 、a3 、a5 软信息由 I 路 信号计算出来,a2 、a4 、a6 的软信息由 Q 路信号计算出来。以 I 路为 例计算相应比特的软信息。星座图如图 2.3 所示,其中 D 1/ 42 。
号代表的比特数。设 n 时刻收到的星座符号为Qn ,包括 I、Q 两路信
号设为 rn(i) 、 rn(q) ,则
r(i) n
s(i) n
n(i) n
r(q) n
s(q) n
n(q) n
其中
s(i) K
、
s(q) K
表示发射信号的
I、Q
两路信号, nn(i)
、 n(q) n
为相互独
立的服从零均值的正态分布的随机序列,其方差 2
图 2-4 BPSK 调制下的 Turbo 码迭代译码原理
2.2 分量译码算法介绍
分量译码算法采用的 SISO 译码算法,主要包括两类,一类是 MAP 算法以及基于 MAP 算法的修正算法;另一类则是基于 Viterbi 算法的 Viterbi 算法(SOVA)以及它的一些修正算法,总的来说, MAP 类算法比 SOVA 算法新能要好,但这是以复杂度来保证的。
卷积码编译码matlab仿真

一、概述卷积码是一种常用的编码技术,用于提高数字通信系统的可靠性和抗干扰能力。
而编码的解码过程则需要运用编译码技术,以恢复原始数据。
Matlab作为一种强大的工程仿真软件,可以用来对卷积码编译码进行仿真分析,帮助工程师们更好地理解和优化卷积码系统,提高通信系统的性能。
二、卷积码原理1. 卷积码的概念卷积码是一种线性块码,它采用移位寄存器和模2加法器进行编码,通过引入冗余比特来提高信号的可靠性。
卷积码的编码过程可以简单描述为:将输入信息数据与特定的生成多项式进行卷积运算,得到编码后的输出数据。
2. 卷积码的特点卷积码具有较高的编码效率和能够很好地控制码长、纠错能力等特性,因此在实际通信系统中得到广泛应用。
三、编译码原理1. Viterbi算法卷积码的译码过程通常采用Viterbi算法,它是一种最大似然译码算法,通过计算最小距离路径的方式来进行译码。
Viterbi算法能够有效地对卷积码进行解码,提高译码的准确性。
2. 编译码的实现在Matlab中,编译码的实现通常是通过编写一定的程序来模拟Viterbi算法的译码过程。
通过仿真分析,可以评估不同的编码方案对通信系统性能的影响。
四、Matlab仿真环境1. Matlab的特点Matlab作为一种强大的仿真软件,具有丰富的工具和函数库,能够方便地进行数字通信系统设计与仿真分析。
Matlab提供了直观的图形界面和强大的数据处理能力,可用于展示仿真结果和进行数据分析。
2. 使用Matlab进行卷积码编译码仿真在Matlab环境中,可以编写程序来实现卷积码的编码和Viterbi算法的译码过程。
通过调用Matlab中的工具函数和绘图函数,可以直观地展示通信系统的性能指标,并对比不同编码方式的性能差异。
五、仿真实例分析1. 卷积码编码仿真我们可以编写Matlab程序,实现对卷积码的编码过程。
通过模拟不同的编码率和约束长度,可以观察到编码后的效果,并评估编码的性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Abstract
Convolutional code has shown its great advantages since it was proposed by P.Elias. Block convolutional codes and Turbo codes are two typical types on the basis of convolutional codes. In the future, the wireless communication system will need better performance to meet the development of communication business, which will lead more codes with better error performance to appear. The decoding algorithms of convolutional codes are mainly researched in this thesis. Firstly, the basic architecture of digital communication is introduced, and channel coding is mainly introduced as an important part of the basic architecture. Convolutional code is a classic type of code and has been used in error control fields widely. Secondly, the principle of convolutional codes and the detailed derivation of decoding algorithm of BCJR are stated, and the error performance are simulated and analyzed under different decoding algorithms such as Max-log-MAP, MAP. Thirdly, the Max-log-MAP decoder for convolutional code (1, 15/13) is designed under the platform of the FPGA, in which the concept of Sliding-Window(including Pre-warming Window and Computing Window) is introduced and time division multiplexing of storage are adopted in order to shorten decoding delay and save hardware resources effectively. Finally, preliminary exploration of the application of SPA in convolutional codes is made in this thesis. Iterate SPA decoding model and non-iterate SPA decoding model are proposed. Furthermore, several convolutional codes with two or more shift registers are simulated respectively. Keywords:Convolutional Codes BCJR Max-log-MAP
本人签名: 导师签名:
日期 日期
第一章 绪论
1
第一章 绪论
1.1 选题背景和研究意义
信道编码是数字通信系统的重要组成部分,随着通信技术的不断发展,信道 编码技术也在不断地发展。在通信系统中,信道传输特性不理想以及噪声的存在, 会导致接收端出现接收信号的错误,因此用于信道纠错的信道编码是数字通信系 统中极为重要的一个环节。二十世纪 40 年代香农定理的出现为人们指出了纠错码 的研究方向。 根据香农的有噪信道编码定理[1],可以推导出一个码率为 R 的编码通信系统 达到无误码传输状态所必须的最小信噪比的理论极限。这个理论极限通常称为香 农限,它说明对一个码率为 R 的编码通信系统,只有当 SNR 超过这个极限值时才 能获得无误码传输。只要 SNR 高于这个极限值,香农的编码定理保证了能够获得 无误码传输的(可能相当复杂)编码通信系统的存在性。另外,香农证明了在采 用无限长的随机编码时,数据可以以接近信道容量的速率几乎无误码的传输,从 而为信道编码的研究奠定了基础。 P.Elias[2]在1955年提出了卷积码,卷积码是一种高效的纠错编码方式,广泛应 用于卫星通信系统、遥测外测系统、移动通信系统和各种数字电视等。卫星通信 系统中使用(2,1,7)和(3,l,7)卷积码作为标准编码方式。第二代移动通信GSM 系统和IS.95 CDMA系统分 别采用(2,1,5)和(2, l,9)卷积码。第三代移动通信 WCDMA系统中上下行链路中分别采用(3,1,9)和(2,l,9)卷积码完成纠错编码。 卷积码有序列译码、门限译码、Viterbi 译码、BCJR 译码等几种译码方法。序 列译码算法[3]是最早提出的卷积码译码算法, 是一种以最大似然译码原理为基础的 准最佳概率译码,R.M.Fano 引入了一种新的序列译码的变型。门限译码算法[4]曾 经是卷积码的第一种实用的译码方法。该算法虽然误码性能稍差但易于实现,使 卷积码在有线和无线信道的数据传输中得到了一些实际应用。 Viterbi 算法[5]也是以 最大似然译码原理为基础,是一种基于码的网格图的最佳概率译码算法。BCJR[6] 算法是一种软输入软输出译码算法,更多地应用于 Turbo 码等的译码中。 在通信系统中,为了提高传输的可靠性,各种纠错编码技术被广泛地采用。 其中卷积码是一种应用非常广泛的性能优良的编码方式,在信道编码技术不断发 展的今天发挥着重要作用,如以卷积码为基础发展起来的Turbo码[15],由于其类随 机特性以及采用迭代译码的思想几乎达到了接近香农限的误码性能[16],因此研究 卷积码的编译码具有重要的意义。本章主要介绍论文的相关背景,信道编码技术 及其发展状况,最后说明本文的结构和主要的研究工作。
西安电子科技大学 硕士学位论文 卷积码的译码算法研究 姓名:李校娟 申请学位级别:硕士 专业:通信与信息系统 指导教师:陈彦辉 首次提出卷积码编码以来,这一编码技术至今仍显示出强大的生命 力,如以卷积码为基础发展起来的 Turbo 码和分组卷积码等。未来的无线通信系 统需要宽带、高速的系统性能来满足诸如数据、声音、图像之类的高质量多媒体 传输业务,这必将导致更多高性能信道编码技术的出现。 本文主要对卷积码的译码算法进行基础性研究。首先介绍了数字通信的基本 结构,强调了信道编码在通信系统中的重要地位,指出卷积码是一种经典码。其 次,详细介绍了卷积码的基本原理,主要是 BCJR 译码算法,并对 Max-log-MAP、 MAP 等译码算法进行误码性能仿真。 另外重点对卷积码(1, 15/13)的 Max-log-MAP 译码器的 FPGA 实现进行设计。文中引入了滑动窗(预热窗和运算窗) ,预热窗为 运算窗提供相对可靠的后向递推初始值,这样的做法在减小译码延时的同时也提 高了译码的正确性。另外,分支转移概率和前向递推值在存储时采用了四个 RAM 轮流读写、分时复用的方法,有效地节约了硬件资源。 最后,本文初步探索了和积算法(SPA)在卷积码中的应用,给出了迭代 SPA 译码和递推 SPA 译码模型,并分别对具有二个或更多个移位寄存器的若干卷积码 进行仿真分析。 关键词:卷积码 BCJR Max-log-MAP 和积算法
2
卷积码的译码算法研究
1.2 信道编码的发展
1948年,信息论的奠基人Shannon在他的开创性论文“通信的数学理论”[7]中, 首次阐明了在有扰信道中实现可靠通信的方法,提出了著名的有扰信道编码定理, 指出了实现最佳编码的三个基本条件:(1)采用随机编码方式;(2)编码长度L→∞, 即码元序列长度无限;(3)译码采用最大似然译码算法。在满足这三个条件的前提 下,香农认为在有噪信道中可以实现无差错传输。 自20世纪50年代以来,编码理论研究与技术应用是长期围绕数字通信业务的 特点和需要而发展的,即以伽罗华域上的代数编码方法为主体,研究适合串行信 道中使用的码率尽可能高、检错纠错能力尽可能强的码型及其译码算法。从结构 上看,码型可划分为分组码和卷积码两大类;译码算法主要分为基于代数的译码 算法和基于概率的译码算法两大类。在分组码研究中,各种好的循环码、能纠正 多重差错的BCH码、RS码[23]等码型都从理论推导到计算机模拟、搜索中找到。分 组码的译码方法可分为代数和非代数两类。代数方法是以求解一组用以确定差错 位置与数值的联立方程为基础的,而非代数方法以更为直接的方式确定差错模式。 非代数方法主要有梅吉特(Meggitt)于1961年首先提出的纠突发差错的梅吉特译 码器、1963年梅茜(Massey)所给出的门限译码器和1962年由布拉格(Prange)首 先介绍的信息组译码法。此外,为了充分利用解调器所能提供的软信息,后来又 陆续推出了一系列分组码软判决译码算法,如梅茜的后验概率(APP)译码算法、 哈特曼(Hartmann)- 鲁道夫(Rudolph)最优逐符号译码算法和威尔顿算法等。 在卷积码研究方面, 随着Viterbi算法的提出及序列译码算法Fano算法的提出,也出 现了以译码算法优化、减少译码复杂度为突破口的一批好的研究成果。为了在译 码复杂性不高的同时获得更好的纠错性能,范尼(Forney)于1966年首先提出级联 码的概念。 20世纪70~80年代,以Goppa为首的学者从理论上构造了一类Goppa码,其中的 一个子类的性能达到了香农信道编码定理中提出的“好码”的标准,具有理论上 的重大意义。这个时期由于大规模集成电路的迅速发展,为信道编码的大规模使 用打下了坚实的基础,如美国在20世纪70年代发射的“旅行者”号宇宙飞船中就 成功地运用了信道编码技术,使宇宙飞船能从遥远的太空传回清晰的照片。同时, 由于数字信号处理技术的发展,信道编码在通信系统中的应用也得到关注,并广 泛用于实际的通信系统中。另外,近几十年来,许多研究学者致力于寻找低编译 码复杂度的实用化编码,先后提出了非规则重复累加码(IRA)[25],以及多维并行 级联单奇偶校验码(M-PC-SPC)等结构。 在 1993 年 IC 国际会议上,法国不列颠通信大学的 C.Berrou、A.Glavieux[8] 等人,首先提出了一种称之为 Turbo 码的编译码方案。Turbo 码的出现,是首次对
