分类资料的Logistic回归分析SPSS
(完整版)spss的logistic分析教程

Logistic回归主要分为三类,一种是因变量为二分类得logistic回归,这种回归叫做二项logistic回归,一种是因变量为无序多分类得logistic回归,比如倾向于选择哪种产品,这种回归叫做多项logistic回归。
还有一种是因变量为有序多分类的logistic回归,比如病重的程度是高,中,低呀等等,这种回归也叫累积logistic回归,或者序次logistic回归。
二值logistic回归:选择分析——回归——二元logistic,打开主面板,因变量勾选你的二分类变量,这个没有什么疑问,然后看下边写着一个协变量。
有没有很奇怪什么叫做协变量?在二元logistic回归里边可以认为协变量类似于自变量,或者就是自变量。
把你的自变量选到协变量的框框里边。
细心的朋友会发现,在指向协变量的那个箭头下边,还有一个小小的按钮,标着a*b,这个按钮的作用是用来选择交互项的。
我们知道,有时候两个变量合在一起会产生新的效应,比如年龄和结婚次数综合在一起,会对健康程度有一个新的影响,这时候,我们就认为两者有交互效应。
那么我们为了模型的准确,就把这个交互效应也选到模型里去。
我们在右边的那个框框里选择变量a,按住ctrl,在选择变量b,那么我们就同时选住这两个变量了,然后点那个a*b的按钮,这样,一个新的名字很长的变量就出现在协变量的框框里了,就是我们的交互作用的变量。
然后在下边有一个方法的下拉菜单。
默认的是进入,就是强迫所有选择的变量都进入到模型里边。
除去进入法以外,还有三种向前法,三种向后法。
一般默认进入就可以了,如果做出来的模型有变量的p值不合格,就用其他方法在做。
再下边的选择变量则是用来选择你的个案的。
一般也不用管它。
选好主面板以后,单击分类(右上角),打开分类对话框。
在这个对话框里边,左边的协变量的框框里边有你选好的自变量,右边写着分类协变量的框框则是空白的。
你要把协变量里边的字符型变量和分类变量选到分类协变量里边去(系统会自动生成哑变量来方便分析,什么事哑变量具体参照前文)。
SPSS做Logistic回归步骤
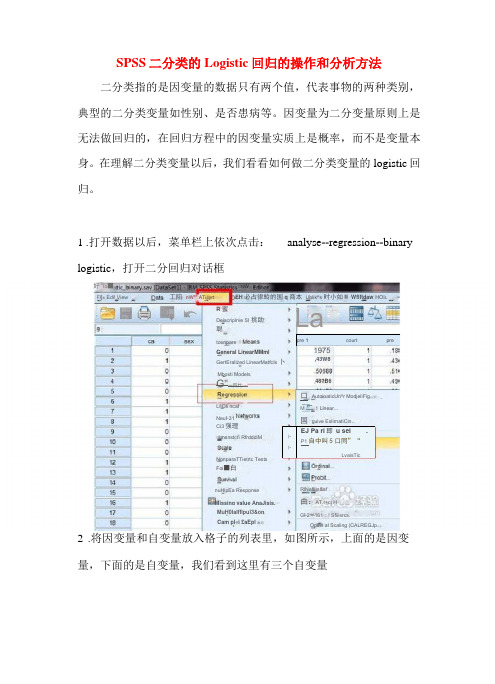
SPSS 二分类的Logistic 回归的操作和分析方法二分类指的是因变量的数据只有两个值,代表事物的两种类别, 典型的二分类变量如性别、是否患病等。
因变量为二分变量原则上是 无法做回归的,在回归方程中的因变量实质上是概率,而不是变量本 身。
在理解二分类变量以后,我们看看如何做二分类变量的logistic 回归。
1 .打开数据以后,菜单栏上依次点击: analyse --regression --binary logistic ,打开二分回归对话框2 .将因变量和自变量放入格子的列表里,如图所示,上面的是因变 量,下面的是自变量,我们看到这里有三个自变量pre 1courtpre卜 卜EJ Pa ri 即 u sei.P1自中叫5口同”“LvaisTic好 Io ■网 □N W□imsnstcri RfrdddiMNonparaTTietrtc Tests Foi ■白MuH0lalfflpul3&on Deiscriplrve SI 挑助聪LfiOli ncaf - Neuf-31 nuHlpEa ResponseMissing value AnaJisis. EH 必占律蛉的国q 商本 Ublik^s 时小如M Wflftdaw HOI LFl[« Edi! View工陷 nW"" ATiilyrtCam pl«i £aEpl 骷与Opsin al Scaling (CALREGJp..R 蜜GertEralized LinearMatfcIs 卜 Mbosti ModelsRlNafllin&af .曲:AT.r+ci HC] 2^^161;! Sfiiisrcs.tosnpareGeneral LinearMMml 48?B6Ci3强理 G"一四忙—一 3 La,43W8口 AutoioaticUn^r ModjeliFig..M 二1 Linear...国 guive EslirnatiCin...C>ep«n (lferit3 .设置回归方法,这里选择最简单的方法:enter ,它指的是将所有的 变量一次纳入到方程。
spss logistic回归分析

变量说明:Y:治愈情况,1=治愈;0=未治愈;; X1:病情严重程度,0=不严重,1=严重;X2:年龄。 X3:治疗方法,0=新疗法,1=旧疗法。
二值 Logistic回归
因变量 协变量(自变量)
注:此处将X1、X3看作为连续变量;采用Enter 法。
OR的95%置信区间
对模型的检验
-2Log likelihood=40.597
实习六
Logistic回归分析
(一)Logistic回归分析的任务
影响因素分析 在流行病学研究中,logistic回归常用于疾病的危险
因素分析,logistic回归分析可以提供一个重要的指标: OR。
(二)Logistic回归分析的基本原理
1.变量特点 因变量:二分类变量,若令因变量为y,研究中,分 别表示病例组和对照组)。
6.OR与RR
Logistic回归模型中,OR=EXP(β)。
当某种疾病的发病率或死亡率很低时,OR≈RR
(三)Logistic回归分析的适用条件
1.经典的Logistic回归分析,要求因变量为二分类变量。但是 其因变量也可以为多分类变量(SPSS中Multinomial Logistic 菜单)。
后退法筛选变量
后退法筛选变量
每步的模型检验、 -2Log likelihood 及拟合分类表
后退法筛选变量
不在模型中的变量
Logistic回归模型为:
Log
P 1− P
= 1.358 −1.832x1
−
2.140x3
逐步前进法筛选变量
逐步前进法筛选变量
不在模型中的变量
Logistic回归模型为:
另法:将X1、X3指定为分类变量。
应用SPSS软件进行多分类Logistic回归分析

e0. 077 e0. 077+ e- 0. 624 +
e0 =
1.
1. 080+
080 0. 536+
1=
0.
413
P (中度) =
01536 11080+ 0. 536+
1=
0.
205
P (重度) =
11080+
1 0.
536+
1=
0.
382
即该初中男生轻度视力低下的概率为 0. 413, 中度视力低
Jou rna l of M a them a tica lM ed icine
V o l. 14 NO. 6 2001
文章编号: 100424337 (2001) 0620548202 中图分类号: T P319 文献标识码: B
应用 SPSS 软件进行多分类 L og ist ic 回归分析
黄 爽 安胜利Ξ
(新乡市卫生监督检验所 新乡 453003)
SPSS 是在W in95 或以上平台下运行的软件, 界面友好、 直观, 操作简便, 非常适合于非统计专业人员应用。 本文结合 具体实例, 介绍如何在 SPSS10. 0 上进行多分类 (反应) logistic 回归分析。
通常意义上的 L ogistic 回归要求因变量 y 只有两种取值 (二分类) , 当 y 的取值有两种以上时, 就要用多分类 L ogistic 回归分析 (M u ltinom ialL og istic R eg ression)。这种分析不仅可 用于医疗卫生领域的研究, 也可应用于社会学、经济学等领域 的研究。例如研究学生龋齿严重程度 (因变量) 与刷牙、饮食习
2. 233 指对于视力低下为中度而不是重度这种情况, 初中生是
spsslogistic回归分析结果解读

spsslogistic回归分析结果解读
本文分析了使用SPSS Logistic回归分析的结果,以了解不同变量之间
是否存在潜在关系。
Logistic回归是一种用于预测调查中的变量组合能够预测调查的结果的
机器学习技术。
在这种情况下,我们使用Logistic回归来预测一个变量
(假设为购买行为)和其他变量(价格,品牌认知度等)之间的关系。
特别是,我们可以评估价格是否是客户决定购买商品的重要影响因素。
SPSS Logistic回归分析的结果表明,在本例中,我们发现价格是一个
重要的影响因素。
我们看到,价格的变化程度会影响客户购买商品的可能性:客户可能更愿意购买相对较低的价格,而对于较高的价格则更不可能购买。
此外,品牌认知度也会影响客户是否愿意购买:客户对品牌认知度越高,购
买概率越高。
这可能是因为客户更倾向于信任已经熟悉的品牌而忽略未熟悉
的品牌,或者可能是因为客户更了解该品牌的商品及其优缺点,因此可以作
出的更明智的购买决策。
因此,本次分析表明,价格和品牌认知度在客户决定购买商品时都有重
要的影响。
商家应考虑这些因素,以确保它们的产品在客户面前具有足够的
吸引力和优势,使其愿意购买。
SPSS--logistic回归分析

小结
谢谢大家!
基础知识
通过下例复习相关概念 如:研究患某疾病与饮酒的关联性
患病率 P1=? P2=?
基础知识
二分类logistic回归模型
回归系数的意义
多因素logistic回归分析时,对回归系数 的解释都是指在其他所有自变量固定的 情况下的优势比。 存在因素间交互作用时,logistic回归系 数的解释变得更为复杂,应特别小心。
适用条件
因变量为二分类变量或某事件的发生率 自变量与Logit(P)之间为线性关系 残差合计为0,且服从二项分布 各观测间相互独立 参数估计方法:最大似然法
例1
研究急性心肌梗塞(AMI)患病与饮酒的关 系,采用横断面调查。
SPSS基本操作
哑变量设置
为了便于解释,对二分类变量按0、1编码 如果对二项分类变量按+1、-1编码,结果? 分类变量必须转化。如地区对血压的影响。 等级资料,当等级之间量度不一时必须转化。 连续资料不宜直接进入方程时,转化为等级 资料或分类资料。
多因素统计分析 1. 因变量为计量资料,多重现性回归 2. 因变量为分类变量,logistic回归
பைடு நூலகம்
Logistic回归模型
按研究设计分类: 1. 非配对设计:非条件logistic回归模型 2. 配对病例对照:条件logistic回归模型
按反应变量分类: 1. 二分类logistic回归模型(常用) 2. 多分类无序logistic回归模型(常用) 3. 多分类有序logistic回归模型(常用)
logistic 回归
海南医学院公共卫生学院 卫生统计学教研室 赵婵娟
chanjuan850@
内容
基本概念 基本步骤 基本操作 基本结果解释
spss二元logistic回归分析结果解读

spss的二元logistic回归
SPSS(Statistical Product and Service Solutions)是一款数据统计与分析软件。
SPSS软件可以提供全面高级的统计分析,方便易用可快速操作,可缩小数据科学与数据理解之间的差距;在具体的应用方向方面,SPSS提供了高级统计分析、大量机器学习算法、文本分析等功能,具备开源可扩展性,可与大数据的集成,并能够无缝部署到应用程序中。
Logistic回归:主要用于因变量为分类变量(如疾病的缓解、不缓解,评比中的好、中、差等)的回归分析,自变量可以为分类变量,也可以为连续变量。
变量为二分类的称为二项logistic回归,因变量为多分类的称为多元logistic回归。
Odds:称为比值、比数,是指某事件发生的可能性(概率)与不发生的可能性(概率)之比。
OR(OddsRatio):比值比,优势比。
二元logistic回归是研究二分类反应变量和多个解释变量间回归关系的统计学分析方法。
logistic回归模型 SPSS例析

Logistic 回归Logistic 回归是多元回归分析的拓展,其因变量不是连续的变量;在logistic 分析中,因变量是分类的变量;logistic 和probit 回归皆为定性回归方程的一种;他们的特点就在于回归因变量的离散型而非连续型。
Logistic 回归又分为binary 和multinominal 两类;1、Logistic 回归原理Logistic 回归Logistic 回归模型描述的是概率P 与协变量12,.......k x x x 之间的关系,考虑到P 的取值在0----1之间,为此要首先把Plogistic 变换为()ln()1pf p p=-,使得它的取值在+∞-∞到之间,然后建立logistic 回归模型P=p(Y=1)()ln()1pf p p=-=011+......k k x x βββ++011011+......+......1k kk kx x x x e p eββββββ++++⇒=+Logistic 回归模型的数据结构观察值个数 取1的观察值个数 取0的观察值个数 协变量12,.......k x x x 的值 N1 r1 n1-ri ……………………… N2 r2 n2-r2 ………………………. . . . . . . . .Nt rt nt-rt ………………………. 根据数据,得到参数0 1....k βββ的似然函数011011011+ (1)+......+......1()()11k ki i ik k k kx x r n r t i x x x x e e eβββββββββ++-=++++∏++使用迭代算法可以求得0 1....k βββ的极大似然估计。
2、含名义数据的logistic 模型婚姻状况是名义数据,分为四种情形:未婚、有配偶、丧偶、离婚;在建立logistic 模型时,定义变量M1、M2、M3,使得(M1=1,M2=0,M3=0)表示未婚; (M1=0,M2=1,M3=0)表示有配偶 (M1=0,M2=0,M3=1)表示丧偶 (M1=-1,M2=-1,M3=-1)表示离婚 也可以将三变量定义为(M1=1,M2=0,M3=0)表示未婚; (M1=0,M2=1,M3=0)表示有配偶 (M1=0,M2=0,M3=1)表示丧偶 (M1=0,M2=0,M3=0)表示离婚 一般来说,只要矩阵[]1111122213331444a b c a b c a b c a b c非奇异,可以定义(M1=a1,M2=b1,M3=c1)表示未婚; (M1=a2,M2=b2,M3=c2)表示有配偶 (M1=a3,M2=b3,M3=c3)表示丧偶 (M1=a4,M2=b4,M3=c4)表示离婚3、含有有序数据的logistic 回归文化程度是有序的定性变量,他有一个顺序,由低到高为文盲、小学、中学、高中、中专;大学。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S PSS 10.0高级教程十三:分类资料的Logistic回归分析(2009-02-05 15:32:54)转载▼所谓Logistic模型,或者说Logistic回归模型,就是人们想为两分类的应变量作一个回归方程出来,可概率的取值在0~1之间,回归方程的应变量取值可是在实数集中,直接做会出现0~1范围之外的不可能结果,因此就有人耍小聪明,将率做了一个Logit变换,这样取值区间就变成了整个实数集,作出来的结果就不会有问题了,从而该方法就被叫做了Logistic回归。
随着模型的发展,Logistic家族也变得人丁兴旺起来,除了最早的两分类Logistic外,还有配对Logistic模型,多分类Logistic模型、随机效应的Logistic模型等。
由于SPSS的能力所限,对话框只能完成其中的两分类和多分类模型,下面我们就介绍一下最重要和最基本的两分类模型。
10.3.1 界面详解与实例例11.1 某研究人员在探讨肾细胞癌转移的有关临床病理因素研究中,收集了一批行根治性肾切除术患者的肾癌标本资料,现从中抽取26例资料作为示例进行logistic回归分析(本例来自《卫生统计学》第四版第11章)。
∙i:标本序号∙x1:确诊时患者的年龄(岁)∙x2:肾细胞癌血管内皮生长因子(VEGF),其阳性表述由低到高共3个等级∙x3:肾细胞癌组织内微血管数(MVC)∙x4:肾癌细胞核组织学分级,由低到高共4级∙x5:肾细胞癌分期,由低到高共4期∙y:肾细胞癌转移情况(有转移y=1; 无转移y=0)。
i x1 x2 x3 x4 x5 y1 592 43.4 2 1 02 36 1 57.2 1 1 03 61 2 190 2 1 04 58 3 128 4 3 15 55 3 80 3 4 16 61 1 94.4 2 1 07 38 1 76 1 1 08 42 1 240 3 2 09 50 1 74 1 1 010 58 3 68.6 2 2 011 68 3 132.8 4 2 012 25 2 94.6 4 3 113 52 1 56 1 1 014 31 1 47.8 2 1 015 36 3 31.6 3 1 116 42 1 66.2 2 1 017 14 3 138.6 3 3 118 32 1 114 2 3 019 35 1 40.2 2 1 020 70 3 177.2 4 3 121 65 2 51.6 4 4 122 45 2 124 2 4 023 68 3 127.2 3 3 124 31 2 124.8 2 3 025 58 1 128 4 3 026 60 3 149.8 4 3 1在菜单上选择Analyze==》Regression==》Binary Logistic...,系统弹出Logistic回归对话框如下:左侧是候选变量框,右上角是应变量框,选入二分类的应变量,下方的Covariates框是用于选入自变量的,只不过这里按国外的习惯被称为了协变量。
两框中间的是BLOCK系列按扭,我在上一课已经讲过了,不再重复。
中下部的>a*b>框是用于选入交互作用的,和其他的对话框不太相同(我也不知道为什么SPSS偏在这里做得不同),下方的Method列表框用于选择变量进入方法,有进入法、前进法和后退法三大类,三类之下又有细分。
最下面的四个按钮比较重要,请大家听我慢慢道来:∙Select>>钮:用于限定一个筛选条件,只有满足该条件的记录才会被纳入分析,单击它后对话框会展开让你填入相应的条件。
不过我觉得该功能纯属多余,和专门的Select 对话框的功能重复了。
∙Categorical钮:如果你的自变量是多分类的(如血型等),你必须要将它用哑变量的方式来分析,那么就要用该按钮将该变量指定为分类变量,如果有必要,可用里面的选择按钮进行详细的定义,如以哪个取值作为基础水平,各水平间比较的方法是什么等。
当然,如果你弄不明白,不改也可以,默认的是以最大取值为基础水平,用Deviance做比较。
o Save钮:将中间结果存储起来供以后分析,共有预测值、影响强度因子和残差三大类。
o Options钮:这一部分非常重要,但又常常被忽视,在这里我们可以对模型作精确定义,还可以选择模型预测情况的描述方式,如Statistics and Plots中的Classification plots 就是非常重要的模型预测工具,Correlations of estimates则是重要的模型诊断工具,Iteration history可以看到迭代的具体情况,从而得知你的模型是否在迭代时存在病态,下方则可以确定进入和排除的概率标准,这在逐步回归中是非常有用的。
好,根据我们的目的,应变量为Y,而X1~X5为自变量,具体的分析操作如下:1.Analyze==》Regression==》Binary Logistic...2.Dependent框:选入Y3.Covariates框:选入x1~x54.OK钮:单击10.3.2 结果解释Logistic Regression上表为记录处理情况汇总,即有多少例记录被纳入了下面的分析,可见此处因不存在缺失值,26条记录均纳入了分析。
上表为应变量分类情况列表,没什么好解释的。
Block 0: Beginning Block此处已经开始了拟合,Block 0拟合的是只有常数的无效模型,上表为分类预测表,可见在17例观察值为0的记录中,共有17例被预测为0,9例1也都被预测为0,总预测准确率为65.4%,这是不纳入任何解释变量时的预测准确率,相当于比较基线。
上表为Block 0时的变量系数,可见常数的系数值为-0.636。
上表为在Block 0处尚未纳入分析方程的侯选变量,所作的检验表示如果分别将他们纳入方程,则方程的改变是否会有显著意义(根据所用统计量的不同,可能是拟合优度,Deviance 值等)。
可见如果将X2系列的哑变量纳入方程,则方程的改变是有显著意义的,X4和X5也是如此,由于Stepwise方法是一个一个的进入变量,下一步将会先纳入P值最小的变量X2,然后再重新计算该表,再做选择。
Block 1: Method = Forward Stepwise (Conditional)此处开始了Block 1的拟合,根据我们的设定,采用的方法为Forward(我们只设定了一个Block,所以后面不会再有Block 2了)。
上表为全局检验,对每一步都作了Step、Block和Model的检验,可见6个检验都是有意义的。
此处为模型概况汇总,可见从STEP1到STEP2,DEVINCE从18降到11,两种决定系数也都有上升。
此处为每一步的预测情况汇总,可见准确率由Block 0的65%上升到了84%,最后达到96%,效果不错,最终只出现了一例错判。
上表为方程中变量检验情况列表,分别给出了Step 1和Step 2的拟合情况。
注意X4的P值略大于0.05,但仍然是可以接受的,因为这里用到的是排除标准(默认为0.1),该变量可以留在方程中。
以Step 2中的X2为例,可见其系数为2.413,OR值为11。
上表为假设将这些变量单独移出方程,则方程的改变有无统计学意义,可见都是有统计学意义的,因此他们应当保留在方程中。
最后这个表格说明的是在每一步中,尚未进入方程的变量如果再进入现有方程,则方程的改变有无统计学意义。
可见在Step 1时,X4还应该引入,而在Step 2时,其它变量是否引入都无关了。
10.3.3 模型的进一步优化与简单诊断10.3.3.1 模型的进一步优化前面我们将X1~X5直接引入了方程,实际上,其中X2、X4、X5这三个自变量为多分类变量,我们并无证据认为它们之间个各等级的OR值是成倍上升的,严格来说,这里应当采用哑变量来分析,即需要用Categorical钮将他们定义为分类变量。
但本次分析不能这样做,原因是这里总例数只有26例,如果引入哑变量模型会使得每个等级的记录数非常少,从而分析结果将极为奇怪,无法正常解释,但为了说明哑变量模型的用法,下面我将演示它是如何做的,毕竟不是每个例子都只有26例。
默认情况下定义分类变量非常容易,做到如上图所示就可以了,此时分析结果中的改变如下:上表为自变量中多分类变量的哑变量取值情况代码表。
左侧为原变量名及取值,右侧为相应的哑变量名及编码情况:以X5为例,表中可见X5=4时,即取值最高的情况被作为了基线水平,这是多分类变量生成哑变量的默认情况。
而X5(1)代表的是X5=1的情况(X5为1时取1,否则取0),X5(2)代表的是X5=2的情况,依此类推。
同时注意到许多等级值有几个记录,显然后面的分析结果不会太好。
相应的,分析结果中也以哑变量在进行分析,如下所示:上表出现了非常有趣的现象:所有的检验P值均远远大于0.05,但是所有的变量均没有被移出方程,这是怎么回事?再看看下面的这个表格吧。
这个表格为方程的似然值改变情况的检验,可见在最后Step 2生成的方程中,无论移出X2还是X4都会引起方程的显著性改变。
也就是说,似然比检验的结果和上面的Walds检验结果冲突,以谁为准?此处应以似然比检验为准,因为它是全局性的检验,且Walds检验本身就不太准,这一点大家记住就行了,实在要弄明白请去查阅相关文献。
请注意:上面的哑变量均是以最高水平为基线水平,这不符合我们的目的,我们希望将最低水平作为基线水平。
比如以肾细胞癌第一期为基线水平,需要这样做只要在Categoriacl框中选中相应的变量,在Reference Category处选择First,再单击Change即可,此时变量旁的标示会做出相应的改变如下:分析结果中也会做出相应的改变,此处略。
10.3.3.2 模型的简单诊断SPSS本身提供了几种用于模型诊断的工具,基本上都集中在Options对话框中,除了大家熟悉的残差分析外,这里这种介绍三种简单而有非常有用的工具:迭代记录、相关矩阵和分类图。
上表为Block 1的迭代记录,可见无论是似然值,还是三个系数值,均是从迭代开始就向着一个方向发展,最终达到收敛,这说明整个迭代过程是健康的,问题不大;如果中途出现波折,尤其是当引入新变量后变化方向改变了,则提示要好好研究。
上表为方程中变量的相关矩阵,可见X2和常数相关性较强,当引入X4后仍然如此,提示要关注这一现象,以防因自变量间的共线性导致方程系数不稳(此时迭代记录多半也会有波动)。
当然,由于本例只有26条记录,这一问题是没有办法深入研究的。
上图是Step 1结束时,即只引入X2时的预测图,0和1代表实际取值,当预测的概率值大于0.5时,则预测结果为1,反之为0,由上图可见,该模型对0的预测是比较好的,多数的概率都在0附近,但对1的预测不准,即使正确的,计算出的概率也在0.8左右,并且有好几个都判错了。
