【精品】湖南省郴州市2017-2018学年高一上学期期末考试数学试题
湖南省郴州市一中2022年高一数学第一学期期末质量检测试题含解析

因为对 , ,故函数 的图象如图所示:
由图可知,当 时,函数 取得最小值 .
故答案为: .
14、2
【解析】由扇形的周长和面积,可求出扇形的半径及弧长,进而可求出该扇形的圆心角.
【详解】设扇形的半径为 ,所对弧长为 ,则有 ,解得 ,故 .
故答案为:2.
1.函数 , 值域是()
A. B.
C. D.
2.已知向量 , ,则 在 方向上的投影为
A. B.8
C. D.
3.若 , ,则下列结论正确的是()
A. B.
C. D.
4.某地一年之内12个月的降水量从小到大分别为:46,48,51,53,53,56,56,56,58,64,66,71,则该地区的月降水量20%分位数和75%分位数为()
故答案为: ,
16、
【解析】设实数x∈[1,9],
经过第一次循环得到x=2x+1,n=2,
经过第二循环得到x=2(2x+1)+1,n=3,
经过第三次循环得到x=2[2(2x+1)+1]+1,n=4此时输出x,
输出的值为8x+7,
令8x+7⩾55,得x⩾6,
由几何概型得到输出的x不小于55的概率为 .
当 时,令 ,即 , ,不在定义域区间内,舍
所以函数 零点所在的区间为
故选:D
9、B
【解析】利用一元二次不等式的解法即得.
【详解】由 可得, ,
故不等式 的解集是 .
故选:B.
10、D
【解析】A项, 可能相交或异面,当 时,存在 , ,故A项错误;
B项, 可能相交或垂直,当 时,存在 , ,故B项错误;
湖南省郴州市2017-2018学年高一上学期期末考试数学试题
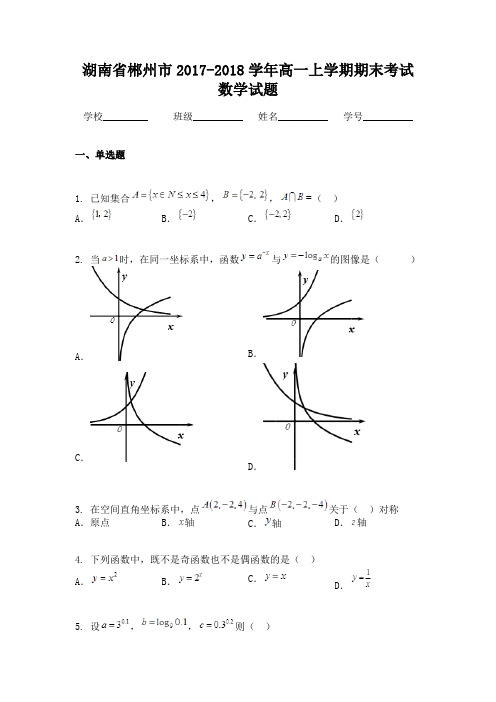
湖南省郴州市2017-2018学年高一上学期期末考试数学试题学校_________ 班级__________ 姓名__________ 学号__________一、单选题1. 已知集合,,()A.B.C.D.2. 当时,在同一坐标系中,函数与的图像是()A.B.C.D.3. 在空间直角坐标系中,点与点关于()对称A.原点B.轴C.轴D.轴4. 下列函数中,既不是奇函数也不是偶函数的是()A.B.C.D.5. 设,,则()A.B.C.D.6. 设是一条直线,,是两个不同的平面,则下列命题中正确的是()A.若,,则B.若,,则C.若,,则D.若,,则7. 中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若取3,其体积为(立方寸),则图中的为()A.B.C.D.8. 将正方形沿对角线折起成直二面角,则直线和平面所成的角的大小为()A.30°B.45°C.60°D.90°9. 已知函数是定义在上的奇函数,且在上是增函数,若实数满足,则实数的取值范围是()A.B.C.D.10. 函数是定义域为R的奇函数,且时,,则函数的零点个数是()A.1 B.2 C.3 D.4二、填空题11. 若幂函数的图像过点,则__________.12. 已知函数,为自然对数的底数,则__________.13. 如图,直四棱柱的底面是边长为1的正方形,侧棱长,则异面直线与的夹角大小等于______.14. 直线与圆有交点,则实数的取值范围是__________.15. 函数的定义域为A,若且时总有,则称为单函数.例如,函数是单函数.下列命题:①函数是单函数;②函数是单函数;③若为单函数,且,则;④若函数在定义域内某个区间D上具有单调性,则一定是单函数. 其中真命题是(写出所有真命题的编号).三、解答题16. 已知函数(Ⅰ)画出函数的大致图象;(Ⅱ)写出函数的最大值和单调递减区间17. 设U= R,A={x |≤1},B= {x |2<x<5},C= {x|a≤x≤a+ 1}(a为实数).(1)求A∩B;(2)若B∪C=B,求a的取值范围.18. 如图,四棱锥中中,底面.底面为梯形,,,,,点在棱上,且.(Ⅰ)求证:平面平面;(Ⅱ)求三棱锥的体积.19. 已知函数是上的奇函数.(Ⅰ)求的值;(Ⅱ)判断并证明的单调性;(Ⅲ)若对任意实数,不等式恒成立,求的取值范围.。
湖南省郴州市2017-2018学年高一上学期期末考试数学试题Word版含解析

郴州市2017年下学期学科教学状况抽测试卷高一数学 (试题卷)、选择题:本大题共 10小题,每小题4分,共40分.在每小题给出的四个选项中,只有 项是符合题目要求的 1.已知集合.\ :. :. 1 : , T :匚匚:,()A. .B. :-二C.D.【答案】D【解析】「:•:「. :•: .■--;.!:, - ,•与 的公共元素为,.厂| = -门 故选D.-■■- -■-丨与点:1- - ■-关于()对称【答案】C 【解析】因为点与点三£ 二H 中,两个点的 值不变, 值与 值互为相反数,所以点- ■ ■■嗚与点 m - ■--关于 轴对称,故选C . 4.下列函数中,既不是奇函数也不是偶函数的是( )2 s 1A.厂B.C. ■/ - ::D. 厂【答案】B, 1【解析】对于 —=J 是偶函数,不合题意;对于 是奇函数,不合题意;对于,是奇函数,不合题意;对于 厂―「鼻i=,且 ,•: 即不是奇函数,又不是偶函数,合题意,故选 B.2.当 时,在同一坐标系中,函数-=:/与的图象是(aB. C. D.【解析】丫 , ■aI 「在定义域上递增,又 丫,::心护在定义域上递减,' 项符合题意,故选 C.A.原点B. 轴C. 轴D. 轴3.在空间直角坐标系中,点5•设•,卜:上“:., •则()A. . ..B. : 1■-C. h ;■ -D. [■ I- :L【答案】A【解析】根据指数函数的性质,.I | H I ,匕Ipf :-::/=「:■- :: ;i,即2 > J.'-,故选A.【方5去点睛】本题主要考查对数函数的性质、指数函数的单调性及比较大小问题r属于中档题*解答比较大小问题•常见思路有两个:一是判断出各个数值所在区间(一般是看三个区间(-co.ojXO.DXl. + «>));二是利用函数的单调性直接解答;数值比较多的比大小问题也可以两种方法综合应用*6. 设是一条直线,■:;,[■是两个不同的平面,则下列命题中正确的是()A.若〔丄二,,则,B. 若,,::挖,贝UC.若,,贝UD. 若I , ,则〕•丨【答案】D【解析】若I , ,则或’•,故错误;若,,则或:,故错误;若,,根据面面平行的性质可得]■ !',故错误,正确,故选D.7. 中国古代数学名著《九章算术)中记载了公元前344年商鞅督造一种标准量器一商鞅铜方升,其三视图如图所示(单位:寸),若可取3,其体积为12.6 (立方寸),则图中的为()卜-----5.4 ------- M y *iiTtoiwntA. 1.2B. 1.6C. 1.8D. 2.4【答案】B【解析】由三视图知,商鞅铜方升由一圆柱和一长方体组合而成,由题意得:;.■■■ ■.:■丨」;]i'-、匚.:■,,故选 B.8. 将正方形O二;沿对角线.折起成直二面角,贝U直线三:与平面所成的角的大小为()A. B. ■ - C. D.【答案】B【解析】设.中点为,连接是正方形,• m.v:,又:折起后it I•是直二面角.【二|平面乂:E,「是2C与平面所成的角,由正方形的性质,可得厲-■::.二‘-m是等腰直角三角形,,即丸;与平面所成的角为..,故选B.9. 已知函数是定义在上的奇函数,且在上是增函数,若实数满足:】l-:g;:I :,则实数的取值范围是()A. j ■二|B. -C. I'-. - ■- ■D. J.…::户【答案】C【解析】:函数是定义在上的奇函数,且在上是增函数,•在:一,|上递增,即在:一® 十心;上递增,一.:0上I • :i 「丨:,化为■: . :■-.! i- ■. : ..I ':■:■:■■ ■'-:'-1:I ' ' I-.二,实数的取值范围是| - ■■ ■,故选C.【方法点睛】本题主要考查抽象函数的奇偶性与单调性的应用,属于难题.将奇偶性与单调性综合考查,一直是命题的热点,解答这种题型往往是根据函数在所给区间上的单调性,利用奇偶性判断出函数在对称区间上的单调性(偶函数在对称区间上单调性相反,奇函数在对称区间单调性相同),然后再根据单调性列不等式求解.10. 已知函数是定义在的奇函数,且当时,匕;「I,则函数的零点个数是()A. 1B. 2C. 3D. 4【答案】C【解析】试题分析:由题意知〔;-1十一—;--1,当时,令;::= * =",即朋】,21 *x令g(冥)=2 (x < O),h(x)二尹 + l(x < 0) , '' g (0)= In2 a ㊁,二当x < 0时,与hb)有1个交点,即X丘0时ffx)有1个零点T又fix)是定义域为R的奇函数、所以函数有3个零点.考点:奇函数的性质、零点问题二、填空题:本大题共5小题,每小题4分,共20分.11..若幕函数y=£的图像过点(2, 8),则日=_________________ .【答案】3【解析】,幕函数的图像过点.•,;—=$*、,故答案为:.12. 已知函数f(x) = L于〔汇1),为自然对数的底数,则___________________.tlnxfx > I)【答案】3【解析】因为函数「7 :,所以• = =1,i i「l ■'宀故答案为:.【思路点睛】本题主要考查分段函数的解析式,属于中档题•对于分段函数解析式的考查是命题的动向之一,这类问题的特点是综合性强,对抽象思维能力要求高,因此解决这类题一定要层次清出,思路清晰•本题解答分两个层次:首先求出的值,进而得到的值•13. 如图,直四棱柱I T'1'i的底面是边长为1的正方形,侧棱长—「,则异面直线4Q与BDj的夹角大小等于____________ .【解析】试题分析:由直四棱柱fEH「匸匸二的底面是边长为1的正方形,侧棱长•…AB 1可得』_ 由■■- ' 1■- ' 'I知」;就是异面直线与的夹角,且■ ■■=:•-_ = 丁所以•三匸:.=60° ,即异面直线“匚:三:.与三二.的夹角大小等于60°.考点:1正四棱柱;2异面直线所成角14. _________________________________________________________________ 直线y=kx+l与圆(X-2卩十『二I有交点,则实数k的取值范围是_________________________________________ .【答案】[-->o【解析】'直线.-:■■■ - ' 1与圆•. - 2 ' ■. ' I有交点,■-圆心到直线,I -八…I的距离小于15. 函数 的定义域为,若, 且 时总有 ,则称 为和谐函数 例如,函数:■.丨「三‘是和谐函数.下列命题: ① 函数:■. I是和谐函数;I x>2② 函数旺x) = ];是和谐函数;x-2:x < 2③ 若 是和谐函数,,;' •—-£::,则<| 1 「:八.④ 若函数 在定义域内某个区间上具有单调性,则一定是和谐函数其中真命题是 ___________ (写出所有真命题的编号) 【答案】③【解析】试题分析:解:①令得:所以,心二-不是单函数;② 因为,所以八一;:-- •,故 不是单函数;③ 与定义是互为逆否命题,是真命题 根据①和②知:若函数 在定义域内某个区间 D 上具有单调性,则 不一定是单函数•所以④ 是假命题. 综上真命题只有:③;故答案应填③考点:1、函数的概念;2、新定义;3、函数的单调性;4、分段函数.三、解答题:本大题共 5小题,共40分,解答应写出文字说明,证明过程或演算步骤(兀X e [Q 2],16.已知函数(I) 画出函数 的大致图像; (n)写出函数的最大值和单调递减区间【答案】(1)见解析(2)的最大值为2.其单调递减区间为或 •或等于半径,即,解得,故答案为k十1 3和12 3【解析】试题分析:(I)禾U用描点法分别作出[jy与;的图象,即可得X到函数的大致图象;(n)根据图象可得函数的最大值和单调递减区间.试题解析:(I)函数的大致图象如图所示.(n)由函数的图象得出,的最大值为2.其单调递减区间为I二.T或17. 设:J—E,心一〔丁乜.;,M —:叩:*门,二―亠十v (为实数)(I)求.I(n)若三•「:_:-三,求的取值范围.【答案】⑴「帚;、…二(2):门2严【解析】试题分析:(I)根据指数函数的性质化简A = :: ■ <打,然后利用交集的定义求解即可;(n)由■■ ■< ■::--:•.得:,根据包含关系列出关于的不等式组求解,即可得到的取值范围.试题解析:(I):匚"I •••'「丨;:•:二•:::(n)由s..-< C-?.得 :•:即.三二軒18. 如图,四棱锥中厂⑴:I】中,底面":、.「.底面t、.T・为梯形,点曰圧,-■- : --二,丨:」厂,点在棱W上,且:「-■ ■ I-.(I)求证:平面KF 平面;(n)求三棱锥F:-的体积.【答案】(1)见解析(2)【解析】试题分析:(I)由面呂三二?可得I:: J IX,结合总三.E1:,利用线面垂直的判定定理可得B 面二*三,再根据面面垂直的判定定理可得平面二匚F 平面二二三;(n )过点,在平面牛三内作壬垂直于.,垂足为尺,由(I)可知丸底面応二,求出,禾U用等3积变换可得;'■ :-.1 根据棱锥的体积公式可得结果•试题解析:(I)证明:•••面=*「,•••■ FA又•••丨「丄.5,且W:- 2. /.B 面又•••;':■「面,•面;"’I 面(n)过点,在平面内作11垂直于,垂足为.由(I)可知刁底面EF 1 l•/ , •- PA 3V33又T 2“. ■ : ■- : -.11 氏厂P 3S AABC =~ X 1* 不==19・已知方程Ill ::(I )若此方程表示圆,求实数 ..的取值范围;(n )若(I )中的圆与直线 ---:相交于、 两点,且』〔c'i (为坐标原点)求实数…的值;(川)在(n )的条件下,求以 二茁为直径的圆的方程.24. ? 4 18【答案】 ⑴"■】;•(2)(3)【解析】试题分析:(1)将圆的方程化为标准方程,利用半径大于零,即可求解实数 .的取值范围;(2)直线方程与圆的方程联立,利用韦达定理及^ ,建立方程,即可求解实数 •的值;(3)写出以为直径的圆的方程,代入条件即可求解结论试题解析:(1)原方程化为、、「•'、、. - .■- 此方程表示圆, •—1. •门,二 山 .. (2)分(2)设心n ,, 则".'l- ■,得;h• s 」p 、:、:;.①x=4 2y2得x +y -2x-4y + m = 0* *16 S I m = … , 24•••「= ,「•;.=.,且丨:广「;:*: mi |,化为 m .. 代入①得:li ,满足1“ —5 5(3)以.为直径的圆的方程为即■-■';!'、、“、 1•••所求圆的方程为 s-y — 7. 考点:圆的综合问题【方法点晴】本题主要考查了圆的综合应用问题,其中解答中涉及到圆的标准方程,表示圆 的条件,直线与圆的位置关系的判定及应用等知识点的综合考查,着重考画出来学生分析问 题和解答问题的能力,以及转化与数形结合思想的应用,本题的解答中涉及圆的标准方程及 直线与圆的位置关系的判定方10分12分-11 -法,灵活应用圆的性质是解答的关键,试题比较解出属于基础口 . 2*_]20.已知函数是上的奇函数. I + 2X(I )求的值;(n )判断并证明 的单调性;(川)若对任意实数,不等式 ::,I' - m''恒成立,求.的取值范围• 【答案】⑴(2)见解析(3)a- 1【解析】试题分析:(I ) Kx )为R 上的奇函数,即一=0,由此得a=】;(n )设萨迪,2 2 2 2则,根据指数函数的性质可得 -------- -- ---- ;,即,\ 21-1戈'十2• 为 上的增函数;(川)不等式 —T :.;:」恒成立等价于,只2 + 12需求出的取值范围,即可得.的取值范围•2 + 1a - 1试题解析:(I ): 为上的奇函数,•,即,由此得 ;2“「1 2(n )由(1)知•••为上的增函数•2X + I2s - 122 2 2证明,设,则 :- 1-— :-— --------------------------- 一2 1十1 2言十1 2亠十1 2 1十I2 2••• ,.•• ,.••2+1 2-1 • 为上的增函数•(川)••• 为上的奇函数•••原不等式可化为丨-■ ■ J- 1',即 ;]二:"二;又••• 为上的增函数,• ',2由此可得不等式 ' -对任意实数恒成立2"+ 12由-12-2 2-2< --- ------ <0=^2 <4 --- ------ <42X + 1 2X + 1.•mW 2.【方法点睛】本题主要考查函数的奇偶性以及函数的单调性,属于中档题 •利用定义法判断函 数的单调性的一般步骤是:(1)在已知区间上任取 ;(2)作差;(3)判断 :的符号(往往先分解因式,再判断各因式的符号) 可得 在已知区间上是增函数,:十心可得 在已知区间上是减函数•- 11 -。
XXX2017-2018学年第一学期期末考试高一数学试卷

XXX2017-2018学年第一学期期末考试高一数学试卷XXX2017-2018学年第一学期期末考试高一年级数学试卷第I卷(选择题共40分)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.已知向量a=(2,1),b=(λ−1,2),若a+b与a−b共线,则λ=()A.−2B.−1C.1D.2改写:向量a=(2,1),向量b=(λ-1,2),若a+b和a-b共线,则λ=() A。
-2 B。
-1 C。
1 D。
22.已知3sinα+4cosα=2,则1-sinαcosα-cos2α的值是() A。
- B。
C。
-2 D。
2改写:已知3sinα+4cosα=2,求1-sinαcosα-cos2α的值,答案为() A。
- B。
C。
-2 D。
23.已知在△ABC中,AB=AC=1,BC=3,则AB·AC=() A。
1/33 B。
- C。
-2 D。
-改写:在△ABC中,AB=AC=1,BC=3,求XXX的值,答案为() A。
1/33 B。
- C。
-2 D。
-4.在△ABC中,若AB2=AB·AC+BA·BC+CA·CB,则△ABC是() A.锐角三角形B.钝角三角形C.直角三角形D.不确定改写:在△ABC中,如果AB2=AB·AC+BA·BC+CA·CB,则△ABC是() A.锐角三角形B.钝角三角形C.直角三角形D.不确定5.已知△ABC中,内角A,B,C所对边的边长分别为a,b,c,且c=7/11,a+b=22/3,XXX-tanA-tanB=3,则△ABC的面积为() A。
3/33 B。
- C。
3 D。
33/2改写:已知△ABC中,内角A,B,C所对边的边长分别为a,b,c,且c=7/11,a+b=22/3,XXX-tanB=3,求△ABC的面积,答案为() A。
3/33 B。
- C。
2017-2018高一数学上学期期末考试试题及答案

2017-2018学年度第一学期期末考试高一数学试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页,满分120分.考试限定用时100分钟.考试结束后,将本试卷和答题纸一并交回.答卷前,考生务必将自己的姓名、座号、考籍号分别填写在试卷和答题纸规定的位置.第Ⅰ卷(选择题 共48分)参考公式:1.锥体的体积公式1,,.3V Sh S h =其中是锥体的底面积是锥体的高 2.球的表面积公式24S R π=,球的体积公式343R V π=,其中R 为球的半径。
一、选择题:本大题共12小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集{0,1,2,3},{1,3}U A ==,则集合U C A = ( )A .{}0B .{}1,2C .{}0,2D .{}0,1,2 2.空间中,垂直于同一直线的两条直线 ( )A .平行B .相交C .异面D .以上均有可能3.已知幂函数()αx x f =的图象经过点错误!,则()4f 的值等于 ( )A .16B 。
错误!C .2D 。
错误!4。
函数()lg(2)f x x =+的定义域为 ( )A 。
(—2,1)B 。
[-2,1]C 。
()+∞-,2 D. (]1,2- 5.动点P 在直线x+y-4=0上,O 为原点,则|OP |的最小值为 ( )AB .CD .26.设m 、n 是两条不同的直线,α、β是两个不同的平面,则下列命题中正确的是 ( )A .若m ∥n ,m ∥α,则n ∥αB .若α⊥β,m ∥α,则m ⊥βC .若α⊥β,m ⊥β,则m ∥αD .若m ⊥n ,m ⊥α, n ⊥β,则α⊥βOOO O1 1117.设()x f 是定义在R 上的奇函数,当0≤x 时,()x x x f -=22,则()1f 等于 ( )A .-3B .-1C .1D .3 8.函数y =2-+212x x⎛⎫⎪⎝⎭的值域是 ( )A .RB .错误!C .(2,+∞)D 。
2017年湖南郴州中考数学试题(解析版)

2017年湖南省郴州市中考数学试卷满分:150分 版本:湘教版第Ⅰ卷(共60分)一、选择题(共8小题,每小题3分,共24分1. 2017的相反数是A ﹣2017B . 2017 C.20171 D. ﹣20171 答案:A ,解析:实数a 的相反数是﹣a .∴2017的相反数是﹣2017.2.下列图形既是轴对称图形又是中心对称图形的是答案:B ,解析:轴对称图形与中心对称图形研究的都是一个图形,识别轴对称图形的关键是找对称轴,若能找到对称轴就是轴对称图形;识别中心对称图形的关键是找旋转中心,若绕某一点旋转180度后能与自身重合,此图形就是中心对称图形.3.某市今年约有140000人报名参加初中学业水平考试,用科学计数法表示140000为A.14×104B.14×103C.1.4×104D.1.4×105答案:D ,解析:用科学记数法表示一个大于10的带单位的较大数,就是将其写成a ×10n 的形式,其中1≤a <10,n 的值为整数位数减1,所以140000=1.4×1054.下列运算正确的是A.()532a a =B.532a a a =⋅C.a a ﹣﹣=1D.(a +b )(a -b )=22b a + 答案:B ,解析:由()mn n ma a =知()632a a =,∴A 错误,由n m n m a a a +=⋅知532a a a =⋅,∴B 正确,由n n aa1=-知a a 11=-,∴C 错误,由平方差公式知(a +b )(a -b )=22b a -,∴D 错误. 5.在创建“全国园林城市期间”郴州市某中学组织共青团员去植树,其中七位同学植树的棵数分别为3,1,1,3,2,3,2,则这则数据中的中位数和众数分别是A B C DA.3,2B.2,3C.2,2D.3,3答案:B ,解析:中位数就是将一组数据按从小到大的顺序排列,处于最中间的一个数(数据个数为奇数)或两个数的平均数(数据个数为偶数);一组数据中出现次数最多的数即为众数.6.已知反比例函数y=x k 的图象经过点A (1,﹣2),则k 的值为 A .1 B.2 C .﹣2 D.﹣1答案:C ,解析:求k 的值,实际就是求反比例函数解析式,将点的坐标代入即可.∵反比例函数y =x k 的图象过点(1,-2),∴-2=1k ,解得k=-2. 7.如图(1)所示的圆锥的主视图是答案:A ,解析:主视图就是从几何体的正面得到的投影,本题中主视图反映的是圆锥的高和底面圆的直径,∴A 符合.8.小明把一幅含45°,30°的直角三角板如图摆放,其中∠C =∠F =90°,∠A =45°,∠D =30°,则∠α+∠β等于A .180°B .210° C. 360° D.270°答案:B 解析:如图,不妨设AB 与DE 交于点G ,由三角形的外角性质可知:∠α=∠A +∠AGD ,∠β=∠B +∠BHF ,由于∠AGD =∠EGH ,∠BHF =∠EHG ,所以∠AGD +∠BHF =∠EGH +∠EHG =180°-∠E =180°-(90°-∠D )=120°,所以∠α+∠β=∠A +∠B +∠AGD +∠BHF =90°+120°=210°,故选B .·αBA FCED β第Ⅱ卷(共90分)二、填空题(每题8分,满分24分,将答案填在答题纸上)9.在平面直角坐标系中,把点A (2,3)向左平移一个单位得到点Aʹ,则点Aʹ的坐标为 . 答案:(1,3)解析:点的平移规律是“左减右加,上加下减”,∴A (2,3)向左平移一个单位得到点Aʹ的坐标是(1,3).10.函数y=1 x 的自变量x 的取值范围是 .答案:x ≥-1,解析:二次根式有意义的条件知x+1≥0,解得x ≥-1.11.把多项式3x 2-12因式分解的结果是 .答案:3(x -2)(x +2),解析:先提取公因式3,再根据平方差公式进行二次分解即可求得答案,注意分解要彻底.12.为从甲乙两名射击运动员中选出一人参加竞标赛,特统计了他们最近10次射击训练的成绩,其中,他们射击的平均成绩为8.9环,方差分别是S 2甲=0.8,S 2乙=13,从稳定性的角度来看, 的成绩更稳定.(填“甲”或“乙”)答案:甲,解析:方差是反映一组数据波动情况的统计量,反差越大,越波动,方差越小,越稳定.S 2甲<S 2乙,所以甲的成绩更稳定.13.如图,直线EF 分别交AB ,CD 于点E ,F ,且AB ∥CD ,若∠1=60°,则∠2 . 答案:120°,解析:由平行线的性质结合图形可知:∠2与∠1的一个邻补角是同位角,相等,∴∠2=180-∠1=180°-60°=120°.14.已知圆锥的母线长为5cm ,高为4cm ,则该圆锥的侧面积为 cm 2(结果保留π). 答案:15π 解析:由圆锥的侧面积公式“圆锥的侧面积=底面周长×母线长÷2”即求出侧面积.∵圆锥的母线长为5cm ,高为4cm ,∴它的底面半径=3cm ,因此圆锥的底面周长=6π,B AE DF C 1 2∴圆锥的侧面积=6π×5÷2=15π.15.从1,﹣1,0三个数中任取两个不同的数作为点的坐标,则该点在坐标轴上的概率是 .答案:32,解析:本题是两步概率问题,借助树状图或列表解决,画树状图如下:可见从三个数中任取两个不同的数作为点的坐标共有6种情况,其中点在坐标轴上的有4种,所以该点在坐标轴上的概率64=32. 16.已知a 1=﹣23,a 2=55,a 3=﹣107,a 4=179,a 5=﹣2611,…… ,则a 8= . 答案:6517,解析:由前5项可得a n =(-1)n ·1122++n n ,当n =8时,a 8=(-1)8·181822++⨯=6517. 三、解答题 (1719题每题6分,2023题每题8分,2425题每题10分,26题12分,共计82分)17.计算:2sin30°+(π-3.14)0+21-+(﹣1)2017.思路分析:先由特殊角的三角函数值、零指数幂的意义、绝对值的意义、乘方的意义对原式化简,在进行实数的运算.解:2sin30°+(π-3.14)0+21-+(﹣1)2017 =2×21+1+2-1-1 =218.先化简,再求值96312---a a ,其中a =1. 思路分析:先对第二个分式的分母因式分解,再找最简公分母,通分,约分化成最简分式,将数值代入求出分式的值.45解:96312---a a =()()33631+---a a a =()()3363+--+a a a =31+a ,当a =1时,原式=41311=+. 19.已知△ABC 中,∠ABC =∠ACB ,点D ,E 分别为边AB ,AC 的中点,求证:BE =CD .思路分析:利用同一三角形中等角对等边说明AB =AC ,再利用中点的性质说明BD =CE ,进而判断△BDC 和△CEB 全等,然后利用全等三角形的性质说明BE =CD .证明:∵∠ABC =∠ACB ,∴AB=AC ,∵点D ,E 分别为边AB ,AC 的中点,∴BD =CE ,在△BDC 和△CEB 中,BD =CE ,∠ABC =∠ACB ,BC=CB ,∴△BDC ≌△CEB ,∴BE =CD .20.某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问题卷调查,调查结果为“A 非常了解”、“B 了解”、“C 基本了解”三个等级,并根据调查结果制作了如下两幅不完整的统计图.(1)这次调查的市民人数为 人,m = ,n = ;(2)补全条形统计图;(3)若该市约有市民1 000 000人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A 非常了解”的程度.· C m % A n % B 56 % AED C B思路分析:(1)根据B 类人数以及B 类所占的百分比可求出总人数,再根据C 类人数占总人数的百分比求得m ,进而求得n ;(2)用A 类人数占总人数的百分比求得A 类人数,从而补全条形统计图;(3)利用样本中A 类人数所占百分比来估计总体中的百分比,从而求出A 类的人数.解:(1)调查总人数=280÷56%=500(人)由于50060×100%=12%,所以m =12 又1-56%-12%=32%,所以n =32故答案为:500, 12, 32(2)由于500×32%=160(人)补全的条形统计图如下:(3)100000×32%=32000(人)因此该市大约有32000人对“社会主义核心价值观”达到“A 非常了解”的程度.21.某工厂有甲种原料130kg ,乙种原料144kg ,现用两种原料生产出A 、B 两种产品共30件,已知生产每件A 产品需甲种原料5kg ,乙种原料4kg ,且每件A 产品可获得700元;生产每件B 产品甲种原料3kg ,乙种原料6kg ,且每件B 产品可获利润900元,设生产A 产品x 件(产品件数为整数件),根据以上信息解答下列问题:(1)生产A 、B 两种产品的方案有哪几种?(2)设生产这30件产品可获利y 元,写出关于x 的函数解析式,写出(1)中利润最大的方案,并求出最大利润.思路分析:(1)由A ,B 两种产品所需甲、乙两种原料的范围,可得出关于x 的一元一次不等式组,解之即可得出x 的取值范围,从而得生产方案;(2)再根据A 、B 两种产品的获利情况,求出y 与x 的函数关系(总利润y =700×A 产品件数+900×B 产品件数),然后利用一次函数的性质即可得出y 的最大值,并选取该方案即可.解:(1)由30件产品中由x 件A 产品,知B 产品有(30-x )件,由题意可得:()()⎩⎨⎧≤-+≤-+14430641303035x x x x ,解得⎩⎨⎧≥≤1820x x ,∴18≤x ≤20,∵产品件数为整数件,∴x 取整数解,∴x=18或x=19或x=20,∴生产A 、B 两种产品的方案有如下三种:方案一:A 产品18件,B 产品12件;方案二:A 产品19件,B 产品11件;方案三:A 产品20件,B 产品10件;(2)由题意可得y=700x +900(30-x )=﹣200x +27 000,∵﹣200<0,y 随x 的增大而减小,又∵18≤x ≤20,∴当x=18时有最大利润,最大利润y=﹣200×18+27 000=23 400,答:利润最大的方案是(1)中的方案一,即:A 产品18件,B 产品12件,最大利润为23 400元.22.如图所示,C 城市在A 城市正东方向,现计划在A 、C 两城市间修建一条高速铁路(即线段AC ),经测量,森林保护区的中心P 在城市A 的北偏东60°方向上,在线段AC 上距A 城市120km 的B 处测得P 在北偏东30°方向上,已知森林保护区是以点P 为圆心,100km为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?(参考数据:1.732=)思路分析:要判断高速铁路是否穿越保护区实际就是判断点P 到线段AC 的最短距离与100的大小关系,若大于,则不穿过,反之穿过.∴过点P 作PH ⊥AC ,通过解直角三角形求得PH 的长.从而判断出这条高速公路会不会穿越保护区.解:如图,过点P 作PH ⊥AC ,交AC 于点H ,C北东由题意得∠EAP=60°,∠FBP=30°,∴∠PAB=30°,∠PBH=60°,∴∠APB=30°,∴AB=PB=120,∴在Rt △PBH 中,PH=PBsin ∠PBH=120×sin60°=603≈103.80,∵103.80>100,∴要修建的这条高速铁路不会穿过森林保护区.23. 如图,AB 是⊙O 的弦,BC 切⊙O 于点B ,AD ⊥BC 垂足为D ,OA 是⊙O 的半径,且OA =3.(1)求证:AB 平分∠OAD ;(2)若点E 是优弧AEB 上一点,且∠AEB =60°,求扇形OAB 的面积(计算结果保留π)思路分析:(1)连接OB ,由切线性质知OB ⊥BC ,结合AD ⊥BC 得AD ∥OB ,即可知∠DAB=∠OBA=∠OAC ,从而得证;(2)点E 是优弧AEB 上一点,且∠AEB =60°,再利用扇形面积公式可求扇形OAB 的面积.解:(1)如图,连结OB ,∵BC 切⊙O 与点B ,·OA DC BE∴OB ⊥BC ,∵AD ⊥BC ,∴AD ∥OB ,∴∠DAB =∠OBA ,∵OA=OB ,∴∠OAB=∠OBA ,∴∠DAB =∠OAB ,∴AB 平分∠OAD ;(2)点E 在弧AEB 上,且∠AEB =60°,∴∠AOB=120°,∴S 扇形OAB =︒︒360120×π×AO 2=31×π×32=3π. 24. 设a ,b 是任意两个实数,用max {a ,b }表示a ,b 两数中较大者,例如:max {﹣1,﹣1}=﹣1,max {1,2}=2,max {4,3}=4,参照上面的材料,解答下列问题:(1)max {5,2}= ,max {0,3}= ;(2)若max {3x +1,﹣x +1}=﹣x +1,求x 的取值范围;(3)求函数y =x 2-2x -4与y =﹣x +2的图象的交点坐标,函数y =x 2-2x -4的图象如下图所示,请你在下图中作出函数y =﹣x +2的图象,并根据图象直接写出max {﹣x +2,x 2-2x +4}的最小值.思路分析:(1)比较5和2、0和3的大小关系即可求得答案;(2)若max {3x +1,-x+1}=-x +1得,-x +1≥3x+1,由此可求得答案;(3)求得抛物线与直线的交点坐标,再利用新定义确定max {-x +2,x 2-2x +4}的最小值.解:(1)5,3;。
2017-2018学年湖南省郴州市高一(上)期末数学试卷(解析版)
2017-2018学年湖南省郴州市高一(上)期末数学试卷一、选择题(本大题共10小题,共40.0分)1.已知集合A={x∈N|1≤x≤4},B={-2,2},A∩B=()A. {1,2}B. {−2}C. {−2,2}D. {2})x与y=log a x的图象是()2.当0<a<1时,在同一坐标系中,函数y=(1aA. B.C. D.3.在空间直角坐标系中,点A(2,-2,4)与点B=(-2,-2,-4)关于()对称A. 原点B. x轴C. y轴D. z轴4.下列函数中,既不是奇函数也不是偶函数的是()A. y=x2B. y=2xC. y=xD. y=1x5.设a=30.1,b=log90.1,c=0.30.2,则()A. a>c>bB. a>b>cC. b>a>cD. b>c>a6.设l是一条直线,α,β是两个不同的平面,则下列命题中正确的是()A. 若l⊥α,α⊥β,则l⊂βB. 若l//α,α//β,则l//βC. 若l⊥α,α//β,则l//βD. 若l⊥α,α//β,则l⊥β7.中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为()A. 1.2B. 1.6C. 1.8D. 2.48.将正方形ABCD沿对角线AC折起成直二面角,则直线BD和平面ABC所成的角的大小为()A. 30∘B. 45∘C. 60∘D. 90∘9. 已知函数f (x )是定义在R 上的奇函数,且在[0,+∞)上是增函数,若实数a 满足3f (log 2a )+f (-log 2a )≥2f (1),则实数a 的取值范围是( )A. (0,2]B. (−∞,2]C. [2,+∞)D. [1,+∞)10. 已知函数f (x )是定义在R 的奇函数,且当x ≤0时,f(x)=2x −12x −1,则函数f(x )的零点个数是( )A. 1B. 2C. 3D. 4 二、填空题(本大题共5小题,共20.0分)11. .若幂函数y =x a 的图象过点(2,8),则a =______.12. 已知函数f(x)={lnx(x >1)3x (x≤1),e 为自然对数的底数,则f [f (e )]=______.13. 如图,直四棱柱ABCD -A 1B 1C 1D 1的底面是边长为1的正方形,侧棱长AA 1=√2,则异面直线A 1B 1与BD 1的夹角大小等于______.14. 直线y =kx +1与圆(x -2)2+y 2=1有交点,则实数k 的取值范围是______.15. 函数f (x )的定义域为A ,若x 1,x 2∈A 且f (x 1)=f (x 2)时总有x 1=x 2,则称f (x )为和谐函数.例如,函数f (x )=x +1(x ∈R )是和谐函数.下列命题:①函数f (x )=x +1(x ∈R )是和谐函数;②函数f(x)={log 12x ,x ≥2x −2,x <2是和谐函数;③若f (x )是和谐函数,x 1,x 2∈A 且x 1≠x 2,则f (x 1)≠f (x 2).④若函数f (x )在定义域内某个区间D 上具有单调性,则f (x )一定是和谐函数. 其中真命题是______(写出所有真命题的编号)三、解答题(本大题共5小题,共40.0分)16. 已知函数f (x )={x ,x ∈[0,2]4x,x ∈(2,4]. (Ⅰ)画出函数f (x )的大致图象;(Ⅱ)写出函数f (x )的最大值和单调递减区间17.设U=R,A={x|2x-3≤1},B={x|2<x<5},C={x|a≤x≤a+1}(a为实数).(Ⅰ)求A∩B;(Ⅱ)若B∪C=B,求a的取值范围.18.如图,四棱锥中P-ABCD中,PA⊥底面ABCD.底面ABCD为梯形,AB∥DC,AB⊥BC,AC=DC=2AB=2,PA=√3,点E在棱PB上,且PE=2EB.(Ⅰ)求证:平面PAB⊥平面PCB;(Ⅱ)求三棱锥A-BCE的体积.19.已知方程x2+y2-2x-6y+m=0.(Ⅰ)若此方程表示圆,求实数m的取值范围;(Ⅱ)若(Ⅰ)中的圆与直线x+2y-4=0相交于M、N两点,且OM⊥ON(O为坐标原点)求实数m的值;(Ⅲ)在(Ⅱ)的条件下,求以MN为直径的圆的方程.20.已知函数f(x)=a⋅2x−1是R上的奇函数.1+2x(Ⅰ)求a的值;(Ⅱ)判断并证明f(x)的单调性;(Ⅲ)若对任意实数,不等式f[f(x)]+f(3-m)>0恒成立,求m的取值范围.答案和解析1.【答案】D【解析】解:∵集合A={x∈N|1≤x≤4}={1,2,3,4},B={-2,2},∴A∩B={2}.故选:D.先求出集合A,由此能求出A∩B.本题考查交集的求法,考查交集定义、不等式性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.2.【答案】C【解析】解:当0<a<1时,函数y=是增函数,过(0,1),函数y=log a x是减函数,过(1,0).由题意可得两个函数的图象是选项C.故选:C.利用指数函数以及对数函数的图象与性质判断即可.本题考查指数函数与对数函数的图象与性质的应用,基本知识的考查.3.【答案】C【解析】解:在空间直角坐标系中,点A(2,-2,4)与点B=(-2,-2,-4)关于y轴对称.故选:C.在空间直角坐标系中,点A(a,b,c)与点(-a,b,-c)关于y轴对称.本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是基础题.4.【答案】B【解析】解:根据题意,依次分析选项:对于A,y=x2,为二次函数,是偶函数,不符合题意;对于B,y=2x,为指数函数,既不是奇函数也不是偶函数,符合题意;对于C,y=x,为正比例函数,是奇函数,不符合题意;对于D,y=,为反比例函数,是奇函数,不符合题意;故选:B.根据题意,依次分析选项中函数的奇偶性,综合即可得答案.本题考查函数的奇偶性的判断,关键是掌握函数奇偶性的定义,属于基础题.5.【答案】A【解析】解:∵a=30.1>1,b=log90.1<0,c=0.30.2∈(0,1).∴a>c>b.故选:A.利用指数函数与对数函数的单调性即可得出.本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.6.【答案】D【解析】解:由l是一条直线,α,β是两个不同的平面,知:在A中,若l⊥α,α⊥β,则l与β相交、平行或l⊂β,故A错误;在B中,若l∥α,α∥β,则l∥β或l⊂β,故B错误;在C中,若l⊥α,α∥β,则l⊥β,故C 错误;在D中,若l⊥α,α∥β,则由线面垂直的判定定理得l⊥β,故D正确.故选:D.在A中,l与β相交、平行或l⊂β;在B中,l∥β或l⊂β;在C中,l⊥β;在D中,由线面垂直的判定定理得l⊥β.本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,是中档题.7.【答案】B【解析】解:由三视图知,商鞅铜方升由一圆柱和一长方体组合而成.由题意得:(5.4-x)×3×1+π•()2x=12.6,解得:x=1.6.故选:B.由三视图知,商鞅铜方升由一圆柱和一长方体组合而成.利用体积求出x.本题考查三视图,考查体积的计算,确定直观图是关键.8.【答案】B【解析】解:如图,当平面BAC⊥平面DAC时,取AC的中点E,则BE⊥平面DAC,故直线BD和平面ABC所成的角为∠DBE,cos∠DBE==,∴∠DBE=45°.故选:B.当平面BAC⊥平面DAC时,取AC的中点E,则BE⊥平面DAC,故直线BD 和平面ABC所成的角为∠DBE,由此能求出结果.本题考查直线与平面所成角的求法,是中档题,解题时要注意空间思维能力的培养.9.【答案】C【解析】解:根据题意,函数f(x)是定义在R上的奇函数,且在[0,+∞)上是增函数,则f(x)在(-∞,0]在R上为增函数,则f(x)在R上增函数,函数f(x)是定义在R上的奇函数,则3f(log2a)+f(-log2a)=3f(log2a)-f(log2a)=2f(log2a),则3f(log2a)+f(-log2a)≥2f(1)⇒f(log2a)≥f(1),又由函数f(x)为R上的增函数;则3f(log2a)+f(-log2a)≥2f(1)⇒log2a≥1,解可得:a≥2,即实数a的取值范围为[2,+∞);故选:C.根据题意,分析可得f(x)在R上增函数,由函数的奇偶性可得3f(log2a)+f (-log2a)≥2f(1)⇒f(log2a)≥f(1),结合函数的单调性可得log2a≥1,解可得a的取值范围,即可得答案.本题考查函数的奇偶性与单调性的综合应用,注意得到关于x的不等式,属于基础题.10.【答案】C【解析】解:函数f(x)是定义在R的奇函数,可得f(0)=0,且f(x)的图象关于原点对称,由x<0时,f(x)=0,即为2x=1+x,由f(0)=0,f(-1)=0.5+0.5-1=0,可得x<0时,f(x)只有有个零点;x>0时,f(x)只有一个零点.则f(x)共有3个零点.故选:C.由奇函数在R上f(0)=0,作出y=2x,y=1+x的图象,结合奇函数的图象关于原点对称,可得所求零点个数.本题考查函数的奇偶性和零点的个数,注意运用方程思想和转化思想,考查数形结合思想方法,属于基础题.11.【答案】3【解析】解:∵幂函数y=x a的图象过点(2,8),∴2a=8,解得a=3.故答案为:3.由幂函数y=x a的图象过点(2,8),推导出2a=8,由此能求出a的值.本题考查实数值的求法,考查幂函数的性质、运算法则等基础知识,考查运算求解能力,是基础题.12.【答案】3【解析】解:根据题意,函数,则f(e)=lne=1,则f[f(e)]=f(1)=3;故答案为:3根据题意,由函数的解析式计算f(e)的值,进而计算f[f(e)]的值,即可得答案.本题考查分段函数的求值,注意分段函数解析式的形式,属于基础题.13.【答案】π3【解析】解:连接BC1,∵A1B1∥C1D1,∴∠BD1C1为异面直线A1B1与BD1所成的角,∵直四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,∴C1D1⊥平面BCC1B1,∴C1D1⊥BC1,在Rt△BC1D1中,BC1=,tan∠BD1C1==,∠BD1C1=.故答案是根据异面直线所成角的定义,证明已知角为异面直线所成的角,再解三角形求角即可.本题考查异面直线所成的角.异面直线所成的角的求法是:1、作角(作平行线);2、证角(符合定义);3、求角(解三角形).14.【答案】[-4,0]3【解析】解:圆(x-2)2+y2=1的圆心坐标为(2,0),半径为1.由圆心到直线y=kx+1的距离d=≤1,解得-≤k≤0.∴实数k的取值范围是[-,0].故答案为:[-,0].由已知圆的方程求得圆心坐标与半径,再由圆心到直线的距离小于等于半径列式求得实数k的取值范围.本题考查直线与圆位置关系的应用,考查点到直线的距离公式,是基础题.15.【答案】①③【解析】解:函数f(x)=x+1(x∈R)满足f(x1)=f(x2)时总有x1=x2,故f(x)是和谐函数,故①正确;函数,由x<2,f(x)递减,x>2时f(x)递增,且f(2)=f(1)=-1,故f(x)不是和谐函数,故②错误;若f(x)是和谐函数,x1,x2∈A且x1≠x2,则f(x1)≠f(x2),故③正确;若函数f(x)在定义域内某个区间D上具有单调性,比如函数,由x<2,f(x)递减,x>2时f(x)递增,则f(x)不一定是和谐函数,故④错误.故答案为:①③.由和谐函数的定义即可判断①;由f(2)=f(1)=-1,结合和谐函数的定义即可判断②;由原命题和其逆否命题等价可判断③;考虑②的函数可判断④.本题考查新定义的理解和运用,考查函数的单调性,主要是对数函数的单调性,考查判断能力,属于基础题.16.【答案】解:(Ⅰ)函数f(x)的大致图象如图所示.(Ⅱ)由函数f(x)的图象得出,f(x)的最大值为2.其单调递减区间为[2,4]或(2,4].【解析】(Ⅰ)根据解析式和定义域范围画图即可;(Ⅱ)通过图象即可写出函数f(x)的最大值和单调递减区间.本题考查了函数图象作图能力和对图象单调性的认识,是基础题.17.【答案】解:(Ⅰ)∵2x-3≤1∴x≤3,∴A∩B={x|2<x≤3};(Ⅱ)由B∪C=B得C⊆B,∴{a+1<5a>2即2<a<4,∴a∈(2,4).【解析】(Ⅰ)先确定集合A,然后直接利用交集运算得答案;(Ⅱ)由B∪C=B得C⊆B得即2<a<4.本题主要考查集合的基本运算,利用集合的关系是解决本题的关键.18.【答案】(Ⅰ)证明:∵PA⊥面ABCD,∴BC⊥PA,又∵BC⊥AB,且AB∩PA=A.∴BC⊥面PAB,又∵BC⊂面PBC,∴面PBC⊥面PAB,(Ⅱ)解:过点E,在平面PAB内作EF垂直于AB,垂足为F.由(Ⅰ)可知EF⊥底面ABCD∵EF PA =13,PA=√3,∴EF=√33.又∵V A-BCE=V E-ABCS△ABC=12×1×√3=√32.∴V A−BCE=V E−ABC=13×√32×√33=16.【解析】(Ⅰ)证明BC⊥PA,结合BC⊥AB,推出BC⊥面PAB,即可证明面PBC⊥面PAB,(Ⅱ)过点E,在平面PAB内作EF垂直于AB,垂足为F.通过V A-BCE=V E-ABC 转化求解即可.本题考查直线与平面垂直的判断定理的应用,几何体的体积的求法,考查空间想象能力以及计算能力.19.【答案】解.(Ⅰ)根据题意,方程x2+y2-2x-6y+m=0,变形可得(x-1)2+(y-3)2=10-m,若此方程表示圆,必有10-m>0,解可得:m<10;(Ⅱ)设M(x1,y1),N(x2,y2),则x1=4-2y1,x2=4-2y2,x1x2=16-8(y1+y2)+4y1y2又由OM⊥ON,则x1x2+y1y2=0即16-8(y1+y2)+5y1y2=0①由{x2+y2−2x−6y+m=0x=4−2y得5y2-18y+m+8=0,所以y1+y2=185,y1y2=m+85,代入①得m=245,(Ⅲ)以MN为直径的圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)=0,即x2+y2-(x1+x2)x-(y1+y2)y=0,所以所求圆的方程为x2+y2−45x−185y=0.【解析】(Ⅰ)根据题意,方程x2+y2-2x-6y+m=0,变形可得(x-1)2+(y-3)2=10-m,由圆的标准方程形式分析可得10-m >0,解可得m 的值,(Ⅱ)设M (x 1,y 1),N (x 2,y 2),由M 、N 在直线上分析可得x 1=4-2y 1,x 2=4-2y 2,则x 1x 2=16-8(y 1+y 2)+4y 1y 2,又由OM ⊥ON ,分析可得16-8(y 1+y 2)+5y 1y 2=0①,联立直线与圆的方程,分析可得5y 2-18y+m+8=0,结合根与系数的关系分析可得,,代入①式中分析可得答案; (Ⅲ)由已知直径端点的圆的方程的形式分析可得要求圆的方程为(x-x 1)(x-x 2)+(y-y 1)(y-y 2)=0,变形可得答案.本题考查直线与圆方程的应用,涉及直线与圆的位置关系,注意将圆的一般方程的形式,属于综合题.20.【答案】解:(Ⅰ)∵f (x )为R 上的奇函数,∴f (0)=0,即a−12=0,由此得a =1 (Ⅱ)由(1)知f(x)=2x −12x +1=1−22x +1∴f (x )为R 上的增函数. 证明,设x 1<x 2,则f(x 1)−f(x 2)=1−22x 1+1−(1−22x 2+1)=22x 2+1−22x 1+1∵x 1<x 2,∴22x 2+1−22x 1+1<0,∴f (x 1)<f (x 2)∴f (x )为R 上的增函数.(Ⅲ)∵f (x )为R 上的奇函数.∴原不等式可化为f [f (x )]>-f (3-m ),即f [f (x )]>f (m -3)又∵f (x )为R 上的增函数,∴f (x )>m -3,由此可得不等式m <f(x)+3=4−22x +1对任意实数x 恒成立由2x >0⇒2x +1>1⇒0<22x +1<2⇒−2<−22x +1<0⇒2<4−22x +1<4 ∴m ≤2【解析】(Ⅰ)利用函数是奇函数,通过f (0)=0,求a 的值;(Ⅱ)利用函数的单调性的定义判断并证明f (x )的单调性;(Ⅲ)若对任意实数,不等式f[f (x )]+f (3-m )>0恒成立,按照m 集项,通过函数的单调性,转化求m 的取值范围.本题考查函数恒成立条件的应用,考查函数的单调性以及函数的奇偶性的应用,转化思想的应用.。
2017-2018学年高一下学期期末考试数学试题(A卷)
第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 以下程序中,输出时的值是输入时的值的()A. 1倍B. 2倍C. 3倍D. 4倍【答案】D【解析】令初始值A=a,则A=2(a+a)=4a.故选D.2. 已知数列是等比数列,,且,,成等差数列,则()A. 7B. 12C. 14D. 64【答案】C【解析】分析:先根据条件解出公比,再根据等比数列通项公式求结果.详解:因为,,成等差数列,所以所以,选C.点睛:本题考查等比数列与等差数列基本量,考查基本求解能力.3. 将1000名学生的编号如下:0001,0002,0003,…,1000,若从中抽取50个学生,用系统抽样的方法从第一部分0001,0002,…,0020中抽取的号码为0015时,抽取的第40个号码为()A. 0795B. 0780C. 0810D. 0815【答案】A【解析】分析:先确定间距,再根据等差数列通项公式求结果.详解:因为系统抽样的方法抽签,所以间距为所以抽取的第40个数为选A.点睛:本题考查系统抽样概念,考查基本求解能力.4. 已知动点满足,则的最大值是()A. 50B. 60C. 70D. 90【答案】D【解析】分析:先作可行域,根据图像确定目标函数所代表直线取最大值时得最优解.详解:作可行域,根据图像知直线过点A(10,20)时取最大值90,选D,点睛:线性规划的实质是把代数问题几何化,即数形结合的思想.需要注意的是:一,准确无误地作出可行域;二,画目标函数所对应的直线时,要注意与约束条件中的直线的斜率进行比较,避免出错;三,一般情况下,目标函数的最大或最小值会在可行域的端点或边界上取得.5. 若干个人站成一排,其中为互斥事件的是()A. “甲站排头”与“乙站排头”B. “甲站排头”与“乙不站排头”C. “甲站排头”与“乙站排尾”D. “甲不站排头”与“乙不站排尾”【答案】A【解析】试题分析:事件A与事件B互斥,其含义是:事件A与事件B在任何一次试验中不会同时发生。
高一数学上学期期末考试试题(含解析)-人教版高一全册数学试题
某某省实验中学2017-2018学年高一数学上学期期末考试试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,,则()A. B. C. D.【答案】A【解析】则故选2. 直线的倾斜角是()A. B. C. D.【答案】C【解析】直线的斜率为直线的倾斜角为:,可得:故选3. 计算,其结果是()A. B. C. D.【答案】B【解析】原式故选4. 已知四面体中,,分别是,的中点,若,,,则与所成角的度数为()A. B. C. D.【答案】D【解析】如图,取的中点,连接,,则,(或补角)是与所成的角,,,,,而故选5. 直线在轴上的截距是()A. B. C. D.【答案】B【解析】直线在轴上的截距就是在直线方程中,令自变量,直线在轴上的截距为故选6. 已知,是两个不同的平面,给出下列四个条件:①存在一条直线,使得,;②存在两条平行直线,,使得,,,;③存在两条异面直线,,使得,,,;④存在一个平面,使得,.其中可以推出的条件个数是()A. 1B. 2C. 3D. 4【答案】B【解析】当,不平行时,不存在直线与,都垂直,,,故正确;存在两条平行直线,,,,,,则,相交或平行,所以不正确;存在一个平面,使得,,则,相交或平行,所以不正确;故选7. 已知梯形是直角梯形,按照斜二测画法画出它的直观图(如图所示),其中,,,则直角梯形边的长度是()A. B. C. D.【答案】B【解析】根据斜二测画法,原来的高变成了方向的线段,且长度是原高的一半,原高为而横向长度不变,且梯形是直角梯形,故选8. 经过点的直线到,两点的距离相等,则直线的方程为()A. B.C. 或D. 都不对【答案】C【解析】当直线的斜率不存在时,直线显然满足题意;当直线的斜率存在时,设直线的斜率为则直线为,即由到直线的距离等于到直线的距离得:,化简得:或(无解),解得直线的方程为综上,直线的方程为或故选9. 已知函数的图象与函数(,)的图象交于点,如果,那么的取值X围是()A. B. C. D.【答案】D【解析】由已知中两函数的图象交于点,由指数函数的性质可知,若,则,即,由于,所以且,解得,故选D.点睛:本题考查了指数函数与对数函数的应用,其中解答中涉及到指数函数的图象与性质、对数函数的图象与性质,以及不等式关系式得求解等知识点的综合考查,着重考查了学生分析问题和解答问题的能力,本题的解答中熟记指数函数与对数函数的图象与性质,构造关于的不等式是解答的关键,试题比较基础,属于基础题.10. 矩形中,,,沿将矩形折成一个直二面角,则四面体的外接球的体积是()A. B. C. D.【答案】B【解析】由题意知,球心到四个顶点的距离相等,球心在对角线上,且其半径为长度的一半为故选11. 若关于的方程在区间上有解,则实数的取值X围是()A. B. C. D.【答案】A【解析】由题意可得:函数在区间上的值域为实数的取值X围是故选点睛:本小题考查的是学生对函数最值的应用的知识点的掌握。
湖南省郴州市高一数学上学期期末试卷(含解析)-人教版高一全册数学试题
某某省某某市2014-2015学年高一上学期期末数学试卷一、选择题(每小题4分,共40分)1.(4分)若集合A={x|﹣2≤x<1},B={x|0<x≤2},则A∩B=()A.{x|﹣2≤x≤2}B.{x|﹣2≤x<0} C.{x|0<x<1} D.{x|1<x≤2}2.(4分)下列函数中,在R上单调递减的是()A.y=|x| B.y=log2x C.y=x D.y=()x3.(4分)函数f(x)=的定义域为()A.③若m⊥α,m∥β,则α⊥β.其中真命题的个数是()A.0 B.1 C.2 D.36.(4分)三视图如图的几何体的全面积是()A.B.C.D.7.(4分)已知正三棱锥的侧棱长是底面边长的2倍,则侧棱与底面所成角的余弦值等于()A.B.C.D.8.(4分)函数f(x)=log3x﹣8+2x的零点一定位于区间()A.(5,6)B.(3,4)C.(2,3)D.(1,2)9.(4分)设点P是Z轴上一点,且点P到M(1,0,2)与点N(1,﹣3,1)的距离相等,则点P的坐标是()A.(﹣3,﹣3,0)B.(0,0,3)C.(0,﹣3,﹣3)D.(0,0,﹣3)10.(4分)设r>0,两圆(x﹣1)2+(y+3)2=r2与x2+y2=16可能()A.相离B.相交C.内切或内含或相交D.外切或外离二、填空题(每小题4分,共20分)11.(4分)如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于.12.(4分)已知点A(1,2)、B(3,1),则线段AB的垂直平分线的方程是.13.(4分)已知函f(x)=,则f(f())=.14.(4分)若f(x)为奇函数,当x<0时,f(x)=x2+ax,且f(3)=6,则实数a的值为.15.(4分)过点的直线l将圆(x﹣2)2+y2=4分成两段弧,当劣弧所对的圆心角最小时,直线l的斜率k=.三、解答题16.(6分)求经过直线l1:3x+2y﹣5=0,l2:3x﹣2y﹣1=0的交点且平行于直线2x+y﹣5=0的直线方程.17.(8分)已知函数f(x)=(a>1)(Ⅰ)判断函数f(x)的奇偶性(Ⅱ)判断f(x)在(﹣∞,+∞)上的单调性,并用定义证明.18.(8分)如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC(Ⅰ)求证:BC⊥PB(Ⅱ)求PC与平面ABCD所成角的余弦值.19.(9分)如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.(1)写出y关于x的函数关系式,并指出这个函数的定义域.(2)当AE为何值时,绿地面积最大?20.(9分)已知圆方程x2+y2﹣2x﹣4y+m=0.(1)若圆与直线x+2y﹣4=0相交于M,N两点,且OM⊥ON(O为坐标原点)求m的值;(2)在(1)的条件下,求以MN为直径的圆的方程.某某省某某市2014-2015学年高一上学期期末数学试卷参考答案与试题解析一、选择题(每小题4分,共40分)1.(4分)若集合A={x|﹣2≤x<1},B={x|0<x≤2},则A∩B=()A.{x|﹣2≤x≤2}B.{x|﹣2≤x<0} C.{x|0<x<1} D.{x|1<x≤2}考点:交集及其运算.专题:集合.分析:由A与B,求出两集合的交集即可.解答:解:∵A={x|﹣2≤x<1},B={x|0<x≤2},∴A∩B={x|0<x<1}.故选:C.点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.2.(4分)下列函数中,在R上单调递减的是()A.y=|x| B.y=log2x C.y=x D.y=()x考点:函数单调性的性质.专题:函数的性质及应用.分析:根据函数单调性的性质分别进行判断即可.解答:解:y=|x|在(﹣∞,0]上为减函数,在分析:利用分式分母不为零,偶次方根非负,得到不等式组,求解即可.解答:解:由题意解得x∈解答:解:a=2﹣1=,b=log3<0,c=()﹣1=,所以b<a<c,故选:B.点评:本题主要考查了指数函数的性质和对数函数的性质,属于基础题.5.(4分)已知直线m、n与平面α,β,给出下列三个命题:①若m∥α,n∥α,则m∥n;②若m∥α,n⊥α,则n⊥m;③若m⊥α,m∥β,则α⊥β.其中真命题的个数是()A.0 B.1 C.2 D.3考点:平面与平面之间的位置关系;空间中直线与平面之间的位置关系.专题:综合题.分析:根据线面平行的性质,线面垂直的性质,面面平行的判定,结合空间点线面之间的关系,我们逐一分析已知中的三个命题即可得到答案.解答:解:m∥α,n∥α,时,m与n可能平行、可能异面也可能相交,故①错误;m∥α,n⊥α时,存在直线l⊂α,使m∥l,则n⊥l,也必有n⊥m,故②正确;m⊥α,m∥β时,直线l⊂β,使l∥m,则n⊥β,则α⊥β,故③正确;故选C点评:本题考查的知识点是平面与平面之间的位置关系,空间中直线与平面之间的位置关系,熟练掌握空间线面关系的判定方法,建立良好的空间想象能力是解答本题的关键.6.(4分)三视图如图的几何体的全面积是()A.B.C.D.考点:由三视图求面积、体积.专题:计算题.分析:由三视图知几何体是一个四棱锥,四棱锥的底面是一个边长为1的正方形,一条侧棱与底面垂直,且侧棱的长是1,另外两条侧棱长,得到表面积.解答:解:由三视图知几何体是一个四棱锥,四棱锥的底面是一个边长为1的正方形,一条侧棱与底面垂直,且侧棱的长是1,∴四棱锥的表面积是1×+2×=2+故选A.点评:本题考查由三视图还原几何体,本题解题的关键是看出几何体的各个部分的长度,本题是一个基础题.7.(4分)已知正三棱锥的侧棱长是底面边长的2倍,则侧棱与底面所成角的余弦值等于()A.B.C.D.考点:棱锥的结构特征.专题:计算题.分析:由题意可知,本题需作辅助线,可以根据三角形的特征,进行求解.解答:解:已知正三棱锥的侧棱长是底面边长的2倍,设底面边长为1,侧棱长为2,连接顶点与底面中心,则侧棱在底面上的射影长为,所以侧棱与底面所成角∠PAO的余弦值等于,故选A.点评:本题考查学生的空间想象能力,以及学生对三角形的利用,是基础题.8.(4分)函数f(x)=log3x﹣8+2x的零点一定位于区间()A.(5,6)B.(3,4)C.(2,3)D.(1,2)考点:根的存在性及根的个数判断.专题:计算题.分析:根据函数零点存在定理,若f(x)=log3x﹣8+2x若在区间(a,b)上存在零点,则f(a)•f(b)<0,我们根据函数零点存在定理,对四个答案中的区间进行判断,即可得到答案.解答:解:当x=3时,f(3)=log33﹣8+2×3=﹣1<0当x=4时,f(4)=log34﹣8+2×4=log34>0即f(3)•f(4)<0又∵函数f(x)=log3x﹣8+2x为连续函数故函数f(x)=log3x﹣8+2x的零点一定位于区间(3,4)故选B点评:本题考查的知识点是零点存在定理,我们求函数的零点通常有如下几种方法:①解方程;②利用零点存在定理;③利用函数的图象,其中当函数的解析式已知时(如本题),我们常采用零点存在定理.9.(4分)设点P是Z轴上一点,且点P到M(1,0,2)与点N(1,﹣3,1)的距离相等,则点P的坐标是()A.(﹣3,﹣3,0)B.(0,0,3)C.(0,﹣3,﹣3)D.(0,0,﹣3)考点:空间两点间的距离公式.专题:空间位置关系与距离.分析:设出M点的坐标,利用点P到M(1,0,2)与点N(1,﹣3,1)的距离相等,列出方程即可求出M的坐标.解答:解:由题意设P(0,0,z),因为点P到M(1,0,2)与点N(1,﹣3,1)的距离相等,所以,=解得z=﹣3.所以P的坐标为(0,0,﹣3).故选:D.点评:本题考查空间两点的距离公式的求法,考查计算能力.10.(4分)设r>0,两圆(x﹣1)2+(y+3)2=r2与x2+y2=16可能()A.相离B.相交C.内切或内含或相交D.外切或外离考点:圆与圆的位置关系及其判定.专题:计算题.分析:先计算两圆的圆心距,再与半径的和差比较,可判断.解答:解:∵两圆圆心坐标为(1,﹣3),(0,0)∴两圆的圆心距的平方为(0﹣1)2+(0+3)2=10,半径分别为4,r,∴当时,两圆相交;当时,两圆内切;当时,两圆内含.故选C.点评:本题主要考查圆与圆的位置关系,利用代数方法可解.二、填空题(每小题4分,共20分)11.(4分)如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于2π.考点:棱柱、棱锥、棱台的体积.专题:空间位置关系与距离.分析:设圆柱的高为:h,轴截面为正方形的圆柱的底面直径为h,由圆柱的侧面积是4π,得h2π=4π,求出h=2,由此能求出圆柱的体积.解答:解:设圆柱的高为h,轴截面为正方形的圆柱的底面直径为:h,因为圆柱的侧面积是4π,所以h2π=4π,∴h=2,所以圆柱的底面半径为:1,圆柱的体积:π×12×2=2π.故答案为:2π.点评:本题考查圆柱的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.12.(4分)已知点A(1,2)、B(3,1),则线段AB的垂直平分线的方程是4x﹣2y﹣5=0.考点:直线的点斜式方程.专题:计算题.分析:要求线段AB的垂直平分线,即要求垂直平分线线上一点与直线的斜率,根据中点坐标公式求出AB的中点M的坐标,利用A与B的坐标求出直线AB的斜率,根据两直线垂直时斜率乘积为﹣1得到垂直平分线的斜率,根据M的坐标和求出的斜率写出AB的垂直平分线的方程即可.解答:解:设M的坐标为(x,y),则x==2,y==,所以M(2,)因为直线AB的斜率为=﹣,所以线段AB垂直平分线的斜率k=2,则线段AB的垂直平分线的方程为y﹣=2(x﹣2)化简得4x﹣2y﹣5=0故答案为:4x﹣2y﹣5=0点评:此题考查学生会利用中点坐标公式求线段中点的坐标,掌握两直线垂直时斜率的关系,会根据一点和斜率写出直线的点斜式方程,是一道中档题.13.(4分)已知函f(x)=,则f(f())=.考点:对数的运算性质;函数的值.专题:函数的性质及应用.分析:利用分段函数直接进行求值即可.解答:解:由分段函数可知f()=,f(f())=f(﹣2)=.故答案为:.点评:本题主要考查分段函数求值,比较基础.14.(4分)若f(x)为奇函数,当x<0时,f(x)=x2+ax,且f(3)=6,则实数a的值为5.考点:函数奇偶性的性质.分析:利用函数是奇函数,由f(3)=6,得到f(﹣3)=﹣f(3)=﹣6,代入表达式即可求解.解答:解:因为f(x)为奇函数,当x<0时,f(x)=x2+ax,且f(3)=6,所以f(﹣3)=﹣f(3)=﹣6,即f(﹣3)=9﹣3a=﹣6,所以3a=15,解得a=5.故答案为:5.点评:本题主要考查函数奇偶性的应用,比较基础.15.(4分)过点的直线l将圆(x﹣2)2+y2=4分成两段弧,当劣弧所对的圆心角最小时,直线l的斜率k=.考点:直线的斜率;直线和圆的方程的应用.专题:压轴题;数形结合.分析:本题考查的是直线垂直时斜率之间的关系,及直线与圆的相关性质,要处理本题我们先要画出满足条件的图形,数形结合容易得到符合题目中的条件的数理关系,由劣弧所对的圆心角最小弦长最短,及过圆内一点最短的弦与过该点的直径垂直,易得到解题思路.解答:解:如图示,由图形可知:点A在圆(x﹣2)2+y2=4的内部,圆心为O(2,0)要使得劣弧所对的圆心角最小,只能是直线l⊥OA,所以.点评:垂径定理及其推论是解决直线与圆关系时常用的定理,要求大家熟练掌握,垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.相关推论,过圆内一点垂直于该点直径的弦最短,且弦所地的劣弧最短,优弧最长,弦所对的圆心角、圆周角最小….三、解答题16.(6分)求经过直线l1:3x+2y﹣5=0,l2:3x﹣2y﹣1=0的交点且平行于直线2x+y﹣5=0的直线方程.考点:待定系数法求直线方程.专题:直线与圆.分析:联立,解得交点坐标(1,1),与直线2x+y﹣5=0平行的直线为:2x+y+m=0,把(1,1)代入解得即可.解答:解:联立,解得,交点坐标(1,1).与直线2x+y﹣5=0平行的直线为:2x+y+m=0,把(1,1)代入可得2+1+m=0,解得m=﹣3.∴所求的直线方程为:2x+y﹣3=0.点评:本题考查了直线的交点坐标、平行线的斜率之间的关系,考查了计算能力,属于基础题.17.(8分)已知函数f(x)=(a>1)(Ⅰ)判断函数f(x)的奇偶性(Ⅱ)判断f(x)在(﹣∞,+∞)上的单调性,并用定义证明.考点:函数单调性的判断与证明;函数奇偶性的判断.专题:函数的性质及应用.分析:(Ⅰ)由题意可得函数的定义域为R,可得f(﹣x)=﹣f(x),可得奇函数;(Ⅱ)设x1,x2∈(﹣∞,+∞)且x1<x2,可判定f(x1)﹣f(x2)的符号,由单调性的定义可得结论.解答:解:(Ⅰ)可得函数的定义域为R,f(﹣x)===﹣=﹣f(x),∴函数f(x)为奇函数;(Ⅱ)函数f(x)在(﹣∞,+∞)为增函数,证明如下:设x1,x2∈(﹣∞,+∞)且x1<x2,则f(x1)﹣f(x2)=﹣==,∵a>1且x1<x2,∴﹣<0,∴<0,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2),∴f(x)在(﹣∞,+∞)上是增函数.点评:本题考查函数的单调性和奇偶性,涉及单调性的定义法证明,属基础题.18.(8分)如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC(Ⅰ)求证:BC⊥PB(Ⅱ)求PC与平面ABCD所成角的余弦值.考点:直线与平面所成的角.专题:空间位置关系与距离;空间角.分析:(Ⅰ)由已知条件AD∥BC,PA⊥AD,从而得到BC⊥PA,再由BC⊥AB,即可得到BC⊥平面PAB,从而得出BC⊥PB;(Ⅱ)由PA⊥AD,PA⊥AB即可得到PA⊥平面ABCD,从而连接AC,∠PCA便是PC与平面ABCD 所成角,从而求出AC,PC的长,在直角三角形PAC中即可求出cos∠PCA.解答:解:(Ⅰ)证明:∵A、D分别是RB、RC的中点;∴AD∥BC,∠PAD=∠RAD=∠RBC=90°;∴PA⊥AD,PA⊥BC;又BC⊥AB,PA∩AB=A;∴BC⊥平面PAB;∵PB⊂平面PAB;∴BC⊥PB;(Ⅱ)由PA⊥A D,PA⊥AB,AD∩AB=A;∴PA⊥平面ABCD;连接AC,则∠PCA是直线PC与平面ABCD所成的角;∵AB=1,BC=2,∴AC=;又PA=1,PA⊥AC,∴PC=;∴在Rt△PAC中,cos;∴PC与平面ABCD所成角的余弦值为.点评:考查三角形中位线的性质,弄清折叠前后不变的量,线面垂直的判定定理及其性质,线面角的概念及求法,直角三角形边的关系.19.(9分)如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.(1)写出y关于x的函数关系式,并指出这个函数的定义域.(2)当AE为何值时,绿地面积最大?考点:函数模型的选择与应用;函数的最值及其几何意义.专题:应用题.分析:(1)先求得四边形ABCD,△AHE的面积,再分割法求得四边形EFGH的面积,即建立y关于x的函数关系式;(2)由(1)知y是关于x的二次函数,用二次函数求最值的方法求解.解答:解:(1)S△AEH=S△CFG=x2,(1分)S△BEF=S△DGH=(a﹣x)(2﹣x).(2分)∴y=S ABCD﹣2S△AEH﹣2S△BEF=2a﹣x2﹣(a﹣x)(2﹣x)=﹣2x2+(a+2)x.(5分)由,得0<x≤2(6分)∴y=﹣2x2+(a+2)x,0<x≤2(7分)(2)当,即a<6时,则x=时,y取最大值.(9分)当≥2,即a≥6时,y=﹣2x2+(a+2)x,在(0,2]上是增函数,则x=2时,y取最大值2a﹣4(11分)综上所述:当a<6时,AE=时,绿地面积取最大值;当a≥6时,AE=2时,绿地面积取最大值2a﹣4(12分)点评:本题主要考查实际问题中的建模和解模能力,注意二次函数求最值的方法.20.(9分)已知圆方程x2+y2﹣2x﹣4y+m=0.(1)若圆与直线x+2y﹣4=0相交于M,N两点,且OM⊥ON(O为坐标原点)求m的值;(2)在(1)的条件下,求以MN为直径的圆的方程.考点:直线和圆的方程的应用.专题:直线与圆.分析:(1)将圆的方程与直线方程联立,设M(x1,y1),N(x2,y2),利用OM⊥ON,可得x1x2+y1y2=0,利用韦达定理,即可求出m的值;(2)确定圆心坐标与半径,即可求以MN为直径的圆的方程.解答:解:(1)由x2+y2﹣2x﹣4y+m=0得(x﹣1)2+(y﹣2)2=5﹣m由5﹣m>0,可得m<5…(2分)于是由题意把x=4﹣2y代入x2+y2﹣2x﹣4y+m=0,得 5y2﹣16y+8+m=0…..(3分)设M(x1,y1),N(x2,y2),则,…(4分)∵OM⊥ON,∴x1x2+y1y2=0…(5分)∴5y1y2﹣8(y1+y2)+16=0∴,满足题意…(8分)(2)设圆心为(a,b),则a=,b=….(9分)半径r==•=…(12分)∴圆的方程…(13分)点评:本题考查直线与圆的位置关系,考查韦达定理的运用,考查圆的方程,正确运用韦达定理是关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
郴州市2017年下学期学科教学状况抽测试卷
高一数学
(试题卷)
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一 项是符合题目要求的.
1. 已知集合{}
4A x N x =∈≤≤,{}2,2B =-,A
B =( )
A . {}12,
B . {}2-
C .{}2,2-
D .{}2
2. 当01a <<时,在同一坐标系中,函数1
()x
y a
=与log a y x =的图象是( )
A .
B .
C .
D .
3. 在空间直角坐标系中,点(2,2,4)A -与点(2,2,4)B =---关于( )对称 A .原点 B .x 轴 C . y 轴 D . z 轴
4. 下列函数中,既不是奇函数也不是偶函数的是( ) A .2y x = B .2x y = C .y x = D .1
y x
= 5. 设0.1
3a =,9log 0.1b =,0.2
0.3c =则( )
A .a c b >>
B .a b c >> C. b a c >> D .b c a >> 6. 设l 是一条直线,α,β是两个不同的平面,则下列命题中正确的是( ) A . 若l α⊥,αβ⊥,则l β⊂ B .若//l α,//αβ,则//l β C. 若l α⊥,//αβ,则//αβ D .若l α⊥,//αβ,则l β⊥
7. 中国古代数学名著《九章算术)中记载了公元前344年商鞅督造一种标准量器—商鞅铜方升,其三视图如图所示(单位:寸),若π可取3,其体积为12.6(立方寸),则图中的x 为( ) A . 1.2 B . 1.6 C. 1.8 D .2.4
8. 将正方形ABCD 沿对角线AC 折起成直二面角,则直线BD 与平面ABC 所成的角的大小为( ) A .30︒ B . 45︒ C. 60︒ D .90︒
9. 已知函数()f x 是定义在R 上的奇函数,且在[)0,+∞上是增函数,若实数a 满足
223(log )+(log )2(1)f a f a f -≥,则实数a 的取值范围是( )
A .(]02,
B .(],2-∞ C.[)2,+∞ D .[)1,+∞ 10. 已知函数()f x 是定义在R 的奇函数,且当0x ≤时,1
()212
x
f x x =--,则函数()f x 的零点个数是( )
A . 1
B .2 C. 3 D .4
二、填空题:本大题共5小题,每小题4分,共20分.
11. .若幂函数a
y x =的图像过点(28),
,则a = . 12. 已知函数3(1)
()ln (1)
x x f x x x ⎧≤=⎨>⎩,e 为自然对数的底数,则[]()f f e .
13. 如图,直四棱柱1111ABCD A BC D -的底面是边长为1的正方形,侧棱长1AA 则异面直线11A B 与1BD 的夹角大小等于 .
14.直线1y kx =+与圆2
2
(2)1x y -+=有交点,则实数k 的取值范围是 .
15.函数()f x 的定义域为A ,若1x ,2x A ∈且12()()f x f x =时总有12x x =,则称()f x 为和谐函数.
例如,函数()1()f x x x R =+∈是和谐函数.下列命题: ①函数()1()f x x x R =+∈是和谐函数;
②函数12log 2()2,2
x x f x x x ⎧≥⎪
=⎨⎪-<⎩,是和谐函数; ③若()f x 是和谐函数,1x ,2x A ∈且12x x ≠,则12()()f x f x ≠.
④若函数()f x 在定义域内某个区间D 上具有单调性,则()f x 一定是和谐函数. 其中真命题是 (写出所有真命题的编号)
三、解答题:本大题共5小题,共40分,解答应写出文字说明,证明过程或演算步骤.
16. 已知函数[](],0,2()4,2,4.x x f x x x ⎧∈⎪
⎨∈⎪⎩
,
(Ⅰ)画出函数()f x 的大致图像;
(Ⅱ)写出函数()f x 的最大值和单调递减区间
17. 设U R =,{}3
21x A x -=≤,{}25B x x =<<,{}
1C x a x a =≤≤+ (a 为实数)
(Ⅰ)求A B ;
(Ⅱ)若B
C B =,求a 的取值范围.
18. 如图,四棱锥中P ABCD -中,PA ⊥底面ABCD .底面ABCD 为梯形,//AB DC ,AB BC ⊥,
22AC DC AB ===
,PA =E 在棱PB 上,且2PE EB =.
(Ⅰ)求证:平面PAB ⊥平面PCB ; (Ⅱ)求三棱锥A BCE -的体积.
19. 已知方程22260x y x y m +--+= (Ⅰ)若此方程表示圆,求实数m 的取值范围;
(Ⅱ)若(Ⅰ)中的圆与直线240x y +-=相交于M 、N 两点,且OM ON ⊥(O 为坐标原点)求实数
m 的值;
(Ⅲ)在(Ⅱ)的条件下,求以MN 为直径的圆的方程.
20. 已知函数21
()12
x x
a f x ⋅-=+是R 上的奇函数. (Ⅰ)求a 的值;
(Ⅱ)判断并证明()f x 的单调性;
(Ⅲ)若对任意实数,不等式[]()(3)0f f x f m +->恒成立,求m 的取值范围.
郴州市2017年下学期学科教学状况抽测试卷
高一数学参考答案及评分细则
一、选择题
1-5: DCCBA 6-10: DBBCC
二、填空题
11. 3 12. 3 13.60︒ 14. 4,03⎡⎤
-
⎢⎥⎣⎦
15. ③ 三、解答题
16. 解:(Ⅰ)函数()f x 的大致图象如图所示.
(Ⅱ)由函数()f x 的图象得出,()f x 的最大值为2. 其单调递减区间为[]24,或(]24,. 17.(Ⅰ)∵3
21x -≤ ∴3x ≤
∴{}23A
B x x =<≤
(Ⅱ)由B C B =得C B ⊆
∴215a a >⎧⎨+<⎩
即24a <<
∴(2,4)a ∈
18. (Ⅰ)证明:∵PA ⊥面ABCD ,∴BC PA ⊥ 又∵BC AB ⊥,且AB
PA A =.∴B BC ⊥面PAB
又∵BC ⊂面PBC ,∴面PBC ⊥面PAB
(Ⅱ)过点E ,在平面PAB 内作EF 垂直于AB ,垂足为F . 由(Ⅰ)可知EF ⊥底面ABCD
∵
1
3
EF PA =,PA =
∴EF =
又∵A BCE E ABC V V --=
1
12ABC S ∆=⨯=
∴11
36
A BCE E ABC V V --==
=
19. 解.(Ⅰ)圆的方程可化为2
2
(1)(3)10x y m -+-=-,∴10m < (Ⅱ)设11(,)M x y ,22(,)N x y ,则1142x y =-,2242x y =-,
121212168()4x x y y y y =-++
∵OM ON ⊥,∴12120x x y y += ∴1212168()50y y y y -++=①
由22
42260x y x y x y m =-⎧
⎨+--+=⎩
得2
51880y y m -++= 所以12185y y +=
,1285m y y +=代入①得24
5
m = (Ⅲ)以MN 为直径的圆的方程为
1212()()()()0x x x x y y y y --+--=
即221212()()0x y x x x y y y +-+-+= 所以所求圆的方程为2
2
418
055
x y x y +-
-=.
20. (Ⅰ)∵()f x 为R 上的奇函数,∴(0)0f =,即
1
02
a -=,由此得1a = (Ⅱ)由(1)知212
()12121
x x x f x -==-++∴()f x 为R 上的增函数. 证明,设12x x <,则1221122222
()()1(1)21212121
x x x x f x f x -=---=-++++ ∵12x x <,∴
21
22
02121
x x -<++,∴12()()f x f x < ∴()f x 为R 上的增函数. (Ⅲ)∵()f x 为R 上的奇函数
∴原不等式可化为[]()(3)f f x f m >--,即[]()(3)f f x f m >- 又∵()f x 为R 上的增函数,∴()3f x m >-, 由此可得不等式2
()3421
x m f x <+=-+对任意实数x 恒成立 由2
202110221
x
x
x
>⇒+>⇒<
<⇒+ 22
202442121
x x -<-<⇒<-<++
∴2m ≤。
