材料力学扭转答案
土木工程师-公共基础-材料力学-扭转
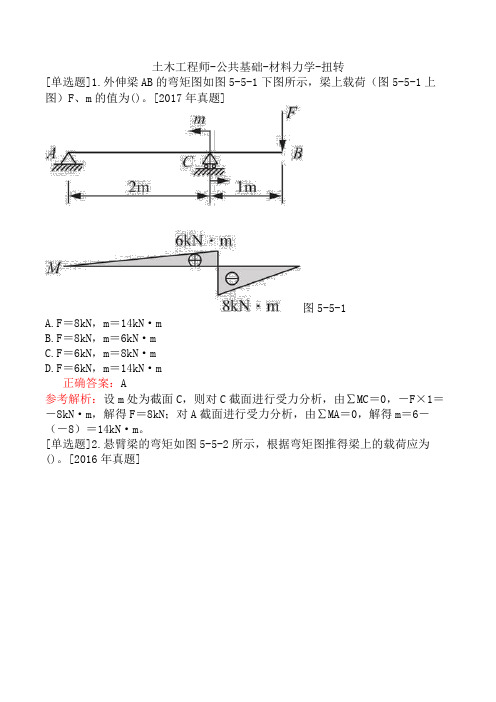
土木工程师-公共基础-材料力学-扭转[单选题]1.外伸梁AB的弯矩图如图5-5-1下图所示,梁上载荷(图5-5-1上图)F、m的值为()。
[2017年真题]图5-5-1A.F=8kN,m=14kN·mB.F=8kN,m=6kN·mC.F=6kN,m=8kN·mD.F=6kN,m=14kN·m正确答案:A参考解析:设m处为截面C,则对C截面进行受力分析,由∑MC=0,-F×1=-8kN·m,解得F=8kN;对A截面进行受力分析,由∑MA=0,解得m=6-(-8)=14kN·m。
[单选题]2.悬臂梁的弯矩如图5-5-2所示,根据弯矩图推得梁上的载荷应为()。
[2016年真题]图5-5-2A.F=10kN,m=10kN·mB.F=5kN,m=10kN·mC.F=10kN,m=5kN·mD.F=5kN,m=5kN·m正确答案:B参考解析:弯矩图在支座C处有一个突变,突变大小即为支座C处的弯矩值,m =10kN·m。
弯矩图的斜率值即为剪力值,显然BC段截面剪力为零,AB段截面剪力为+5kN(顺时针),因此根据B点截面处的竖向力平衡,可算得:F=5kN。
[单选题]3.简支梁AB的剪力图和弯矩图如图5-5-3所示,该梁正确的受力图是()。
[2016年真题]图5-5-3 A.B.C.D.正确答案:C参考解析:弯矩图在中间处突变,则构件中间有集中力偶大小为50kN·m;剪力图中间有突变,则说明构件中间有集中力,大小为100kN。
根据中间截面处的左右两侧剪力(顺时针为正)与集中荷载的平衡,则集中荷载竖直向下,C项正确。
[单选题]4.承受均布载荷的简支梁如图5-5-4(a)所示,现将两端的支座同时向梁中间移动l/8,如图(b)所示。
两根梁的中点(l/2处)弯矩之比Ma/Mb 为()。
[2013年真题]图5-5-4(a)图5-5-4(b)A.16B.4C.2D.1正确答案:C参考解析:支座未移动前中点处弯矩Ma=ql2/8,移动后中点处弯矩变为:Mb=(-ql/8)×(l/16)+q(l-2l/8)2/8=ql2/16,故Ma/Mb=2。
材料力学拉伸与扭转题目答案

75
2
3
1
A
B
C
P
40
80
80
变形相容条件 变形后三根杆与梁 仍绞接在一起。 变形几何方程
2 l2 l1 l3
2
3
1
A
B
C
l1
P
l2
l3
40
80
80
75
2 l2 l1 l3
补充方程
2 N 2 l2 N1l1 N3l3 EA EA EA
静力平衡方程
N1 N2 N3 P 0 2N2 4N3 P 0
2
3
1
A
B
C
P
40
80
80
N1
N2
N3
P
75
3、阶梯形圆杆AE段为空心,外径 D =140mm,内径 d=100mm。BC段为实心,直径 d=100mm。外力偶矩 mA=18KN.m,mB=32KN.m,mC=14KN.m。已知许用切应力 []=80MPa 。试校核轴的强度。
mA
D
d
A
E
mB mC
二、计算题
1:悬臂吊车如图所示。G=20KN,许用应力 []=120MPa,弹性模量E=200GPa。AB杆为圆钢。试设计 AB杆的直径并计算其伸长量l
A
C
300
3m
D B
2m
G
1、解:计算AB杆的轴力
A
mc 0
3N AB sin300 5G 0
C
300
D
NAB=66.7KN (1) 设计AB杆的直径
d
C B
mAB =18KN.m ,mBD =14KN.m
BC
M nBC Wn
材料力学答案03

T2 = M B + M C = 764 N ⋅ m Tmax = 764 N ⋅ m
其绝对值比第(1)种情况小,即对轴的受力有利。 3-3 试绘出图示截面上切应力的分布图,其中 T 为截面的扭矩。
(a1)
(b1)
(c1)
3-4 图示圆截面轴, AB 与 BC 段的直径分别为 d1 与 d 2 ,且 d1 = 4d 2 / 3 。求轴内的 最大扭转切应力。
ϕ = ∫ dϕ = ∫
l l
T (x ) dx GI p ( x )
上式适用于等截面圆轴和截面变化不大的圆锥截面轴。对等截面圆轴,若在长 l 的两横截面 间的扭矩 T 为常量,则
ϕ=
圆轴扭转的刚度条件为
Tl GI p
⎟ ≤ [θ ] θ max = ⎜ ⎜ GI ⎟ ⎝ p ⎠ max
⎛ T ⎞
对于等截面圆轴为 或
28
答 同一变速箱中的高速轴与低速轴指相对转速高低,其传递的功率相同(不计功率损 耗) ,啮合处线速度相同。要啮合处产生相同的线速度,则高速轴的啮合半径就较小;又因 为啮合处相互作用力相同,该作用力对啮合半径就较小的高速轴线产生的外力偶矩就较小, 从而在高速轴中产生的扭矩较小,故高速轴可做得较细。 3-12 图示轴 A 和套筒 B 牢固地结合在一起,两者切变模量分别为 G A 和 G B ,两端受扭 转力偶矩,为使轴和套筒承受的扭转相同而必须满足的条件是什么?
(
)
16 × 500 = 194 MPa ⎡ ⎛ 40 ⎞ 4 ⎤ 3 −9 π × 42 × 10 × ⎢1 − ⎜ ⎟ ⎥ ⎢ ⎝ 42 ⎠ ⎦ ⎥ ⎣
(2)若考虑薄壁 ,可求其平均扭转切应力
τ=
Me = 2 πR 2δ
材料力学-扭转-计算公式及例题

求 AB段Mn(1-1剖面)
K N·m 4.50 背向剖切面为正
求 BC段Mn(2-2剖
面) K N·m
-4.50
求 CD段Mn(3-3剖面)
K N·m -1.50
D>=103mm
已知 CD段Mn(3-3剖面)
K N·m -1.5
求
IP m4 1.19E-05
求 φB-A
° 0.216
求 ΦC-B
K N·m
K N·m
K N·m
K N·m
数值
0.62
2.05
1.43
0.62
横截面上的力偶矩的方向,为外力偶矩(如T1,T2,T3)指向剖切面为负,背向剖切面为正
校核AC段 的强度(实
数据状态
代号
单位
数值 校核DB段 的强度(实
数据状态
代号
单位
已知 d1 mm 40
已知 d2 mm
已知 Mn(AC) K N·m 0.62
°/m
m4
1.05E+01 5.00E-01 1.50E-08
,试设 计截面的内
求 D0 mm 63.38
求 d mm 60.44
求 A1/A2
mm 0.51
d2=70mm。 。材料的许用切应 轴的强度和刚度。
。材料的许用切应 轴的强度和刚度。
求 CD段Mn(2-2剖面)
K N·m 0.62 背向剖切面为正
° -0.270
求 φD-C
° -0.108
强度计算 序号
名称
代号
单位
max
M n max Wp
[ ]
1
横截面上的最大扭 矩
Mn max
《材料力学》第3章 扭转 习题解
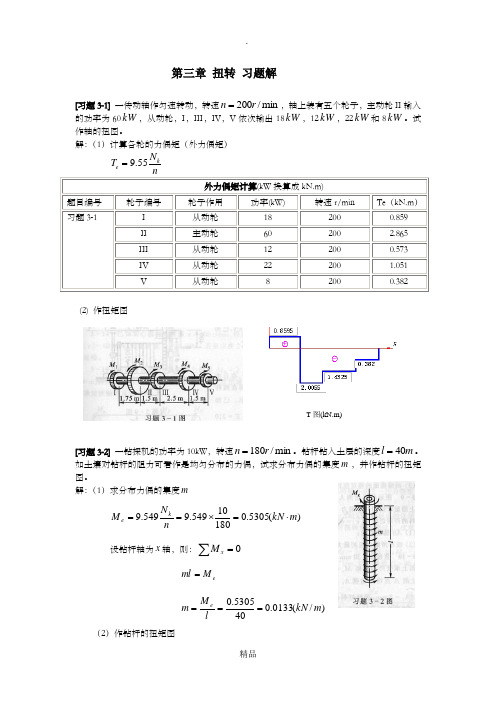
第三章扭转 习题解[习题3-1] 一传动轴作匀速转动,转速min /200r n =,轴上装有五个轮子,主动轮II 输入的功率为60kW ,从动轮,I ,III ,IV ,V 依次输出18kW ,12kW ,22kW 和8kW 。
试作轴的扭图。
解:(1)计算各轮的力偶矩(外力偶矩) nN T ke 55.9= 外力偶矩计算(kW 换算成kN.m)题目编号 轮子编号轮子作用 功率(kW) 转速r/minTe (kN.m ) 习题3-1I 从动轮 18 200 0.859 II 主动轮 60 200 2.865 III 从动轮 12 200 0.573 IV 从动轮 22 200 1.051 V从动轮82000.382(2) 作扭矩图[习题3-2] 一钻探机的功率为10kW ,转速min /180r n =。
钻杆钻入土层的深度m l 40=。
如土壤对钻杆的阻力可看作是均匀分布的力偶,试求分布力偶的集度m ,并作钻杆的扭矩图。
解:(1)求分布力偶的集度m)(5305.018010549.9549.9m kN n N M k e ⋅=⨯== 设钻杆轴为x 轴,则:0=∑xMe M ml =)/(0133.0405305.0m kN l M m e ===(2)作钻杆的扭矩图T 图(kN.m)x x lM mx x T e0133.0)(-=-=-=。
]40,0[∈x 0)0(=T ; )(5305.0)40(m kN M T e ⋅-==扭矩图如图所示。
[习题3-3] 圆轴的直径mm d 50=,转速为120r/min 。
若该轴横截面上的最大切应力等于60MPa ,试问所传递的功率为多大? 解:(1)计算圆形截面的抗扭截面模量:)(245445014159.3161161333mm d W p =⨯⨯==π (2)计算扭矩2max /60mm N W Tp==τ )(473.1147264024544/6032m kN mm N mm mm N T ⋅=⋅=⨯=(3)计算所传递的功率 )(473.1549.9m kN nN M T ke ⋅=== )(5.18549.9/120473.1kW N k =⨯=[习题3-4] 空心钢轴的外径mm D 100=,内径mm d 50=。
材料力学复习题第三章 扭 转

第三章 扭 转一、判断题1.圆杆受扭时,杆内各点均处于纯剪切状态。
( ) 2.非圆截面杆不能应用圆杆扭转切应力公式,是因为非圆截面杆扭转时“平面假设”不能成立。
( ) 3.当剪应力超过材料的剪切比例极限时,剪应力互等定律亦成立。
( ) 4.一点处两个相交面上的剪应力大小相等,方向指向(或背离)该两个面的交线。
( ) 5.直径和长度相同,材料不同的两根轴,受相同的扭转力偶矩作用,它们的最大剪应力和最大扭转角都相同。
6. 杆件受扭时,横截面上最大切应力发生在距截面形心最远处。
( )7. 薄壁圆管和空心圆管的扭转切应力公式完全一样。
( )8. 圆杆扭转变形实质上是剪切变形。
( )9. 横截面的角点处的切应力必为零。
( ) 1.√ 2.√ 3.√ 4.× 5.× 6.×(非圆截面) 7.× 8.√ 9.× 二、单项选择题1. 图示圆轴曲面C 左、右两侧的扭矩MC+和M C-的( )。
A .大小相等,正负号相同;B .大小不等,正负号相同; C .大小不等,正负号不同;D .大小相等,正负号不同。
2. 直径为D 的实心圆轴,两端受扭转力矩作用。
轴内最大剪应力τ,若轴的直径改为D/2,则轴内的最大剪应力变为( )。
A .2τ; B .τ; C . 8τ; D .16τ。
3. 阶梯圆轴的最大切应力发生在( )。
A .扭矩最大的截面;B .直径最小的截面;C .单位长度扭转角最大的截面;D .不能确定。
4.空心圆轴的外径为D ,内径为d,α=d/D 。
其抗扭截面系数为( )。
A .()απ-=1163D W P ;B 。
()23116απ-=D W P ;C 。
()33116απ-=D W PD .()43116απ-=D WP5.扭转的切应力公式ρτρPPI M =适用于( )杆件。
A .任意截面; B .任意实心截面;C .任意材料的圆截面; D .线弹性材料的圆面。
材料力学精选试题及答案-剪切与挤压的实用计、扭转

剪切与挤压的实用计算1.图示木接头,水平杆与斜杆成(A )bh ;(B )tan bh ;(C )cos bh;(D )cos sin bh。
答:C2.图示铆钉连接,铆钉的挤压应力bs(A )22π Fd ;(B )2Fd;(C )2Fb;(D )24πFd 。
答:B3.切应力互等定理是由单元体(A )静力平衡关系导出的;(B )几何关系导出的;4.5.6.7. 图示直径为d 的圆柱放在直径为3D d ,厚度为 的圆形基座上,地基对基座的支反力为均匀分布,圆柱承受轴向压力F ,则基座剪切面的剪力S F 。
答: 22S 2π 48π 49D dF F F D8. 拉杆及头部均为圆截面,已知40 mm D ,20 mm d ,15 mm h 。
材料的许用切应力[]100 MPa ,许用挤压应力bs []240 MPa ,试由拉杆头的强度确定许用拉力F 。
解:S π []94.3 kN F d h22bsbs π[]226 kN 4D d F取[]94.3 kN F 。
9. 图示在拉力F 的作用下的螺栓,已知螺栓的许用切应力[] 是拉伸许用应力的0.6倍。
试求螺栓直径d 和螺栓头高度h 的合理比值。
解:24[]πF d 因为,0.6[]πFd h所以在正应力和切应力都达到各自许用应力时,有241π0.6πFd F dh , 2.4d h 。
10. 图示键的长度30 mm l ,键许用切应力[]80 MPa ,许用挤压应力bs []200 MPa ,试求许可载荷][F 。
解:以手柄和半个键为隔离体, S 0, 204000O M F F取半个键为隔离体,bs S 20F F F由剪切:S []sFA ,720 N F由挤压:bs bs bs bs [][], 900N FF A取[]720N F 。
材料力学习题册答案-第3章 扭转

第三章扭转一、是非判断题1.圆杆受扭时,杆内各点处于纯剪切状态。
(×)2.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
(×)3.薄壁圆管和空心圆管的扭转切应力公式完全一样。
(×)4.圆杆扭转变形实质上是剪切变形。
(×)5.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
(√)6.材料相同的圆杆,他们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
(×)7.切应力互等定理仅适用于纯剪切情况。
(×)8.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
(√)9.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
(√)10.受扭圆轴的最大切应力只出现在横截面上。
(×)11.受扭圆轴内最大拉应力的值和最大切应力的值相等。
(√)12.因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭距达到某一极限值时,圆杆将沿轴线方向出现裂纹。
(×)二、选择题1.内、外径之比为α的空心圆轴,扭转时轴内的最大切应力为τ,这时横截面上内边缘的切应力为 ( B )A τ;B ατ;C 零;D (1- 4α)τ 2.实心圆轴扭转时,不发生屈服的极限扭矩为T ,若将其横截面面积增加一倍,则极限扭矩为( C )0 B 20T 0 D 40T 3.两根受扭圆轴的直径和长度均相同,但材料C 不同,在扭矩相同的情况下,它们的最大切应力τ、τ和扭转角ψ、ψ之间的关系为( B )A 1τ=τ2, φ1=φ2B 1τ=τ2, φ1≠φ2C 1τ≠τ2, φ1=φ2D 1τ≠τ2, φ1≠φ2 4.阶梯圆轴的最大切应力发生在( D ) A 扭矩最大的截面; B 直径最小的截面; C 单位长度扭转角最大的截面; D 不能确定。
5.空心圆轴的外径为D ,内径为d, α=d /D,其抗扭截面系数为 ( D ) A ()31 16p D W πα=- B ()321 16p D W πα=-C ()331 16p D W πα=- D ()341 16pD Wπα=-6.对于受扭的圆轴,关于如下结论: ①最大剪应力只出现在横截面上;②在横截面上和包含杆件的纵向截面上均无正应力;③圆轴内最大拉应力的值和最大剪应力的值相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-1 一传动轴作匀速转动,转速,轴上装有五个轮子,主动轮Ⅱ输入的功率为60kW,从动轮,Ⅰ,Ⅲ,Ⅳ,Ⅴ依次输出18kW,12kW,22kW和8kW。
试作轴的扭矩图。
解:kN
kN
kN
kN
返回
3-2(3-3) 圆轴的直径,转速为。
若该轴横截面上的最大切应力等于,试问所传递的功率为多大
解:故
即
又
故返回
3-3(3-5) 实心圆轴的直径mm,长m,其两端所受外力偶矩,材料的切变模量。
试求:
(1)最大切应力及两端截面间的相对扭转角;
(2)图示截面上A,B,C三点处切应力的数值及方向;
(3)C点处的切应变。
解:=
返回
3-4(3-6) 图示一等直圆杆,已知,,,。
试求:
(1)最大切应力;
(2)截面A相对于截面C的扭转角。
解:(1)由已知得扭矩图(a)
(2)
返回
3-5(3-12) 长度相等的两根受扭圆轴,一为空心圆轴,一为实心圆轴,两者材料相同,受力情况也一样。
实心轴直径为d;空心轴外径
为D,内径为,且。
试求当空心轴与实心轴的最大切应力均达到材料的许用切应力),扭矩T相等时的重量比和刚度比。
解:重量比=
因为
即
故
故
刚度比=
=
返回
3-6(3-15) 图示等直圆杆,已知外力偶矩,,许用切应力,许可单位长度扭转角,切变模量。
试确定该轴的直径d。
解:扭矩图如图(a)
(1)考虑强度,最大扭矩在BC段,且
(1)
(2)考虑变形
(2)比较式(1)、(2),取
返回
3-7(3-16) 阶梯形圆杆,AE段为空心,外径D=140mm,内径d=100mm;BC段为实心,直径d=100mm。
外力偶矩,,。
已知:,,。
试校
核该轴的强度和刚度。
解:扭矩图如图(a)
(1)强度
=
,BC段强度基本满足
=
故强度满足。
(2)刚度
BC段:
BC段刚度基本满足。
AE段:
AE段刚度满足,显然EB段刚度也满足。
返回
3-8(3-17) 习题3-1中所示的轴,材料为钢,其许用切应力,切变模量,许可单位长度扭转角。
试按强度及刚度条件选择圆轴的直径。
解:由3-1题得:
故选用。
返回
3-9(3-18) 一直径为d的实心圆杆如图,在承受扭转力偶矩后,测得圆杆表面与纵向线成方向上的线应变为。
试导出以,d 和表示的切变模量G的表达式。
解:圆杆表面贴应变片处的切应力为
圆杆扭转时处于纯剪切状态,图(a)。
切应
变
(1)
对角线方向线应变:
(2)
式(2)代入(1):
返回
3-10(3-19) 有一壁厚为25mm、内径为250mm的空心薄壁圆管,其长度为1m,作用在轴两端面内的外力偶矩为180。
试确定管中的最大切应力,并求管内的应变能。
已知材料的切变模量。
解:
3-11(3-21) 簧杆直径mm的圆柱形密圈螺旋弹簧,受拉力作用,弹簧的平均直径为mm,材料的切变模量。
试求:
(1)簧杆内的最大切应力;
(2)为使其伸长量等于6mm所需的弹簧有效圈数。
解:,
故
因为
故圈
返回
3-12(3-23) 图示矩形截面钢杆承受一对外力偶矩。
已知材料的切变模量,试求:
(1)杆内最大切应力的大小、位置和方向;
(2)横截面矩边中点处的切应力;
(3)杆的单位长度扭转角。
解:,,
由表得
MPa。
