材料力学答案3扭转
合集下载
材料力学 第03章 扭转
sin 2 , cos 2
由此可知：
sin 2 , cos 2
(1) 单元体的四个侧面( = 0°和 = 90°)上切 应力的绝对值最大； (2) =-45°和 =+45°截面上切应力为零，而 正应力的绝对值最大；
[例5-1]图示传动轴，主动轮A输入功率NA=50 马力，从 动轮B、C、D输出功率分别为 NB=NC=15马力 ，ND=20马 力，轴的转速为n=300转/分。作轴的扭矩图。
解：
NA 50 M A 7024 7024 1170 N m n 300 NB 15 M B M C 7024 7024 351 m N n 300 NC 20 M D 7024 7024 468N m n 300
第3章
扭
转
§3.1
一、定义 二、工程实例 三、两个名词
概
述
一、定义
Me Me
扭转变形 ——在一对大小相等、转向相反的外力偶矩
作用下，杆的各横截面产生相对转动的
变形形式，简称扭转。
二、工程实例
1、螺丝刀杆工作时受扭。
Me
主动力偶
阻抗力偶
2、汽车方向盘的转动轴工作时受扭。
3、机器中的传动轴工作时受扭。
公式的使用条件：
1、等直的圆轴， 2、弹性范围内工作。
圆截面的极惯性矩 Ip 和抗扭截面系数Wp
实心圆截面：
2 A
I p d A (2π d )
2
d 2 0
O
2 π(
4
d /2
4
)
0
πd 4 32
d
d A 2π d
材料力学第三章 扭转
n
250
横截面上的最大切应力为
max
T Wt
T (D4 d 4)
16D
16 0.55573000 Pa 19.2MPa [ ] 50MPa (0.554 0.34 )
满足强度要求。
跟踪训练 7.机车变速箱第II轴如图所示，轴所传递的功率为
p 5.5KW,转速n 200r / min，材料为45钢，
（3）主动轮放在两从动轮之间可使最大扭矩取最小值
B
A
C
Me2
Nm
M e1
Me3
4220
2810
本章小结
1.外力偶矩的计算 内力的计算——扭矩图
P M e 9549 n (N m)
2.圆轴扭转切应力公式的建立
τρ
Tρ Ip
强度条件的应用
max
Tmax Wt
[ ]
刚度条件的应用
' max
T
180 [']
（3）主动轮和从动轮应如何安排才比较合理。
再根据平衡条件，可得 Me1 Me2 Me3 (2810 4220)N m 7030N m
所作扭矩图如右图
（1）试确定AB段的直径d1和BC段的直径d2。
根据强度条件确定AB直径d1
AB
TAB Wt
16TAB
d12
[ ]
根据刚度条件确定AB直径d1
mB
(a)
1
350 2
C
1
2
T1
11463
446
A
D
3
mB
(b)
(c) mB
mC
T2
mC
mA T3
mD
T1 350N m 350 1 350 2
材料力学-第三章扭转
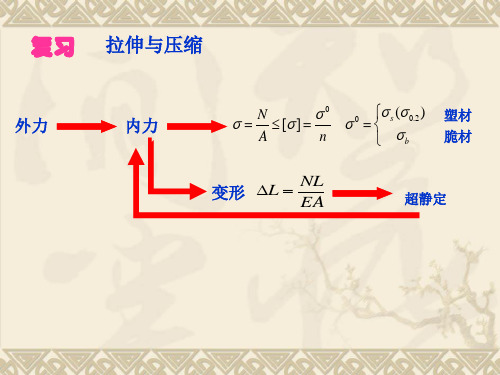
3、物理方程 mA a mA a AC 2GI p GI p
BC
2 mB a GI p
4 解得： m A 7 T 3 mB T 7
AB AC BC 0
例：由实心杆 1 和空心杆 2 组成的组合轴，受扭矩 T， 两者之间无相对滑动，求各点切应力。 T 解: 设实心杆和空心杆承担的扭矩分别为 G 2 Ip 2 M n 1 、 M n2 。 R2
二 刚度条件
M 180 刚度 n 0.50～1.0 / m 一般轴 l G Ip 条件
0.25～0.5 / m 精密轴
1.0 ～3.0 / m 粗糙轴
例 传动主轴设计，已知:n = 300r/m，P1 = 500kW，P2=200kW P3=300kW，G=80GPa [ ] 40MPa , [] 0.3 求：轴的直径d 解：1、外力分析
圆轴扭转的强度条件
max
Mn D Mn I p 2 Wp
Wp
2I p D
Mn
D 3 D 3 Wp 1 4 抗扭截面系数Wp : W p 16 16
强度条件：
Mn max Wp
例 已知汽车传动主轴D = 90 mm, d = 85 mm [ ] 60MPa, T = 1.5 kNm
Mn d
3
圆形优于矩形
Aa
= 0.208
3
a
3
4
3
d 0.886 d
2
Mn
a
2
Mn 0.208 0.886 d
b
6.913
材料力学第3章扭转
试问：纵向截面里的切应力是由什么内力平衡的？
§3.8 薄壁杆件的自由扭转
薄壁杆件：杆件的壁厚远小于截面的其它尺寸。 开口薄壁杆件：杆件的截面中线是不封闭的折线或曲
线，例如：工字钢、槽钢等。 闭口薄壁杆件：杆件的截面中线是封闭的折线或曲线，
例如：封闭的异型钢管。
一、开口薄壁杆的自由扭转
＝ Tl
GI t
变形特点：截面发生绕杆轴线的相对转动 本章主要研究圆截面等直杆的扭转
§3.2 外力偶矩的计算 扭矩和扭矩图
功率： P(kW) 角速度：ω 外力偶矩：Me
P = Meω
转速：n(r/min)
2n/ 60
Me
1000 P＝9549
P n
(N
m)
内力偶矩：扭矩 T 求法：截面法
符号规则： 右手螺旋法则 与外法线同向“ + ” 与外法线反向“－”
max
T max
It
It
1 3
hi
3 i
二、闭口薄壁杆的自由扭转
max
T
2 min
TlS
4G 2
其中：ω截面为中线所围的面积
S 截面为中线的长度
闭口薄壁杆的应力分布：
例： 截面为圆环形的开口和闭口薄壁杆件如图所 示，设两杆具有相同平均半径 r 和壁厚δ，试 比较两者的扭转强度和刚度。
开＝3 r 闭 开＝3( r )2 闭
8FD3n Gd 4
C
ห้องสมุดไป่ตู้
Gd 4 8D3n
F C
§3.7 矩形截面杆扭转的概念
1) 翘曲
变形后杆的横截面不再保持为平面的现象。
2) 自由扭转和约束扭转
自由扭转：翘曲不受限制的扭转。 各截面翘曲程度相同，纵向纤维无伸缩， 所以，无正应力，仅有切应力。
材料力学 扭转3
T i L i j = å i (GI P )i
二、刚度条件 对于传动轴，有时即使满足了强度条件，还不一定能保证它 正常工作。例如：机器的传动轴如有过大的扭转角，将会使机器 在运转中产生较大的振动；精密机床上的轴若变形过大，则将影 响机器的加工精度等。因此对传动轴的扭转变形要加以限制。 一般地说：标志杆件扭转变形的物理量有两个： 绝对扭转角 相对扭转角
4
d 2 = 76 mm
5.选同一直径时
d = d . 4 mm 1 = 86
d1
6.将主动轮按装在 两从动轮之间
C
M e 2
(- )
d 2 B
M e 3
A
M e 1
4580 N × m 7640 N × m
d1 C
受力合理
M e 2
A
M e 1
1.5kN∙m
j AC = j AB + j BC = 0. 0239 rad 0318 rad - 0 . 0079 rad = 0.
&
例题2
M 2
图示一空心传动轴，轮1为主动轮，力偶矩M1＝9KN∙m，轮2、轮 3、轮4为从动轮,力偶矩分别为M2＝4KN∙m，M3＝3.5KN∙m，M4＝ 1.5KN∙m。已知空心轴内外径之比d/D＝1/2，试设计此轴的外径D，并 求出全轴两端的相对扭转角φ24。G＝80GPa，［τ］＝60MPa。
t t¢
等直圆杆扭转时的应变能
x
dx
2 2
V e dAdx e = ò v e dV = ò ò v
V l A
1 = tg g 2
Tr = I P
=
材料力学答案03
T2 = M B + M C = 764 N ⋅ m Tmax = 764 N ⋅ m
其绝对值比第（1）种情况小，即对轴的受力有利。 3-3 试绘出图示截面上切应力的分布图，其中 T 为截面的扭矩。
(a1)
(b1)
(c1)
3-4 图示圆截面轴， AB 与 BC 段的直径分别为 d1 与 d 2 ，且 d1 = 4d 2 / 3 。求轴内的 最大扭转切应力。
ϕ = ∫ dϕ = ∫
l l
T (x ) dx GI p ( x )
上式适用于等截面圆轴和截面变化不大的圆锥截面轴。对等截面圆轴，若在长 l 的两横截面 间的扭矩 T 为常量，则
ϕ=
圆轴扭转的刚度条件为
Tl GI p
⎟ ≤ [θ ] θ max = ⎜ ⎜ GI ⎟ ⎝ p ⎠ max
⎛ T ⎞
对于等截面圆轴为 或
28
答 同一变速箱中的高速轴与低速轴指相对转速高低，其传递的功率相同（不计功率损 耗） ，啮合处线速度相同。要啮合处产生相同的线速度，则高速轴的啮合半径就较小；又因 为啮合处相互作用力相同，该作用力对啮合半径就较小的高速轴线产生的外力偶矩就较小， 从而在高速轴中产生的扭矩较小，故高速轴可做得较细。 3-12 图示轴 A 和套筒 B 牢固地结合在一起，两者切变模量分别为 G A 和 G B ，两端受扭 转力偶矩，为使轴和套筒承受的扭转相同而必须满足的条件是什么？
(
)
16 × 500 = 194 MPa ⎡ ⎛ 40 ⎞ 4 ⎤ 3 −9 π × 42 × 10 × ⎢1 − ⎜ ⎟ ⎥ ⎢ ⎝ 42 ⎠ ⎦ ⎥ ⎣
（2）若考虑薄壁 ，可求其平均扭转切应力
τ=
Me = 2 πR 2δ
材料力学第三章剪切和扭转
T
Ⅰ
T
d1
(a)
l
T (b)
D2
Ⅱ
T
l
36
3.3 等直圆杆扭转时的应力
解：
Wp1
πd13 16
Wp2
πD23 14
16
1,maxW Mpt11
T Wp1
16T πd13
2,ma xW M pt2 2W Tp2πD 2 311T 6 4
D 2 31 4 d 1 3
螺栓连接[图(a）]中，螺栓主要受剪切及挤压（局部压
缩）。
F
3
3.1 剪切
键连接[图(b）]中，键主要受剪切及挤压。
4
3.1 剪切
剪切变形的受力和变形特点： 作用在构件两侧面上的外力的合力大小相等、方向相 反，作用线相隔很近，并使各自推动的部分沿着与合 力作用线平行的受剪面发生错动。
受剪面上的内力称为剪力； 受剪面上的应力称为切应力；
3.3 等直圆杆扭转时的应力
传动轴的外力偶矩：
已知：
T2
T1
从动轮
n 主动轮
T3 从动轮
传动轴的转速 n ；某一轮上 所传递的功率
NK (kW)
作用在该轮上的外力偶矩T 。
一分钟内该轮所传递的功率等于其上外力偶矩所 作的功：
NK60 13 0(J)T2πn(Nm)
33
3.3 等直圆杆扭转时的应力
26
3.3 等直圆杆扭转时的应力
dj M t
d x GI pBiblioteka G djdx
GGMItp
Mt
Ip
等直圆杆扭转时横截面上切应力计算公式
Mt
O
材料力学_陈振中_习题第三章扭转
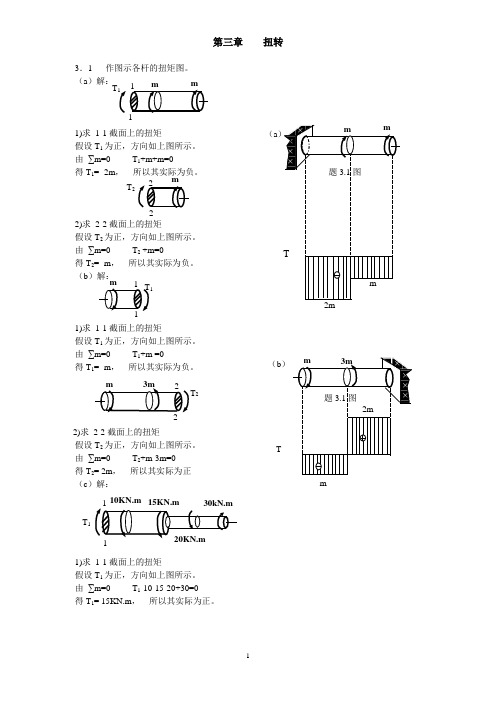
第三章 扭转3．1 作图示各杆的扭矩图。
（a ）解：1)求 1-1截面上的扭矩假设T 1为正，方向如上图所示。
由 ∑m=0 T 1+m+m=0得T 1= -2m ， 所以其实际为负。
2)求 2-2截面上的扭矩假设T 2为正，方向如上图所示。
由 ∑m=0 T 2 +m=0得T 2= -m ， 所以其实际为负。
（b ）解：1)求 1-1截面上的扭矩假设T 1为正，方向如上图所示。
由 ∑m=0 T 1+m =0得T 1= -m ， 所以其实际为负。
2)求 2-2截面上的扭矩假设T 2为正，方向如上图所示。
由 ∑m=0 T 2+m-3m=0 得T 2= 2m ， 所以其实际为正 （c ）解：1)求 1-1截面上的扭矩假设T 1为正，方向如上图所示。
由 ∑m=0 T 1-10-15-20+30=0得T 1= 15KN.m ， 所以其实际为正。
T 1T 2（a2（b ）mTT 12)求 2-2截面上的扭矩假设T 2为正，方向如上图所示。
由 ∑m=0 T 2-15-20+30=0得T 2= 5KN.m ， 所以其实际为正。
3)求 3-3截面上的扭矩 假设T 3为正，方向如上图所示。
由 ∑m=0 T 3-20+30=0得T 3= -10KN.m ， 所以其实际为负。
4)求 4-4截面上的扭矩假设T 4为正，方向如上图所示。
由 ∑m=0 T 4 +30=0得T 4= -30KN.m ， 所以其实际为负。
3.2 T 为圆杆横截面上的扭矩，试画出截面上与T 对应的剪应力分布图。
解：3.5 D=50mm 直径的圆轴，受到扭矩T=2.15KN .m 的作用。
试求在距离轴心10mm 处的剪应力，并求轴横截面上的最大剪应力。
T 230kN.m T 3T 4（题3.2图（a ） （b ）解：求距离轴心10mm 处的剪应力， 由 I P =πD 4/32=π×0.054/32=6.13×10-7 m 4 W t = I P /R=6.13×10-7/0.025=2.454×10-5 m 3τρ=Tρ/ I P =2.15×103×10×10-3/(6.13 ×10-7 ) =35MPa求轴横截面上的最大剪应力τmax =T/ W t =2.15×103/(2.454 ×10-5 ) =87.6MPa3.8 阶梯形圆轴直径分别为d 1=40mm ，d 2=70mm ，轴上装有三个皮带轮，如图所示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
π 2 则 ( D −d2 ) ×6 V 空 = 4 = 0.389 π 2 π 2 V 实 d1 ×4+ d2 ×2 4 4
T:
由于材料长度相同，所以空心轴的重量为实轴重量的38.9%。 由于材料长度相同，所以空心轴的重量为实轴重量的38.9%。
34
◆ 圆轴扭转时的强度和刚度设计
例题3 如图，已知M0=10KN·m， [τ]=60MPa，试绘扭矩图。 如图，已知M 10KN·m， ]=60MPa，试绘扭矩图。
解：此属于一次超静定。 此属于一次超静定。 静力方程， （1）静力方程，由∑Mx = 0 得 -MA-M0+M0+MB=0 MA=MB （2）变形几何方程 ） ϕAC +ϕCD +ϕDB = 0 （3）物理方程
MA ⋅ a ϕAC = GIp
(MA + M0)⋅ a ϕCD = GIp
MB ⋅ a ϕDB = GIp
dϕ T θ= = ≤ [θ ] dx GI P
θ max
Tmax 180 = × ≤ [θ ] GI P π
(° m)
29
◆ 圆轴扭转时的强度和刚度设计
已知：机床主轴箱内第4轴的传 例 题 1 已知：机床主轴箱内第 轴的传 动示意如图， 动示意如图，PⅡ ＝ 0.756kW， ， P Ⅳ ＝2.98kW, n=180.5 r/min,材 材 料为45钢 料为 钢，G=80GPa， ， [τ]=40MPa，[θ]=1.5(°)/m。 ， ° 。 设计轴的直径。 求: 设计轴的直径。 解：1）计算外力偶矩 ）
5
◆外力偶矩、扭矩、扭矩图 外力偶矩、扭矩、
扭 矩
截面法
T = Me
符号规定
6
◆外力偶矩、扭矩、扭矩图 外力偶矩、扭矩、
扭矩图 传动轴如图a 传动轴如图 所 示，主动轮 A 输入功 率为P 率为 A=36kW，从动 ， 轮输出功率为P 轮输出功率为 B= PC= 11kW， PD=14kW ， ， 轴的转速为 n=300r/min。 。 试画出轴的扭矩图。 试画出轴的扭矩图。
截面翘曲
矩形截面轴的自由扭转
切应力分布特点： 切应力分布特点：
1)沿边走 沿边走 2)角点为 角点为0 角点为 3)长边中点最大 长边中点最大 4)短边中点较大 短边中点较大
τmax
T = W t
T θ= GIt
It——相当极惯性矩 相当极惯性矩
39
◆ *非圆截面杆扭转时的切应力
狭长矩形截面
切应力表达式
a b
横截面保持平面， 横截面保持平面 ， 只能 发生刚性转动。 发生刚性转动。
c d
a b
c
γ
d
角应变γ (剪应变、切应变)：微元的 剪应变、切应变) 直角改变量
14
◆ 圆轴扭转时的应力
圆轴扭转变形特征
15
◆ 圆轴扭转时的应力
几何关系－ 几何关系－变形协调方程
dϕ γ (ρ) = ρ dx
16
◆ 圆轴扭转时的强度和刚度设计
例题2
BC段：同理，由扭转强度条件得 BC段 同理， 由扭转刚度条件得
d2 ≥ 67 (m ) m
d2 ≥ 74.5 (m ) m
取d2 = 74.5 (m ) m
（2）外径 D=84.6 mm，则内径 mm，
d = D⋅α = 0.8×84.6 = 67.68 (m ) m
◆ 圆轴扭转时的应力
物理关系－ 物理关系－剪切胡克定律
dϕ γ (ρ) = ρ dx
τ = Gγ
dϕ τ = Gγ = Gρ dx
17
◆ 圆轴扭转时的应力
静力关系－ 静力关系－静力学方程
静力关系
dϕ τ = Gγ = Gρ dx
dϕ T = dx G P I G---剪切弹模 ---剪切弹模 GIP—扭转刚度
2 A
其中：α = d / D
21
◆ 圆轴扭转时的应力 最大切应力
τmax
W = P
圆轴扭转时横截面上 的切应力表达式
Tρm T ax = = IP W P
扭截面系数 ρm 抗扭截面系数 ax
IP
πd3 实心圆截面 W = P 16
πD3 1 α4 － W= 圆环截面 P 16
(
)
其中：α = d / D
P 2 = 39.3 N⋅ m n P Me4 = 9549 4 =155 N⋅ m n Me3 = Me2 + Me4 =194.3 N⋅ m Me2 = 9549
2）画扭矩图 ） 3）强度校核 ） T 16 T τmax = max = max ≤[τ] W πD3 p
30
◆ 圆轴扭转时的强度和刚度设计
22
◆ 圆轴扭转时的应力
圆轴扭转时横截面上 的切应力表达式
切应力公式适用条件： 切应力公式适用条件：
Tρ τ(ρ) = IP
弹性范围 小变形 圆截面
23
◆ 圆轴扭转时的应力 纵截面上应力分布？ 纵截面上应力分布？
圆轴扭转时横截面上 的切应力表达式
切应力互等定理
τ =τ ′
24
◆ 圆轴扭转时的强度和刚度设计
例题1
16Tm ax D≥ = 27.2 m m π[τ ]
3
4）刚度计算 ）
θmax =
D≥ 4
T ax 180 m × ≤[θ] GIp π
32Tm ×180 ax = 29.5 m m 2 G [ϕ′] π
选 D=30 mm。
31
◆ 圆轴扭转时的强度和刚度设计
如图， 马力， 马力， ， 马力 马力 例 题 2 如图，传动轴 n=500r/min， P1=500马力， P2=200马力， P3=300马力，已知 [τ]=70MPa，[θ]=1o/m，G=80GPa。 马力， 马力 ， ， 。 求（1）确定 段，BC段直径。 确定AB段 段直径。 段直径 轴改为外径D=84.6mm， （2）轴改为外径 ， α=0.8的空心轴，比较两轴重量之比。 的空心轴， 的空心轴 比较两轴重量之比。 解（1） 1）计算外力偶矩
4
◆外力偶矩、扭矩、扭矩图 外力偶矩、扭矩、
外力偶矩 外力偶矩
1.功率为千瓦 1.功率为千瓦 n 2π × × M e = P × 1000 60
P(kW ) Me = 9549 (N⋅ m ) n (r/m ) in
2.功率为马力 2.功率为马力
P(马 ) 力 Me = 7024 (N⋅ m ) n (r/ m ) in
35
◆ 圆轴扭转时的强度和刚度设计
例题4 由几何和物理关系得补充方程
MA ⋅ a (MA +M0)⋅ a MB ⋅ a + + =0 GIp GIp GIp
2MA + M0 + MB = 0
MA=MB
M0 联立解得 MA = MB = − <0 3
“-”表示真实方向与假设的方向相反， 表示真实方向与假设的方向相反， 绘制扭矩图如图所示， 绘制扭矩图如图所示， 由图可知CD段为危险段。 由图可知CD段为危险段。 段为危险段
T 16T τmax = = 3 ≤[τ ] W πd1 t
16T 3 16×7024 d1 ≥ 3 = ≈80 (m ) m 6 π[τ ] π×70×10
T 180o ϕp = × ≤[ϕ] 4 πd1 π G 32
由扭转刚度条件
T:
d1 ≥ 84.6 (m ) m
取d1= 84.6 （mm）
33
1 3 It = hδ 3
τmax
T = δ It
T θ= GIt
40
◆ *非圆截面杆扭转时的切应力
切应力表达式
开口薄壁截面
1 3 It =η⋅ ∑ hδi i i= 3 1
41
n
◆ 圆轴扭转时的强度和刚度设计
已知： ＝ 已知：P＝7.5kW， n=100r/min， ， ， [τ]=40MPa，空心圆轴的内外直径 ， 之比 α = 0.5。二轴长度相同。 。二轴长度相同。 实心轴的直径d 求: 实心轴的直径 1和空心轴的外 直径D 确定二轴的重量之比。 直径 2；确定二轴的重量之比。 2）对于空心轴 ） 解：首先由轴所传递的功率计 ： 算作用在轴上的扭矩 16T T τmax 2 = = ≤[τ] P W 2 πD3(1−α4) Me =T = 9549× = 716.2 N⋅ m p 2 n 1）实心轴 ） 16T 3 D≥ = 0.046 m= 46 m m 2 4 T 16T π(1-α )[τ] τmax1 = = 3 ≤[τ] W1 πd1 3）重量之比 ） p
36
截面 扭转 的
矩形截面轴的扭转简介
平 面 假 设 不 再 存 在
37
◆ *非圆截面杆扭转时的切应力
截面翘曲
变形特征－翘曲
扭转后，横截面将不再保持平面 扭转后， 无正应力 自由扭转 ：翘曲程度相同 ——无正应力 翘曲程度相同
约束扭转 ：翘曲程度不同 ——有正应力 有正应力 翘曲程度不同
38
◆ *非圆截面杆扭转时的切应力
∫ (τdA)ρ ＝T
A
IP = ∫ ρ dA
2 A
18
◆ 圆轴扭转时的应力
切应力表达式
圆轴扭转时横截面上 的切应力表达式
dϕ 几何关系 γ (ρ) = ρ dx
物理关系
τ = Gγ
dϕ T = dx G P I
Tρ τ(ρ) = IP
静力关系
19
◆ 圆轴扭转时的应力
圆轴扭转时横截面上 的切应力表达式
P MeA = 7024 1 = 7024 (N⋅ m ) n
T:
Hale Waihona Puke MeB = 7024P 2 = 2809.6(N⋅ m ) n P MeC = 7024 3 = 4214.4(N⋅ m ) n
T:
由于材料长度相同，所以空心轴的重量为实轴重量的38.9%。 由于材料长度相同，所以空心轴的重量为实轴重量的38.9%。
34
◆ 圆轴扭转时的强度和刚度设计
例题3 如图，已知M0=10KN·m， [τ]=60MPa，试绘扭矩图。 如图，已知M 10KN·m， ]=60MPa，试绘扭矩图。
解：此属于一次超静定。 此属于一次超静定。 静力方程， （1）静力方程，由∑Mx = 0 得 -MA-M0+M0+MB=0 MA=MB （2）变形几何方程 ） ϕAC +ϕCD +ϕDB = 0 （3）物理方程
MA ⋅ a ϕAC = GIp
(MA + M0)⋅ a ϕCD = GIp
MB ⋅ a ϕDB = GIp
dϕ T θ= = ≤ [θ ] dx GI P
θ max
Tmax 180 = × ≤ [θ ] GI P π
(° m)
29
◆ 圆轴扭转时的强度和刚度设计
已知：机床主轴箱内第4轴的传 例 题 1 已知：机床主轴箱内第 轴的传 动示意如图， 动示意如图，PⅡ ＝ 0.756kW， ， P Ⅳ ＝2.98kW, n=180.5 r/min,材 材 料为45钢 料为 钢，G=80GPa， ， [τ]=40MPa，[θ]=1.5(°)/m。 ， ° 。 设计轴的直径。 求: 设计轴的直径。 解：1）计算外力偶矩 ）
5
◆外力偶矩、扭矩、扭矩图 外力偶矩、扭矩、
扭 矩
截面法
T = Me
符号规定
6
◆外力偶矩、扭矩、扭矩图 外力偶矩、扭矩、
扭矩图 传动轴如图a 传动轴如图 所 示，主动轮 A 输入功 率为P 率为 A=36kW，从动 ， 轮输出功率为P 轮输出功率为 B= PC= 11kW， PD=14kW ， ， 轴的转速为 n=300r/min。 。 试画出轴的扭矩图。 试画出轴的扭矩图。
截面翘曲
矩形截面轴的自由扭转
切应力分布特点： 切应力分布特点：
1)沿边走 沿边走 2)角点为 角点为0 角点为 3)长边中点最大 长边中点最大 4)短边中点较大 短边中点较大
τmax
T = W t
T θ= GIt
It——相当极惯性矩 相当极惯性矩
39
◆ *非圆截面杆扭转时的切应力
狭长矩形截面
切应力表达式
a b
横截面保持平面， 横截面保持平面 ， 只能 发生刚性转动。 发生刚性转动。
c d
a b
c
γ
d
角应变γ (剪应变、切应变)：微元的 剪应变、切应变) 直角改变量
14
◆ 圆轴扭转时的应力
圆轴扭转变形特征
15
◆ 圆轴扭转时的应力
几何关系－ 几何关系－变形协调方程
dϕ γ (ρ) = ρ dx
16
◆ 圆轴扭转时的强度和刚度设计
例题2
BC段：同理，由扭转强度条件得 BC段 同理， 由扭转刚度条件得
d2 ≥ 67 (m ) m
d2 ≥ 74.5 (m ) m
取d2 = 74.5 (m ) m
（2）外径 D=84.6 mm，则内径 mm，
d = D⋅α = 0.8×84.6 = 67.68 (m ) m
◆ 圆轴扭转时的应力
物理关系－ 物理关系－剪切胡克定律
dϕ γ (ρ) = ρ dx
τ = Gγ
dϕ τ = Gγ = Gρ dx
17
◆ 圆轴扭转时的应力
静力关系－ 静力关系－静力学方程
静力关系
dϕ τ = Gγ = Gρ dx
dϕ T = dx G P I G---剪切弹模 ---剪切弹模 GIP—扭转刚度
2 A
其中：α = d / D
21
◆ 圆轴扭转时的应力 最大切应力
τmax
W = P
圆轴扭转时横截面上 的切应力表达式
Tρm T ax = = IP W P
扭截面系数 ρm 抗扭截面系数 ax
IP
πd3 实心圆截面 W = P 16
πD3 1 α4 － W= 圆环截面 P 16
(
)
其中：α = d / D
P 2 = 39.3 N⋅ m n P Me4 = 9549 4 =155 N⋅ m n Me3 = Me2 + Me4 =194.3 N⋅ m Me2 = 9549
2）画扭矩图 ） 3）强度校核 ） T 16 T τmax = max = max ≤[τ] W πD3 p
30
◆ 圆轴扭转时的强度和刚度设计
22
◆ 圆轴扭转时的应力
圆轴扭转时横截面上 的切应力表达式
切应力公式适用条件： 切应力公式适用条件：
Tρ τ(ρ) = IP
弹性范围 小变形 圆截面
23
◆ 圆轴扭转时的应力 纵截面上应力分布？ 纵截面上应力分布？
圆轴扭转时横截面上 的切应力表达式
切应力互等定理
τ =τ ′
24
◆ 圆轴扭转时的强度和刚度设计
例题1
16Tm ax D≥ = 27.2 m m π[τ ]
3
4）刚度计算 ）
θmax =
D≥ 4
T ax 180 m × ≤[θ] GIp π
32Tm ×180 ax = 29.5 m m 2 G [ϕ′] π
选 D=30 mm。
31
◆ 圆轴扭转时的强度和刚度设计
如图， 马力， 马力， ， 马力 马力 例 题 2 如图，传动轴 n=500r/min， P1=500马力， P2=200马力， P3=300马力，已知 [τ]=70MPa，[θ]=1o/m，G=80GPa。 马力， 马力 ， ， 。 求（1）确定 段，BC段直径。 确定AB段 段直径。 段直径 轴改为外径D=84.6mm， （2）轴改为外径 ， α=0.8的空心轴，比较两轴重量之比。 的空心轴， 的空心轴 比较两轴重量之比。 解（1） 1）计算外力偶矩
4
◆外力偶矩、扭矩、扭矩图 外力偶矩、扭矩、
外力偶矩 外力偶矩
1.功率为千瓦 1.功率为千瓦 n 2π × × M e = P × 1000 60
P(kW ) Me = 9549 (N⋅ m ) n (r/m ) in
2.功率为马力 2.功率为马力
P(马 ) 力 Me = 7024 (N⋅ m ) n (r/ m ) in
35
◆ 圆轴扭转时的强度和刚度设计
例题4 由几何和物理关系得补充方程
MA ⋅ a (MA +M0)⋅ a MB ⋅ a + + =0 GIp GIp GIp
2MA + M0 + MB = 0
MA=MB
M0 联立解得 MA = MB = − <0 3
“-”表示真实方向与假设的方向相反， 表示真实方向与假设的方向相反， 绘制扭矩图如图所示， 绘制扭矩图如图所示， 由图可知CD段为危险段。 由图可知CD段为危险段。 段为危险段
T 16T τmax = = 3 ≤[τ ] W πd1 t
16T 3 16×7024 d1 ≥ 3 = ≈80 (m ) m 6 π[τ ] π×70×10
T 180o ϕp = × ≤[ϕ] 4 πd1 π G 32
由扭转刚度条件
T:
d1 ≥ 84.6 (m ) m
取d1= 84.6 （mm）
33
1 3 It = hδ 3
τmax
T = δ It
T θ= GIt
40
◆ *非圆截面杆扭转时的切应力
切应力表达式
开口薄壁截面
1 3 It =η⋅ ∑ hδi i i= 3 1
41
n
◆ 圆轴扭转时的强度和刚度设计
已知： ＝ 已知：P＝7.5kW， n=100r/min， ， ， [τ]=40MPa，空心圆轴的内外直径 ， 之比 α = 0.5。二轴长度相同。 。二轴长度相同。 实心轴的直径d 求: 实心轴的直径 1和空心轴的外 直径D 确定二轴的重量之比。 直径 2；确定二轴的重量之比。 2）对于空心轴 ） 解：首先由轴所传递的功率计 ： 算作用在轴上的扭矩 16T T τmax 2 = = ≤[τ] P W 2 πD3(1−α4) Me =T = 9549× = 716.2 N⋅ m p 2 n 1）实心轴 ） 16T 3 D≥ = 0.046 m= 46 m m 2 4 T 16T π(1-α )[τ] τmax1 = = 3 ≤[τ] W1 πd1 3）重量之比 ） p
36
截面 扭转 的
矩形截面轴的扭转简介
平 面 假 设 不 再 存 在
37
◆ *非圆截面杆扭转时的切应力
截面翘曲
变形特征－翘曲
扭转后，横截面将不再保持平面 扭转后， 无正应力 自由扭转 ：翘曲程度相同 ——无正应力 翘曲程度相同
约束扭转 ：翘曲程度不同 ——有正应力 有正应力 翘曲程度不同
38
◆ *非圆截面杆扭转时的切应力
∫ (τdA)ρ ＝T
A
IP = ∫ ρ dA
2 A
18
◆ 圆轴扭转时的应力
切应力表达式
圆轴扭转时横截面上 的切应力表达式
dϕ 几何关系 γ (ρ) = ρ dx
物理关系
τ = Gγ
dϕ T = dx G P I
Tρ τ(ρ) = IP
静力关系
19
◆ 圆轴扭转时的应力
圆轴扭转时横截面上 的切应力表达式
P MeA = 7024 1 = 7024 (N⋅ m ) n
T:
Hale Waihona Puke MeB = 7024P 2 = 2809.6(N⋅ m ) n P MeC = 7024 3 = 4214.4(N⋅ m ) n