分子动力学模拟实验报告doc
分子动力学模拟分析

分子动力学模拟分析分子动力学模拟(Molecular Dynamics Simulation,简称MD)是一种计算模拟分子运动的方法,可以研究分子的结构、动力学和相互作用等,对物质性质和功能的研究有重要作用。
在材料科学、化学、生物学等领域中得到广泛应用。
本文将从MD模拟基础、模拟流程及分析研究结果三个方面进行阐述。
一、MD模拟基础MD模拟的基础是牛顿力学和统计物理学,其中牛顿三定律和万有引力定律描述了分子的运动和相互作用;玻尔兹曼分布定律、统计力学中的最大熵原理以及热力学第二定律等描述了系统的宏观性质和热力学性质。
MD模拟将牛顿力学和统计物理学相结合,通过数值计算方法,从初状态的分子坐标、速度和势能等信息出发,重复计算分子在某个温度、压力下的运动轨迹和性质,模拟时间可以从纳秒到毫秒,有关联的分子之间,模拟精度可达到亚埃。
二、模拟流程MD模拟的主要流程包括体系构建、体系平衡和体系生产等阶段。
体系构建需要先定义体系的边界、所包含分子种类及其数量、分子初始坐标等,这一阶段可以是手动构建,也可以是从实验数据中获取分子坐标信息进行加工。
体系平衡一般需要先进行一个大规模的能量最小化,在此基础上,对体系进行一个温度和压力逐步升高或下降的过程,使体系逐步达到平衡态,也可以调整体系的偏倚参数,如盒子尺寸等,最终得到较为合理的平衡态体系。
在体系平衡的基础上,进行体系生产,对于所需要的性质,如动力学参数、能量铁达方程、径向分布函数、自相关函数等,在进行生产时需要对体系进行约束,如固定温度、压力、含水量等,得到精确的分子性质描述。
三、分析研究结果对MD模拟结果的分析对研究者而言极为重要,主要是对数据的可视化及其统计分析。
一般可以采用分析软件如VMD、GROMACS等对MD的轨迹文件进行可视化,对于分子的运动、某些物理性质的演化、分子图像变化等,可以做出一系列的动画或动图。
对于性质的统计分析,一般需要进行采样过程,对一定时刻内的数值进行平均,这样可减小误差。
分子动力学模拟

分子动力学模拟分子动力学模拟是一种重要的计算方法,用来研究分子体系的运动和相互作用。
该方法基于牛顿力学和统计力学的原理,通过数值模拟来预测和描述分子在不同条件下的行为。
在分子动力学模拟中,通过计算每个分子的受力和相互作用,可以得到关于分子位置、速度和能量等物理量的时间演化。
这些信息可以被用来研究分子体系的动力学、热力学和结构性质等。
为了进行分子动力学模拟,需要确定分子的力场和初始状态。
力场是一组描述分子分子间相互作用的数学函数,包括键的强度、键角的刚度、电荷分布等。
初始状态则是给定分子的初始位置和速度。
在分子动力学模拟中,分子受到的力主要来自于势能函数的梯度。
通过运用牛顿运动方程,可以计算得到每个分子的加速度,并进一步更新位置和速度。
这个过程重复进行,直到达到所需的模拟时间。
分子动力学模拟可以用来研究各种不同类型的分子体系。
例如,可以模拟液体中分子的运动和结构,以研究其流变性质和相变行为。
还可以模拟气体中分子的运动和相互作用,以研究化学反应和传输过程。
此外,分子动力学模拟还可以用来研究固体材料的力学性质和热导率等。
通过模拟材料内部原子的动力学行为,可以计算材料的弹性模量、杨氏模量等力学性质。
同时,还可以计算材料的热导率,从而了解其热传导性能。
分子动力学模拟已经成为了许多领域的重要工具。
它在材料科学、生物科学、化学工程和环境科学等领域中都得到了广泛应用。
通过模拟和理解分子体系的行为,我们可以更好地设计新材料、药物和催化剂,以及解决各种科学和工程问题。
然而,分子动力学模拟也有一些局限性。
首先,模拟的时间尺度受到限制,通常只能模拟纳秒或微秒级别的时间。
其次,模拟的精度也受到一定的限制,特别是在处理量子效应和极化效应等方面。
为了克服这些限制,研究人员正在发展和改进分子动力学模拟的方法。
例如,开发更精确的势能函数和更高效的计算算法,可以提高模拟的时间尺度和精度。
同时,与实验相结合,通过验证和修正模型,也可以提高模拟的可靠性和预测能力。
分子动力学模拟实验的原理与方法

分子动力学模拟实验的原理与方法一、引言分子动力学模拟实验是一种基于分子运动规律的计算方法,通过模拟分子间相互作用力和运动轨迹,可以研究物质的结构、性质和动力学过程。
本文将介绍分子动力学模拟实验的原理与方法,包括模拟算法、模拟体系的构建和模拟结果的分析。
二、分子动力学模拟的原理分子动力学模拟实验基于牛顿力学和统计力学的原理,通过求解分子系统的运动方程,模拟分子间相互作用力和运动轨迹。
其基本原理可以概括为以下几点:1. 分子运动方程分子动力学模拟实验中,每个分子都被看作是一个质点,其运动方程可以由牛顿第二定律得到。
根据分子的质量、受力和加速度,可以得到分子的位置和速度随时间的变化。
2. 分子间相互作用力分子间的相互作用力可以通过势能函数来描述,常见的势能函数包括Lennard-Jones势和Coulomb势。
这些势能函数描述了分子间的吸引力和排斥力,从而影响分子的相互作用和运动。
3. 温度和压力控制分子动力学模拟实验中,为了模拟实际系统的温度和压力条件,需要引入温度和压力控制算法。
常见的温度控制算法包括Berendsen热浴算法和Nosé-Hoover热浴算法,压力控制算法包括Berendsen压力控制算法和Parrinello-Rahman压力控制算法。
三、分子动力学模拟的方法分子动力学模拟实验的方法包括模拟算法、模拟体系的构建和模拟结果的分析。
下面将对这些方法进行介绍。
1. 模拟算法分子动力学模拟实验中,常用的模拟算法包括经典力场方法和量子力场方法。
经典力场方法基于经验势能函数,适用于大尺度的分子系统,如蛋白质和溶液。
量子力场方法基于量子力学原理,适用于小尺度的分子系统,如分子反应和电子结构计算。
2. 模拟体系的构建模拟体系的构建是分子动力学模拟实验中的重要步骤,包括选择模拟系统、确定初始结构和参数设置。
模拟系统的选择应根据研究的目的和问题,可以是单个分子、溶液系统或固体表面。
初始结构可以通过实验数据、计算方法或模型生成,参数设置包括力场参数、温度和压力等。
分子模拟综合实验
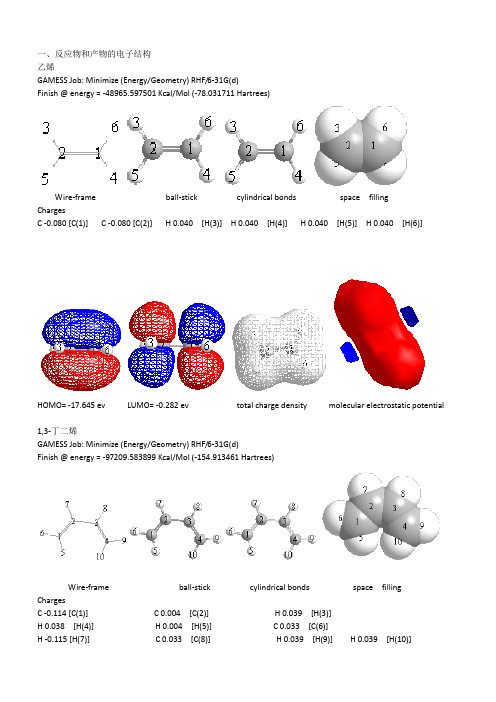
一、反应物和产物的电子结构乙烯GAMESS Job: Minimize (Energy/Geometry) RHF/6-31G(d)Finish @ energy = -48965.597501 Kcal/Mol (-78.031711 Hartrees)Wire-frame ball-stick cylindrical bonds space fillingChargesC -0.080 [C(1)] C -0.080 [C(2)] H 0.040 [H(3)] H 0.040 [H(4)] H 0.040 [H(5)] H 0.040 [H(6)]HOMO= -17.645 ev LUMO= -0.282 ev total charge density molecular electrostatic potential1,3-丁二烯GAMESS Job: Minimize (Energy/Geometry) RHF/6-31G(d)Finish @ energy = -97209.583899 Kcal/Mol (-154.913461 Hartrees)Wire-frame ball-stick cylindrical bonds space fillingChargesC -0.114 [C(1)] C 0.004 [C(2)] H 0.039 [H(3)]H 0.038 [H(4)] H 0.004 [H(5)] C 0.033 [C(6)]H -0.115 [H(7)] C 0.033 [C(8)] H 0.039 [H(9)] H 0.039 [H(10)]HOMO= -15.068 ev LUMO= -3.719ev total charge density molecular electrostatic potential环己烯GAMESS Job: Minimize (Energy/Geometry) RHF/6-31G(d)Finish @ energy = -146221.8807 Kcal/Mol (-233.019592 Hartrees)Wire-frame ball-stick cylindrical bonds space fillingChargesC -0.059 [C(1)] C -0.059 [C(2)] H -0.073 [H(3)] C -0.073 [C(4)]C -0.082 [C(5)] H 0.030 [H(6)] H -0.082 [H(7)] C 0.030 [C(8)]H 0.052 [H(9)] H 0.052 [H(10)] H 0.052 [H(11)] H 0.052 [H(12)]H 0.040 [H(13)] C 0.040 [C(14)] H 0.040 [H(15)] H 0.040 [H(16)]HOMO= -14.895 ev LUMO= 1.618 ev total charge density molecular electrostatic potential从分子轨道的对称性来看,乙烯的HOMO轨道关于镜面呈对称,LUMO反对称,丁二烯的HOMO反对称,LUMO 对称,环己烯HOMO对称,LUMO反对称。
分子动力学模拟实验报告doc

分子动力学模拟实验报告篇一:分子动力学实验报告 md2分子动力学实验报告( XX 至 XX 学年第_2_学期)班级:姓名:学号:实验名称:晶体点缺陷成绩:一、实验目的计算空位形成能和间隙原子形成能。
探究形成的空位和间隙原子所在的位置不同其形成能的变化。
以及空位和间隙原子的浓度不同时其空位能和间隙原子形成能的变化。
二、实验原理点缺陷普遍存在于晶体材料中,它是晶体中最基本的结构缺陷,对材料的物理和化学性质影响很大。
根据点缺陷相对于理想晶格位置可能出现的几种主要偏差状态,可将其命名如下:(1)空位:正常节点位置上出现的原子空缺。
(2)间隙原子(离子):指原子(离子)进入正常格点位置之间的间隙位(本文来自:小草范文网:分子动力学模拟实验报告)置。
(3)杂质原子(离子):晶体组分意外的原子进入晶格中即为杂质,杂质原子若取代晶体中正常格点位置上的原子(离子)即为置换原子(离子),也可进入正常格点位置之间的间隙位置而成为填隙的杂质原子(离子)。
一般情况下,空位、间隙原子都是构成晶体的原子或离子偏离原有格点所形成的热缺陷。
在一定温度下,晶体中各原子的热振动状态和能量并不同,遵循麦克斯韦分布规律。
热振动的原子某一瞬间可能获得较大的能量,这些较高能量的原子可以挣脱周围质点的作用而离开平衡位置,进入到晶格内的其他位置,于是在原来的平衡格点位置上留下空位。
根据原子进入晶格内的不同位置,可以将缺陷分为弗伦克尔(Frenkel)缺陷和肖特基(Schottky)缺陷。
点缺陷都只有一个原子大小的尺度,因此不容易通过实验对其进行直接的观察。
而且实验方法研究缺陷时利用较多的还是缺陷对晶体性质的影响。
例如,通过测量晶体的膨胀率和电阻率的变化规律,即可对点缺陷的存在、运动和相互作用等方面展开间接的研究。
分子动力学方法对金属材料原子尺度物理和化学过程的研究具有实验法无法比拟的优势,可直观的模拟和分析晶体中的点缺陷。
若我们搭建完整晶体的原子个数为N,能量为E1,通过删除和增加一个原子得到空位和间隙原子,充分弛豫后体系能量为E2,则空位形成能Ev 和间隙原子形成能Ei分别为:三、实验过程(1)进入2_point文件夹$cd口2_point(2)运行in.inter文件,得到Cu的八面体间隙原子的图像,以及体系的总能量的变化,计算出八面体间隙原子的形成能。
分子动力学模拟

qk2
π k1 4π ε 0
校正项
Vcorrection
2π 3L3
|
N i 1
qi 4π ε 0
ri
|2
能量极小化
Energy Minimization
最速下降法方法, Steepest Descent 3N 笛卡尔坐标 沿负梯度方向
方向
Sk
gk | gk
|
X k1 X k λ k Sk
截断半径
范德华相互作用 0.8A
静电
1.4A
Ewald加和
Ewald 1921提出用于一个粒子与盒子中其它粒子以及 周期性盒子中其它粒子的相互作用
立方体边长 (iL, jL,kL) i,j,k=0,1,2,3….
在中心盒中有N个电荷,电荷-电荷相互作用
V 1 N N qi q j
3
exp(
α
2r
2
)
π2
实空间
V 1 N N qi q j erf c(α | rij nL)
2 i1 4 j 1 |n|0 ε 0
| rij nL
误差函数
erf c(x)
2 exp(t 2 )dt
x
收敛快, 收敛快慢取决于高斯函 数的宽度α越大收敛越快
]T (t)
λ {1 2Cvdf t [ T0
1
1]}2
1
Cvdf
t [
T0
1]
kb τ T T (t)
kb τ T T (t)
vnew λ
vold
{1
Cvdf kb
t τT
[ T0 T (t)
1]}vold
分子动力学计算(实验报告)

4.使用LST/QST/CG方法计算过渡态结构a.Calculation,setup选项卡,Task改为TS Search。
more中确保Search protocol设置为Complete LST/QST,Quality设置为Mediumb.Job control选项卡,确保Automatic未被选中,输入TS作为Job description。
点击run第二部分:实验调试与结果分析三、调试过程(包括调试方法描述、实验数据记录,实验现象记录,实验过程发现的问题等)1.建立气体H2模型。
为使缩放过程明显,将H-H键长设为0.8埃Calculation中设置如下,模拟结构中原子在计算力影响下的移动2.建立Pd(111)表面模型,真空厚度为7.00埃3.将a=0.56, b=0.47, c=0.70的H1和a=0.47, b=0.56, c=0.70的H2原子到reactants中Pd表面。
后束缚全部的Pd原子。
4.在products中改变两个H原子的坐标,并使每个H原子键合一个Pd原子再使用CASTEP|Calculation优化几何结构,设置截图如下对reactants执行相同优化。
优化后两个原子文档如下5.对products和reactants的优化结构中的原子进行配对。
可见开始时0个原子被配对,8个原子未配对Auto Find后对对应的原子set match, 使两个文档中所有原子配对配对后Preview,事先确保number of frame值为10,得reactants-products.xtd轨迹文件6.使用LST/QST/CG方法计算过渡态结构。
设置截图如下得TS.xsd文档。
对此文档进行Analysis,选择Energy evolution,点击view, 得TS.xtd及TS TSSeaarch.xcd图表文件。
点击图上不同点可查看轨迹文件中相应结构四、实验结果及分析(包括结果描述、实验现象分析、影响因素讨论、综合分析和结论等)1.在TS.CASTEP中搜索Transition State Found,结果如下:得(1)反应能量:0.06565eV(2)来自反应物的能垒:0.03465eV(3)来自产物的能垒:-0.03100eV2.点击TS Search图中不同点,可在TS.xtd中查看相应结构通过TS Search亦可得出反应活化能(起始点至反应峰顶):E a=-4815.97-(-4819.59)=3.62eV五.思考题1.反应势垒是什么?答:物质在发生化学反应时,需要先破坏原有的化学键,这样就需要一定的能量,这个能量称之为化学势垒2.研究和了解反应的过渡态有什么意义?反应的过渡态:在反应物相互接近的反应进程中,出现一个能量比反应物与生成物均高的势能最高点,此势能最高点相对应的结构称为过渡态。
分子动力学模拟(两篇)

引言概述:分子动力学模拟(MD)是一种模拟系统内原子或分子运动的计算方法,通过计算原子之间的相互作用力和运动方程,可以研究材料的物理和化学性质、相互作用和动态行为等。
本文将深入探讨分子动力学模拟的相关内容,包括模拟算法、分子模型构建、初始条件设定、系统参数调优、结果分析等。
正文内容:一、模拟算法1.1简单分子动力学模拟算法:介绍经典分子动力学模拟的基本原理和算法。
1.2高级模拟算法:介绍一些基于统计力学和量子力学原理的高级分子动力学模拟算法,如MonteCarlo方法和量子分子动力学模拟。
二、分子模型构建2.1原子选择:根据研究对象和目的,选择适合的原子种类。
2.2原子间相互作用模型:介绍常用的原子间相互作用势函数模型,如LennardJones势和Coulomb势等。
2.3拓扑构建:说明如何根据分子结构构建拓扑,包括原子连接方式和键长、键角、二面角等参数。
三、初始条件设定3.1初始构型:介绍如何原子或分子的初始位置和速度。
3.2温度控制:讨论如何在模拟中控制温度,包括使用温度计算公式和应用恒温算法等。
3.3压力控制:介绍如何在模拟中控制压力,包括应用压力计算公式和应用恒压算法等。
四、系统参数调优4.1时间步长选择:讲解如何选择合适的时间步长,以确保模拟结果的准确性和稳定性。
4.2模拟时间长度:介绍如何选取适当的模拟时间长度,以获得足够的统计样本。
4.3系统尺寸选择:探讨系统尺寸对模拟结果的影响,包括边界条件的选择和静电相互作用的处理。
五、结果分析5.1动力学参数计算:介绍如何通过模拟数据计算动力学参数,包括径向分布函数和速度自相关函数等。
5.2结构参数分析:讨论如何分析模拟结果中的结构特征,如配位数、键长分布和角度分布等。
5.3物理性质计算:讲解如何通过模拟数据计算材料的物理性质,如热力学性质和动力学性质等。
总结:分子动力学模拟是一种强大的计算工具,可以模拟和研究材料的动态行为和性质。
从模拟算法、分子模型构建、初始条件设定、系统参数调优到结果分析,每个步骤都需要仔细考虑和调整,以保证模拟结果的准确性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分子动力学模拟实验报告篇一:分子动力学实验报告 md2分子动力学实验报告( XX 至 XX 学年第_2_学期)班级:姓名:学号:实验名称:晶体点缺陷成绩:一、实验目的计算空位形成能和间隙原子形成能。
探究形成的空位和间隙原子所在的位置不同其形成能的变化。
以及空位和间隙原子的浓度不同时其空位能和间隙原子形成能的变化。
二、实验原理点缺陷普遍存在于晶体材料中,它是晶体中最基本的结构缺陷,对材料的物理和化学性质影响很大。
根据点缺陷相对于理想晶格位置可能出现的几种主要偏差状态,可将其命名如下:(1)空位:正常节点位置上出现的原子空缺。
(2)间隙原子(离子):指原子(离子)进入正常格点位置之间的间隙位(本文来自:小草范文网:分子动力学模拟实验报告)置。
(3)杂质原子(离子):晶体组分意外的原子进入晶格中即为杂质,杂质原子若取代晶体中正常格点位置上的原子(离子)即为置换原子(离子),也可进入正常格点位置之间的间隙位置而成为填隙的杂质原子(离子)。
一般情况下,空位、间隙原子都是构成晶体的原子或离子偏离原有格点所形成的热缺陷。
在一定温度下,晶体中各原子的热振动状态和能量并不同,遵循麦克斯韦分布规律。
热振动的原子某一瞬间可能获得较大的能量,这些较高能量的原子可以挣脱周围质点的作用而离开平衡位置,进入到晶格内的其他位置,于是在原来的平衡格点位置上留下空位。
根据原子进入晶格内的不同位置,可以将缺陷分为弗伦克尔(Frenkel)缺陷和肖特基(Schottky)缺陷。
点缺陷都只有一个原子大小的尺度,因此不容易通过实验对其进行直接的观察。
而且实验方法研究缺陷时利用较多的还是缺陷对晶体性质的影响。
例如,通过测量晶体的膨胀率和电阻率的变化规律,即可对点缺陷的存在、运动和相互作用等方面展开间接的研究。
分子动力学方法对金属材料原子尺度物理和化学过程的研究具有实验法无法比拟的优势,可直观的模拟和分析晶体中的点缺陷。
若我们搭建完整晶体的原子个数为N,能量为E1,通过删除和增加一个原子得到空位和间隙原子,充分弛豫后体系能量为E2,则空位形成能Ev 和间隙原子形成能Ei分别为:三、实验过程(1)进入2_point文件夹$cd口2_point(2)运行in.inter文件,得到Cu的八面体间隙原子的图像,以及体系的总能量的变化,计算出八面体间隙原子的形成能。
$lmp口-i口in.inter(3)为了使八面体间隙原子的形成能最小,使得八面体间隙原子充分弛豫,修改八面体插入原子的坐标,改为(0.5,0.25,0.5)运行文件,得到相应的图像及体系变化前后的能量,计算出八面体间隙原子的形成能。
$gedit口in.inter(4)修改输入文件in.inter,将增加的原子坐标改为0.25 0.25 0.25.之后重复上述步骤,得到四面体间隙原子的图像以及体系能量的改变前后的能量,计算出四面体间隙原子的形成能。
$gedit口in.inter(5)再次打开in.inter文件,修改原子的位置,将插入的原子坐标修改为(0.5,0.25,0.5),再次运行文件,得到相应的图像与变化前后的能量,得到体系最稳定的状态,此时八面体间隙原子的形成能最小。
$gedit口in.inter(6)之后继续尝试,加入两个八面体间隙原子,修改坐标使得两个八面体间隙原子分别在一个晶胞的体心和棱上(坐标分别为(0.5,0.5,,05),(1,1,0.5)),两个八面体间隙原子在相邻的两个晶胞中的体心(坐标分别为(0.5,0.5,0.5),(0.5,1.5,0.5)),两个八面体间隙原子在同一个晶胞内的相邻的两条棱上(坐标分别为(1,1,0.5),(1,2,0.5)),两个八面体间隙原子在相隔较远的两个晶胞之内(1.5,1.5,1.5),(3.5,3.5,3.5)。
得到相应的效果图并计算出每种情况下的间隙原子的形成能。
$gedit口in.inter(7)仿照八面体间隙原子,修改四面体间隙原子的坐标,使得两个原子的相对位置分别为再同一个晶胞中,两个四面体间隙原子的插入位置分别为为相邻(两个原子的坐标为(0.25,0.25,0.25),(0.75,0.25,0.25)),在面对角线上(两个原子的坐标分别为(0.75,0.75,0.25)),在体对角线上(坐标分别为(0.25,0.25,0.25),(0.75,0.75,0.75))和在相隔较远的两个晶胞中的四面体间隙原子(坐标分别为(1.25,1.25,1.25),(4.25,4.25,4.25))。
得到相应的效果图并计算出每一种情况下的间隙原子的形成能。
$gedit口in.inter(8)改变体系的大小以改变八面体间隙原子的浓度,将晶胞的个数分别改为3×3×3,4×4×4,5×5×5,7×7×7,8×8×8,分别运行,分别计算出相应的体系的间隙原子的形成能。
$gedit口in.inter(9)运行in.vacancy文件,得到空位的图像和体系改变前后的能量,并计算出空位的行成能。
$lmp口-i口in.vacancy(10)修改in.vacancy文件,加入region centerpoint2 block 1 1.05 2 2.05 1 1.05 delete_atoms region centerpoint2增加一个空位之后运行文件,得到相应的效果图和体系变化前后的能量并计算空位形成能。
$lmp口-i口in.vacancy(11)修改in.vacancy文件,改变体系的大小以改变考位的浓度,将晶胞的个数分别改为3×3×3,4×4×4,5×5×5,7×7×7,8×8×8,分别运行,计算出每种浓度下空位的形成能。
$lmp口-i口in.vacancy四、实验结果1.间隙原子(1)八面体间隙原子效果图四面体间隙原子效果图:Ev=3.297eVEv=3.618eV(2)八面体间隙原子能量最低时效果图(呈哑铃形)Ev=3.1197eV(3)八面体原子对效果图:a(分别在一个晶胞内的体心和棱上),b(在相邻两个晶胞的体心),c(一个晶胞内的相邻两条棱),d(距离较远的两个晶胞中)a .Ev=2.92eVb. Ev=3.06eVc.Ev=2.96eVd.Ev=3.15eV(4)四面体间隙原子对效果图:a(同一个晶胞中的两个四面体间隙原子,相邻),b(同一个晶胞中的两个四面体间隙原子,面对角线),c(同一个晶胞中的两个四面体间隙原子,体对角线),d(相隔较远的两个晶胞中的四面体间隙原子)a.Ev=3.285eVb.Ev=2.87c.Ev=3.649eVd.Ev=3.645eV篇二:MS计算模拟实验报告固体结构及电子态计算模拟实验报告一、实验目的通过实际操作初步地了解和掌握Materials Studio,特别是其中的Dmol3和Castep模块的工作原理和操作步骤。
通过学习Materials Studio软件,能够自己独立地进行简单的固体结构模型的构造和相关电子结构的计算和分析。
二、实验原理第一性原理的理论计算的主要理论基础是量子力学的基本方程和相对论效应,在第一性原理的发展过程中,相继提出了变分原理、泡利不相容原理、Hartree-Fock近似、Slater矩阵、关联相互能、密度泛函理论以及含时密度泛函理论等。
其基本思路就是它的基本思想是将多原子构成的实际体系理解为由电子和原子核组成的多粒子系统,运用量子力学等基本的物理原理最大限度地对问题进行“非经验”处理。
密度泛函理论现在已经成为计算凝聚态物理的重要理论基础,并被广泛应用于原子、分子、团簇、固体和表面的几何结构和电子结构的计算。
随着计算机的高速发展,使得计算物理成为可能。
依靠高性能计算机强大的计算能力,市场上研发出了很多基于第一性原理计算(尤其是密度泛函理论方法)的软件包。
其中最具代表性的就是Materials studio。
其模块中的Dmol3程序是一个先进的密度泛函框架下的量子力学程序,它不仅可以模拟固体、表面、低维体系,而且能够模拟气相和液相。
它可以计算体系的能量,能带结构,态密度,磁性等。
三、实验主要步骤⑴建立α石英晶体:①选择P3221空间群;②确定晶格参数;③加入Si和O原子,确定相关参数;⑵ AlAs半导体能带结构及相关计算①导入AlAs半导体结构,并选择单胞;②在Dmol3模块中选择Calculation,设置能带结构计算的相关参数;③计算完毕,选中得到的*.xsd文件;④在Dmol3没款中选择analysis,选择Band structure 后点击View,得到能带图;⑤同理可以计算AlAs的电子态密度、电子密度等。
四、数据分析及实验结果展示图为α石英晶体,其中黄色+是硅原子,红色+是氧原子。
如图是Materials studio 7 中系统自带的α石英晶体的空间结构。
发现跟之前做的略有差别,结构图中还包含了Si-O键,其中各个原子在空间上的位置与上图是一一对应的。
为了画出系统自带α石英晶体空间结构图的效果,需要对图形做一些修饰。
右击背景选择Display Style 可以对atom和lattice的样式作出修改。
在菜单build中选择bond,画出Si-O键后,与系统自带的标准图就十分相似了。
左图是AlAs空间结构图;右图是AlAs在单胞中的空间结构图。
如图,是通过Dmol3模块计算得到的AlAs能带结构(纵坐标的能量单位是Hartree,1Hartree=27.2eV)。
从图中可以看出AlAs的价带顶和导带底之间存在一定宽度的能隙,宽度大约为0.1Ha(2.2eV),能隙宽度正好是半导体材料范围,所以从能带中可以看出AlAs材料是一种半导体。
如图,是通过Dmol3模块计算得到的AlAs电子态密度图。
电子态密度图在-0.4-0.35Ha之间有一个峰,在0-0.1Ha有个谷,基本上和能带结构相吻合。
如图,是通过Dmol3计算得到的电子密度图。
五、体会和评论Materials studio作为一个成熟的商业化科研软件,的确非常好用,大量的图形界面便于初学者快速上手。
因为研究方向相近(分子动力学模拟)的缘故,平时也经常需要进行大量运算,所用的软件为Gromacs和NAMD。
由于都是开源软件,其使用起来就没有那么方便,都需要在Linux系统下通过命令行来完成任务,图形显示也需要借助第三方软件才能完成。
分子动力学模拟的理论基础是牛顿第三定律为中心的经典力学,研究原子之间的相互作用,整个体系通常会包含几千甚至几万个原子。
而第一性原理计量是基于量子力学,虽然研究的体系相对小,但是计算量也非常大,对于较为复杂的系统单单依靠PC端是无法完成的,所以特别了解了下,Materials studio也有Linux系统下的版本,支持多核多节点运算。
