七年级数学上册整式计算题专项练习(有答案)
七年级数学上册整式计算题专项练习(含答案)
整式的乘除计算训练（1）1. )2()(b a b a -++-2. (x+2)(y+3)-(x+1)(y-2)3. 22)2)(2(y y x y x ++-4. x(x －2)－(x+5)(x －5)5. ⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--y x y x 224 6. )94)(32)(23(22x y x y y x +--- 7. ()()3`122122++-+a a 8. ()()()2112+--+x x x9. (x －3y)(x+3y)－(x －3y)2 10. 23(1)(1)(21)x x x +--- 11. 22)23()23(y x y x --+ 12. 22)()(y x y x -+13. 0.125100×8100 14. 30022)2(21)x (4554---÷⎪⎭⎫ ⎝⎛--π-+⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛ 15. (1211200622332141）（）（）（）-⨯+---- 16—19题用乘法公式计算16.999×1001 17.1992-18.298 19.2010200820092⨯-20.化简求值：)4)(12()12(2+-+-a a a ，其中2-=a 。
21. 化简求值2(2)2()()2(3)x y x y x y y x y +--++-,其中12,2x y =-=。
22. 5(x －1)(x +3)－2(x －5)(x －2) 23. (a －b )(a 2+ab +b 2)24. (3y +2)(y －4)－3(y －2)(y －3) 25. a (b －c )+b (c －a )+c (a －b )26. (－2mn 2)2－4mn 3(mn +1) 27. 3xy (－2x )3·(－41y 2)228. (－x －2)(x +2) 29. 5×108·(3×102)30. (x －3y )(x +3y )－(x －3y )2 31. (a +b －c )(a －b －c )答案1. 2. 3. 4.5. 6. 7. 8.9. 10. 11. 12.13. 14. 15.16. 原式=(1000-1)(1000+1) 17. 原式=(99+1)(99-1)=1000000-1 =10098=999999 =980018. 原式=(900-2)2 19. 原式=20092-(2009+1)(2009-1)=10000-400+4 =20092-20092+1=9604 =120.原式=，当时，原式=21.原式=，当，时，原式=22. 23. 24. 25. 026. 27. 28. 29.30. 31.2014年北师大七年级数学上册《整式及其加减》计算题专项练习一一．解答题（共12小题）1．计算题①12﹣（﹣8）+（﹣7）﹣15；②﹣12+2×（﹣5）﹣（﹣3）3÷；③（2x﹣3y）+（5x+4y）；④（5a2+2a﹣1）﹣4（3﹣8a+2a2）．2．（1）计算：4+（﹣2）2×2﹣（﹣36）÷4；（2）化简：3（3a﹣2b）﹣2（a﹣3b）．3．计算：（1）7x+4（x2﹣2）﹣2（2x2﹣x+3）；（2）4ab﹣3b2﹣[（a2+b2）﹣（a2﹣b2）]；（3）（3mn﹣5m2）﹣（3m2﹣5mn）；（4）2a+2（a+1）﹣3（a﹣1）．4．化简（1）2（2a2+9b）+3（﹣5a2﹣4b）（2）3（x3+2x2﹣1）﹣（3x3+4x2﹣2）5．（2009•柳州）先化简，再求值：3（x﹣1）﹣（x﹣5），其中x=2．6．已知x=5，y=3，求代数式3（x+y）+4（x+y）﹣6（x+y）的值．7．已知A=x2﹣3y2，B=x2﹣y2，求解2A﹣B．8．若已知M=x2+3x﹣5，N=3x2+5，并且6M=2N﹣4，求x．9．已知A=5a2﹣2ab，B=﹣4a2+4ab，求：（1）A+B；（2）2A﹣B；（3）先化简，再求值：3（A+B）﹣2（2A﹣B），其中A=﹣2，B=1．10．设a=14x﹣6，b=﹣7x+3，c=21x﹣1．（1）求a﹣（b﹣c）的值；（2）当x=时，求a﹣（b﹣c）的值．11．化简求值：已知a、b满足：|a﹣2|+（b+1）2=0，求代数式2（2a﹣3b）﹣（a﹣4b）+2（﹣3a+2b）的值．12．已知（x+1）2+|y﹣1|=0，求2（xy﹣5xy2）﹣（3xy2﹣xy）的值．2014年北师大七年级数学上册《整式及其加减》计算题专项练习一参考答案与试题解析一．解答题（共12小题）1．计算题①12﹣（﹣8）+（﹣7）﹣15；②﹣12+2×（﹣5）﹣（﹣3）3÷；③（2x﹣3y）+（5x+4y）；④（5a2+2a﹣1）﹣4（3﹣8a+2a2）．考点：整式的加减；有理数的混合运算．专题：计算题．分析：（1）直接进行有理数的加减即可得出答案．（2）先进行幂的运算，然后根据先乘除后加减的法则进行计算．（3）先去括号，然后合并同类项即可得出结果．（4）先去括号，然后合并同类项即可得出结果．解答：解：①原式=12+8﹣7﹣15=﹣2；②原式=﹣1﹣10+27÷=﹣11+81=70；③原式=2x﹣3y+5x+4y=7x+y；④原式=5a2+2a﹣1﹣12+32a﹣8a2=﹣3a2+34a﹣13．点评：本题考查了整式的加减及有理数的混合运算，属于基础题，解答本题的关键熟记去括号法则，熟练运用合并同类项的法则，这是各地中考的常考点．2．（1）计算：4+（﹣2）2×2﹣（﹣36）÷4；（2）化简：3（3a﹣2b）﹣2（a﹣3b）．考点：整式的加减；有理数的混合运算．分析：（1）按照有理数混合运算的顺序，先乘方后乘除最后算加减；（2）运用整式的加减运算顺序计算：先去括号，再合并同类项．解答：解：（1）原式=4+4×2﹣（﹣9）=4+8+9=17；（2）原式=9a﹣6b﹣2a+6b=（9﹣2）a+（﹣6+6）b=7a．点评：在混合运算中要特别注意运算顺序：先三级，后二级，再一级；熟记去括号法则：﹣﹣得+，﹣+得﹣，++得+，+﹣得﹣；及熟练运用合并同类项的法则：字母和字母的指数不变，只把系数相加减．3．计算：（1）7x+4（x2﹣2）﹣2（2x2﹣x+3）；（2）4ab﹣3b2﹣[（a2+b2）﹣（a2﹣b2）]；（3）（3mn﹣5m2）﹣（3m2﹣5mn）；（4）2a+2（a+1）﹣3（a﹣1）．考点：整式的加减．分析：（1）先去括号，再合并同类项即可；（2）先去括号，再合并同类项即可；（3）先去括号，再合并同类项即可；（4）先去括号，再合并同类项即可．解答：解：（1）7x+4（x2﹣2）﹣2（2x2﹣x+3）=7x+4x2﹣8﹣4x2+2x﹣6=9x﹣14；（2）4ab﹣3b2﹣[（a2+b2）﹣（a2﹣b2）]=4ab﹣3b2﹣[a2+b2﹣a2+b2]=4ab﹣3b2﹣2b2=4ab﹣5b2；（3）（3mn﹣5m2）﹣（3m2﹣5mn）=3mn﹣5m2﹣3m2+5mn=8mn﹣8m2；（4）2a+2（a+1）﹣3（a﹣1）=2a+2a+2﹣3a+3=a+5．点评：本题考查了整式的加减，解决此类题目的关键是熟记去括号法则，熟练运用合并同类项的法则，这是各地中考的常考点．4．化简（1）2（2a2+9b）+3（﹣5a2﹣4b）（2）3（x3+2x2﹣1）﹣（3x3+4x2﹣2）考点：整式的加减．专题：计算题．分析：（1）原式利用去括号法则去括号后，合并同类项即可得到结果；（2）原式利用去括号法则去括号后，合并同类项即可得到结果．解答：解：（1）原式=4a2+18b﹣15a2﹣12b=﹣11a2+6b；（2）原式=3x3+6x2﹣3﹣3x3﹣4x2+2=2x2﹣1．点评：此题考查了整式的加减，涉及的知识有：去括号法则，以及合并同类项法则，熟练掌握法则是解本题的关键．5．（2009•柳州）先化简，再求值：3（x﹣1）﹣（x﹣5），其中x=2．考点：整式的加减—化简求值．分析：本题应对方程去括号，合并同类项，将整式化为最简式，然后把x的值代入即可．解答：解：原式=3x﹣3﹣x+5=2x+2，当x=2时，原式=2×2+2=6．点评：本题考查了整式的化简．整式的加减运算实际上就是去括号、合并同类项，这是各地中考的常考点．6．已知x=5，y=3，求代数式3（x+y）+4（x+y）﹣6（x+y）的值．考点：整式的加减—化简求值．分析：先把x+y当作一个整体来合并同类项，再代入求出即可．解答：解：∵x=5，y=3，∴3（x+y）+4（x+y）﹣6（x+y）=x+y=5+3=8．点评：本题考查了整式的加减的应用，主要考查学生的计算能力，用了整体思想．7．已知A=x2﹣3y2，B=x2﹣y2，求解2A﹣B．考点：整式的加减．分析：直接把A、B代入式子，进一步去括号，合并得出答案即可．解答：解：2A﹣B=2（x2﹣3y2）﹣（x2﹣y2）=2x2﹣6y2﹣x2+y2=x2﹣5y2．点评：此题考查整式的加减混合运算，掌握去括号法则和运算的方法是解决问题的关键．8．若已知M=x2+3x﹣5，N=3x2+5，并且6M=2N﹣4，求x．考点：整式的加减；解一元一次方程．专题：计算题．分析：把M与N代入计算即可求出x的值．解答：解：∵M=x2+3x﹣5，N=3x2+5，∴代入得：6x2+18x﹣30=6x2+10﹣4，解得：x=2．点评：此题考查了整式的加减，熟练掌握运算法则是解本题的关键．9．已知A=5a2﹣2ab，B=﹣4a2+4ab，求：（1）A+B；（2）2A﹣B；（3）先化简，再求值：3（A+B）﹣2（2A﹣B），其中A=﹣2，B=1．考点：整式的加减；整式的加减—化简求值．专题：计算题．分析：（1）把A与B代入A+B中计算即可得到结果；（2）把A与B代入2A﹣B中计算即可得到结果；（3）原式去括号合并得到最简结果，把A与B的值代入计算即可求出值．解答：解：（1）∵A=5a2﹣2ab，B=﹣4a2+4ab，∴A+B=5a2﹣2ab﹣4a2+4ab=a2+2ab；（2）∵A=5a2﹣2ab，B=﹣4a2+4ab，∴2A﹣B=10a2﹣4ab+4a2﹣4ab=14a2﹣8ab；（3）原式=3A+3B﹣4A+2B=﹣A+5B，把A=﹣2，B=1代入得：原式=2+5=7．点评：此题考查了整式的加减，熟练掌握运算法则是解本题的关键．10．设a=14x﹣6，b=﹣7x+3，c=21x﹣1．（1）求a﹣（b﹣c）的值；（2）当x=时，求a﹣（b﹣c）的值．考点：整式的加减；代数式求值．专题：计算题．分析：（1）把a，b，c代入a﹣（b﹣c）中计算即可得到结果；（2）把x的值代入（1）的结果计算即可得到结果．解答：解：（1）把a=14x﹣6，b=﹣7x+3，c=21x﹣1代入得：a﹣（b﹣c）=a﹣b+c=14x﹣6+7x﹣3+21x﹣1=42x﹣10；（2）把x=代入得：原式=42×﹣10=10.5﹣10=0.5．点评：此题考查了整式的加减，以及代数式求值，熟练掌握运算法则是解本题的关键．11．化简求值：已知a、b满足：|a﹣2|+（b+1）2=0，求代数式2（2a﹣3b）﹣（a﹣4b）+2（﹣3a+2b）的值．考点：整式的加减—化简求值；非负数的性质：绝对值；非负数的性质：偶次方．专题：计算题．分析：原式去括号合并得到最简结果，利用非负数的性质求出a与b的值，代入计算即可求出值．解答：解：原式=4a﹣6b﹣a+4b﹣6a+4b=﹣3a+2b，∵|a﹣2|+（b+1）2=0，∴a=2，b=﹣1，则原式=﹣6﹣2=﹣8．点评：此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．12．已知（x+1）2+|y﹣1|=0，求2（xy﹣5xy2）﹣（3xy2﹣xy）的值．考点：整式的加减—化简求值；非负数的性质：绝对值；非负数的性质：偶次方．分析：因为平方与绝对值都是非负数，且（x+1）2+|y﹣1|=0，所以x+1=0，y﹣1=0，解得x，y的值．再运用整式的加减运算，去括号、合并同类项，然后代入求值即可．解答：解：2（xy﹣5xy2）﹣（3xy2﹣xy）=（2xy﹣10xy2）﹣（3xy2﹣xy）=2xy﹣10xy2﹣3xy2+xy=（2xy+xy）+（﹣3xy2﹣10xy2）=3xy﹣13xy2，∵（x+1）2+|y﹣1|=0∴（x+1）=0，y﹣1=0∴x=﹣1，y=1．∴当x=﹣1，y=1时，3xy﹣13xy2=3×（﹣1）×1﹣13×（﹣1）×12=﹣3+13=10．答：2（xy﹣5xy2）﹣（3xy2﹣xy）的值为10．点评：整式的加减运算实际上就是去括号、合并同类项，这是各地中考的常考点．代入求值时要化简．。
人教版数学七年级上册整式计算专项练习200题及答案详解
1当2已知，当3当4当5当当6若代数式7已知当8当9 C. D.如图所示的运算程序中，若开始输入的10B.C. D.按如图所示的程序计算：若开始输入的11 B.C.D.已知，则代数式的值是（）．12 B.C.D.已知，则式子的值为（）．13不能确定已知代数式的值是，则代数式的值是（）．14当时，代数式值为，那么当时，代数式的值是 （）．1516化简17当18已知19已知代数式20化简21若22已知23如果24已知代数式25若代数式26整式化简求值：先化简，再求值：27已知整式化简求值：先化简，再求值：28已知三个有理数29已知30先化简，再求值31已知代数式32按照如图的运算顺序，输入33如图是一个数值转换机．若输入的34当35若36已知37已知多项式时，多项式的值是38已知．3940设41用整体思想解题：为了简化问题，我们往往把一个式子看成一个数42已知当43已知当44已知45先化简再求值：46设若代数式47若48已知49先化简再求值50若51已知52先化简，再求值：53先化简，在求值：5456当57化简求值：58化简：59请回答下列各题：60已知62已知63先化简，再求值：64先化简，再求值：65先化简，再求值：66回答下面问题；67先化简，再求值：68先化简，再求值：69化简再求值：70阅读框图并回答下列问题：．71先化简，再求值：72先化简，再求值．求73对于74先化简，再求值：75若76已知77已知78已知79奕铭在化简多项式80先化简，再求值81先化简，再求值：82先化简，再求值：83若84已知：85先化简再求值：86先化简，再求值：87已知88已知89已知90先化简，再求值：91已知92先化简，再求值：93若单项式94求多项式95设96已知97已知98求99若100若代数式1 23 4 5 67 8 9 10 11 1213 14 15 16 17 18 1920 21 22 23 24 25 26 2728 29 30 31 32 33 34 3536 37 38 39 40 41 4243 44 45 46 47 48 4950 51 52 53 54 55 5657 58 59 60 61 62 63 6465 66 67 68 69 70 7173 74 75 76 77 78 7981 82 83 84 85 8687 88 89 90 91 9293 94 9596 9798 99 100。
七年级数学专题训练：整式的加减计算题100题(含答案)
题减整式的加计算1、已知A ＝4x 2－4xy ＋y 2，B ＝x 2－xy －5y 2，求3A －B2、已知A＝x 2＋xy ＋y 2，B＝－3xy －x 2，求2A－3B．3、已知1232+-=a a A ，2352+-=a a B ，求BA 32-4、已知325A x x =-，2116B x x =-+，求：⑴A＋2B；⑵、当1x =-时，求A＋5B 的值。
5、)(4)()(3222222y z z y y x ---+-6、2(a 2b ＋2b 3－ab 3)＋3a 3－(2ba 2－3ab 2＋3a 3)－4b 3，其中a ＝－3，b ＝27、-)32(3)32(2a b b a -+-8、21x －2(x －31y 2)＋(－23x ＋31y 2)，其中x ＝－2，y ＝－32．9、222213344a b ab ab a b ⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭10、()()323712p p p p p +---+11、21x－3(2x－32y 2)＋(－23x＋y 2)12、5a-[6c－2a－(b－c)]－[9a－(7b＋c)]13、2237(43)2x x x x ⎡⎤----⎣⎦14、-22225(3)2(7)a b ab a b ab ---15、2（-a 3+2a 2）-（4a 2-3a+1）16、（4a 2-3a+1）-3（1-a 3+2a 2）．17、3（a 2-4a+3）-5（5a 2-a+2）18、3x 2-[5x-2（14x -32）+2x 2]19、7a ＋（a 2－2a ）－5（a －2a 2）20、－3（2a ＋3b ）－31（6a －12b ）21、222226284526x y xy x y x xy y x x y+---+-22、3(2)(3)3ab a a b ab -+--+；23、22112()822a ab a ab ab ⎡⎤--+-⎢⎥⎣⎦；24、（a 3-2a 2+1）-2(3a 2-2a +21)25、x-2(1-2x+x 2)+3(-2+3x-x 2)26、)24()215(2222ab ba ab b a +-+-27、-4)142()346(22----+m m m m28、)5(3)8(2222xy y x y x xy ++--+-29、ba ab b a ab ab b a 222222]23)35(54[3--+--30、7xy+xy 3+4+6x-25xy 3-5xy-331、-2（3a 2－4）＋（a 2－3a）－（2a 2-5a＋5）32、-12a 2b-5ac-(-3a 2c-a 2b)+(3ac-4a 2c)33、2(-3x 2-xy)-3(-2x 2+3xy)-4[x 2-(2x 2-xy+y 2)]34、-2(4a-3b)+3(5b-3a)35、52a -[2a +（32a -2a）-2（52a -2a）]36、-5xy 2-4[3xy 2-（4xy 2-2x 2y）]+2x 2y-xy37、),23()2(342222c a ac b a c a ac b a +-+---38、(2)()xy y y yx ---+39、2237(43)2x x x x ⎡⎤----⎣⎦40、7-3x-4x 2+4x-8x 2-1541、2(2a 2-9b)-3(－4a 2+b)42、8x 2-[-3x-(2x 2-7x-5)+3]+4x43、)(2)(2b a b a a +-++；44、)32(2[)3(1yz x x xy +-+--]45、)32(3)23(4)(5b a b a b a -+--+；46、)377()5(322222a b ab b ab a a ---+--47、)45()54(3223--++-x x x x 48、)324(2)132(422+--+-x x x x49、)69()3(522x x x +--++-.50、)35()2143(3232a a a a a a ++--++-51、)(4)(2)(2n m n m n m -++-+52、]2)34(7[522x x x x ----53、(2)(3)x y y x ---54、()()()b a b a b a 4227523---+-55、()[]22222223ab b a ab b a ---56、2213[5(3)2]42a a a a ---++57、()()()xy y x xy y xy x -+---+-2222232258、－32ab ＋43a 2b ＋ab ＋(－43a 2b )－159、已知m+n =－3，mn=2,求116432n mn mn m ⎛⎫⎛⎫--+- ⎪ ⎪⎝⎭⎝⎭的值；60、(2x 2－21＋3x )－4(x －x 2＋21)；61、2x －(3x －2y ＋3)－(5y －2)；62、已知()()()2222A=232B=231A 22x xy y x xy y B A B A -++-+--，，求；63、已知()()222222120522422a b a b a b ab a b ab ⎡⎤++-=-----⎣⎦，求；64、1－3(2ab ＋a )十[1－2(2a －3ab )]．65、3x 2－［7x －(4x －3)－2x 2］．66、已知323243253A a a a B a a a =--++=--，，当a =－2时，求A－2B 的值.67、已知xy=2，x＋y=－3，求整式（4xy＋10y）＋[5x－（2xy＋2y－3x）]的值.68、已知2222224132a ab b ab a b a ab b +=+=--++，，求及的值.69、221131222223233x y x y x y ⎛⎫⎛⎫--+-+=-= ⎪ ⎪⎝⎭⎝⎭，，70、()()232334821438361a a a a a a a -+---+-=-，其中71、已知()()()()23412043535712714m n m m n m n m n ++--=---+++-，求的值72、已知222232542A b a ab B ab b a =-+=--，，当a=1，b =－1，求3A－4B 的值.73、已知222A=23B=25C=1276x x x x x ----+，，，求A－（B－4C）的值.74、已知22A=23211x kx x B x kx +--=-+-，，且2A+4B 的值与x 无关，求k 的值.75、()()2221254322x x x x x x -----+=，其中．76、已知()()()222222120745223a a b a b a b ab a b ab -++=--+--，求的值.77、2222220A=3B=23A B C a b c a b c ++=+---+已知，且，，求C.78、()()22221532722a b ab a b ab a b ---==，且，79、(5x-3y-2xy)-(6x+5y-2xy)，其中5-=x ，1-=y 80、若()0322=++-b a ，求3a 2b－[2ab 2－2（ab－1.5a 2b）+ab]+3ab 2的值；81、233(4333)(4),2;a a a a a a +----+=-其中82、22222222(22)[(33)(33)],1, 2.x y xy x y x y x y xy x y ---++-=-=其中83、()()()2222223224b ab a ab b a b ab a +-+-+----其中4.0,41=-=b a 84、3－2xy ＋2yx 2＋6xy －4x 2y ，其中x ＝－1，y ＝－2．85、(－x 2＋5＋4x 3)＋(－x 3＋5x －4)，其中x ＝－2；86、(3a 2b －ab 2)－(ab 2＋3a 2b )，其中a ＝－3，b ＝－287、已知222244,5A x xy y B x xy y =-+=+-，其中1122x y ==-，，求3A －B88、已知A ＝x 2＋xy ＋y 2，B ＝－3xy －x 2，其中，113x y =-=-，，求2A －3B ．89、有两个多项式：A ＝2a 2－4a ＋1，B ＝2(a 2－2a )＋3，当a 取任意有理数时，请比较A 与B 的大小．90、x x x x x x 5)64(213223312323-++-⎪⎭⎫ ⎝⎛---其中x ＝－121；91、21x 2－2⎪⎭⎫ ⎝⎛+--⎪⎭⎫ ⎝⎛-222231322331y x y x ，其中x ＝－2，y ＝－3492、2(a 2b ＋2b 3－ab 3)＋3a 3－(2ba 2－3ab 2＋3a 3)－4b 3，其中a ＝－3，b ＝293、()()233105223xy x y xy y x xy y x =-+=++-+-⎡⎤⎣⎦已知，，求的值94、已知()()22222322322A x xy y B x xy y A B B A =-+=+-+---⎡⎤⎣⎦，，求95、已知()222232232M a ab b N a ab b M N M M N =-+=+-----⎡⎤⎣⎦，，化简96、小美在计算某多项式减去2235a a +-的差时，误认为加上2235a a +-，得到答案是24a a +-，问正确答案是多少？97、已知2222113532A a b abB ab a b x y =-=+==-，，当，，求5A－3B 的值.98、已知2223226mx xy y x nxy y +--+-+的值与x 的取值无关，求22m n -的值99、已知231x x -=，求326752019x x x +-+的值100、()()11111111321014122m n n m m n x y y x x y m n +--++-⎛⎫+---- ⎪⎝⎭，其中为自然数，为大于的整数整式的加减计算100题答案1、2211118x xy y -+2、225112x xy y ++3、2954a a -+-4、()()3231322122553084x x x x x --+--+；，5、222325x y z +-6、322312ab ab -+，7、－13a+12b8、24369x y -+，9、22122a b ab -10、325797p p p +--11、273x y -+12、－2a＋8b－6c13、2533x x --14、22729a b ab -+15、3231a a -+-16、323232a a a ---17、22271a a ---18、2932x x --19、211a 20、－8a－5b 21、2224382x xy x y y x ---+22、3a＋b23、2592a ab -24、32524a a a --+25、25148x x -+-26、2232a b ab+27、2261213m m --+28、22272x xy y --29、2231532a b ab+30、332615y xy x +++31、2723a a -++32、22122a b ac a c --33、224154x xy y -+34、－17a+21b 35、2112a a -36、226xy x y xy ---37、22474a b ac a c--38、xy39、2533x x --40、2128x x -+-41、21621a b -42、2108x -43、a－b44、1－3x－3xy－6yz45、－a＋4b 46、2266a ab b -+47、32341x x -+48、－8x－249、2534x x -++50、32941a a a --++51、4m＋4n 52、2733x x --53、4x－3y 54、4a－b 55、22710a b ab -56、2912a a -+57、225x xy y -+58、113ab -59、2660、21622x x --61、－x－3y－162、2222424109x xy y x xy y ---+；63、221462a b ab -+；64、2－7a 65、2533x x --66、7967、－2068、5，269、24369x y -+；70、－5371、－1.7572、2221716a ab b --+；73、2473026x x -+74、2/575、－2.576、22710a b ab +-；77、222a c --78、221352a b ab -；79、－x－8y；1380、212ab ab +；81、327353a a a -++-；5582、222x y xy -+；83、22478150a ab b --；84、224315x y xy -++；--21---21-85、3235137x x x -++-；86、2224ab -；87、22111388x xy y -+；88、228511289x y y ++；89、A<B90、323668x x x +-+；91、2211226x y --；827-92、232223a b ab ab -+；4893、2294、224611x xy y +-95、2221614a ab b -+96、2356a a --+97、23-98、－899、2022100、118m n x y +--+。
七年级上册 数学 第二章 整式的加减-专项练习100题含答案
整式的加减专项练习1、3（a+5b）-2（b-a）2、3a-（2b-a）+b3、2（2a2+9b）+3（-5a2-4b）4、（x3-2y3-3x2y）-（3x3-3y3-7x2y）5、3x2-[7x-（4x-3）-2x2]6、（2xy-y）-（-y+yx）7、5（a2b-3ab2）-2（a2b-7ab）8、（-2ab+3a）-2（2a-b）+2ab 9、（7m2n-5mn）-（4m2n-5mn）10、（5a2+2a-1）-4（3-8a+2a2）．11、-3x2y+3xy2+2x2y-2xy2；12、2（a-1）-（2a-3）+3．13、-2（ab-3a2）-[2b2-（5ab+a2）+2ab]14、（x2-xy+y）-3（x2+xy-2y）15、3x2-[7x-（4x-3）-2x2]16、a2b-[2（a2b-2a2c）-（2bc+a2c）]；17、-2y3+（3xy2-x2y）-2（xy2-y3）．18、2（2x-3y）-（3x+2y+1）19、-（3a2-4ab）+[a2-2（2a+2ab）]．20、5m-7n-8p+5n-9m-p ；21、（5x 2y-7xy 2）-（xy 2-3x 2y ）； 22、3（-3a 2-2a ）-[a 2-2（5a-4a 2+1）-3a]．23、3a 2-9a+5-（-7a 2+10a-5）； 24、-3a 2b-（2ab 2-a 2b ）-（2a 2b+4ab 2）．25、（5a-3a 2+1）-（4a 3-3a 2）； 26、-2（ab-3a 2）-[2b 2-（5ab+a 2）+2ab]27、(8xy －x 2＋y 2)＋(－y 2＋x 2－8xy )； 28、(2x 2－21＋3x )－4(x －x 2＋21)；29、3x 2－［7x －(4x －3)－2x 2］． 30、5a+（4b-3a ）-（-3a+b ）；31、（3a 2-3ab+2b 2）+（a 2+2ab-2b 2）； 32、2a 2b+2ab 2-[2（a 2b-1）+2ab 2+2]．33、（2a 2-1+2a ）-3（a-1+a 2）； 34、2（x 2-xy ）-3（2x 2-3xy ）-2[x 2-（2x 2-xy+y 2）]．35、 －32ab ＋43a 2b ＋ab ＋(－43a 2b )－1 36、(8xy －x 2＋y 2)＋(－y 2＋x 2－8xy )；37、2x －(3x －2y ＋3)－(5y －2)； 38、－(3a ＋2b )＋(4a －3b ＋1)－(2a －b －3)39、4x 3－(－6x 3)＋(－9x 3) 40、3－2xy ＋2yx 2＋6xy －4x 2y41、 1－3(2ab ＋a )十[1－2(2a －3ab )]．42、 3x －[5x ＋(3x －2)]；43、(3a 2b －ab 2)－(ab 2＋3a 2b ) 44、()[]{}y x x y x --+--3233245、(－x 2＋5＋4x 3)＋(－x 3＋5x －4) 46、（5a 2-2a+3）-（1-2a+a 2）+3（-1+3a-a 2）．47、5（3a 2b-ab 2）-4（-ab 2+3a 2b ）． 48、4a 2+2（3ab-2a 2）-（7ab-1）．49、 21xy+（-41xy ）-2xy 2-（-3y 2x ） 50、5a 2-[a 2-（5a 2-2a ）-2（a 2-3a ）]51、5m-7n-8p+5n-9m+8p 52、（5x 2y-7xy 2）-（xy 2-3x 2y ）53、 3x2y-[2x2y-3（2xy-x2y）-xy] 54、5556、（a2+4ab-4b2）-3（a2+b2）-7（b2-ab）．57、a2+2a3+（-2a3）+（-3a3）+3a2；58、5ab+（-4a2b2）+8ab2-（-3ab）+（-a2b）+4a2b2； 59、（7y-3z）-（8y-5z）；60、-3（2x2-xy）+4（x2+xy-6）．61、（x3+3x2y-5xy2+9y3）+（-2y3+2xy2+x2y-2x3）-（4x2y-x3-3xy2+7y3）62、-3x2y+2x2y+3xy2-2xy2； 63、3（a2-2ab）-2（-3ab+b2）；64、5abc-{2a2b-[3abc-（4a2b-ab2]}．65、5m2-[m2+（5m2-2m）-2（m2-3m）]．66、-[2m-3（m-n+1）-2]-1．67、31a-( 21a-4b-6c)+3(-2c+2b) 68、 -5a n -a n -（-7a n ）+（-3a n ） 69、x 2y-3xy 2+2yx 2-y 2x70、 41a 2b-0.4ab 2- 21a 2b+ 52ab 2；71、3a-{2c-[6a-（c-b ）+c+（a+8b-6）]}72、-3（xy-2x 2）-[y 2-（5xy-4x 2）+2xy]；73、化简、求值21x 2－2212- (x + y )2⎡⎤⎢⎥⎣⎦－23(－32x 2＋31y 2)，其中x ＝－2， y ＝－3474、化简、求值21x －2(x －31y 2)＋(－23x ＋31y 2)，其中x ＝－2，y ＝－32．75、x x x x x x 5)64(213223312323-++-⎪⎭⎫ ⎝⎛---其中x ＝－121；76、 化简，求值（4m+n ）-[1-（m-4n ）]，m=52 n=-13177、化简、求值2(a2b＋2b3－ab3)＋3a3－(2ba2－3ab2＋3a3)－4b3，其中a＝－3，b＝278、化简，求值：（2x3-xyz）-2（x3-y3+xyz）+（xyz-2y3），其中x=1，y=2，z=-3．79、化简，求值：5x2-[3x-2（2x-3）+7x2]，其中x=-2．80、若两个多项式的和是2x2+xy+3y2，一个加式是x2-xy，求另一个加式．81、若2a2-4ab+b2与一个多项式的差是-3a2+2ab-5b2，试求这个多项式．82、求5x2y－2x2y与－2xy2＋4x2y的和．83、求3x2＋x－5与4－x＋7x2的差．84、计算 5y+3x+5z2与12y+7x-3z2的和85、计算8xy2+3x2y-2与-2x2y+5xy2-3的差86、 多项式-x 2+3xy-21y 与多项式M 的差是-21x 2-xy+y ，求多项式M87、当3（x 2-2xy ）-[3x 2-2y+2（xy+y ）]的值．88、化简再求值5abc-{2a 2b-[3abc-（4ab 2-a 2b ）]-2ab 2}，其中a=-2，b=3，c=-4189、已知A=a 2-2ab+b 2，B=a 2+2ab+b 2（1）求A+B ； （2）求41(B-A)；90、小明同学做一道题，已知两个多项式A ，B ，计算A+B ，他误将A+B 看作A-B ，求得9x 2-2x+7，若B=x 2+3x-2，你能否帮助小明同学求得正确答案？91、已知：M=3x 2+2x-1，N=-x 2-2+3x ，求M-2N ．92、已知222244,5A x xy y B x xy y =-+=+-，求3A －B93、已知A ＝x 2＋xy ＋y 2，B ＝－3xy －x 2，求2A －3B ．94、已知2 a ＋(b ＋1)2＝0，求5ab 2－[2a 2b －(4ab 2－2a 2b )]的值．95、化简求值：5abc-2a 2b+[3abc-2（4ab 2-a 2b ）]，其中a 、b 、c 满足|a-1|+|b-2|+c 2=0．96、已知a ，b ，z 满足：（1）已知|x-2|+（y+3）2=0，（2）z 是最大的负整数，化简求值：2（x 2y+xyz ）-3（x 2y-xyz ）-4x 2y ．97、已知a+b=7，ab=10，求代数式（5ab+4a+7b ）+（6a-3ab ）-（4ab-3b ）的值．98、已知m 2+3mn=5，求5m 2-[+5m 2-（2m 2-mn ）-7mn-5]的值99、设A=2x 2-3xy+y 2+2x+2y ，B=4x 2-6xy+2y 2-3x-y ，若|x-2a|+（y-3）2=0，且B-2A=a ，求a 的值．100、有两个多项式：A ＝2a 2－4a ＋1，B ＝2(a 2－2a )＋3，当a 取任意有理数时，请比较A 与B 的大小．整式的加减专项练习答案：1、3（a+5b ）-2（b-a ）=5a+13b2、3a-（2b-a ）+b=4a-b ．3、2（2a 2+9b ）+3（-5a 2-4b ）=—11a 2+6b 2 4、（x 3-2y 3-3x 2y ）-（3x 3-3y 3-7x 2y ）= -2x 3+y 3+4x 2y5、3x 2-[7x-（4x-3）-2x 2] = 5x 2 -3x-36、（2xy-y ）-（-y+yx ）= xy7、5（a 22b-3ab 2）-2（a 2b-7ab ） = -a 2b+11ab 8、（-2ab+3a ）-2（2a-b ）+2ab= -2a+b9、（7m 2n-5mn ）-（4m 2n-5mn ）= 3m 2n10、（5a 2+2a-1）-4（3-8a+2a 2）= -3a 2+34a-1311、-3x 2y+3xy 2+2x 2y-2xy 2= -x 2y+xy 212、2（a-1）-（2a-3）+3．=413、-2（ab-3a 2）-[2b 2-（5ab+a 2）+2ab]= 7a 2+ab-2b 214、（x 2-xy+y ）-3（x 2+xy-2y ）= -2x 2-4xy+7y15、3x 2-[7x-（4x-3）-2x 2]=5x 2-3x-3 16、a 2b-[2（a 2b-2a 2c ）-（2bc+a 2c ）]= -a 2b+2bc+6a 2c17、-2y 3+（3xy 2-x 2y ）-2（xy 2-y 3）= xy 2-x 2y18、2（2x-3y ）-（3x+2y+1）=2x-8y-1 19、-（3a 2-4ab ）+[a 2-2（2a+2ab ）]=-2a 2-4a20、5m-7n-8p+5n-9m-p = -4m-2n-9p21、（5x 2y-7xy 2）-（xy 2-3x 2y ）=4xy 2-4x 2y22、3（-3a 2-2a ）-[a 2-2（5a-4a 2+1）-3a]=-18a 2 +7a+223、3a 2-9a+5-（-7a 2+10a-5）=10a 2-19a+1024、-3a 2b-（2ab 2-a 2b ）-（2a 2b+4ab 2）= -4a 2b-64ab 225、（5a-3a 2+1）-（4a 3-3a 2）=5a-4a 2+126、-2（ab-3a 2）-[2b 2-（5ab+a 2）+2ab]=7a 2+ab-2b 2 27、(8xy －x 2＋y 2)＋(－y 2＋x 2－8xy )=028、(2x 2－21＋3x )－4(x －x 2＋21) = 6x 2-x-25 29、3x 2－［7x －(4x －3)－2x 2］= 5x 2－3x －330、5a+（4b-3a ）-（-3a+b ）= 5a+3b31、（3a 2-3ab+2b 2）+（a 2+2ab-2b 2）= 4a 2-ab32、2a 2b+2ab 2-[2（a 2b-1）+2ab 2+2]．= -133、（2a 2-1+2a ）-3（a-1+a 2）= -a 2-a+234、2（x 2-xy ）-3（2x 2-3xy ）-2[x 2-（2x 2-xy+y 2）]=-2x 2+5xy-2y 235、－32ab ＋43a 2b ＋ab ＋(－43a 2b )－1 = 31ab-1 36、(8xy －x 2＋y 2)＋(－y 2＋x 2－8xy )=037、2x －(3x －2y ＋3)－(5y －2)=-x-3y-138、－(3a ＋2b )＋(4a －3b ＋1)－(2a －b －3)= -a-4b+439、4x 3－(－6x 3)＋(－9x 3)＝ x 340、3－2xy ＋2yx 2＋6xy －4x 2y = -2 x 2y+441、 1－3(2ab ＋a )十[1－2(2a －3ab )]=2-7a42、 3x －[5x ＋(3x －2)]=-5x+243、(3a 2b －ab 2)－(ab 2＋3a 2b )= -2ab 244、()[]{}y x x y x --+--32332 = 5x+y45、(－x 2＋5＋4x 3)＋(－x 3＋5x －4)= 3x 3－x 2＋5x+146、（5a 2-2a+3）-（1-2a+a 2）+3（-1+3a-a 2）=a 2+9a-147、5（3a 2b-ab 2）-4（-ab 2+3a 2b ）．=3a 2b-ab 248、4a 2+2（3ab-2a 2）-（7ab-1）=1-ab49、 21xy+（-41xy ）-2xy 2-（-3y 2x ）=41xy+xy 2 50、5a 2-[a 2-（5a 2-2a ）-2（a 2-3a ）]=11a 2-8a51、5m-7n-8p+5n-9m+8p=-4m-2n59、（7y-3z ）-（8y-5z ）=-y+2z60、-3（2x 2-xy ）+4（x 2+xy-6）=-2x 2+7xy-24 61、（x 3+3x 2y-5xy 2+9y 3）+（-2y 3+2xy 2+x 2y-2x 3）-（4x 2y-x 3-3xy 2+7y 3）=0 62、-3x 2y+2x 2y+3xy 2-2xy 2 = -x 2y+xy 263、3（a 2-2ab ）-2（-3ab+b 2）=3a 2-2b 264、5abc-{2a 2b-[3abc-（4a 2b-ab 2]}=8abc-6a 2b+ab 265、5m 2-[m 2+（5m 2-2m ）-2（m 2-3m ）]=m 2-4m66、-[2m-3（m-n+1）-2]-1=m-3n+467、31a-( 21a-4b-6c)+3(-2c+2b)= -61a+10b 68、 -5a n -a n -（-7a n ）+（-3a n ）= -2a n69、x 2y-3xy 2+2yx 2-y 2x=3x 2y-4xy 271、 41a 2b-0.4ab 2- 21a 2b+ 52ab 2 = -41a 2b 71、3a-{2c-[6a-（c-b ）+c+（a+8b-6）]}= 10a+9b-2c-672、-3（xy-2x 2）-[y 2-（5xy-4x 2）+2xy]= 2x 2-y 2 73、化简、求值21x 2－2212- (x + y )2⎡⎤⎢⎥⎣⎦－23(－32x 2＋31y 2)，其中x ＝－2， y ＝－34 原式=2x 2＋21y 2－2 =698 74、化简、求值21x －2(x －31y 2)＋(－23x ＋31y 2)，其中x ＝－2，y ＝－32． 原式=-3x+y 2=694 75、x x x x x x 5)64(213223312323-++-⎪⎭⎫ ⎝⎛---其中x ＝－121； 原式=x 3+x 2-x+6=683 76、 化简，求值（4m+n ）-[1-（m-4n ）]，m=52 n=-131 原式=5m-3n-1=577、化简、求值2(a 2b ＋2b 3－ab 3)＋3a 3－(2ba 2－3ab 2＋3a 3)－4b 3，其中a ＝－3，b ＝2原式=-2ab 3+3ab 2＝1278、化简，求值：（2x 3-xyz ）-2（x 3-y 3+xyz ）+（xyz-2y 3），其中x=1，y=2，z=-3．原式=-2xyz=679、化简，求值：5x 2-[3x-2（2x-3）+7x 2]，其中x=-2．原式=-2x 2+x-6=-1680、若两个多项式的和是2x 2+xy+3y 2，一个加式是x 2-xy ，求另一个加式．（2x 2+xy+3y 2 ） ——（ x 2-xy ）= x 2+2xy+3y 281、若2a 2-4ab+b 2与一个多项式的差是-3a 2+2ab-5b 2，试求这个多项式．（ 2a 2-4ab+b 2 ）—（-3a 2+2ab-5b 2）=5a 2 －6ab+6b 282、求5x 2y －2x 2y 与－2xy 2＋4x 2y 的和．（5x 2y －2x 2y ）+（－2xy 2＋4x 2y ）=3xy 2＋2x 2y83、 求3x 2＋x －5与4－x ＋7x 2的差．（3x 2＋x －5）—（4－x ＋7x 2）=—4x 2＋2x －984、计算 5y+3x+5z 2与12y+7x-3z 2的和（5y+3x+5z 2）+（12y+7x-3z 2）=17y+10x+2z 285、计算8xy 2+3x 2y-2与-2x 2y+5xy 2-3的差（8xy 2+3x 2y-2）—（-2x 2y+5xy 2-3）=5x 2y+3xy 2+186、 多项式-x 2+3xy-21y 与多项式M 的差是-21x 2-xy+y ，求多项式M23y 87、当3（x 2-2xy ）-[3x 2-2y+2（xy+y ）]的值． 原式=-8xy+y= —1588、化简再求值5abc-{2a 2b-[3abc-（4ab 2-a 2b ）]-2ab 2}，其中a=-2，b=3，c=-41 原式=83abc-a 2b-2ab 2=3689、已知A=a 2-2ab+b 2，B=a 2+2ab+b 2 （1）求A+B ；（2）求41(B-A)； A+B=2a 2+2b 2 41(B-A)=ab 90、小明同学做一道题，已知两个多项式A ，B ，计算A+B ，他误将A+B 看作A-B ，求得 9x 2-2x+7，若B=x 2+3x-2，你能否帮助小明同学求得正确答案？A=10x 2+x+5 A+B=11x 2+4x+391、已知：M=3x 2+2x-1，N=-x 2-2+3x ，求M-2N ．M-2N=5x 2－4x+392、已知222244,5A x xy y B x xy y =-+=+-，求3A －B3A －B=11x 2-13xy+8y 293、已知A ＝x 2＋xy ＋y 2，B ＝－3xy －x 2，求2A －3B ．2A －3B= 5x 2＋11xy ＋2y 294、已知2-a ＋(b ＋1)2＝0，求5ab 2－[2a 2b －(4ab 2－2a 2b )]的值． 原式=9ab 2－4a 2b=3495、化简求值：5abc-2a 2b+[3abc-2（4ab 2-a 2b ）]，其中a 、b 、c 满足|a-1|+|b-2|+c 2=0． 原式=8abc-8a 2b=-3296、已知a ，b ，z 满足：（1）已知|x-2|+（y+3）2=0，（2）z 是最大的负整数，化简求值： 2（x 2y+xyz ）-3（x 2y-xyz ）-4x 2y ．原式=-5x 2y+5xyz=9097、已知a+b=7，ab=10，求代数式（5ab+4a+7b ）+（6a-3ab ）-（4ab-3b ）的值． 原式=10a+10b-2ab=5098、已知m 2+3mn=5，求5m 2-[+5m 2-（2m 2-mn ）-7mn-5]的值原式=2m 2+6mn+5=1599、设A=2x 2-3xy+y 2+2x+2y ，B=4x 2-6xy+2y 2-3x-y ，若|x-2a|+（y-3）2=0，且B-2A=a ，求a 的值． B-2A=-7x-5y=-14a-15=a a=-1100、有两个多项式：A ＝2a 2－4a ＋1，B ＝2(a 2－2a )＋3，当a 取任意有理数时，请比较A与B 的大小． A=2a 2－4a ＋1 B ＝2a 2－4a ＋3 所以A<B。
七年级上册数学整式加减计算题
七年级上册数学整式加减计算题一、整式加减基础运算题（1 - 10）1. 计算：(3a + 2b)-(a - b)- 解析：- 去括号法则：括号前是正号，把括号和它前面的正号去掉后，原括号里各项的符号都不改变；括号前是负号，把括号和它前面的负号去掉后，原括号里各项的符号都要改变。
- 所以(3a + 2b)-(a - b)=3a + 2b - a + b。
- 然后合并同类项，3a - a+2b + b = 2a+3b。
2. 计算：2(x^2-3x + 1)-3(2x^2+x - 4)- 解析：- 先使用乘法分配律去括号，2(x^2-3x + 1)=2x^2-6x + 2，3(2x^2+x -4)=6x^2+3x - 12。
- 然后进行整式的减法：(2x^2-6x + 2)-(6x^2+3x - 12)=2x^2-6x + 2 - 6x^2-3x + 12。
- 合并同类项得(2x^2-6x^2)+(-6x - 3x)+(2 + 12)= - 4x^2-9x + 14。
3. 计算：(5a^2-3b^2)+(a^2+b^2)-(5a^2+3b^2)- 解析：- 先去括号，(5a^2-3b^2)+(a^2+b^2)-(5a^2+3b^2) = 5a^2-3b^2+a^2+b^2-5a^2-3b^2。
- 再合并同类项，(5a^2+a^2-5a^2)+(-3b^2+b^2-3b^2)=a^2-5b^2。
4. 计算：3x^2y-(2xy - 2(xy-(3)/(2)x^2y)+xy)- 解析：- 先去小括号，3x^2y-(2xy - 2(xy-(3)/(2)x^2y)+xy)=3x^2y-(2xy-2xy +3x^2y+xy)。
- 再去中括号，3x^2y - 2xy + 2xy - 3x^2y - xy=-xy。
5. 计算：(4m^3-2m^2+m - 1)-(2m^3+3m^2-m + 2)- 解析：- 去括号得4m^3-2m^2+m - 1 - 2m^3-3m^2+m - 2。
北师大版七年级数学上册整式计算题专项练习(附答案)
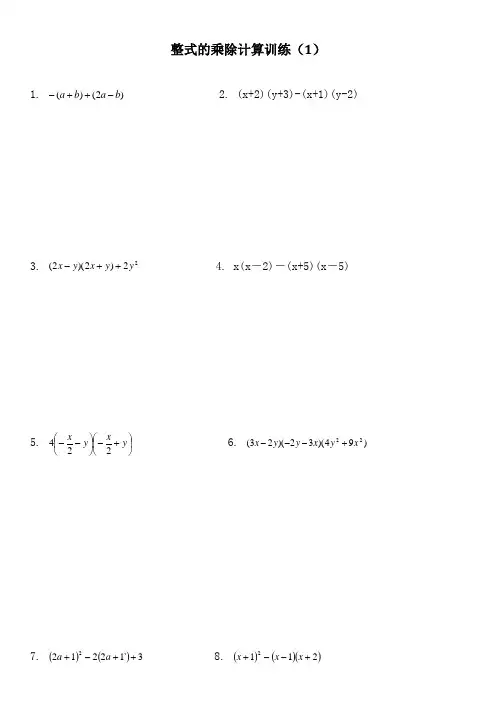
整式的乘除计算训练（1）1. )2()(b a b a -++-2. (x+2)(y+3)-(x+1)(y-2)3. 22)2)(2(y y x y x ++-4. x(x －2)－(x+5)(x －5)5. ⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--y x y x224 6. )94)(32)(23(22x y x y y x +---7. ()()3`122122++-+a a 8. ()()()2112+--+x x x9. (x －3y)(x+3y)－(x －3y)2 10. 23(1)(1)(21)x x x +---11. 22)23()23(y x y x --+ 12. 22)()(y x y x -+13. ×810014. 3022)2(21)x (4554---÷⎪⎭⎫⎝⎛--π-+⎪⎭⎫⎝⎛-÷⎪⎭⎫ ⎝⎛15. (1211200622332141）（）（）（）-⨯+----16—19题用乘法公式计算×1001 17.1992-18.298 19.2010200820092⨯-20.化简求值：)4)(12()12(2+-+-a a a ，其中2-=a 。
21. 化简求值2(2)2()()2(3)x y x y x y y x y +--++-,其中12,2x y =-=。
22. 5(x －1)(x +3)－2(x －5)(x －2) 23. (a －b )(a 2+ab +b 2)24. (3y+2)(y－4)－3(y－2)(y－3) 25. a(b－c)+b(c－a)+c(a－b)1y2)226. (－2mn2)2－4mn3(mn+1) 27. 3xy(－2x)3·(－428. (－x－2)(x+2) 29. 5×108·(3×102) 30. (x－3y)(x+3y)－(x－3y)2 31. (a+b－c)(a－b－c)答案1. a-2b2. 5x+y+83. 4x2+y24. -2x+255. x2-4y26. 16y4-81x47. 4a2+28. x+39. 6xy-18y2 10. -x2+4x-4 11. 24xy 12. x4-2x2y2+y413. 1 14. 10 15. 161216. 原式=(1000-1)×(1000+1) 17. 原式=(99+1)×(99-1)=1000000-1 =100×98=999999 =980018. 原式=(900-2)2 19. 原式=20092-(2009+1)(2009-1)=10000-400+4 =20092-20092+1=9604 =120.原式=6a2+3a-3，当a=2时，原式=6×(-2)2+3×(-2)-3=1521.原式=-x2+6xy，当x=2，y=12时，原式=-(-2)2+6×(-2)×12=-1022. -3x2+24x-35 23. a3-b3 24. 5y-26 25. 026. -4mn3 27. -3x4y5 28. -x2-4x-4 29. 1.5×1011230. 6xy-18y2 31. a2-2ac+c2-b22014年北师大七年级数学上册《整式及其加减》计算题专项练习一一．解答题（共12小题）1．计算题①12﹣（﹣8）+（﹣7）﹣15；②﹣12+2×（﹣5）﹣（﹣3）3÷；③（2x﹣3y）+（5x+4y）；④（5a2+2a﹣1）﹣4（3﹣8a+2a2）．2．（1）计算：4+（﹣2）2×2﹣（﹣36）÷4；（2）化简：3（3a﹣2b）﹣2（a﹣3b）．3．计算：（1）7x+4（x2﹣2）﹣2（2x2﹣x+3）；（2）4ab﹣3b2﹣[（a2+b2）﹣（a2﹣b2）]；（3）（3mn﹣5m2）﹣（3m2﹣5mn）；（4）2a+2（a+1）﹣3（a﹣1）．4．化简（1）2（2a2+9b）+3（﹣5a2﹣4b）（2）3（x3+2x2﹣1）﹣（3x3+4x2﹣2）5．（2009?柳州）先化简，再求值：3（x﹣1）﹣（x﹣5），其中x=2．6．已知x=5，y=3，求代数式3（x+y）+4（x+y）﹣6（x+y）的值．7．已知A=x2﹣3y2，B=x2﹣y2，求解2A﹣B．8．若已知M=x2+3x﹣5，N=3x2+5，并且6M=2N﹣4，求x．9．已知A=5a2﹣2ab，B=﹣4a2+4ab，求：（1）A+B；（2）2A﹣B；（3）先化简，再求值：3（A+B）﹣2（2A﹣B），其中A=﹣2，B=1．10．设a=14x﹣6，b=﹣7x+3，c=21x﹣1．（1）求a﹣（b﹣c）的值；（2）当x=时，求a﹣（b﹣c）的值．11．化简求值：已知a、b满足：|a﹣2|+（b+1）2=0，求代数式2（2a﹣3b）﹣（a﹣4b）+2（﹣3a+2b）的值．12．已知（x+1）2+|y﹣1|=0，求2（xy﹣5xy2）﹣（3xy2﹣xy）的值．2014年北师大七年级数学上册《整式及其加减》计算题专项练习一参考答案与试题解析一．解答题（共12小题）1．计算题①12﹣（﹣8）+（﹣7）﹣15；②﹣12+2×（﹣5）﹣（﹣3）3÷；③（2x﹣3y）+（5x+4y）；④（5a2+2a﹣1）﹣4（3﹣8a+2a2）．考点：整式的加减；有理数的混合运算．专题：计算题．分析：（1）直接进行有理数的加减即可得出答案．（2）先进行幂的运算，然后根据先乘除后加减的法则进行计算．（3）先去括号，然后合并同类项即可得出结果．（4）先去括号，然后合并同类项即可得出结果．解答：解：①原式=12+8﹣7﹣15=﹣2；②原式=﹣1﹣10+27÷=﹣11+81=70；③原式=2x﹣3y+5x+4y=7x+y；④原式=5a2+2a﹣1﹣12+32a﹣8a2=﹣3a2+34a﹣13．点评：本题考查了整式的加减及有理数的混合运算，属于基础题，解答本题的关键熟记去括号法则，熟练运用合并同类项的法则，这是各地中考的常考点．2．（1）计算：4+（﹣2）2×2﹣（﹣36）÷4；（2）化简：3（3a﹣2b）﹣2（a﹣3b）．考点：整式的加减；有理数的混合运算．分析：（1）按照有理数混合运算的顺序，先乘方后乘除最后算加减；（2）运用整式的加减运算顺序计算：先去括号，再合并同类项．解答：解：（1）原式=4+4×2﹣（﹣9）=4+8+9=17；（2）原式=9a﹣6b﹣2a+6b=（9﹣2）a+（﹣6+6）b=7a．点评：在混合运算中要特别注意运算顺序：先三级，后二级，再一级；熟记去括号法则：﹣﹣得+，﹣+得﹣，++得+，+﹣得﹣；及熟练运用合并同类项的法则：字母和字母的指数不变，只把系数相加减．3．计算：（1）7x+4（x2﹣2）﹣2（2x2﹣x+3）；（2）4ab﹣3b2﹣[（a2+b2）﹣（a2﹣b2）]；（3）（3mn﹣5m2）﹣（3m2﹣5mn）；（4）2a+2（a+1）﹣3（a﹣1）．考点：整式的加减．分析：（1）先去括号，再合并同类项即可；（2）先去括号，再合并同类项即可；（3）先去括号，再合并同类项即可；（4）先去括号，再合并同类项即可．解答：解：（1）7x+4（x2﹣2）﹣2（2x2﹣x+3）=7x+4x2﹣8﹣4x2+2x﹣6=9x﹣14；（2）4ab﹣3b2﹣[（a2+b2）﹣（a2﹣b2）]=4ab﹣3b2﹣[a2+b2﹣a2+b2]=4ab﹣3b2﹣2b2=4ab﹣5b2；（3）（3mn﹣5m2）﹣（3m2﹣5mn）=3mn﹣5m2﹣3m2+5mn=8mn﹣8m2；（4）2a+2（a+1）﹣3（a﹣1）=2a+2a+2﹣3a+3=a+5．点评：本题考查了整式的加减，解决此类题目的关键是熟记去括号法则，熟练运用合并同类项的法则，这是各地中考的常考点．4．化简（1）2（2a2+9b）+3（﹣5a2﹣4b）（2）3（x3+2x2﹣1）﹣（3x3+4x2﹣2）考点：整式的加减．专题：计算题．分析：（1）原式利用去括号法则去括号后，合并同类项即可得到结果；（2）原式利用去括号法则去括号后，合并同类项即可得到结果．解答：解：（1）原式=4a2+18b﹣15a2﹣12b=﹣11a2+6b；（2）原式=3x3+6x2﹣3﹣3x3﹣4x2+2=2x2﹣1．点评：此题考查了整式的加减，涉及的知识有：去括号法则，以及合并同类项法则，熟练掌握法则是解本题的关键．5．（2009?柳州）先化简，再求值：3（x﹣1）﹣（x﹣5），其中x=2．考点：整式的加减—化简求值．分析：本题应对方程去括号，合并同类项，将整式化为最简式，然后把x的值代入即可．解答：解：原式=3x﹣3﹣x+5=2x+2，当x=2时，原式=2×2+2=6．点评：本题考查了整式的化简．整式的加减运算实际上就是去括号、合并同类项，这是各地中考的常考点．6．已知x=5，y=3，求代数式3（x+y）+4（x+y）﹣6（x+y）的值．考点：整式的加减—化简求值．分析：先把x+y当作一个整体来合并同类项，再代入求出即可．解答：解：∵x=5，y=3，∴3（x+y）+4（x+y）﹣6（x+y）=x+y=5+3=8．点评：本题考查了整式的加减的应用，主要考查学生的计算能力，用了整体思想．7．已知A=x2﹣3y2，B=x2﹣y2，求解2A﹣B．考点：整式的加减．分析：直接把A、B代入式子，进一步去括号，合并得出答案即可．解答：解：2A﹣B=2（x2﹣3y2）﹣（x2﹣y2）=2x2﹣6y2﹣x2+y2=x2﹣5y2．点评：此题考查整式的加减混合运算，掌握去括号法则和运算的方法是解决问题的关键．8．若已知M=x2+3x﹣5，N=3x2+5，并且6M=2N﹣4，求x．考点：整式的加减；解一元一次方程．专题：计算题．分析：把M与N代入计算即可求出x的值．解答：解：∵M=x2+3x﹣5，N=3x2+5，∴代入得：6x2+18x﹣30=6x2+10﹣4，解得：x=2．点评：此题考查了整式的加减，熟练掌握运算法则是解本题的关键．9．已知A=5a2﹣2ab，B=﹣4a2+4ab，求：（1）A+B；（2）2A﹣B；（3）先化简，再求值：3（A+B）﹣2（2A﹣B），其中A=﹣2，B=1．考点：整式的加减；整式的加减—化简求值．专题：计算题．分析：（1）把A与B代入A+B中计算即可得到结果；（2）把A与B代入2A﹣B中计算即可得到结果；（3）原式去括号合并得到最简结果，把A与B的值代入计算即可求出值．解答：解：（1）∵A=5a2﹣2ab，B=﹣4a2+4ab，∴A+B=5a2﹣2ab﹣4a2+4ab=a2+2ab；（2）∵A=5a2﹣2ab，B=﹣4a2+4ab，∴2A﹣B=10a2﹣4ab+4a2﹣4ab=14a2﹣8ab；（3）原式=3A+3B﹣4A+2B=﹣A+5B，把A=﹣2，B=1代入得：原式=2+5=7．点评：此题考查了整式的加减，熟练掌握运算法则是解本题的关键．10．设a=14x﹣6，b=﹣7x+3，c=21x﹣1．（1）求a﹣（b﹣c）的值；（2）当x=时，求a﹣（b﹣c）的值．考点：整式的加减；代数式求值．专题：计算题．分析：（1）把a，b，c代入a﹣（b﹣c）中计算即可得到结果；（2）把x的值代入（1）的结果计算即可得到结果．解答：解：（1）把a=14x﹣6，b=﹣7x+3，c=21x﹣1代入得：a﹣（b﹣c）=a﹣b+c=14x﹣6+7x﹣3+21x﹣1=42x﹣10；（2）把x=代入得：原式=42×﹣10=﹣10=．点评：此题考查了整式的加减，以及代数式求值，熟练掌握运算法则是解本题的关键．11．化简求值：已知a、b满足：|a﹣2|+（b+1）2=0，求代数式2（2a﹣3b）﹣（a﹣4b）+2（﹣3a+2b）的值．考点：整式的加减—化简求值；非负数的性质：绝对值；非负数的性质：偶次方．专题：计算题．分析：原式去括号合并得到最简结果，利用非负数的性质求出a与b的值，代入计算即可求出值．解答：解：原式=4a﹣6b﹣a+4b﹣6a+4b=﹣3a+2b，∵|a﹣2|+（b+1）2=0，∴a=2，b=﹣1，则原式=﹣6﹣2=﹣8．点评：此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．12．已知（x+1）2+|y﹣1|=0，求2（xy﹣5xy2）﹣（3xy2﹣xy）的值．考点：整式的加减—化简求值；非负数的性质：绝对值；非负数的性质：偶次方．分析：因为平方与绝对值都是非负数，且（x+1）2+|y﹣1|=0，所以x+1=0，y﹣1=0，解得x，y的值．再运用整式的加减运算，去括号、合并同类项，然后代入求值即可．解答：解：2（xy﹣5xy2）﹣（3xy2﹣xy）=（2xy﹣10xy2）﹣（3xy2﹣xy）=2xy﹣10xy2﹣3xy2+xy=（2xy+xy）+（﹣3xy2﹣10xy2）=3xy﹣13xy2，∵（x+1）2+|y﹣1|=0∴（x+1）=0，y﹣1=0∴x=﹣1，y=1．∴当x=﹣1，y=1时，3xy﹣13xy2=3×（﹣1）×1﹣13×（﹣1）×12=﹣3+13=10．答：2（xy﹣5xy2）﹣（3xy2﹣xy）的值为10．点评：整式的加减运算实际上就是去括号、合并同类项，这是各地中考的常考点．代入求值时要化简．。
七年级数学(上)《整式》测试题含答案
七年级数学（上）《整式》测试题班级 学号 姓名 分数一．判断题(1)31+x 是关于x 的一次两项式． ( ) (2)－3不是单项式．( )(3)单项式xy 的系数是0．( ) (4)x 3＋y 3是6次多项式．( ) (5)多项式是整式．( )二、选择题1．在下列代数式：21ab ，2b a +，ab 2+b+1，x 3+y2，x 3+ x 2－3中，多项式有（ ） A ．2个 B ．3个 C ．4个 D5个 2．多项式－23m 2－n 2是（ ）A ．二次二项式B ．三次二项式C ．四次二项式D 五次二项式 3．下列说法正确的是（ ）A ．3 x 2―2x+5的项是3x 2，2x ，5 B ．3x －3y 与2 x 2―2x y －5都是多项式 C ．多项式－2x 2+4x y 的次数是３D ．一个多项式的次数是6，则这个多项式中只有一项的次数是6 4．下列说法正确的是（ ） A ．整式abc 没有系数 B ．2x +3y +4z不是整式 C ．－2不是整式 D ．整式2x+1是一次二项式5．下列代数式中，不是整式的是（ ）A 、23x -B 、745b a -C 、xa 523+D 、－20056．下列多项式中，是二次多项式的是（ ） A 、132+xB 、23xC 、3xy －1D 、253-x7．x 减去y 的平方的差，用代数式表示正确的是（ ） A 、2)(y x - B 、22y x -C 、y x -2D 、2y x -8．某同学爬一楼梯，从楼下爬到楼顶后立刻返回楼下。
已知该楼梯长S 米，同学上楼速度是a 米/分,下楼速度是b 米/分,则他的平均速度是（ ）米/分。
A 、2b a + B 、b a s + C 、b s a s + D 、bs a s s +29．下列单项式次数为3的是( )A.3abcB.2×3×4C.41x 3y D.52x10．下列代数式中整式有( )x1， 2x +y ， 31a 2b ， πy x -， x y 45， 0.5 ， aA.4个B.5个C.6个D.7个11．下列整式中，单项式是( )A.3a +1B.2x －yC.0.1D.21+x 12．下列各项式中，次数不是3的是( )A ．xyz ＋1B ．x 2＋y ＋1C ．x 2y －xy 2D ．x 3－x 2＋x －1 13．下列说法正确的是( ) A ．x(x ＋a)是单项式 B ．π12+x 不是整式 C ．0是单项式 D ．单项式－31x 2y 的系数是31 14．在多项式x 3－xy 2＋25中，最高次项是( )A ．x 3B ．x 3，xy 2C ．x 3，－xy 2D ．2515．在代数式yy y n x y x 1),12(31,8)1(7,4322++++中，多项式的个数是( ) A ．1B ．2C ．3D ．416．单项式－232xy 的系数与次数分别是( )A ．－3，3B ．－21，3C ．－23，2D ．－23，3 17．下列说法正确的是( )A ．x 的指数是0B ．x 的系数是0C ．－10是一次单项式D ．－10是单项式 18．已知：32y x m-与nxy 5是同类项，则代数式n m 2-的值是( )A 、6-B 、5-C 、2-D 、5 19．系数为－21且只含有x 、y 的二次单项式，可以写出( )A ．1个B ．2个C ．3个D ．4个20．多项式212x y -+的次数是（ ）A 、1B 、 2C 、－1D 、－2三．填空题1．当a ＝－1时，34a ＝ ； 2．单项式： 3234y x -的系数是 ，次数是 ； 3．多项式：y y x xy x +-+3223534是 次 项式； 4．220053xy 是 次单项式；5．y x 342-的一次项系数是 ，常数项是 ； 6．_____和_____统称整式.7．单项式21xy 2z 是_____次单项式.8．多项式a 2－21ab 2－b 2有_____项，其中－21ab 2的次数是 .9．整式①21，②3x －y 2,③23x 2y ,④a ,⑤πx +21y ,⑥522a π,⑦x +1中 单项式有 ，多项式有 10．x+2xy +y 是 次多项式. 11．比m 的一半还少4的数是 ；12．b 的311倍的相反数是 ；13．设某数为x ，10减去某数的2倍的差是 ； 14．n 是整数，用含n 的代数式表示两个连续奇数 ； 15．42234263y y x y x x --+-的次数是 ； 16．当x ＝2，y ＝－1时，代数式||||x xy -的值是 ；17．当t ＝ 时，31tt +-的值等于1； 18．当y ＝ 时，代数式3y －2与43+y 的值相等； 19．－23ab 的系数是 ，次数是 次． 20．把代数式2a 2b 2c 和a 3b 2的相同点填在横线上：（1）都是 式；（2）都是 次． 21．多项式x 3y 2－2xy 2－43xy－9是___次___项式，其中最高次项的系数是 ，二次项是 ，常数项是 ．22.若2313m x y z -与2343x y z 是同类项,则m = .23．在x 2， 21 (x ＋y)，π1，－3中，单项式是 ，多项式是 ，整式是 ．24．单项式7532c ab 的系数是____________，次数是____________．25．多项式x 2y ＋xy －xy 2－53中的三次项是____________． 26．当a=____________时，整式x 2＋a －1是单项式． 27．多项式xy －1是____________次____________项式． 28．当x ＝－3时，多项式－x 3＋x 2－1的值等于____________．29．如果整式(m －2n)x 2y m+n-5是关于x 和y 的五次单项式，则m+n 30．一个n 次多项式，它的任何一项的次数都____________．31．系数是－3，且只含有字母x 和y 的四次单项式共有 个，分别是 ．32．组成多项式1－x 2＋xy －y 2－xy 3的单项式分别是 ．四、列代数式1． 5除以a 的商加上323的和；2．m 与n 的平方和；3．x 与y 的和的倒数；4．x 与y 的差的平方除以a 与b 的和，商是多少。
初一《整式的加减》专项练习题(有答案)
整式的加减专项练习100题1、3（a+5b）-2（b-a）2、3a-（2b-a）+b3、2（2a2+9b）+3（-5a2-4b）4、（x3-2y3-3x2y）-（3x3-3y3-7x2y）5、3x2-[7x-（4x-3）-2x2]6、（2xy-y）-（-y+yx）7、5（a2b-3ab2）-2（a2b-7ab）8、（-2ab+3a）-2（2a-b）+2ab9、（7m2n-5mn）-（4m2n-5mn）10、（5a2+2a-1）-4（3-8a+2a2）．11、-3x2y+3xy2+2x2y-2xy2；12、2（a-1）-（2a-3）+3．13、-2（ab-3a2）-[2b2-（5ab+a2）+2ab]14、（x2-xy+y）-3（x2+xy-2y）15、3x2-[7x-（4x-3）-2x2]16、a2b-[2（a2b-2a2c）-（2bc+a2c）]；17、-2y3+（3xy2-x2y）-2（xy2-y3）．18、2（2x-3y）-（3x+2y+1）19、-（3a2-4ab）+[a2-2（2a+2ab）]．20、5m-7n-8p+5n-9m-p；21、（5x2y-7xy2）-（xy2-3x2y）；22、3（-3a2-2a）-[a2-2（5a-4a2+1）-3a]．23、3a2-9a+5-（-7a2+10a-5）；24、-3a 2b-（2ab 2-a 2b ）-（2a 2b+4ab 2）．25、（5a-3a 2+1）-（4a 3-3a 2）； 26、-2（ab-3a 2）-[2b 2-（5ab+a 2）+2ab] 27、(8xy －x 2＋y 2)＋(－y 2＋x 2－8xy )； 28、(2x 2－21＋3x )－4(x －x 2＋21)；29、3x 2－［7x －(4x －3)－2x 2］．30、5a+（4b-3a ）-（-3a+b ）；31、（3a2-3ab+2b2）+（a2+2ab-2b2）；32、2a2b+2ab2-[2（a2b-1）+2ab2+2]．33、（2a 2-1+2a ）-3（a-1+a 2）；34、2（x 2-xy ）-3（2x 2-3xy ）-2[x 2-（2x 2-xy+y 2）]．35、 －32ab ＋43a 2b ＋ab ＋(－43a 2b )－136、(8xy －x 2＋y 2)＋(－y 2＋x 2－8xy )； 37、2x －(3x －2y ＋3)－(5y －2)；38、－(3a ＋2b )＋(4a －3b ＋1)－(2a －b －3)39、4x 3－(－6x 3)＋(－9x 3) 40、3－2xy ＋2yx 2＋6xy －4x 2y 41、 1－3(2ab ＋a )十[1－2(2a －3ab )]． 42、 3x －[5x ＋(3x －2)]； 43、(3a 2b －ab 2)－(ab 2＋3a 2b ) 44、()[]{}y x x y x --+--3233245、(－x 2＋5＋4x 3)＋(－x 3＋5x －4)46、（5a 2-2a+3）-（1-2a+a 2）+3（-1+3a-a 2）．47、5（3a 2b-ab 2）-4（-ab 2+3a 2b ）． 48、4a 2+2（3ab-2a 2）-（7ab-1）． 49、 21xy+（-41xy ）-2xy 2-（-3y 2x ）50、5a 2-[a 2-（5a 2-2a ）-2（a 2-3a ）] 51、5m-7n-8p+5n-9m+8p 52、（5x 2y-7xy 2）-（xy 2-3x 2y ） 53、 3x 2y-[2x 2y-3（2xy-x 2y ）-xy]5556、（a 2+4ab-4b 2）-3（a 2+b 2）-7（b 2-ab ）． 57、a 2+2a 3+（-2a 3）+（-3a 3）+3a 2；58、5ab+（-4a 2b 2）+8ab 2-（-3ab ）+（-a 2b ）+4a 2b 2； 59、（7y-3z ）-（8y-5z ）； 60、-3（2x 2-xy ）+4（x 2+xy-6）． 61、（x 3+3x 2y-5xy 2+9y 3）+（-2y3（-2y 3+2xy 2+x 2y-2x 3）-（4x 2y-x 3-3xy 2+7y 3）62、-3x 2y+2x 2y+3xy 2-2xy 2； 63、3（a 2-2ab ）-2（-3ab+b 2）；64、5abc-{2a 2b-[3abc-（4a 2b-ab 2]}．65、5m 2-[m 2+（5m 2-2m ）-2（m 2-3m ）]．66、-[2m-3（m-n+1）-2]-1．67、31a-( 21a-4b-6c)+3(-2c+2b) -5a n -a n -（-7a n ）+（-3a n ）69、x 2y-3xy 2+2yx 2-y 2x70、 41a 2b-0.4ab 2- 21a 2b+ 52ab 2；71、3a-{2c-[6a-（c-b ）+c+（a+8b-6）]}72、-3（xy-2x 2）-[y 2-（5xy-4x 2）+2xy]；73、化简、求值21x 2－2212- (x + y )2⎡⎤⎢⎥⎣⎦－23(－32x 2＋31y 2)，其中x ＝－2， y ＝－3474、化简、求值21x －2(x －31y 2)＋(－23x ＋31y 2)，其中x ＝－2，y ＝－32．75、化简、求值xx x x x x 5)64(213223312323-++-⎪⎭⎫ ⎝⎛---其中x ＝－121；76、 化简，求值（4m+n ）-[1-（m-4n ）]，m=52 n=-13177、化简、求值2(a 2b ＋2b 3－ab 3)＋3a 3－(2ba 2－3ab 2＋3a 3)－4b 3，其中a ＝－3，b ＝278、化简，求值：（2x 3-xyz ）-2（x 3-y 3+xyz ）+（xyz-2y 3），其中x=1，y=2，z=-3．79、化简，求值：5x 2-[3x-2（2x-3）+7x 2]，其中x=-2．80、若两个多项式的和是2x 2+xy+3y 2，一个加式是x 2-xy ，求另一个加式．81、若2a 2-4ab+b 2与一个多项式的差是-3a 2+2ab-5b 2，试求这个多项式．82、求5x 2y －2x 2y 与－2xy 2＋4x 2y 的和．83、 求3x 2＋x －5与4－x ＋7x 2的差．84、计算 5y+3x+5z 2与12y+7x-3z 2的和85、计算8xy 2+3x 2y-2与-2x 2y+5xy 2-3的差86、 多项式-x 2+3xy-21y 与多项式M 的差是-21x 2-xy+y ，求多项式M87、当3（x 2-2xy ）-[3x 2-2y+2（xy+y ）]的值．88、化简再求值5abc-{2a 2b-[3abc-（4ab 2-a 2b ）]-2ab 2}，其中a=-2，b=3，c=-4189、已知A=a 2-2ab+b 2，B=a 2+2ab+b 2（1）求A+B ；（2）求41(B-A)；90、小明同学做一道题，已知两个多项式A ，B ，计算A+B ，他误将A+B 看作A-B ，求得9x 2-2x+7，若B=x 2+3x-2，你能否帮助小明同学求得正确答案？91、已知：M=3x 2+2x-1，N=-x 2-2+3x ，求M-2N ．92、已知222244,5A x xy y B x xy y =-+=+-，求3A －B93、已知A ＝x 2＋xy ＋y 2，B ＝－3xy －x 2，求2A －3B ．94、已知2-a ＋(b ＋1)2＝0，求5ab 2－[2a 2b －(4ab 2－2a 2b )]的值．95、化简求值：5abc-2a 2b+[3abc-2（4ab 2-a 2b ）]，其中a 、b 、c 满足|a-1|+|b-2|+c 2=0．96、已知a，b，z满足：（1）已知|x-2|+（y+3）2=0，（2）z是最大的负整数，化简求值：2（x2y+xyz）-3（x2y-xyz）-4x2y．97、已知a+b=7，ab=10，求代数式（5ab+4a+7b）+（6a-3ab）-（4ab-3b）的值．98、已知m2+3mn=5，求5m2-[+5m2-（2m2-mn）-7mn-5]的值99、设A=2x2-3xy+y2+2x+2y，B=4x2-6xy+2y2-3x-y，若|x-2a|+（y-3）2=0，且B-2A=a，求a的值．100、有两个多项式：A＝2a2－4a＋1，B＝2(a2－2a)＋3，当a取任意有理数时，请比较A 与B的大小．答案：1、3（a+5b ）-2（b-a ）=5a+13b2、3a-（2b-a ）+b=4a-b ．3、2（2a 2+9b ）+3（-5a 2-4b ）=—11a 2+6b 24、（x 3-2y 3-3x 2y ）-（3x 3-3y 3-7x 2y ）= -2x 3+y 3+4x 2y5、3x 2-[7x-（4x-3）-2x 2] = 5x 2 -3x-36、（2xy-y ）-（-y+yx ）= xy7、5（a 22b-3ab 2）-2（a 2b-7ab ） = -a 2b+11ab8、（-2ab+3a ）-2（2a-b ）+2ab= -2a+b9、（7m 2n-5mn ）-（4m 2n-5mn ）= 3m 2n10、（5a 2+2a-1）-4（3-8a+2a 2）= -3a 2+34a-1311、-3x 2y+3xy 2+2x 2y-2xy 2= -x 2y+xy 2 12、2（a-1）-（2a-3）+3．=413、-2（ab-3a 2）-[2b 2-（5ab+a 2）+2ab]= 7a 2+ab-2b 2 14、（x 2-xy+y ）-3（x 2+xy-2y ）= -2x 2-4xy+7y 15、3x 2-[7x-（4x-3）-2x 2]=5x 2-3x-316、a 2b-[2（a 2b-2a 2c ）-（2bc+a 2c ）]= -a 2b+2bc+6a 2c 17、-2y 3+（3xy 2-x 2y ）-2（xy 2-y 3）= xy 2-x 2y 18、2（2x-3y ）-（3x+2y+1）=2x-8y-1 19、-（3a 2-4ab ）+[a 2-2（2a+2ab ）]=-2a 2-4a20、5m-7n-8p+5n-9m-p = -4m-2n-9p 21、（5x 2y-7xy 2）-（xy 2-3x 2y ）=4xy 2-4x 2y22、3（-3a 2-2a ）-[a 2-2（5a-4a 2+1）-3a]=-18a 2 +7a+2 23、3a 2-9a+5-（-7a 2+10a-5）=10a 2-19a+1024、-3a 2b-（2ab 2-a 2b ）-（2a 2b+4ab 2）= -4a 2b-64ab 2 25、（5a-3a 2+1）-（4a 3-3a 2）=5a-4a 2+1 26、-2（ab-3a 2）-[2b 2-（5ab+a 2）+2ab]=7a 2+ab-2b 227、(8xy －x 2＋y 2)＋(－y 2＋x 2－8xy )=028、(2x 2－21＋3x )－4(x －x 2＋21) = 6x 2-x-2529、3x 2－［7x －(4x －3)－2x 2］= 5x 2－3x －3 30、5a+（4b-3a ）-（-3a+b ）= 5a+3b 31、（3a 2-3ab+2b 2）+（a 2+2ab-2b 2）= 4a 2-ab32、2a 2b+2ab 2-[2（a 2b-1）+2ab 2+2]．= -133、（2a 2-1+2a ）-3（a-1+a 2）= -a 2-a+234、2（x 2-xy ）-3（2x 2-3xy ）-2[x 2-（2x 2-xy+y 2）]=-2x 2+5xy-2y 235、－32ab ＋43a 2b ＋ab ＋(－43a 2b )－1 = 31ab-136、(8xy －x 2＋y 2)＋(－y 2＋x 2－8xy )=037、2x －(3x －2y ＋3)－(5y －2)=-x-3y-138、－(3a ＋2b )＋(4a －3b ＋1)－(2a －b －3)= -a-4b+4 39、4x 3－(－6x 3)＋(－9x 3)＝ x 340、3－2xy ＋2yx 2＋6xy －4x 2y = -2 x 2y+4 41、 1－3(2ab ＋a )十[1－2(2a －3ab )]=2-7a 42、 3x －[5x ＋(3x －2)]=-5x+2 43、(3a 2b －ab 2)－(ab 2＋3a 2b )= -2ab 244、()[]{}y x x y x --+--32332 = 5x+y45、(－x 2＋5＋4x 3)＋(－x 3＋5x －4)= 3x 3－x 2＋5x+146、（5a 2-2a+3）-（1-2a+a 2）+3（-1+3a-a 2）=a 2+9a-1 47、5（3a 2b-ab 2）-4（-ab 2+3a 2b ）．=3a 2b-ab 2 48、4a 2+2（3ab-2a 2）-（7ab-1）=1-ab49、 21xy+（-41xy ）-2xy 2-（-3y 2x ）=41xy+xy 250、5a 2-[a 2-（5a 2-2a ）-2（a 2-3a ）]=11a 2-8a60、-3（2x 2-xy ）+4（x 2+xy-6）=-2x 2+7xy-2461、（x 3+3x 2y-5xy 2+9y 3）+（-2y 3+2xy 2+x 2y-2x 3）-（4x 2y-x 3-3xy 2+7y 3）=062、-3x 2y+2x 2y+3xy 2-2xy 2 = -x 2y+xy 263、3（a 2-2ab ）-2（-3ab+b 2）=3a 2-2b 264、5abc-{2a 2b-[3abc-（4a 2b-ab 2]}=8abc-6a 2b+ab 2 65、5m 2-[m 2+（5m 2-2m ）-2（m 2-3m ）]=m 2-4m 66、-[2m-3（m-n+1）-2]-1=m-3n+467、31a-( 21a-4b-6c)+3(-2c+2b)= -61a+10b68、 -5a n -a n -（-7a n ）+（-3a n ）= -2a n 69、x 2y-3xy 2+2yx 2-y 2x=3x 2y-4xy 270、 41a 2b-0.4ab 2- 21a 2b+ 52ab 2 = -41a 2b71、3a-{2c-[6a-（c-b ）+c+（a+8b-6）]}= 10a+9b-2c-672、-3（xy-2x 2）-[y 2-（5xy-4x 2）+2xy]= 2x 2-y 273、化简、求值21x 2－2212- (x + y )2⎡⎤⎢⎥⎣⎦－23(－32x 2＋31y 2)，其中x ＝－2， y ＝－34原式=2x 2＋21y 2－2 =69874、化简、求值21x －2(x －31y 2)＋(－23x ＋31y 2)，其中x ＝－2，y ＝－32．原式=-3x+y 2=69475、x x x x x x 5)64(213223312323-++-⎪⎭⎫ ⎝⎛---其中x ＝－121；原式=x 3+x 2-x+6=68376、 化简，求值（4m+n ）-[1-（m-4n ）]，m=52 n=-131原式=5m-3n-1=577、化简、求值2(a 2b ＋2b 3－ab 3)＋3a 3－(2ba 2－3ab 2＋3a 3)－4b 3，其中a ＝－3，b ＝2原式=-2ab 3+3ab 2＝1278、化简，求值：（2x 3-xyz ）-2（x 3-y 3+xyz ）+（xyz-2y 3），其中x=1，y=2，z=-3． 原式=-2xyz=679、化简，求值：5x 2-[3x-2（2x-3）+7x 2]，其中x=-2．原式=-2x 2+x-6=-1680、若两个多项式的和是2x 2+xy+3y 2，一个加式是x 2-xy ，求另一个加式．（2x 2+xy+3y 2 ） ——（ x 2-xy ）= x 2+2xy+3y 281、若2a 2-4ab+b 2与一个多项式的差是-3a 2+2ab-5b 2，试求这个多项式．（ 2a 2-4ab+b 2 ）—（-3a 2+2ab-5b 2）=5a 2 －6ab+6b 282、求5x 2y －2x 2y 与－2xy 2＋4x 2y 的和．（5x 2y －2x 2y ）+（－2xy 2＋4x 2y ）=3xy 2＋2x 2y83、 求3x 2＋x －5与4－x ＋7x 2的差．（3x 2＋x －5）—（4－x ＋7x 2）=—4x 2＋2x －984、计算 5y+3x+5z 2与12y+7x-3z 2的和（5y+3x+5z 2）+（12y+7x-3z 2）=17y+10x+2z 285、计算8xy 2+3x 2y-2与-2x 2y+5xy 2-3的差（8xy 2+3x 2y-2）—（-2x 2y+5xy 2-3）=5x 2y+3xy 2+186、 多项式-x 2+3xy-1y 与多项式M 的差是-21x 2-xy+y ，求多项式M23y 87、当3（x 2-2xy ）-[3x 2-2y+2（xy+y ）]的值． 15 88、化简再求值5abc-{2a 2b-[3abc-（4ab 2-a 2b ）]-2ab 2}，其中a=-2，b=3，c=-41 原式=83abc-a 2b-2ab 2=3689、已知A=a 2-2ab+b 2，B=a 2+2ab+b 2（1）求A+B ； （2）求41(B-A)； A+B=2a 2+2b 241(B-A)=ab 90、小明同学做一道题，已知两个多项式A ，B ，计算A+B ，他误将A+B 看作A-B ，求得 9x 2-2x+7，若B=x 2+3x-2，你能否帮助小明同学求得正确答案？A=10x 2+x+5 A+B=11x 2+4x+391、已知：M=3x 2+2x-1，N=-x 2-2+3x ，求M-2N ．M-2N=5x 2－4x+3 92、已知222244,5A x xy y B x xy y =-+=+-，求3A －B3A －B=11x 2-13xy+8y 293、已知A ＝x 2＋xy ＋y 2，B ＝－3xy －x 2，求2A －3B ．2A －3B= 5x 2＋11xy ＋2y 294、已知2-a ＋(b ＋1)2＝0，求5ab 2－[2a 2b －(4ab 2－2a 2b )]的值．原式=9ab 2－4a 2b=3495、化简求值：5abc-2a 2b+[3abc-2（4ab 2-a 2b ）]，其中a 、b 、c 满足|a-1|+|b-2|+c 2=0． 原式=8abc-8a 2b=-3296、已知a ，b ，z 满足：（1）已知|x-2|+（y+3）2=0，（2）z 是最大的负整数，化简求值： 2（x 2y+xyz ）-3（x 2y-xyz ）-4x 2y ． 原式=-5x 2y+5xyz=9097、已知a+b=7，ab=10，求代数式（5ab+4a+7b ）+（6a-3ab ）-（4ab-3b ）的值． 原式=10a+10b-2ab=5098、已知m 2+3mn=5，求5m 2-[+5m 2-（2m 2-mn ）-7mn-5]的值原式=2m 2+6mn+5=1599、设A=2x2-3xy+y2+2x+2y，B=4x2-6xy+2y2-3x-y，若|x-2a|+（y-3）2=0，且B-2A=a，求a 的值．B-2A=-7x-5y=-14a-15=a a=-1100、有两个多项式：A＝2a2－4a＋1，B＝2(a2－2a)＋3，当a取任意有理数时，请比较A 与B的大小．A=2a2－4a＋1 B＝2a2－4a＋3 所以A<B。
人教版数学七年级上册整式计算专项练习200题及答案解析
1写出下列单项式的系数和次数：2找出下列各代数式中的单项式（画3把多项式4计算：5化简：6解答下列问题：7解答下列各题：8请回答下列问题：9先化简，再求值：10先化简后求值：已知11已知12化简：13化简：14已知15合并同类项．16“1718先化简，再求值：19已知当20已知21先化简再求值．22化简：23已知24课堂上李老师给出了一道整式求值的题目，李老师把要求的整式25若关于26先化简，再求值：27已知28有这样一道题29有这样一道题：30先化简，再求值31已知32小明做一道题33已知多项式34先化简，再求值：35已知老师在黑板上书写了一个正确的演算过程随后用手掌捂住了如图所示的一个二次三项式，形式如36化简：37计算：38计算：39计算：40计算：41化简下列各式4243先化简，再求值：44若多项式45已知46已知47小红做一道数学题48先化简，再求值：49先化简，再求值：50已知：51先化简，后求值：已知52若53先化简再求值：54先化简，再求值：55解答下列各题：56完成下列小题．57化简求值，先化简代数式：58先化简，再求值：59先化简，再求值：60小明同学做数学题：已知两个多项式61回答问题．62先化简，再求值：63先化简，再求值：64先化简，再求值：65先化简，再求值：66化简：67先化简，再求值：68先化简，再求值：先化简，再求值：69化简：70已知：多项式71先化简，再求值：72先化简，再求值：73化简求值：74先化简，再求值：7576化简：77计算：78先化简，再求值：79化简：80已知81化简：82先化简，再求值：83阅读下面的解题过程并回答问题．84计算：8586解答下列问题．先化简，再求值：87先化简，再求值：88下列去括号正确的是（89下列去括号或添括号：90当9192如果单项式93单项式9495关于多项式9697先化简，再求值：98若代数式99若100观察下列运算并填空．1 23 4 5 67 8 9 10 11 1213 14 15 16 17 18 1920 21 22 23 24 25 26 2728 29 30 31 32 33 34 3536 37 38 39 40 41 4243 44 45 46 47 48 4950 51 52 53 54 55 5657 58 59 60 61 62 63 6465 66 67 68 69 70 7173 74 75 76 77 78 7981 82 83 84 85 8687 88 89 90 91 9293 94 9596 9798 99 100。
七年级上册数学整式的加减计算题50道(含答案)
七年级数学整式的加减计算题50道1.化简求值：−12a−2(a−12b2)−(32a−13b2)，其中a=−2，b=32．2.已知a、b互为相反数，x、y互为倒数，m的绝对值是2，求：13(a+b)2−6xy+m3的值。
3.已知代数式A=x2+xy−2y，B=2x2−2xy+x−1(1)求2A−B；(2)若2A−B的值与x的取值无关，求y的值．4.计算：(1)12+(−34)+(−23)(2)(3x2−xy−2y2)−2(x2+xy−2y2)5.先化简，再求值：(3a2−ab+7)−(−4a2+2ab+7)，其中a=−1，b=26.化简：(1)−3m+3n−5m−7n(2)5a2−[3a−2(a−3)+4a2]7.若−2a m b与a2b n是同类项，求2mn2−[2m2n−3(m2n−2mn2)]的值．8.化简下列各式(1)3ab−a2−2ab−3a2(2)−2(x2−3xy)+6(x2−12 xy)9.计算与化简：(1)30−48×(16+34−112)(2)−14−2×(−3)2÷(−16)(3)5(x+y)−4(3x−2y)+3(2x−y)(4)6ab2−[a2b+2(a2b−3ab2)]10.化简11.先化简，再求值：5x2−[2xy−3(13xy+2)+4x2]。
其中x=−2，y=12。
12.化简(1)4x2y−8xy2−9−4x2y+12xy2+5；(2)−(2a2b−5ab)+2(−ab+a2b−1)．13.计算：(1)(3a−2)−3(a−5)(2)(4a2b−5ab2)−(3a2b−4ab2)14. 合并下列多项式中的同类项：(1)3a 2+4b 2+ab −3a 2−4b 2;．15. 已知A =3ax 3−bx ，B =−ax 3−2bx +8．(1)求A +B ；(2)当x =−1时，A +B =10，求代数式3b −2a 的值．16. 计算：(1)16÷(−12)×(−38)−(+4)(2)−12020÷(−5)2×(−53)−|0.8−1| (3)2a +(3a 1)(a 5)(4)3x 2y 4xy 23+5x 2y +2xy 2+5．17.化简．(1)(8a−7b)−(−4a+5b)(2)a+(2a+b)−2(a−2b)18.化简：(l)m−2n+3(m+n)；(2)5(a2b−ab)−2(−a2b+3ab)。
北师大版七年级数学上册整式计算题专项练习(附答案)
北师大版七年级数学上册整式计算题专项练习(附答案)1.将表达式化简：$-a-b+2a-b=-b+a$2.将表达式化简：$(x+2)(y+3)-(x+1)(y-2)=xy+3x+2y+6-xy+x-2y+2=x+3x+2+6+x-2y+2=4x-2y+10$3.将表达式化简：$(2x-y)(2x+y)+2y2=4x2-y2+2y2=4x2$4.将表达式化简：$\frac{x(x-y)}{x-2}+\frac{2y}{x-2}=\frac{x(x-y)+2y}{x-2}=\frac{x^{2}-xy+2y}{x-2}$6.将表达式化简：$(2a+1)^{2}-2(2a+1)+3=4a^{2}+8a+4-4a-2+3=4a^{2}+4a+5$8.将表达式化简：$-(x-5)(x+5)-\frac{(3x-2y)(-2y-3x)}{x+1}=\frac{-(x^{2}-25)(x+1)+(9x^{2}-12xy+4y^{2})}{x+1}=\frac{-x^{3}-10x^{2}-21x+4y^{2}}{x+1}$10.将表达式化简：$3(x+1)(x-1)-(2x-1)(x+y)2(x-y)2=3(x^{2}-1)-2x^{3}+x^{2}y+xy^{2}-2xy^{2}+2y^{3}=3x^{2}-3-2x^{3}+x^{2}y-y^{2}$15.将表达式化简：$-\frac{1}{2}-(-1)^{2006}+\frac{2^{11}\times(-3)^{432}}{2}= -\frac{1}{2}-1+2^{10}\times3^{432}=2^{10}\times3^{432}-\frac{3}{2}$20.将表达式化简：$(2a-1)^{2}+(2a-1)(a+4)=4a^{2}-4a+1+2a^{2}+7a-4=6a^{2}+3a-3$21.将表达式化简：$(x+2y)^{2}-2(x-y)(x+y)+2y(x-3y)=x^{2}+4xy+4y^{2}-2(x^{2}-y^{2})+2xy-6y^{2}=x^{2}+6xy-8y^{2}$22.将表达式化简：$5(x-1)(x+3)-2(x-5)(x-2)=5(x^{2}+2x-3)-2(x^{2}-3x+10)=3x^{2}+16x-40$23.将表达式化简：$(a-b)(a^{2}+ab+b^{2})=a^{3}-b^{3}$24.将表达式化简：$(3y+2)(y-4)-3(y-2)(y-3)=3y^{2}-5y-18$25.将表达式化简：$a(b-c)+b(c-a)+c(a-b)=ab-ac+bc-bc+ac-ab=0$26.将表达式化简：$(-2mn^{2})^{2}-4mn^{3}(mn+1)=4m^{2}n^{4}-4m^{2}n^{4}-4mn^{3}= -4mn^{3}$28.将表达式化简：$-(x+2)(x-2)=-(x^{2}-4)=-x^{2}+4$30.将表达式化简：$(x-3y)(x+3y)-(x-3y)=x^{2}-9y^{2}-x+3y$1.原式=2.原式=-400+4=9604；原式=-+1=13.原式=900×219；原式=-(2009+1)(2009-1)=2xxxxxxxxxxxx=-xxxxxxx4.原式=6a^2+3a-3，当a=2时，原式=6×(-2)^2+3×(-2)-3=24-6-3=155.原式=-x^2+6xy，当x=2，y=2时，原式=-(-2)^2+6×(-2)×2=-4-24=-286.原式=-3x^2+24x-357.原式=a^3-b3=(a-b)(a^2+ab+b^2)8.原式=5y-269.原式=6xy-18y210.原式=(a-c+b)^2-b^2=a^2-2ac+2bc+c^2-b^211.原式=15×10^912.原式=2a+2解答题：1.①原式=12-(-8)+(-7)-15=38②原式=-1+2×(-5)-(-3)÷(-1)=-1+(-10)-3=-14③原式=2x-3y+5x+4y=7x+y④原式=5a+2a^-1-4(3-8a+2a)=5a+2a^-1-12+32a-8a=34a+2a^-1-122.1) 原式=4-2×2-(-36)÷4=4-4+9=92) 原式=9a-6b-2a+6b=7a3.①原式=7x+4(x-2)-2(2x-x+3)=7x+4x-8-2x+2=9x-6②原式=4ab-3b-[(a+b)-(a-b)]=4ab-3b-a-b+a+b=4ab-3b-a③原式=3mn-5m-3m+5mn=8mn-8m④原式=2a+2(a+1)-3(a-1)=2a+2a+2-3a+3=4a+54.①原式=4a+18b-15a-12b=4a-15a+18b-12b=-11a+6b②原式=3x+6x^-1-3x-4x^-1=2x+2x^-15.原式=3(x-1)-(x-5)=3x-3-x+5=2x+26.原式=3(x+y)+4(x+y)-6(x+y)=7(x+y)=7(5+3)=567.原式=2(x-3y)-(x-y)=2x-6y-x+y=x-5y8.由6M=2N-4得M=N/3-2/3，代入M=x+3x-5和N=3x+5中得到：x+3x-5=N/3-2/3+3x-5解得x=7/69.原式=A+B=5a-2ab-4a+4ab=a先化简，再求值：3（A+B）﹣2（2A﹣B），其中A=﹣2，B=1．分析：先代入数值，再按照整式的加减运算顺序进行计算．解答：代入A=﹣2，B=1得：3（A+B）﹣2（2A﹣B）=3（﹣2+1）﹣2（2（﹣2）﹣1）=3﹣4﹣（﹣5）=9．点评：本题考查了整式的加减及代数式的化简，解答本题的关键在于熟练掌握整式的加减运算顺序及代入数值的方法．10．设a=14x﹣6，b=﹣7x+3，c=21x﹣1．1）求a﹣（b﹣c）的值；2）当x=时，求a﹣（b﹣c）的值．分析：先代入数值，再按照整式的加减运算顺序进行计算．解答：代入a=14x﹣6，b=﹣7x+3，c=21x﹣1得：1）a﹣（b﹣c）=14x﹣6﹣（﹣7x+3﹣21x+1）=14x﹣6﹣﹣7x+3﹣21x﹣1=6x﹣4；2）当x=时，a﹣（b﹣c）=6×﹣4﹣4=﹣28．点评：本题考查了整式的加减及代数式的化简，解答本题的关键在于熟练掌握整式的加减运算顺序及代入数值的方法．11．化简求值：已知a、b满足：|a﹣2|+（b+1）=0，求代数式2（2a﹣3b）﹣（a﹣4b）+2（﹣3a+2b）的值．分析：先化简|a﹣2|+（b+1）=0得a=2，b=﹣1，再代入求值．解答：代入a=2，b=﹣1得：2（2a﹣3b）﹣（a﹣4b）+2（﹣3a+2b）=2（2×2﹣3（﹣1））﹣（2﹣4（﹣1））+2（﹣3×2+2（﹣1））=4+9+6=19．点评：本题考查了整式的加减及代数式的化简，解答本题的关键在于熟练掌握绝对值的性质及代入求值的方法．12．已知（x+1）+|y﹣1|=0，求2（xy﹣5xy）﹣（3xy﹣xy）的值．分析：先解方程|x﹣1|+（y+1）=0，得x=﹣1，y=﹣2，再代入求值．解答：解方程得x=﹣1，y=﹣2，代入得：2（xy﹣5xy）﹣（3xy﹣xy）=2（﹣1×﹣2﹣5﹣1×﹣2）﹣（3﹣1×﹣2）=4﹣（3+2）=﹣1．点评：本题考查了整式的加减及代数式的化简，解答本题的关键在于熟练掌握绝对值的性质及代入求值的方法．解答：将3（x+y）+4（x+y）﹣6（x+y）化简得：(3+4-6)(x+y)=x+y=-2代入x=5，y=3，得到3（5+3）+4（5+3）﹣6（5+3）=24 所以，代数式3（x+y）+4（x+y）﹣6（x+y）的值为24.点评：本题考查了整式的加减、化简和求值，需要熟练掌握去括号、合并同类项和代入数值的方法。
初中数学七年级上册整式练习题含答案
初中数学七年级上册整式练习题含答案学校：__________ 班级：__________ 姓名：__________ 考号：__________1. 单项式−xy2的系数是（）A.−3B.−2C.−1D.02. 下列各式中，次数为3的单项式是( )A.−15abB.3a2b2C.4x3−3D.3x2y53. 下列说法正确的是( )A.多项式x2+2x2y+1是二次三项式B.单项式2x2y的次数是2C.0是单项式D.单项式−3πx2y的系数是−34. 下列说法中正确的是（）A.5不是单项式B.x−1是整式C.x2y的系数是0D.x+y2是单项式5. 多项式x2+3kxy−y2−9xy+10中，不含xy项，则k＝（）A.0B.2C.3D.46. 下列说法正确的是（）A.−2vt3的系数是−2 B.32ab3的次数是6次C.x+y5是多项式 D.x2+x−1的常数项为17. 下列式子：x2−1，1a ，2ab23，0，−5x中，整式的个数是()A.2B.3C.4D.58. 下列判断中错误的是（）A.1−a−ab是二次三项式B.−a2b2c是单项式C.a+b2是多项式 D.34πr2中，系数是349. 下列说法中正确的是（ ）A.5πx 的系数是5B.单项式x 的系数为1，次数为0C.xy 2的次数是2D.xy +x −1是二次三项式10. 在代数式2xy,0,−x 3，8y 2，1xy ，x +2y 中，整式共有（ ）A.5B.4C.6D.3 11. 一个关于b 的二次三项式的二次项系数是−2，一次项系数是−0.5，常数项是3，则这个多项式是________．12. 下列各式−14，3xy ，a 2−b 2，3x−y 5，2x >1，−x ，0.5+x 中，是整式的有________个，是单项式的有________个，是多项式的有________个．13. 已知代数式：−x ，b 2a ，2ab 23，a 2−12，x +5y ，5π，−xy 2z 5，a 2+2ab +b 2，单项式有________，多项式有________．14. 已知多项式−13x 2y m+1+xy 2−3x 3−6是五次四项式，单项式0.4x 2n y 5−m 的次数与这个多项式的次数相同，则m =________，n =________．15. 在下列各式：①π−3；②ab ＝ba ；③x ；④2m −1>0；⑤x−y x+y ；⑥8(x 2+y 2)中，整式有________．16. 单项式−x 2yz 32是________次单项式．17. 关于x 的多项式 k(k +1)x 3+kx 2+x 2−4x −3 是关于x 的二次多项式.（1）直接写出k 的值为______.（2）若该多项式的值为7，则 2019k −12x 2+2x 的值为________.18. 多项式−x2+xy−y次数、项数、第一项的系数分别是________、________、________．19. 单项式−23x2y的系数与次数的乘积是________．20. 观察下列单项式的特点：2x3y，−4x4y2，8x5y3，−16x6y4，…请写出第七个单项式________，试猜想第n个单项式为________．21. 先化简，再求值：(2a+3b)2−(2a+b)(2a−b)，其中a=13，b=−12．22. 若(x m+2y2)3⋅(x2y n−3)2=x13y8，求m−n的值．23. 填表．24. 已知多项式−3x2+mx+nx2−x+3的值与x取值无关，求(2m−n)2012的值．25. 把下列等式填入相应的圈内：ab+c，2m，9x2+c，−ab2c，a，0，−12x，y+2．26. 若多项式5x2y|m|+(n−3)y2−2是关于x、y的四次二项式，求m2−2mn+n2的值．27. −5x2y m+1+xy2−3x3−6是六次四项式，且3x2n y5−m的次数跟它相同（1）求m，n的值（2）求多项式的常数项以及各项的系数和．28. 一个单项式中，所有字母的指数的和叫做这个单项式的次数，那么单项式−3x2y3，abc，2xy23，πmn2中所有字母的指数的和各是多少？29. 下列代数式中哪些是单项式，哪些是多项式？它们的次数分别是多少？a2b+a2−2；−3x；−2x+y2；2xy2；25.30.(1)已知多项式−2x2y m+1+xy2−3x3−6是六次四项式，单项式−x2n y5−n与该多项式的次数相同，求m−n的值.(2)已知关于x，y的多项式3mx2+nxy−x+2xy−x2+y+3不含二次项，求6m−2n+1的值．31. （1）若3x2−x−ax2+bx+1是一个二次多项式，求a的值； 31.（2）若上述多项式是一次二项式，求a、b的值．32. 已知关于x的多项式−2x2+nx2−5x−1为一次多项式．(1)求n的值；(2)求该多项式各项系数之和．33. 已知多项式x2y m+2+xy3−3x4−5是五次四项式，且单项式5x2n−3y4−m的次数与该多项式的次数相同，求m，n的值．34. 指出下列多项式是几次几项式．（1）x2−3x+1；（2）2x−2y3；（3）4x2y−5xy3+2x2y+1．35. 已知多项式−x2y2m+1+xy−6x3−1是五次四项式，且单项式πx n y4m−3与多项式的次数相同，求m，n的值．36. 一个三位数，它的十位数字是百位数字的平方，个位数字比百位数字的2倍少1，如果记百位数字是x，先按字母x的降幂排列写出这个三位数的表达式，再写出所有满足条件的三位数．37. 已知代数式M=(a−16)x3+20x2+10x+5是关于x的二次多项式，且二次项的系数为b. 如图，在数轴上有A，B，C三个点，且A，B，C三点所表示的数分别为a，b，c. 已知AC=6AB.(1)求a，b，c的值；(2)若动点P，Q分别从C，O两点同时出发，向右运动，且点Q不超过点A．在运动过程中，点E为线段AP的中点，点F为线段BQ的中点，若动点P的速度为每秒2个单位长度，的值；动点Q的速度为每秒3个单位长度，求BP−AQEF(3)若动点P，Q分别自A，B同时出发，都以每秒2个单位长度向左运动，动点M自点C时，出发，以每秒6个单位长度的速度沿数轴向右运动，设运动时间为t（秒），3<t<72数轴上有一点N与点M的距离始终为2，且点N在点M的左侧，点T为线段MN上一点（点T不与点M，N重合），在运动的过程中，若满足MQ−NT=3PT（点T不与点P重合），求出此时线段PT的长度．38. 观察下列单项式−2x，4x2，−8x3，16x4，−32x5，64x6，…（1）分别指出单项式的系数和指数是怎样变化的？（2）写出第10个单项式；（3）写出第n个单项式．39. 写出系数为2011，只含有字母x，y，且x，y都含有的所有四次单项式．40. 观察下列单项式：−2x，22x2，−23x3，24x4，…，−219x19，你能写出第n个单项式吗？并写出第2013个单项式为解决这个问题，我们不妨从系数和次数两个方面入手进行探究，从中发现规律，经过归纳，猜想出结论．（1）系数规律有两条：①系数的符号规律是________；②系数的绝对值规律是________．（2）次数的规律是________．（3）根据上面的规律，猜想出第n个单项式．（4）求第2013个单项式．参考答案与试题解析初中数学七年级上册整式练习题含答案一、选择题（本题共计 10 小题，每题 3 分，共计30分）1.【答案】C【考点】单项式【解析】此题暂无解析【解答】此题暂无解答2.【答案】D【考点】单项式的系数与次数单项式的概念的应用【解析】此题暂无解析【解答】此题暂无解答3.【答案】C【考点】单项式的概念的应用多项式的项与次数单项式的系数与次数【解析】此题暂无解析【解答】此题暂无解答4.【答案】A【考点】单项式的系数与次数【解析】此题暂无解析【解答】此题暂无解答5.C【考点】多项式【解析】此题暂无解析【解答】此题暂无解答6.【答案】C【考点】单项式的系数与次数多项式的概念的应用多项式的项与次数【解析】此题暂无解析【解答】此题暂无解答7.【答案】C【考点】整式的概念【解析】此题暂无解析【解答】此题暂无解答8.【答案】D【考点】单项式多项式【解析】此题暂无解析【解答】此题暂无解答9.【答案】D【考点】单项式的系数与次数多项式的项与次数此题暂无解析【解答】此题暂无解答10.【答案】A【考点】整式的概念【解析】此题暂无解析【解答】此题暂无解答二、填空题（本题共计 10 小题，每题 3 分，共计30分）11.【答案】−2b2−0.5b+3【考点】多项式【解析】此题暂无解析【解答】此题暂无解答12.【答案】6,3,3【考点】整式的概念多项式的概念的应用单项式的概念的应用【解析】此题暂无解析【解答】此题暂无解答13.【答案】−x，2ab23，5π，−xy2z5,a2−12，a2+2ab+b2【考点】多项式单项式【解析】此题暂无解析【解答】此题暂无解答14.【答案】2,1【考点】单项式单项式的系数与次数多项式的项与次数【解析】此题暂无解析【解答】此题暂无解答15.【答案】①、③、⑥【考点】整式的概念【解析】此题暂无解析【解答】此题暂无解答16.【答案】6【考点】单项式单项式的系数与次数【解析】此题暂无解析【解答】此题暂无解答17.【答案】解：(1)0.(2)−5.【考点】多项式的概念的应用【解析】此题暂无解析【解答】此题暂无解答18.【答案】2,3,−1【考点】多项式多项式的项与次数单项式【解析】此题暂无解析【解答】此题暂无解答19.【答案】−2【考点】单项式的概念的应用有理数的乘法【解析】此题暂无解析【解答】此题暂无解答20.【答案】128x9y7,(−1)n+12n x n+2y n【考点】单项式【解析】此题暂无解析【解答】此题暂无解答三、解答题（本题共计 20 小题，每题 10 分，共计200分）21.【答案】解：原式=12ab+10b2，当a=13，b=−12时，原式=12．【考点】整式的概念【解析】此题暂无解析【解答】此题暂无解答22.【答案】解：原式=x3(m+2)y6⋅x4y2(n−3)=x13y8，∴{3(m+2)+4=13，2(n−3)+6=8，解得{m=1，n=4，∴m−n=1−4=−3. 【考点】单项式的系数与次数整式的混合运算同底数幂的乘法二元一次方程组的解【解析】此题暂无解析【解答】此题暂无解答23.【答案】解：4xy−15=15(4xy−1)=45xy−15，故这个多项式的项为45xy，−15⋅【考点】多项式【解析】此题暂无解析【解答】此题暂无解答24.【答案】解：合并同类项得(n−3)x2+(m−1)x+3，根据题意得n−3=0，m−1=0，解得m=1，n=3，所以(2m−n)2012=(−1)2012=1．【考点】多项式【解析】此题暂无解析【解答】此题暂无解答25.【答案】解：根据题意如下：【考点】多项式单项式【解析】此题暂无解析【解答】此题暂无解答26.【答案】解：由多项式是关于x，y的四次二项式知：2+|m|=4，n−3=0，∴m=2或m=−2，n=3，∴m2−2mn+n2=22−2×2×3+32=4−12+9=1，∴m2−2mn+n2=(−2)2−2×(−2)×3+32=25，∴求m2−2mn+n2的值是1，或25．【考点】多项式【解析】此题暂无解析【解答】此题暂无解答27.【答案】解：（1）由题意可知：该多项式时六次多项式，∴2+m+1=6，∴m=3，∵3x2n y5−m的次数也是六次，∴2n+5−m=6，∴n=2∴m=3，n=2（2）该多项式为：−5x2y4+xy2−3x3−6常数项−6，各项系数为：−5，1，−3，−6，故系数和为：−5+1−3−6=−13【考点】多项式单项式【解析】此题暂无解析【解答】此题暂无解答28.【答案】解：单项式−3x2y3，abc，2xy23，πmn2中所有字母的指数的和分别是：5，3，3，2．【考点】单项式【解析】此题暂无解析【解答】此题暂无解答29.【答案】解：单项式有：−3x，2xy2，25，次数分别是：1，3，0；多项式有：a2b+a2−2，−2x+y2，次数分别是：3，2.【考点】单项式的概念的应用多项式的概念的应用【解析】此题暂无解析【解答】此题暂无解答30.【答案】解：(1)∵多项式−2x2y m+1+xy2−3x3−6是六次四项式，单项式−x2n y5−n与该多项式次数相同，∴2+m+1=6，2n+5−n=6，解得：m=3，n=1∴m−n=2.(2)原式=(3m−1)x2+(n+2)xy−x+y+3.由题意得3m−1=0，n+2=0，解得m=13，n=−2，所以6m−2n+1=6×13−2×(−2)+1=7.【考点】多项式的项与次数多项式单项式【解析】此题暂无解析【解答】此题暂无解答31.【答案】3x2−x−ax2+bx+1是一个二次多项式，则3−a≠0，解得：a≠3；∵上述多项式是一次二项式，∴3−a＝0，b−1≠0，解得：a＝3，b≠1．【考点】多项式的概念的应用【解析】此题暂无解析【解答】此题暂无解答32.【答案】解：(1)由多项式的概念应用可知，n−2=0，则n=2.(2)由(1)可知该多项式为−5x−1．则(−5)+(−1)=−6．【考点】多项式的概念的应用【解析】此题暂无解析【解答】此题暂无解答33.【答案】解：因为x2y m+2+xy3−3x4−5是五次四项式，所以m+2=3，解得m=1.因为单项式5x2n−3y4−m的次数与该多项式的次数相同，所以2n−3+4−m=5，即2n+1−1=5，解得n=5.2【考点】多项式的概念的应用单项式的系数与次数多项式的项与次数【解析】此题暂无解析【解答】此题暂无解答34.【答案】解：（1）x2−3x+1是二次三项式；是一次二项式；（2）2x−2y3（3）4x2y−5xy3+2x2y+1是四次三项式．【考点】多项式【解析】此题暂无解析【解答】此题暂无解答35.【答案】解：∵−x2y2m+1+xy−6x3−1是五次四项式，∴2m+1=3，m=1，∴4m−3=1.∵单项式πx n y4m−3与多项式−x2y2m+1+xy−6x3−1的次数相同，∴n+1=5，n=4，∴m=1，n=4.【考点】多项式的项与次数单项式的系数与次数【解析】此题暂无解析【解答】此题暂无解答36.【答案】解：由题意得，十位上的数字是x2，个位上的数字是(2x−1)，则按字母x的降幂排列写出这个三位数的表达式为：10x2+100x+2x−1=10x2+ 102x−1．当x=1时，这个三位数是111；当x=2时，这个三位数是243；当x=3时，这个三位数是395．【考点】多项式【解析】此题暂无解析【解答】此题暂无解答37.【答案】解：(1)∵M=(a−16)x3+20x2+10x+5是关于x的二次多项式，二次项的系数为b，∴a=16，b=20，∴AB=4.∵AC=6AB，∴AC=24，即16−c=24，∴c=−8.(2)由题意得：EF=AE−AF=12AP−12BQ+AB=12(24−2t)−12(20−3t)+4=6+t2，∴BP−AQ=(28−2t)−(16−3t)=12+t，∴BP−AQEF=2.(3)P点表示的数为16−2t，Q点表示的数为20−2t，M点表示的数为6t−8，N点表示的数为6t−10，T点表示的数为x，∴MQ=28−8t，NT=x−6t+10，PT=|16−2t−x|.∵MQ−NT=3PT，∴28−8t−(x+10−6t)=3|16−2t−x|，∴x=15−2t或x=332−2t，∴PT=1或PT=12．【考点】数轴多项式的概念的应用【解析】此题暂无解析【解答】此题暂无解答38.【答案】解：（1）系数为：−2，4=(−2)2，−8=(−3)3，16=(−2)4，−32=(−2)5…指数分别是：1，2，3，4，5，6…（2）第10个单项式为：(−2)10x10=1024x10；（3）第n个单项式为：(−2)n x n．【考点】单项式【解析】此题暂无解析【解答】此题暂无解答39.【答案】解：符合题意的式子有：2011x3y；2011x2y2；2011xy3．【考点】单项式【解析】此题暂无解析【解答】此题暂无解答40.【答案】(−1)n,2n第n个为n次（3）由（1）知第n个单项式是=(−1)n×2n x n；（4）∵由（1）知第n个单项式是=(−1)n×2n x n，∴第2013个单项式为=(−1)2013×22013x2013=−22013x2013．【考点】单项式【解析】此题暂无解析【解答】此题暂无解答。
人教版数学七年级上册第二章《整式的加减》计算题专项训练
人教版七年级数学上册《整式的加减》计算题训练附答案解析第二章整式的加减第一节整式的加减法（高效训练1--20）1、计算下列各式2、化简：1、计算下列各式2、化简：3、先化简再求值：其中，4、先化简，再求值．，其中与互为相反数1、合并同类项2、化简：先化简，后求值：，其中．3、有这样一道题：计算的值，其中。
某同学把抄成了，但计算结果也是正确的，试说明理由，并求出这个结1、计算下列各式2、计算下列各式3、已知a是绝对值等于4的负数，b是最小的正整数，c的倒数的相反数是，求a，b，c的值；求：、1、计算下列各式计算：计算：化简：化简并求值：；其中，；2、计算下列各式3、先化简，再求值．已知，求的值．1、计算下列各式2、计算下列各式3、已知：，求的值；若的值与x无关，求y的值．1、计算下列各式若，，求：当时，的值．已知，，求代数式的值．2、在关于x，y的多项式中，无论x，y取任何数，多项式的值都不变，求a，b的值．3、已知，求的值1、计算下列各式(2)2、合并下列多项式中的同类项．3、先化简，再求值：，其中，1、计算下列各式2、化简：3、化简求值：已知，求代数式的值1、计算下列各式2、已知代数式，马小虎同学在做整式加减运算时，误将“”看成“”了，计算的结果是．请你帮马小虎同学求出正确的结果；是最大的负整数，将x代入问的结果求值3、已知，，且，求C1、计算下列各式2、计算下列各式化简：先化简，再求值：，其中，3、已知：已知，．求B；当时，求的1、计算下列各式2、化简下列各式：．3、老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了如图所示的一个二次三项式，形式如图：求所捂的二次三项式；若，求所捂二次三项式的值1、计算下列各式2、化简下列各式先化简，再求值．，其中，．已知，，求代数式的值3、已知，．求；若，求的值；试将用A与B的式子表示出来．1、计算下列各式2、求值：，其中，3、先化简，再求值：，其中．，其中，．1、计算下列各式2、已知，，按要求完成下列各小题．若的结果中不存在含x的一次项，求a的值；当时，求的结果．3、已知，求的值．1、先化简，再求值：，其中．，其中，2、先化简，再求值：，其中，．有一道题是一个多项式减去“”，小强误当成了加法计算，得到的结果是“”，请求出正确的计算结果．3、已知，．若化简是常数的结果中没有常数项，求m的值；当时，求的值．1、计算下列各式，其中．，其中，．2、若代数式中不含xy项，求：的值．3、已知多项式与多项式A的和为，且式子的计算结果中不含关于x的一次项，求多项式A．求m的值1、计算下列各式2、已知，．求；若，求的值．3、化简或求值化简：；化简求值：，其中，．1、计算下列各式2、已知，求的值3、如果代数式的值与字母x取值无关，试求代数式的值．4、若，求的值高效训练20 第周星期1、计算下列各式先化简，再求值：，其中，．已知整式，整式M与整式N之差是，求出整式N．2、有这样一道题：计算的值，其中，甲同学把“”错抄成了“”但他计算的结果也是正确的，请你通过计算说明原因．3、已知：，求的值；当x的取任意数值，的值是一个定值时，求的值4、如果关于x的多项式的值与x的取值无关，且该多项式的次数是三次．求m，n的值．参考答案与解析高效训练11.原式原式原式原式原式原式2.解：原式；原式．高效训练21.原式；原式．2.原式原式3.解：4.解：原式，，，原式高效训练31.原式．原式原式原式2.原式；原式；原式，原式．3.．当时，原式．因为化简的结果中不含x，所以原式的值与x值无关．高效训练41.（1）．（2）．（3）．2.（1）；（2）．3.由题意可知：，，当，，时，原式高效训练51.原式；原式；原式；原式．原式．2.原式原式．3.=10高效训练61.解：原式；原式；原式原式2.原式；原式3.原式；原式要使原式的值与x无关，则，解得：．高效训练71.原式；原式；，，，当时，原式；，，原式．2.解：，无论x，y取任何数，多项式的值都不变，，，解得：，3.解：，，原式高效训练81.（1）；（2）；；（4）．2.原式；原式；原式；原式．3.原式原式高效训练91.原式；原式；原式；原式；原式；原式．2.原式；原式；原式；原式．3.原式原式高效训练101.原式；原式；原式；原式；原式；原式．2.根据题意知，则；是最大的负整数，，则原式．3.，，，高效训练111.原式；原式；原式；原式．2.原式；原式，原式．3.（1）B；（2），原式．高效训练121.原式原式原式．2.（1）原式（2）原式（3）原式．3.根据题意得：；当时，原式．高效训练131.原式；原式；原式；原式2.原式，当，时，原式；原式，当，时，原式．3.（1）（2）原式；．高效训练141.（1）．（2）（3）．（4）．2.原式，当，时，原式3.（1），当时，原式．（2），当，时，原式．高效训练151.原式；原式；原式；原式．2.，，，由结果中不含x的一次项，得到，解得：；，，，3.原式，当，时，原式．高效训练161.原式，原式；原式，当，时，原式．2.原式，当，时，原式；原式则正确的计算结果．3.（1），由结果不含常数项，得到，解得：；（2）原式，当时，原式．高效训练171.原式当时，原式．原式当，时，原式．2.原式，由结果不含xy项，得到，解得：，则原式．3.根据题意得：；，结果不含关于x的一次项，，即高效训练181.原式；原式；原式；原式．2.(2)解得，，．3.（1）；（2）；（3）．高效训练191.原式；原式2.原式当时，原式3.，根据题意知且，解得：、，4.，，，，当，时，原式．高效训练201.(1)，当，时，原式；整式．2.原式，此题的结果与x的取值无关．3.．．当x的取任意数值，的值是一个定值，即的值是一个定值，．4.由题意得，，，解得，，．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
整式的乘除计算训练（1）1. )2()(b a b a -++-2. (x+2)(y+3)-(x+1)(y-2)3. 22)2)(2(y y x y x ++-4.x(x －2)－(x+5)(x －5)5. ⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛--y x y x224 6.)94)(32)(23(22x y x y y x +---7. ()()3`122122++-+a a 8.()()()2112+--+x x x9. (x －3y)(x+3y)－(x －3y)2 10. 23(1)(1)(21)x x x +---11. 22)23()23(y x y x --+ 12.22)()(y x y x -+13. 0.125100×810014. 3022)2(21)x (4554---÷⎪⎭⎫⎝⎛--π-+⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛15. (1211200622332141）（）（）（）-⨯+----16—19题用乘法公式计算16.999×1001 17.1992-18.298 19.2010200820092⨯-20.化简求值：)4)(12()12(2+-+-a a a ，其中2-=a 。
21. 化简求值2(2)2()()2(3)x y x y x y y x y +--++-,其中12,2x y =-=。
22. 5(x－1)(x+3)－2(x－5)(x－2) 23. (a－b)(a2+ab+b2)24. (3y+2)(y－4)－3(y－2)(y－3) 25. a(b－c)+b(c－a)+c(a－b)1y2)2 26. (－2mn2)2－4mn3(mn+1) 27. 3xy(－2x)3·(－428. (－x－2)(x+2) 29. 5×108·(3×102) 30. (x－3y)(x+3y)－(x－3y)231. (a+b－c)(a－b－c)答案1. 2. 3. 4.5. 6. 7. 8.9. 10. 11. 12.13. 14. 15.16. 原式=(1000-1)(1000+1) 17. 原式=(99+1)(99-1)=1000000-1 =10098=999999 =980018. 原式=(900-2)2 19. 原式=20092-(2009+1)(2009-1)=10000-400+4 =20092-20092+1=9604 =120.原式=，当时，原式=21.原式=，当，时，原式=22. 23. 24. 25. 0 26. 27. 28. 29.30. 31.北师大七年级数学上册《整式及其加减》计算题专项练习一一．解答题（共12小题）1．计算题①12﹣（﹣8）+（﹣7）﹣15；②﹣12+2×（﹣5）﹣（﹣3）3÷；③（2x﹣3y）+（5x+4y）；④（5a2+2a﹣1）﹣4（3﹣8a+2a2）．2．（1）计算：4+（﹣2）2×2﹣（﹣36）÷4；（2）化简：3（3a﹣2b）﹣2（a﹣3b）．3．计算：（1）7x+4（x2﹣2）﹣2（2x2﹣x+3）；（2）4ab﹣3b2﹣[（a2+b2）﹣（a2﹣b2）]；（3）（3mn﹣5m2）﹣（3m2﹣5mn）；（4）2a+2（a+1）﹣3（a﹣1）．4．化简（1）2（2a2+9b）+3（﹣5a2﹣4b）（2）3（x3+2x2﹣1）﹣（3x3+4x2﹣2）5．（2009•柳州）先化简，再求值：3（x﹣1）﹣（x﹣5），其中x=2．6．已知x=5，y=3，求代数式3（x+y）+4（x+y）﹣6（x+y）的值．7．已知A=x2﹣3y2，B=x2﹣y2，求解2A﹣B．8．若已知M=x2+3x﹣5，N=3x2+5，并且6M=2N﹣4，求x．9．已知A=5a2﹣2ab，B=﹣4a2+4ab，求：（1）A+B；（2）2A﹣B；（3）先化简，再求值：3（A+B）﹣2（2A﹣B），其中A=﹣2，B=1．10．设a=14x﹣6，b=﹣7x+3，c=21x﹣1．（1）求a﹣（b﹣c）的值；（2）当x=时，求a﹣（b﹣c）的值．11．化简求值：已知a、b满足：|a﹣2|+（b+1）2=0，求代数式2（2a﹣3b）﹣（a﹣4b）+2（﹣3a+2b）的值．12．已知（x+1）2+|y﹣1|=0，求2（xy﹣5xy2）﹣（3xy2﹣xy）的值．北师大七年级数学上册《整式及其加减》计算题专项练习一参考答案与试题解析一．解答题（共12小题）1．计算题①12﹣（﹣8）+（﹣7）﹣15；②﹣12+2×（﹣5）﹣（﹣3）3÷；③（2x﹣3y）+（5x+4y）；④（5a2+2a﹣1）﹣4（3﹣8a+2a2）．考点：整式的加减；有理数的混合运算．专题：计算题．分析：（1）直接进行有理数的加减即可得出答案．（2）先进行幂的运算，然后根据先乘除后加减的法则进行计算．（3）先去括号，然后合并同类项即可得出结果．（4）先去括号，然后合并同类项即可得出结果．解答：解：①原式=12+8﹣7﹣15=﹣2；②原式=﹣1﹣10+27÷=﹣11+81=70；③原式=2x﹣3y+5x+4y=7x+y；④原式=5a2+2a﹣1﹣12+32a﹣8a2=﹣3a2+34a﹣13．点评：本题考查了整式的加减及有理数的混合运算，属于基础题，解答本题的关键熟记去括号法则，熟练运用合并同类项的法则，这是各地中考的常考点．2．（1）计算：4+（﹣2）2×2﹣（﹣36）÷4；（2）化简：3（3a﹣2b）﹣2（a﹣3b）．考点：整式的加减；有理数的混合运算．分析：（1）按照有理数混合运算的顺序，先乘方后乘除最后算加减；（2）运用整式的加减运算顺序计算：先去括号，再合并同类项．解答：解：（1）原式=4+4×2﹣（﹣9）=4+8+9=17；（2）原式=9a﹣6b﹣2a+6b=（9﹣2）a+（﹣6+6）b=7a．点评：在混合运算中要特别注意运算顺序：先三级，后二级，再一级；熟记去括号法则：﹣﹣得+，﹣+得﹣，++得+，+﹣得﹣；及熟练运用合并同类项的法则：字母和字母的指数不变，只把系数相加减．3．计算：（1）7x+4（x2﹣2）﹣2（2x2﹣x+3）；（2）4ab﹣3b2﹣[（a2+b2）﹣（a2﹣b2）]；（3）（3mn﹣5m2）﹣（3m2﹣5mn）；（4）2a+2（a+1）﹣3（a﹣1）．考点：整式的加减．分析：（1）先去括号，再合并同类项即可；（2）先去括号，再合并同类项即可；（3）先去括号，再合并同类项即可；（4）先去括号，再合并同类项即可．解答：解：（1）7x+4（x2﹣2）﹣2（2x2﹣x+3）=7x+4x2﹣8﹣4x2+2x﹣6=9x﹣14；（2）4ab﹣3b2﹣[（a2+b2）﹣（a2﹣b2）]=4ab﹣3b2﹣[a2+b2﹣a2+b2]=4ab﹣3b2﹣2b2=4ab﹣5b2；（3）（3mn﹣5m2）﹣（3m2﹣5mn）=3mn﹣5m2﹣3m2+5mn=8mn﹣8m2；（4）2a+2（a+1）﹣3（a﹣1）=2a+2a+2﹣3a+3=a+5．点评：本题考查了整式的加减，解决此类题目的关键是熟记去括号法则，熟练运用合并同类项的法则，这是各地中考的常考点．4．化简（1）2（2a2+9b）+3（﹣5a2﹣4b）（2）3（x3+2x2﹣1）﹣（3x3+4x2﹣2）考点：整式的加减．专题：计算题．分析：（1）原式利用去括号法则去括号后，合并同类项即可得到结果；（2）原式利用去括号法则去括号后，合并同类项即可得到结果．解答：解：（1）原式=4a2+18b﹣15a2﹣12b=﹣11a2+6b；（2）原式=3x3+6x2﹣3﹣3x3﹣4x2+2=2x2﹣1．点评：此题考查了整式的加减，涉及的知识有：去括号法则，以及合并同类项法则，熟练掌握法则是解本题的关键．5．（2009•柳州）先化简，再求值：3（x﹣1）﹣（x﹣5），其中x=2．考点：整式的加减—化简求值．分析：本题应对方程去括号，合并同类项，将整式化为最简式，然后把x的值代入即可．解答：解：原式=3x﹣3﹣x+5=2x+2，当x=2时，原式=2×2+2=6．点评：本题考查了整式的化简．整式的加减运算实际上就是去括号、合并同类项，这是各地中考的常考点．6．已知x=5，y=3，求代数式3（x+y）+4（x+y）﹣6（x+y）的值．考点：整式的加减—化简求值．分析：先把x+y当作一个整体来合并同类项，再代入求出即可．解答：解：∵x=5，y=3，∴3（x+y）+4（x+y）﹣6（x+y）=x+y=5+3=8．点评：本题考查了整式的加减的应用，主要考查学生的计算能力，用了整体思想．7．已知A=x2﹣3y2，B=x2﹣y2，求解2A﹣B．考点：整式的加减．分析：直接把A、B代入式子，进一步去括号，合并得出答案即可．解答：解：2A﹣B=2（x2﹣3y2）﹣（x2﹣y2）=2x2﹣6y2﹣x2+y2=x2﹣5y2．点评：此题考查整式的加减混合运算，掌握去括号法则和运算的方法是解决问题的关键．8．若已知M=x2+3x﹣5，N=3x2+5，并且6M=2N﹣4，求x．考点：整式的加减；解一元一次方程．专题：计算题．分析：把M与N代入计算即可求出x的值．解答：解：∵M=x2+3x﹣5，N=3x2+5，∴代入得：6x2+18x﹣30=6x2+10﹣4，解得：x=2．点评：此题考查了整式的加减，熟练掌握运算法则是解本题的关键．9．已知A=5a2﹣2ab，B=﹣4a2+4ab，求：（1）A+B；（2）2A﹣B；（3）先化简，再求值：3（A+B）﹣2（2A﹣B），其中A=﹣2，B=1．考点：整式的加减；整式的加减—化简求值．专题：计算题．分析：（1）把A与B代入A+B中计算即可得到结果；（2）把A与B代入2A﹣B中计算即可得到结果；（3）原式去括号合并得到最简结果，把A与B的值代入计算即可求出值．解答：解：（1）∵A=5a2﹣2ab，B=﹣4a2+4ab，∴A+B=5a2﹣2ab﹣4a2+4ab=a2+2ab；（2）∵A=5a2﹣2ab，B=﹣4a2+4ab，∴2A﹣B=10a2﹣4ab+4a2﹣4ab=14a2﹣8ab；（3）原式=3A+3B﹣4A+2B=﹣A+5B，把A=﹣2，B=1代入得：原式=2+5=7．点评：此题考查了整式的加减，熟练掌握运算法则是解本题的关键．10．设a=14x﹣6，b=﹣7x+3，c=21x﹣1．（1）求a﹣（b﹣c）的值；（2）当x=时，求a﹣（b﹣c）的值．考点：整式的加减；代数式求值．专题：计算题．分析：（1）把a，b，c代入a﹣（b﹣c）中计算即可得到结果；（2）把x的值代入（1）的结果计算即可得到结果．解答：解：（1）把a=14x﹣6，b=﹣7x+3，c=21x﹣1代入得：a﹣（b﹣c）=a﹣b+c=14x﹣6+7x﹣3+21x﹣1=42x ﹣10；（2）把x=代入得：原式=42×﹣10=10.5﹣10=0.5．点评：此题考查了整式的加减，以及代数式求值，熟练掌握运算法则是解本题的关键．11．化简求值：已知a、b满足：|a﹣2|+（b+1）2=0，求代数式2（2a﹣3b）﹣（a﹣4b）+2（﹣3a+2b）的值．考点：整式的加减—化简求值；非负数的性质：绝对值；非负数的性质：偶次方．专题：计算题．分析：原式去括号合并得到最简结果，利用非负数的性质求出a与b的值，代入计算即可求出值．解答：解：原式=4a﹣6b﹣a+4b﹣6a+4b=﹣3a+2b，∵|a﹣2|+（b+1）2=0，∴a=2，b=﹣1，则原式=﹣6﹣2=﹣8．点评：此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．12．已知（x+1）2+|y﹣1|=0，求2（xy﹣5xy2）﹣（3xy2﹣xy）的值．考点：整式的加减—化简求值；非负数的性质：绝对值；非负数的性质：偶次方．分析：因为平方与绝对值都是非负数，且（x+1）2+|y﹣1|=0，所以x+1=0，y﹣1=0，解得x，y的值．再运用整式的加减运算，去括号、合并同类项，然后代入求值即可．解答：解：2（xy﹣5xy2）﹣（3xy2﹣xy）=（2xy﹣10xy2）﹣（3xy2﹣xy）=2xy﹣10xy2﹣3xy2+xy=（2xy+xy）+（﹣3xy2﹣10xy2）=3xy﹣13xy2，∵（x+1）2+|y﹣1|=0∴（x+1）=0，y﹣1=0∴x=﹣1，y=1．∴当x=﹣1，y=1时，3xy﹣13xy2=3×（﹣1）×1﹣13×（﹣1）×12=﹣3+13=10．答：2（xy﹣5xy2）﹣（3xy2﹣xy）的值为10．点评：整式的加减运算实际上就是去括号、合并同类项，这是各地中考的常考点．代入求值时要化简．。