实验三控制系统的稳定性分析
计算机控制系统性能分析

南京邮电大学自动化学院实验报告课程名称:计算机控制系统实验名称:计算机控制系统性能分析所在专业:自动化学生姓名:**班级学号:B************: ***2013 /2014 学年第二学期实验一:计算机控制系统性能分析一、 实验目的:1.建立计算机控制系统的数学模型;2.掌握判别计算机控制系统稳定性的一般方法3.观察控制系统的时域响应,记录其时域性能指标;4.掌握计算机控制系统时间响应分析的一般方法;5.掌握计算机控制系统频率响应曲线的一般绘制方法。
二、 实验内容:考虑如图1所示的计算机控制系统图1 计算机控制系统1. 系统稳定性分析(1) 首先分析该计算机控制系统的稳定性,讨论令系统稳定的K 的取值范围; 解:G1=tf([1],[1 1 0]);G=c2d(G1,0.01,'zoh');//求系统脉冲传递函数 rlocus(G);//绘制系统根轨迹Root LocusReal AxisI m a g i n a r y A x i s-7-6-5-4-3-2-1012-2.5-2-1.5-1-0.500.511.522.5将图片放大得到0.750.80.850.90.9511.051.11.151.21.25-0.15-0.1-0.050.050.10.15Root LocusReal AxisI m a g i n a r y A x i sZ 平面的临界放大系数由根轨迹与单位圆的交点求得。
放大图片分析: [k,poles]=rlocfind(G)Select a point in the graphics window selected_point = 0.9905 + 0.1385i k =193.6417 poles =0.9902 + 0.1385i 0.9902 - 0.1385i 得到0<K<193(2) 假设不考虑采样开关和零阶保持器的影响,即看作一连续系统,讨论令系统稳定的K 的取值范围; 解:G1=tf([1],[1 1 0]); rlocus(G1);-1.2-1-0.8-0.6-0.4-0.200.2-0.8-0.6-0.4-0.20.20.40.60.8Root LocusReal AxisI m a g i n a r y A x i s由图片分析可得,根轨迹在S 平面左半面,系统是恒稳定的,所以: 0<K<∞(3) 分析导致上述两种情况下K 取值范围差异的原因。
机械工程控制基础实验指导书

《机械工程控制基础》实验指导书青岛科技大学前言机械工程控制基础是针对过程装备与控制工程专业而开设的一门专业基础课,主要讲解自动控制原理的主要内容,是一门理论性较强的课程,为了帮助学生学好这门课,能够更好的理解理论知识,在课堂教学的基础上增加了该实验环节。
《机械工程控制基础》实验指导书共编写了4个实验,有实验一、典型环节模拟研究实验二、典型系统动态性能和稳定性分析实验三、控制系统的频率特性分析实验四、调节器参数对系统调节质量的影响《机械工程控制基础》实验指导书的编写主要依据“控制工程基础”教材的内容,结合本课程教学大纲的要求进行编写。
利用计算机和MATLAB程序完成实验。
注:1)每个实验的实验报告均由5部分组成,最后一部分“实验数据分析”或“思考题”必须写。
2)每个实验所记录的图形均需标出横轴和纵轴上的关键坐标点。
目录实验一典型环节模拟研究 (4)一、实验目的二、实验要求三、实验原理四、实验内容及步骤五、实验报告要求实验二典型系统动态性能和稳定性分析 (7)一、实验目的二、实验要求三、实验原理四、实验内容及步骤五、实验报告要求实验三控制系统的频率特性分析 (9)一、实验目的二、实验要求三、实验原理四、实验内容及步骤五、实验报告要求实验四调节器参数对系统调节质量的影响 (11)一、实验目的二、实验要求三、实验原理四、实验内容及步骤五、实验报告要求附录一:MATLAB6.5的使用 (13)实验一典型环节模拟研究一、实验目的1.熟悉各种典型环节的阶跃响应曲线2.了解参数变化对典型环节动态特性的影响。
二、实验要求1.观测并记录各种典型环节的阶跃响应曲线2.观测参数变化对典型环节阶跃响应的影响,测试并记录相应的曲线三、实验原理1.惯性环节(一阶环节),如图1-1所示。
(a) 只观测输出曲线(b) 可观测输入、输出两条曲线图1-1 惯性环节原理图2.二阶环节,如图1-2所示。
或图1-2 二阶环节原理图3.积分环节,如图1-3所示。
自动控制原理实验实验指导书

自动控制原理实验目录实验一二阶系统阶跃响应(验证性实验) (1)实验三控制系统的稳定性分析(验证性实验) (9)实验三系统稳态误差分析(综合性实验) (15)预备实验典型环节及其阶跃响应一、实验目的1.学习构成典型环节的模拟电路,了解电路参数对环节特性的影响。
2.学习典型环节阶跃响应测量方法,并学会由阶跃响应曲线计算典型环节传递函数。
二、实验内容搭建下述典型环节的模拟电路,并测量其阶跃响应。
1.比例(P)环节的模拟电路及其传递函数示于图1-1。
2.惯性(T)环节的模拟电路及其传递函数示于图1-2。
3.积分(I)环节的模拟电路及其传递函数示于图1-3。
4. 比例积分(PI)环节的模拟电路及其传递函数示于图1-4。
5.比例微分(PD)环节的模拟电路及其传递函数示于图1-5。
6.比例积分微分(PID)环节的模拟电路及其传递函数示于图1-6。
三、实验报告1.画出惯性环节、积分环节、比例积分环节、比例微分环节、比例积分微分环节的模拟电路图,用坐标纸画出所记录的各环节的阶跃响应曲线。
2.由阶跃响应曲线计算出惯性环节、积分环节的传递函数,并与由模拟电路计算的结果相比较。
附1:预备实验典型环节及其阶跃响应效果参考图比例环节阶跃响应惯性环节阶跃响应积分环节阶跃响应比例积分环节阶跃响应比例微分环节阶跃响应比例积分微分环节阶跃响应附2:由模拟电路推导传递函数的参考方法1. 惯性环节令输入信号为U 1(s) 输出信号为U 2(s) 根据模电中虚短和虚断的概念列出公式:整理得进一步简化可以得到如果令R 2/R 1=K ,R 2C=T ,则系统的传递函数可写成下面的形式:()1KG s TS =-+当输入r(t)为单位脉冲函数时 则有输入U 1(s)=1输出U 2(s)=G(s)U 1(s)= 1KTS-+由拉氏反变换可得到单位脉冲响应如下:/(),0t TK k t e t T-=-≥ 当输入r(t)为单位阶跃函数时 则有输入U 1(s)=1/s输出U 2(s)=G(s)U 1(s)= 11K TS s-+由拉氏反变换可得到单位阶跃响应如下:/()(1),0t T h t K e t -=--≥当输入r(t)为单位斜坡函数时 则有输入U 1(s)=21s输出U 2(s)=G(s)U 1(s)=2323R R C T R R =+2Cs12Cs-(s)U R10-(s)U 21R R +-=12212)Cs (Cs 1(s)U (s)U )(G R R R s +-==12212)Cs 1((s)U (s)U )(G R R R s +-==由拉氏反变换可得到单位斜坡响应如下:/()(1),0t T c t Kt KT e t -=--≥2. 比例微分环节令输入信号为U 1(s) 输出信号为U 2(s) 根据模电中虚短和虚断的概念列出公式:(s)(s)(s)(s)(s)U100-U U 0U 2=1R1R23(4)CSU R R '''---=++由前一个等式得到 ()1()2/1U s U s R R '=- 带入方程组中消去()U s '可得1()1()2/11()2/12()1134U s U s R R U s R R U s R R R CS+=--+由于14R C〈〈,则可将R4忽略,则可将两边化简得到传递函数如下: 2()23232323()(1)1()11123U s R R R R R R R R G s CS CS U s R R R R R ++==--=-++如果令K=231R R R +, T=2323R R C R R +,则系统的传递函数可写成下面的形式:()(1)G s K TS =-+当输入r(t)为单位脉冲函数时,单位脉冲响应不稳定,讨论起来无意义 当输入r(t)为单位阶跃函数时 则有输入U 1(s)=1/s输出U 2(s)=G(s)U 1(s)=(1)K TS S-+由拉氏反变换可得到单位阶跃响应如下:()(),0h t KT t K t δ=+≥当输入r(t)为单位斜坡函数时 则有输入U 1(s)=21s输出U 2(s)=G(s)U 1(s)=2(1)K TS S -+由拉氏反变换可得到单位斜坡响应如下:(),0c t Kt KT t =+≥实验一 二阶系统阶跃响应(验证性实验)一、实验目的研究二阶系统的两个重要参数阻尼比ξ和无阻尼自然频率n ω对系统动态性能的影响。
控制系统CAD实验报告
控制系统CAD实验报告一、实验目的1. 掌握如何使用Matlab进行系统的根轨迹分析。
2. 掌握如何使用Matlab进行系统的稳定性分析。
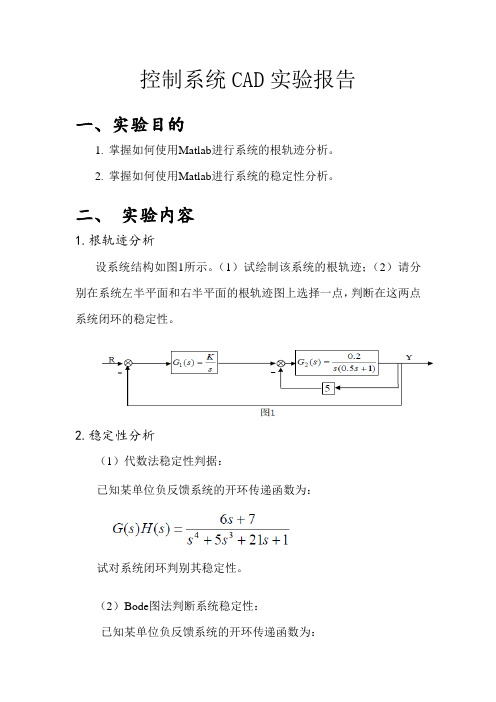
二、实验内容1.根轨迹分析设系统结构如图1所示。
(1)试绘制该系统的根轨迹;(2)请分别在系统左半平面和右半平面的根轨迹图上选择一点,判断在这两点系统闭环的稳定性。
2.稳定性分析(1)代数法稳定性判据:已知某单位负反馈系统的开环传递函数为:试对系统闭环判别其稳定性。
(2)Bode图法判断系统稳定性:已知某单位负反馈系统的开环传递函数为:试绘制系统的Bode图和Nyquist曲线,分别用两种方法判断闭环系统的稳定性,并求出系统的频域性能指标w,γ与时域性能指标σ%、s t。
c三、预习报告1.根轨迹分析g1=tf(1,[1 0])g2=tf(0.2,[0.5 1 0])sys=g1*g2+5*g2rlocus(sys)Gridnyquist(G)2.稳定性分析(1)G=tf([6 7],[1 5 0 27 8]) %闭环环传递函数den=[1 5 0 27 8]p=roots(den)i=find(real(p)>=0)n=length(i)if(n>0) disp('系统不稳定,不稳定根个数为:')nelse disp('系统稳定')end四、上机实验结果1.根轨迹分析2.稳定性分析(1)代数法稳定性判据:Transfer function:6 s + 7----------------------s^4 + 5 s^3 + 27 s + 8den =1 5 0 27 8p =-5.76950.5307 + 2.1137i0.5307 - 2.1137i-0.2920i =23n = 2系统不稳定,不稳定根个数为:n =2(2)Transfer function:0.3 s + 1------------------s^3 + 12 s^2 + 5 s Gm = Inf Pm = 69.1650 Wcg =InfWcp =0.1842五、实验总结对知识的掌握不足,对知识点理解错误。
第五章 控制系统的稳定性分析

arctan
b a
2
arctan
j
b a
jw
1
s1 tan1 b
b
a
a Re
22
若上式b为负值,则角增量为
2
2
arctan
b a
如图:
j
jw
a
2
Re
tan1 b
s2
a b
23
若根在右半平面,其角增量如图所示,
j jw
tan1 b
3
b
a
a
Re
为
2
2
arctan
b a
24
现考虑n次多项式 Ds,且在原点有q个零点,可表示为
代入D(s)并命w从0增大到 时,复数D(s)的角连续增
大 ng
2
二 乃奎斯特稳定判据
1 反馈系统开环和闭环的特征方程式
Xi s
X0 s
27
该单位反馈系统的开环传递函数为
G
s
MK s DK S
闭环传递函数为
s
Gs 1Gs
DK
MK s s Mk
s
MK s Db s
令:F
s
1
G
s
1
MK DK
s s
arg1 G( j。w) 90o
列 系统的开环传递函数为
Go
(s)
(T1s
K 1)(T2s 1)(T3s
1)
讨论开环增益K的大小对系 统稳定性的影响
解:这是一个三阶系统,没有开环零点,且开环极点全部 位于左半s平面,因此是最小相位系统。 作极坐标草图,先计算极限值:
32
=0时,有
A(0) K
实验一_系统响应及系统稳定性实验报告

实验一_系统响应及系统稳定性实验报告一、实验目的本实验旨在通过研究系统响应及系统稳定性的实验,掌握系统的动态特性及如何评价系统的稳定性。
二、实验仪器和器材1.计算机2.MATLAB软件3.稳态平台三、实验原理系统的响应是指系统对输入信号的反应。
在控制系统中,动态性能是系统的重要指标之一,它描述了系统响应的速度和稳定性。
首先通过给定的输入信号,将其输入到待测系统中,并记录系统的输出信号。
然后,通过分析输入信号和输出信号的关系,得到系统的动态性能参数,如过渡过程的时间、超调量等。
系统的稳定性是指系统在受到外界扰动时,能够保持稳定状态、不产生过大的波动。
一般通过稳定度来衡量系统的稳定性,而稳定度又可分为绝对稳定和相对稳定两种情况。
在稳定度分析中,通常使用稳定图的方式进行。
四、实验步骤1.运行MATLAB软件,打开控制系统实验模块。
2.设计一个给定的输入信号。
3.将输入信号输入待测系统中,记录系统的输出信号。
4.分析输入信号和输出信号的关系,得到系统的动态性能参数,如过渡过程的时间、超调量等。
5.通过稳态平台绘制系统的稳定图,评价系统的稳定性。
五、实验结果与分析通过实验我们得到了系统的动态性能参数,并绘制了系统的稳定图。
根据动态性能参数和稳定图来评价系统的动态特性和稳定性。
六、实验总结通过本次实验,我们学习了如何评价系统的动态性能和稳定性。
同时,我们也发现系统的动态特性和稳定性对于控制系统的性能起到了重要的影响。
在实际的控制系统设计中,需要充分考虑系统的动态特性和稳定性,以保证系统的性能和可靠性。
通过本次实验,我们进一步加深了对系统的理解,为日后的控制系统设计与优化提供了参考。
自动控制系统的稳定性和稳态误差分析

实验三 自动控制系统的稳定性和稳态误差分析一、实验目的1、研究高阶系统的稳定性,验证稳定判据的正确性;2、了解系统增益变化对系统稳定性的影响;3、观察系统结构和稳态误差之间的关系。
二、实验任务1、稳定性分析欲判断系统的稳定性,只要求出系统的闭环极点即可,而系统的闭环极点就是闭环传递函数的分母多项式的根,可以利用MATLAB 中的tf2zp 函数求出系统的零极点,或者利用root 函数求分母多项式的根来确定系统的闭环极点,从而判断系统的稳定性。
(1)已知单位负反馈控制系统的开环传递函数为0.2( 2.5)()(0.5)(0.7)(3)s G s s s s s +=+++,用MATLAB 编写程序来判断闭环系统的稳定性,并绘制闭环系统的零极点图。
在MATLAB 命令窗口写入程序代码如下: z=-2.5p=[0,-0.5,-0.7,-3] k=0.2 Go=zpk(z,p,k) Gc=feedback(Go,1) Gctf=tf(Gc) 运行结果如下: Transfer function: 0.2 s + 0.5 --------------------------------------- s^4 + 4.2 s^3 + 3.95 s^2 + 1.25 s + 0.5s^4 + 4.2 s^3 + 3.95 s^2 + 1.25 s + 0.5是系统的特征多项式,接着输入如下MATLAB程序代码:den=[1,4.2,3.95,1.25,0.5]p=roots(den)运行结果如下:p =-3.0058-1.0000-0.0971 + 0.3961i-0.0971 - 0.3961ip为特征多项式dens的根,即为系统的闭环极点,所有闭环极点都是负的实部,因此闭环系统是稳定的。
下面绘制系统的零极点图,MATLAB程序代码如下:z=-2.5p=[0,-0.5,-0.7,-3]k=0.2Go=zpk(z,p,k)Gc=feedback(Go,1)Gctf=tf(Gc)[z,p,k]=zpkdata(Gctf,'v')pzmap(Gctf)grid运行结果如下:z =-2.5000p =-3.0058-1.0000-0.0971 + 0.3961i-0.0971 - 0.3961ik =0.2000输出零极点分布图如图3-1所示。
自动机实验报告(3篇)

第1篇一、实验目的1. 理解自动机的概念和分类。
2. 掌握有限自动机(FA)和正规文法(CFG)的基本原理。
3. 学习自动机的应用,如词法分析、语法分析等。
4. 通过实验加深对自动机理论的理解。
二、实验内容1. 有限自动机(FA)- 实验一:设计并实现一个识别特定字符串的有限自动机实验步骤:(1)根据题目要求,确定输入字母表和输出字母表。
(2)设计有限自动机的状态转移图。
(3)编写代码实现有限自动机的状态转移功能。
(4)测试有限自动机对特定字符串的识别能力。
- 实验二:分析并验证有限自动机的正确性实验步骤:(1)根据实验一的结果,分析有限自动机的状态转移图。
(2)验证有限自动机是否满足题目要求。
(3)如果有限自动机不满足要求,修改状态转移图,重新进行实验。
2. 正规文法(CFG)- 实验一:设计并实现一个正规文法实验步骤:(1)根据题目要求,确定正规文法中的非终结符、终结符和产生式。
(2)编写代码实现正规文法的生成功能。
(3)测试正规文法生成的句子是否满足题目要求。
- 实验二:将正规文法转换为有限自动机实验步骤:(1)根据实验一的结果,分析正规文法。
(2)将正规文法转换为有限自动机。
(3)测试有限自动机对句子进行词法分析的能力。
三、实验结果与分析1. 实验一:有限自动机- 在实验一中,我们成功设计并实现了识别特定字符串的有限自动机。
通过测试,我们发现有限自动机能够正确识别给定的字符串。
- 在实验二中,我们分析了有限自动机的状态转移图,并验证了其正确性。
我们发现有限自动机满足题目要求,能够正确识别给定的字符串。
2. 实验二:正规文法- 在实验一中,我们成功设计并实现了正规文法。
通过测试,我们发现正规文法能够生成满足题目要求的句子。
- 在实验二中,我们将正规文法转换为有限自动机,并测试了其对句子进行词法分析的能力。
我们发现有限自动机能够正确对句子进行词法分析。
四、实验总结通过本次实验,我们掌握了有限自动机和正规文法的基本原理,并学会了如何将它们应用于实际问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三控制系统的稳定性分析
实验报告
1画出步骤5的模拟电路图。
2 •画出系统增幅或减幅振荡的波形图。
C=1uf 时:
R3=50K K=5:
段弋三«LSn:rKim^- VunV rlRr^lK :IQ口口
关粹:远口口f IQ tn;
R3=100KK=10
ltirn SODO '6 ODO[□MJ gciao lc aod
-1DC0
-2DC0
-3DC0
Xl ¥l a xa
5»g Yz
eg
■5QW
looaa
D lU'.O ZDOC JOO0 驷 口。
5OD0
6OOD [C ™ 6DQO
gciao lc aod
R3=200K K=20:
D
10QO tDdC
E0C0
瓦鲨三 HIMPZ : K IM - * UhV 目佗证■ iooa mV 灵禅:HCICICI 十 io tn ;
■QW
3 oco
-2-QC€
>3000
■叫 DC 口
TWM
Xi
a xa mg
locaa
¥1
5oca TE 卫oc
IrIXlOO
®;0M
4 口
Cd
30M
1DCC
a
-1DC0
-2DCO
•3DCC
■叫口 t 口
Xl Y1 a Xi 50da Tg
gg
-■5QW
looaa
jrIXIg
6OCD R CPO B DQ 4
»oao
■Z
DbDCll - T ;CKJC&- S£DOOS TA
DO&OT »scr EX D TX
0 口口CH ODQkd wag 00091 口口QE OQQE ODQa OCDT a
:>izis=ed :鑒缈劇蓊
C=0.1uf 时:
R3=50k:
ltirn 1OO J SODO '6
ODO
[□MJ gciao lc aod sow段弋三«LSn:rKim^- VunV 同:1 ana
mV 共.桿;H£I口口f ia tn;
35M
-1DCO
-2DCQ
-SDC-Cl
■^.OCQ
Xl
Y1
口Xl
5DC0 TS■5Q0C
iooaa
JrIXIg
R3=100K:
a iaao EDQO
WP 4£三和t(E; »C K TK-V Ltn# 冃用宅
压:IMQ inv 石祥:IOQO ia tXl£
Hl DOO
^□OD5OO
口
6OOD ?ooe B DOO lc^io
-
■Da
e
2DCO
long
-3 口爾
■■二•
口口Cl
■300
c
MD00
-«.DCO
Xl
Y1
1'KOC
50dQ T2
locao
i-
ooaa
R3U200K
f
l a n s t
s Q G lal c
l o o hl n n n
• ■a n n
Luu
•
|.||4:|口
<
■
sct
K r r
e
F.
u c r H Gr ll
庐■詩「x l r
w M
m < mrK
申 Ado
■口
E
潘
#
* 日
<3\ 戸口
015
u r £
□£
L
P O
D D C I h-
Q 口门
D
F-H S
D
迤昴箫餾-R3U400K
B 1M& 35»
3 •计算系统的临界放大系数,并与步骤 5中测得的临界放大系数相比较。
实际测了得,临界放大系数是 2.17,计算得系统的放大系数是
2,相差不大,在可允许
的误差范围内。
Z.
PE
屮口口匚
gaoo
•咖O
-莎
DO
•』口 □匚
T m r T
1
Xs=
欝
li»5? T? IDcg。
