实验三 基于Matlab的控制系统实验研究综合 北工大
北京理工大学信号与系统实验报告

实验1 信号的时域描述与运算一、实验目的1、掌握信号的MATLAB表示及其可视化方法。
2、掌握信号基本时域运算的MATLAB实现方法。
3、利用MATLAB分析常用信号,加深对信号时域的理解。
二、实验原理1、连续时间的MATLAB表示连续时间信号指的是在连续时间范围内有定义的信号,即除若干个不连续点外,在任何信号都有意义。
在MATLAB中,连续时间信号可以用两种方法来表示,即向量表示法和符号对象表示法。
向量表示法:严格意义上来说,MATLAB并不能处理连续时间信号,都必须是用信号等时间间隔采样后的采样值来近似表示的,采样时间间隔足够小的时候,这些采样值就可以近似地表示出连续时间信号。
例如:>>t=0:0.01:10;>>x=sin(t);此时利用plot(t,x)命令即可绘制上述信号的时域波形。
符号对象表示法:连续时间信号先用表达式表示出来,然后采用符号表达式来表示信号。
例如:>>sym t;>>x=xin(t);此时利用ezplot(x)命令即可绘制上述信号的时域波形。
常用的信号产生函数:2、连续时间信号的时域运算对连续时间信号的运算包括量信号想家、相乘、微分、积分以及位移反转、尺度变换(尺度伸缩)等1)相加和相乘信号的相加和相乘指两个信号对应时刻的值相加和相乘,对于两个采用向量表示的可以直接使用算术运算的运算符“+”和“•”来计算,此时要求表示两信号的向量时间范围和采样间隔相同,采用符号对象表示的两个信号,可以直接根据符号对象的运算规则运算。
2)微分和积分对于向量表示发表示的连续时间信号,可以用过数值计算的方法计算信号的微分和积分。
这里由时间向量[t1,t2,…,t N]和采样值向量[x1,x2,…,x N]表示的连续信号的微分是利用差分来近似求取的。
MATLAB里用diff来计算差分x(k+1)-x(k)。
连续信号的定积分可以由MATLAB的quad函数实现,调用格式为quad(‘functions_name’,a,b)其中,functions_name为被积函数名,a、b为积分区间。
北工大自控matlab实验报告

自动控制原理实验报告一、试验设计构造一个二阶闭环系统,使得该系统的%30≥p M对于任意二阶系统,其闭环传递函数为2222)(G nn nc s s s ωξωω++=,其中ξ为二阶系统的阻尼比,n ω为二阶系统的无阻尼振荡频率,该系统的超调量为πξξ21--=e M p 。
若要%30≥p M ,则0.36≤ξ。
取0.3=ξ,又n ω任意,所以取20=n ω,则要求设计的闭环传递函数为40012400)(2++=s s s G c 。
二、实验内容及步骤1.以MATLAB 命令行的方式,进行系统仿真,确定系统时域性能指标 num=[400]; den=[1 12 400]; step(num,den)由图可知,该系统的超调量为%30%37>=p M ,满足要求,上升时间为0985.0=r t ,峰值时间为164.0=p t ,调节时间为0.472=s t 。
2.通过改变系统的开环放大倍数K (分增大和减小两种情况)和系统的阻尼比系数(分增大和减小两种情况),进行系统仿真分析,确定新的性能指标,并与原构造系统的进行比较,根据响应曲线分析并说明出现的现象 (1)增大开环放大倍数num=[500]; den=[1 12 500]; step(num,den)由图可知,该系统的超调量为%30%42>=p M ,上升时间为0858.0=r t ,峰值时间146.0=p t ,调节时间0.48=s t 。
(2)减小开环放大倍数 num=[300]; den=[1 12 300]; step(num,den)由图可知,该系统的超调量为%30%31>=p M ,上升时间为119.0=r t ,峰值时间为0.1921=p t ,调节时间为0.455=s t 。
(3)增大阻尼比 num=[400];den=[1 12.4 400]; step(num,den)由图可知,该系统的超调量为%30%36>=p M ,上升时间为0995.0=r t ,峰值时间为0.163=p t ,调节时间为0.486=s t 。
MATLAB实验报告3-控制系统仿真
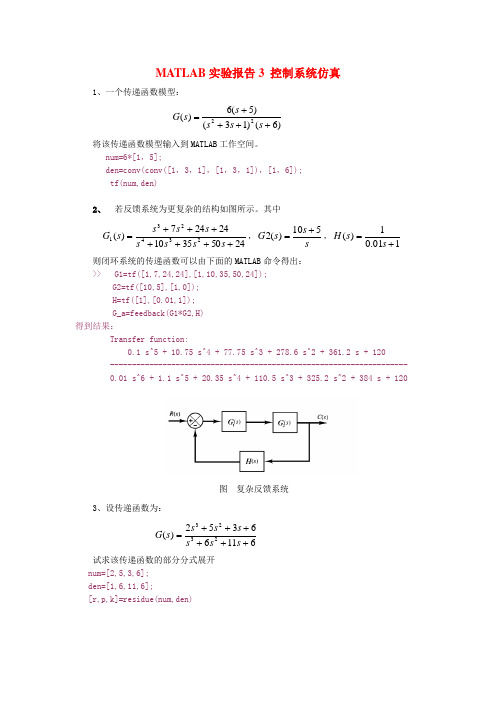
MATLAB 实验报告3 控制系统仿真1、一个传递函数模型: )6()13()5(6)(22++++=s s s s s G 将该传递函数模型输入到MATLAB 工作空间。
num=6*[1,5];den=conv(conv([1,3,1],[1,3,1]),[1,6]);tf(num,den)2、 若反馈系统为更复杂的结构如图所示。
其中2450351024247)(234231+++++++=s s s s s s s s G ,s s s G 510)(2+=,101.01)(+=s s H 则闭环系统的传递函数可以由下面的MATLAB 命令得出:>> G1=tf([1,7,24,24],[1,10,35,50,24]);G2=tf([10,5],[1,0]);H=tf([1],[0.01,1]);G_a=feedback(G1*G2,H)得到结果:Transfer function:0.1 s^5 + 10.75 s^4 + 77.75 s^3 + 278.6 s^2 + 361.2 s + 120 -------------------------------------------------------------------- 0.01 s^6 + 1.1 s^5 + 20.35 s^4 + 110.5 s^3 + 325.2 s^2 + 384 s + 1203、设传递函数为:61166352)(2323++++++=s s s s s s s G 试求该传递函数的部分分式展开num=[2,5,3,6];den=[1,6,11,6];[r,p,k]=residue(num,den)图 复杂反馈系统4、给定单位负反馈系统的开环传递函数为:)7()1(10)(++=s s s s G 试画出伯德图。
利用以下MATLAB 程序,可以直接在屏幕上绘出伯德图如图20。
>> num=10*[1,1];den=[1,7,0];bode(num,den)5、已知三阶系统开环传递函数为:)232(27)(23+++=s s s s G画出系统的奈氏图,求出相应的幅值裕量和相位裕量,并求出闭环单位阶跃响应曲线。
北京理工大学自动控制原理实验报告
本科实验报告实验名称:控制理论基础实验实验时间:课程名称:控制理论基础任课教师:实验地点:实验教师:实验类型:□原理验证□综合设计学生姓名:□自主创新组号:学号/班级:学院:同组搭档:专业:成绩:实验1控制系统的模型建立一、实验目的1、掌握利用MATLAB建立控制系统模型的方法。
2、掌握系统的各种模型表述及相互之间的转换关系。
3、学习和掌握系统模型连接的等效变换。
二、实验原理1、系统模型的MATLAB描述系统的模型描述了系统的输入、输出变量以及内部各变量之间的关系,表征一个系统的模型有很多种,如微分方程、传递函数模型、状态空间模型等。
这里主要介绍系统传递函数(TF)模型、零极点增益(ZPK)模型和状态空间(SS)模型的MATLAB描述方法。
1)传递函数(TF)模型传递函数是描述线性定常系统输入-输出关系的一种最常用的数学模型,其表达式一般为在MATLAB中,直接使用分子分母多项式的行向量表示系统,即num=[bm,bm-1,…b1,b0]den=[an,an-1,…a1,a0]调用tf函数可以建立传递函数TF对象模型,调用格式如下:Gtf=tf(num,den)Tfdata函数可以从TF对象模型中提取分子分母多项式,调用格式如下:[num,den]=tfdata(Gtf)返回cell类型的分子分母多项式系数[num,den]=tfdata(Gtf,'v')返回向量形式的分子分母多项式系数2)零极点增益(ZPK)模型传递函数因式分解后可以写成式中,z1,z2,…,z m称为传递函数的零点,p1,p2,…,p n称为传递函数的极点,k为传递系数(系统增益)。
在MATLAB中,直接用[z,p,k]矢量组表示系统,其中z,p,k分别表示系统的零极点及其增益,即:z=[z1,z2,…,zm];p=[p1,p2,…,pn];k=[k];调用zpk函数可以创建ZPK对象模型,调用格式如下:Gzpk=zpk(z,p,k)同样,MATLAB提供了zpkdata命令用来提取系统的零极点及其增益,调用格式如下:[z,p,k]=zpkdata(Gzpk)返回cell类型的零极点及增益[z,p,k]=zpkdata(Gzpk,’v’)返回向量形式的零极点及增益函数pzmap可用于求取系统的零极点或绘制系统得零极点图,调用格式如下:pzmap(G)在复平面内绘出系统模型的零极点图。
基于MATLAB控制系统仿真实验报告

中南大学计算机控制系统仿真实验报告信息科学与工程学院自动化0903班实验一 MATLAB 语言编程一、 实验目的1、熟悉Matlab 语言及其环境,掌握编程方法。
2、要求认真听取实验指导老师讲解与演示。
二、具体实验内容、步骤、要求1、运行交互式学习软件,学习MATLAB 语言;2、在MATLAB 的命令窗口下键入如下命令:INTRO (注意:intro 为一个用MATLAB 语言编写的幻灯片程序,主要演示常用的MATLAB 语句运行结果。
)然后,根据现实出来的幻灯片右面按钮进行操作,可按START ——NEXT ——NEXT 按钮一步步运行,观察。
3、自编程序并完成上机编辑,调试,运行,存盘: (1)用MATLAB 命令完成矩阵的各种运算,例如:⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎪⎪⎬⎫=44434241343332312423222114131211A求出下列运算结果,并上机验证。
解:实验程序如下:function chengxu1A=[11 12 13 14;21 22 23 24;31 32 33 34;41 42 43 44]; a1=A(:,1) a2=A(2,:)a3=A(1:2,2:3) a4=A(2:3,2:3) a5=A(:,1:2) a6=A(2:3) a7=A(:) a8=A(:,:) a9=ones(2,2) a10=eye(2)实验结果如下:(1) A(:,1)=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡41312111 (2) A(2,:)= []24232221(3) A(1:2,2:3)= ⎥⎦⎤⎢⎣⎡23221312 (4) A(2:3,2:3)= ⎥⎦⎤⎢⎣⎡33322322 (5) A(:,1:2)= ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡4241323122211211(6) A(2:3)= []3121 (7) A(:)=⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎫44342414433323134232221241312111 (8) A(:,:)=⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎪⎪⎬⎫44434241343332312423222114131211(9) ones(2,2)=⎥⎦⎤⎢⎣⎡1111 (10) eye(2)=⎥⎦⎤⎢⎣⎡1001 (2)、绘制数学函数的图形,例如:y(t)=1-2e-tsin(t) (0<=t<=8) 理解数组运算与矩阵运算功能。
《MATLAB与控制系统仿真》实验报告

《MATLAB与控制系统仿真》实验报告一、实验目的本实验旨在通过MATLAB软件进行控制系统的仿真,并通过仿真结果分析控制系统的性能。
二、实验器材1.计算机2.MATLAB软件三、实验内容1.搭建控制系统模型在MATLAB软件中,通过使用控制系统工具箱,我们可以搭建不同类型的控制系统模型。
本实验中我们选择了一个简单的比例控制系统模型。
2.设定输入信号我们需要为控制系统提供输入信号进行仿真。
在MATLAB中,我们可以使用信号工具箱来产生不同类型的信号。
本实验中,我们选择了一个阶跃信号作为输入信号。
3.运行仿真通过设置模型参数、输入信号以及仿真时间等相关参数后,我们可以运行仿真。
MATLAB会根据系统模型和输入信号产生输出信号,并显示在仿真界面上。
4.分析控制系统性能根据仿真结果,我们可以对控制系统的性能进行分析。
常见的性能指标包括系统的稳态误差、超调量、响应时间等。
四、实验步骤1. 打开MATLAB软件,并在命令窗口中输入“controlSystemDesigner”命令,打开控制系统工具箱。
2.在控制系统工具箱中选择比例控制器模型,并设置相应的增益参数。
3.在信号工具箱中选择阶跃信号,并设置相应的幅值和起始时间。
4.在仿真界面中设置仿真时间,并点击运行按钮,开始仿真。
5.根据仿真结果,分析控制系统的性能指标,并记录下相应的数值,并根据数值进行分析和讨论。
五、实验结果与分析根据运行仿真获得的结果,我们可以得到控制系统的输出信号曲线。
通过观察输出信号的稳态值、超调量、响应时间等性能指标,我们可以对控制系统的性能进行分析和评价。
六、实验总结通过本次实验,我们学习了如何使用MATLAB软件进行控制系统仿真,并提取控制系统的性能指标。
通过实验,我们可以更加直观地理解控制系统的工作原理,为控制系统设计和分析提供了重要的工具和思路。
七、实验心得通过本次实验,我深刻理解了控制系统仿真的重要性和必要性。
MATLAB软件提供了强大的仿真工具和功能,能够帮助我们更好地理解和分析控制系统的性能。
MATLAB控制系统仿真实验报告

练习 A:
(1) help rand,然后随机生成一个 2×6 的数组,观察 command window、command history 和 workspace 等窗口的变化结果 (2) 学习使用 clc、clear,了解其功能和作用 (3) 输入一个 2 维数值数组,体会标点符号的作用(空格和逗号的作用)。 (4) 一维数组的创建和寻访,创建一个一维数组(1×8)X,查询 X 数组的第 2 个 元素,查询 X 数组的第 3 个元素到第 6 个元素,查询 X 数组的第 5 个元素到最 后一个元素,查询 X 数组的第 3、2、1 个元素,查询 X 数组中≤5 元素,将 X 数组的第 2 个元素重新赋值为 111,实例 expm1。 (5) 二维数组的创建和寻访,创建一个二维数组(4×8)A,查询数组 A 第 2 行、 第 3 列的元素, 查询数组 A 第 2 行的所有元素, 查询数组 A 第 6 列的所有元素, 查询数组 A 按列拉长形成新的数组 B(1×8),查询数组 A 按行拉长形成新的数 组 C(1×8),以全元素赋值的方式对数组 A 赋值。 (6) 两种运算指令形式和实质内涵的比较。设有 3 个二维数组 A2×4,B2×4,C2×2, 写出所有由 2 个数组参与的合法的数组运算和矩阵指令 (7) 学习使用表 8 列的常用函数(通过 help 方法) (8) 学习使用表 9 数组操作函数 (9) 学习字符串的创建,a='This is an example.'
实验时间:2015.10.19 上午 8:30—9:30 实验地点:黄岛老校区计算中心
二、实验目的:
1、 熟悉 MATLAB 程序编辑与设计环境 2、 掌握各种编程语句语法规则及程序设计方法 3、 函数文件的编写和设计 4、 了解和熟悉跨空间变量传递和赋值
北京工业大学自动控制原理实验八--基于MATLAB的PID控制研究

实验八 基于MATLAB 的PID 控制研究一、 实验目的:1 理解PID 的基本原理2 研究PID 控制器的参数对于系统性能的影响二、 实验设备1 pc 机一台(含有软件“matlab ”) 三、 实验内容1 利用matlab 软件,针对控制对象设计单闭环PID 控制系统2 通过调节PID 控制器的参数,研究PID 控制参数对系统性能的影响四、 实验原理 1 PID 的原理单闭环PID 的控制系统的作用框图如下:比例(P)控制比例控制是一种最简单的控制方式,其控制器的输出与输入误差信号成比例关系。
当仅有比例控制时系统输出存在稳态误差(Steady-state error)。
比例控制作用及时,能迅速反应误差,从而减小稳态误差。
但是,比例控制不能消除稳态误差。
其调节器用在控制系统中,会使系统出现余差。
为了减少余差,可适当增大P K ,P K 愈大,余差就愈小;但P K 增大会引起系统的不稳定,使系统的稳定性变差,容易产生振荡。
积分(I)控制在积分控制中,控制器的输出与输入误差信号的积分成正比关系。
输入—积分控制的作用是消除稳态误差。
只要系统有误差存在,积分控制器就不断地积累,输出控制量,以消除误差。
积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。
这样,即便误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减小,直到等于零。
因而,只要有足够的时间,积分控制将能完全消除误差,使系统误差为零,从而消除稳态误差。
积分作用太强会使系统超调加大,甚至使系统出现振荡。
微分(D)控制在微分控制中,控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系。
自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳。
其原因是由于存在有较大惯性组件(环节)或有滞后(delay)组件,具有抑制误差的作用,其变化总是落后于误差的变化。
解决的办法是使抑制误差的作用的变化“超前”,即在误差接近零时,抑制误差的作用就应该是零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.实验内容
Ⅰ阶跃响应
01
1.二阶系统的闭环传递函数为:G(s)=
1).系统闭环根s=-1±3i阻尼比ζ=
无阻尼振荡频率ωn=
阶跃响应曲线如下:
Δ=±5%
Δ=±2%
实际值
理论值峰值Cmax
1.35 1.35峰值时间t p
1.06 1.04过渡时间t s Δ=±2%
3.544Δ=±5% 2.523
2修改参数,分别实现ζ=1、ζ=2的响应曲线,并与原有系统响应曲线记录在同一幅图中
修改参数,分别实现ωn1=12
ωn.ωn1=2ωn 的响应曲线,并于原系统记录在同一幅图中
3试做出系统的脉冲响应曲线和斜坡响应曲线.
1)脉冲响应
2)斜坡响应
4在SIMULINK环境下(如下图),构造系统的结构图,作时域仿真并与命令行方式取得的响应曲线进行对比
Ⅱ根轨迹
1.系统开环传递函数为G(s)=
(s 1)(s 2)
k s ++1)绘制系统的根轨迹
2)根据根轨迹图可知:分离点坐标为s =-0.423对应的增益为0.385
3)确定临界稳定时的根轨迹增益:由图可得临界根轨迹增益K gL =6.07
2.系统开环传函为G 02(s)=
(s 1)(s 1)²)
46(1s k s s +++-系统根轨迹:
系统稳定的根轨迹增益范围由根轨迹图可得为23<k <35.6
Ⅲ博德图
1.开环传递函数为:G(s)=²²211T s Ts ζ++,T =0.1ζ=2,1,0.5,0.1,0.01
2.开环传递函数为:G(s)=
31.6 (0.011)(0.11) s s s
++
作博德图:
由图中坐标可得:
1)初始段斜率为:-20.03高频段斜率为:-60.01开环截止频率ωc=16.2rad/s
中频段穿越斜率:-40.05
低频段渐进相位角:-900;高频段渐进相位角:-2700;-1800线的穿越频率:319.rad/s
2)由稳定裕度命令计算系统的稳定裕度Lg=10.9dBγc=22.30系统稳定
3)在图上作近似折现特性相比较
在博德图分段添加斜率-20-40-60的直线,比较发现直线和命令行模拟线基本吻合,存在一定误差。
