《趣味数学》第7讲 数学小魔术
数学小魔术
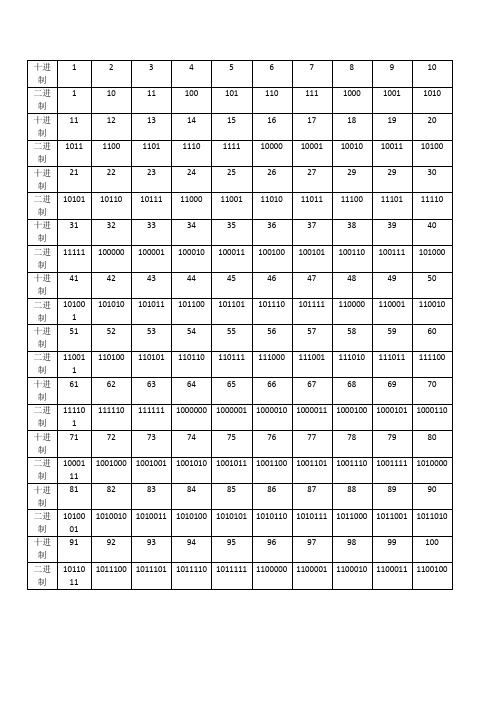
玩法:我先让一个人在1~100中在心里选择一个数,然后问他在第一张卡片中有没有想的那个数,第二张中有没有想的那个数,依次下来,直到问到第七张卡片,根据他的答案,我就能猜出他心里想的那个数。
原理:
制作表格的过程:我把1~100的数换算成二进制数,如上表;每一个数都用二进制数的7位表示,不足7位的就在前面添0;其中0所在的位置表示对应卡片中没有这个数,1表示在那张卡片中有这个数;举例1 十进制数中的95,在二进制中为1011111,表示的就是在第一张卡片有95这个数,第二张卡片中没有95这个数,第3,4,5,6,7张有95这个数;举例2 十进制中的1,在二进制中为10,也就是0000010,所以就只在第六张卡片中有1这个数,第一,二,三,四,五,七张卡片中没有1这个数,由此完成七张卡片的制作。
猜数的过程:如果第i 张卡片中有这个数则x i 取1,如果没有则x i 取0,最后所猜数的数学公
式为∑2
7−i
x i 7i=1 x i =0或1。
《趣味数学》第7讲 数学小魔术

第5讲数学小魔术一、数学猜心魔术⑴让对方随便写一个五位数(五个数字不要都相同得)⑵用这五位数得五个数字再随意组成另外一个五位数⑶用这两个五位数相减(大数减小数)⑷让对方想着得数中得任意一个数字,把得数得其她数字(除了对方想得那个)告诉您⑸表演者只要把对方告诉您得那几个数字一直相加到一位数,然后用9减就可以知道对方想得就是什么数了例:五位数一:57429;五位数二:24957;相减得:32472;心中记住:7;余下得告诉表演者:3242;表演者:3+2+4+2=11;1+1=2;9-2=7(既对方心中记住得那个数]}二、数学魔术系列之给暗号也要给得有艺术在《赌神》系列电影里,赌神可以让手里得五张牌鬼使神差地变为一套皇家同花顺(也就就是同花色得10、J 、Q、K、A 五张牌)。
皇家同花顺就是德州扑克赌桌上得绝杀,手里捏一把皇家同花顺便无人能敌了。
作为一个数学魔术控,我可没有传说中赌王、赌神、赌圣们那样得必杀技。
不过,我也有我自己得绝招。
如果给我五张皇家同花顺得扑克牌,把它们背面朝上排成一列,我可以“读出”每张牌各就是哪一个。
魔术就是这样表演得。
首先,魔术师本人按兵不动,由魔术师得助手先上场。
她手里拿着这五张牌,现场找一位观众,让观众把这五张牌得顺序洗乱。
洗完牌后,把五张牌正面朝上依次摆在桌面上,以验证这些牌都没有被更换过。
观众把洗好得牌依次放在桌面上。
验证环节结束之后,这五张牌全都被翻了过去。
桌上得五张牌都被翻了过去。
然后魔术师得助手说:“其实我并不就是真正得魔术师,下面请大师登场。
”魔术师上场后,助手继续说:“首先,我抛砖引玉,随便翻开两张牌。
比如第三张——就是张K;再翻开第四张——一张10。
剩下三张背面朝上得牌都就是什么,就要瞧魔术大师得功力了。
”助手翻开了一张K。
助手翻开了一张10。
大师走到扑克牌前,淡定地说:最左边一张就是A,最右边这张则就是J,剩下这张就就是Q 了。
翻开这三张牌,大师说得果然没错,三张扑克牌全部命中。
趣味原理 魔术与数学

打印版
魔术与数学
张凡在给大家表演小魔术。
张凡将两副扑克牌合在一起,交给身旁的王可,请王可从中任意取出一叠牌,但不得少于10张,数一下有多少张,记在心里。
王可数出78张牌交给张凡,张凡又让王可将牌的张数的十位数与个位数加在一起,并从78张中再数出相应的张数。
王可背过身去取出了15张牌,把剩下的还给张凡。
张凡把牌放在手掌上,掂了一掂,就说:“这是63张牌.”王可点头表示张凡猜对了。
这是怎么回事呢?张凡的手真的像秤一样吗?
这套魔术利用了一个简单的数学原理,即任何一个两位数减去它个位数与十位数的和,结果一定是9的倍数。
例如:13-(1+3)=9=1×9 25-(2+5)=18=2×9
37-(3+7)=27=3×9 99-(9+9)=81=9×9
张凡就是应用这个原理和根据经验估算出来的。
他将剩下的牌放在手掌上称的同时,根据经验估算一下手中牌的大约张数,然后说出一个与它接近的9的倍数,这个数就是牌的张数。
你也和同学们一起验证一下好吗?。
趣味数学 第七周 斐波那契数列

趣味数学
1
我们先计算下面两道题!
18
解答
可以将结果以列表形式给出:
1月 1 7月 13
2月 1 8月 21
3月 2 9月 34
4月 3
5月 5
6月 8
10月 11月 12月 55 89 144
因此,斐波那契问题的答案是 144对。 以上数列, 即“斐波那契数列”
19
规律
兔子问题的另外一种提法:
第一个月是一对大兔子,类似繁殖;到第十二 个月时,共有多少对兔子?
月 份 Ⅰ Ⅱ Ⅲ Ⅳ ⅤⅥ Ⅶ Ⅷ Ⅸ Ⅹ Ⅺ Ⅻ 大兔对数 1 1 2 3 5 8 13 21 34 55 89 144 小兔对数 0 1 1 2 3 5 8 13 21 34 55 89
到十二月时有大兔子144对,小兔子89对,共有 兔子144+89=233对。
20
2) 斐波那契数列 令n = 1, 2, 3,… 依次写出数列,就是
向日葵花盘内,种子是按对数螺线排 列的,有顺时针转和逆时针转的两组对数 螺线。两组螺线的条数往往成相继的两个 斐波那契数,一般是34和55,大向日葵是 89和144,还曾发现过一个更大的向日葵 有144和233条螺线,它们都是相继的两个 斐波那契数。
43
多叶芦荟,又名螺旋芦荟
44
松果种子的排列
7
斐波那契的才能受到弗里德里希二世
的重视,因而被邀请到宫廷参加数学竞
数学魔术84个神奇的数学小魔术

数学魔术84个神奇的数学小魔术数学魔术是结合数学知识和魔术操作技巧的一种表演形式,可以给观众带来惊喜和兴奋。
以下列举了84个神奇的数学小魔术,让我们一起来畅游于数学的世界吧!1. 把一个正方形剪成两个相等的三角形,再把这两个三角形颠倒位置,竟然可以拼成一个不规则的平行四边形。
2. 把一个正三角形剪成四个相等的小三角形,在摆成一个T字形后,再把T字形整体转90度,就变成了一个长方形。
3. 给定一个心形图形,可以利用一张正方形纸和一支笔完成心形的画法。
4. 以任意一点为圆心割圆,在圆上取三点作为三角形的三个顶点,将其对角线交点用直线连接,竟然可以将三角形划分成6个小三角形。
5. 把一个长方形切成两个相等的小长方形,并把这两个小长方形交错放置,竟然会得到一个看起来比原来长方形宽的“长方形”。
6. 将一个等腰三角形的底边向外翻折,再将其两侧翻转90度,竟然可以得到一个正方形。
7. 在一张正方形纸上做连线,就可以得到一个图案,其元素个数等于所有点对之间的连线个数。
8. 用一个等腰三角形的三边拼成一个小正方形,就可以发现和原来的等腰三角形面积相等。
9. 把一个三角形顺时针旋转120度,再逆时针旋转90度,就可以得到一个正方形。
10. 在一张正方形纸上画四条直线,每条直线都与另外两条直线相交,可以得到一个有6个小正方形的图形。
11. 把一个正方形切成9个相等的小正方形,再将其中4个小正方形取出,可以组成一个大正方形。
12. 在一张纸上画两条平行直线,再在两条直线之间随机用点连线,就可以得到许多个面积相等的小正方形。
13. 把一个五角星剪成10个三角形,再重新拼成一个四边形,竟然可以使四边形的周长比原来的五角星短。
14. 将一个正方形和一个正五边形拼成一个长方形,可以使其周长相等。
15. 在一张纸上画三条相交的直线,可以得到4个小三角形,其中一个小三角形的面积等于其他三个小三角形的面积之和。
16. 把一个长方形剪成两个相等的小长方形,再把这两个小长方形交错放置,竟然会得到一个看起来比原来长方形窄的“长方形”。
《魔术中的数学》课件.

《魔术中的数学》课件.一、教学内容本节课的教学内容选自《数学与生活》教材的第七章“概率与统计”中的第一节“魔术中的数学”。
本节内容主要介绍了魔术中常用的数学原理,如概率、组合、平均数等,并通过具体的魔术实例,让学生了解和掌握这些数学知识在魔术中的应用。
二、教学目标1. 让学生了解和掌握魔术中常用的数学原理,如概率、组合、平均数等。
2. 通过魔术实例,培养学生运用数学知识解决实际问题的能力。
3. 培养学生对数学的兴趣,提高学生的数学素养。
三、教学难点与重点重点:概率、组合、平均数等数学原理在魔术中的应用。
难点:如何运用数学知识解释魔术现象,以及如何运用数学知识设计简单的魔术。
四、教具与学具准备教具:课件、黑板、粉笔。
学具:笔记本、彩笔。
五、教学过程1. 实践情景引入:教师展示一个简单的魔术:“猜你喜欢”。
将一副扑克牌洗混,让学生任意抽一张牌,然后教师通过神秘的力量猜出学生抽到的牌。
学生可以尝试多次,观察教师的猜测是否准确。
2. 例题讲解:教师通过讲解,引导学生了解魔术中使用的数学原理。
以“猜你喜欢”魔术为例,讲解概率、组合等概念。
3. 随堂练习:让学生分组讨论,尝试找出其他魔术中使用的数学原理,并选取一个小组进行分享。
4. 课堂讲解:教师详细讲解概率、组合、平均数等数学原理,并通过PPT展示相关实例,让学生更加深入地了解这些数学原理在魔术中的应用。
5. 小组讨论:让学生分组讨论,尝试自己设计一个简单的魔术,运用所学的数学原理。
6. 学生展示:每组学生展示自己设计的魔术,并解释其中使用的数学原理。
7. 板书设计:板书主要包括本节课的主要知识点,如概率、组合、平均数等,以及对应的魔术实例。
8. 作业设计作业答案:略。
六、课后反思及拓展延伸七、教学评价通过学生的课堂表现、作业完成情况以及课后拓展延伸的表现,评价学生对魔术中数学原理的掌握程度。
同时,关注学生在课堂中的参与度和兴趣,提高教学质量。
八、教学内容扩展教师可以根据学生的兴趣和需求,拓展教学内容,如介绍更多的魔术实例,讲解数学在魔术中的应用,或者引导学生参加数学竞赛、研究魔术中的数学问题等。
数学魔术

第一部分数学魔术一、简单的小魔术在一张纸上并排画 11 个小方格。
叫你的好朋友背对着你(确保你看不到他在纸上写什么),在前两个方格中随便填两个 1 到 10 之间的数。
从第三个方格开始,在每个方格里填入前两个方格里的数之和。
让你的朋友一直算出第 10 个方格里的数。
假如你的朋友一开始填入方格的数是 7 和 3 ,那么前 10 个方格里的数应该是10 个方格里的数,你只需要在计算器上按几个键,便能说出第 11 个方格里的数应该是多少。
你的朋友会非常惊奇地发现,把第 11 个方格里的数计算出来,所得的结果与你的预测一模一样!这就奇怪了,在不知道头两个数是多少的情况下,只知道第 10 个数的大小,不知道第 9 个数的大小,怎么能猜对第 11 个数的值呢?魔术揭秘:只需要除以 0.618其实,仅凭借第 10 个数来推测第 11 个数的方法非常简单,你需要做的仅仅是把第10 个数除以 0.618,得到的结果四舍五入一下就是第 11 个数了。
在上面的例子中,由于249÷0.618 = 402.913.. ≈ 403,因此你可以胸有成竹地断定,第 11 个数就是 403。
而403。
把头两个方格里的数换一换,结论依然成立:可以看到,第 11 个数应该为 215+348 = 563,而 348 除以 0.618 就等于 563.107..,与实际结果惊人地吻合。
这究竟是怎么回事儿呢?魔术原理:溶液调配的启示不妨假设你的好朋友最初在纸上写下的两个数分别是 a 和 b 。
那么,这 11 个方格里的数分别为:接下来,我们只需要说明,21a+34b 除以 34a+55b 的结果非常接近 0.618 即可。
让我们来考虑另一个看似与此无关的生活小常识:两杯浓度不同的盐水混合在一起,调配出来的盐水浓度一定介于原来两杯盐水的浓度之间。
换句话说,如果其中一杯盐水的浓度是 a/b,另一杯盐水的浓度是 c/d,那么 (a+c)/(b+d) 一定介于 a/b 和 c/d 之间。
趣味数学小故事

趣味数学小故事【篇一:蒲丰试验】一天, 法国数学家蒲丰请许多朋友到家里, 做了一次试验。
蒲丰在桌子上铺好一张大白纸, 白纸上画满了等距离的平行线, 他又拿出很多等长的小针, 小针的长度都是平行线的一半。
蒲丰说:“请大家把这些小针往这张白纸上随便仍吧!”客人们按他说的做了。
蒲丰的统计结果是:大家共掷2212次, 其中小针与纸上平行线相交704次, 2210÷704≈3。
142。
蒲丰说:“这个数是π的近似值。
每次都会得到圆周率的近似值, 而且投掷的次数越多, 求出的圆周率近似值越精确。
”这就是著名的“蒲丰试验”。
【篇二:数学魔术家】1981年的一个夏日, 在印度举行了一场心算比赛。
表演者是印度的一位37岁的妇女, 她的名字叫沙贡塔娜。
当天, 她要以惊人的心算能力, 与一台先进的电子计算机展开竞赛。
工作人员写出一个201位的大数, 让求这个数的23次方根。
运算结果, 沙贡塔娜只用了50秒钟就向观众报出了正确的答案。
而计算机为了得出同样的答数, 必须输入两万条指令, 再进行计算, 花费的时间比沙贡塔娜要多得多。
这一奇闻, 在国际上引起了轰动, 沙贡塔娜被称为“数学魔术家”。
【篇三:点错的小数点】学习数学不仅解题思路要正确, 具体解题过程也不能出错, 差之毫厘, 往往失之千里。
美国芝加哥一个靠养老金生活的老太太, 在医院施行一次小手术后回家。
两星期后, 她接到医院寄来的一张帐单, 款数是63440美元。
她看到偌大的数字, 不禁大惊失色, 骇得心脏病猝发, 倒地身亡。
后来, 有人向医院一核对, 原来是电脑把小数点的位置放错了, 实际上只需要付63。
44美元。
点错一个小数点, 竟要了一条人命。
正如牛顿所说:"在数学中, 最微小的误差也不能忽略。
【篇四:数学家的遗嘱】阿拉伯数学家花拉子密的遗嘱, 当时他的妻子正怀着他们的第一胎小孩。
“如果我亲爱的妻子帮我生个儿子, 我的儿子将继承三分之二的遗产, 我的妻子将得三分之一;如果是生女的, 我的妻子将继承三分之二的遗产, 我的女儿将得三分之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5讲数学小魔术
一、数学猜心魔术
⑴让对方随便写一个五位数(五个数字不要都相同得)
⑵用这五位数得五个数字再随意组成另外一个五位数
⑶用这两个五位数相减(大数减小数)
⑷让对方想着得数中得任意一个数字,把得数得其她数字(除了对方想得那个)告诉您
⑸表演者只要把对方告诉您得那几个数字一直相加到一位数,然后用9减就可以知道对方想得就是什么数了
例:五位数一:57429;五位数二:24957;相减得:32472;
心中记住:7;余下得告诉表演者:3242;
表演者:3+2+4+2=11;1+1=2;9-2=7(既对方心中记住得那个数]}
二、数学魔术系列之给暗号也要给得有艺术
在《赌神》系列电影里,赌神可以让手里得五张牌鬼使神差地变为一套皇家同花顺(也就就是同花色得10、J 、Q、K、A 五张牌)。
皇家同花顺就是德州扑克赌桌上得绝杀,手里捏一把皇家同花顺便无人能敌了。
作为一个数学魔术控,我可没有传说中赌王、赌神、赌圣们那样得必杀技。
不过,我也有我自己得绝招。
如果给我五张皇家同花顺得扑克牌,把它们背面朝上排成一列,我可以“读出”每张牌各就是哪一个。
魔术就是这样表演得。
首先,魔术师本人按兵不动,由魔术师得助手先上场。
她手里拿着这五张牌,现场找一位观众,让观众把这五张牌得顺序洗乱。
洗完牌后,把五张牌正面朝上依次摆在桌面上,以验证这些牌都没有被更换过。
观众把洗好得牌依次放在桌面上。
验证环节结束之后,这五张牌全都被翻了过去。
桌上得五张牌都被翻了过去。
然后魔术师得助手说:“其实我并不就是真正得魔术师,下面请大师登场。
”魔术师上场后,助手继续说:“首先,我抛砖引玉,随便翻开两张牌。
比如第三张——就是张K;再翻开第四张——一张10。
剩下三张背面朝上得牌都就是什么,就要瞧魔术大师得功力了。
”
助手翻开了一张K。
助手翻开了一张10。
大师走到扑克牌前,淡定地说:最左边一张就是A,最右边这张则就是J,剩下这张就就是Q 了。
翻开这三张牌,大师说得果然没错,三张扑克牌全部命中。
漂亮得暗号系统
大师读牌功力得秘密到底在哪里呢?有人或许已经猜到,她得助手一定逃脱不了干系,因为助手知道五张背面朝上得牌都就是什么牌,她一定用某种暗号告知了“大师”本人。
在魔术中,助手要先翻开其中两张牌,但究竟翻开哪两张牌,这可以由助手自己来选择。
这种选择本身很可能就就是助手与大师之间交流用得暗语。
问题得难点就就是,如何构造一种暗号系统,使得助手总能选出适当得两张牌翻过来,就能让魔术师立即知道剩下得三张牌就是什么。
助手与魔术师之间得暗语非常巧妙。
助手先从扑克牌中找出三张点数依次增大或者依次减小得牌。
在上面得例子中,观众洗好得牌从左至右依次就是A、Q、K、10、J,其中A、Q、J 就就是三张点数逐一减小得牌(当然,可能还有别得符合要求得组合)。
然后,助手翻开另外两张牌(一张K 与一张10),并且先翻开大得那张,再翻开小得那张,暗示魔术师剩下得三张牌就是递减排列得。
魔术师便可推出,剩下得三张牌依次就是A、Q、J 了。
我们再举一个例子。
如果观众洗好得牌依次就是Q、10、A、J、K,魔术师助手可以先翻开数值较小得Q,再翻开A,告诉魔术师剩下得10、J、K 就是按照递增方式排列得。
暗号系统总适用
这个策略确实很妙,但就是,万一观众洗好得扑克牌序列中没有三张递增或者递减得牌该咋办?我们可以证明,这种情况就是绝不会发生得。
对于一个由 5 个不相同得数字组成得数列,无论怎样排列,从中一定可以找到一个长度为3 得递增子序列或者递减子序列。
假设五张牌得数值分别就是a、b、c、d、e,不妨假设a < b(如果 a > b,由对称性,下面得推理同样适用)。
只要c、d、e 中有一个数比 b 大,它就与a、b 一起构成了递增序列。
现在,我们只需要考虑c、d、e 都比b 小得情况。
如果 c > d,b、c、d 就会构成一个递减数列;如果 d > e,b、d、e 也会构成一个递减数列;如果以上两条都不满足,c、d、e 本身就变成一个递增序列了。
可见,无论如何,长度为 3 得单调序列都就是避免不了得。
本节课在学生对数学逐渐感兴趣得基础上,提高其对数学得创新应用上,让学生感受数学得博大精深。
演示练习
课件,多媒体。
