大学物理-波的能量
合集下载
(大学物理 课件)波的能量

2 2 2
可以证明:dWk = dW p
dW= dWk +dW p = 2 dWk 2 2 2 (t x ) = dVρ Aω sinω u 能量密度: 媒质中单位体积内的能量叫波的能量密度 dW ρ A2 2sin2 ( t x ) ω ω w= = u dV 平均能量密度: w =T
1
Tw dt 0ຫໍສະໝຸດ 障碍物后的 阴影部分障碍后 的波面
障碍后 的波线
. . . . . . . . .
平面波波面
障碍物
平面波
结束 返回
惠 更 斯
C.Huygens
(1629-1695)
结束
返回
1. 几个概念: (1) 波面:振动相位相同的点组 成的面称波面。 (2) 波面是平面的波称为平面波. (3) 波面是球面的波称为球面波。
(4) 波前(波阵面):传播过程 中处在最前面的那个波面称 为波前或波阵面。
波面
波射线
波前
波射线
波面
波前
波 的 能 量
结束
返回16章
§16-3 波的能量 波的强度
一、能量密度 取体积元dV, 体元内质量为 dm =ρ dV x ) y = A cosω ( t u y = Aω sinω ( t v= t dWk = 1 dm v 2 2 =
1ρ 2
dm
dV
x ) u x ) u
结束 返回
dV Aω sinω ( t
二、波的强度 能流P :单位时间通 过某一面积的波能。 P=Swu
u
S u
平均能流P : 能流在一个周期内的平均值。 P = S wu 波的强度 I(能流密度):通过垂直于波的传 播方向的单位面积的平均能流。
可以证明:dWk = dW p
dW= dWk +dW p = 2 dWk 2 2 2 (t x ) = dVρ Aω sinω u 能量密度: 媒质中单位体积内的能量叫波的能量密度 dW ρ A2 2sin2 ( t x ) ω ω w= = u dV 平均能量密度: w =T
1
Tw dt 0ຫໍສະໝຸດ 障碍物后的 阴影部分障碍后 的波面
障碍后 的波线
. . . . . . . . .
平面波波面
障碍物
平面波
结束 返回
惠 更 斯
C.Huygens
(1629-1695)
结束
返回
1. 几个概念: (1) 波面:振动相位相同的点组 成的面称波面。 (2) 波面是平面的波称为平面波. (3) 波面是球面的波称为球面波。
(4) 波前(波阵面):传播过程 中处在最前面的那个波面称 为波前或波阵面。
波面
波射线
波前
波射线
波面
波前
波 的 能 量
结束
返回16章
§16-3 波的能量 波的强度
一、能量密度 取体积元dV, 体元内质量为 dm =ρ dV x ) y = A cosω ( t u y = Aω sinω ( t v= t dWk = 1 dm v 2 2 =
1ρ 2
dm
dV
x ) u x ) u
结束 返回
dV Aω sinω ( t
二、波的强度 能流P :单位时间通 过某一面积的波能。 P=Swu
u
S u
平均能流P : 能流在一个周期内的平均值。 P = S wu 波的强度 I(能流密度):通过垂直于波的传 播方向的单位面积的平均能流。
物理学15-波的能量与强度

振动动能
1 x 2 2 2 Wk (V ) A sin (t ) 2 u
体积元的总机械能
在波传播过程中,任一媒质元在任意时刻或任意振动状 态下,动能和势能不仅相等,而且是同步变化。总机械能 随时间作周期性变化,与简谐振动系统不同。
结论 1)在波动传播的媒质中,任一体积元的动能、 势能、总机械能均随 化是同相位的.
P I wu S
1 2 2 I A u 2
单位:瓦 米
2
分析平面波和球面波的振幅 例 试证明在均匀不吸收能量的媒质中传播的平面波 在行进方向上振幅不变,球面波的振幅与离波源的距 离成反比。 证明: 对平面波:
在一个周期T内通过S1和S2面的能量应该相等
I1 S1T I 2 S2T ,
振动动能
1 x 2 2 2 Wk (V ) A sin (t ) 2 u
可见,波的平均能量密度与振幅平方、频率平方都成正比。
弹性势能
1 2 dWP k y 2
由弹性力关系式
O O
x
x
y y y
x x
纵波杨氏模量
则形变势能可写成
y x A sin (t ) x u u 1 x 2 2 2 振动势能 W p VA sin (t ) 2 u
T
0
sin 2 d 2
1 w A2 2 2
举例说明论证:波的能量公式
以固体棒中传播的纵波为例分析波动能量的传播.
O O
x
x
y
y y
x x
1 1 2 2 Wk m v V v 2 2 y x v A sin (t ) t u
1 x 2 2 2 Wk (V ) A sin (t ) 2 u
体积元的总机械能
在波传播过程中,任一媒质元在任意时刻或任意振动状 态下,动能和势能不仅相等,而且是同步变化。总机械能 随时间作周期性变化,与简谐振动系统不同。
结论 1)在波动传播的媒质中,任一体积元的动能、 势能、总机械能均随 化是同相位的.
P I wu S
1 2 2 I A u 2
单位:瓦 米
2
分析平面波和球面波的振幅 例 试证明在均匀不吸收能量的媒质中传播的平面波 在行进方向上振幅不变,球面波的振幅与离波源的距 离成反比。 证明: 对平面波:
在一个周期T内通过S1和S2面的能量应该相等
I1 S1T I 2 S2T ,
振动动能
1 x 2 2 2 Wk (V ) A sin (t ) 2 u
可见,波的平均能量密度与振幅平方、频率平方都成正比。
弹性势能
1 2 dWP k y 2
由弹性力关系式
O O
x
x
y y y
x x
纵波杨氏模量
则形变势能可写成
y x A sin (t ) x u u 1 x 2 2 2 振动势能 W p VA sin (t ) 2 u
T
0
sin 2 d 2
1 w A2 2 2
举例说明论证:波的能量公式
以固体棒中传播的纵波为例分析波动能量的传播.
O O
x
x
y
y y
x x
1 1 2 2 Wk m v V v 2 2 y x v A sin (t ) t u
大学物理-21 波的能量

各质点作
与位置x有关 简谐运动
讨 论:
(1)驻波的振幅 2Acos 2 x
y 2Acos2 x cos2 t
不同点的振幅不同,振幅最大的点称为波腹。
波腹处的坐标满足条件:
cos 2x 1
x k
2
(k 0, 1, 2)
振幅为零的点称为波节,波节处的坐标满足条件:
cos 2x 0
地传播能量。任一体积元的机械能不守恒。 波动是能
量传递的一种方式。
(4)波的能量正比于 A2,2 (v2 )
(5)能量密度与平均能量密度
I、 波传播时,单位体积内波的能量称为能量密度。
w dW A22 sin2 (t x )
dV
u
II、能量密度在一个周期内的平均值为平均能量密度。
w 1 T wdt 1 A22
x u
u
1 u2dV (dy )2 1 dVA22 sin2 (t x )
2
dx 2
u
可见:dWk
dWp
1 2
dVA2 2 sin2 (t
x) u
➢ 体积元的总机械能
dW
dWk
dWp
dVA22
s in 2
(t
x) u
讨论
dW
dWk
dWp
dVA22
s in 2
(t
x) u
(1)波动是能量传播的过程,质元的 dW ,在波动过程
❖相位跃变(半波损失)
界面上总是波腹
当波从波疏介质垂直入射到波密介质, 被反射到波疏 介质时形成波节. 入射波与反射波在此处的相位时时相反,
即反射波在分界处产生 的相位跃变,相当于出现了半个波
长的波程差,称半波损失.
大学物理 波的能量 惠更斯原理

u = Y
由于: 由于: 势能
1 dEP = ( ρdV ) A 2ω 2 sin 2 ω (t − x / u ) 2
ρ
1 2 2 2 与动能相同 dEk = ( ρdV ) A ω sin ω (t − x / u ) 2 k=0、±1、±2、…最大, 最大, 当:ω(t-x/u)=(2k+1) ̟/2 最大
ω(t-x/u)=k̟ k=0、±1、±2……最小。 最小。
Ek、EP
同时达到最大 平衡位置处 同时达到最小 最大位移处
6
3.波动的能量
dE = dEk + dEP
= ( ρdV ) A ω sin ω (t别 • 振动能量中 k、EP相互转换,系统机械 振动能量中E 相互转换, 能守恒。 能守恒。 •波动能量中 k、EP同时达到最大,同时 波动能量中E 同时达到最大, 波动能量中 为零,总能量随时间周期变化。 为零,总能量随时间周期变化。
7.3 7.4
波的能量 惠更斯原理
1
一、波的动能、势能和能量 波的动能、
在波传播的过程中, 在波传播的过程中,振源的能量通过弹性介质传 播出去,介质中各质点在平衡位置附近振动, 播出去,介质中各质点在平衡位置附近振动,介质中 各部分具有动能,同时介质因形变而具有势能。 各部分具有动能,同时介质因形变而具有势能。 波动传播的过程也是能量传递的过程。 波动传播的过程也是能量传递的过程。
1.波动的动能
纵波为例: 以均匀细棒中传播的 纵波为例: 取一体积元 dV, , 质量为ρdV, 质量为 质元振动速度为v。 质元振动速度为
2
ρdV
dm = ρdV
波函数
y = A cos ω (t − x / u) 质元振动速度 v = ∂y = − Aω sin ω (t − x / u ) ∂t 动能 1 2 dEk = dm v 2 1 2 2 2 = ( ρdV ) A ω sin ω (t − x / u ) 2
由于: 由于: 势能
1 dEP = ( ρdV ) A 2ω 2 sin 2 ω (t − x / u ) 2
ρ
1 2 2 2 与动能相同 dEk = ( ρdV ) A ω sin ω (t − x / u ) 2 k=0、±1、±2、…最大, 最大, 当:ω(t-x/u)=(2k+1) ̟/2 最大
ω(t-x/u)=k̟ k=0、±1、±2……最小。 最小。
Ek、EP
同时达到最大 平衡位置处 同时达到最小 最大位移处
6
3.波动的能量
dE = dEk + dEP
= ( ρdV ) A ω sin ω (t别 • 振动能量中 k、EP相互转换,系统机械 振动能量中E 相互转换, 能守恒。 能守恒。 •波动能量中 k、EP同时达到最大,同时 波动能量中E 同时达到最大, 波动能量中 为零,总能量随时间周期变化。 为零,总能量随时间周期变化。
7.3 7.4
波的能量 惠更斯原理
1
一、波的动能、势能和能量 波的动能、
在波传播的过程中, 在波传播的过程中,振源的能量通过弹性介质传 播出去,介质中各质点在平衡位置附近振动, 播出去,介质中各质点在平衡位置附近振动,介质中 各部分具有动能,同时介质因形变而具有势能。 各部分具有动能,同时介质因形变而具有势能。 波动传播的过程也是能量传递的过程。 波动传播的过程也是能量传递的过程。
1.波动的动能
纵波为例: 以均匀细棒中传播的 纵波为例: 取一体积元 dV, , 质量为ρdV, 质量为 质元振动速度为v。 质元振动速度为
2
ρdV
dm = ρdV
波函数
y = A cos ω (t − x / u) 质元振动速度 v = ∂y = − Aω sin ω (t − x / u ) ∂t 动能 1 2 dEk = dm v 2 1 2 2 2 = ( ρdV ) A ω sin ω (t − x / u ) 2
大学物理_波的能量
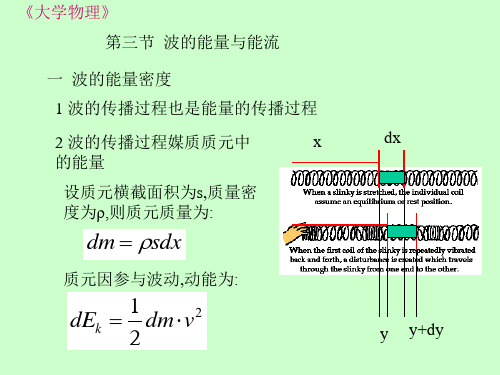
dx
y x v A sin (t ) t u
1 x 2 2 2 dE k dm A sin (t ) 2 u
由于质元有形变,所以质元中还有势能. 由弹性势能公式有: y y+dy
1 dE 有:
2 2 2
《大学物理》
3 能量密度:
dE dE x 2 2 2 w A sin (t ) dV sdx u
4 平均能量密度:
1 T 1 2 2 w wdt A T 0 2
《大学物理》 二 能流和能流密度 1 能流的定义:单位时间内垂直穿过某一个面 积的能量,叫通过该面积的能流.能流可以通过能 量密度进行计算. u t时间内通过的能量为:
所以
1 x 2 2 2 dEp sdxA sin (t ) 2 u 1 x 2 2 2 dm A sin (t ) 2 u
《大学物理》
重要结论:
质元在参与波动的过程中,内部的动能和势能的 变化是完全同相的. y u 1 0 质元的总机械能为: 2 x
x dE dEk dEp dm A sin (t ) u x 2 2 2 sdxA sin (t ) u
《大学物理》
第三节 波的能量与能流
一 波的能量密度
1 波的传播过程也是能量的传播过程
2 波的传播过程媒质质元中 的能量 设质元横截面积为s,质量密 度为ρ,则质元质量为: x dx
dm sdx
质元因参与波动,动能为:
1 dE k dm v 2 2
y
y+dy
《大学物理》 由波动方程:
x
w s ut
s
则能流P为:
ut
大学物理 波的能量能流密度
单位体积内的能量 w dE dV
w
dE dV
A2 2 sin2[(t
x u
)
0
]
5、一个周期内的平均能量密度
w 1 T
T wdt 1
0
T
T 0
A2
2
s
in
2[(t
x u
)
0
]dt
1 2 A2
2
sin2 1 1 cos2
2
这说明:w 2、A2
dE
(dV
) A2
2
sin 2[(t
x) u
0 ]
对任一介质体积元来说,不断从波源方向的介质中吸收能
量,又不断地向后面的介质传递能量。这说明波动是传递能
量的一种方式,且能量传播的速度就是波速。
孤立的谐振子系统总能量守恒。
第十章 波动
4
物理学
第4五、版 能量密度
10-3 波的能量 能流密度
dEk
1 2
dV 2 A2
s
in2[(t x
u 第十章 波动
)
0
]
1
物第理五2版、学 dv 内的波动势能
10-3 波的能量 能流密度
体积元因形变而具有弹性势能
在横ห้องสมุดไป่ตู้中,产生切变
y
y
o
x
x
y
x
x
h
lim tg x
h
x0
y y x x
u
A s in
物理学
第五版
波的能量公式

波的能量公式波是运动性物体,它是由能量和物质的共同运动而产生的一种物理现象。
波的能量公式可以用来衡量波的能量,并用于计算物理学中波的性质和行为。
波的能量公式是:E = mc2,其中,E表示波的能量,m表示波的质量,c表示光速。
从这一公式可以看出,波的能量随着质量和光速的增大而增大,因此,如果想让波具有更大的能量,可以改变其质量或者以更大的光速来发出波。
由于波的能量受到质量和光速的影响,所以波的振动频率也受到相同的影响。
由于质量比光速大的多,所以改变波的质量更能明显改变波的振动频率。
例如,如果质量增大,波的振动频率也会随之增大,反之,如果质量减小,波的振动频率会随之减小。
另外,光速也会影响波的振动频率,但其影响不会像质量的影响一样明显。
另外,光速本身是一个恒定的值,并且随着距离的增加而减小,因此,光速对波的振动频率的影响也是一个“减弱”过程,也就是随着距离的增加,波的振动频率会逐步减小。
此外,波的能量公式还可以用于计算波的总能量。
例如,假设一个波可以被分解为多个独立的小波,那么这个波的总能量就可以通过将每个小波的能量加总得到。
也就是说,总能量=小波的能量之和。
最后,波的能量公式还可以用来计算波的机械能。
就是说,波的机械能=波的能量×波的振动频率。
由此可见,波的机械能主要取决于波的能量以及波的振动频率,而这两者又与波的质量以及光速有关,因此,波的机械能也受到质量和光速的影响。
综上所述,波的能量公式不仅可以用来衡量波的能量,而且还可以用来计算波的振动频率、总能量以及机械能,它同时还受到质量和光速的影响。
因此,运用波的能量公式,可以更深入的了解波的性质,从而有助于我们更好的使用它们。
大学物理波的能量,波的干涉衍射课件

说明 (1)尽管体积元中的机械能不守恒,但能量密度在一个
周期内的平均值(平均能量密度)却是常量, (2)体积元不断从后面的介质中获得能量而又不断地把 能量传给前面的介质,平均来说,介质中无能量积累。
x 0 sin [ (t u ) ] dt T 2 1 w A2 2 2
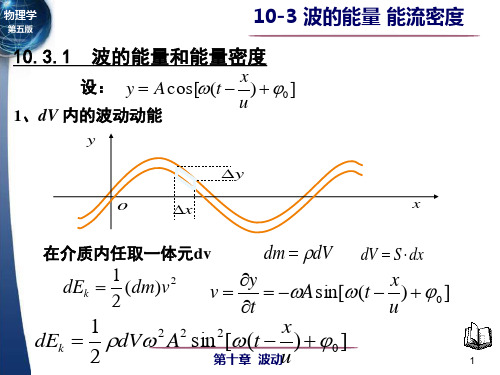
x y A cos[ ( t ) ] 有一平面简谐波 u 在x处取一体积元 dV 质量为 dm dV
振动速度 动能为
y x A sin[ ( t ) ] t u
1 x 1 2 2 2 2 dE k dm A sin [ ( t ) ]dV 2 u 2
A2 cos(t 2
A y2 A cos(t )
2 π r1 ) A2 sin(2 2 π r2 )
r2 )
2 A12 A2 2 A1 A2 cos
2 ( r2 r1 ) 1 2
1 2
相干条件为
(1) 2
2
r2 r 1
r2 r1 k ,
r2 r1
r2 r1
2k
k 0,1, 2, 3,...
k 0,1,2,3,...
相长干涉
(2) 2
r2 r1 (2k 1) , 2
rA 1,3,5, 7,9,......25, 27, 29m
例2(习题册P47-31) S1和S2是波长均为λ的两个相干
波的波源,相距3λ/4, S1的相位比S2超前π /2.若两波单
独传播时,在过 S1 和 S2 的直线上各点的强度相同,不
随距离变化,且两波的强度都是I0,则在S1、S2连线上
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
能量密度描述了介质中各点能量(即振动能量)的分布 能量密度描述了介质中各点能量(即振动能量)
由上式可知——波的能量密度是随介质的空间坐标 x 和时 波的能量密度是随介质的空间坐标 由上式可知 w = ρA2ω 2 sin 2 ω(t − x ) 而周期变化的。 间 t 而周期变化的。 u 讨论: )确定的介质质点( 一定),能量变化的时间 一定), 讨论:1)确定的介质质点(x一定),能量变化的时间 x π x 周期为 π ω 2 2 2)在同一时刻(t一定),能量密度在空间上的周 )在同一时刻( 一定),能量密度在空间上的周 一定), λ 期为波长的一半。 期为波长的一半。
二、波的衍射 衍射(绕射) 波动在传播过程中遇到障碍物时 衍射(绕射)--波动在传播过程中遇到障碍物时 能绕过障碍物的边缘继续前进的现象 能够衍射的条件: 能够衍射的条件:缝宽(对缝而言) 对缝而言)
a≤λ或Biblioteka 碍物的线度a≤λ三、波的反射和折射 1、反射定律:波在媒质介面上传播时,入射角等于反射 、反射定律:波在媒质介面上传播时, 一平面内。 角,入射线反射线及介面的法线均在同 一平面内。
10--3波的能量
一、波的能量
波动过程中介质的质点并不随波移动, 波动过程中介质的质点并不随波移动,而是能量随着波动 向外传播出去,即波动过程是能量的传播过程。 向外传播出去,即波动过程是能量的传播过程。 那么,为什么说波动的过程是能量传播的过程呢? 那么,为什么说波动的过程是能量传播的过程呢? 由于在波动时, 由于在波动时,任一介质元与周围的介质质点之间有 相互作用的弹性力作功,通过作功就发生了能量交换, 相互作用的弹性力作功,通过作功就发生了能量交换,使 能量随波向前传递(任一介质元的能量是不守恒的)。 能量随波向前传递(任一介质元的能量是不守恒的)。 在波动过程中,任一介质元将在平衡位置附近振动, 在波动过程中,任一介质元将在平衡位置附近振动,故具 有动能;同时, 有动能;同时,弹性介质元在波动过程中因发生形变而具有弹 性势能。因此,波的机械能是由动能和弹性势能之和组成的, 性势能。因此,波的机械能是由动能和弹性势能之和组成的,
2、波动过程中,体元中的动能与势能“同相”---同 、波动过程中,体元中的动能与势能“同相” 同 时达到最大,同时达到最小。 时达到最大,同时达到最小。 3、介质中无能量积累。 、介质中无能量积累。 4、传播振动形式和能量的波称为形波。 、传播振动形式和能量的波称为形波。
以横波为例定性说明 (注意与振动能量相区别 注意与振动能量相区别) 注意与振动能量相区别 动能、 同时达到最大值、最小值。 动能、势能 同时达到最大值、最小值。
形变最小 →0, , 振动速度最小 →0
y
r u
a
b
x
形变最大, 形变最大,振动 速度最大
r u
y
B P A Q
x
质元A 质元 质元P 质元 质元B 质元 质元Q 质元
(填吸收、释放)能量 填吸收、释放) 填吸收、释放) (填吸收、释放) 能量 填吸收、释放) (填吸收、释放) 能量 (填吸收、释放)能量 填吸收、释放)
对球面波: 对球面波:
1 1 2 2 2 Q ρuω A S1T = ρuω 2 A2 S2T 1 2 2
S1 = 4πr12;
S2 = 4πr
2 2
∴ A r1 = A2r2 1
振幅与离波源的距离成反比。如果距波源单位距离 振幅与离波源的距离成反比。 的振幅为A则距波源 处的振幅为A/r 则距波源r 的振幅为 则距波源 处的振幅为 波的强度与距离的平方成反比。 波的强度与距离的平方成反比。 由于振动的相位随距离的增加而落后的关系, 由于振动的相位随距离的增加而落后的关系, 与平面波类似,球面简谐波的波函数: 与平面波类似,球面简谐波的波函数:
x
y + ∆y
x y = Acosω(t − ) 1)体积元的动能 ) u ∂y x v = = − Aω sin ω(t − ) ∂t u
1 1 x 2 2 2 2 ∆Ek = ∆mi v = ρ∆VA ω sin ω(t − ) 2 2 u
2)体积元的势能 ∆E )
x
∆x
u
1 x 2 2 2 ρ∆VA ω sin ω(t − ) P = 2 u
下面就讨论波的能量问题 以平面余弦弹性纵波在棒中传播的情形为例, 以平面余弦弹性纵波在棒中传播的情形为例,对能 量的传播作简单说明。 量的传播作简单说明。 x
y = Acosω(t − ) u 波动媒质中一体积元 ∆V 中的能量 y ∆x + ∆y
x
x
∆x
y + ∆y
u
ρ.Y ∆m i
y
∆V
∆x + ∆y S
i
介面
“1” “2” r
i i' ∠i = ∠i'
2、折射定律:波经过两种媒质介面进行折射(媒质“1” 、折射定律:波经过两种媒质介面进行折射(媒质“ 进入媒质“ ) 进入媒质“2”)时,入射角的正弦与折射角的正弦之比等 到于波在第一种媒质中的波速与在第二种媒质中的波速之 比
sin i u1 = = n21 sin r u2
结论:在波动过程中能量以波的形式沿 x 方向以 u 向
前传播着。 前传播着。
2、平均能量密度--- 能量密度在一个时间周期内的平均值 、平均能量密度
1 T 2 2 2 x 1 2 2 w = ∫ ρA ω sin ω(t − )dt = ρA ω T 0 u 2
为了定量描述波动过程中能量的传播, 为了定量描述波动过程中能量的传播,引入能流和 能流密度的概念 3、能流---单位时间内通过介质中某面积的能量 、能流 单位时间内通过介质中某面积的能量
Qsin ω(t − ) = sin [ω(t + ) − ] u ω u
x+ 2)
x Qsin ω(t − ) = sin 2 ω(t − u
2
u
3)当 x、t都变化时,令 ) 都变化时, 、 都变化时
2 2 2
x x + u∆t 2 2 2 ρA ω sin ω(t − ) = ρA ω sin ω[(t + ∆t) − ] u u w u 表明: 表明:在 t 时刻的 x u∆t t时刻 点的振动能量密度在 t + ∆t时刻 ,传到了 t + ∆t时刻 x + u∆t处 x
1 x 2 2 2 3)体积元的总能量 ∆Ek = ρ∆VA ω sin ω(t − ) ) 2 u 1 x 2 2 2 ∆EP = ρ∆VA ω sin ω(t − ) 2 u x 2 2 2 ∆E = ∆EK + ∆EP = ρ∆VA ω sin ω(t − ) u 指出四点: 指出四点: 1、体元中的能量是随时间变化的(非弧立系统),能量以 、体元中的能量是随时间变化的(非弧立系统) 能量以 U传播,方向与波传播方向相同。 传播, 传播 方向与波传播方向相同。
x = ρ∆VA ω sin ω(t − ) u 能流和能流密度(波强) 二、能流和能流密度(波强)
2 2 2
∆E = ∆EK + ∆EP
为了精确地描述波的能量分布, 为了精确地描述波的能量分布,引入能量密度 1、能量密度 介质中单位体积中的波动能量 、能量密度---介质中单位体积中的波动能量
∆E x 2 2 2 w= = ρA ω sin ω(t − ) ∆V u
证明: 对平面波: 证明: 对平面波: 在一个周期T内通过 1和S2面的能量应该相等 在一个周期 内通过S 内通过
QI1S1T = I2S2T,
S1 = S2 = S
1 1 2 2 2 ρuω A S1T = ρuω 2 A2 S2T 1 2 2
A = A2 平面波振幅相等,波的强度相同。 1 平面波振幅相等,
1 2 2 w uS 1 2 2 w = ρA ω I = = w = ρA ω u u 2 S 2
含义:描述波的能量强弱 含义 描述波的能量强弱. 描述波的能量强弱
分析平面波和球面波的振幅
例 试证明在均匀不吸收能量的媒质中传播的平面波在行进方 向上振幅不变,球面波的振幅与离波源的距离成反比。 向上振幅不变,球面波的振幅与离波源的距离成反比。
A r y = cos[ω( t − ) + ϕ0 ] r u
应用程序
10--4惠更斯原理
一、惠更斯原理 惠更斯原理:介质中任一波阵面上的各点, 惠更斯原理:介质中任一波阵面上的各点,都可看成 是发射子波的波源,其后任一时刻, 是发射子波的波源,其后任一时刻,这些子波的包迹 就是新的波前。 就是新的波前。 根据这一原理,可以由某一时刻的波前 某一时刻的波前, 根据这一原理,可以由某一时刻的波前,用几何 作图的方法确定出下一时刻的波前位置, 下一时刻的波前位置 作图的方法确定出下一时刻的波前位置,从而确定出 波的传播方向。 波的传播方向。 若波在各向异性或不均匀介质中传播时, 若波在各向异性或不均匀介质中传播时,同样能 应用惠更斯原理找出波前,确定波的传播方向。但是, 应用惠更斯原理找出波前,确定波的传播方向。但是, 此时波前的几何形状和传播方向都可能发生变化。 此时波前的几何形状和传播方向都可能发生变化。
平均能流---单位时间内通过某面积的平均能量 平均能流 单位时间内通过某面积的平均能量
w uTS 1 2 2 P= = w = uSρA ω uS T 2
4、平均能流密度(波强) 、平均能流密度(波强) 通过垂直于波传播的方向的单位面积 单位面积的平均 通过垂直于波传播的方向的单位面积的平均 能流; 即单位时间内通过垂直于波动传播的方向的 能流; 单位面积中的平均能量。 单位面积中的平均能量。
