第19讲 相干和非相干光学处理
物理学中的相干光学

物理学中的相干光学相干光学是物理学领域中的一个重要分支,它研究的是光的相干性及其在传播、干涉和衍射等现象中的应用。
相干光学对于解释和研究光的性质以及应用于光学仪器和技术方面都具有重要意义。
在本文中,我们将探讨相干光学的基本概念、干涉现象和衍射现象,以及一些应用于实践中的相关内容。
一、相干光学的基本概念在相干光学中,相干性是一个核心概念。
相干性指的是光波的频率、幅度和相位之间存在的关系。
当两个或多个光波在同一点重合时,它们的相位关系会决定它们的干涉效应。
如果两个光波的相位关系保持不变,它们就是相干的;反之,则是不相干的。
二、干涉现象干涉是相干光学中的重要现象之一。
当两束或多束光波相遇时,它们会产生干涉现象。
干涉实验可以通过一个分波器将一束光分成两束,然后再将它们重新交叉来实现。
干涉现象的主要表现形式是明暗条纹,这是由于光波的相位差所引起的。
根据光波的相位差,干涉现象可以分为相长干涉和相消干涉。
三、衍射现象衍射现象是光波遇到障碍物或通过狭缝时发生的现象。
衍射是光经过障碍物或狭缝后发生弯曲和扩散的过程,它会导致光波在屏幕上形成一系列的亮暗条纹。
衍射现象是相干光学中的另一个重要现象,它在光学领域中有着广泛的应用,例如光学显微镜和光栅等。
四、相干光学的应用相干光学在现代科技和实验研究中有着广泛的应用。
它在激光技术、光学成像和光学通信等方面都发挥着重要作用。
例如,在激光技术中,利用相干光的特性可以实现高质量和稳定的激光束;在光学成像中,相干光学可以用于增强图像的清晰度和对比度;在光学通信中,相干光学是实现高速、高容量光纤通信的基础。
总结相干光学作为物理学中的一个重要分支,研究光的相干性及其在传播、干涉和衍射等现象中的应用。
它的基本概念包括相干性、干涉现象和衍射现象。
相干光学在现代科技领域中有着广泛的应用,对于实现高质量的光学仪器和技术具有重要作用。
随着科技的不断进步,相干光学的研究和应用将会继续取得新的突破和进展。
光学相干性和干涉现象

光学相干性和干涉现象在物理学中,光学相干性和干涉现象是一种非常重要的现象。
干涉现象是指两束光线相交所产生的互相干扰和干涉现象。
而光学相干性则是指在时间序列上,两个光束之间的相位差固定不变的现象。
这些现象在光学领域的应用非常广泛。
首先,让我们来看看干涉现象。
在干涉现象中,光线在相遇时会互相干扰,产生强化或减弱的效果。
这是由于光线的波动性质所引起的。
当两束光线在相遇时,它们会在相交处形成明暗条纹。
当两束光的相位相同,它们会互相增强,而当两束光的相位相差π,它们会互相抵消。
这个原理在干涉仪中得到了广泛的应用。
干涉仪是一种利用干涉现象测量物体形状和光学性质的装置。
它由两个镜子构成,在光线经过其中一个镜子后,又经过一个光屏。
根据光在不同的路程中的相位差,可以得到物体的形状和光学性质的信息。
除了干涉现象,光学相干性也是光学领域中非常重要的现象。
光学相干性是指在时间序列上,两个光束之间的相位差固定不变的现象。
这种相位差可以是由两条光路的长度差或者两个不同的频率引起的。
当两条光路的长度差非常小(小于光波长的一半)时,它们会出现相干性。
这个现象在激光技术中被广泛应用。
激光的产生和稳定依赖于光学相干性。
激光通过谐振腔中的两个反射镜反复来回反射,使光的相位差保持不变。
这个稳定的相位差是激光的重要特征,它为激光的合成和调制提供了基础。
光学相干性也被应用于激光干涉术。
这种技术利用激光的相干性来测量非常小的位移或变形。
在激光干涉术中,激光通过反射或透射到目标物体上,然后再回到激光干涉仪中。
根据光的相位差,可以计算出目标物体的位移或变形。
这种技术被广泛应用于地震和建筑结构的监测和测量。
总之,光学相干性和干涉现象是光学领域中非常重要的现象。
它们被广泛应用于各种光学仪器和技术中,例如激光技术和激光干涉术。
这些现象的研究和应用将为我们理解光学的基本特性和发展光学技术提供帮助。
相干光学原理及应用

相干光学原理及应用相干光学原理基于光的干涉现象,研究光波之间的相位关系和干涉效应。
干涉是指两束或多束光波相遇时,根据它们的相位关系而产生互相增强或抵消的现象。
光的相干性是指两个或多个光波之间具有确定的相位关系,即它们在时间和空间上的相位差保持稳定。
相干性可以理解为两个光波之间存在一种协同的关系,类似于音乐中的和谐乐声。
相干光学的应用非常广泛。
以下是一些常见的应用领域:1. 干涉仪:干涉仪是相干光学最常见的应用之一。
根据干涉现象,干涉仪可用于测量光的波长、薄膜的厚度、形态学的变化等。
著名的干涉仪包括迈克尔逊干涉仪和杨氏双缝干涉仪。
2. 光学显微镜:相干光学在显微镜领域有重要应用。
相干光的使用可以提高显微镜的分辨率,使得微小的结构能够更清晰地观察到。
相干显微镜可用于生物学、材料科学等领域的研究。
3. 光学显示技术:相干光学可用于光学图片处理和显示技术。
通过相干光的干涉现象,可以实现全息投影、全息实时显示等技术。
全息技术在三维成像、虚拟现实等领域有广泛应用。
4. 激光干涉测量:相干光学在测量领域的应用十分重要。
激光干涉技术可以用于测量长度、位移、形变等。
例如,激光干涉测量可以用于检测工件表面的微小缺陷,实现高精度的尺寸测量。
5. 光学通信:相干光学在光纤通信领域有很多应用。
由于相干性可以保持光信号的稳定性,相干光可以在长距离传输中保持较低的信号衰减和失真。
相干光学使得光纤通信能够实现高速、高带宽的数据传输。
总之,相干光学原理的研究和应用在现代光学中起着重要作用。
通过深入理解和应用相干光学原理,我们可以进一步拓展光学技术的领域,并推动光学应用的发展。
相干成像与非相干成像的比较

光学信息处理
第三章
Transfer Function of Optical Imaging System
光学成像系统的传递函数
§ 6. 相干成像与非相干成像的比较
a.截止频率
相 干: Hc (,)=F{hi(xi,yi)}
非相干:
ℋ (,)=
2
jφ )
x 1 .92
x 1 .92
由于相位差的影响,应具体问题具体分析,不能瑞利判据来表述分辨 率。
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
§ 6. 相干成像与非相干成像的比较
相干成像与非相干成像由于照明方式有本质的不同,是不 能直接进行比较的! 这里主要是从量上进行对比,以加深对几个同名参数的 理解与记忆!
§ 6. 相干成像与非相干成像的比较
b.像的强度谱
例题:物体的复振幅透过率为:t1 ( x )
cos
2
x b
当此物通过一横向放大率为1的光学系统成像,系统的出瞳是半径为
di b
ห้องสมุดไป่ตู้
a
2di b
的圆孔, di 为出瞳到像面的距离,试问对该物体成像,是采用相干照明好还是
非相干照明好?
在相干照明下:
c
a di
§ 6. 相干成像与非相干成像的比较
c.分辨率
非相干: I( x ) [ 2J1( x 1.92 ) ] 2 [ 2J1( x 1.92 ) ] 2
x 1.92
x 1.92
可以用瑞利判据: σ 1 .22 λ d i
D
相 干:
I( x )
[ 2 J 1 ( x 1 .92 ) ] [ 2 J 1 ( x 1 .92 ) ] exp(
第19讲相干和非相干光学处理

图像相减的应用
图像相减操作在许多方面已经得到应用: 通过对卫星拍摄的照片的图像相减处理,可用于监测海洋面积的改变、 陆地板块移动的速度 用于对各种自然灾害灾情的监测,如森林大火、洪水等灾情的发展, 地壳运动的变迁,如山脉的升高或降低
对侦察卫星发回的照片进行相减操作,可提高监测敌方军事部署变化 的敏感度和准确度
1 [rect( x3 ) comb( x3 )] 2 16 4
答案
(c)高通滤波挡住零频分量,输出平面复振幅和光强分布表达式
t (x3) =
x 1 [rect( x3 ) comb( 3 )] 4 4
2
- rect(
1 4
x3 ) 4
I = | t (x3) |
由于a = d / 4 ,强度将出现对比度反转,像光栅常数仍为d = 4, 线宽为a’= 3
t0(x',y')
若输入光信号t(x0,y0)≠ t0(x0,y0),则P3 平面得到 u3 = t(x',y')* t0*(-x',-y') = t(x',y')☆t0(x',y') 是两个不同图像的互相关运算,在P3平面上呈现为弥散的亮斑。
匹配滤波器的制作
匹配滤波器是物函数的傅里叶变换的复共轭,可用计算全息方法制作, 也可用光学全息法制作 光学全息制作的方法:先将与之匹配的目标物t0(x0,y0)制成透明片, 再用光学全息法制作它的傅里叶变换全息图(第5章5.4.4P139)
1 1 1 1 1 T ( f x ) = {sinc( f x ) + sinc( ) ( f x - ) + sinc( ) ( f x + ) +• • • } 4 4 4 4 4
5.6__相干成像和非相干成像的比较 PPT课件
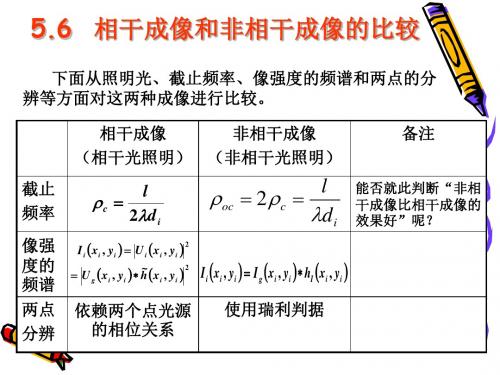
相干光照明下,
像的强度为
Ii U g h~ 2
像强度的频谱为 Gi , Gg , H , Gg , H ,
瞳是半径为a 的圆形孔径,并且 di a 2di
b
b
。d i
为出瞳到像面的距离, 为照明光波波长,请问对
该物体成像,采用相干光和非相干光照明,哪一种方
式更好?
t1x
x
分析:首先,该系统的出瞳是圆孔.
相干光照明时, 截止频率为
c
a
di
a
因为题目给出了条件:di a 2di
(相干光照明) (非相干光照明)
备注
截止 频率
像强 度的 频谱 两点 分辨
c
l
2d i
oc
2c
l
di
能否就此判断“非相 干成像比相干成像的 效果好”呢?
Ii xi , yi Ui xi , yi 2
U g xi , yi h~xi , yi 2 Ii xi , yi Ig xi , yi hI xi , yi
b
b
所以得到
1 2
c
1 b
c
(1)
接着,将物函数分解为余弦函数的线性组合,即将其展 开成傅立叶级数,得
tix
cos 2
x b
4
1 2
1 cos 4
13
x b
1 cos 6
第十章 非相干光学处理

第十章 非相干光学处理一、 相干光处理与非相干光处理的比较1.相干光系统输入为()y x u i ,,输出为()y x u ,,则:()(),,i iu x y u x y =∑即:输出的合成复振幅()y x u ,满足复振幅叠加原则。
而光强为:()()()22,,,∑==i y x u y x u y x I()()()2*,,,i i j ii ju x y u x y u x y ≠=+∑∑()()*,,i i j ii jI u x y u x y ≠=+∑∑在相干处理系统中,输出光强除了是输入光强i I 的叠加外,还存在相干项*j i u u ⋅的影响。
2.非相干光系统对于非相干光系统,由于输入图像各点的光互不相干,所以上式中的互相关项(第二项)的平均值为零。
即()()∑=ii i i y x I y x I ,,即:非相干光处理系统是强度的线性系统,满足强度叠加原理。
3.比较:相干——振幅叠加——可正可负——可完成加、减、乘、除、微分、卷积等运算 非相干——光强叠加——实函数—— 无上述运算4.相干光处理系统存在的不足 1) 噪声太大相干噪声:由光路中的尘埃,指纹,擦痕,元件的缺陷,气泡等引起得干涉。
散班噪声:由漫射物体表面的起伏粗糙而引起的无规干涉。
2)只能处理透明图片(复振幅分布)而不能利用光强接收器得到的信号做为输入信号,(如CRT 、LED 、CCD )3)只能处理单色图象,对彩色图象则无能为力。
4)而非相干系统正好可弥补相干系统的上述不足,即不存在上述不足。
问题:能不能找到一个系统:即能象相干系统一样,存在一个频谱面,可进行各种处理,又能象非相干系统一样,去掉讨厌的噪声干扰-----部分相干系统----白光处理系统二、 白光光学信息处理技术白光光学处理采用宽谱带白光光源,但采用微小的光源尺寸以提高空间相干性。
另一方面在输入平面上引入光栅来提高时间相干性。
这样即不存在相干噪声,又在某种程度上保留了相干光学处理系统对复振幅进行运算的能力,运算灵活性好。
8.6 非相干光学处理

天狼星离我们8.6光年, 光年, 天狼星离我们 光年 是第五近的恒星。 是第五近的恒星。因 为它本身发光很强, 为它本身发光很强, 又距离近, 又距离近,才显得很 明亮耀眼. 明亮耀眼
希腊诗人埃斯库罗斯 (Aeschylus)称天狼 ) 星为‘炽热的犬’ 星为‘炽热的犬’,因 为它是大犬星座α星 为它是大犬星座 星, 在最热的七八月份黎明 前升起。 前升起。 古埃及人称它为索提斯 ),意为 (sothis),意为‘水 ),意为‘ 上之星’ 上之星’
2
功率谱相关器的优点:见教材P 功率谱相关器的优点:见教材P334。 。
光瞳平面上放透过率为t 光瞳平面上放透过率为 2的透明片
x y h1 ( x, y) ∝ T2 , λf λf
2
系统最终输出为
I i ( x , y ) = I g ( x , y ) ∗ h1 ( x , y ) ξ η x − ξ y −η = ∫∫ T1 λ f , λf ⋅ T2 λ f , λf dξdη
在非相干光学处理系统中,我们也同样 在非相干光学处理系统中, 可以在频域综合出所需要的OTF,即实现 可以在频域综合出所需要的 , 各种形式的滤波。 各种形式的滤波。
OTF等于光瞳函数的归一化自相关函数,即 等于光瞳函数的归一化自相关函数, 等于光瞳函数的归一化自相关函数
∫∫ P (λd α , λd β )P (λd (ξ + α ), λd (ξ + β ))dαdβ Η (ξ ,η ) = ∫∫ P (λd α , λd β ) dαdβ
i i i i 2 i i
是系统的出瞳到像面的距离。 式中di 是系统的出瞳到像面的距离。对半径为a 的圆形光瞳,其光学传递函数如图所示: 的圆形光瞳,其光学传递函数如图所示:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相干光学信息处理采用的方法多为频域调制,即对输入光信号的频 谱进行复空间滤波,得到所需要的输出 相干光学信息处理系统的结构是根据具体的图像处理要求而定的, 这里只介绍最基本的一种。由于相干处理是在频域进行调制,通常 采用三透镜系统 输出平面上将得到输入图像与滤波器逆变换的卷积
u 3’= F-1[T(fx,fy)· F(fx,fy)] = F-1[T(fx,fy)] * F-1[F(fx,fy)] = t(x',y')* f(x',y')
t ( x' , y ' ) F j 2πf xT f x , f y x'
置于频谱面上的滤波器的振幅透过率应为
G(xf,yf)=j2 xf /f
微分滤波器的制作
微分滤波器可用光学全息方法,也可用计算全息方法制作。 光学全息方法制作全息微分滤波器实际上是作复合光栅,制作复合 光栅的光路如下图示。 第一次曝光时,干板对于两束光呈对称状态;第二次曝光前将平 台转过一微小角度,曝光后经处理便得到复合光栅,也就是微 分滤波器。
光学微分的应用
实际上,光学微分是用差分近似的结果,原理和图像相减是一回 事。
人的视觉对于轮廓十分敏感,轮廓也是物体的重要特征之一,只 要能看到轮廓线,便可大体分辨出是何种物体。因而将模糊图片 进行光学微分,得出轮廓来进行识别,可以大大压缩图象的信息 量
提取轮廓的其它方法也由光学微分发展而来
微分滤波用于位相物,也有应用价值。例如,用光学微分检测透 明光学元件内部缺陷或折射率不均匀性,用于检测位相型光学元 件的加工是否符合设计要求等等
使A的正一级像与B的负一级像在像面原点重叠
当两者位相相反时,得到相减的结果 当两者位相相同时,得到相加的结果 通过改变调制光栅在频谱面的横向位置,控制两者的位相关系。 当调制光栅的 1/4 周期处于原点位置时,可在像平面得到相减结 果;而当调制光栅的零点处于原点时,可在像平面得到相加结果
一维光栅实现图像相加和相减示意图
图像相减的应用
图像相减操作在许多方面已经得到应用: 通过对卫星拍摄的照片的图像相减处理,可用于监测海洋面积的改变、 陆地板块移动的速度 用于对各种自然灾害灾情的监测,如森林大火、洪水等灾情的发展, 地壳运动的变迁,如山脉的升高或降低
对侦察卫星发回的照片进行相减操作,可提高监测敌方军事部署变化 的敏感度和准确度
特征识别光学系统
光学图像的特征加以识别,是图像处理的一个重要的应用方
面
这种识别大多体现在输出光信号出现较高的峰值,即其自相 关出现较其它信号强得多的峰值 进行光学图像的特征识别处理,采用4f 系统较为方便,下图 是特征识别系统示意图
光学图像识别
特征识别的关键元件是匹配滤波器,用其产生自(互)相关信号 匹配滤波器的振幅透过率F(fx,fy)与输入信号t0(x0,y0)的傅里 叶变换T0(fx,fy)应相互共轭,数学表示为 F(fx,fy)= T0*(fx,fy)= [F{ t0(x0,y0)}]* 将匹配滤波器置于4f系统的P2 平面,P2 后的光场为: u2' = T0(fx,fy) T0*(fx,fy) 在P 3平面上得到 u3 = t0(x',y')* t0*(-x',-y')= t0(x',y')☆ 这是物的自相关,呈现为一个亮点。
复合光栅作微分滤波的机理
置于原点的物的频谱受一个复合光栅调制后,在输出面可得到六 个衍射像:两个零级像在原点,两套正、负一级像对称分布于两 侧。 两个同级衍射像沿x方向只错开很小的距离。当复合光栅位置调节 适当时,可使两个同级衍射像正好相差位相,相干迭加时重叠 部分相消,只余下错开的部分,因而转换成强度时形成很细的亮 线,构成了光学微分图形。
式中
f(x',y')= F-1[F(fx,fy)]
多重像的产生
利用正交光栅调制输入图像的频谱,可以得到多重像的输出
正交朗奇光栅的频谱形成一个Sinc函数的阵列,可近似看成是δ 函数阵列(书上公式8.26有错误请同学自己找,作为练习),物 函数与之卷积的结果是在P3平面上构成输入图形的多重像
图像的相加和相减--一维光栅调制法
图像的相加和相减—复合光栅调制法
所谓复合光栅,是指两套取向一致、但空间频率有微小差异的一维 正弦光栅迭合在同一张底片上制成的光栅,设两套光栅的空间频 率分别为0和0-,由于莫尔效应,在复合光栅表面可见到粗大 的条纹结构,称为“莫尔条纹”。将图像A、B对称置于输入面上 坐标原点两侧,间距为x,并使它与x满足关系式 x = λ f 在频谱面后得到复合光栅透过率G与图像频谱的乘积 u 2'= TG 式中 T 表示将 A 、 B 看成是同一幅图像时的频谱, P3 平面上的 光扰动应为
又如对人体内部器官的检查,可通过不同时期的X 光片进行相减处理, 及时发现病变的所在 用于检测工件的加工,可通过与标准件图片的相减结果检查工件外形 加工是否合格,并能显示出缺陷之所在
ห้องสมุดไป่ตู้学微分—像边缘增强
光学微分的光路系统仍采用4f 系统,待微分的图像置于输入面的 原点位置,微分滤波器置于频谱面上 设输入图像为t0(x0,y0),它的傅里叶频谱为T(fx,fy),输出 图像是T(fx,fy)的逆变换,若想得到图像的微分输出,那么在 P2平面后的光扰动必须满足 t ( x' , y' ) u2 ' F x ' 根据傅里叶变换微商定理
= F -1[T ]* F-1[ G ] 因为 G 是两套光栅复合而成,因而它的傅里叶逆变换应包括六项, 即每套光栅都各有一个零级,一个正一级和一个负一级衍射斑, 出现六重图像
3
u
复合光栅实现图像相加和相减示意图
当复合光栅相对坐 标原点的位移量恰 等于半个莫尔条纹 时,两个正一级像 的位相差等于π, 该处得到图像A、 B的相减结果;而 当复合光栅恢复到 坐标原点位置时, 两个像的位相差为 0,得到图像A、B 的相加的结果 。
将两个需相减操作的图像A、B对称地置于输入面上,中心分别在 x0 = + l 处;频谱面上置一正弦型振幅光栅,其线密度 0 (亦 称空间频率)应满足关系式; ν 0 = l /λ f ,其中 f 为透镜焦距, λ 为光源的波长。一定条件下在输出面的原点处可得到A、B图像 相减的结果 正弦型光栅的频谱包括三项:零级、正一级和负一级。
