(第九章)相干光学处理.
物理学中的相干光学

物理学中的相干光学相干光学是物理学领域中的一个重要分支,它研究的是光的相干性及其在传播、干涉和衍射等现象中的应用。
相干光学对于解释和研究光的性质以及应用于光学仪器和技术方面都具有重要意义。
在本文中,我们将探讨相干光学的基本概念、干涉现象和衍射现象,以及一些应用于实践中的相关内容。
一、相干光学的基本概念在相干光学中,相干性是一个核心概念。
相干性指的是光波的频率、幅度和相位之间存在的关系。
当两个或多个光波在同一点重合时,它们的相位关系会决定它们的干涉效应。
如果两个光波的相位关系保持不变,它们就是相干的;反之,则是不相干的。
二、干涉现象干涉是相干光学中的重要现象之一。
当两束或多束光波相遇时,它们会产生干涉现象。
干涉实验可以通过一个分波器将一束光分成两束,然后再将它们重新交叉来实现。
干涉现象的主要表现形式是明暗条纹,这是由于光波的相位差所引起的。
根据光波的相位差,干涉现象可以分为相长干涉和相消干涉。
三、衍射现象衍射现象是光波遇到障碍物或通过狭缝时发生的现象。
衍射是光经过障碍物或狭缝后发生弯曲和扩散的过程,它会导致光波在屏幕上形成一系列的亮暗条纹。
衍射现象是相干光学中的另一个重要现象,它在光学领域中有着广泛的应用,例如光学显微镜和光栅等。
四、相干光学的应用相干光学在现代科技和实验研究中有着广泛的应用。
它在激光技术、光学成像和光学通信等方面都发挥着重要作用。
例如,在激光技术中,利用相干光的特性可以实现高质量和稳定的激光束;在光学成像中,相干光学可以用于增强图像的清晰度和对比度;在光学通信中,相干光学是实现高速、高容量光纤通信的基础。
总结相干光学作为物理学中的一个重要分支,研究光的相干性及其在传播、干涉和衍射等现象中的应用。
它的基本概念包括相干性、干涉现象和衍射现象。
相干光学在现代科技领域中有着广泛的应用,对于实现高质量的光学仪器和技术具有重要作用。
随着科技的不断进步,相干光学的研究和应用将会继续取得新的突破和进展。
相干与非相干光学处理

Optical Information Processing
光学信息处理
第九章
Incoherent Optical information Processing
非相干光学信息处理
: 光学信息处理从光源的空间和时间相干性来分类
0
i1
另外,不同噪声之间互不相关,因此有
N
E nin j
i1
0上面分析可知,单一通道上的信噪比为 s 2 / 2
当引入N个通道后,信噪比为 Ns 2 / 2
这这一一点点在在光光学学系系统统中中是是容容易易理理解解的的。。
扩扩展展光光源源引引入入的的多多余余通通道道
(1) 相干噪声和散斑噪声问题 (2) 输入和输出上存在的问题
(3) 对色彩信息难以处理
(1)相干噪声和散斑噪声问题.
在光学系统中,透镜、反射镜和分束器等不可避免地存在一些缺陷,如气泡、 擦痕以及尘埃、指印或霉斑等.
当用相干光照明时,这些缺陷将产生衍射,而这些衍射波之间又会互相干涉,从 而形成一系列杂乱条纹与图像重叠在一起,无法分开.这就是所谓相干噪声。
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
c.非相干光学处理系统的特征
照明光波场:非单色光
光学处理对象:光强 作用:完成运算(非负实函数运算处理)
特点:
1.无相干噪声,抗干扰能力强 2.系统简单,具有很强的灵活性
3.色彩信息量高。
。 混合处理系统,可以直接使用这类非相干信号
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
(第九章)相干光学处理

第九章
Coherent Optical Information Processing
相干光学信息处理
内容提要
1. 光的强度、位相、颜色和偏振等都是光信息。光信息可以通过 记录介质进行记录。本章讨论的光信息都是记录在感光胶片上的 图像,即具有一定复振幅或光强透过率的透明片。
2. 信息处理的内容,包括对信息进行加工、变换、识别、增强和 复原,等等。信息处理主要是对输入信息进行各种变换或处理。 就其数学本质来说,就是用某种适当算符作用于输入信号,因而 又是一种“运算”,通过某种系统实现的数学“运算”。 3. 光学信息处理,处理的是光学信息——图像透明片;处理的手 段是光学手段——光学系统;处理后得到的结果仍是光学信息— —光学图像的复振幅或光强分布。
g xi , yi F
1 A x y
F
F f , f H f , f F f , f exp j exp j F F F f , f
1 x y x y
1 A x y
exp j f A xi , yi
9.1 图像周期性网点的消除
9.1.1 图像中周期性网点
周期性网点频谱的特点: 周期性网点,其间隙(距)很小,是一种高频信号。
9.1.2 图像中周期性网点的消除
周期性网点的消除: 方法:低通滤波器 光路:4f系统
Po
Pi
9.1.2 图像中周期性网点的消除 在4f系统中,将记录有周期性网点图像的透明胶片放在 输入平面Po上。设原图像的分布函数为 f ( x0 , y0 )。 大量周 期性网点组成的图像,相当于一幅抽样图像,忽略每个 网点的大小,其复振幅透过率为:
9.2.1 利用干涉仪实现图像相加减
相干光学原理及应用

相干光学原理及应用相干光学原理基于光的干涉现象,研究光波之间的相位关系和干涉效应。
干涉是指两束或多束光波相遇时,根据它们的相位关系而产生互相增强或抵消的现象。
光的相干性是指两个或多个光波之间具有确定的相位关系,即它们在时间和空间上的相位差保持稳定。
相干性可以理解为两个光波之间存在一种协同的关系,类似于音乐中的和谐乐声。
相干光学的应用非常广泛。
以下是一些常见的应用领域:1. 干涉仪:干涉仪是相干光学最常见的应用之一。
根据干涉现象,干涉仪可用于测量光的波长、薄膜的厚度、形态学的变化等。
著名的干涉仪包括迈克尔逊干涉仪和杨氏双缝干涉仪。
2. 光学显微镜:相干光学在显微镜领域有重要应用。
相干光的使用可以提高显微镜的分辨率,使得微小的结构能够更清晰地观察到。
相干显微镜可用于生物学、材料科学等领域的研究。
3. 光学显示技术:相干光学可用于光学图片处理和显示技术。
通过相干光的干涉现象,可以实现全息投影、全息实时显示等技术。
全息技术在三维成像、虚拟现实等领域有广泛应用。
4. 激光干涉测量:相干光学在测量领域的应用十分重要。
激光干涉技术可以用于测量长度、位移、形变等。
例如,激光干涉测量可以用于检测工件表面的微小缺陷,实现高精度的尺寸测量。
5. 光学通信:相干光学在光纤通信领域有很多应用。
由于相干性可以保持光信号的稳定性,相干光可以在长距离传输中保持较低的信号衰减和失真。
相干光学使得光纤通信能够实现高速、高带宽的数据传输。
总之,相干光学原理的研究和应用在现代光学中起着重要作用。
通过深入理解和应用相干光学原理,我们可以进一步拓展光学技术的领域,并推动光学应用的发展。
物理实验技术中的光学相干实验方法与技巧

物理实验技术中的光学相干实验方法与技巧光学作为一门古老而又重要的科学,已经为人类的生活和科技发展做出了巨大贡献。
而光学相干实验作为光学研究的一种基础实验方法,具有重要的意义和广泛的应用。
本文将介绍一些光学相干实验的方法与技巧。
光学相干实验的基本原理是利用光波的相干性质,通过干涉与衍射的现象来研究光的特性和性质。
在进行光学相干实验前,我们首先需要准备一些实验器材,如激光器、偏振器、光阑等。
值得注意的是,由于光学相干实验对实验环境的要求较高,因此在实验前需选择一个较为稳定的实验室环境。
在进行光学相干实验时,我们经常会用到一种重要的实验方法,即自发光法。
这种方法通过调整实验条件,使得光源自己发出相干光,从而减少实验过程中可能存在的干扰因素。
例如,在利用干涉仪进行光学相干实验中,我们可以将光源置于一个黑暗的容器中,通过适当的调整,使得光源只发出特定波长的相干光。
这样一来,我们就可以在实验中更准确地研究光波的相干性质。
在进行光学相干实验时,我们还需要注意一些实验技巧。
首先,要避免实验过程中的光波损耗。
光学相干实验中,往往需要将光波引入到某个光学元件中,因此光波的损耗会直接影响实验结果的准确性。
为了避免这一问题,我们可以采用低损耗的光纤或反射镜等器材,减小光波的传输损耗。
其次,要合理选择光学元件的位置和角度。
实验中,各个光学元件的位置和角度的微小变化都可能对实验结果产生影响。
因此,在进行光学相干实验时,我们需要通过仔细调整光学元件的位置和角度,使得光波可以准确地通过或反射。
这样一来,我们就能够获得更准确的实验结果。
最后,要注意实验环境的干扰因素。
光学相干实验对实验环境的要求较高,因此我们在进行实验前要尽量避免一些可能引起实验干扰的因素。
例如,我们可以将实验器材放置在一个稳定的平台上,避免来自地震或其他振动的干扰;另外,我们还可以在实验室中设置一些吸收和隔离装置,减小外界光线的影响。
总结来说,在物理实验技术中的光学相干实验方法与技巧方面,我们需要注意实验器材的准备、实验方法的选择以及实验技巧的掌握。
光学相干性分析

光学相干性分析光学相干性分析是一种重要的光学技术,广泛应用于光学系统的研究与设计、光通信、医学影像等领域。
本文将从基本原理、实用方法和应用案例等方面,深入探讨光学相干性分析的概念及其在科学研究和工程实践中的价值。
一、基本原理光学相干性是指光波的干涉现象。
当两束光波在空间中相遇时,根据各个点上的光场振幅以及相位差的差别,会出现干涉现象。
光学相干性分析正是通过对这种干涉现象的观察和测量,来研究光波的传播特性和光学系统的性能。
光学相干性分析的基本原理之一是光的干涉原理。
根据光波的干涉特性,当两束光波相遇时,它们的振幅会叠加产生干涉图样。
通过观察和分析干涉图样的变化,可以获得光波的相位、波长、振幅等信息。
光学相干性分析的另一个基本原理是光的干涉标准。
为了准确定义和描述干涉现象,人们引入了相干函数或互相关函数,用来描述光波的相干性。
这些函数可以通过光学元件、干涉仪等设备进行测量和分析。
二、实用方法在光学相干性分析中,有许多常用的实用方法。
其中最常见的包括:自由空间干涉法、干涉仪法、相位微分法、激光多普勒血流仪等。
自由空间干涉法是最简单和常见的光学相干性分析方法之一。
通过将样品放置在自由空间中,并观察干涉图样的变化,可以获得样品的光学特性信息。
这种方法适用于工程实践中对光学元件、光学材料等的表面形貌和光学性能进行分析。
干涉仪法是一种更为精确和定量的光学相干性分析方法。
通过使用干涉仪设备,可以实现对光波的相位、幅度等参数的高精度测量。
干涉仪法广泛应用于光通信、激光技术、光学成像等领域。
相位微分法是一种利用光场的相位差来分析光学系统特性的方法。
通过测量光场在不同位置的相位变化,可以获得样品的形貌信息。
相位微分法在科学研究和工程实践中有重要应用,特别是在材料表面形貌研究、生物医学影像等领域。
激光多普勒血流仪是一种基于光学相干性分析的医学影像技术。
通过测量光场在血液中的散射和干涉特性,可以实现对血流速度、血管形态等信息的获取。
相干处理光学系统的象质评价和计算程序

相干处理光学系统的象质评价和计算程序随着现代高科技的不断发展,光学系统的应用领域变得愈加广泛。
为了确保系统的性能,光学系统的象质评价和计算处理变得愈加重要。
以下是对光学系统的象质评价和计算程序的相关处理方面的详细分析:一、光谱分析光谱分析是光学系统中最重要的概念之一,是评价光系统象质的依据。
光谱分析可以帮助研究者了解光系统中各种成分的组成及其强度分布,是一种有效的检测方法。
二、图像拼接图像拼接技术是用来评估光学系统的一种测量方法,它既可以观察图像的恒定性,又能够检测系统中的不良元件和结构,衡量光学系统背后的隐形结构。
经过图像拼接,研究者可以更好地了解光学系统的结构象质,并将图像与其他测量方法结合进行象质评价。
三、图像处理图像处理是评估光学系统象质的一个重要组成部分。
它包括对图像空间分块、色彩校正、噪声处理等步骤,以提取有效信息。
它能够清晰地显示象质的变化,改善图像的清晰度、增强图像的性能,从而更好地评估系统的象质性能。
四、像差分析像差分析是一种常用的测量方法,可以从不同的位置进行定量检测。
通过测量物体在不同实验条件下的像差,可以获得物体的绝对误差、相对误差和形变等信息,从而有效进行象质评价。
五、计算处理通过使用计算机等多媒体设备,可以进行关于光学系统的定量分析和计算模拟。
它可以大大提高测量精度和系统效率,帮助研究者减少测量时间,准确分析光学系统的象质状况,有效改进和提升系统性能。
以上就是对光学系统的象质评价和计算程序的相关处理方面的分析。
由此可见,光学系统的象质评价和计算处理对于实现系统性能具有重要意义。
在未来,我们将会更多地利用光谱分析、图像拼接、图像处理及计算机等技术来优化系统的象质和性能。
大学物理光学课件 (PDF格式)
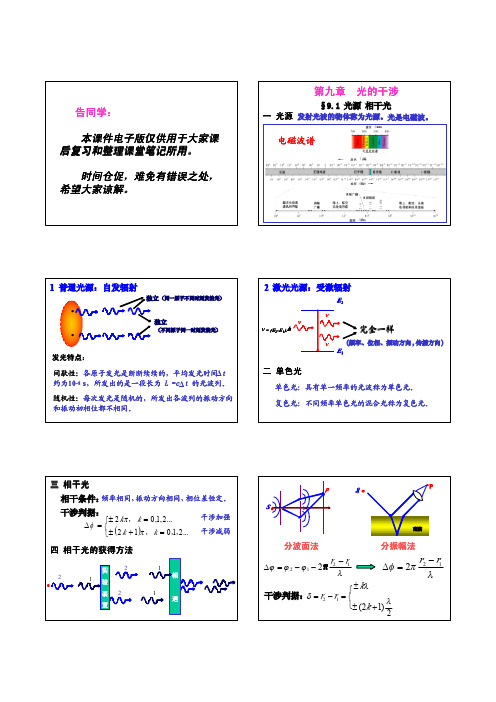
2.干涉明暗条纹的位置 2.1 波程差的计算
p
1
x
d δ
θ
r
·x
x
r
2
o D
S*
S1 *
k= 0
I
设实验在真空(或空气)中进行,则波程差为:
S2 *
k=-1 k=-2
δ = r2 − r1 ≈ d sin θ ≈ d tg θ = d ⋅
x D
2.2 明暗条纹条件
δ = r2 −r1 ≈d sinθ ≈ d tgθ = d ⋅
r
B
(4)
E
(5)
,条纹的移动: k一 定, e ↑ → i ↑ → rk 膜厚变化时, • 膜厚变化时 : 波长对条纹的影响: • 波长对条纹的影响
k, e 一 定, λ ↑ → i ↓→ rk ↓
利用薄膜干涉使反射光减小, 这样的薄膜称为增透膜。
2 、多层高反射膜
H L H ZnS MgF 2 ZnS MgF 2
AD = AC sin i
δ = 2 n2 AB − n1 AD +
P Q
sin i n2 = sin r n1
n1 n2 n2 > n1
e λ = 2n2 ⋅ − n1 ⋅ 2e ⋅ tan r sin i + cos r 2
= 2e λ ( n − n sin r sin i ) + cos r 2 1 2 2e sin i λ = ( n − n sin 2 r )+ cos r 2 1 sin r 2
2 2 = 2e n2 2 − n1 sin i + λ / 2
δ = 2 n 2 AB − n1 AD + λ 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章
Coherent Optical Information Processing
相干光学信息处理
内容提要
1. 光的强度、位相、颜色和偏振等都是光信息。光信息可以通过 记录介质进行记录。本章讨论的光信息都是记录在感光胶片上的 图像,即具有一定复振幅或光强透过率的透明片。
2. 信息处理的内容,包括对信息进行加工、变换、识别、增强和 复原,等等。信息处理主要是对输入信息进行各种变换或处理。 就其数学本质来说,就是用某种适当算符作用于输入信号,因而 又是一种“运算”,通过某种系统实现的数学“运算”。
在物平面Po上,沿xo方向相对于坐标原点对称放置记录着图像 信息的A和B,它的中心离开坐标原点的距离都等于
b f0 f
(9.2.4)
式中, 是单色照明光波长; f0 为光栅空间频率; f 为透
镜焦距。
9.2.1 利用光栅滤波实现图像相加减
在频谱平面P1上,放置忽略了有限尺寸的正弦振幅型光栅, 其复振幅透过率函数可写为
H
fx, fy
1 2
1
cos
2
f0x1
(9.2.5)
1 2
1
1 2
exp
j 2
f0 x1
1 2
exp
j 2
f0 x1
其中,
fx
x1
f
,
f y
y1
f
,
为光栅条纹的初相位,它由光栅
相对于频谱坐标原点的位置决定。
正弦振幅型光栅可通过全息的方法制得。
9.2.1 利用光栅滤波实现图像相加减
3. 光学信息处理,处理的是光学信息——图像透明片;处理的手 段是光学手段——光学系统;处理后得到的结果仍是光学信息— —光学图像的复振幅或光强分布。
9.1 图像周期性网点的消除
9.1.1 图像中周期性网点
周期性网点频谱的特点: 周期性网点,其间隙(距)很小,是一种高频信号。
9.1.2 图像中周期性网点的消除
f x, y fA x, y fB x, y
输出获得图像相减
特点 :( 1 )光路,原理简单 ( 2 )调节困难,(精确重合)
(9.2.1) (9.2.2) (9.2.3)
9.2.1 利用光栅滤波实现图像相加减
x1
处理系统如图
9.2.2所示。它
是一个4f相干
处理系统。
Po
y1 P1
Pi
图9.2.2 用光栅实现图像相加减
0
x0
,
y0
comb
x0 a
comb y0 b
f
x0 , y0
(9.1.1)
式子,a、b分别表示网点沿xo,yo方向的间距。
9.1.2 图像中周期性网点的消除
(9.1.1)式表明,网点图像由δ函数阵列构成。利用傅里叶变换 的卷积定理,在频谱面上的频谱为
F0
fx, fy
comb
x0 a
9.2 图像的相加减
• 两幅图A、B,有相同部分,又有不 同部分
• 取相同部分,弃去不同部分,用相 加法
• 取不同部分,弃去相同部分,用相 减法
9.2.1 利用干涉仪实现图像相加减
利用马赫干涉仪实现两幅
图像的加减,基本光路如
图9.2.1所示。其中,S为点
光源,L1为准直透镜。BS1, BS2分别为分束器。q为位相 补偿器。M1,M2为平面反射
PB Pi
镜。PA,PB是记录着复振幅
透过率为fA(x,y)和fB(x,y)的
PA
两幅图像透明片,他们通过 成像透镜L2同时以放大率
图9.2.1
用马赫特干涉仪实现图像相加减
为1成像在Pi平面上。
设照射到PA与PB上为 单位振幅平面波,两路光的位相差为 ,其 值可通过位相补偿器调节,则在像面Pi上光场的复振幅分布为:
间滤波的方法,从Fo中抽取原函数频谱F,阻挡其它频谱,再由 F求出原函数。具体来说,就是采用开孔适当大小的低通滤波
器H(fx,fy),只让中心(m=n=0)的一个F(fx,fy)通过,即,
F0 fx, fy H fx, fy fx , fy F fx , fy
F f x , f y
comb
y0 b
f
x0
,
y0
comb
x0 a
comb
y0 b
F
fx, fy
acombafx bcomb bfy
fy
m b
F
fx, fy
n
m
F
fx
n a
,
fy
m b
(9.1.2)
频谱平面上图像的频谱F是以 (n/a,m/b)点为中心,周期性的重复出 现。沿fx方向的周期间隔为1/a,沿fy方向的周期间隔为1/b.
9.1.2 图像中周期性网点的消除
一副实际图像分布一定是带限函数。它的频谱只在频谱平面的 一个有限区域上不为零。设这个区域为矩形,并以2A,2B分别 表示这个最小区域在fx和fy方向上的宽度,则当
1 2A 1 2B 即 a 1
b 1 时 (9.1.3)
a
b
2A
2B
Fo中各频谱区域就不出现重叠现象。实际上网点距离比较小, 上述条件通常时得到满足的。因而个频谱区域分开,可以用空
(9.1.4)
9.1.2 图像中周期性网点的消除
最后在输出像平面Pi上得
g xi , yi F 1 F0 fx, fy H fx, fy F 1 F fx, fy
f xi , yi
这样就获得了一幅没有网点得图像分布。而将其网点、扫描线 等噪声去掉。
图9.1.1给出了两幅分别为经网络滤波处理前后的对比图像。
设fA(xo,yo)和fB(xo,yo)分别为图像A和B的复振幅透过率函数,在 单位振幅平面波垂直照明下,物平面输入光场分布为
f x0 , y0 f A x0 b, y0 f B x0 b, y0 (9.2.6)
9.2.1 利用干涉仪实现图像相加减
f x, y fA x, y exp j fB x, y
当 n 2时,(n为整数)
e(i) cos j sin 1
f x, y fA x, y fB x, y
输出获得图像相加
当 (2n 1),(n为正整数)
e(i) cos j sin 1
周期性网点的消除: 方法:低通滤波器 光路:4f系统
Po
Pi
9.1.2 图像中周期性网点的消除
在4f系统中,将记录有周期性网点图像的透明胶片放在 输入平面Po上。设原图像的分布函数为 f (x0, y0 )。大量周 期性网点组成的图像,相当于一幅抽样图像,忽略每个 网点的大小,其复振幅透过率为:
f
