同济版大学物理学第五章练习题
大学物理第五章习题解答
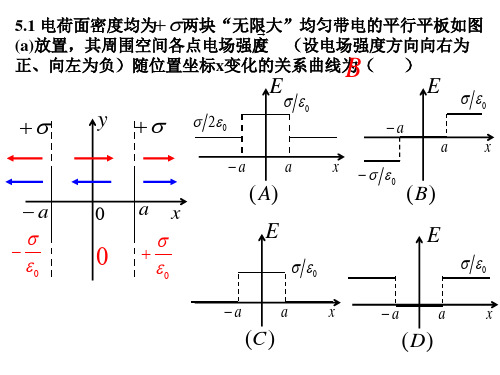
R1 4 0r 2
R2 4 0r 2
Q1 Q2
4 0 R1 4 0 R2
Q1 Q2
R2
(2)
R1
r
R2
,
V E dl
R2
E
dl
E dl
r
r
R2
R2 r
Q1
4 0r 2
er
drer
R2
Q1 Q2
4 0r 2
er
drer
Q1
4 0r
Q2
4 0 R2
(3)r R2 ,
5.1 电荷面密度均为两块“无限大”均匀带电的平行平板如图
(a)放置,其周围空间各点电场强度E (设电场强度方向向右为
B 正、向左为负)随位置坐标x变化的关系曲线为( )
E
y 20
0
E 0
a
ax
a
a
x 0
( A)
(B)
a 0 a x
0
0
0
E
0
E
0
a a x
(C )
a a x
(D)
B 5.2 下列说法正确的是( )
解:电荷分布具有轴对 称,作同轴的封闭圆柱 面
-+
l
-
+ +
-+
R1 R2
作Gauss面,该Gauss面底面半径为 r,高度范围 l。
由 高斯 定理:SE
dS
q内
0
上E dS 下E dS 侧E dS 侧E dS E 2rl
E q内
2 0rl
全空间分为3个区域来讨论 (1)r R1
圆环: ( p159 )
E
1
大学物理习题册第五章习题详解共26页

OR
真空中的静电场(二)
第五章 真空中的静电场
7.图示为一边长均为a的等边三角形,其三个顶点分 别放置着电荷为q、2q、3q的三个正点电荷,若将一电 荷为Q的正点电荷从无穷远处移至三角形的中心O处, 则外力需作功A=__________.
3 1 3
q 1 5
(B)
4pe 0l
5
(D)
q
4pe 0l
5 1 5
D l
C l -q
B l A +q
E lF
pe pepe A qC FC FC F 4 q 0 lq 4 q 0 l 4 1-1q 0 题5 图l
真空中的静电场(二)
第五章 真空中的静电场
真空中的静电场(二)
第五章 真空中的静电场
2.在一个带有负电荷的均匀带电球外,放置一电偶极
子,其电矩 的方向如图所示.当电偶极子被释放后,该
电偶极子将
(A) 沿逆时针方向旋转直到电矩 p 沿径向指向球面
而停止.
(B)沿逆时针方向旋转至 p 沿径向指向球面,同时沿
电场线方向向着球面移动.
(C) 沿逆时针方向旋转至 p 沿径向指向球面,同时
2 2
;
x
真空中的静电场(二)
第五章 真空中的静电场
3.地球表面上晴空时,地球表面以上10km范围内的
电场强度都约为100V/m。此电场的能量密度为
;
在该范围内电场所储存的能量共有
kw·h。
e w e 1 20 E 2 1 2 8 .8 1 5 10 2 12 0 4 .4 0 2 1 8 5 J 03 /m
度为d(d<<R).环上均匀带正电,总电量为q.则圆
心O处的场强大小E=
大学物理课后习题答案第五章

第五章 机械波5.1 已知一波的波动方程为y = 5×10-2sin(10πt – 0.6x ) (m). (1)求波长、频率、波速及传播方向;(2)说明x = 0时波动方程的意义,并作图表示. [解答](1)与标准波动方程比较得:2π/λ = 0.6, 因此波长为:λ = 10.47(m);圆频率为:ω = 10π,频率为:v =ω/2π = 5(Hz);波速为:u = λ/T = λv =52.36(m·s -1).且传播方向为x 轴正方向.(2)当x = 0时波动方程就成为该处质点的振动方程: y = 5×10-2sin10πt = 5×10-2cos(10πt – π/2), 振动曲线如图.5.2 一平面简谐波在媒质中以速度为u = 0.2m·s -1沿x 轴正向传播,已知波线上A 点(x A = 0.05m )的振动方程为(m).试求:(1)简谐波的波动方程;(2)x = -0.05m 处质点P 处的振动方程.[解答](1)简谐波的波动方程为:; 即 = 0.03cos[4π(t – 5x ) + π/2]. (2)在x = -0.05m 处质点P 点的振动方程为:y = 0.03cos[4πt + π + π/2] =0.03cos(4πt - π/2).5.3 已知平面波波源的振动表达式为(m).求距波源5m 处质点的振动方程和该质点与波源的位相差.设波速为2m·s -1.[解答]振动方程为: , 位相差为 Δφ = 5π/4(rad).5.4 有一沿x 轴正向传播的平面波,其波速为u = 1m·s -1,波长λ = 0.04m ,振幅A = 0.03m .若以坐标原点恰在平衡位置而向负方向运动时作为开始时刻,试求:(1)此平面波的波动方程;(2)与波源相距x = 0.01m 处质点的振动方程,该点初相是多少?[解答](1)设原点的振动方程为:y 0 = A cos(ωt + φ),其中A = 0.03m .由于u = λ/T ,所以质点振动的周期为:T = λ/u = 0.04(s),圆频率为:ω = 2π/T = 50π.当t = 0时,y 0 = 0,因此cos φ = 0;由于质点速度小于零,所以φ = π/2. 原点的振动方程为:y 0 = 0.03cos(50πt + π/2), 平面波的波动方程为:= 0.03cos[50π(t – x ) + π/2).(2)与波源相距x = 0.01m 处质点的振动方程为:y = 0.03cos50πt . 该点初相φ = 0.2cos()xy A t πωλ=-0.03cos(4)2A y t ππ=-cos[()]Ax x y A t uωϕ-=-+0.050.03cos[4()]0.22x y t ππ-=--20 6.010sin 2y t π-=⨯26.010sin()2xy t u π-=⨯-50.06sin()24t ππ=-0.03cos[50()]2x y t u ππ=-+t /s y /cm5 0 0.1 0.2 0.35.5 一列简谐波沿x 轴正向传播,在t 1 = 0s ,t 2 = 0.25s 时刻的波形如图所示.试求:(1)P 点的振动表达式; (2)波动方程;(3)画出O 点的振动曲线.[解答](1)设P 点的振动方程为 y P = A cos(ωt + φ), 其中A = 0.2m .在Δt = 0.25s 内,波向右传播了Δx = 0.45/3 = 0.15(m),所以波速为u = Δx/Δt = 0.6(m·s -1).波长为:λ = 4Δx = 0.6(m), 周期为:T = λ/u = 1(s), 圆频率为:ω = 2π/T = 2π.当t = 0时,y P = 0,因此cos φ = 0;由于波沿x 轴正向传播,所以P 点在此时向上运动,速度大于零,所以φ = -π/2.P 点的振动表达式为:y P = 0.2cos(2πt - π/2). (2)P 点的位置是x P = 0.3m ,所以波动方程为. (3)在x = 0处的振动方程为y 0 = 0.2cos(2πt + π/2),曲线如图所示.5.6 如图所示为一列沿x 负向传播的平面谐波在t = T /4时的波形图,振幅A 、波长λ以及周期T 均已知.(1)写出该波的波动方程;(2)画出x = λ/2处质点的振动曲线;(3)图中波线上a 和b 两点的位相差φa – φb 为多少? [解答](1)设此波的波动方程为: ,当t = T /4时的波形方程为:. 在x = 0处y = 0,因此得sin φ = 0,解得φ = 0或π.而在x = λ/2处y = -A ,所以φ = 0. 因此波动方程为:. (2)在x = λ/2处质点的振动方程为:, 曲线如图所示.(3)x a = λ/4处的质点的振动方程为;0.2cos[2()]2P x x y t u ππ-=--100.2cos(2)32t x πππ=-+cos[2()]t xy A T πϕλ=++cos(2)2xy A ππϕλ=++sin(2)xA πϕλ=-+cos 2()t x y A T πλ=+cos(2)cos 2t t y A A T Tπππ=+=-cos(2)2a t y A T ππ=+x /m y /m0.2O t 1=0 0.45 t 2=0.25P 图5.5 t /sy /m0.2O 0.5 1xy AO bau图5.6y Ax b = λ处的质点的振动方程为. 波线上a 和b 两点的位相差φa – φb = -3π/2.5.7 已知波的波动方程为y = A cosπ(4t – 2x )(SI ).(1)写出t = 4.2s 时各波峰位置的坐标表示式,并计算此时离原点最近的波峰的位置,该波峰何时通过原点?(2)画出t = 4.2s 时的波形曲线.[解答]波的波动方程可化为:y = A cos2π(2t – x ),与标准方程比较,可知:周期为T = 0.5s ,波长λ = 1m .波速为u = λ/T = 2m·s -1. (1)当t = 4.2s 时的波形方程为y = A cos(2πx – 16.8π)= A cos(2πx – 0.8π). 令y = A ,则cos(2πx – 0.8π) = 1,因此 2πx – 0.8π = 2k π,(k = 0, ±1, ±2,…), 各波峰的位置为x = k + 0.4,(k = 0, ±1, ±2,…).当k = 0时的波峰离原点最近,最近为:x = 0.4(m).通过原点时经过的时间为:Δt = Δx/u = (0 – x )/u = -0.2(s), 即:该波峰0.2s 之前通过了原点.(2)t = 0时刻的波形曲线如实线所示.经过t = 4s 时,也就是经过8个周期,波形曲线是重合的;再经Δt = 0.2s ,波形向右移动Δx = u Δt = 0.4m ,因此t = 4.2s 时的波形曲线如虚线所示.[注意]各波峰的位置也可以由cos(2πx – 16.8π) = 1解得,结果为x = k + 8.4,(k = 0, ±1, ±2,…),取同一整数k 值,波峰的位置不同.当k = -8时的波峰离原点最近,最近为x = 0.4m .5.8 一简谐波沿x 轴正向传播,波长λ = 4m ,周期T = 4s ,已知x = 0处的质点的振动曲线如图所示. (1)写出时x = 0处质点的振动方程;(2)写出波的表达式;(3)画出t = 1s 时刻的波形曲线.[解答]波速为u = λ/T = 1(m·s -1).(1)设x = 0处的质点的振动方程为y = A cos(ωt + φ), 其中A = 1m ,ω = 2π/T = π/2.当t = 0时,y = 0.5,因此cos φ = 0.5,φ = ±π/3.在0时刻的曲线上作一切线,可知该时刻的速度小于零,因此φ = π/3.振动方程为:y = cos(πt /2 + π/3). (2)波的表达式为:.(3)t = 1s 时刻的波形方程为cos(22)b ty A Tππ=+cos[2()]t x y A T πϕλ=-+cos[2()]t xy A T πϕλ=-+cos[()]23t x ππ=-+xy A O ut =0 t =4.2s 0.51 t /s y /m1 O -10.5 图5.8x /my /m 1O -10.5u2/3,波形曲线如图所示.5.9 在波的传播路程上有A 和B 两点,都做简谐振动,B 点的位相比A 点落后π/6,已知A 和B 之间的距离为2.0cm ,振动周期为2.0s .求波速u 和波长λ.[解答] 设波动方程为:, 那么A 和B 两点的振动方程分别为:,.两点之间的位相差为:,由于x B – x A = 0.02m ,所以波长为:λ = 0.24(m).波速为:u = λ/T = 0.12(m·s -1).5.10 一平面波在介质中以速度u = 20m·s -1沿x 轴负方向传播.已知在传播路径上的某点A 的振动方程为y = 3cos4πt .(1)如以A 点为坐标原点,写出波动方程;(2)如以距A 点5m 处的B 点为坐标原点,写出波动方程; (3)写出传播方向上B ,C ,D 点的振动方程. [解答](1)以A 点为坐标原点,波动方程为 .(2)以B 点为坐标原点,波动方程为. (3)以A 点为坐标原点,则x B = -5m 、x C = -13m 、x D = 9m ,各点的振动方程为, ,.[注意]以B 点为坐标原点,求出各点坐标,也能求出各点的振动方程.5.11 一弹性波在媒质中传播的速度u = 1×103m·s -1,振幅A = 1.0×10-4m ,频率ν= 103Hz .若该媒质的密度为800kg·m -3,求:(1)该波的平均能流密度;(2)1分钟内垂直通过面积S = 4×10-4m 2的总能量.[解答](1)质点的圆频率为:ω = 2πv = 6.283×103(rad·s -1), 波的平均能量密度为:= 158(J·m -3), 平均能流密度为:= 1.58×105(W·m -2).(2)1分钟内垂直通过面积S = 4×10-4m 2的总能量为:E = ItS = 3.79×103(J).5cos()26y x ππ=-cos[2()]t xy A T πϕλ=-+cos[2()]A A xt y A T πϕλ=-+cos[2()]B B xt y A T πϕλ=-+2(2)6B A x x πππλλ---=-3cos 4()3cos(4)5x x y t t u πππ=+=+3cos 4()Ax x y t u π-=+3cos(4)5x t πππ=+-3cos 4()3cos(4)BB x y t t u πππ=+=-33cos 4()3cos(4)5C C x y t t u πππ=+=-93cos 4()3cos(4)5D D x y t t u πππ=+=+2212w A ρω=I wu =x5m A B C D8m 9m图5.105.12 一平面简谐声波在空气中传播,波速u = 340m·s -1,频率为500Hz .到达人耳时,振幅A = 1×10-4cm ,试求人耳接收到声波的平均能量密度和声强?此时声强相当于多少分贝?已知空气密度ρ = 1.29kg·m -3.[解答]质点的圆频率为:ω = 2πv = 3.142×103(rad·s -1), 声波的平均能量密度为:= 6.37×10-6(J·m -3), 平均能流密度为:= 2.16×10-3(W·m -2),标准声强为:I 0 = 1×10-12(W·m -2), 此声强的分贝数为:= 93.4(dB).5.13 设空气中声速为330m·s -1.一列火车以30m·s -1的速度行驶,机车上汽笛的频率为600Hz .一静止的观察者在机车的正前方和机车驶过其身后所听到的频率分别是多少?如果观察者以速度10m·s -1与这列火车相向运动,在上述两个位置,他听到的声音频率分别是多少?[解答]取声速的方向为正,多谱勒频率公式可统一表示为, 其中v S 表示声源的频率,u 表示声速,u B 表示观察者的速度,u S 表示声源的速度,v B 表示观察者接收的频率.(1)当观察者静止时,u B = 0,火车驶来时其速度方向与声速方向相同,u S = 30m·s -1,观察者听到的频率为= 660(Hz). 火车驶去时其速度方向与声速方向相反,u S = -30m·s -1,观察者听到的频率为= 550(Hz). (2)当观察者与火车靠近时,观察者的速度方向与声速相反,u B = -10m·s -1;火车速度方向与声速方向相同,u S = 30m·s -1,观察者听到的频率为= 680(Hz). 当观察者与火车远离时,观察者的速度方向与声速相同,u B = 10m·s -1;火车速度方向与声速方向相反,u S = -30m·s -1,观察者听到的频率为= 533(Hz). [注意]这类题目涉及声速、声源的速度和观察者的速度,规定方向之后将公式统一起来,很容易判别速度方向,给计算带来了方便.5.14.一声源的频率为1080Hz ,相对地面以30m·s -1速率向右运动.在其右方有一反射面相对地面以65m·s -1的速率向左运动.设空气中声速为331m·s -1.求:(1)声源在空气中发出的声音的波长; (2)反射回的声音的频率和波长.[解答](1)声音在声源垂直方向的波长为:λ0 = uT 0 = u /ν0 = 331/1080 = 0.306(m); 在声源前方的波长为:λ1 = λ0 - u s T 0 = uT 0 - u s T 0 = (u - u s )/ν0 = (331-30)/1080 = 0.2787(m); 在声源后方的波长为:λ2 = λ0 + u s T 0 = uT 0 + u s T 0 = (u + u s )/ν0= (331+30)/1080 = 0.3343(m).2212w A ρω=I wu =010lgIL I =BB S Su u u u νν-=-33060033030B S S u u u νν==--33060033030B S S u u u νν==-+3301060033030B B S S u u u u νν-+==--3301060033030B B S S u u u u νν--==-+u Bu Su(2)反射面接收到的频率为= 1421(Hz).将反射面作为波源,其频率为ν1,反射声音的频率为= 1768(Hz).反射声音的波长为=0.1872(m).或者 = 0.1872(m). [注意]如果用下式计算波长=0.2330(m), 结果就是错误的.当反射面不动时,作为波源发出的波长为u /ν1 = 0.2330m ,而不是入射的波长λ1.5.15 S 1与S 2为两相干波源,相距1/4个波长,S 1比S 2的位相超前π/2.问S 1、S 2连线上在S 1外侧各点的合成波的振幅如何?在S 2外侧各点的振幅如何?[解答]如图所示,设S 1在其左侧产生的波的波动方程为,那么S 2在S 1左侧产生的波的波动方程为,由于两波源在任意点x 产生振动反相,所以合振幅为零.S 1在S 2右侧产生的波的波动方程为,那么S 2在其右侧产生的波的波动方程为,由于两波源在任意点x 产生振动同相,所以合振幅为单一振动的两倍.5.16 两相干波源S 1与S 2相距5m ,其振幅相等,频率都是100Hz ,位相差为π;波在媒质中的传播速度为400m·s -1,试以S 1S 2连线为坐标轴x ,以S 1S 2连线中点为原点,求S 1S 2间因干涉而静止的各点的坐标.[解答]如图所示,设S 1在其右侧产生的波的波动方程为 ,那么S 2在其左侧产生的波的波动方程为.1033165108033130B S u u u u νν++==⨯--`11331142133165B u u u νν==⨯--`1111331651421BBu u u uλννν--=-==`1`13311768uλν==`111650.27871768Bu λλν=-=-1cos[2()]t xy A T πϕλ=++2/4cos[2()]2t x y A T λππϕλ-=++-cos[2()]t xA T πϕπλ=++-1cos[2()]t xy A T πϕλ=-+2/4cos[2()]2t x y A T λππϕλ-=-+-cos[2()]t xA T πϕλ=-+1/2cos[2()]x l y A t u πνϕ+=-+5cos(2)24A t x πππνϕ=-+-2/2cos[2()]x l y A t u πνϕπ-=+++cos(2)24A t x πππνϕ=++-u BuxS 1 xS 2λ/4 x xS 1x 2l两个振动的相差为Δφ = πx + π,当Δφ = (2k + 1)π时,质点由于两波干涉而静止,静止点为x = 2k , k 为整数,但必须使x 的值在-l /2到l /2之间,即-2.5到2.5之间.当k = -1、0和1时,可得静止点的坐标为:x = -2、0和2(m).5.17 设入射波的表达式为,在x = 0处发生反射,反射点为一自由端,求:(1)反射波的表达式; (2)合成驻波的表达式.[解答](1)由于反射点为自由端,所以没有半波损失,反射波的波动方程为.(2)合成波为y = y 1 + y 2,将三角函数展开得,这是驻波的方程.5.18 两波在一很长的弦线上传播,设其表达式为:,,用厘米、克、秒(cm,g,s )制单位,求:(1)各波的频率,波长、波速;(2)节点的位置;(3)在哪些位置上,振幅最大?[解答](1)两波可表示为:,, 可知它们的周期都为:T = 0.5(s),频率为:v = 1/T = 2(Hz);波长为:λ = 200(cm);波速为:u = λ/T = 400(cm·s -1).(2)位相差Δφ = πx /50,当Δφ = (2k + 1)π时,可得节点的位置x = 50(2k + 1)(cm),(k = 0,1,2,…).(3)当Δφ = 2k π时,可得波腹的位置x = 100k (cm),(k = 0,1,2,…).(注:可编辑下载,若有不当之处,请指正,谢谢!)1cos 2()t xy A T πλ=+2cos 2()t xy A T πλ=-222coscosy A x t Tππλ=1 6.0cos(0.028.0)2y x t π=-2 6.0cos(0.028.0)2y x t π=+1 6.0cos 2()0.5200t x y π=-2 6.0cos 2()0.5200t x y π=+。
大学物理第五章习题答案

大学物理第五章习题答案大学物理第五章习题答案第一题:题目:一个质量为m的物体以速度v水平运动,撞到一个质量为M的静止物体,两物体发生完全弹性碰撞,求碰撞后两物体的速度。
解答:根据动量守恒定律,碰撞前后动量的总和保持不变。
设碰撞后物体m的速度为v1,物体M的速度为V1,则有mv = mv1 + MV1。
由于碰撞是完全弹性碰撞,动能守恒定律也成立,即(mv^2)/2 = (mv1^2)/2 + (MV1^2)/2。
将第一个方程代入第二个方程,可得到关于v1和V1的方程组。
解方程组即可得到碰撞后两物体的速度。
第二题:题目:一个质量为m的物体以速度v1撞击一个质量为M的静止物体,碰撞后物体m的速度变为v2,求物体M的速度。
解答:同样利用动量守恒定律和动能守恒定律,设碰撞后物体m的速度为v2,物体M的速度为V2,则有mv1 = mv2 + MV2,以及(mv1^2)/2 = (mv2^2)/2 + (MV2^2)/2。
将第一个方程代入第二个方程,解方程组即可得到物体M的速度V2。
第三题:题目:一个质量为m的物体以速度v撞击一个质量为M的静止物体,碰撞后两物体粘在一起,求粘在一起后的速度。
解答:根据动量守恒定律,碰撞前后动量的总和保持不变。
设碰撞后两物体的速度为V,则有mv = (m+M)V。
解方程即可得到粘在一起后的速度V。
第四题:题目:一个质量为m的物体以速度v撞击一个质量为M的静止物体,碰撞后物体m的速度变为v2,求物体M的速度。
解答:同样利用动量守恒定律和动能守恒定律,设碰撞后物体m的速度为v2,物体M的速度为V,则有mv = mv2 + MV,以及(mv^2)/2 = (mv2^2)/2 +(MV^2)/2。
将第一个方程代入第二个方程,解方程组即可得到物体M的速度V。
第五题:题目:一个质量为m的物体以速度v撞击一个质量为M的静止物体,碰撞后物体m的速度变为v2,求碰撞后两物体的动能变化。
解答:碰撞前物体m的动能为(mv^2)/2,碰撞后物体m的动能为(mv2^2)/2,两者之差即为动能变化。
大学物理习题册第五章习题详解ppt课件
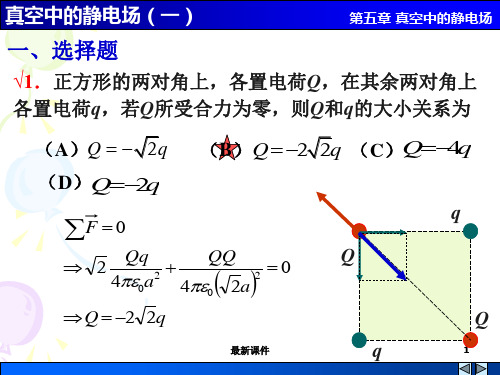
球心处于O点.△AOP是边长为a的等边三角形.为了
使P点处场强方向垂直于OP,则l和Q的数量之间应满
足____l__=_Q__/a____关系,且l与Q为___异____号电荷。
由图示几何关系有, EQElsin30
Aλ
Q 1 l 40a2 2 20a
a
a
OQ a
P
ቤተ መጻሕፍቲ ባይዱQal
最新课件
10
真空中的静电场(一)
面上,在此气球被吹大的过程中,被气球表面掠过的
点(该点与球中心距离为r),其电场强度的大小将
由
变为
.
SEd SE4r2q 0 E4rq 20
r q0
最新课件
14
真空中的静电场(一)
第五章 真空中的静电场
7.已知均匀带正电圆盘的静电场的电力线分布如图所 示.由这电力线分布图可断定圆盘边缘处一点P的电势
半径为R,则b点处的电势 =___________.
由电势的叠加原理有,
i i4 0 q 1 2 R 4 q 02 2 R 4 0 q 3 2 R q 2
2q1q3q2
80R
q1
O
q3
最新课件
b
16
真空中的静电场(一)
第五章 真空中的静电场
9. 一半径为R的均匀带电圆盘,电荷面密度为s,设无 穷远处为电势零点,则圆盘中心O点的电势=__.
sR/(20)
dr dqs2πrdr
x2 r2
ro
R
x
Px
P
1
4π0
R 0
s2πrdr
x r 2 2 最新课件
s
20
x2R2 x
17
真空中的静电场(一)
大学物理课后习题(第五章)

第五章 静电场选择题5-1 关于电场强度定义式0q =FE ,下列说法中正确的是 ( B ) (A) 电场强度E 的大小与检验电荷的电荷量0q 成反比;(B) 对电场中某点,检验电荷所受的力F 与其电荷量0q 的比值不因0q 的改变而变化; (C) 检验电荷在电场中某点所受电场力F 的方向就是该处电场强度E 的方向; (D) 若电场中某点不放检验电荷,则0=F ,因而0=E .5-2 下述关于某点的电势正负的陈述,正确的是 ( C ) (A) 电势的正负决定于检验电荷的正负;(B) 电势的正负决定于外力对检验电荷所做的功的正负; (C) 在电场中,空间某点的电势的正负,决定于电势零点的选取;(D) 电势的正负决定于带电体所带电荷的正负,带正电的物体周围的电势一定是正的,带负电的物体的周围的电势一定为负.5-3 在正六边形的顶角上,相间放置电荷相等的正负点电荷,则中心处 ( C ) (A) 电势为零,电场强度不为零; (B) 电势不为零,电场强度为零; (C) 电势为零,电场强度也为零; (D) 电势不为零,电场强度也不为零.5-4 一电子逆着电场线进入匀强电场,在前进过程中,其动能 ( B ) (A) 先增大后减小; (B) 越来越大; (C) 越来越小; (D) 先减小后增大.5-5 处于静电场中的平面1S 和曲面2S 有共同的边界,则 ( B ) (A) 穿过平面1S 的电场强度通量比穿过曲面2S 的电场强度通量大; (B) 穿过平面1S 的电场强度通量与穿过曲面2S 的电场强度通量相等;(C) 穿过平面1S 的电场强度通量比穿过曲面2S 的电场强度通量小;(D) 若电场是匀强的,穿过平面1S 的电场强度通量与穿过曲面2S 的电场强度通量相等,否则不相等.5-6 下列叙述中,正确的是 ( D ) (A) 在匀强电场中,两点之间的电势差为零; (B) 电场强度等于零的地方,电势也为零; (C) 电场强度较大的地方,电势也较高; (D) 在电场强度为零的空间,电势处处相等.5-7 无限长均匀带电的直线的电荷线密度为λ.在距离该直线为r 处,电场强度的大小为 ( D )(A)204πr λε; (B) 04πr λε; (C) 202πr λε; (D) 02πrλε.5-8 若两块无限大均匀带电平行平板的电荷面密度分别为σ和σ-,则两平板之间的电场强度和两平板之外的电场强度大小分别为 ( A )(A)0σε, 0 ; (B) 0 2σε, 02σε; (C) 0σε , 0σε; (D) 02σε, 0 . 5-9 在电荷面密度分别为σ-和σ+的两块无限大均匀带电平行平板之间的电场中,在任一条电场线上的不同点 ( B )(A) 电场强度E 相同,电势U 相同; (B) 电场强度E 相同,电势U 不同; (C) 电场强度E 不同,电势U 相同; (D) 电场强度E 不同,电势U 不同.5-10 如图所示,负的点电荷q 的电场中有A 、B 两点.下面的说法正确的是 ( C ) (A) 点B 场强的大小比点A 的小, 点B 的电势比点A 的高; (B) 点B 场强的大小比点A 的小, 点B 的电势比点A 的低; (C) 点B 场强的大小比点A 的大, 点B 的电势比点A 的低; (D) 点B 场强的大小比点A 的大, 点B 的电势比点A 的高.5-11 半径为R 的球面上均匀分布电荷q ,球心处的电势为 ( C ) (A) 0; (B)04πq R ε-; (C) 04πq R ε; (D) 02πqRε.5-12 两块相互平行的无限大均匀带电平板,它们的电荷面密度分别为σ±,若平板之间距离为d ,则两平板之间的电势差为 ( B )(A)02d σε; (B) 0d σε; (C) 02d σε; (D) 04dσε. 5-13 一半径为R 的均匀带电圆环,所带电荷为q ,环心处的电场强度大小和电势分别为 ( D )(A) 204πq E R ε=, 04πqV Rε=; (B) 0E =, 0V =;(C) 204πq E R ε=, 0V =; (D) 0E =, 04πqV Rε=.5-14 关于真空平行板电容器,下面说法正确的是 ( C ) (A) 极板上的电荷增加一倍,其电容也增加一倍; (B) 极板之间的电压增加一倍,其电容也增加一倍; (C) 极板的面积增加一倍,其电容也增加一倍; (D) 极板之间的距离增加一倍,其电容也增加一倍.5-15 一真空平行板电容器的电容为0C ,充电至极板间电势差为0U 时和电源断开,保持极板上的电荷不变.若在其极板间充满相对电容率为r ε的电介质,则其电容C 和极板间电势差U 分别为 ( B )(A) r 0C C ε=, r 0ε=U U ; (B) r 0C C ε=, 0rε=U U ;(C) 0rC C ε=, 0rε=U U ; (D) 0rC C ε=, r 0ε=U U ;5-16 平行板电容器充电后仍与电源连接.若用绝缘手柄将两极板的间距拉大,则极板上电荷Q ,极板间的电场强度E 的大小和电场能量e W 的变化为 ( B )(A) Q 增大, E 增大, e W 增大; (B) Q 减小, E 减小, e W 减小;(C) Q 增大, E 减小, e W 增大; (D) Q 减小, E 增大, e W 增大.计算题5-17 电荷为61 2.010C q -=⨯和62 4.010C q -=⨯的两个点电荷,相距10cm ,求两点电荷连线上电场强度为零的点的位置.解 设场强为零的点到1q 的距离为x ,则12220004π4π()q q x d x εε-=-式中10cm d =.解方程,可得cm 4.14cm x ===5-18 如图所示,两个等量异号的点电荷q ±,相距为l .求两点电荷的连线上距离中点O 为x 的点P 的电场强度.若x l >>,这两个点电荷组成的系统可看成电偶极子,求此情况下,点P 处的电场强度表达式.解 以O P →为Ox 轴正向,q 在点P 的电场强度为1204π2q E l x ε=⎛⎫- ⎪⎝⎭q -在点P 的电场强度为2204π2q E l x ε-=⎛⎫+ ⎪⎝⎭点P 的电场强度为12222202002π4π4π224q q q xlE E E l l l x x x εεε-=+=+=⎛⎫⎛⎫⎛⎫-+- ⎪⎪⎪⎝⎭⎝⎭⎝⎭0E >,说明其方向沿O P →.若x l >>,则33002π2πql pE x xεε== 式中p ql =,为偶极子的电矩p 的大小;若写成矢量式,则为302πxε=p E .5-19 一半径为R ,圆心角为2π3的圆环上均匀分布电荷q -.求圆心处的电场强度E . 解 取坐标如图.圆环上单位长度电荷绝对值为322ππ3q qRR λ==.如图所示,在θ处取d d q R λθ=,其在环心O 处的电场强度d E 方向如图,大小为22000d d d d 4π4π4πq R E R R Rλθλθεεε=== 由于对称, 圆环上的电荷在环心O 处的电场强度沿Ox 方向的分量d 0x x E E ==⎰.在Oy 方向上0cos d d d cos 4πy E E Rλθθθε==圆环上的电荷在环心O 处的电场强度沿Oy 方向的分量为π3π220003cos d 4π4π8πy E R R R λθθεεε-===⎰圆环上的电荷在环心O 处的电场强度为2208πy E Rε==E j j 5-20 正电荷q 均匀地分布在长度为L 的细棒上.求证在棒的延长线上,距离棒中心为r 处的电场强度的大小为2201π4qE r L ε=-证 取坐标如图所示.在棒上x 处取微元d x ,其上的电荷为d d d qq x x Lλ==.d q 在棒的延长线上距中心r 处的点C 的电场强度沿Ox 轴正向,为20d d 4π()xE r x λε=-整个棒上的电荷在点C 的电场强度为22002222200d 114π()4π2241 4π4π4L L x E L L r x r r L q r L r L λλεελεε-⎛⎫⎪==- ⎪- ⎪-+⎝⎭==--⎰5-21 如图所示,一细线被弯成半径为R 的半圆形,其上部均匀分布有电荷q ,下部均匀分布电荷q -.求圆心O 处的电场强度E .解 半圆细线关于Ox 轴对称.取对称的大小相等的正负电荷微元,它们在圆心O 处的电场强度之和沿Oy 轴负向.由此可见,所有电荷在圆心O 处的电场强度,也一定沿Oy 轴负向.上半部分带正电荷,电荷线密度为2ππ2q qR R λ+==.在圆弧上取微元d d l R θ=,其上所带电量为d d d q l R λλθ==.d q 在圆心处产生的电场强度1d E 的大小为1200d d d 4π4πR E R Rλθλθεε== 1d E 沿Oy 方向的分量为10d d cos 4πy E Rλθθε=-式中θ为d q 到Oy 轴的角距离.对上面的四分之一圆弧积分,即得所有正电荷在圆心O 处的电场强度沿Oy 方向的分量为π21000cos 4π4πy E d R Rλλθθεε=-=-⎰ 同样的方法,可求得所有负电荷在圆心O 处的电场强度沿Oy 方向的分量为204πy E Rλε=-整个半圆环上的电荷在圆心O 处的电场强度为()1222002ππy y qE E R R λεε=+=-=-E j j j5-22 边长为a 的正方体的中心,放置一点电荷Q .求穿过正方体各个侧面的电场强度通量.若点电荷Q 放在正方体的顶点A 上,如图所示,则穿过侧面BCDE 的电场强度通量为多少?解 若点电荷放置在正方体的中心,则正方体表面包围的电荷为Q ,穿过表面的电场强度通量为e 0QΦε=穿过各侧面的电场强度通量相等,为e106QΦε=若点电荷放在正方体的顶点A 上,则可设想点电荷处于另一个大正方体的中心,这个大正方体是原来的小正方体的8倍.穿过这个大正方体表面的电场强度通量为e 0QΦε=,穿过大正方体一个侧面的电场强度通量为e6Φ.每个侧面都是由4个BCDF 这样的正方形对称地拼铺而成.因此, 穿过BCDF 的电场强度通量是穿过一个侧面的电场强度通量的14,为 e e e201462424QΦΦΦε=⨯==5-23 电场强度大小为1300V m -⋅的匀强电场中,有一半径为20.0cm 的圆周,电场强度与圆平面的夹角为o30.求穿过以该圆周为边界的曲面的电场强度通量e Φ.解 电场穿过以圆周为边界的任何曲面的电场强度通量都与穿过圆平面的电场强度通量相等.电场强度与圆平面的法线间的夹角为ooo(9030)60θ=-=,因此()2o e 21o cos πcos 60 300π2.010cos 60 V m 18.85 V mΦES E R θ-=⋅===⨯⋅=⋅E S5-24 相互平行的两条无限长直线,相距为a ,其上均匀带电,电荷线密度分别为λ和λ-.求距离两直线均为a 的点P 的电场强度.解 二带电直线在点P 的电场强度1E 和2E 如图所示.二者大小相等,为1202πE E aλε==.总电场强度E 是1E 和2E 的矢量和,方向如图,垂直于二直线且与二直线组成的平面平行;由几何关系可知,E 大小与1E 和2E 相同,亦为02πE a λε=5-25 如图所示,相互平行的两条无限长直线,相距为d ,其上均匀带电,电荷线密度分别为λ和λ-.求在两直线所决定的平面上的电场强度分布.解 取坐标如图所示.在两条带电直线所在的平面上, 两条带电直线的电场强度1E 和2E 的方向均沿Ox 轴.左边的均匀带电无限长直线在x 处的电场强度为()10 02πE x xλε=≠ 右边的均匀带电无限长直线在x 处的电场强度为()()20 2πE x d x d λε-=≠-两条带电直线决定的的平面上的电场强度为()()1200011 0,2π2π2πE E E x x d x x d x x d λλλεεε-⎛⎫=+=+=-≠≠ ⎪--⎝⎭5-26 如图所示,两块相互平行的无限大均匀带电平面上,电荷面密度分别为σ和2σ-.求图中三个区域的电场强度.解 两块电荷均匀分布的无限大平板的电场均为匀强场.如图所示,左边平板的电场方向如图上实箭头所指,大小为02σε,右边平板的电场方向如图上虚箭头所指,大小为0σε.如图所示,取Ox 轴与平面垂直,则三个区域的电场强度均沿Ox 轴.由叠加原理,各区域的场强为:Ⅰ区域100022E σσσεεε⎛⎫=+-=⎪⎝⎭ Ⅱ区域2000322E σσσεεε⎛⎫=+=⎪⎝⎭ Ⅲ区域300022E σσσεεε⎛⎫-=-+=⎪⎝⎭ 5-27 如图所示,两个电偶极矩大小均为p ql =的电偶极子在一条直线上,方向相反,且负电荷重合.求在它们的延长线上距离负电荷为r (r l >>)的点P 的电势.解 从左到右三个点电荷的电场在点P 的电势分别为()104πqV r l ε=+2024πq V r ε-=()304πqV r l ε=-点P 的电势为()()()12300022202 4π4π4π 2πV V V V q q qr l r r l ql r r l εεεε=++-=+++-=- 因为r l >>,所以可近似为233002π2πql pl V r r εε==5-28 如图所示,电荷为q ±的两个点电荷分别位于点D 和点O ,2DO R =.若将带电粒子0q 从DO 的中点A ,沿以点O 为圆心,R 为半径的圆弧ABC 移至点C ,求电场力对它所做的功.解 q +和q -的电场中,点A 的电势0A V =,点C 的电势为00114π36πC q qV R R Rεε--⎛⎫=+= ⎪⎝⎭ 将0q 从点A 经点B 沿圆弧移至点C ,电场力对它所做的功为()0006πA C q qA q V V Rε=-=5-29 一均匀带电的半圆环,半径为R ,所带电荷为Q ,求环心处的电势. 解 半圆环上的电荷元d q 的电场中,圆心O 处的电势为0d d 4πqV Rε=带电半圆环的电场中,圆心O 处的电势为00d d 4π4πLq QV V R Rεε===⎰⎰5-30 电荷q 均匀地分布在半径为R 的细圆环上.求细圆环轴线上,距中心为x 的点P 的电势.解 取坐标如图所示.在园环上取电荷元d q ,其电场在Ox 轴上x 处的点P 处的电势为0d d 4πq V r ε==整个园环上的电荷的电场在点P 处的电势为d V q ===⎰⎰圆环也可以用电势定义d P P L V ∞=⋅⎰E l 来求.在例5-4中,已经求得带电圆环轴线上距中心为x 处的场强为()322204πqx E x Rε=+若选积分路径为从点P 沿轴线延伸到∞的直线,则d d x =l i ,于是()32220d d 4πqx x x Rε⋅=+E l点P 处的电势为()322021d d 4πP P x Lqx xV P xRε∞∞=⋅==+⎰⎰E l点P 是任意的,因此V =5-31 如图所示,平面曲线ABMCD 上均匀带电,电荷线密度为λ.BMC 是半径为R 的半圆弧,AB 、CD 和圆心O 在同一条直线上,AB CD R ==.求圆心O 处的电场强度和电势.解 AB 和CD 上的电荷,在圆心O 处产生的电场强度,大小相等方向相反,相互抵消.因此圆心O 处总的电场强度与半圆弧BMC 上的电荷在此产生的电场强度相等,方向垂直AD 向下.如题5—19,可求得该电场强度的大小为02πE Rλε=.在AB 上距离A 为x 出取d x ,其上电荷为d d q x λ=.d q 的电场中,圆心O 处的电势为0d d 4π(2)xV R x λε=-.AB 上的电荷的电场中,圆心O 处的电势为1000d ln 24π(2)4πRxU R x λλεε==-⎰同样的方法可求得CD 上的电荷的电场中,圆心O 处的电势为20ln 24πV λε=半圆弧BMC 上电荷的电场中,圆心O 处的电势为 300π4π4R V R λλεε==圆心O 处的总电势为12300022ln 2ln 214π44πV V V V λλλεεε⎛⎫=++=⨯+=+ ⎪⎝⎭5-32 无限长直线均匀带电,电荷线密度为λ.求其电场中距离直线分别为a 和b 的两点之间的电势差.解 均匀带电线密度为λ的无限长直线周围的电场,沿以该直线为轴的柱坐标的径向,到带电直线的距离为r 的点上,电场强度的大小为02πE rλε=到带电直线的距离为a 和b 的两点之间的电势差为00d d d ln 2π2πb b bab aaabU E r r r aλλεε=⋅=⋅==⎰⎰⎰E l 5-33 在平行板电容器极板之间充填两种电容率分别为1ε和2ε的电介质,每一种电介质各占一半体积.若电介质如图(a)分布,两种电介质中的电场能量密度之比是多少?若电介质按图(b)分布,则两种电介质中电场能量密度之比又是多少?解 (a) 极板间的电势差相同,因此板间的电场强度相等,12E E =.由2e 12E ε=w ,可得两种介质中的电场的能量密度之比为e1e212::εε=w w(b) 电介质中的电场强度为E σε=,因此两种介质中的电场强度之比为121211::E E εε=.由2e 12E ε=w ,可得两种介质中的电场的能量密度之比为 22e1e21122211211::::E E εεεεεε===w w5-34 一个标有“10μF,450V ”的电容器,当充电到电势差400V U =时,它所储存的电场能为多少?若是平行板电容器,极板之间的距离为320010cm d .-=⨯,充填的电介质的相对电容率为r 520.ε=,则极板之间电场的能量密度为多大?解 电容器储存的电场能为262e 111010400J 0.8 J 22W CU -==⨯⨯⨯=极板之间的电场强度为UE d=,电场的能量密度为 22e r 0r 0212333511221400 52088510J m 92010J m 220010U E d ....εεεε----⎛⎫== ⎪⎝⎭⎛⎫=⨯⨯⨯⨯⋅=⨯⋅ ⎪⨯⎝⎭w。
大学物理第五章课后习题答案

第五章课后习题答案5.1 解:以振动平衡位置为坐标原点,竖直向下为正向,放手时开始计时。
设t 时刻砝码位置坐标为x ,由牛顿第二定律可知: 220)(dtx d mx x k mg =+-其中0x 为砝码处于平衡位置时弹簧的伸长量,所以有 0kx mg = 解出0x 代入上式,有:022=+x mk dtxd 其中 mk =ω可见砝码的运动为简谐振动简谐振动的角频率和频率分别为: s r a d x g mk /9.90===ω Hz 58.12==πων振动微分方程的解为)c o s (ϕω+=t A x由起始条件 t =0 时,,1.00m x x -=-= 0=v得: A =0.1m ,πϕ=振动方程为:)9.9cos(1.0π+=t x5.2 证明:取手撤去后系统静止时m 的位置为平衡位置,令此点为坐标原点,此时弹簧伸长为x ,则有: 0sinkx mg =θ (1)当物体沿斜面向下位移为x 时,则有: ma T mg =-1sin θ (2) βJ R T R T =-21 (3) )(02x x k T += (4)R a β= (5) 将(2)与(4)代入(3),并利用(5),可得: k x R R kx mgR a RJ mg --=+0sin )(θ利用(1)式可得 x RJ mR kR dtx d a +-==22所以物体作简谐振动因为 R J mR kR +=ω 所以振动周期为 ωπ2=T5.3 解: 因为 mk ππων212==所以 :1221m m =νν22121)(m m νν==2 Kg5.4 解:(1) 由振动方程)420cos(01.0ππ+=t x 可知:振幅A =0.01m ;圆频率 πω20=; 周期 s T 1.02==ωπ频率Hz 10=ν ;初相40πϕ=(2)把t =2s 分别代入可得:2005.0)420cos(01.0|2=+==ππt x t m2314.0)420sin(2.0|2-=+-===πππt dt dx v t m/s)420sin(4|22πππ+===t dtdv a t5.5 解: T =2s ,ππω==T2设振动方程为:)cos(10ϕπ+=t x则速度为:)s i n (10ϕππ+-=t v加速度为: )c o s (102ϕππ+-=t a根据t =0 时,x =5cm ,v < 0 的条件,得振动的初相为 3πϕ=,故振动方程为:)3cos(10ππ+=t x设在 1t 时刻振子位于cm x 6-=处,并向x 轴负方向运动,则有:53)3'c o s (-=+ππt 54)3's i n (=+ππt故有 s cm t v /1.25)3'sin(10-=+-=πππ22/2.59)3'cos(10s cm t a =+-=πππ设弹簧振子回到平衡位置的时刻为2t ,则有πππ2332=+t ,从上述位置回到平衡位置所需时间为: st t 8.0/)]3)53(arccos()323[(12=----=-ππππ5.6。
大学物理第五章习题答案

L
o
y
x
22
在锥体上 z 坐标处任取半径为 r高为 dz 的小柱体,则
L z 2 dm dv r dz ( R ) dz L 根据质心定义得
2
z
1 zC M
L
0
1 zdm M
L
L
0
L z 2 z ( R ) dz L
r
dz
L
R ML2 0 L L R 2 L 2 2 3 x [ zL dz 2 Lz dz z dz ] 2 0 0 0 ML R 2 L4 2 L4 L4 R 2 2 3 M L [ ] L L 2 ML 2 3 4 12 M 12 M 4
11
如果一个长度已知的不规则物体的重量超过一个弹簧秤的最大 量度,问怎样用这弹簧秤称出该物体的重量? F 上图,根据合力矩为零得
Gx Fl
N
下图,根据合力矩为零得
F l G(l x )
x
F
l
整理可得:
G F F
G
N
G
课后习题
12
5-3:静止的电动机皮带轮半径为 5 cm,接通电源后做匀变速 转动,30 s 后转速达到152 rad / s,求: 1)30 s 内电动机皮带轮转过的转数; 2)通电后 20 s 时皮带轮的角速度; 3)通电后 20 s 时皮带轮边缘上一点的速度、切向加速度和法 向加速度。 解:皮带轮的角加速度为 152 t 0 t t 5 (rad/s 2 )
8
来复线的作用是增加炮弹的射程和准确性。由于炮弹射出时 绕自身轴线高速转动,空气阻力产生的对质心的力矩使炮弹 围绕前进方向产生进动效应,弹头的轴线始终围绕着弹道切 线向前且做锥形运动,从而能克服空气阻气,保证弹头稳定 地向前飞行,避免大的偏离,提高射程与准确性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章 静电场
一、选择题
1. 关于电场线, 以下说法中正确的是
[ ] (A) 电场线一定是电荷在电场力作用下运动的轨迹
(B) 电场线上各点的电势相等
(C) 电场线上各点的电场强度相等
(D) 电场线上各点的切线方向一定是处于各点的点电荷在电场力作用下运动的加速度方向
2. 高斯定理(in )
01d i s S E S q ε⋅=⋅∑⎰⎰r r Ò, 说明静电场的性质是 [ ] (A) 电场线是闭合曲线 (B) 库仑力是保守力
(C) 静电场是有源场 (D) 静电场是保守场
3. 根据高斯定理(in )
01d i s S E S q ε⋅=⋅∑⎰⎰r r Ò,下列说法中正确的是 [ ] (A) 通过闭合曲面的电通量仅由面内电荷的代数和决定
(B) 通过闭合曲面的电通量为正时面内必无负电荷
(C) 闭合曲面上各点的场强仅由面内的电荷决定
(D) 闭合曲面上各点的场强为零时, 面内一定没有电荷
4. 高斯定理成立的条件是
[ ] (A) 均匀带电球面或均匀带电球体所产生的电场
(B) 无限大均匀带电平面产生的电场
(C) 高斯面的选取必须具有某些简单的对称性
(D) 任何静电场
5. 将点电荷Q 从无限远处移到相距为2l 的点电荷+和-q 的中点处, 则电势能的增加量为
[ ] (A) 0 (B) l q 0π4ε (C) l Qq 0π4ε (D) l
Qq 0π2ε 6. 下面关于某点电势正负的陈述中, 正确的是
[ ] (A) 电势的正负决定于试探电荷的正负
(B) 电势的正负决定于移动试探电荷时外力对试探电荷做功的正负
(C) 空间某点电势的正负是不确定的, 可正可负, 决定于电势零点的选取
(D) 电势的正负决定于带电体的正负
7. 由定义式⎰∞
⋅=R R l E U ρρd 可知
8. 静电场中某点电势的数值等于
[ ] (A) 试验电荷q 0置于该点时具有的电势能
(B) 单位试验电荷置于该点时具有的电势能
(C) 单位正电荷置于该点时具有的电势能
(D) 把单位正电荷从该点移到电势零点外力所做的功
9. 在电场中有a 、b 两点, 在下述情况中b 点电势较高的是
[ ] (A) 正电荷由a 移到b 时, 外力克服电场力做正功
(B) 正电荷由a 移到b 时, 电场力做正功
(C) 负电荷由a 移到b 时, 外力克服电场力做正功
(D) 负电荷由a 移到b 时, 电场力做负功
10. 已知一负电荷从图5-1-48所示的电场中M 点移到N 点.有人根据这个图得出下列几点结论,其中哪一点是正确的? [ ] (A) 电场强度E M < E N ; (B) 电势U M < U N ;
(C) 电势能W M < W N ; (D) 电场力的功A > 0. 11. 关于电场强度和电势的关系, 下列说法中正确的是 [ ] (A) 电势不变的空间, 电场强度一定为零 (B) 电势不变的空间, 电场强度不为零
(C) 电势为零处, 电场强度一定为零
(D) 电场强度为零处, 电势一定为零
12. 一点电荷在电场中某点所受的电场力为零, 则该点
[ ] (A) 场强一定为零, 电势一定为零
(B) 场强不一定为零, 电势一定为零
(C) 场强一定为零, 电势不一定为零
(D) 场强不一定为零, 电势不一定为零
13. 如图5-1-54所示, 在一条直线上的连续三点A 、B 、C 的电势关系为U A >U B >U C . 若将一负电荷放在中间点B 处, 则此电荷将
[ ] (A) 向A 点加速运动 (B) 向A 点匀速运动
(C) 向C 点加速运动 (D) 向C 点匀速运动
14. 关于电荷仅在电场力作用下运动的下列几种说法中, 错误的是
[ ] (A) 正电荷总是从高电势处向低电势处运动
(B) 正电荷总是从电势能高的地方向电势能低的地方运动
(C) 正电荷总是从电场强的地方向电场弱的地方运动
(D) 正电荷加速的地方总是与等势面垂直
15. 边长为a 的正方体中心放置一电荷Q , 则通过任一个侧面S 的电通量
⎰⎰⋅s S E ϖϖd 为 [ ] (A) 04εQ (B) 06εQ (C) 08εQ (D) 6
Q 16. 真空中一“无限大”均匀带负电荷的平面如图所示,其电场的场强分布图线应是(设场强方向向右为正、向左为负) [ ] 二、填空题 1. 半径为R 的均匀带电球面, 若其面电荷密度为σ, 则在球面外距离球面R 处的电场强度大小为 .
图5-1-54 B C x (D)
x (C)0
2εσx (B)x (A)
x 图5-1-48
2. 两个同心均匀带电球面,半径分别为a R 和b R (b a R R <) , 所带电荷量分别为a Q 和b Q ,设某点与球心相距r , 当b a R r R <<时, 该点的电场强度的大小为 .
3. 一长为L 、半径为R 的圆柱体,置于电场强度为E 的均匀电场中,圆柱体轴线与场强方向平行.则:(A) 穿过圆柱体左端面的E 通量为 ;
(B) 穿过圆柱体右端面的E 通量为 ; (C) 穿过圆柱体侧面的E 通量为 ;
(D) 穿过圆柱体整个表面的E 通量为 .
4. 真空中一半径为R 的均匀带电球面,总电荷量为Q (Q > 0).今在球面上挖去非常小块的面积S ∆(连同电荷),且假设不影响原来的电荷分布,则挖去S ∆后球心处电场强度的大小E = ,其方向为 .
5. 有一个球形的橡皮膜气球,电荷q 均匀地分布在球面上,在此气球被吹大的过程中, 被气球表面掠过的点(该点与球中心距离为r ),其电场强度的大小将由 变 为 .
第五章补充习题答案
一、选择
DCADA CDCAC ACACB D
二、填空
1.
4εσ 2. 20π41r
Q a ⋅ε 3. (1) 2πR E - (2) 2πR E (3) 0 (4) 0 O S R
图5-2-9
4. 402π16R S Q ε∆, 圆心O 点指向S ∆
5. 20π4r q ε, 0。
