2019届高考数学专题14外接球
2019届高考数学专题十四外接球精准培优专练理201811081151

培优点十四 外接球1.正棱柱,长方体的外接球球心是其中心例 1:已知各顶点都在同一球面上的正四棱柱的高为 4 ,体积为16,则这个球的表面积是 ()A .16πB . 20πC . 24πD .32π【答案】C 【解析】Va 2h 16, a 2 , 4R 2 a 2 a 2 h 2 4 4 16 24 , S 24π ,故选 C .2.补形法(补成长方体)PPPPO 2ccAbCCa bAAaB aBBbc C AaB bcC图 1 图 2 图 3 图 4例 2:若三棱锥的三个侧面两两垂直,且侧棱长均为 3 ,则其外接球的表面积是 .【答案】9π 【解析】 4R 23 3 3 9 , S 4πR 2 9π .3.依据垂直关系找球心 例 3:已知三棱锥 PABC 的四个顶点均在同一个球面上,底面△ABC 满足BA BC,π 6ABC,若该三棱锥体积的最大值为 3,则其外接球的体积为2()16 3A .8πB .16πC .πD . 32 3π【答案】D1 【解析】因为△ABC 是等腰直角三角形,所以外接球的半径是 r,设外接球的 12 32半径是R,球心O到该底面的距离d,如图,则11V S h 6h 3△,ABC361S△63,BD 3,由题设ABC21最大体积对应的高为SD h3,故R2d23,即233R R,解之得R2,2所以外接球的体积是4π332πR,故答案为D.33对点增分集训一、单选题1.棱长分别为2、3、5的长方体的外接球的表面积为()A.4πB.12πC.24πD.48π【答案】B2 222【解析】设长方体的外接球半径为R,由题意可知:2R235,则:R23,该长方体的外接球的表面积为S4πR24π312π.本题选择B选项.2.设三棱柱的侧棱垂直于底面,所有棱的长都为23,顶点都在一个球面上,则该球的表面积为()A.12πB.28πC.44πD.60π【答案】B【解析】设底面三角形的外接圆半径为r,由正弦定理可得:2r23sin60,则r2,2设外接球半径为R,结合三棱柱的特征可知外接球半径R23227,外接球的表面积S4πR228π.本题选择B选项.3.把边长为3的正方形ABCD沿对角线AC对折,使得平面ABC平面ADC,则三棱锥2D ABC的外接球的表面积为()A.32πB.27πC.18πD.9π【答案】C【解析】把边长为3的正方形ABCD沿对角线AC对折,使得平面ABC 平面ADC,则三棱锥D ABC的外接球直径为AC 32,外接球的表面积为4πR218π,故选C.4.某几何体是由两个同底面的三棱锥组成,其三视图如下图所示,则该几何体外接球的面积为()A.a2πB.2a2πC.3a2πD.4a2π【答案】C【解析】由题可知,该几何体是由同底面不同棱的两个三棱锥构成,其中底面是棱长为2a的正三角形,一个是三条侧棱两两垂直,且侧棱长为a的正三棱锥,另一个是棱长为2a的正四面体,如图所示:该几何体的外接球与棱长为푎的正方体的外接球相同,因此外接球的直径即为正方体的体对角线,所以222233R a a aa Ra,所以该几何体外接球面积22232S 4πR 4πa3aπ2,故选C.5.三棱锥A BCD的所有顶点都在球O的表面上,AB 平面BCD,BC BD 2,3AB 2CD 4 3 ,则球 O 的表面积为() A .16π B .32πC . 60πD . 64π【答案】D22 22 3122【解析】因为 BC BD 2 ,CD 2 3 ,所以CBDcos2 2 22,2πCBD,3因此三角形 BCD 外接圆半径为1 CD 2sin CBD2,设外接球半径为 R ,则2R2 =22 +4 12 16 ,S =4πR 264π ,故选D .AB26.如图 ABCD A B C D 是边长为 1的正方体, SABCD 是高为 1的正四棱锥,若点S ,1 1 1 1A ,B 1 ,C 1 ,D 1 在同一个球面上,则该球的表面积为()19 A . 16 π25 16 B .π49 16 C .π81 D . π16【答案】D【解析】如图所示,连结A C,B1D1,交点为M,连结SM,11易知球心O在直线SM上,设球的半径R OS x,在R t△OMB中,由勾股定理有:142222OMB MB O ,即:22 22 xx ,解得: 1129x ,则该球的表面积82SR4π 4ππ .本题选择 D 选项.29 81 8167.已知球 O 的半径为 R , A , B , C 三点在球 O 的球面上,球心 O 到平面 ABC 的距离为1 2R ,AB AC 2 , BAC 120,则球 O 的表面积为( )16 9 A . π 16 3 B . πC .649 π D . 64 3 π 【答案】D【解析】由余弦定理得: BC4 4 222cos1202 3 ,设三角 ABC 外接圆半径为 r ,由正弦定理可得: 2 3 sin1202r,则 r2,又 R 21 R2 4 ,解得: R 216 ,则球的表面积 4π 2 64 π SR.本题选择 D 选项.4338.已知正四棱锥 P ABCD (底面四边形 ABCD 是正方形,顶点푃在底面的射影是底面的中心) 的各顶点都在同一球面上,底面正方形的边长为 10 ,若该正四棱锥的体积为 50 3,则此球的 体积为( )A .18πB .8 6C .36πD .32 3π【答案】C 【解析】如图,设正方形 ABCD 的中点为 E ,正四棱锥 P ABCD 的外接球心为 O ,底面正方形的边长为10,EA5,正四棱锥的体积为5031250,V10PE,P ABCD335则 PE 5 ,OE 5 R ,在△AOE中由勾股定理可得:VR5 R5 R ,解得 R3 ,4 π336π 22球,故选 C .39.如图,在△ABC 中, AB BC 6 , ABC 90 ,点 D 为 AC 的中点,将△ABD 沿 BD折起到 △PBD 的位置,使 PC PD ,连接 PC ,得到三棱锥 P BCD .若该三棱锥的所有顶点都在同一球面上,则该球的表面积是( )A . 7πB .5πC .3πD . π【答案】A【解析】由题意得该三棱锥的面 PCD 是边长为 3 的正三角形,且 BD 平面 PCD ,设三棱锥 P BDC 外接球的球心为 O , △PCD 外接圆的圆心为O ,则OO 1 面 PCD ,∴四边形OO 1DB 为直角梯形,17由 BD 3 ,O D ,及OB OD ,得OB,∴外接球半径为1 1 2∴该球的表面积4π 2 4π 7 7π S R.故选 A .47 R,210.四面体 A BCD 中, ABCABDCBD 60 , AB3 ,CB DB2 ,则此四面体外接球的表面积为( ) 19 2 A . π 19 38π B .2417 17π C .17πD .6【答案】A 【解析】由题意,△BCD中,CB DB2,CBD60,可知△BCD是等边三角形,BF3,6∴△BCD 的外接圆半径 FE, r 2 3BE ,3 33∵ ABCABD 60,可得 AD AC7 ,可得 AF6 ,∴ AFFB ,∴ AFBCD ,∴四面体 A BCD 高为 AF6 .设外接球 R , O 为球心,OEm ,可得: r 2 m 2 R 2 ……①,2226πEFR ……②由①②解得:SR.故选 A .R 19 .四面体外接球的表面积:4π219 π 8211.将边长为 2的正 △ABC 沿着高 AD 折起,使 BDC 120 ,若折起后 A 、B 、C 、D 四点都在球 O 的表面上,则球 O 的表面积为( )A . 7 2 π13 B . 7πC . π213 D . π3【答案】B【解析】△BCD 中, BD1,CD1, BDC120 ,底面三角形的底面外接圆圆心为 M ,半径为 r ,由余弦定理得到 BC 3 ,再由正弦定理得到3 sin1202r r1,见图示:AD 是球的弦, DA 3 ,将底面的圆心 M 平行于 AD 竖直向上提起,提起到 AD 的高度的一3半,即为球心的位置 O ,∴OM ,在直角三角形OMD 中,应用勾股定理得到OD ,OD 2即为球的半径.37OD.该球的表面积为 4πOD 27π ;故选 B .∴球的半径14212.在三棱锥A BCD中,AB CD6,AC BD AD BC5,则该三棱锥的外接球的表面积为()7A .43 43π 24 B .43 43π 6 C .43π 2D . 43π【答案】D【解析】分别取 AB ,CD 的中点 E , F ,连接相应的线段CE , ED , EF , 由条件, ABCD4 , BCACAD BD5 ,可知, △ABC 与△ADB ,都是等腰三角形,AB 平面 ECD ,∴ AB EF ,同理CD EF ,∴ EF 是 AB 与CD 的公垂线,球心G 在 EF 上,推导出△AGB ≌△CGD ,可以证明G 为 EF 中点,DE 25 9 4 , DF3, EF 16 9 7 ,∴GF7 ,球半径 7 9 43 2 4 2故选 D .二、填空题13.棱长均为 6的直三棱柱的外接球的表面积是_________. 【答案】84π16 1 6 【解析】由正弦定理可知底面三角形的外接圆半径为r2 sin6023 22 3 ,2则外接球的半径R 32 391221 ,2则外接球的表面积为 S4πR 24π 21 84π .14.已知棱长都相等正四棱锥的侧面积为16 3 ,则该正四棱锥内切球的表面积为________.【答案】32 16 3π【解析】设正四棱锥的棱长为 a ,则 43216 3 a,解得 a 4 .4于是该正四棱锥内切球的大圆是如图△PMN的内切圆,8其中MN 4,PM PN 23.∴PE 22.设内切圆的半径为r,由△PFO △PEN,得FO PO,即r 22r,EN PN22322解得r 6231,2 ∴内切球的表面积为Sr2.4π4π6232163π15.已知三棱柱A BC A B C的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为1113,AB 2,AC 1,BAC 60,则此球的表面积等于______.【答案】8π【解析】∵三棱柱A BC A B C的侧棱垂直于底面,棱柱的体积为3,AB 2,AC1,1111BAC 60,21sin603,,AA AA1 212BC2AB2AC22AB ACcos60412,BC 3,BC设△ABC外接圆的半径为R,则=2R ,R 1,sin602∴外接球的半径为112,∴球的表面积等于4π28π.故答案为8π.16.在三棱锥A BCD中,AB AC,DB DC,AB DB 4,AB BD,则三棱锥A BCD外接球的体积的最小值为_____.82π【答案】3【解析】如图所示,三棱锥A BCD的外接圆即为长方体的外接圆,外接圆的直径为长方体的体对角线AD,9设 AB AC x ,那么 DB DC 4 x , AB BD ,所以 ADAB 2 DB 2 .由题意,体积的最小值即为AD 最小, 24AD xx ,所以当 x 2 时, AD 的最小值为 2 2 ,所以半径为 2 ,28 2π 故体积的最小值为3.10。
高考数学专题突破:外接球题型总结

高考数学专题突破:外接球模型模板一:即一、题型描述几何体的外接球问题:题目中涉及几何体外接球体,或者球内接几何体,再或者说成球面上有几个点围成几何体,这类题型称之为几何体的外接球问题。
二、模法讲解以下这幅图,大家应该都能看明白吧!一个底面半径为,高为的圆柱,求它的外接球半径。
那么问题来了?这个式子怎么来的。
那么这个式子有何妙用?1、如果我们对圆柱上下底面对应位置处,取相同数量的点,比如都取三个点,如图所示:我们可以得到(直)三棱柱,它的外接球其实就是这个圆柱的外接球,所以说直棱柱的外接球求半径符合这个模型。
在这里棱柱的高就是公式中h的,而棱柱底面外接圆的半径则是公式中的r(至于怎么求外接圆半径可以用正弦定理。
2、我们再继续进行,如果我把刚刚那个三棱柱上面的两点去掉,我将得到三棱锥,如图:这个三棱锥的特点是AA1⊥底面ABC,即有一根侧棱⊥底面的锥体,依然符合这个模型。
那条竖直棱AA1就是公式中的h,而底面ABC的外接圆半径是公式中的r。
3、题目还喜欢这么干:面PAD垂直面ABCD。
它非常符合圆柱外接球模型!我们知道,这里的r为PAD的外接圆半径,h为AB或者CD为的长。
接着看,当我对第二幅图中的三棱柱 ABC-A1B1C1只去掉C1这个点,会得到什么呢?没错!这就是刚刚那个四棱锥放倒了!它的特点是:底面A1B1AB⊥CAB侧面,出题的时候则不会这么仁慈,就会像上一幅图那样,有一个侧面⊥矩形底面的四棱锥!圆柱外接球模型——适用于:①圆柱-------r,h自带②直棱柱-------r:底面外接圆半径;h:直棱柱的高③一根侧棱⊥底面的锥体-------r:底面外接圆半径;h:垂直于底面的那条侧棱④一个侧面⊥矩形底面的四棱锥-------r:垂直底面的侧面的外接圆半径;h:垂直于那个侧面的底边长那么接下来第二步就是找到,求出,而又怎么求呢?用正弦定理。
可以说正弦定理求外接圆半径这种方法咱们基本上就在高一学的时候提及过,根本就没用过它!告诉你,几乎整个高考也就此处求外接球题型可以用它来求求那个了。
高考数学 核心考点 外接球与内切球的计算

A微专题 与球相关的外接与内切问题知识梳理1、若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体, 这个球是这个多面体的外接球,计算外接球的两大方法:构造法、球心定位法。
2、若一个多面体的各面都与内部的一个球相切,那么这个球叫做这个多面体的内切球。
3、球的性质:球心到截面的距离d 与球的半径R 及截面圆的半径r 的关系:222dr R +=题型归纳方法一 构造法(补形法)处理外接球问题事实:正方体或长方体的外接球的球心是其体对角线的中点. 类型一:三棱相互垂直型【例1】如图所示,设A ,B ,C ,D 为球O 上四点,AB ,AC ,AD 两两垂直,且AB =AC =3, 若AD =R(R 为球O 的半径),则球O 的表面积为( )A .πB .2πC .4πD .8π【解析】因为AB ,AC ,AD 两两垂直,所以以AB ,AC ,AD 为棱构建一个长方体,如图所示,则长方体的各顶点均在球面上,AB =AC =3,所以AE =6,AD =R ,DE =2R ,则有R 2+6=(2R)2,解得R =2,所以球的表面积S =4πR 2=8π.故选D 。
【点评】当一三棱锥的三侧棱a 、b 、c 两两垂直时,可将三棱锥补成一个长方体,将问题转化为长方体(正方体)来解,长方体的外接球即为该三棱锥的外接球,满足2222)2(c b a R ++=关系式。
变式1:如图所示,已知三棱锥A-BCD 的四个顶点A ,B ,C ,D 都在球O 的表面上,AC ⊥平面BCD , BC ⊥CD ,且AC =3,BC =2,CD =5,则球O 的表面积为( )A .12πB .7πC .9πD .8π【解析】由AC ⊥平面BCD ,BC ⊥CD 知三棱锥A-BCD 可以补成以AC ,BC ,CD 为三条棱的长方体,设球O 的半径为R ,则有(2R)2=AC 2+BC 2+CD 2=3+4+5=12,所以S 球=4πR 2=12π.故选A 。
高中数学空间几何体的外接球专题(附经典例题与解析)

高中数学空间几何体的外接球专题(附经典例题与解析)球的性质回顾:球心O和小圆O'的连线OO'垂直于圆O'所在平面。
外接球半径的求法是利用直角三角形的勾股定理,在Rt△OAO'中,OA^2=OO'^2+O'A^2.常见平面几何图形的外接圆半径(r)的求法:1.三角形:1) 等边三角形:内心、外心、重心、垂心、中心重合于一点。
外接圆半径通常结合重心的性质(2:1)进行求解:r=a*(2/3)^(1/2) (其中a为等边三角形的边长)。
2) 直角三角形:外接圆圆心位于斜边的中点处,r=斜边/2.3) 等腰三角形:外接圆圆心位于底边的高线(即中线)上。
r=a/(2sin(A/2)) (其中A为顶角)。
4) 非特殊三角形:可使用正弦定理求解,XXX)。
2.四边形:常见具有外接圆的四边形有正方形、矩形、等腰梯形。
其中正方形与长方形半径求解方法转化为直角三角形。
几何体的外接球球心与底面外心的连线垂直于底面,即球心落在过底面外心的垂线上。
练:2.半径为2的球的内接三棱锥P-ABC,PA=PB=PC=2,AB=AC=BC,则三棱锥的高为3.1.三棱柱ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱AA1垂直于底面ABC,且AA1=4,则此三棱柱外接球的表面积为8π。
本文介绍了三棱锥的外接球的求解方法,其中包括侧棱垂直底面的三棱锥、正三棱锥和侧面垂直于底面的三棱锥三种类型。
对于侧棱垂直底面的三棱锥,可以采用补形法或通过确定底面三角形的外心来求解外接球的半径。
补形法是指将该几何体转化为原三棱柱的外接球,从而求出外接球的半径。
而通过确定底面三角形的外心,则可以通过勾股定理求解外接球的半径。
对于正三棱锥,可以通过底面正三角形的边长来求解内切球的半径,然后再利用勾股定理求解外接球的半径。
对于侧面垂直于底面的三棱锥,则需要确定△ABC和△PAB的外心分别为O’和O’’,并通过勾股定理求解OO’的长度,从而求解外接球的半径。
高中数学空间几何体的外接球专题(附经典例题与解析)
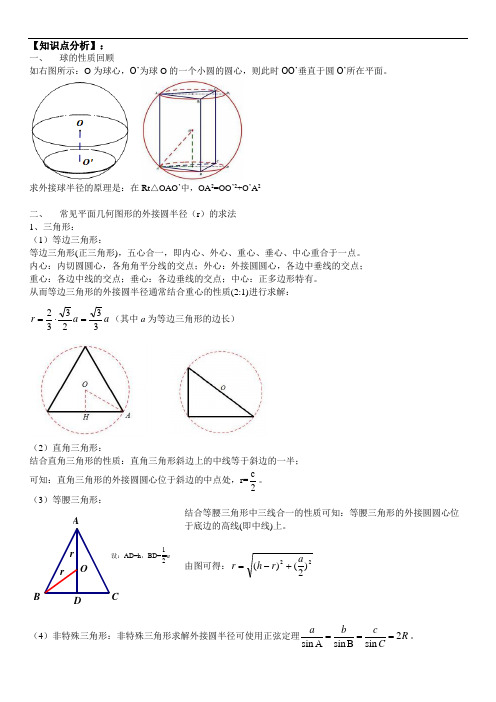
【知识点分析】: 一、 球的性质回顾如右图所示:O 为球心,O’为球O 的一个小圆的圆心,则此时OO’垂直于圆O’所在平面。
求外接球半径的原理是:在Rt △OAO ’中,OA 2=OO ’2+O ’A 2二、 常见平面几何图形的外接圆半径(r )的求法1、三角形:(1)等边三角形:等边三角形(正三角形),五心合一,即内心、外心、重心、垂心、中心重合于一点。
内心:内切圆圆心,各角角平分线的交点;外心:外接圆圆心,各边中垂线的交点;重心:各边中线的交点;垂心:各边垂线的交点;中心:正多边形特有。
从而等边三角形的外接圆半径通常结合重心的性质(2:1)进行求解:a a r 332332=⋅=(其中a 为等边三角形的边长)(2)直角三角形:结合直角三角形的性质:直角三角形斜边上的中线等于斜边的一半;可知:直角三角形的外接圆圆心位于斜边的中点处,r=2c 。
(3)等腰三角形: 结合等腰三角形中三线合一的性质可知:等腰三角形的外接圆圆心位于底边的高线(即中线)上。
由图可得:22)2()(a r h r +-=(4)非特殊三角形:非特殊三角形求解外接圆半径可使用正弦定理2sin sin sin a b c R C===A B 。
rrAD=h ,BD=12a B CO2、四边形常见具有外接圆的四边形有:正方形、矩形、等腰梯形,其中正方形与长方形半径求解方法转化为直角三角形,等腰梯形的外接圆圆心不在中学考察范围内。
外接圆圆心是在圆心到各个顶点距离相同的点;外接球球心则是球心到几何体各个顶点距离相同的点。
结论:几何体的外接球球心与底面外心的连线垂直于底面,(也即球心落在过底面外心的垂线上,)简单称之为:球心落在底面外心的正上方。
【相似题练习】2.半径为2的球的内接三棱锥P﹣ABC,PA=PB=PC=2,AB=AC=BC,则三棱锥的高为()A.3B.C.2D.3【知识点分析】:类型一:直(正)棱柱:上下两底面三角形的外心连线与侧棱平行与底面垂直,从而球心O 必位于上下两底面外心连线的中点处,即121'AA OO =,从而R 可求.【相似题练习】1.三棱柱ABC ﹣A 1B 1C 1中,底面ABC 是边长为2的正三角形,侧棱AA 1垂直于底面ABC ,且AA 1=4,则此三棱柱外接球的表面积为( )A .B .C .D .【知识点分析】:类型二:侧棱垂直底面的三棱锥,法一:补形法:该几何体可由正三棱柱沿平面PBC 切割得来,故可转化为原三棱柱的外接球;法二:先确定底面三角形ABC 的外心O’,从而球心位于O’的正上方,即OO’ ⊥平面ABC ,同时:OP=OA ,故,过O 作OM ⊥PA 于M ,此时M 必为PA 中点,从而四边形OMAO’为矩形,所以PA AM OO 21'==,在直角三角形OO’A 中有:222'OO r R +=.【相似题练习】2.已知在三棱锥P ﹣ABC 中,△ABC 是边长为2的正三角形,若PA ⊥底面ABC 且PA =2,则该三棱锥的外接球的表面积为( )A .32πB .28πC .24πD .20π3.在三棱锥P ﹣ABC 中,PA ⊥平面ABC ,PA =2,AB =4,AC =3,∠BAC =,则三棱锥P ﹣ABC 的外接球的半径R =( )A .B .C .D .【知识点分析】:类型三:正三棱锥:由底面正三角形边长可得r ,在直角三角形OO’A 中,222'OO r R +=,故只需确定OO’的长度即可,结合图形,OO’=PO’-OP=H-R ,代入222)(R H r R -+=即可求解.【相似题练习】3.正三棱锥P ﹣ABC 侧棱长为,侧棱与底面ABC 所成的角为60°,则该正三棱锥外接球半径为 .2.某几何体的三视图如图所示,其中网格纸上小正方形的边长为1,则该几何体的外接球的表面积为( )【知识点分析】:类型四:侧面垂直于底面的三棱锥:设△ABC和△PAB的外心分别为O’,O’’,则PM⊥AB,球心设为O,则OO’ ⊥平面ABC,OO’’⊥平面PAB,从而四边形OO’MO’’是矩形,可得:OO’=O’’M,在Rt△OO’C中用勾股定理求解.【讲透例题】1.在四面体A﹣BCD中,AB=5,BC=CD=3,DB=2,AC=4,∠ACD=60°,则该四面体的外接球的表面积为.解析:如图:取AB的中点O,在△ACD中,由余弦定理得:AD2=AC2+CD2﹣2×AC×CD cos60°=13,在△ABD中,∵AB2=BD2+AD2,∴∠ADB=90°,∴OA=OB=OD,在△ABC中,∵AB2=BC2+AC2,∴∠ACB=90°,∴OA=OB=OC,∴OA=OB=OC=OD,∴O为四面体ABCD的外接球的球心,其半径R=AB=,∴S球=4πR2=4π()2=25π.故答案为:25π.【相似题练习】4.在三棱锥P-ABC中,面PAB⊥面ABC,三角形ABC和三角形PAB均为等边三角形,且AB=3,求该几何体外接球半径.2.在边长为2的菱形ABCD中,,将菱形ABCD沿对角线AC折起,使得平面ABC⊥平面ACD,则所得三棱锥A﹣BCD的外接球表面积为()A.B.C.D.1.已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2,PC=,则三棱锥P﹣ABC外接球的表面积为.5、如图,在四棱锥P﹣ABCD中,底面ABCD为长方形,PA⊥底面ABCD,AD=AP=2,AB=2,E为棱PD中点.(1)求证:PD⊥平面ABE;(2)求四棱锥P﹣ABCD外接球的体积.1.如图,在正四棱锥P﹣AMDE,底面AMDE的边长为2,侧棱PA=,B,C分别为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.(1)求证:AB∥FG;(2)求正四棱锥P﹣AMDE的外接球的表面积.1.如图,四凌锥P﹣ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.(Ⅰ)求证:平面PAD⊥平面PCD;(Ⅱ)在AD=2,AB=4,求三棱锥P﹣ABD的体积;(Ⅲ)在条件(Ⅱ)下,求四棱锥P﹣ABCD外接球的表面积.7、如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是()A.B.C.19πD.22π课后作业:1.如图,一个正三棱柱的主视图是长为,宽为2的矩形,俯视图是边长为的正三角形,则它的外接球的表面积等于()A.16πB.12πC.8πD.4π2.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为()A.πB.3πC.πD.π3.某四棱锥的三视图如图所示,则该棱锥的外接球的表面积为()A.3πB.C.6πD.12π4.四棱锥P﹣ABCD中,ABCD为矩形,AD=2,AB=2,PA=PD,∠APD=,且平面PAD⊥平面ABCD.(1)证明:PA⊥PC;(2)求四棱锥P﹣ABCD的外接球的体积.参考答案与解析12.(5分)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为()A.64πB.48πC.36πD.32π【解答】解:由题意可知图形如图:⊙O1的面积为4π,可得O1A=2,则AO1=AB sin60°,,∴AB=BC=AC=OO1=2,外接球的半径为:R==4,球O的表面积:4×π×42=64π.故选:A.1.1.一个几何的三视图如图所示,它们都是腰长为1的等腰直角三角形,则该几何体的外接球的体积等于()A.B.C.πD.2π解析:由三视图可知:该几何体是一个如图所示的三棱锥,其中底面是一个两直角边都为1的直角三角形,PC⊥底面ABC,且PC=1.将此三棱锥恢复为棱长为1的正方体,可知该正方体的外接球的直径即为正方体的对角线,∴V外接球==.故选:B.1.半径为2的球的内接三棱锥P﹣ABC,PA=PB=PC=2,AB=AC=BC,则三棱锥的高为()A.3B.C.2D.3【解答】解:三棱锥P﹣ABC中,PA=PB=PC=2,AB=AC=BC,如图,过点p作PM⊥平面ABC的垂足为M,则球O的内接三棱锥P﹣ABC的球心O在PM所在直线上,∵球O的半径为2,∴OB=OP=2,∴由余弦定理得cos∠BPM==∴∠BPM=30°,∴在Rt△PMB中,∠PBM=60°,∴PM=PB sin∠PBM=3.故选:D.1.三棱柱ABC﹣A1B1C1中,底面ABC是边长为2的正三角形,侧棱AA1垂直于底面ABC,且AA1=4,则此三棱柱外接球的表面积为()A.B.C.D.【解答】解:∵正三棱柱ABC﹣A1B1C1的中,底面边长为2,高为4,由题意可得:三棱柱上下底面中心连线的中点,到三棱柱顶点的距离相等,说明中心就是外接球的球心,∴正三棱柱ABC﹣A1B1C1的外接球的球心为O,外接球的半径为r,表面积为:4πr2.球心到底面的距离为2,底面中心到底面三角形的顶点的距离为:=,所以球的半径为r==.外接球的表面积为:4πr2=π故选:D.2.已知在三棱锥P﹣ABC中,△ABC是边长为2的正三角形,若PA⊥底面ABC且PA=2,则该三棱锥的外接球的表面积为()A.32πB.28πC.24πD.20π【解答】解:由正弦定理可知,正△ABC的外接圆的直径为,∵PA⊥平面ABC,所以,该三棱锥的外接球的直径为,则.因此,该三棱锥的外接球的表面积为4πR2=20π.故选:D.3.在三棱锥P﹣ABC中,PA⊥平面ABC,PA=2,AB=4,AC=3,∠BAC=,则三棱锥P﹣ABC的外接球的半径R=()A.B.C.D.【解答】解:∵AC=3,AB=4,∠BAC=,∴由余弦定理可得BC=,∴△ABC外接圆的半径r=,设球心到平面ABC的距离为d,则d=PA=1.由勾股定理可得R =,故选:D .3.正三棱锥P ﹣ABC 侧棱长为,侧棱与底面ABC 所成的角为60°,则该正三棱锥外接球半径为 1 . 【解答】解:过点P 作PH ⊥平面ABC 于H ,则∵AH 是PA 在平面ABC 内的射影 ∴∠PAH 是直线PA 与底面ABC 所成的角,得∠PAH =60°, ∴Rt △PAH 中,AH =PA cos60°=,PH =PA sin60°=设三棱锥外接球的球心为O ,∵PA =PB =PC ,∴P 在平面ABC 内的射影H 是△ABC 的外心由此可得,外接球心O 必定在PH 上,连接OA 、OB 、OC ∵△POA 中,OP =OA , ∴∠OAP =∠OPA =30°,可得PA =OA =,∴三棱锥外接球的半径R =OA =1故答案为:1.2.某几何体的三视图如图所示,其中网格纸上小正方形的边长为1,则该几何体的外接球的表面积为( )A .16πB .12πC .9πD .8π【解答】解:根据几何体的三视图转换为直观图为:该几何体为底面为等腰直角三角形,高为2的三棱锥体. 如图所示:所以该三棱锥体的外接球的球心为O ,外接球的半径为OA =r ,则:,解得.故S =.故选:C .4.在三棱锥P-ABC 中,面PAB ⊥面ABC ,三角形ABC 和三角形PAB 均为等边三角形,且AB=3,求该几何体外接球半径.由题可得:333,2331'''=====AB r PM M O OO ,所以215'22=+=OO r R2.在边长为2的菱形ABCD中,,将菱形ABCD沿对角线AC折起,使得平面ABC⊥平面ACD,则所得三棱锥A﹣BCD的外接球表面积为()A.B.C.D.【解答】解:∵在边长为2的菱形ABCD中,;如图,由已知可得,△ABC与△ACD均为等边三角形,取AC中点G,连接BG,DG,则BG⊥AC,∴DG=⇒cos∠GDA=⇒∠GDA=⇒∠ADC=;∵二面角B﹣AC﹣D为直二面角,则BG⊥平面ACD,分别取△BCD与△ABD的外心E,F,过E,F分别作两面的垂线,相交于O,则O为三棱锥A﹣BCD的外接球的球心,由△BCA与△ACD均为等边三角形且边长为2,可得OE=OF=DG=.∴DE=DG﹣GE=.∴OD===.∴三棱锥A﹣BCD的外接球的表面积为4π×R2=4π×()2=.故选:C.1.已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2,PC=,则三棱锥P﹣ABC外接球的表面积为10π.【解答】解:因为O为△ABC外接圆的圆心,且平面PBC⊥平面ABC,过O作面ABC的垂线l,则垂线l一定在面PBC内,根据球的性质,球心一定在垂线l,∵球心O1一定在面PBC内,即球心O1也是△PBC外接圆的圆心,在△PBC中,由余弦定理得cos B=,⇒sin B=,由正弦定理得:,解得R=,∴三棱锥P﹣ABC外接球的表面积为s=4πR2=10π,故答案为:10π.1.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP=2,AB=2,E为棱PD 中点.(1)求证:PD⊥平面ABE;(2)求四棱锥P﹣ABCD外接球的体积.【解答】证明:(1)∵PA⊥底面ABCD,AB⊂底面ABCD,∴PA⊥AB,又∵底面ABCD为矩形,∴AB⊥AD,PA∩AD,又PA⊂平面PAD,AD⊂平面PAD,∴AB⊥平面PAD,又PD⊂平面PAD,∴AB⊥PD,AD=AP,E为PD中点,∴AE⊥PD,AE∩AB=A,AE⊂平面ABE,AB⊂平面ABE,∴PD⊥平面ABE.解:(II)四棱锥P﹣ABCD外接球球心是线段BD和线段PA的垂直平分线交点O,由已知BD===4,设C为BD中点,∴AM=2,OM=AP=1,∴OA===3,∴四棱锥P﹣ABCD外接球的体积是=36π.1.如图,在正四棱锥P﹣AMDE,底面AMDE的边长为2,侧棱PA=,B,C分别为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.(1)求证:AB∥FG;(2)求正四棱锥P﹣AMDE的外接球的表面积.【解答】(1)证明:在正方形AMDE中,因为B是AM的中点,所以AB∥DE.又因为AB⊄平面PDE,DE⊂平面PDE,所以AB∥平面PDE.因为AB⊂平面ABF,且平面ABF∩平面PDE=FG,所以AB∥FG.(2)解:连接AD,EM,相交于O′,易得AO′=,PO′=.由正四棱锥P﹣AMDE的对称性,得正四棱锥P﹣AMDE得外接球球心在线段PO′上,不妨设为O点.设OA=OP=R,则OO′=﹣R,∵AO2=AO′2+OO′2,∴R2=2+(﹣R)2,∴R=∴S=4πR2=,∴正四棱锥P﹣AMDE的外接球的表面积为.1.如图,四凌锥P﹣ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.(Ⅰ)求证:平面PAD⊥平面PCD;(Ⅱ)在AD=2,AB=4,求三棱锥P﹣ABD的体积;(Ⅲ)在条件(Ⅱ)下,求四棱锥P﹣ABCD外接球的表面积.【解答】解:(I)∵四边形ABCD是矩形,∴AD⊥CD,又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊂平面ABCD,∴CD⊥平面PAD,∵CD⊂平面PCD,∴平面PAD⊥平面PCD.(II)过P作PE⊥AD,垂足为E,∵△PAD是等腰直角三角形,∠APD=90°,∴PE==1.∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PE⊂平面PAD,PE⊥AD,∴PE⊥平面ABCD,∴V棱锥P﹣ABD=S△ABD•PE=••2•4•1=.(III)取BD中点M,过M作MN⊥平面ABCD,则球心O在直线MN上,连接AM,则AM==.∵PE⊥平面ABCD,∴MN∥PE.∵四棱锥P﹣ABCD内接于球,,∴OA==.∴S⊙O=4πOA2=20π.∴E为外心,∴OM=1.如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是()A.B.C.19πD.22π【解答】解:几何体的直观图如图:是长方体的一部分,上底面PCD的外接圆的半径:O1D==,几何体的外接球的半径为:OD==,该四棱锥的外接球的表面积是:4=π.故选:A.课后作业答案:1.如图,一个正三棱柱的主视图是长为,宽为2的矩形,俯视图是边长为的正三角形,则它的外接球的表面积等于()A.16πB.12πC.8πD.4π【解答】解:设正三棱柱的外接球的半径为R,则∵俯视图是边长为的正三角形∴底面三角形外接圆的半径为=1,∵正三棱柱的高为2∴正三棱柱的外接球的半径为=∴正三棱柱的外接球的表面积等于4π×=8π故选:C.2.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为()A.πB.3πC.πD.π【解答】解:由三视图可知:该四面体是正方体的一个内接正四面体.∴此四面体的外接球的直径为正方体的对角线长=.∴此四面体的外接球的表面积为表面积==3π.故选:B.3.某四棱锥的三视图如图所示,则该棱锥的外接球的表面积为()A.3πB.C.6πD.12π【解答】解:由题意可知,几何体的直观图如图:是四棱锥D1﹣ABCD,是棱长为1的正方体的一部分,外接球奇数正方体的外接球,取得直径是体对角线,r=,外接球的表面积为:4=3π.故选:A.4.四棱锥P﹣ABCD中,ABCD为矩形,AD=2,AB=2,PA=PD,∠APD=,且平面PAD⊥平面ABCD.(1)证明:PA⊥PC;(2)求四棱锥P﹣ABCD的外接球的体积.【解答】证明:(1)设AD的中点为E,则∵PA=PD,∴PE⊥AD,∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴PE⊥平面ABCD,∵PA在平面ABCD内的射影为AE,AE⊥CD,∴PA⊥CD,∵PA⊥PD,CD∩PD=D,∴PA⊥平面PCD∴PA⊥PC;解:(2)连接AC交BD于F,球心O在底面的射影必为点F,取截面PEF,PE=,EF=1.假设OF=x,则由OA2=x2+4=1+得x=0,∴球的半径为2,∴四棱锥P﹣ABCD的外接球的体积为=.。
2019-2020学年高三下学期高考数学之空间几何体的外接球专题课件

│课堂互动│
空间几何体的外接球问题
类型一:补形为正方体、长方体的类型(学生做,完成后直接对答案)
1.棱长为 2 2 的正四面体的顶点在同一球面上,则该球面的表面积为
A.12 B. 32 C.8 D. 4
3
【详解】 如图,将正四面体补成正方体 ,
设正方体的棱长为 a ,
则 a2 a2 (2 2)2,a 2 .
该外接球的半径 R 1 PB 1 PD2 AB2 AD2 1
2
2
2
∴该外接球的体积V
4 3
R
3
4 3
33
36 ,
11 9 16 3 ,
│学习目标│➯│新课引入│➯│课本预习│➯│预习评价│➯│知识导出│➯│课堂互动│➯│课堂小结│
│课堂互动│
空间几何体的外接球问题
类型一:补形为正方体、长方体的类型(学生做,完成后直接对答案)
学情分析: 空间几何体的外接球问题是历年常考的题型,是热点知识点, 本专题由浅入深,分类型突破,清晰的为学生解读了空间几何体的 外接球的几种常见的类型!
│学习目标│➯│新课引入│➯│课本预习│➯│预习评价│➯│知识导出│➯│课堂互动│➯│课堂小结│
│新课引入│
空间几何体的外接球问题
知识引入:
(1)球的性质(如图)___R__2__=___r_2__+__d__2____;
4.直三棱柱 ABC A1B1C1 的 6 个顶点在球O 的球面上.若 AB 3 ,
AC 4 . AB AC , AA1 12 ,则球O 的表面积为( )
A.169 B.169 C. 288 D. 676
4
【详解】
解:将直三棱柱补形为长方体 ABEC A1B1E1C1 , 所以体对角线 BC1 的长为球O的直径.
2019届高考数学专题十四-外接球总结-练习题及答案

【解析】由余弦定理得: BC 4 4 2 2 2cos120 2 3 ,
设三角 ABC 外接圆半径为 r ,由正弦定理可得: 2 3 2r ,则 r 2,
sin120
又 R2 1 R2 4 ,解得: R2 16 ,则球的表面积 S 4πR2 64 π .本题选择
4
3
3
D 选项.
42
12.在三棱锥 A BCD 中, AB CD 6 , AC BD AD BC 5 ,则该三棱
锥的外接球的表面积为( )
A. 43 43π
24
【答案】D
B. 43 43π
6
C. 43π
2
D. 43π
【解析】分别取 AB , CD 的中点 E , F ,连接相应的线段 CE , ED,
EF ,
△PCD 外接圆的圆心为 O1 ,则 OO1 面 PCD ,∴四边形 OO1DB 为直角梯 形,
由 BD
3 , O1D 1 ,及 OB OD ,得 OB
7 ,∴外接球半径为 R
2
7,
2
∴该球的表面积 S 4πR2 4π 7 7π .故选 A.
4
10.四面体 A BCD 中, ABC ABD CBD 60, AB 3 , CB DB 2 ,
则此四面体外接球的表面积为( )
A. 19 π
2
【答案】A
B. 19 38π
24
C.17π
D. 17 17π
6
【解析】
由题意,△BCD 中, CB DB 2 , CBD 60 ,可知△BCD 是等边三角 形, BF 3 ,
9
∴ △BCD 的外接圆半径 r 2 3 BE , FE 3 ,
将△ABD沿 BD折起到△PBD的位置,使 PC PD ,连接 PC ,得到三棱锥
玩转外接球、内切球、棱切球经典问题--高一数学微专题(十四大题型)(解析版)

玩转外接球、内切球、棱切球经典问题【题型归纳目录】题型一:正方体、长方体模型题型二:正四面体模型题型三:对棱相等模型题型四:直棱柱模型题型五:直棱锥模型题型六:正棱锥与侧棱相等模型题型七:侧棱为外接球直径模型题型八:共斜边拼接模型题型九:垂面模型题型十:最值模型题型十一:二面角模型题型十二:圆锥圆柱圆台模型题型十三:锥体内切球题型十四:棱切球【方法技巧与总结】技巧总结一:正方体、长方体外接球1.正方体的外接球的球心为其体对角线的中点,半径为体对角线长的一半.2.长方体的外接球的球心为其体对角线的中点,半径为体对角线长的一半.3.补成长方体(1)若三棱锥的三条侧棱两两互相垂直,则可将其放入某个长方体内,如图1所示.(2)若三棱锥的四个面均是直角三角形,则此时可构造长方体,如图2所示.(3)正四面体P -ABC 可以补形为正方体且正方体的棱长a =PA2,如图3所示.(4)若三棱锥的对棱两两相等,则可将其放入某个长方体内,如图4所示图1图2图3图4技巧总结二:正四面体外接球如图,设正四面体ABCD 的的棱长为a ,将其放入正方体中,则正方体的棱长为22a ,显然正四面体和正方体有相同的外接球.正方体外接球半径为R =22a ⋅32=64a ,即正四面体外接球半径为R =64a .技巧总结三:对棱相等的三棱锥外接球四面体ABCD中,AB=CD=m,AC=BD=n,AD=BC=t,这种四面体叫做对棱相等四面体,可以通过构造长方体来解决这类问题.如图,设长方体的长、宽、高分别为a,b,c,则b2+c2=m2a2+c2=n2a2+b2=t2,三式相加可得a2+b2+c2=m2+n2+t22,而显然四面体和长方体有相同的外接球,设外接球半径为R,则a2+b2+c2=4R2,所以R=m2+n2+t28.技巧总结四:直棱柱外接球如图1,图2,图3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)图1图2图3第一步:确定球心O的位置,O1是ΔABC的外心,则OO1⊥平面ABC;第二步:算出小圆O1的半径AO1=r,OO1=12AA1=12h(AA1=h也是圆柱的高);第三步:勾股定理:OA2=O1A2+O1O2⇒R2=h22+r2⇒R=r2+h2 2,解出R技巧总结五:直棱锥外接球如图,PA⊥平面ABC,求外接球半径.解题步骤:第一步:将ΔABC 画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:O 1为ΔABC 的外心,所以OO 1⊥平面ABC ,算出小圆O 1的半径O 1D =r (三角形的外接圆直径算法:利用正弦定理,得a sin A =b sin B =c sin C =2r ),OO 1=12PA ;第三步:利用勾股定理求三棱锥的外接球半径:①(2R )2=PA 2+(2r )2⇔2R =PA 2+(2r )2;②R 2=r 2+OO 12⇔R =r 2+OO 12.技巧总结六:正棱锥与侧棱相等模型1.正棱锥外接球半径:R =r 2+h 22h.2.侧棱相等模型:如图,P 的射影是ΔABC 的外心⇔三棱锥P -ABC 的三条侧棱相等⇔三棱锥P -ABC 的底面ΔABC 在圆锥的底上,顶点P 点也是圆锥的顶点.解题步骤:第一步:确定球心O 的位置,取ΔABC 的外心O1,则P ,O ,O 1三点共线;第二步:先算出小圆O1的半径AO1=r,再算出棱锥的高PO1=h(也是圆锥的高);第三步:勾股定理:OA2=O1A2+O1O2⇒R2=(h-R)2+r2,解出R=r2+h2 2h.技巧总结七:侧棱为外接球直径模型方法:找球心,然后作底面的垂线,构造直角三角形.技巧总结八:共斜边拼接模型如图,在四面体ABCD中,AB⊥AD,CB⊥CD,此四面体可以看成是由两个共斜边的直角三角形拼接而形成的,BD为公共的斜边,故以“共斜边拼接模型”命名之.设点O为公共斜边BD的中点,根据直角三角形斜边中线等于斜边的一半的结论可知,OA=OC=OB=OD,即点O到A,B,C,D四点的距离相等,故点O就是四面体ABCD外接球的球心,公共的斜边BD就是外接球的一条直径.技巧总结九:垂面模型如图1所示为四面体P-ABC,已知平面PAB⊥平面ABC,其外接球问题的步骤如下:(1)找出△PAB和△ABC的外接圆圆心,分别记为O1和O2.(2)分别过O1和O2作平面PAB和平面ABC的垂线,其交点为球心,记为O.(3)过O1作AB的垂线,垂足记为D,连接O2D,则O2D⊥AB.(4)在四棱锥A-DO1OO2中,AD垂直于平面DO1OO2,如图2所示,底面四边形DO1OO2的四个顶点共圆且OD为该圆的直径.图1图2技巧总结十:最值模型这类问题是综合性问题,方法较多,常见方法有:导数法,基本不等式法,观察法等技巧总结十一:二面角模型如图1所示为四面体P-ABC,已知二面角P-AB-C大小为α,其外接球问题的步骤如下:(1)找出△PAB和△ABC的外接圆圆心,分别记为O1和O2.(2)分别过O1和O2作平面PAB和平面ABC的垂线,其交点为球心,记为O.(3)过O1作AB的垂线,垂足记为D,连接O2D,则O2D⊥AB.(4)在四棱锥A-DO1OO2中,AD垂直于平面DO1OO2,如图2所示,底面四边形DO1OO2的四个顶点共圆且OD为该圆的直径.技巧总结十二:圆锥圆柱圆台模型1.球内接圆锥如图1,设圆锥的高为h,底面圆半径为r,球的半径为R.通常在△OCB中,由勾股定理建立方程来计算R.如图2,当PC>CB时,球心在圆锥内部;如图3,当PC<CB时,球心在圆锥外部.和本专题前面的内接正四棱锥问题情形相同,图2和图3两种情况建立的方程是一样的,故无需提前判断.由图2、图3可知,OC=h-R或R-h,故(h-R)2+r2=R2,所以R=h2+r2 2h.2.球内接圆柱如图,圆柱的底面圆半径为r,高为h,其外接球的半径为R,三者之间满足h2+r2=R2.3.球内接圆台R 2=r 22+r 22-r 21-h 22h 2,其中r 1,r 2,h 分别为圆台的上底面、下底面、高.技巧总结十三:锥体内切球方法:等体积法,即R =3V 体积S 表面积技巧总结十四:棱切球方法:找切点,找球心,构造直角三角形【典型例题】题型一:正方体、长方体模型1(2024·天津市第一中学滨海学校高一阶段练习)正方体外接球的体积是323π,那么外接球的直径为,正方体的表面积为.【答案】 4 32【解析】解:正方体外接球的体积是323π,设外接球的半径为R ,则43πR 3=323π,解得R =2,则外接球的直径2R =4,即正方体的体对角线的长为4,设正方体的棱长为a ,则a 2+a 2+a 2=4,解得a =433或a =-433(舍去);所以正方体的表面积S =6a 2=6×4332=32;故答案为:4;32.2(2024·辽宁·东港市第二中学高一阶段练习)在长方体ABCD -A 1B 1C 1D 1中,AB =2,BC =CC 1=1;点E ,F 分别为AB 、CD 中点;那么长方体ABCD -A 1B 1C 1D 1外接球表面积为;三棱锥的D 1-BEF外接球的体积为.【答案】 6π11116π【解析】长方体对角线长为l =22+12+12=6,所以长方体外接球半径为R =l 2=62,表面积为S =4π×62 2=6π;如图,G ,H ,I ,J 分别是A 1D 1,AD ,BC ,B 1C 1中点,则GHIJ 是矩形,平面GHIJ ⎳平面CDD 1C 1,E ,F 分别是AB ,CD 中点,则EF ⎳AD ,而AD ⊥平面CDD 1C 1,所以EF ⊥平面CDD 1C 1,所以EF ⊥平面GHIJ ,而EF ⊂平面D 1EF ,EF ⊂平面BEF ,所以平面D 1EF ⊥平面GHIJ ,平面BEF ⊥平面GHIJ ,由EF ⊥平面CDD 1C 1,D 1F ⊂平面CDD 1C 1,得EF ⊥D 1F ,而EF ⊥EB ,设平面GHIJ 与D 1E ,BF ,EF 的交点分别为N ,M ,Q ,则N ,M ,Q 分别是D 1E ,BF ,EF 的中点,所以N ,M 分别是△D 1EF 和△EFB 的外心,在平面GHIJ 内过N 作PN ⊥NQ ,过M 作PM ⊥QM 交PN 于点P ,由EF ⊥平面CDD 1C 1,得EF ⊥PN ,EF ⊥PM ,而NQ ∩EF =Q ,NQ ,EF ⊂平面D 1EF ,所以PN ⊥平面D 1EF ,同理PM ⊥平面BEF ,所以P 是三棱锥D 1-BEF 的外接球球心.四边形PMQN 是圆内接四边形,由长方体性质知∠NQH =∠D 1FD =π4,所以∠NQM =3π4,NQ =12D 1F =22,MQ =12,MN =12+14-2×22×12×cos 3π4=52,由PM ⊥平面BEF ,BM ⊂平面BEF ,得PM ⊥BM ,PQ =MNsin ∠NQM=52sin 3π4=102,PM =PQ 2-QM 2=32,BM =12BF =22,所以PB =PM 2+BM 2=112,所以三棱锥的D 1-BEF 外接球的体积为V =4π3×1123=11116π.故答案为:6π;11116π.3(2024·湖南·高一阶段练习)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,书中将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵;将底面为矩形,一侧棱垂直于底面的四棱锥称为阳马;将四个面均为直角三角形的四面体称为鳖臑.如图,在堑堵ABC -A 1B 1C 1中,AC ⊥BC ,AA 1=6,AB =8,则鳖臑A 1CBC 1外接球的表面积为,阳马A 1-BCC 1B 1体积的最大值为.【答案】 100π 64【解析】鳖臑A 1CBC 1外接球即为堑堵ABC -A 1B 1C 1的外接球,可将堑堵ABC -A 1B 1C 1补成长方体,则外接球直径为A 1B =62+82=10,∴其表面积为S =100π.∵64=AC 2+BC 2≥2AC ⋅BC ,当且仅当AC =BC =42时取等号,所以AC ⋅BC ≤32,∴阳马A 1-BCC 1B 1的体积为13BC ⋅BB 1⋅A 1C 1=13AC ⋅BC ⋅AA 1≤64.故答案为:100π,64题型二:正四面体模型1(江苏省镇江市2023-2024学年高一学期期末数学试题)一个正四面体的四个顶点都在一个表面积为24π的球面上,则该四面体的体积为.【答案】1623【解析】设正四面体的棱长为a ,外接球半径为R ,如图正四面体ABCD 中,E 为CD 的中点,M 为△BCD 的中心,连接AM ,则AM ⊥平面BCD ,O 为正四面体ABCD 外接球的球心,连接OB ,则BM =23BE =23×32a =33a ,所以AM =AB 2-BM 2=a 2-39a 2=63a ,因为正面体外接球的表面积为24π,所以4πR 2=24π,得R =6,所以AO =OB =6,所以OM =AM -OA =63a -6,在Rt △OBM 中,OM 2+BM 2=OB 2,则63a -6 2+33a 2=6 2,解得a =4或a =0(舍去),所以该四面体的体积为13S △BCD ⋅AM =13×34×42×63×4=1632,故答案为:16232(2024·天津南开·高二学业考试)表面积为43的正四面体外接球的体积为.【答案】6π【解析】设正四面体的边长为a ,△ABC 的外接圆圆心为D ,正四面体外接球的球心为O ,半径为R ,如图所示:因为4×12a2×32=43,解得a=2.因为2sin60°=2CD,所以CD=233,SD=22-2332=236.在RT△COD中,236-R2+233 2=R2解得R=62.正四面体外接球的体积V=43π×623=6π.故答案为:6π3(2024·辽宁鞍山·二模)已知正四面体ABCD的表面积为23,且A,B,C,D四点都在球O的球面上,则球O的体积为.【答案】3 2π【解析】正四面体各面都是全等的等边三角形,设正四面体的棱长为a,所以该正四面体的表面积为S=4×12×a×a2-a2 2=3a2,所以a=2,又正方体的面对角线可构成正四面体,若正四面体棱长为2,可得正方体的棱长为1,所以正方体的外接球即为该正四面体的外接球,所以外接球的直径为3,半径为3 2,所以球O的体积为32π.故答案为:3 2π题型三:对棱相等模型1如图,在三棱锥P-ABC中,PA=BC=3,PB=AC=2,PC=AB=5,则三棱锥P-ABC外接球的体积为()A.2πB.3πC.6πD.6π【解析】解:由题意,PA=BC=3,PB=AC=2,PC=AB=5,将三棱锥P-ABC放到长方体中,可得长方体的三条对角线分别为3,2,5,即a2+b2=3,a2+c2=2,c2+b2=5,解得:a=1,b=2,c=3.外接球的半径R=12×a2+b2+c2=62.∴三棱锥P-ABC外接球的体积V=43πR3=6π.故选:C.2(2024•永安市校级期中)在三棱锥P-ABC中,PA=BC=4,PB=AC=5,PC=AB=11,则三棱锥P-ABC的外接球的表面积为()A.26πB.12πC.8πD.24π【解析】解:∵三棱锥P-ABC中,PA=BC=4,PB=AC=5,PC=AB=11,∴构造长方体,使得面上的对角线长分别为4,5,11,则长方体的对角线长等于三棱锥P-ABC外接球的直径.设长方体的棱长分别为x,y,z,则x2+y2=16,y2+z2=25,x2+z2=11,∴x2+y2+z2=26,∴三棱锥P-ABC外接球的直径为26,∴三棱锥P-ABC外接球的表面积为4π2622=26π.故选:A.3(2024•五华区校级期中)如图,蹴鞠,又名“蹋鞠”、“蹴球”、“蹴圆”、“筑球”、“踢圆”等,“跳”有用脚蹴、蹋、踢的含义,“鞠”最早系皮革外包、内实米糠的球.因而“蹴鞠”就是指古人以脚蹴、蹋、踢皮球的活动,类似今日的足球.2006年5月20日,蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家级非物质文化遗产名录.若将“鞠”的表面视为光滑的球面,已知某“鞠”表面上的四个点A,B,C,D满足AB=CD =13cm,BD=AC=25cm,AD=BC=5cm,则该“鞠”的表面积为()A.20πcm2B.24πcm2C.27πcm2D.29πcm2【解析】解:因为鞠表面上的四个点A,B,C,D满足AB=CD=13cm,BD=AC=25cm,AD=BC=5cm,所以可以把A,B,C,D四点放到长方体的四个顶点上,则该长方体的体对角线就是鞠的直径,设该长方体的长、宽、高分别为x,y,z,鞠的半径为R,则(2R)2=x2+y2+z2,由题意得x2+y2=20,x2+z2=13,y2+z2=25,所以(2R)2=x2+y2+z2=29,即4R2=29,所以该鞠的表面积为4πR2=29πcm2,故选:D.题型四:直棱柱模型1(2024·辽宁·昌图县第一高级中学高一阶段练习)已知直三棱柱ABC-A1B1C1的6个顶点都在球O 的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的表面积为()A.36πB.144πC.169πD.256π【答案】C【解析】如图,取B1C1,BC的中点分别为O1,O2,根据题意,它们分别是△A1B1C1,△ABC的外心,因为B1O1⎳BO1,B1O1=BO2,所以四边形BO2O1B1是平行四边形,所以B1B⎳O1O2,B1B=O1O2,而B1B⊥底面ABC,所以O1O2⊥底面ABC,取O1O1的中点O,于是点O为该直三棱柱外接球的球心.连接OB,容易求得OO2=6,BO2=12AC=1232+42=52,则外接球半径OB=OO22+BO22=36+254,于是外接球的表面积为4π×36+25 4=169π.故选:C.2(2024·广西桂林·高二期末)直三棱柱ABC-A1B1C1的各个顶点都在同一个球面上,若AB=AC= AA1=2,∠BAC=120°则此球的表面积为()A.20πB.200πC.10πD.30π【答案】A【解析】由题意,棱柱底面三角形中BC=23,底面外接圆半径r=BC2sin∠BAC=2,又ABC-A1B1C1为直三棱柱且AA1=2,所以其外接球半径R=r2+AA122=5,故球体表面积为4πR2=20π.故选:A3(2024·河北·张北县第一中学高一阶段练习)已知正三棱柱ABC-A1B1C1所有棱长都为6,则此三棱柱外接球的表面积为()A.48π B.64πC.84πD.144π【答案】C【解析】如图,D 为棱BC 的中点,G 为正△ABC 的中心,O 为外接球的球心根据直棱柱外接球的性质可知OG ∥AA 1,OG =12AA 1=3,外接球半径R =OC ,∵正△ABC 的边长为6,则CG =23∴R 2=OC 2=OG 2+CG 2=21外接球的表面积S =4πR 2=84π故选:C .题型五:直棱锥模型1(2024·全国·高三专题练习)在四棱锥P -ABCD 中,已知底面ABCD 为矩形,PA ⊥底面ABCD ,PA =6,AB =1,AD =3,则四棱锥P -ABCD 的外接球O 的表面积是()A.80π B.160π C.60πD.40π【答案】D【解析】由题意底面矩形的外接圆半径r =121+3=1,则原四棱锥外接球半径R =r 2+h 22=10,S =4πR 2=40π故选:D2(2024·河南·濮阳一高高一期中)已知三棱锥D -ABC 中,AD ⊥底面ABC ,AD =2,BC =1,∠BAC =30°,则此几何体外接球的体积为()A.43π B.4πC.82π3D.8π【答案】C【解析】解:设底面△ABC 外接圆的半径为r ,则2r =BC sin ∠BAC=112=2,设外接球的半径为R ,则2R 2=2r 2+AD 2,即2R 2=22+22=8,所以R =2,所以外接球的体积V =4πR 33=4π2 33=82π3;故选:C3(2024·黑龙江·勃利县高级中学高一期中)据《九章算术》记载,“鳖臑”为四个面都是直角三角形的三棱锥.如图所示,现有一个“鳖臑”,PA⊥底面ABC,AB⊥BC,且PA=AB=BC=2,三棱锥外接球表面积为()A.10πB.12πC.14πD.16π【答案】B【解析】如图,将三棱锥补形为正方体,则外接球半径R=PC2=AP2+AB2+BC22=4+4+42=3.所以三棱锥外接球表面积S=4πR2=4π×3=12π.故选:B.题型六:正棱锥与侧棱相等模型1(2024·江苏南通·高三期末)已知正四棱锥P-ABCD的底面边长为22,侧棱PA与底面ABCD所成的角为45°,顶点P,A,B,C,D在球O的球面上,则球O的体积是()A.16πB.323π C.8π D.823π【答案】B【解析】在正四棱锥P-ABCD中,连接AC,BD,AC∩BD=O ,连PO ,如图,则有PO ⊥平面ABCD ,∠PAO 为侧棱PA 与底面ABCD 所成的角,即∠PAO =45°,于是得O P =O A =O B =O C =O D =22AB =2,因此,顶点P ,A ,B ,C ,D 在以O 为球心,2为半径的球面上,即点O 与O 重合,所以球O 的体积是V =43π×23=323π.故选:B2(2024·江苏·扬中市第二高级中学高二阶段练习)已知正三棱锥P -ABC 的四个顶点都在半径为R 的球面上,且AB =2,若三棱锥P -ABC 体积为32R ,则该球的表面积为()A.32π9B.64π9C.64π27D.16π9【答案】B【解析】如图,PG 为正三棱锥P -ABC 的高,则其外接球的球心O 在PG 上,且OA =OP ,延长AG 交BC 于D ,则AD =32AB =3,所以AG =23AD =233,因为三棱锥P -ABC 体积为32R ,所以13S △ABC ⋅PG =13×34×22⋅PG =32R ,得PG =32R ,在直角△AOG 中,AG 2+OG 2=OA 2,所以233 2+32R -R 2=R 2,解得R 2=169,所以该球的表面积为4πR 2=4π⋅169=64π9,故选:B3(2024·重庆市实验中学高一阶段练习)三棱锥P -ABC 体积为36,且PA =PB =PC ,AB =AC =1,BC =3,则三棱锥外接球的表面积为.【答案】254π【解析】三棱锥P -ABC 中,取BC 中点D ,连PD ,连AD 并延长至O 1,使DO 1=AD ,连接BO 1,CO 1,PO 1,如图:于是得四边形ABO 1C 为平行四边形,而AB =AC =1,▱ABO 1C 是菱形,在△ABC 中,BC =3,由余弦定理有cos ∠BAC =AB 2+AC 2-BC 22AB ⋅AC=-12,即∠BAC =120°,则∠ABO 1=60°,△ABO 1是正三角形,O 1A =O 1B =O 1C =1,于是得O 1是△ABC 外接圆圆心,因PA =PB =PC ,D 为BC 中点,则PD ⊥BC ,又AO 1⊥BC ,PD ∩AO 1=D ,PD ,AO 1⊂平面PAO 1,从而有BC ⊥平面PAO 1,PO 1⊥BC ,同理PO 1⊥AC ,而AC ∩BC =C ,从而得PO 1⊥平面ABC ,由球的截面小圆性质知,三棱锥P -ABC 外接球球心O 在直线PO 1上,又S △ABC =12AB ⋅AC sin120°=34,则V P -ABC =13PO 1⋅S △ABC =36,解得PO 1=2,设球O 的半径为R ,则OB =OP =R ,OO 1=|R -2|,Rt △OO 1B 中,O 1B 2+O 1O 2=OB 2,即1+(R -2)2=R 2,解得R =54,则球O 的表面积为S =4πR 2=25π4,所以三棱锥外接球的表面积为254π.故答案为:254π题型七:侧棱为外接球直径模型1(2024•本溪月考)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,ΔABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2;则棱锥V O -ABC :V O -SAB =()A.1:1B.1:2C.2:1D.1:3【解析】解:根据题意作出图形:设球心为O ,过ABC 三点的小圆的圆心为O 1,则OO 1⊥平面ABC ,延长CO 1交球于点D ,则SD ⊥平面ABC .∵CO 1=23×32=33,∴OO1=12-33 2=63,∴高SD=2OO1=263,∵ΔABC是边长为1的正三角形,∴SΔABC=34,∴V S-ABC=13×34×263=26.V O-ABC=13×34×63=212,∴V O-SAB=V S-ABC-V O-ABC=26-212=212,∴棱锥V O-ABC:V O-SAB=1:1.故选:A.2(2024•云南校级月考)已知三棱锥S-ABC的所有顶点都在球O的球面上,ΔABC是边长为2的正三角形,SC为球O的直径,且SC=4,则此棱锥的体积为()A.423B.433C.823D.42【解析】解:因为ΔABC是边长为2的正三角形,所以ΔABC外接圆的半径r=23 3,所以点O到平面ABC的距离d=R2-r2=26 3,SC为球O的直径,点S到平面ABC的距离为2d=463,此棱锥的体积为V=13SΔABC×2d=13×3×463=423,故选:A.3(2024•防城港模拟)体积为26的三棱锥S-ABC的所有顶点都在球O的球面上,已知ΔABC是边长为1的正三角形,SC为球O的直径,则球O的表面积为()A.πB.2πC.4πD.6π【解析】解:根据题意作出图形:设球心为O,球的半径r.过ABC三点的小圆的圆心为O1,则OO1⊥平面ABC,延长CO1交球于点D,则SD⊥平面ABC.∵CO1=23×32=33,∴OO1=r2-13,∴高SD=2OO1=2r2-13,∵ΔABC是边长为1的正三角形,∴SΔABC=34,∴V三棱锥S-ABC =13×34×2r2-13=26,∴r=1.则球O的表面积为4π故选:C.题型八:共斜边拼接模型1(2024·安徽·芜湖一中高二期中)已知三棱锥P-ABC中,PA=1,PB=3,PC=5,AB=22,CA=CB=2,则此三棱锥的外接球的表面积为()A.14π3B.28π3C.9πD.12π【答案】C【解析】因为PA=1,AB=22,PB=3,则PB2=PA2+AB2,所以PA⊥AB,又因为AB=22,BC=2,AC=2,则AB2=BC2+AC2,所以AC⊥BC,由PA=1,AC=2,PC=5,则PC2=PA2+AC2,所以PA⊥AC,又由PC=5,BC=2,PB=3,则PB2=PC2+BC2,所以PC⊥BC,可得PB为三棱锥P-ABC的外接球的直径,又由PC2=PA2+AC2+BC2=1+4+4=9,所以此三棱锥的外接球半径为R=4+4+12=32,所以球的表面积为S=4πR2=9π.故选:C.2(2024·江西赣州·高二期中)在三棱锥A -SBC 中,AB =10,∠ASC =∠BSC =π4,AC =AS ,BC =BS 若该三棱锥的体积为153,则三棱锥A -SBC 外球的体积为()A.πB.π3C.5πD.43π【答案】D【解析】如图所示:设SC 的中点为O ,AB 的中点为D ,连接OA 、OB 、OD ,因为∠ASC =∠BSC =π4,AC =AS ,BC =BS ,所以∠SAC =∠SBC =π2,则OA =OB =OC =OS ,所以O 为其外接球的球心,设球的半径为R ,因为OD ⊥AB ,AB =10,所以AD =DB =102,OD =R 2-102 2,所以S △AOB =12⋅AB ⋅OD =1210R 2-25,因为SC ⊥OA ,SC ⊥OB ,OA ∩OB =O ,所以SC ⊥平面AOB ,所以V A -SBC =13⋅S AOB ⋅SC =13⋅1210R 2-25⋅2R =153,解得R =3,所以其外接球的体积为V =43⋅π⋅R 3=43π,故选:D3(2024·全国·高三专题练习)三棱锥D-ABC中,AB=DC=3,AC=DB=2,AC⊥CD,AB⊥DB.则三棱锥D-ABC外接球的表面积是( ).A.9πB.13πC.36πD.52π【答案】B【解析】取AD的中点为O,连接OC,OB,因为AC⊥CD,AB⊥DB∴OC=OA=OD=OB即O为棱锥D-ABC外接球的球心,又AB=DC=3,AC=DB=2,∴AD=22+32=13,∴三棱锥D-ABC外接球的表面积为13π.故选:B.题型九:垂面模型1(2024·全国·高三专题练习)四棱锥P-ABCD的底面ABCD是矩形,侧面PAD⊥平面ABCD,∠APD=120°,AB=PA=PD=2,则该四棱锥P-ABCD外接球的体积为()A.32π3B.205π3C.86πD.36π【答案】B【解析】取AD的中点E,连接PE,△PAD中,∠APD=120°,PA=PD=2∴PE=1,AD=23,设ABCD的中心为O ,球心为O,则O B=12BD=2,设O到平面ABCD的距离为d,则R2=d2+22=22+(2-d)2,∴d=1,R=5,∴四棱锥P-ABCD的外接球的体积为43πR3=2053π.故选:B.2(2024·山西·祁县中学高三阶段练习(文))已知四棱锥P-ABCD的底面为矩形,平面PBC⊥平面ABCD,PE⊥BC于E,EC=1,AB=26,BC=3,PE=2,则四棱锥P-ABCD外接球的表面积为()A.36πB.39πC.42πD.66π【答案】A【解析】如图,设ΔPBC外接圆圆心为O1,半径为r,因为BC=3,EC=1,所以BE=2,又PE⊥BC,PE=2,所以∠PBE=45°,由正弦定理可得:PCsin∠PBC =2r,即2r=PCsin∠PBE=PE2+EC2sin45°=522=10,所以r=10 2,因为底面ABCD为矩形,则四棱锥P-ABCD外接球的球心到平面PBC的距离与到AD的距离相等,设四棱锥P-ABCD外接球的球心为O,半径为R,则易知:OO1=12AB=262,所以有R2=r2+OO12=1022+262 2=9,所以外接球表面积为S=4πR2=36π.故选:A3(2024·福建·厦门一中高三阶段练习(理))三棱锥P-ABC中,PA=PB=22,AB=4,BC=3,AC=5,若平面PAB⊥平面ABC,则三棱锥P-ABC外接球的表面积为.【答案】25π【解析】由AB=4,BC=3,AC=5,可知△ABC是角B为直角的直角三角形.即BC⊥AB.取AC中点F,则F是△ABC的外心.取AB中点E,连接PE,EF,则PE⊥AB.在Rt△PAE,PA=22,AE=2,所以PE=2.又平面PAB⊥平面ABC,∴PE⊥平面ABC.又PE⊂平面ABC所以PE⊥EF.由E,F分别为AB,AC的中点,则EF⎳BC.则EF=3 2,所以在直角△PEF中,PF=EF2+PE2=322+22=52又在直角三角形△ABC中,F是AC中点.所以AF=AC=BF=12AC=52所以AF=AC=BF=PF=5 2所以三棱锥P-ABC外接球的球心为点F,半径为5 2所以三棱锥P-ABC外接球的表面积为S=4π×522=25π故答案为:25π题型十:最值模型1(2024·贵州遵义·高三开学考试)已知三棱锥S-ABC的四个顶点均在体积为323π的球面上,AB=BC=1,AC=3,则三棱锥S-ABC的体积的最大值为()A.23+312B.3+14C.23+34D.3+112【答案】A【解析】若球体半径为R,则43πR3=323π,可得R=2,而底面ABC中AB=BC=1,AC=3,易得:cos B=AB2+BC2-AC22AB⋅BC=-12,又0<B<π,故B=120°,则底面外接圆半径为r=AC2sin B=1,要使三棱锥S-ABC的体积的最大,只需S在球面上离面ABC最远,而R2-r2=3,所以S在球面上离面ABC最远距离为3+2,故最大体积V S -ABC =13×(3+2)×12×1×1×sin120°=3+2312.故选:A2(2024·全国·三模)已知三棱锥S -ABC 的体积为2833,其外接球的体积为5003π,若AB =AC =4,∠BAC =120°,则线段SA 的长度的最小值为()A.8 B.52C.6D.42【答案】B【解析】如图,O 1是△ABC 所在截面圆圆心,O 是球心,OO 1⊥平面ABC ,SH ⊥平面ABC ,H 为垂足,连接HA ,HO 1,则SH ⊥AH ,SH ⊥O 1H ,则OO 1⎳SH ,AB =AC =4,∠BAC =120°,则BC =2AB sin60°=43,2O 1A =BC sin ∠BAC ,O 1A =432sin120°=4,S △ABC =12×4×4×sin120°=43,由V S -ABC =13S △ABC⋅SH 得SH =7,由球体积V =43πR 3得43πR 3=5003π,R =5,即OS =OA =5,OO 1=OA 2-O 1A 2=52-42=3,在直角梯形SOO 1H 中,O 1H =OO 12-(SH -OH )2=3,即H 在以O 1为圆心,3为半径的圆上,AH min =AO 1-O 1H =4-3=1,所以SA min =72+12=52.故选:B .3(2024·辽宁抚顺·一模)已知三棱柱ABC -A 1B 1C 1的顶点都在球O 的表面上,且AC =BC ,∠ACB =2π3,若三棱柱ABC -A 1B 1C 1的侧面积为12+63,则球O 的表面积的最小值是()A.8πB.12πC.24πD.32π【答案】C【解析】依题意可知三棱柱ABC -A 1B 1C 1是直三棱柱,设其高为h ,设AB =c ,AC =BC =a ,则a +a +c ×h =12+63,h =12+632a +c,h 24=14×12+632a +c 2=6+332a +c 2=63+3634a 2+c 2+4ac,由余弦定理得c2=a2+a2-2a2cos 2π3,即c2=3a2,c=3a,设三角形ABC的外接圆半径为r,则csin2π3=2r,r=c3,所以球O的半径R2=r2+h22=c23+h24=c23+63+363 4a2+c2+4ac=a2+63+3637+43a2=a2+9a2≥2a2⋅9a2=6,当且仅当a4=9,a2=3,a=3时等号成立.所以球O的表面积的最小值为4π×6=24π.故选:C题型十一:二面角模型1(2024·全国·高三专题练习)在三棱锥P-ABC中,△ABC为等腰直角三角形,AB=AC=2,△PAC为正三角形,且二面角P-AC-B的平面角为π6,则三棱锥P-ABC的外接球表面积为()A.529π B.49π C.283π D.329π【答案】C【解析】如图所示,△ABC为直角三角形,又AB=AC=2,所以BC=22,因为△PAC为正三角形,所以PA=PC=AC=2,连接PD,DE,D为AC的中点,E为BC中点,则PD⊥AC,DE⊥AC,所以∠PDE为二面角P-AC-B的平面角所以∠PDE=30°.因为△ABC为直角三角形,E为BC中点,所以点E为△ABC的外接圆的圆心,设G为△PAC的中心,则G为△PAC的外接圆圆心.过E作面ABC的垂线,过G作面PAC的垂线,设两垂线交于O.则O即为三棱锥P-ABC的外接球球心.设GO与DE交于点H,GD =13PD =33,DH =DG cos30°=33×23=23,所以HE =DE -DH =13,OE =HE ×tan60°=33,∴R 2=CO 2=CE 2+EO 2=2+13=73.所以S =4πR 2=283π,故选:C .2(2024·江苏·南京市金陵中学河西分校高三阶段练习)在三棱锥A -BCD 中,△BCD 是边长为3的正三角形,且AD =3,AB =23,二面角A -BD -C 的大小为π3,则此三棱锥外接球的体积为.【答案】1313π6【解析】根据题意,AD 2+BD 2=AB 2,所以AD ⊥BD ,取BD 中点为E ,AB 中点M ,则ME ⎳AD ,ME =12AD =32,ME ⊥DB ,△BCD 是正三角形,CE ⊥DB ,∠MEC 是二面角A -BD -C 的平面角,∠MEC =60°,∠ADB =90°,M 是△ADB 的外心,设N 是△DBC 的外心,设过M 与平面ABD 垂直的直线与过N 垂直于平面BCD 的直线交于点O ,则O 是三棱锥A -DBC 外接球球心,CN =BN =33×3=3,EN =32,又EM =32,由于平面MNO 与MEO 同时垂直于BD ,所以M 、E 、N 、O 共面,在四边形MENO 中,由∠MEC =60°,EN =32,ME =32,∠OME =∠ONE =900,可得:ON =12,外接球半径为r =OB =BN 2+ON 2=3+14=132,体积为V =43π×132 3=13136π.故答案为:13136π3(2024·全国·高三专题练习)四边形ABDC 是菱形,∠BAC =60°,AB =3,沿对角线BC 翻折后,二面角A -BD -C 的余弦值为-13,则三棱锥D -ABC 的外接球的体积为.【答案】6π【解析】如图,取BC 的中点为M ,连接AM ,DM ,则AM ⊥BC ,DM ⊥BC ,则二面角A -BC -D 的平面角为∠AMD ,AB =3,由四边形ABDC 是菱形,∠BAC =60°可知△ABC ,△DBC 为正三角形,设球心O 在平面ABC 内的射影为O 1,在平面BCD 内的射影为O 2,则O 1,O 2为△ABC ,△DBC 的中心,所以DM =32,DO 2=1,O 2M =12,由于二面角A -BD -C 的余弦值为-13,故设∠AMD =2θ,θ∈π4,π2 ,则cos2θ=2cos 2θ-1=-13,cos 2θ=13,故sin 2θ=23,则tan θ=2,∴OO 2=O 2M tan θ=22,球O 的半径R =DO 22+OO 22=62,所求外接球的体积为V =43π623=6π,题型十二:圆锥圆柱圆台模型1(2024·全国·高三专题练习)如图,半径为4的球O 中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与圆柱的表面积之差为()A.64πB.48πC.32πD.16π【答案】D 【解析】如图.设圆柱底面半径为r ,球的半径与圆柱底面夹角为∠OMN =α,则MN =r =R ⋅cos α=4cos α,ON =R ⋅sin α=4sin α,∴圆柱的高h =8sin α,∴圆柱的侧面积为S =2π⋅r ⋅h =32π⋅sin2α,当且仅当α=π4时,sin2α=1,圆柱的侧面积最大,为32π,球的表面积与圆柱的表面积之差为4πR 2-2πrh -2×π(22)2=64π-32π-16π=16π.故选:D .2(2024·云南昆明·高三开学考试)“云南十八怪”描述的是由云南独特的地理位置、民风民俗所产生的一些特有的现象或生活方式,是云南多元民族文化的写照.“云南十八怪”中有一怪“摘下草帽当锅盖”所指的锅盖是用秸秆或山茅草编织成的,因其形状酷似草帽而传为佳话.一种草帽锅盖呈圆锥形,其母线长为6dm ,侧面积为183πdm 2,若此圆锥的顶点和底面圆都在同一个球面上,则该球体的表面积等于dm 2.【答案】144π【解析】设圆锥的底面半径为r ,由πr ×6=183π,解得r =33πdm ,如图AB =33πdm ,设外接球的球心为O 半径为R ,由PB ⊥圆B 得AB 2+PB 2=AP 2,即27+PB 2=36,解得PB =3,由AB 2+R -PB 2=R 2得R =6,所以该球体的表面积等于4π×62=144πdm 2 .3(2024·全国·高三专题练习)已知圆台上底半径为1,下底半径为3,高为2,则此圆台的外接球的表面积为.【答案】40π【解析】如图所示,设外接球半径为r ,球心到上底的距离为h ,则球心到下底的距离为|h -2|则有r 2=1+h 2,r 2=9+(2-h )2,解得h =3,r =10.所以外接球的表面积为4πr 2=40π.故答案为:40π题型十三:锥体内切球1(2024·全国·高三专题练习)已知三棱锥A -BCD 中,AB =CD =2,AD =AC =BC =BD =3,则该三棱锥内切球的表面积为.【答案】7π8【解析】如图,在长方体AHDG -EBFC 中,设EC =c ,EB =b ,EA =a ,则a 2+b 2=4,c 2+b 2=9,a 2+c 2=9,所以a =b =2,c =7,故四面体ABCD 的体积V =abc -4×13×12abc =273,四面体ABCD 的表面积S =4S △ABC =4×12×2×32-12=82,设三棱锥内切球的半径为r ,由等体积可得273=13×82r ,解得r =742,所以三棱锥内切球的表面积为4π×7422=7π8.故答案为:7π8.2(2024·全国·高三专题练习)已知△ABC 中,AB =4,BC =3,AC =5,以AC 为轴旋转一周得到一个旋转体,则该旋转体的内切球的表面积为()A.4936π B.57649π C.57625π D.34525π【答案】B【解析】旋转体的轴截面如图所示,其中O 为内切球的球心,过O 作AB ,BC 的垂线,垂足分别为E ,F ,则OE =OF =r (r 为内切球的半径),故AO =r sin ∠BAC =53r ,CO =r sin ∠BCA =54r ,故5=AO +OC =53r +54r ,故5=AO +OC =53r +54r ,故r =127,故旋转体的内切球的表面积为4π×127 2=57649π,故选:B3(2024·甘肃酒泉·模拟预测)三棱锥A -BCD 中,AB ⊥平面BCD ,BC ⊥CD ,且AB =CD =4,BC =3,则该三棱锥内切球的表面积为()A.916π B.94π C.169π D.43π【答案】B 【解析】由AB⊥平面BCD,CD⊂平面BCD,得AB⊥CD.又BC⊥CD,且AB,BC⊂平面ABC,AB∩BC= B,所以CD⊥平面ABC,又AC⊂平面ABC,所以CD⊥AC.由AB=CD=4,BC=3,得AC=BD=5,所以三棱锥A-BCD的表面积S=2×12×3×4+2×12×4×5=32,三棱锥A-BCD的体积V=13×12×3×4×4=8.设三棱锥内切球球心为O,半径为r,由V=V O-ABC+V O-ABD+V O-ACD+V O-BCD=13Sr,得r=3VS=34,所以该三棱锥内切球的表面积S球=4πr2=4π×916=94π.故选:B.题型十四:棱切球1(2024·江西·进贤县第一中学高二期中)球与棱长为32的正四面体各条棱都相切,则该球的表面积为()A.6πB.18πC.9πD.10π【答案】C【解析】将正四面体补形为一个正方体如图所示(红色线条表示正四面体),则正四面体的棱为正方体的面对角线,因为球与正四面体的各条棱都相切,所以球与正方体的各个面都相切,所以所求的球为正方体的内切球,又因为正方体的棱长为322=3,所以球的半径R=32,所以球的表面积为:4π⋅322=9π,故选:C.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
又 R2 1 R2 4 ,解得: R2 16 ,则球的表面积 S 4πR2 64 π .本题选择 D 选项.
4
3
3
8.已知正四棱锥 P ABCD (底面四边形 ABCD 是正方形,顶点 在底面的射影是底面的中
心)的各顶点都在同一球面上,底面正方形的边长为 10 ,若该正四棱锥的体积为 50 ,则此 3
∵ ABC ABD 60 ,可得 AD AC 7 ,可得 AF 6 ,∴ AF FB ,∴ AF BCD ,
∴四面体 A BCD 高为 AF 6 .
设外接球 R , O 为球心, OE m,可得: r2 m2 R2 ……①,
6 π 2 EF 2 R2 ……②
由①②解得: R 19 .四面体外接球的表面积: S 4πR2 19 π .故选 A.
球的体积为( )
A.18π
B. 8 6
C. 36π
D. 32 3π
【答案】C
【解析】
如图,设正方形 ABCD 的中点为 E ,正四棱锥 P ABCD 的外接球心为 O ,
底面正方形的边长为 10 ,EA 5 ,
正四棱锥的体积为
50 3
,VP ABCD
1 3
10
2
PE
50
,
3
则 PE 5 ,OE 5 R ,
D. 64π
【解析】因为 BC BD 2, CD 2
22 22 3 ,所以 cosCBD
2
2
3 1 ,
222
2
CBD 2π , 3
因此三角形 BCD 外接圆半径为 1 CD 2 , 2 sinCBD
设外接球半径为
R
,则
R2
=22
+
AB 2
2
4
12
16
, S =4πR2
64π
在 △AOE
中由勾股定理可得: 5
R2
5
R2
,解得
R
3 ,V球
4 3
πR3
36π
,故选
C.
9.如图,在 △ABC 中, AB BC 6 ,ABC 90 ,点 D 为 AC 的中点,将 △ABD 沿 BD
折起到 △PBD 的位置,使 PC PD ,连接 PC ,得到三棱锥 P BCD .若该三棱锥的所有
则外接球的半径 R
32
2
2
3
9 12
21 ,
则外接球的表面积为 S 4πR2 4π 21 84π .
14.已知棱长都相等正四棱锥的侧面积为16 3 ,则该正四棱锥内切球的表面积为________.
【答案】 32 16 3 π
【解析】设正四棱锥的棱长为
a
,则
4
3 4
a2
16
A. a2π 【答案】C
B. 2a2π
C. 3a2π
D. 4a2π
【解析】由题可知,该几何体是由同底面不同棱的两个三棱锥构成,其中底面是棱长为 2a
的正三角形,一个是三条侧棱两两垂直,且侧棱长为 a 的正三棱锥,另一个是棱长为 2a 的 正四面体,如图所示: 该几何体的外接球与棱长为 的正方体的外接球相同,因此外接球的直径即为正方体的体对 角线,所以 2R a2 a2 a2 3a R 3 a ,所以该几何体外接球面积
易知球心 O 在直线 SM 上,设球的半径 R OS x ,在 Rt△OMB1 中,由勾股定理有:
OM
2
B1M 2
B1O2
,即: 2
x2
2 2
2
x2
,解得:
x
9 8
,则该球的表面积
S
4πR2
4π
9 2 8
81 π .本题选择 16
D
选项.
7.已知球 O 的半径为 R ,A ,B ,C 三点在球 O 的球面上,球心 O 到平面 ABC 的距离为 1 R , 2
设外接球半径为 R ,结合三棱柱的特征可知外接球半径 R2 3 2 22 7 ,
外接球的表面积 S 4πR2 28π .本题选择 B 选项.
3.把边长为 3 的正方形 ABCD 沿对角线 AC 对折,使得平面 ABC 平面 ADC ,则三棱锥
D ABC 的外接
球的表面积为( )
A. 32π
2
3
5 2 ,则:R2 3 ,
该长方体的外接球的表面积为 S 4πR2 4π 3 12π .本题选择 B 选项.
2.设三棱柱的侧棱垂直于底面,所有棱的长都为 2 3 ,顶点都在一个球面上,则该球的表
面积为( )
A.12π
B.28π
C.44π
D.60π
【答案】B
【解析】设底面三角形的外接圆半径为 r ,由正弦定理可得: 2r 2 3 ,则 r 2 , sin60
由 BD
3 , O1D 1 ,及 OB OD ,得 OB
7 ,∴外接球半径为 R 2
7, 2
∴该球的表面积 S 4πR2 4π 7 7π .故选 A. 44 - 让每个人平等地提升自我!
10.四面体 A BCD 中, ABC ABD CBD 60, AB 3 , CB DB 2 ,则此四面
3 ,解得 a 4 .
于是该正四棱锥内切球的大圆是如图 △PMN 的内切圆,
其中 MN 4 , PM PN 2 3 .∴ PE 2 2 .
设内切圆的半径为 r ,由 △PFO △PEN ,得 FO PO ,即 r 2 2 r ,
EN PN2 236 - 让每个人平等地提升自我!
【答案】 8π
【解析】∵三棱柱 ABC A1B1C1 的侧棱垂直于底面,棱柱的体积为 3 , AB 2 , AC 1 ,
BAC
60
,
1 2
2
1
sin
60
AA1
3 , AA1 2 ,
BC2 AB2 AC2 2AB AC cos 60 4 1 2 ,BC 3 ,
设 △ABC 外接圆的半径为 R ,则 BC =2R ,R 1, sin 60
A. 8π
B.16π
C. 16 π 3
D. 32 π 3
【答案】D
【解析】因为△ABC 是等腰直角三角形,所以外接球的半径是 r 1 12 3 ,设外接球
2
的半径是
R ,球心 O 到该底面的距离 d
,如图,则 S△ABC
16 2
3,
BD
3 ,由题设
V
1 3
S△ABC
h
1 6
6h
3
,
最大体积对应的高为 SD h 3,故 R2 d 2 3,即 R2 3 R2 3 ,解之得 R 2 ,
,故选
D.
6.如图 ABCD A1B1C1D1 是边长为 1 的正方体, S ABCD 是高为 1 的正四棱锥,若点 S ,
A1 , B1 , C1 , D1 在同一个球面上,则该球的表面积为( )
A. 9 π 16
【答案】D
B. 25 π 16
C. 49 π 16
D. 81 π 16
【解析】如图所示,连结 A1C1 , B1D1 ,交点为 M ,连结 SM ,
体外接球的表面积为( )
A. 19 π 2
【答案】A
B. 19 38π 24
C.17π
D. 17 17π 6
【解析】
由题意, △BCD 中, CB DB 2 , CBD 60 ,可知△BCD 是等边三角形, BF 3 ,
∴ △BCD 的外接圆半径 r 2 3 BE , FE 3 ,
3
3
顶点都在同一球面上,
则该球的表面积是( )
A. 7π
B. 5π
C. 3π
D. π
【答案】A
【解析】由题意得该三棱锥的面 PCD 是边长为 3 的正三角形,且 BD 平面 PCD ,
设三棱锥 P BDC 外接球的球心为 O ,
△PCD 外接圆的圆心为 O1 ,则 OO1 面 PCD ,∴四边形 OO1DB 为直角梯形, - 让每个人平等地提升自我!
培优点十四 外接球
1.正棱柱,长方体的外接球球心是其中心
例 1:已知各顶点都在同一球面上的正四棱柱的高为 4 ,体积为16 ,则这个球的表面积是
()
A.16π
B. 20π
Байду номын сангаас
C. 24π
D. 32π
【答案】C
【解析】V a2h 16 , a 2 , 4R2 a2 a2 h2 4 4 16 24 , S 24π ,故选 C.
所以外接球的体积是 4 πR3 32π ,故答案为 D.
3
3
一、单对选点题增分集训
1.棱长分别为 2、 3 、 5 的长方体的外接球的表面积为(
A. 4π 【答案】B
B.12π
C. 24π
) D. 48π1 - 让每个人平等地提升自我!
【解析】设长方体的外接球半径为 R ,由题意可知:2R2 22
得到 3 2r r 1, sin120
见图示:
AD 是球的弦, DA 3 ,将底面的圆心 M 平行于 AD 竖直向上提起,提起到 AD 的高度的
一半,即为球心的位置 O ,∴ OM 3 ,在直角三角形 OMD 中,应用勾股定理得到 OD , 2
OD 即为球的半径. ∴球的半径 OD 1 3 7 .该球的表面积为 4π OD2 7π ;故选 B.
DE 25 9 4 , DF 3, EF 16 9 7 ,
∴ GF 7 ,球半径 DG 7 9 43 ,∴外接球的表面积为 S 4π DG2 43π .
2
4
2
故选 D.
二、填空题
13.棱长均为 6 的直三棱柱的外接球的表面积是_________.
