静电场作业
第5章 静电场作业答案
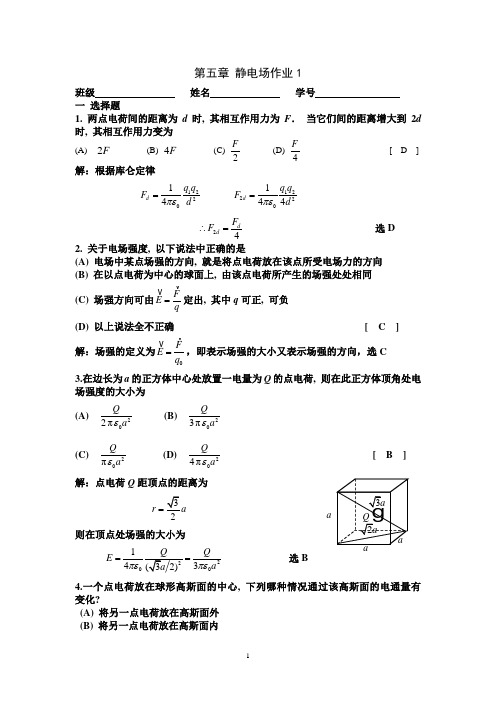
第五章 静电场作业1班级 姓名 学号 一 选择题1. 两点电荷间的距离为d 时, 其相互作用力为F ． 当它们间的距离增大到2d 时, 其相互作用力变为(A) F 2 (B) F 4 (C) 2F (D) 4F[ D ]解：根据库仑定律122014d q q F d πε=12220144dq q F d πε= 24dd F F ∴=选D 2. 关于电场强度, 以下说法中正确的是(A) 电场中某点场强的方向, 就是将点电荷放在该点所受电场力的方向 (B) 在以点电荷为中心的球面上, 由该点电荷所产生的场强处处相同(C) 场强方向可由FE q= 定出, 其中q 可正, 可负(D) 以上说法全不正确 [ C ]解：场强的定义为0FE q = ，即表示场强的大小又表示场强的方向，选C3.在边长为a 的正方体中心处放置一电量为Q 的点电荷, 则在此正方体顶角处电场强度的大小为 (A)202πQ a ε (B) 203πQaε (C)20πQ a ε (D) 204πQa ε [ B ] 解：点电荷Q 距顶点的距离为2r a =则在顶点处场强的大小为203QE aπε== 选B 4.一个点电荷放在球形高斯面的中心, 下列哪种情况通过该高斯面的电通量有变化?(A) 将另一点电荷放在高斯面外 (B) 将另一点电荷放在高斯面内a(C) 将中心处的点电荷在高斯面内移动(D) 缩小高斯面的半径 [ B ]解：根据高斯定理d iSq E S ε⋅=∑⎰，高斯面内的电荷变化，则通过该高斯面的电通量有变化。
选B二 填空题1.一长为L 、半径为R 的圆柱体，置于电场强度为E 的均匀电场中，圆柱体轴线与场强方向平行．则：(1) 穿过圆柱体左端面的E 通量为2R Επ-； (2) 穿过圆柱体右端面的E 通量为2R Επ；解：1）穿过左端面的电通量为21ΕS R ΕΦπ=⋅=-2）穿过右端面的电通量为21ΕS R ΕΦπ=⋅=2. 一个薄金属球壳，半径为1R ，带有电荷1q ，另一个与它同心的薄金属球壳，半径为2R )(12R R >，带有电荷2q 。
物理作业静电场基础练习2
物理作业内容：静电场基础练习2制作人：袁瑛 学生姓名： 班级：1.如图所示，水平放置的平行板电容器相距h ，上极板A 带正电，下极板B 带等量的负电。
现有质量为m ，带电量为+q 的小球从B 板下方H 处以初速度V 0竖直向上从B 板小孔进入板间电场，欲使小球刚好打到A 板，求A 、B 间电势差U AB 。
2.电量为c q 9102-⨯-=的电荷从电场中a 点运动到b 点时，电场力做功J 7105.1-⨯,从b 点移动到c 点时克服电场力做功J 7100.4-⨯。
求a 、c 两点间的电势差ac U 。
3.如图所示，Q A =3×10-8C ，Q B =－3×10-8C ，A ，B 两球相距6cm ，在水平方向的匀强电场作用下A 、B 保持静止且绝缘悬线竖直，求A ，B 连线中点的合场强。
（两带电小球可看作点电荷，229/109c m N k ⋅⨯=）4.如图，在O 处放一个与水平地面绝缘的物块，物块质量g m 10=、带电量C q 8105-⨯+=且电量始终保持不变、与水平面间的动摩擦因数4.0=μ。
空间存在水平向右的匀强电场，场强大小C N E /105=。
现给物块一个向右的初速度，大小为s m v /20=，求（1）物块运动的时间。
（2）物块最终停止时的位置。
(g 取2/10s m )5. 如图所示，一个电子以100ev 的初动能从A 点垂直电场线方向飞入匀强电场，在B 点离开电场时，其运动方向与电场线成1500角，则A 与B 两点间的电势差多大?10月19日物理作业答案：1、AB2、D3、B4、C5、D6、B7、C8、C9、BC 10、BC 11、ABD10月20日物理作业答案：1、 AB U =q h H mg mv 2)(220+-2、125V3、对于A ：20E AB BA A r Q kQ Q =，C N E /105.740⨯=∴，方向向左。
设向右为矢量正方向，在AB 中点有0E E E E B A -+=即C N E r kQ r kQ E AB BAB A /1025.5)2()2(5022⨯=-+=4、设向右为矢量正方向，对物块有ma F =-f 电①q F E =电② ，N f μ=③，0=-N mg ④由①②③④的2/5.3a s m -= （1） 由at v +=00得s t 57.0=（2） 由as v 2020=-得m s 57.0=，物体最终停止在O 点右侧0.57m 处。
静电场及其应用单元作业设计案例
静电场及其应用单元作业设计案例一、作业设计目标。
1. 让同学们对静电场的基本概念（如电荷、电场强度、电势等）有更深入的理解，就像让他们跟这些概念成为好朋友一样熟悉。
2. 能够熟练运用相关公式解决静电场中的一些简单问题，这就好比给他们一把钥匙，让他们可以轻松打开静电场问题的小盒子。
3. 培养同学们对静电场在实际生活中应用（像静电除尘、静电复印等）的观察力和思考能力，让他们知道静电场可不是只存在于书本里的枯燥知识，而是像个小魔法师，在生活中到处施展魔法呢。
二、作业内容。
（一）基础知识巩固。
1. 电荷的奥秘。
（1）选择题。
有两个完全相同的金属小球A和B，带电量分别为 +Q和 3Q。
当它们相距r时（r 远大于小球半径），它们之间的库仑力为F。
若把它们接触后再放回原处，则它们之间的库仑力变为（）A. F/3.B. F/2.C. F.D. 3F.这就像两个性格不同（一个带正电一个带负电）的小伙伴，先互相吸引（有库仑力），然后手拉手（接触中和电荷），再分开看看彼此的关系（新的库仑力）有没有变化呢。
（2）填空题。
元电荷的电量是_______。
这个就像是静电世界里的最小货币单位，所有的电荷电量都是它的整数倍哦。
2. 电场强度的探索。
（1）概念解释。
用自己的话描述一下电场强度这个概念。
就像是你要给一个外星人介绍什么是电场强度，要简单易懂，让它一听就明白电场强度是描述电场什么特性的一个家伙。
（2）计算题。
在一个电场中，有一点P，已知放在P点的电荷q = 3×10⁻⁶ C时，它受到的电场力F = 6×10⁻³ N。
求P点的电场强度E。
这就像是一场力量与电量的小竞赛，通过它们之间的关系算出电场强度这个“裁判”的数值。
（二）能力提升。
1. 电势的高低判断。
（1）给出一个电场的等势面分布图，图中有A、B、C三个点。
让同学们判断这三个点电势的高低顺序。
这就像是在一个高低起伏的静电小山坡上，找到不同位置的高度（电势）排序。
静电场练习题
1 q q dE cos 2 4 0 ( x 2 R 2 )3 2 4 0 r
可得该带电圆环在P点产生场强dE的大小为
由于dq为正，故dE方向沿X轴正方向。 将dq带入上式，可得:
注意: dq dE cos 斜边 2 4 0 R
1
则整个半球面在球心P点处产生的场强的大小为:
补充题
q 4π 0 r 2 E q r 4π 0 R 3
(r R)
(r<R)
.p
V E dl E d r E dr E dr
p
p
r
R
R
q(3R 2 r 2 ) V 8 0 R3
9
补充题 两个均匀带电的同心球面，内半径为 R1 ，外半径 为 R2 ， 电量分别为 q1 ， q2 。求内球和外球的电势。
方向沿X轴正方向。
7
均匀带电球面的半径为 R, 总电荷量为 q. 求电场中任 .p 一点p处的电势,并作出V-r图.
补充题
解
： 据高斯通量定理，得
q R
1 q 4 0 r 2 E 0
(r R)
.p
(r R)
Vp E dl E d r Edr
因此，该系统在P点产生总场强的大小为:
x 2 rdr E dE 2 2 3/ 2 4 ( x r ) 0 R
x 2 2 1/ 2 2 0 ( x R )
方向沿X轴正方向。
6
解法二 半径为R的圆孔可以看成是其上均匀地分布 着电荷面密度为+σ和-σ的两种电荷。
解:取坐标轴OX，将带电半球面分成许多宽度 极窄的半径不同的带电圆环，其上任意一个 dq dS 圆环上的带电量为: 为便于计算，可采用角量描述。 因为: dS 2 R sin Rd
第七章静止电荷的电场作业题目及解答
（3）金属球的电势
R Q Q Q 1 1 r U E d l dr dr ( ) 2 2 r R R 4 r 4 r 4 R R 0 r 0 0 r
e e e ee e
C F 7-64 电容 的电容器在800V的电 1 4 差下充电，然后切断电源，并将此电容器 的两个极板分别和原来不带电、电容为 的C 6 F 电容器两极板相连，求： 2 （1）每个电容器极板所带电荷量； （2）连接前后的静电场能
0
ε
q´
0
0
题号 结束
7-20 在半径为R，电荷体密度为ρ 的均 匀带电球内，挖去一个半径为 r 的小球，如 图所示。试求：O、O′、P、 P′各点的场 强。 O、O′、P、 P′在一条直线上。
P′.
P O . O . .′ r R
题号 结束
解：
E1 E2
带电荷-ρ 的小球的场强 带电荷ρ 的大球的场强
0 0
r1 . P
O O′ . . r R
0
ρ r2 E2 =
3 ε E1
0
EP = E2 =
r2 P.
3 ε
ρ
r2
0
r3 r12
O O′ . . r R
题号 结束
(4)P ´点的场强： 3 4 r 1 2 π r 1 r E1 4 π 1 = ρ ε 3 r 2 O O ′ P ′ 3 . . ρ . r E1 = r 2 r R 3 ε 1
UP =
4 π ε r> > re a = re cosq
0
1
q (r 1
Байду номын сангаас
2q + q ) r r2 r1 r a
大物静电场作业解答
一半径为R的无限长带电圆柱，其体电荷密度为 = 0 r ( r R )， 0为常数，求其圆柱体内的场强（r R），圆柱体外的场强为（r > R）。
R
解：取同轴高斯面r R，由高斯定理得
h
解：取同轴高斯面r > R，由高斯定理得
三.计算题:
真空中一高 h 等于 20 cm ,底面半径 R = 10cm 的圆锥体, 在其顶点与底面中心连线的中点上置一 q ＝ 10-5 C 的点电荷,求通过该圆锥体侧面的电场强度通量.( 0 = 8.85×10-12 N -1 • m -2 )
8
4.在静电场中，下列说法中哪一个是正确的？ [ D ]
5. 有四个等量点电荷在OXY平面上的四种不同组态,所有点电荷均与原点等距,设无穷远处电势为零,则原点O处电场强度和电势为零的组态是: [ D ]
-q
-q
+q
+q
O
-q
+q
-q
+q
O
+q
-q
+q
-q
O
+q
-q
-q
+q
O
则通过圆锥侧面的电场强度通量就等于对整个球面的通量减去通过圆锥底面所截球冠的通量 .
以为圆心、为 半径作球面。
r 由几何关系 h
2. 图示一厚度为d 的"无限大"均匀带电平面,电荷密度为,试求板内外的场强分布.并画出场强在x轴的投影值随坐标变化的图线,即Ex-x图线.(设原点在带电平板的中央平面上,ox轴垂直于平板)
,不是 y!
设在均匀电场中，场强E与半径为R的半球面的轴相平行，通过此半球面的电场强度通量为 [ ] 解：利用高斯定理，穿过圆平面的电力线必通过半球面，因此在圆平面上 所以通过此半球面的电通量为
第5章 真空中的静电场作业题
第５章 真空中的静电场作业题（注：带“*”号的适用多学时）一、选择题1. 图中所示为一沿 x 轴放置的“无限长”分段均匀带电直线，电荷线密度分别为+λ（x >0）和 -λ（x < 0），则 oxy 坐标平面上点（0，a ）处的场强E 的方向为（ ）( A )x 正方向 （B ） x 负方向（C ）y 正方向 （D ）y 负方向2.如图所示，一个带电量为q 的点电荷位于正立方体的中心上，则通过其中一侧面的电场强度通量等于：（ ）（A ）06εq (B)08εq (C) 024εq (D) 027εq 3．关于高斯定理0ε∑⎰⎰=⋅=Φi s e q s d E ，下列说法中正确的是（ ）（A ）如果高斯面内的电荷为零，则高斯面上的电场强度处处为零（B ）如果高斯面上的电场强度处处为零，则高斯面内电量的代数和为零（C ）若通过高斯面的电通量为零，则高斯面上的电场强度处处为零（D ）以上都正确4．关于电场和电势，下列说法中正确的是（ ）（A ）电场强度为0的点，电势也一定为0（B ）等势面上电场强度大小一定相等（C ）电势为0的点，则电场强度也一定为0（D ）电场强度的方向总是指向电势下降的方向。
5.一导体放在静电场中，当达到静电平衡时（ ）（A ）整个导体都是等势体、导体表面是等势面（B ）导体内部场强处处为零（C ）导体内部无电荷，电荷只能分布在导体表面上（D ）以上均正确6、均匀带电圆环一半带正电，一半带负电，则中心处的场强和电势分别有（ ）(A) 场强为零，电势为零。
（B ）场强为零，电势不为零。
(C) 场强不为零，电势不为零。
（D ）场强不为零，电势为零。
*7.关于平板电容器的电容，正确的是（）（A）电容的大小与极板上带的电量成正比（B）电容的大小与极板上所加的电压成反比（C）电容的大小与极板的面积成反比（D）电容的大小与极板之间的距离成反比二填空题*1.如图所示均匀带电量为Q的细棒，长为L，求其延长线上距杆端点为L的位置A的场强__________，若在A处放一点电荷q,则电荷收到的电场力为_____________*2.一半径为R的均匀带电圆环，带电量为q，圆心处的电场强度大小为______________ ，方向为____________，电势为____________。
物理作业静电场基础练习1
物理作业内容：静电场基础练习1制作人：袁瑛 学生姓名： 班级：每小题给出的四个选项中，有的只有一个选项正确，有的有多个选项正确1.关于电场强度的表达式①q F E =、②2r kq E =、③d U E =，以下叙述正确的是 A. ①式中的q 代表试探电荷的电量 B. ②式中的q 代表场源电荷的电量C. ①、②式中的q 都代表试探电荷的电量D. ③式只适用于匀强电场, 并且式中的d 代表电场中两点间的距离 2.以下表述正确的是A. 电荷在电场中某点的电势能等于把此电荷从无穷远移到该点过程中电场力做的功B. 电势、电势差、电势能都只由电场性质决定C. 电势为零的地方场强也为零D.场强为零的地方电势可以不为零3.图示为点电荷a 、b 所形成电场的电场线，下列说法中正确的是 A ．a 、b 为异种电荷，a 带电量大于b 的带电量 B ．a 、b 为异种电荷，a 带电量小于b 的带电量 C ．a 、b 为同种电荷，a 带电量大于b 的带电量 D ．a 、b 为同种电荷，a 带电量小于b 的带电量4.已知四个点电荷q 、q 、q -、q 分别分布于边长为a 的正方形的四个顶点A 、B 、C 、D 处，则正方形中心处的场强大小为A.223a kqB. 225a kqC. 24a kqD. 05.如图，在场强为E 匀强电场中有一个质量为m 的带正电小球A 悬挂在绝缘细线上，当小球静止时，细线与竖直方向成300角，己知此电场方向恰使小球受到的电场力最小，则小球所带的电量应为A 、E mgB 、E mg 3C 、E mg 2D 、E mg26.如图所示，在竖直放置的光滑半圆弧绝缘细管的圆心O 处放一点电荷，将质量为m ，带电量为q 的小球从圆弧管的水平直径端点C 由静止释放，小球沿细管滑到最低点B 时，对管壁恰好无压力。
则放于圆心处的点电荷在C 点产生的场强大小为A 、2/mg qB 、3/mg qC 、q mg /4D 、q mg /5BC7.在如图所示的电场线中a 、b 两点的电势分别为V a 50=ϕ、V b 20=ϕ，则a 、b 连线的中点c 的电势应该 A. V c35>ϕ B. V c 35=ϕ C. V c35<ϕ D. 无法判断的高低8.如图所示，实线为电场线，虚线表示等势面，相邻两个等势面之间的电势差相等，有一个运动的正电荷在等势面3l上某点的动能为20J,运动至等势面1l 上的某一点时动能变为0，若取2l 为零势面，则此电荷的电势能为4J 时，其动能为A.16JB.10JC.6JD.4J9. 如图所示，两个等量异种点电荷连线的垂直平分线上有a 、b 、c 三点，下列说法正确的是 A ．a 点电势比b 点高 B ．a 、b 、c 三点电势相等C ．a 、b 两点的场强方向相同，b 点场强比a 点大D ．一个电子在a 点无初速释放，则它将在c 点上下往复运动10.如图所示，一平行板电容器两板间有匀强电场．其中有一个带电液滴处于静止状态，当发生下列哪些变化时，液滴将向上运动 A.将电容器下极板稍稍下移 B.将电容器上极板稍稍下移C.将S 断开，并把电容器的下极板稍稍向左水平移动D.将S 断开，并把电容器的上极板稍稍下移11. 如图，电子在电势差为U1的加速电场中由静止开始运动，然后射入电势差为U2的两块平行极板间的电场中，入射方向与极板平行，整个装置处于真空中，重力不计，在满足电子能射出平行板区域的条件下，下述四种情况中，一定能使电子的偏转角θ变大的是 A ．其它条件不变，U1变小 B ．其它条件不变，U2变大C ．其它条件不变，U1变大同时U2变小D ．其它条件不变，U1变小同时U2变大 10月19日物理作业答案：1、AB 2、D 3、B 4、C 5、D 6、B 7、C 8、C 9、BC 10、BC 11、ABDabc。
大学物理II第10章静电场 作业题
10.1 四个点电荷到坐标原点的距离均为d ，如题10.1图所示，求点O 的电场强度的大小和方向 。
题图10.1解：由图所示x 轴上两点电荷在O 点产生场强为i d q i d q i d q i E i E E q q2020*********πεπεπε=+=+=-y 轴上两点电荷在点O 产生场强为j dq j d q j d q j E j E E q q2020*********πεπεπε-=--=+=- 所以，点O 处总场强为j dq i d q E E E O2020214343πεπε-=+= 大小为202221423dq E E E O πε=+=,方向与x 轴正向成045-角。
10.4 正方形的边长为a ，四个顶点都放有电荷，求如题10.4图所示的4种情况下，其中心处的电场强度。
q qq q (a ) (b ) (c ) (d )题图10.4解：在四种情况下，均以中心O 为坐标原点，水平向右为x 轴正方向，竖直向上为y 轴正方向建立坐标系，则有（a ）根据对称性，四个顶点处的电荷在中心处产生的场强两两相互抵消。
所以0=a E(b ) 根据对称性，电荷在中心处产生的场强在x 轴上抵消，只有y 轴上的分量，所以[]j aq j a a q j E E qy b20220245cos )2/()2/(444πεπε-=+-=-= (c ) 根据对称性，对角线上的电荷在中心处的场强可以相互抵消，所以0=c E(d ) 根据对称性，电荷在中心处产生的场强在y 轴上抵消，只有x 轴上的分量，所以[]i aq i a a q i E E qx d20220245sin )2/()2/(444πεπε=+== 10.5 一半径为R 的半圆细环上均匀地分布电荷+Q ，求环心处的电场强度。
题图10.5解：以环心O 为原心，取如图所示的坐标轴。
在环上取一线元dl ，其所带电量为RQdldq π=，它在环心O 处的电场强度E d 在y 轴上的分量为θππεsin 14120R R Qdl dE y =由于环对y 轴对称，电场强度在x 轴上的分量为零。
大学物理静电场作业题参考答案
解得 q 2l sin 4 0mg tan 7.3.4 长 l =15.0cm的直导线AB上均匀地分布着线密度 =5.0x10-9C·m-1的正电荷．试
求：(1)在导线的延长线上与导线B端相距 a1 =5.0cm处 P 点的场强；(2)在导线的垂直 平分线上与导线中点相距 d2 =5.0cm 处 Q 点的场强．
S
(D) 曲 面 S 的 电 场 强 度 通 量 不 变 ， 曲 面 上 各 点 场 强 变
化．
题 7.1（2）图
[答案 D ]
（3）在电场中的导体内部的 [ ] （A）电场和电势均为零； （B）电场不为零，电势均为零； （C）电势和表面电势相等； （D）电势低于表面电势。 [答案：C]
（4）两个同心均匀带电球面，半径分别为 Ra 和 Rb (Ra＜Rb), 所带电荷分别为 Qa 和
Uo
4U1
4
8.99
109
1.25 5
108 102
8.99 103V
(2)根据电势差的定义，有UO q0 (U UO )
选取无穷远处为电势零点WO q0 (U UO ) 8.99 106 J
电场力做负功，说明实际需要外力克服电场力做功。
题 7.3.11 图 7.3.11 如题7.3.11图所示，在 A ，B 两点处放有电量分别为+ q ,- q 的点电荷，AB
解：如题 7.3.4 图所示
(1) 在带电直线上取线元 dx ，其上电量 dq 在 P 点产生场强为 dEP
1 4π 0
dx (a x)2
EP
dE P
4π 0
l 2 l 2
dx (a x)2
4π 0
[ a
1
l
1 a
第10章-静电场-1作业答案
§10.2 电场 电场强度一．选择题和填空题1. 下列几个说法中哪一个是正确的？（A ）电场中某点场强的方向，就是将点电荷放在该点所受电场力的方向.（B ）在以点电荷为中心的球面上， 由该点电荷所产生的场强处处相同．(C) 场强可由q F E / =定出，其中q 为试验电荷，q 可正、可负，F为 试验电荷所受的电场力．(D) 以上说法都不正确． [ C ]2. 如图所示，在坐标(a ，0)处放置一点电荷+q ，在坐标(-a ，0)处放置另一点电荷－q ．P 点是x 轴上的一点，坐标为(x ，0)．当x >>a 时，该点场强的大小为：(A)x q 04επ． (B) 30xqaεπ． (C) 302x qaεπ．(D)204x qεπ． [ B ]3. 两个平行的“无限大”均匀带电平面， 其电荷面密度分别为＋和＋2，如图所示，则A 、B 、C 三个区域的电场强度分别为：E A ＝－3/ (20)_，E B ＝_－ / (2) ，E C ＝_3 / (2)_ (设方向向右为正)．4. 一半径为R 的带有一缺口的细圆环，缺口长度为d (d<<R)环上均匀带有正电，电荷为q ，如图所示．则圆心O 处的场强大小E ＝()30220824R qdd R R qd εεπ≈-ππ，场强方向为_____从O 点指向缺口中心点_________________．二．计算题1. 如图所示，真空中一长为L 的均匀带电细直杆，总电荷为q ，试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度．１、解：设杆的左端为坐标原点O ，x 轴沿直杆方向．带电直杆的电荷线密度为=q / L ，在x 处取一电荷元d q = d x = q d x / L ，它在P 点的场强： ()204d d x d L q E -+π=ε()204d x d L L x q -+π=ε 总场强为 ⎰+π=Lx d L x L q E 020)(d 4－ε()d L d q +π=04ε 方向沿x 轴，即杆的延长线方向．Ox-a -q+q +ax P (x ,0)y+σ +2σA B CR OqLd PＰL d d q x (L+d －x )d ExO2．一环形薄片由细绳悬吊着，环的外半径为R ，内半径为R /2，并有电荷Q 均匀分布在环面上．细绳长3R ，也有电荷Q 均匀分布在绳上，如图所示,试求圆环中心O 处的电场强度(圆环中心在细绳延长线上)．解：先计算细绳上的电荷在O 点产生的场强．选细绳顶端作坐标原点O ，x 轴向下为正．在x 处取一电荷元 d q = d x = Q d x /(3R ) 它在环心处的场强为 ()20144d d x R qE -π=ε ()20412d x R R xQ -π=ε 整个细绳上的电荷在环心处的场强()203020116412R Qx R dx R Q E R εεπ=-π=⎰圆环上的电荷分布对环心对称，它在环心处的场强E 2=0由此，合场强 i R Qi E E20116επ==方向竖直向下．三．理论推导与证明题一半径为R 的均匀带电圆环，总电荷为Q . 选x 轴沿圆环轴线, 原点在环心. 证明其轴线上任一点的场强为:()2/32204xR QxE +=πε 并说明在什么条件下, 带电圆环可作为点电荷处理.证：选环心作原点，x 轴沿圆环轴线方向，y 、z 轴如图所示．在环上任取一电荷元d q =(Q d ) / (2)，设P 点位于x 处，从电荷元d q 到P 点的矢径为r，它在P 点产生的场强为r r Q r r q E ˆ8d ˆ4d d 20220εθεπ=π=r ˆ为矢径r 方向上的单位矢量．d E 沿x 轴的分量为 d E x =d E cos 为矢径r 与x 轴正向夹角)由对称性容易证明 E y =0 E z =0 因而有 E =E x 20202024cos d 8cos r Q r Q εφθεθππ=π=⎰O R 3RR /2 E 1x R3R x xP x φR z d q θ d θ y rE d()2/32204xR Qx+π=ε当x >>R 时，可得 E ≈Q / (40x 2)这相当于一个位于原点O 的带电量为Q 的点电荷在P 点产生的场强．§10.3 电通量 高斯定理一. 选择题和填空题 1.一电场强度为E 的均匀电场，E的方向与沿x 轴正向，如图所示．则通过图中一半径为R 的半球面的电场强度通量为(A) R 2E ． (B) R 2E / 2． (C) 2R 2E ． (D) 0． [ D ]2. 两个同心均匀带电球面，半径分别为R a 和R b (R a ＜R b ), 所带电荷分别为Q a 和Q b ．设某点与球心相距r ，当R a ＜r ＜R b 时，该点的电场强度的大小为： (A)2041r Q Q b a +⋅πε． (B) 2041rQ Q ba -⋅πε． (C)⎪⎪⎭⎫ ⎝⎛+⋅π22041b b a R Q r Q ε．(D)2041r Q a⋅πε． [ D ] 3. 根据高斯定理的数学表达式⎰∑⋅=Sq S E 0/d ε可知下述各种说法中，正确的是：(A) 闭合面内的电荷代数和为零时，闭合面上各点场强一定为零． (B) 闭合面内的电荷代数和不为零时，闭合面上各点场强一定处处不为零． (C) 闭合面内的电荷代数和为零时，闭合面上各点场强不一定处处为零． (D) 闭合面上各点场强均为零时，闭合面内一定处处无电荷． [ C ] 4. 图示为一具有球对称性分布的静电场的E ～r 关系曲线．请指出该静电场是由下列哪种带电体产生的． (A) 半径为R 的均匀带电球面． (B) 半径为R 的均匀带电球体． (C) 半径为R 的、电荷体密度为＝A r (A 为常数)的非均匀带电球体． (D) 半径为R 的、电荷体密度为＝A/r (A 为常数)的非均匀带电球体 ． [ B ]5. 如图所示，在边长为a 的正方形平面的中垂线上，距中心O点a /2处，有一电荷为q 的正点电荷，则通过该平面的电场强度通量为q/(6) ．xOEOR rE E ∝1/r 2a qa/2O6. 一半径为R 的均匀带电球面，其电荷面密度为．该球面内、外的场强分布为(r表示从球心引出的矢径)：()r E ＝ 0 (r <R )， ()r E ＝0202302ˆr rR r r R εσεσ= (r >R )． 7. 有一个球形的橡皮膜气球，电荷q 均匀地分布在表面上，在此气球被吹大的过程中，被气球表面掠过的点(该点与球中心距离为r )，其电场强度的大小将由204r q επ变为__0．二. 计算题1.一半径为R 的带电球体，其电荷体密度分布为=Ar (r ≤R ) ， =0 (r ＞R )A 为一常量．试求球体内外的场强分布．解：在球内取半径为r 、厚为d r 的薄球壳，该壳内所包含的电荷为r r Ar V q d 4d d 2π⋅==ρ在半径为r 的球面内包含的总电荷为403d 4Ar r Ar dV q rVπ=π==⎰⎰ρ (r ≤R)以该球面为高斯面，按高斯定理有 0421/4εAr r E π=π⋅ 得到()0214/εAr E =， (r ≤R )方向沿径向，A >0时向外, A <0时向里．在球体外作一半径为r 的同心高斯球面，按高斯定理有 0422/4εAR r E π=π⋅ 得到 ()20424/r AR E ε=， (r >R ) 方向沿径向，A >0时向外，A <0时向里．2. 两个带有等量异号电荷的无限长同轴圆柱面，半径分别为1R 和2R （21R R <），单位长度上的电荷为λ。
《静电场》同步作业2库仑定律Word版带答案
作业2 库仑定律一、选择题(每小题5分，共50分)1.关于对元电荷的理解，下列说法正确的是( )A .元电荷就是电子B .元电荷就是质子C .元电荷是表示跟电子所带电荷量数值相等的电荷量D .元电荷是带电荷量最小的带电粒子答案:C2.关于库仑定律的公式221r Q Q k F ，下列说法中正确的是( )A .当真空中两个电荷间距离r →∞时，它们间的静电力F →0B .当真空中两个电荷间距离r →0时，它们间的静电力F →∞C .当两个电荷间的距离r →∞时，库仑定律的公式就不适用了D .当两个电荷间的距离r →0时，电荷不能看成是点电荷，库仑定律的公式就不适用了 答案:AD3.要使真空中的两个点电荷间的库仑力增大到原来的4倍，下列方法中可行的是( )A .每个点电荷的带电荷量都增大到原来的2倍，电荷间的距离不变B .保持点电荷的带电荷量不变，使两个点电荷间的距离增大到原来的2倍C .使一个点电荷的带电荷量加倍，另一个点电荷电荷量保持不变，同时将两点电荷间的距离减小为原来的21 D .保持点电荷的带电荷量不变，将两点电荷间的距离减小为原来的21 答案:AD4.两个大小相同、可看成是点电荷的金属小球a 和b ，分别带有等量异种电荷，被固定在绝缘水平面上，这时两球间静电引力的大小为F .现用一个不带电、同样大小的绝缘金属小球C 先与a 球接触，再与b 球接触后移去，则a 、b 两球间静电力大小变为( )A .F 21B .F 83C .F 41D .F 81答案:D5.如图所示，两根细线拴着两个质量相同的小球A 、B ，上、下两根细线中的拉力分别是T A 、T B ，现在使A 、B 带同种电荷，此时上、下细线受力分别为T A ′、T B ′，则( )A .T A ′=T A ，TB ′>T B B .T A ′=T A ，T B ′<T BC .T A ′<T A ，T B ′>T BD .T A ′>T A ，T B ′<T B答案:A6.两个大小相同的小球带有同种电荷，质量分别为m 1和m 2，带电荷量分别是q 1和q 2，用绝缘细线悬挂后，由于静电斥力而使两悬线张开，分别与铅垂线方向成夹角а1和а2，且两球处于同一水平线上，如图所示，а1=а2，则下列关系正确的是( )A .q 1一定等于q 2B .m 1一定等于m 2C .一定满足2211m q m q =D .一定同时满足q 1=q 2，m 1=m 2答案:B7.固定的A 和B 两个点电荷都带正电，相距8cm 今将第三个点电荷C 放在A 与B 连线上，A 的内侧距A2cm 处，C 恰好处于静止状态,则必有( )A .C 应带正电，且31q q B A = B .C 应带负电，且91q q B A = C .C 带电可正可负，且91q q B A = D .C 带电可正可负，且31q q B A = 答案:C8.两个点电荷，电荷量分别为q A =4×10-9C ，q B =-9×10-9，两者固定于距离为20cm 的a 和b两点上今有一个点电荷放在a 与b 连线上并处于静止不动，则该点电荷所处的位置是( )A .距a 点外侧40cm 处B .距a 点内侧8cm 处C .距b 点外侧20cm 处D .无法确定答案:A9.在光滑且绝缘的水平面上，有两个金属小球A 、B ，它们用一绝缘的轻弹簧相连，如图所示在A 、B 带有等量同种电荷后，弹簧伸长x 1时小球平衡如果小球A 、B 带电荷量加倍，它们重新平衡时弹簧伸长为x 2，则x 1和x 2的关系为( )A .x 2=2x 1B .x 2=4x 1C .x 2<4x 1D .x 2>4x 1答案:C10.如图所示，墙壁上的Q 处有一固定的质点A ，在Q 上方P 点用绝缘丝线悬挂另一质量的小球B ，A 、B 带同种电荷后而使悬线与竖直方向成β角.由于漏电使带电荷量逐渐减少，在电荷漏完之前悬线对P 点的拉力大小()A .保持不变B .先变小后变大C .逐渐减小D .逐渐增大答案:A二、填空题(每空4分，共24分)11.两个相同的金属小球，带电荷量之比为1:7，相距为r ，两者相互接触后再放回原来的位置上，则它们间的库仑力变为原来的______答案:71679或 12.光滑绝缘水平面上有两个带电小球A 、B ，相距为L ，A 球质量为m .A 、B 两球由静止开始释放，释放时，A 、B 的加速度分别为a 和4a ，经时间t ，B 的速度为v ，加速度为a ，则此时A 的速度为______，加速度为______.此过程中电场力做的功为______答案:2mv 325;a 41;v 41 13.真空中有两个点电荷，带电荷量分别为q 1=5×10-3，q 2=-2×10-2C ，它们相距15cm ，现引入第三个点电荷则它的带电荷量应为______，放在______位置才能使三个点电荷都处于静止状态答案:-2×10-2C ;在q 1,q 2的连线上，且在q 1的外侧15cm 处三、计算题(每小题13分，共26分)14.如图所示，A 、B 是带等量同种电荷的小球，A 固定在竖直放置的10cm长的绝缘支杆上，B 平衡于绝缘的倾角为30°的光滑斜面上时，恰与A等高，若B 的质量为g 330，则B 带电荷量是多少?(g 取10m /s 2)答案:如图所示，小球B 受三个力而平衡︒=∴mgtan30F 库①据库仑定律得22)hcot30(q k F ︒=库② 由①②得C 100.1C 31010100.9331010330hcot30k mgtan30q 6293---⨯=⨯⨯⨯⨯⨯⨯⨯=︒•︒=15.两根光滑绝缘棒在同一竖直平面内，两棒与水平面间均成45°角，棒上各穿有一个质量为m 、带电荷量为Q 的相同小球，如图所示.现让两球同时从同一高度由静止开始下滑,则当两球相距多大时，小球的速度达到最大值?答案:如图所示，小球在三个力作用下先做加速度减小的变加速运动，当a =0时，速度达最大.此时，︒mgtan45F 库①由库仑定律得22rQ k F =库 由①、②得 mg kQ r 2=。
大学物理下作业答案.docx
静电场(一)一. 选择题:1.解:在不考虑边缘效应的情况下，极板间的电场等同于电荷均匀分布，密度为o = ±q/S的两面积无限大平行薄板之间的电场一-匀强电场，一板在另一板处之电场强度为£ = o/(2s0)，方向垂直于板面.所以，极板间的相互作用力F =q・E = q2 /(2件)。
故选(B)。
2.解：设置八个边长为a的立方体构成一个大立方体，使A(即Q)位于大立方体的中心.所以通过大立方体每一侧面的电场强度通量均为q/(6&o),而侧面abed是大立方体侧面的1/4,所以通过侧面abed的电场强度通量等于q/(24%).选(C)。
3.解:寸亘•丞=jpdV/£°适用于任何静电场.选(A)。
4.解：选(B)。
5.解:据高斯定理知：通过整个球面的电场强度通=q/&. ■内电荷通过昂、&的电通量相等且大于零; 外电荷对品的通量为负，对&的通量为正. 所以0>1 <0>2 •故(D)对。
二. 填空题：1.解：无限大带电平面产生的电场E= —2&oA L 八(5 2(5 3(5A 区：E A= ------------------ = ------2s0 2s02g0CL L b 2b bB 区：E R = ------------ = ------2s0 2s 02s0C区"c=三+至=至2s n 2s n 2s n2.解：据题意知，P点处场强方向若垂直于OP,则入在P点场强的OP分量与Q在P点的场强E QP一定大小相等、方向相反.即Jcp = ------------- c os——= ----------- =也冲= -------- , O — aA .2%。
3 4%。
4%。
之3. 解：无限长带电圆柱体可以看成由许多半径为r 的均匀带电无限长圆筒叠加而成，因此 其场强分布是柱对称的，场强方向沿圆柱半径方向，距轴线等距各点的场强大学相等。
静电场(二)作业解答
E2 q
q
4 0
(1 r
1) R
与外球壳带电量无关！
1. 球对称模型的电场强度的计算 2. 电势差的计算
3. 真空中有一点电荷Q，在与它相距为r 的a点处有一试验电荷q. 现使试验电荷q 从a点沿半圆弧轨道运动到b点，如图所 示，则电场力对q 做功为 [ D ]
(A)
Qq r 2 (B)
s 0
i
dxi
0 a
s 0 dx
s 0
a
方向由圆心指向缝隙
2. 点电荷电场强度的计算
三、计算题
1．正电荷均匀分布在半径为R的球
1
2
形体积中（如图），电荷体密度为r，
求球内a点和球外b点的电势差。
解：
1区 2区 U ab
ab44Errd22ElE 12rRarQE0V01drr34r0RRr0b3E34r2drr3E62Er10
rr 3 0
点）。
解： 吹前 r1
E
Q
40 R 2
+Q 高斯球面
U
Q
4 0
R
吹后
+Q
吹后求内区！
r2
E1 E2 1.带电球面，内外区电场
R
强度的计算
高斯球面
2.带电球面，内外区电势 的计算
E1 0
U
r2 R
E1
dr
E r2 2
dr
Q 4πε0r2
内区是等势体
5. 一均匀静电场，电场强度 E (400i 600 j ) V/ m，则点a
一.选择题:
1. 某电场的电力线分布情况如图所示。 一负电荷从 M 点移到 N 点。有人根据 这个图作出下列几点结论，其中哪点
习题课后作业(静电场中的导体和电介质)
习题课后作业(静电场中的导体和电介质)1、一个平行板电容器的电容值C ＝100Pf ，面积S ＝100cm 2，两板间充以相对电容率为εr ＝6的云母片，当把它接到50V 的电源上时，云母中电场强度大小E ＝9.42×103v/m ，金属板上的自由电荷量q ＝5.00×10-9C 。
(CU q =εDE =εσ==Sqr 0εε)2、一空气平行板电容器，电容为C ，两极板间距离为d ，充电后，两极板间相互作用力为F ，则两极板间的电势差为 C Fd 2，极板上的电荷量大小为FCd 2。
3、一平行板电容器，两极板间电压为U 12，其间充满相对电容率为εr 的各向同性均匀电介质，电介质厚度为d ，则电介质中的电场能量密度为221202d U w r εε= (d U E 12=, 2/20E w r εε=)4、如图，在与电源连接的平行板电容器中，填入两种不同的均匀的电介质，则两种电介质中的场强相等,电位移不相等。
(填相等或不相等)dUE E ==21,011E D r εε=, 2022E D r εε=, 12r r εε≠ , 21D D ≠∴5、平行板电容器在接入电源后,把两板间距拉大,则电容器( D )(A)电容增大； (B)电场强度增大；(C)所带电量增大 (D)电容、电量及两板内场强都减小。
由dSC 0ε=, U =Ed , q =CU 可见,接入电源后,U 不变,若d 增大,则C 减小, E 减小,Q 减小6、如图所示，一内半径为a ，外半径为b 的金属球壳，带有电量Q ，在球壳空腔内距离球心为r 处有一点电荷q ，设无限远处为电势零点。
试求：(1)球壳外表面上的电荷；(2)球心O 点处由球壳内表面上电荷产生的电势； (3)球心O 点处的总电势。
解: (1) 设球壳内、外表面电荷分别为q 1 , q 2,以O 为球心作一半径为R (a <R <b )的高斯球面S,由高斯定理 ⎰+=⋅S oq q S d E ε1 ,根据导体静电平衡条件,当a <R <b 时,0=E .则0=⋅⎰S S d E.即1=+q q ,得q q -=1根据电荷守恒定律,金属球壳上的电量为21q q Q +=q Q q Q q +=-=∴12(2)在内表面上任取一面元,其电量为dq ,在O 点产生的电势为:adq dU o πε411=q 1在O 点产生的电势aq aq adq dU U o o o πεπεπε4441111-====⎰⎰内内(3) 同理,外球面上的电荷q 2在O 点产生的电势bqQ bq U o o πεπε4422+== 点电荷q 在O 点产生的电势rq U o q πε4=∴ O 点的总点势o q U U U U πε41210=++=(b q Q aq r q ++-)7、一平行板电容器，两极板间的距离d ＝5.00mm 板面积100cm 2，以300V 电源使之充电。
课后作业20-静电场中导体
作业20 静电场中导体姓名 班级 学号 教学班序号20-1（1）如图所示，一带正电荷的物体M ，靠近一原不带电的金属导体N ，N 的左端感生出负电荷，右端感生出正电荷．若将N 的左端接地，则（A ）N 上有正电荷入地； （B ）N 上有负电荷入地；（C ）N 上的电荷不动； （D ）N 上所有电荷都入地。
［ ］（2）半径分别为R 和r 的两个金属球，相距很远．用一根细长导线将两球连接在一起并使它们带电．在忽略导线的影响下，两球表面的电荷面密度之比σR / σr 为(A) r / R ； (B) r 2 / R 2； (C) R / r ； (D) R 2 / r 2。
［ ］ （3）两个同心薄金属球壳，半径分别为R 1和R 2 (R 2 > R 1 )。
若分别带上电荷q 1和q 2，选无穷远处为电势零点，则两者的电势分别为U 1和U 2。
现用导线将两球壳相连接，则它们的电势为(A) U 1； (B) U 2； (C))(2121U U +； (D) U 1 + U 2 ［ ］（4）半径为R 的均匀带电球面，若其电荷面密度为σ，则在距离球面R 处的电场强度大小为： (A)εσ； (B)02εσ； (C) 04εσ； (D)8εσ［ ］ （5）有三个直径相同的金属小球．小球1和小球2带等量异号电荷，两者的距离远大于小球直径，相互作用力为F ．小球3不带电并装有绝缘手柄．用小球3先和小球1碰一下，接着又和小球2碰一下，然后移去。
则此时小球1和2之间的相互作用力为(A) 0； (B) F / 8； (C) F /4； (D) F / 2 ［ ］20-2（1）如图所示，两同心导体球壳，内球壳带电荷+q ，外球壳带电荷-2q 。
静电平衡时，外球壳的电荷分布为： 内表面___________ ； 外表面___________ 。
（2）如图所示，半径为r 的导体球与半径为R 的薄导体球壳，(R ＞r )，同心放置，球壳上有一小孔，用细导线穿过小孔(绝缘)将导体球接地。
静电场作业
E内＝0 UAB 0 (2) A带+q，B球内表面感应-q，外表面感应+q，有
E内＝
q
4
r
2
UAB
B
E dl
q
(1 1)
A
4 R0 R1
7．如图所示，金属球A和金属球壳B同心放置，它们原 先都不带电。设球A的半径为Ro, ，球壳B的内、外半径 分别为R1和R2. 。求在下列情况下，A、B的电势差 (1)使B带电+q;(2)使A带电+q; (3)使A带电+q，使B带电-q; (4)使A带电-q，将B外表面接地。
B.只适用于真空中的静电场
C.只适用于具有球对称性、轴对称性和平面
D.只适用于虽然不具有（C）中所述的对称性、
但可以找到合适的高斯面的静电场
6．两无限大均匀带电的平行平面A和Ｂ，电荷面
密度分别为＋σ和－σ，若在两平面的中间插入另
一电荷面密度为＋σ的平行平面C后，
P点的场强的大小将是
A．不变
B．原来的 1/2
(3) A带+q，B带-q，分布在B球的内表面上，有
E内＝
q
4
r
2
UAB
B
q1 1
E dl ( )
A
4 R0 R1
(4) A带-q，B球的内表面感应+q，外表面感应的-q与地
中和，UB=0，则有
E内＝-
q
4 r2
U AB
B
E dl
q
(1 1)
A
4 R0 R1
C．原来的2倍 D．零
7．静电场中a、b两点的电势差 Ua U b 取决于
A.零电势位置的选取 C.a、b两点场强的值
静电场作业
静电场作业1.如题6.1.2图所示，在点电荷＋q 的电场中，若取图中P 点处为电势零点，则M 点的电势为( )(A)q 4πε0a . (B)q 8πε0a . (C)－q 4πε0a . (D)－q 8πε0a. 题6.1.1图题6.1.2图2.如题6.1.3图所示，两个同心球壳，内球壳半径为R 1，均匀带有电量Q ；外球壳半径为R 2，壳的厚度忽略，原先不带电，但与地相连接．设地为电势零点，则在两球之间、距离球心为r 的P 点处电场强度的大小与电势分别为( )(A)E ＝Q 4πε0r 2， U ＝Q 4πε0r . (B)E ＝Q 4πε0r 2， U ＝Q 4πε0r ⎝⎛⎭⎫1R 1－1r . (C)E ＝Q 4πε0r 2， U ＝Q 4πε0⎝⎛⎭⎫1r －1R 2. (D)E ＝0， U ＝Q 4πε0R 2. 题6.1.3图3.4．如题6.1.4图所示，边长为a 的等边三角形的三个顶点上，放置着3个正的点电荷，电量分别为q ，2q ，3q ，若将另一正点电荷Q 从无穷远处移到三角形的中心O 处，外力所做的功为( ) (A)23qQ 4πε0a . (B)43qQ 4πε0a . (C)63qQ 4πε0a . (D)83qQ 4πε0a. 题6.1.4图5、一边长为 a 的正方形平面，其中垂线上距中心 O点 a / 2 处有一点电荷 -2q ，如图所示，则通过该平面的电场强度通量为（）A 、03εqB 、03πεqC 、04πεqD 、06εq 6、如题图所示，在点电荷+2q 的电场中，若取图中 M 点处的电势为 0，则 P 点的电势为（）A 、a q 043πε B 、a q 02πε- C 、a q08πε D 、a q08πε-7、真空中两块相互平行的“无限大”均匀带电平面 A 、B 。
A 平面的电荷面密度为2 σ ，B 平面的电荷面密度为σ ，两平面间的距离为 d 。
当点电荷 q 从 A 面移到 B 面时，电场力做的功为（）A 、0εσdq B 、0εσd q - C 、02εσd q D 、02εσd q - 8、关于高斯定理的理解有下面几种说法，其中正确的是： (A) 如果高斯面上处处为零，则该面内必无电荷 (B) 如果高斯面内无电荷，则高斯面上处处为零 (C) 如果高斯面上处处不为零，则高斯面内必有电荷(D) 如果高斯面内有净电荷，则通过高斯面的电场强度通量必不为零9、如图所示，两个同心的均匀带电球面，内球面半径为R 1、带电荷Q 1，外球面半径为R 2、带电荷Q 2 .设无穷远处为电势零点，则在两个球面之间、距离球心为r 处的P 点的电势U 为： (A) (B) (C) (D)10、电荷分别为q 1，q 2，q 3的三个点电荷分别位于同一圆周的三个点上，如图所示。
静电场三作业解
（C）空心球电量多；
（D）实心球电量多。
两球相互接触后，由于电荷仅分布在两球外表面，而 两球外表面完全相同，则均匀分配。
二、填空题：
1.一平行板电容器，极板面积为 S，相距为 d，若 B 板接地， 且保持 A 板的电势 UA= U0 不变，如图，把一块面积相同的带 电量为 Q 的导体薄板 C 平行的插入两板中间，则导体薄板的 电势 UC= _____.
uA
E1
d 2
2Q 1
3 0S
d 2
Qd
3 0 S
（2）若在A、B间充以相对介电常数为 r 的均匀电介质，再
求B板和C板上的感应电荷Q´B、Q ´ C 、及A板的电势U´A 。
uAC uAB
d E1 2 E2d
E1
q1
0S
E2
q2
0 r S
q1 d q2 d
0S 2 0 r S
CA B q1 q2
反证法：设这样一条电力线，在导体内
补线，形成闭合环路。计算该环路环流，
与静电场环路定理比较。
LE dl 0
违反了静电场环路定理，所以不存在这
样一条电力线。
压增大，电容减少。
与电源断开，极板上电量保持不变，则电容器中的场强
E
0
保持不变
C Q 0S
Ud
d增大，电容减小，Q不变，U增大。所以 [ E ] 正确。
5. 有两个带电不等的金属球，直径相等。但一个是空心
的，一个是实心的。现使它们互相接触，则这两个金属球
上的电荷
[B]
（A）不变化；
（B）平均分配；
⑴. 离球心30cm处的场强； ⑵. 两球间的电势差; ⑶. A球的电势。
(1) E Q1 Q2 5.998103v / m
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
AB 2l ,OCD是以B为中心，l为半经 3．如图所示， 的半圆，A点有正电荷+q，B点有负电荷-q，求： （1）把单位正电荷从O点沿OCD移到D点，电场 力对它作的功？ （2）把单位正电荷从D点沿AB的延长线移到无穷 C 远去，电场力对它作的功？ q 解：（1） A q( U0 U D ) A q O D B l 2l q U D 6 0 l
Q dV Ar 4r dr
2
V
R
0
AR
4
7．把一个均匀带电量＋Q的球形肥皂泡由半径r1 吹胀到r2，则半径为R（r1＜R＜r2）的高斯球面 2 Q / 4 R 上任一点的场强大小E由_______ 变 0 Q / 40 r2 Q / 40 R 变为_______ 为__ 0 ；电势U由_________ R r1 (选无穷远处为电势零点)。
5．两无限大均匀带电的平行平面A和B，电荷面密度分 别为＋σ和－σ，若在两平面的中间插入另一电荷面密度 为＋σ的平行平面C后，P点的场强的大小将是 A．不变 B．原来的 1/2 C．原来的2倍 D．零 6．静电场中a、b两点的电势差 Ua Ub 取决于 A.零电势位臵的选取 B.检验电荷由a移到b路径 C.a、b两点场强的值 b D． E dl (任意路径)
2.图中所示为一沿 x 轴放臵的长度为l的不均匀带 电细棒，其电荷线密度为= 0(x-a)， 0为一常 量。取无穷远处为电势零点，求坐标原点O处 的电势。
a
O
l
x
U dU 解： q
a l
a
0 l 0 a al ln 4 0 4 0 a
dx 4 0 x
8. 有两个点电荷电量都是 +q，相距为2a。今以左边的点 电荷所在处为球心，以a为半径作一球形高斯面， 在球 面上取两块相等的小面积S1和S2, 其位臵如图所示。设通 过S1 和 S2的电场强度通量分,则 A. Φ Φ , Φ q /
S2
I II
III
x
4．半径为R1和R2的两个同轴金属圆筒，其间充 满着相对介电常数为r的均匀介质，设两筒上单 位长度带电量分别为+ 和-，则介质中的电位移 矢量的大小D＝ / 2 r ,电场强度大小E＝ / 20 r r.
5．在场强为E的均匀电场中，A、B两点间距离 为d，A、B连线方向与E方向一致，从A点经任意 路径到B点的场强线积分 Ed . AB E dl =____ 6．半径为R的不均匀带电球体，电荷体密度分布 为＝Ar，式中r为离球心的距离，(r≤R)、A为一 4 常数，则球体上的总电量Q＝ A R 。
r2
8．有两根均匀带等量异号电荷的长直直线，其电 荷线密度分别为+、-，相距R，O点为带电直线 垂线的中点，则通过以O为圆心，R为 0 ， 半径的高斯面的电场强度通量为___ 球面上A点的电场强度的大小为 2 ， 3 0 R 水平向左 。 方向为_________
9．两根互相平行的长直导线，相距为a， 1 2 其上均匀带电，电荷线密度分别为1和2， 则导线单位长度所受电场力的大小为F0 a ＝ 12 / 20 a 。 E1 1 / 20 a F E1dq2 E1q2 12 l / 20 a F0 F 12 / 20 a q l
a
7．半径为r的均匀带电球面1,带电量为q;其 外有一同心的半径为R的均匀带电球面2,带 电量为Q,则此两球面之间的电势差U1－U2为
A. q 1 1 4 0 r R
R
q r Q q D. 4 0 r
Q 1 1 B. 4 0 R r
1 q Q C. 4 0 r R
10．有一电荷q，旁边有一金属导体A，且A处于静电平 衡，则（ ） A．导体内E1=0，q不在导体内产生场强 B．导体内E1≠0，q在导体内产生场强 C．导体内E1=0，q在导体内产生场强 D．导体内E1≠0 ，q不在导体内产生场强
11. 真空中一半径为R的球面均匀带电Q，在球心O处有 一带电量为q的点电荷，如图所示。设无穷远处为电势 零点，则在球内离球心O距离为r的P点处电势为 q q q Q A. B. ( ) C. q Q Q 4 0 r 4 0 r R p 4 0 r r q q Qq o R D. ( ) 4 0 r R 12. 在带电量为－Q的点电荷A的静电场中，将另一带电 量为q 的点电荷B从 a点移到 b点，a、b两点距离点电荷 A的距离分别为 r1和 r2，如图所示。则在电荷移动过程 中电场力做的功为 A r1 a qQ 1 1 Q 1 1 A. ( ) B. ( ) -Q 4 0 r1 r2 4 0 r1 r2 qQ 1 1 qQ r2 C. ( ) D. b 4 0 r1 r2 4 0 ( r2 r1 )
E内＝0 U AB 0
(2) A带+q，B球内表面感应-q，外表面感应+q，有 B q q 1 1 E内＝ U AB E dl ( ) 2 A 4 r 4 R0 R1
R 0
D内 4 r 4 r dr Ar 4 0
2 2
r
S内
U内 E内dr＋ E外dr
r R
R
D外 4 r 2 4 r 2 dr AR4
AR4 AR4 D外 ; E外 . 2 2 4r 4 0 r
A( R 3 r 3 ) AR 3 ＝ 12 4 0 AR4 U 外 E外dr r 4 0 r
q
O
S1
q
a 2a
x
C. Φ1 Φ2 , ΦS q / 0 D. Φ1 Φ2 , ΦS q / 0
B. Φ1 Φ2 , ΦS 2q / 0
1
2
S
0
9．一均匀带电球面，若球内电场强度处处为零，则球面 上的带电量dS的面元在球面内产生的电场强度是 A．处处为零 B．不一定为零 C．一定不为零 D．是常数
（2） A q( U D U ) 6 l
0
q
4. 一厚度为d 的无限大平板，平板内均匀带电， 电荷体密度为，求板内、外场强的分布。
2 Ds s d d D外 d , E外 2 2 0 s x q 板内： D d s 2 Dds i
三、计算题 1．一半径为R的带电球体，其电荷体密度分布为 Ar ( r R, ) ,A为一常数,试求球体内外的场强 R 0 ( r R, 0 ) 分布和电势分布。
解：
D dS qi
S
r
Ar 2 Ar 2 D内 ; E内＝ 4 4
3．在真空中的静电场中，作一封闭的曲面，则下 列结论中正确的是( ) A.通过封闭曲面的电通量仅是面内电荷提供的 B.封闭曲面上各点的场强是面内电荷激发的 C.由高斯定理求得的场强仅由面内电荷所激发的 D.由高斯定理求得的场强是空间所有电荷共同激发 4．高斯定理 S D ds V dV （ ） A．适合于任何静电场； B．只适用于真空中的静电场； C．只适用于具有球对称、轴对称和平面对称的静电场 D．只适用于虽然不具有(c)中所述的对称性，但可 找到合适的高斯面的静电场
s
板外： D ds 2 Dds q
s
s
s内
o
s
（侧视图）
2 Ds s 2 x x D内 x , E内
s内
5. 图示一球形电容器，在外球壳的内半径b和内外 导体间的电压U维持恒定的条件下，内球半径a为 多大时，才能使内球面上的电场强度最小？这个 最小的电场强度和相应的电场能量各是多少？
S S Q 2 4 0 R 4 0 R 2 4R 2
O
R
S
3. 两块“无限大”的带电平行电板，其电荷面密 度分别为(>0) 及－ 2 ，如图所示，试写出各 区域的电场强度 E 2 І区 E的大小 E / 2 0 ，方向 x轴正向. Π区 E的大小 E 3 / 2 0，方向 x轴正向. Ш区 E 的大小 E / 2 0 ，方向 x轴负向 .
m
12．有一内外半径分别为R及2R的金属球壳，在 离其球心O为R/2处放一电量为q的点电荷，则球 心O处的电势U0=_________ 3q / 8 0 R 。在离球心O为3R处 2 q / 12 0 R。 的电场强度大小E=________ q / 36 0 R ，电势U=________
二、填空题 1．真空中有一半径为R均匀带正电的细圆环，其 电荷线密度为λ，则电荷在圆心处产生的电场强 度 E 的大小为 0 。 2. 真空中一半径为R的均匀带电球面，总电量为 Q(Q > 0)。今在球面上挖去非常小块的面积ΔS (连同电荷)，且假设不影响原来的电荷分布，则 S 挖去ΔS后球心处电场强度的大小E= 2 ， 4 0 R 其方向为 指向S 。
解：E内面
CU 2 4 a 4 a 2
q
b
U a
4 abU bU 2 4 a ( b a ) ( b a )a
E 4 U 0 a b / 2 E Emin a b 1 4 ab 2 2 1 2 U 2 bU We CU 2 ba 2
10. 图示为一边长均为a的等边三角形，其三个顶点分别 放臵着电量为q、2q、3q的三个正点电荷若将一电量为Q 3 q 的正点电荷从无穷远处移至三角形的 中心O处，则外力需作功A＝3 3 qQ
2 0 a
q
a
a
O
a
2q
11．一质量为m、电量为q的小球，在电场力作 用下，从电势为U的a点，移动到电势为零的b点 ，若已知小球在b点的速率为b，则小球在a点的 速率a＝ 2 2qU 。 Aab q( Ua Ub ) 1 m b2 1 m a2 b 2 2