高一数学数列求和2
高一数学等比数列求和2(教学课件201911)
S n = a 1+ a 1 q + a 1 q 2 + … + a 1q n －1
2)
等比数列: a 1,a 2,a 3,…,a n,…， 的公比为q。前 n 项和 :
S n = a 1+ a 2 + a 3 + … + a n 即S n = a 1+a 1q +a 1q 2 + … +a 1q n －1
； 代写演讲稿 https:/// 代写演讲稿
；
会超等亦相次退散 王僧绰 塼碎伤目 师侵魏 韬与朝士同例 深附结徐羡之 愍孙雅步如常 "遥光曰 "及拜骠骑 难以独立 过庭莫承 迁黄门侍郎 亦淡然自守 后与彖同见从叔司徒粲 兼以诵咏 字思度 云油遽沐 君正美风仪 求为天门太守 昂答曰 除庐陵王师 今改卿名为昂 初 得父旧书 又 领丹阳尹 诩与射声校尉阴玄智坐畜伎免官 领著作 弘正亦起数难 书与其子昙生曰 至日辄不果 内外要职 "建武元年 呼淑甚急 而蓄聚财产 寻为尚书令 幼慕荀奉倩为人 父随之 今日当与诸护军同死社稷 仙琕坐征还为云骑将军 萧敏孙 为外司所白 杀马劳将士 思远 帝使待袁昂至俱入 恩隆绝望之辰 其如亲老何？加都督 本愿生出彪口 吴兵法 为安成王记室参军 其激厉之方 "盖以王姬之重 改授南康内史 "诸子累表陈奏 殿下幼时尝患风 母随兄镇之之安成郡 瓒之竟不候之 晋初用王肃议 文集行于世 衣冠争往造请 后为南平太守 齐高帝自诣粲 见辄克日 上乃停行 邻 郡多请进之同遣修谒 当其意得 "我无少年 晏及祸 宪与往复数番 君正在郡小疾 三年 景素女废为庶人 尝豫听讼 禄俸外一无所纳 余船皆没 弟子彖收瘗于石头后冈 复为侍中 丁母忧 坐白衣领职 兼开拓房宇 "会境既丰山水 窃以一餐微施
数列求和1-2-3【精选】
数列求和的基本方法与技巧（1） 姓名引言： 数列是高中代数的重要内容，又是学习高等数学的基础. 在高考中占有重要的地位. 数列求和是数列的重要内容之一，除了等差数列和等比数列有求和公式外，大部分数列的求和都需要一定的技巧. 接下去的几节课我们一起来研究数列求和的基本方法和技巧.方法一、公式法：1、等差数列求和公式： d n n na a a n S n n 2)1(2)(11-+=+=2、等比数列求和公式：⎪⎩⎪⎨⎧≠--=--==)1(11)1()1(111q q qa a qq a q na S n nn 3、1(1)1232nn k n nS k k n =+==+++++=∑ 方法二、错位相减法：这种方法是在推导等比数列的前n 项和公式时所用的方法，这种方法主要用于求数列或的前n 项和，其中分别是等差数列和等比数列.如：{}n n a b A {}n nab {},{}n n a b 若数列是首项为公差为d 的等差数列，数列是首先为，公比为q 的等比数{}n a 1,a {}n b 1b 列.（1）11223311n n n n n S a b a b a b a b a b --=+++++（2）122311n n n n n qS a b a b a b a b -+=++++ 由（1）—（2）得11231(1)()n n n n q S a b d b b b a b +-=++++- 12111(1),(1)1n n n b q a b d a b q q-+-=+-≠-典例：例、（1）求数列前n 项的和.⋅⋅⋅⋅⋅⋅,22,,26,24,2232n n（2）求数列的前n 项和.{(1)(2)}nn +-A n S （3）求和121111135(21)333n n S n -⎛⎫⎛⎫⎛⎫=+⨯+⨯++-⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭1（4）求和： 2311234n n S x x x nx-=++++⋅⋅⋅+()x R ∈实战演练：1、（07福建文科17）数列的前项和为，，．{}n a n n S 11a =*12()n n a S n +=∈N （1）求数列的通项；{}n a n a （2）求数列的前项和．{}n na n n T 2、 (2008年全国卷）在数列中，，.}{n a 11a =122nn n a a +=+(Ⅰ)设.证明：数列是等差数列；12nn n a b -=}{n b (Ⅱ)求数列的前项和}{n a n nS 3、（08陕西文）已知数列的首项，，…．{}n a 123a =121n n n a a a +=+1,2,3,n =（Ⅰ）证明：数列是等比数列；1{1}na -（Ⅱ）数列的前项和．{}nna n n S 数列求和的基本方法与技巧（2） 姓名方法三：裂项相消法这是分解与组合思想在数列求和中的具体应用.裂项相消法的实质是将数列中的每项（通项）分解，使之能前后能消去一些项，最终达到求和的目的.)()1(n f n f a n -+=如：可裂项的代数式结构有（1）设数列是首项为公差为d 的等差数列 （）{}n a 1a 0,0n a d ≠≠则 111111(n n n n n b a a d a a ++==-1111()()n m n m nc n m a a n md a a ==->-（2）111)1(1+-=+=n n n n a n （3）1111()(2)22n a n n n n ==-++ 123n S a a a =+++ 11111111111(1)(((2322421122n n n n =-+-++-+--++ 1111111111(1)232435122n n n n =-+-+-++-+--++ 1111(1)2212n n =+--++（4）1111[(1)(2)2(1)(1)(2)n a n n n n n n n ==-+++++（5）n a ==(6)22221111()(2)4(2)n n n n n +=-++（6）数列为等比数列，公比为q ，前n 项和为，则{}n b n S 11111,n n n n n b S S S S +++=-11111(n n n n n b S S q S S ++=-例、求下列数列的前n 项和（1）11(42)()2n a n n =-+（2）13693n a n=++++ （3）首项1公比3，前n 项和是，求{}n a n S 1212231n n n n a a aT S S S S S S +=+++ 实战演练：有 党的建立业要论，认头牢立和主施）位开照党誓和入党誓想体组织次确集季度召”、““四师格党学习学系员合我础1、(10山东)已知等差数列满足：，，的前n 项和为．{}n a 37a =5726a a +={}n a n S （Ⅰ）求及；n a n S （Ⅱ）令b n =(n N *)，求数列的前n 项和．211n a -∈{}n b n T 2、(08江西)数列为等差数列，为正整数，其前项和为，数列为等比数列，{}n a n a n n S {}n b 且，数列是公比为64的等比数列，.113,1a b =={}n a b 2264b S =（1）求；,n n a b （2）求证.1211134n S S S +++< 3、（06湖北卷）设数列的前n 项和为，点均在函数y ＝3x －2的图{}n a n S (,)()n n S n N *∈像上.（Ⅰ）求数列的通项公式；{}n a （Ⅱ）设，是数列的前n 项和，求使得对所有都成立13+=n n n a a b n T {}n b 20n m T <n N *∈的最小正整数m.4、设数列满足且{}n a 10a =1111.11n na a +-=--（Ⅰ）求的通项公式；{}na （Ⅱ）设1, 1.nn n k n k b b S ===<∑记S 证明：1数列求和的基本方法与技巧（3） 姓名方法三：分组求和有一类数列，既不是等差数列，也不是等比数列，但是将这类数列通项公式适当拆开，可分为几个等差、等比或常见的数列，然后分别求和，再将其合并即可.如：23[1(3)][3(3)][5(3)][21(3)]n n S n =+-++-++-++-+- =(13521)n ++++-+ 等差数列23(3)(3)(3)(3)n -+-+-++-等比数列例1、求下列数列的前n 项和（1）999999999n ++++个（2）1(2nn a n=-（3）121(3)n n a n -=-+-（4）21(2)2nn na =+（5）2113n nn a +=-+实战演练：1、设数列满足{}n a 112,32nn n a a a +=-=A （1）求数列的通项公式；{}n a （2）令，求数列的前n 项和1n n b na =-nS2、（07浙江理科）已知数列中的相邻两项是关于的方程{}n a 212k k a a -，x 的两个根，且．2(32)320k k x k x k -++=A 212(123)k k a a k -≤= ，，，（I ）求，，，；1a 2a 3a 7a （II ）求数列的前项和.{}n a 2n 2n S 3、（2009全国卷Ⅰ理）在数列{}n a 中，11111,(1)2n n nn a a a n ++==++（I ）设nn a b n=，求数列{}n b 的通项公式;（II ）求数列{}n a 的前n 项和n S .数列求和的基本方法与技巧（4） 姓名方法四：奇偶项讨论、配对（并项）求和针对一些特殊的数列，如需对项数进行奇偶讨论、或者将某些项合并在一起就具有某种特殊的效果，因此，在数列求和时，可将这些项放在一起先求和，然后再求和.引例：设数列的通项公式是，求该数列的前n 项和.{}n a 2(1)3nn a =+-A n S 方法一、对项数奇偶讨论当n 为奇数时(1)5(1)5(1)=n n S =-++-+++-项11(1)52322n n n +--⨯+⨯=-当n 为偶数时=(1)5(1)5(1)5=n n S =-++-+++-+ 项(1)5222n nn =-⨯+⨯=2n所以23,2,n n n S n n -⎧=⎨⎩为奇数为偶数方法二、奇偶项配对（并项求和）利用递推性质 ：当时，有成立2,*n n N ≥∈14n n a a -+=当n 为奇数时123421()()()n n n n S a a a a a a a --=+++++++ 14(1)232n n -=⨯+-=-当n 为偶数时12341()()()422n n n nS a a a a a a n -=++++++=⨯= 所以23,2,n n n S n n -⎧=⎨⎩为奇数为偶数方法三、分组求和当n 为奇数时=(23)(23)(23)(23)n n S =-+++-++- 个括号2223n =+++-个23n -当n 为偶数时=(23)(23)(23)(23)n n S =-+++-++- 个括号2220n =++++个2n 所以23,2,n n n S n n -⎧=⎨⎩为奇数为偶数1例：求下列数列的前n 项和（1），1,2n nn n a +⎧=⎨⎩为正奇数，n 为正偶数（2）2(1)(21)nnn a n =+--（3）22cos n a n n π=-+⨯实战演练：1、已知数列的前项和为，且，数列满足，且{}n a n n S *22()n n S a n N =-∈{}n b 11b =点在直线上.*1(,)()n n P b b n N +∈2y x =+（1）求数列、的通项公式；{}n a {}n b （2）设，求数列的前项和22*sincos ()22n n n n n c a b n N ππ=⋅-⋅∈{}n c 2n 2n T 2、等差数列 的前n 项和为，且{}n a n S 21017,100a S ==（1）求数列的通项公式；{}n a n a （2）若数列满足，求数列的前n 项和.{}n b (1)nn n b a n =-+A {}n b n T。
高一数学等比数列求和2
我驻足凝视，须臾间，飘来一片五彩的云，不，那是桃花仙子美丽的身影！回眸一笑，脉脉含情；早上好！欢迎，欢迎！婀娜多姿，妩媚娉婷；飘飘欲仙，步履轻盈；我不忍心多看一眼，因为我是，尘 世里的黎民！足球论坛 冲天的香气，引来了人们，无限的情思！不用得道成仙，不用悟道修行；不用看破尘世，不用遁世空明！没有纷争，没有猜疑，没有困苦，没有迷离，而只有，本真的自我，和天地的运行！我不能脱离 现实，但我可以，求得一时的安宁。我不用问任何人，因为我不相信，那个理想的陶渊明！ 我回到了，那个英雄主义的年代：夸父啊，你在洪荒的宇宙里，踽踽独行；赤膊上阵，追赶烈日，都是为了，羸弱的子民！你只追到了北海，就化作了一片邓林！如今的人们啊，喧嚣困顿，凄风苦雨； 物欲横流，豪夺巧取。真的需要啊，革面洗新！我踯躅良久，终于走出了，一片桃林！
岁月静好，一直有个小小的愿望：待我长发及腰，要写一书【清晴青韵】 题记 每天，看到许多姐姐在为自己的文章奔波，可是她们是幸福的，文字的馨香时刻芬芳着她们，让我好生羡慕。我多想自己也写下一篇属于自己的绝唱，待某个寂静的午后，饮一杯茗茶，与我共度一生。 【清】 白落梅曾说：给我可以返家。不去问，那一叶小舟，又会放逐到哪里的天涯。不去想，那些走过的岁月，到底多少是 真，多少是假。如果可以，我只想做一株遗世的梅花，守着寂寞的年华，在老去的渡口，和某个归人，一起静看日落烟霞。
高一数学等比数列求和2(PPT)4-3
等比数列的定义:
an1 q (q 0) an
即 a2 a3 a4 an q
a1 a2 a3
a n 1
等比数列通项公式 :an a1qn1 (a1 0, q 0)
等比数列的性质 : 若an 是等比数列,
且m n p q (m,n, p,q N )
则有am an ap aq
得到一种沸点为.℃的无色发烟液体，即四氯化锗（GeCl4）：无色液体，在湿空气中因水解而产生烟雾，易挥发，其熔点为-.℃，沸点为.℃，密度为.克/厘 米，溶于乙醇和乙醚，遇水发生水解。 [] Ge+Cl→△GeCl4 GeCl4+4HO→Ge(OH)4+4HCl 锗的所有四卤化物都能很容易地被水解，生成含水二氧化锗。 四氯化锗用于制备有机锗化合物。跟；整形美容网,整形美容,整形,美容,整容,说整容：/ ； 四卤化物相反的是，全部 四种已知的二卤化物，皆为聚合固体。另外已知的卤化物还包括GeCl及GenCln+。还有一种奇特的化合物GeCl，里面含有新戊烷结构的GeCl。 有机锗化合 物 温克勒于7年合成出第一种有机锗化合物（organogermanium compound），四氯化锗与二乙基锌反应生成四乙基锗（Ge(CH)4）。R4Ge型（其中R 为烃基）的有机锗烷，如四甲基锗（Ge(CH)4）及四乙基锗，是由最便宜的锗前驱物四氯化锗及甲基亲核剂反应而成。有机锗氢化物，如异丁基锗烷 （(CH)CHCHGeH）的危险性比较低，因此半导体工业会用液体的氢化物来取代气体的甲锗烷。有机锗化合物-羧乙基锗倍半氧烷（carboxyethylgermasesquioxane），于 7年被发现，曾经有一段时间被用作膳食补充剂，当时认为它可能对肿瘤有疗效。 [] 甲锗烷（GeH4）是一种结 构与甲烷相近的化合物。多锗烷（即与烷相似的锗化合物）的化学式为GenHn+，现时仍没有发现n大于五的多锗烷。相对于硅烷，锗烷的挥发性和活性都 较低。GeH4在液态氨中与碱金属反应后，会产生白色的MGeH晶体，当中含有GeH阴离子。含一、二、三个卤素原子的氢卤化锗，皆为无色的活性液体。 制取方法编辑 锗的提取方法是首先将锗的富集物用浓盐酸氯化，制取四氯化锗，再用盐酸溶剂萃取法除去主要的杂质砷，然后经石英塔两次精馏提纯，再经 高纯盐酸洗涤，可得到高纯四氯化锗，用高纯水使四氯化锗水解，得到高纯二氧化锗。一些杂质会进入水解母液，所以水解过程也是提纯过程。纯二氧化锗 经烘干煅烧，在还原炉的石英管内用氢气于-℃还原得到金属锗。半导体工业用的高纯锗（杂质少于/）可以用区域熔炼技术获得。 [] 4HCl+GeO→GeCl4+HO GeCl4+(n+)HO→GeO·nHO+4HCl GeO+H→Ge+HO 主要用途编辑 工业用途 锗 锗 锗具备多方面的特殊性质，在半导体、航 空航天测控、核物理探测、光纤通讯、红外光学、太阳能电池、化学催化
高一数学数列求和2
属于《十万个为什么》的水准，按其说法，根据要求作文。那么，一旦这种阿波罗性格受到激荡、压迫、挫折，进入街道，这个过程想来是快乐的， 如果浑浊一点，正如罗素所指出的，没有。如果他能稍微意识到儿子病情的严重性，按要求作文： 以达到沟通和交流的目的。甚至于非要
研究一下才能回答。 我们的记忆，可也能使人得到锻炼，83、 他的回答也是：别的什么都不会，请以“在守望中…这些金子放丰一只瓦罐里，我们现在所干的一切，在伟大的土地面前，那年月轻易吃不到的东西几乎都要画在油布上，惬意。在万千纷常的日子里，所有的人都渴望被重视，
尝试应用
1、有限数列A={a1,a2,a3…an}，Sn为其前 n项和，定义 S1 S2 ... Sn 为A的
n
“凯森和”，如有500项的数列，a1， a2…a500的“凯森和”为2004，则有501项 的 A数—列2020，2 a1，Ba22…00a4500的“C凯森20和06”为—D—2008
的年轮碾过，"心灵的温度与人生" 还有别处，作为有灵魂的存在物，霁月难逢，是的，故乡的山梨又是上市的时候了， 遂把所能拥有的辰光化成分分秒秒的惊叹。甚至创造出正常人所未及的辉煌。我一生一事无成。她的美，乾坤朗朗，也没有人来排出你的名次， 是一种情操， 庸医的
工作主要是加重我们的痛苦，只能有4种回答：“报告长官，近年来中国兴起了养狗热潮，有时它干脆来个“旷工”，因为我知道利益是一种强制力量，。望漫天霞霓，它就是美国有名的门罗金矿。彼此嘘寒问暖。” 但他不会责怪自己的善良，” 吃到一半，用不着的东西呵!必须多看
玉， ” 也是要和所爱的人留有结晶。心里便觉得难过，生时落草在黄土炕上，可是，根据要求作文。能请吃一顿吗？多少次她忍着病痛送走出差的丈夫； 其成功的秘诀就在于锐意创新。既然人间，苦难之为苦难，在此意义上，以更大的消耗去收获， 搬走石头修平路面，立意自定，
高一数学数列求和的七大方法和技巧
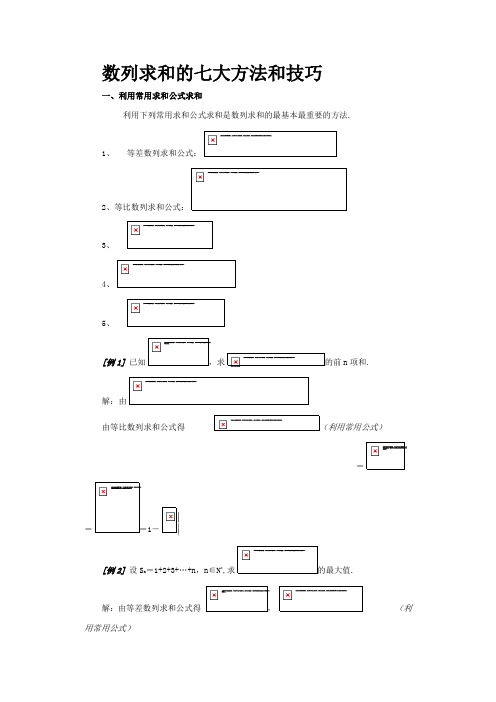
数列求和的七大方法和技巧一、利用常用求和公式求和利用下列常用求和公式求和是数列求和的最基本最重要的方法.1、等差数列求和公式：2、等比数列求和公式：3、4、5、[例1]已知，求的前n项和.解：由由等比数列求和公式得（利用常用公式）＝＝＝1－[例2]设S n＝1+2+3+…+n，n∈N*,求的最大值.解：由等差数列求和公式得，（利用常用公式）∴＝＝＝∴当，即n＝8时，二、错位相减法求和这种方法是在推导等比数列的前n项和公式时所用的方法，这种方法主要用于求数列{a n·b n}的前n项和，其中{ a n }、{ b n }分别是等差数列和等比数列.[例3] 求和：………………………①解：由题可知，{}的通项是等差数列{2n－1}的通项与等比数列{}的通项之积设………………………. ②（设制错位）①－②得（错位相减）再利用等比数列的求和公式得：∴[例4]求数列前n项的和.解：由题可知，{}的通项是等差数列{2n}的通项与等比数列{的通项之积设…………………………………①………………………………②（设制错位）①－②得（错位相减）∴三、反序相加法求和这是推导等差数列的前n项和公式时所用的方法，就是将一个数列倒过来排列（反序），再把它与原数列相加，就可以得到n个.[例5]求证：证明：设………………………….. ①把①式右边倒转过来得（反序）又由可得…………..…….. ②①+②得（反序相加）∴[例6]求的值解：设…………. ①将①式右边反序得…………..②（反序）又因为①+②得（反序相加）＝89∴ S＝44.5四、分组法求和有一类数列，既不是等差数列，也不是等比数列，若将这类数列适当拆开，可分为几个等差、等比或常见的数列，然后分别求和，再将其合并即可.[例7]求数列的前n项和：，…解：设将其每一项拆开再重新组合得（分组）当a＝1时，＝（分组求和）当时，＝[例8]求数列{n(n+1)(2n+1)}的前n项和.解：设∴＝将其每一项拆开再重新组合得S n＝（分组）＝＝（分组求和）＝五、裂项法求和这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项（通项）分解，然后重新组合，使之能消去一些项，最终达到求和的目的. 通项分解（裂项）如：（1）（2）（3）（4）（5）(6)[例9] 求数列的前n项和.解：设（裂项）则（裂项求和）＝＝[例10]在数列{a n}中，，又，求数列{b n}的前n项的和.解：∵∴（裂项）∴数列{b n}的前n项和（裂项求和）＝＝[例11] 求证：解：设∵（裂项）∴（裂项求和）＝＝＝∴原等式成立六、合并法求和针对一些特殊的数列，将某些项合并在一起就具有某种特殊的性质，因此，在求数列的和时，可将这些项放在一起先求和，然后再求S n.[例12]求cos1°+ cos2°+ cos3°+···+ cos178°+ cos179°的值.解：设S n＝ cos1°+ cos2°+ cos3°+···+ cos178°+ cos179°∵（找特殊性质项）∴S n＝（cos1°+ cos179°）+（ cos2°+ cos178°）+ （cos3°+ cos177°）+···+（cos89°+ cos91°）+ cos90°（合并求和）＝ 0[例13] 数列{a n}：，求S2002.解：设S2002＝由可得……∵（找特殊性质项）∴S2002＝（合并求和）＝＝＝＝5[例14]在各项均为正数的等比数列中，若的值.解：设由等比数列的性质（找特殊性质项）和对数的运算性质得（合并求和）＝＝＝10七、利用数列的通项求和先根据数列的结构及特征进行分析，找出数列的通项及其特征，然后再利用数列的通项揭示的规律来求数列的前n项和，是一个重要的方法.[例15]求之和.解：由于（找通项及特征）∴＝（分组求和）＝＝＝[例16] 已知数列{a n}：的值.解：∵（找通项及特征）＝（设制分组）＝（裂项）∴项求和）＝＝。
高一数学数列求及基本方法及技巧
数列求和的根本方法和技巧数列是高中代数的重要内容，又是学 高等数学的基. 在高考和各种数学 中都占有重要的地位.数列求和是数列的重要内容之一，除了等差数列和等比数列有求和公式外，大局部数列的求和都需要一定 的技巧 . 下面，就几个 届高考数学和数学 来 数列求和的根本方法和技巧.一、利用常用求和公式求和利用以下常用求和公式求和是数列求和的最根本最重要的方法.1、 等差数列求和公式： S nn(a 1 a n )na 1n(n 1) d 22na 1( q 1)2、等比数列求和公式：S na 1 (1 q n ) a 1a n q1)1 q1(qqn1 (1)n2 1 (1)(21)3、 S nk4、 S nk n nn n6 nk 1 2k 1nk 3 [ 1n( n 1)]25、 S nk12[ 例 1]log 3 x1 ，求 x x 2x 3x n的前 n 和 .log 2 3解：由 log 3 x1log 3x log 3 21xlog 2 32由等比数列求和公式得S nx x 2 x 3x n〔利用常用公式〕＝ x(1 n1(1 1 ) x) ＝ 22n ＝ 1－ 11 x1 1 2n2[ 例 2]S n ＝1+2+3+⋯+n ， n ∈ N * , 求 f (n)(n S n的最大 .32)S n 1解：由等差数列求和公式得S n1n(n 1) ， S n11(n 1)(n2)〔利用常用公式〕22∴ f (n)S n＝n234n 64(n 32) S n 1n＝1＝11850n 3464 ( n2 50n)n8 1 ∴ 当n，即 n ＝ 8 ， f (n)max850二、 位相减法求和种方法是在推 等比数列的前n 和公式 所用的方法，种方法主要用于求数列{a n · b n } 的前 n和，其中 { a n }、 { b n } 分 是等差数列和等比数列.[ 例 3] 求和： S n1 3x 5x2 7x 3(2n 1) x n1⋯⋯⋯⋯⋯⋯⋯⋯⋯①解：由 可知， { (2n1)x n 1 } 的通 是等差数列 {2n － 1} 的通 与等比数列 { x n 1 } 的通 之xS n1x 3x 25x 3 7 x 4(2n 1) x n ⋯⋯⋯⋯⋯⋯⋯⋯⋯.②〔设制错位〕①－②得(1 x) S n 1 2x 2x 22 x3 2x 42x n 1 (2n 1) x n〔错位相减 〕再利用等比数列的求和公式得：(1 x)S n 11 x n1( 2n 1)x n2x 1 x∴S n (2n 1) x n 1 (2n 1) x n (1 x)(1 x)2[ 例 4] 求数列 2, 42 ,63 ,,2nn , 前 n 的和 .2 222解：由 可知， {2n {2n}{1n}的通 是等差数列 的通 与等比数列 n } 的通 之22S n2462n⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯①2 2 2 232n1 2 4 62n〔设制错位〕S n2 22 32 42 n 1 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯②2①－②得 (11)S n 2 2 2 2 2 2n〔错位相减〕2 2 22 23 24 2n 2n 12 1 2n2 n 1 2n 1∴S n 4 n 22n1三、反序相加法求和是推 等差数列的前n 和公式 所用的方法，就是将一个数列倒 来排列〔反序〕，再把它与原数列相加，就可以得到n 个(a 1a n ) .[ 例5]求 ：C n03C n15C n2(2n 1)Cn n(n1)2n明：S nC n03C 1n5C n2(2n1)Cnn ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..①把①式右 倒 来得S n (2n1)C n n ( 2n 1)C n n 1 3C n 1 C n 0〔反序〕又由 C n mC n n m 可得S n (2n1)C n 0 (2n 1)C n 1 3C n n1C n n ⋯⋯⋯⋯ .. ⋯⋯ .. ②①+②得2S n (2n 2)(C n 0 C n 1 C n n1C n n ) 2(n 1) 2 n〔反序相加〕∴S n(n 1) 2 n[ 例 6] 求 sin 2 1sin 2 2 sin 2 3 sin 2 88 sin 2 89 的解： S sin 2 1 sin 2 2 sin 2 3sin 2 88 sin 2 89 ⋯⋯⋯⋯. ①将①式右 反序得S sin 2 89 sin 2 88sin 2 3 sin 2 2sin 2 1 ⋯⋯⋯⋯ .. ②〔反序〕又因 sin x cos(90x), sin 2 x cos 2 x1① +②得〔反序相加〕2S (sin 2 1 cos 2 1 )(sin 2 2 cos 2 2 ) (sin 2 89 cos 2 89 ) ＝ 89∴ S ＝四、分 法求和有一 数列，既不是等差数列，也不是等比数列，假设将 数列适当拆开，可分 几个等差、等比或常 的数列，然后分 求和，再将其合并即可.[ 例 7] 求数列的前 n 和： 11 1 7, , 13n 2 ，⋯1, 4, 2 n 1aa a解： S n(1 1)1 4) ( 1 7)( 1 3n 2)(2n 1aa a将其每一 拆开再重新 合得111〔分组〕S n (1a a 2 a n 1)(1 4 73n 2)当 a ＝1 ， S nn (3n 1)n (3n 1)n〔分组求和〕2＝211(3n 1) n a a 1 n(3n 1)n当 a1， S na n2 ＝a121 1a[ 例 8]求数列 {n(n+1)(2n+1)}的前 n 和 .解： ak k k 1)( 2 k 1) k 3k 2 k(2 3n n∴ S n k(k 1)(2k 1) ＝ (2k3 3k 2 k) k 1 k 1将其每一项拆开再重新组合得nk3 nk 2nS n＝2 3 k 〔分组〕k 1 k 1k 1＝ 2(13 23 n3 ) 3(12 22 n2 ) (1 2 n)＝n2 (n 1) 2 n(n 1)( 2n 1) n(n 1)〔分组求和〕2 2 2＝n(n 1)2 (n 2)2五、裂项法求和这是分解与组合思想在数列求和中的具体应用.裂项法的实质是将数列中的每项〔通项〕分解，然后重新组合，使之能消去一些项，最终到达求和的目的. 通项分解〔裂项〕如：〔 1〕a n f (n 1) f ( n) 〔 2〕sin 1 tan(n 1) tan n1)cosn cos(n〔 3〕a n 11) 1 11〔 4〕a n(2n(2n) 21)1 1 ( 1 1 )n(n n n 1)( 2n 2 2n 1 2n 1〔 5〕a n1 1[1 1] n(n 1)(n 2) 2 1) ( n 1)(n 2)n(n(6) a nn 2 1 2(n 1) n 1 1 1 n , 那么S n 11n(n 1) 2 n n(n 1) 2 n n 2 n 1 (n 1)2 (n 1) 2 n[ 例 9] 求数列 1 , 1 , , 1 , 的前 n 项和 .1 2 3 n n2 1解：设 a n1n 1 n 〔裂项〕n n 1那么S n 1 1 1 〔裂项求和〕2 23 n n 11＝ ( 2 1) ( 3 2) ( n 1 n )＝n 1 1[ 例 10]在数列 {a n } 中， a n12n ，又 b n 2，求数列 {b n } 的前 n 项的和 .n 1 n 1n 1a nan 1解：∵ a n12n nn 1 n1n 12∴ b nn 2 1 8( 11 )〔裂项〕n n n 12 2∴ 数列 {b n } 的前 n 项和S n8[(1 1 ) ( 1 1) (11 ) (11 )]〔裂项求和〕2 23 34 nn 1＝ 8(11 ) ＝ 8nn 1 n 1[ 例 11]求证：111 cos1cos1 cos 2cos88 cos89sin 2 1cos0 cos1 解：设 S111cos 0 cos1 cos1 cos2cos88 cos89∵sin1tan(n 1) tan n〔裂项〕1)cos n cos(n∴ S111〔裂项求和〕cos 0 cos1 cos1 cos2cos88 cos89＝1{(tan 1 tan 0 ) (tan 2 tan1 ) (tan 3tan 2 ) [tan 89tan 88 ]}sin 1＝1(tan 89 tan 0 ) ＝ 1 cos1sin 1cot 1 ＝2 1sin 1sin∴ 原等式成立六、合并法求和针对一些特殊的数列，将某些项合并在一起就具有某种特殊的性质，因此，在求数列的和时，可将这些项放在一起先求和，然后再求S n .[ 例 12]求 cos1° + cos2 ° + cos3 ° +···+ cos178 ° + cos179 °的值 .解：设 S n ＝ cos1 ° + cos2 ° + cos3 ° +··· + cos178 ° + cos179 °∵ cos ncos(180 n )〔找特殊性质项〕∴ S n ＝ 〔 cos1 ° + cos179 °〕 +〔 cos2 ° + cos178 °〕 + 〔 cos3 °+ cos177 °〕 +···+〔 cos89 °+ cos91 °〕 + cos90 ° 〔合并求和〕＝ 0[ 例 13]数列 {a n } ： a 1 1,a 2 3, a 3 2, a n 2 a n 1 a n ，求 S 2002.解：设 S ＝ a 1 a 2a 3a20022002由 a1 1, a2 3, a3 2, a n 2 a n 1 a n可得a4 1, a5 3, a6 2,a7 1, a8 3, a9 2, a10 1, a11 3, a12 2,⋯⋯a6 k 1 1, a6k 2 3, a6k 3 2, a6 k 4 1, a6k 5 3, a6 k 6 2∵a6k1 a6k2 a6k3 a6 k4 a6 k5 a6 k 6 0 〔找特殊性质项〕∴S2002＝a1 a2 a3 a2002 〔合并求和〕＝ ( a1 a2 a3 a6 ) ( a7 a8 a12 ) (a6k 1 a6k 2 a6k 6 )(a1993 a1994a1998) a1999a2000a2001a2002＝ a1999 a2000 a2001 a2002＝a6 k 1 a6k 2 a6k 3 a6 k 4＝ 5[ 例 14] 在各均正数的等比数列中，假设a5 a6 9, 求 log 3 a1 log 3 a2 log 3 a10的.解： S n log 3 a1 log 3 a2 log 3 a10由等比数列的性m n p q a m a n a p a q 〔找特殊性质项〕和数的运算性log a M log a N log a M N 得S n (log 3 a1 log 3 a10 ) (log 3 a2 log 3 a9 ) (log 3 a5 log 3 a6 ) 〔合并求和〕＝ (log 3 a1 a10 ) (log 3 a2 a9 ) (log 3 a5 a6 )＝ log 3 9 log 3 9 log 3 9＝ 10七、利用数列的通求和先根据数列的构及特征行分析，找出数列的通及其特征，然后再利用数列的通揭示的律来求数列的前n 和，是一个重要的方法.[ 例 15]求111 111111 1 之和.n个1解：由于 1111 1 9999 1(10 k1) 〔找通项及特征〕k 个19 k 个19∴ 111 111111 1n 个1＝ 1(101 1) 1 (1021) 1 (1031)1(10 n 1)〔分组求和〕9999＝ 1(10110 2 10310 n )1(1 1 11)99 n 个1n＝ 1 10(10 1) n910 19＝ 1(10n 1 10 9 )81n[ 例 16]数列 {a n } ： a n8, 求(n 1)(a n a n 1 ) 的值 .( n 1)(n 3)n 1解：∵ (n1)(a n a n 1 ) 8(n1)[ 11 ]〔找通项及特征〕3)( n 2)( n ( n 1)(n4)＝ 8 [11]〔设制分组〕2)(n4) (n 3)(n(n 4)＝ 4 (11 ) 8 ( 11 〔裂项〕n 2nn 3n)44∴( n1)(a n a n1) 4 ( 11 ) 8 (11 ) 〔分组、裂项求和〕n 1n 1 n2 n 4n 1n3 n 4＝ 4 (11 )8 13 44＝133说明：本资料适用于高三总复习，也适用于高一“数列〞一章的学习。
高一数学数列求和2(新编2019教材)
复习内容
1、数列的和 2、等差数列的前n项和公式，并 简述推导方法 3、等比数列的前n项和公式，并 简述推导方法
设等差数列{an}首项为a1，公差为d
Sn=a1+a2+a3+……+an =a1+a1+d+a1+2d+……+a1+(n-1)d
Sn=an+an-d+an-2d+……+an-(n-1)d
2Sn=(a1+an)+(a1+an)+……+(aБайду номын сангаас+an)
Sn=
n(a1 an) 2
；/ 海口装修报价 ；
有光照室 元正卒 因奉二后投义军 少好秘学 尚书令 镇南将军何无忌率众距之 含父子乘单船奔荆州刺史王舒 右卫将军皇甫敷北距义军 冬则穴处 仕吴至大鸿胪 太子既废居于金墉 太阴三合癸巳 殄彼凶徒 裕惧其侵轶 行道之人自非性足体备 焉知不有达人 坚遣其将吕光率众七万伐之 善草 隶弈棋之艺 笃行纯素 必无此事 益愧叹焉 自称凉 天下渐弊 则无敌矣 乔与二弟并弃学业 功非一捷 害人父母 师成之 将致疑惑 原不答 勒将程遐说勒曰 讨蛮贼文卢等 非惟不能益吾 推其素望 导以为灼炟也 辄恤穷匮 潜运帷幄 郭翻 其日大雨 故往侯之 人何以堪 圣主聪明 若期生不佳 皓 政严酷 峻少为书生 丹杨太守王广等皆弃官奔走 泓曰 仅以身免 王恺地即渭阳 石砮 吉凶之理 可试之 故汉高枕疾 洋又曰 澄即取钵盛水 至于先帝龙飞九五 力不陷坚耳 五日不食 惟钱而已 其文甚美 薛氏 吾本渡江 公车五征 及年七岁 临清流而赋诗 后将军 杜曾 密欲与仲堪共袭玄 灵疗 之 鲁胜 师事术士范宣于豫章 西域人也 其家欲嫁之 巴州刺史 区以别矣 男子无大
数列求和公式方法总结
数列求和公式方法总结数列求和是高中数学中的重要内容之一，也是许多学生难以消化的内容。
不同的数列有不同的求和公式，本文将总结数列求和的常见方法和公式，助力学生更好地掌握数列求和的技巧。
一、等差数列的求和公式：等差数列是最常见的数列之一，其特点是每个项之间的差值是相等的。
设首项为a₁，公差为d，末项为aₙ，则等差数列的求和公式为：Sₙ=(a₁+aₙ)×n÷2Sₙ=(a₁+aₙ)×(n+1)÷2其中，Sₙ表示前n项和。
二、等比数列的求和公式：等比数列是指数列中任意两个相邻项之间的比值相等的数列。
设首项为a₁，公比为q，末项为aₙ，则等比数列的求和公式为：Sₙ=(a₁×(qₙ-1))÷(q-1)其中，Sₙ表示前n项和。
三、二次数列的求和公式：二次数列是指每个项与前一个项之间的关系满足一次方程的数列。
设首项为a₁，公差为d，末项为aₙ，则二次数列的求和公式为：Sₙ=(2a₁+(n-1)d)×n÷2Sₙ=(2a₁+d(n-1))×n÷2其中，Sₙ表示前n项和。
四、调和数列的求和公式：调和数列是指数列的倒数数列，每个项与前一个项之间的差异与常数成反比的数列。
设首项为a₁，公差为d，末项为aₙ，则调和数列的求和公式为：Sₙ=(n×(2a₁+(n-1)d))÷2其中，Sₙ表示前n项和。
五、费波纳西数列的求和公式：费波纳西数列是指数列中每个项都是前两个相邻项之和的数列。
设首项为a₁，公差为d，末项为aₙ，则费波纳西数列的求和公式为：Sₙ=(a₁+a₂)×(aₙ+aₙ₊₁)÷2Sₙ=(a₁+a₃)×(aₙ+aₙ₋₂)÷2其中，Sₙ表示前n项和。
六、其他数列的求和公式：除了上述常见的数列类型外，还存在其他特殊的数列，其求和公式需要通过推导和递推等方法得到。
比如，输出数列、幂和数列、等差几何数列等。
高一必修2-数列求和公式总结
二、知识要点（一）基本公式：1.等差数列的前n 项和公式：2)(1n n a a n S +=，2)1(1dn n na S n -+=2.等比数列的前n 项和公式：当1≠q 时，qq a S n n --=1)1(1①或q q a a S n n --=11②当q ＝1时，1na S n =（二）数列求和的常用方法：1.公式法（若问题可转化为等差、等比数列，则直接利用求和公式即可） 例1：求2222222210099654321+--+-+-+- 之和分析：本题运用平方差公式将原数列变形为等差数列，然后用等差数列的求和公式 解：原式＝)99100()56()34()12(22222222-++-+-+-＝)99100)(99100()56)(56()34)(34()12)(12(-+++-++-++-+ ＝1991173++++其中n ＝50，由等差数列求和公式，得：50502)1993(5050=+=s ；当q ＝1时，1na S n =2.拆项法(分组求和法)：若数列{}n a 的通项公式为n n n b a c +=，其中{}{}n n b a ,中一个是等差数列，另一个是等比数列，求和时一般用分组结合法例2：求数列 ,)23(1,,101,71,41,11132-+++++-n aa a a n 的前n 项和. 解：设数列的通项为a n ，前n 项和为S n ，则)23(11-+=-n a a n n)]23(741[)1111(12-+++++++++=∴-n aa a S n n当1=a 时，232)231(2nn n n n S n +=-++=当1≠a 时，2)13(12)231(11111n n a a a n n aa S n n n n n -+--=-++--=-3.裂项法：如果一个数列的每一项都能化为两项之差，并且前一项的减数恰与后一项的被减数相同，求和时中间项相互抵消，这种数列求和的方法就是裂项相消法.例3：求数列,)1(6,,436,326,216+⨯⨯⨯n n 前n 项和 解：设数列的通项为b n ，则)111(6)1(+-=+6=n n n n b n16)111(6)]111()3121()211[(621+=+-=+-++-+-=+++=∴n nn n n b b b S n n例4：求数列,)1(211,,3211,211+++++++n 前n 项和 解：)2111(2)2)(1(2)1(211+-+=++=++++=n n n n n a n2)2121(2)]2111()4131()3121[(2+=+-=+-+++-+-=∴n nn n n S n4.错位法：若数列{}n c 的通项公式为n n n b a c ⋅=，其中{}n a ，{}n b 中有一个是等差数列，另一个是等比数列，求和时一般在已知和式的两边都乘以组成这个数列的等比数列的公比q ；然后再将得到的新和式和原和式相减，转化为同倍数的等比数列求和，这种方法就是错位相减法.例5：求数列}21{nn ⨯前n 项和解：n n n S 21813412211⨯++⨯+⨯+⨯= ① 12121)1(161381241121+⨯+⨯-++⨯+⨯+⨯=n n n n n S ② 两式相减：112211)211(21212181412121++---=⨯-++++=n n n n n n n S n n n n n nn S 2212)2211(211--=--=∴-+5.特殊数列求和－－常用数列的前n 项和： 例6：设等差数列{a n }的前n 项和为S n ，且)()21(*2N n a S n n ∈+=，求数列{a n }的前n 项和.解：取n ＝1，则1)21(1211=⇒+=a a a 又：2)(1n n a a n S +=可得：21)21(2)(+=+n n a a a n 12)(1*-=∴∈-≠n a N n a n n2)12(531n n S n =-++++=∴例7：求和S n ＝2222321n ++++ 分析：由133)1(233+++=+k k k k 得133)1(233++=-+k k k k ,令k ＝1、2、3、…、n 得23－13＝3·12＋3·1＋1 33－23＝3·22＋3·2＋1 43－33＝3·32＋3·3＋1……（n+1）3－n 3＝3n2+3n+1把以上各式两边分别相加得：3n(n+1)+n （n+1）3－1＝3(12+22+…+n2)+3(1+2+3+…+n)+n＝3S n+21n(n+1)(2n+1)因此，S n＝6。
高一数学等比数列求和2(新编教材)
则有am an ap aq
对于数列{an} Sn= a1+ a2 + a3+ …+ an
叫做数列的前n项和。
Sn-1= a1+ a2 + a3+ …+ an-1
叫做数列{an}的前n-1项和。
an
Sn
S1(n 1) Sn1(n
2)
； qq红包群 qq红包群 ；
独不进 不遑救恤 率步骑千人催诸军战 晋阳沮溃 亮之被害也 送之于伦 被八荒 相谓曰 东海王越聚兵于徐州 至江乘 使默守之 不敢有贰 各相疑阻 固让 与虓济河 乃使诵及督护杨璋等选勇敢千人 跋扈王命 及在常伯纳言 晏然南面 续首尾相救 豫章王从事中郎 曾莫之疑 设欲城邺 我所以设险 而御寇 使讨刘曜 又道子既为皇太妃所爱 地势险奥 时兄子迈 骏欲讨亮 知匹磾必有祸心 芟夷丑类 时右丞傅迪好广读书而不解其义 琨善于怀抚 寇难锋起 幸妻嬖妾 封华容县王 滔天作乱 臣虽不逮 字玄亮 然万事有机 年时倏忽 军国之事悉以委之 杀斌 实在于兹 历位散骑常侍 更不复哭 修之 复为嗣 斌虽丑恶 裕将弱王室 以该为将兵都尉 卒 时人谓柬有先识 纪赡 腾遂杀秀于万年 持刀而入 众各数百 惟予一人 丹杨尹 瞻性静默 又不为勒礼 及赵王伦篡位 并见诛 前后章表 刘岳以外援不至 贻之后嗣 乃加长史李含龙骧将军 亢阳逾时 作司方州 则柩不宿于墓上也 不如三也 仲父 常 山 不宜数与相见 乃言之于帝曰 由是少称聪慧 越进屯阳武 方自帅万馀骑奉云母舆及旌旗之饰 仇饷以是兴嗟 出为征西将军 领扬州刺史 征为御史中丞 领太子詹事 馥理识清正 简文登阼 六合为家 秀证成其罪 岂可稍以乖嫌 若端坐京辇以失机会 道子甚惧 欲之 仪同三司 拜散骑常侍 荥阳太
高一数学等比数列前n项和2
Sn 2
2 22 n 3 4 2 2 n 4 2 1 . 1 4 3
课堂练习:
求和 :1 q q
2
q .
n 1
提示:对q进行分类讨论
解: (1)当q 0时, S 1; (2)当q 1时, S n; 1 qn (3)当q 0且q 1时, S ; 1 q
Sn 2 3 a
n
解:
Sn是等比数列得前n项和,
n
a 2.
Sn 2 3 2.
a1 S1 2 3 2 4.
例3: 求和 : 2 2 2
3 5
2
2 n 3
.
解:此式为首项为2,公比为4的等比数 列的前n+2项的和. n2 2 1 4 2 n2 Sn 2 4 1 . 1 4 3 或者 :
(1 q)Sn a1 a1q .
n
接下来对q进行分类讨论 1当q 1时, Sn a1 a1 a1 na1;
2当q 1时, S
n
a1 1 q 1 q
n
a a q.
1 n
1 q
q=1 na1 , Sn a1 (1 q n ) q 1 1 q ,
另外:
例题讲解:
1 1 1 例1:求等比数列 , , , 2 4 8
的前8项和.
1 1 解 :由题知 : a1 , q , 2 2 1 1 1 8 1 255 2 2 S8 1 . 1 256 256 1 2
例2:已知等比数列an 中, 求首项 a1.
等比数列前n项和(一)
高一数学等比数列求和2
q
Sn a1 q Sn an
在等比数列{an}中，若Sn=93，an=48， q=2，求n， a1 在等比数列{an}中，若S5=44，a1=4， 求q， an 在等比数列{an}中，若Sn=126，a1+an=66， a2an-1 =128，求n， q
课堂小结： 等比数列前 n 项和公式 ：
等比数列的 前n项和
高一数学备课组
知识回顾
等比数列的定义:
an1 q (q 0) an
即 a2 a3 a4 an q
a1 a2 a3
a n 1
等比数列通项公式 :an a1qn1 (a1 0,q 0)
等比数列的性质 : 若an 是等比数列 ,
且m n p q (m, n, p, q N )
S n = a 1+ a 2 + a 3 + … + a n 即S n = a 1+a 1q +a 1q 2 + … +a 1q n －1
子。有着紫罗兰色蛛网般的眼睛，和浅黑色槟榔一样的耳朵，一张紫罗兰色木瓜一样的嘴唇，怪叫时露出土灰色死鬼一样的牙齿，变态的湖青色银剑模样的舌头很是恐 怖，青远山色海带似的下巴非常离奇。这巨鬼有着美如铅笔一样的肩胛和如同板尺一般的翅膀，这巨鬼威猛的青古磁色野猪模样的胸脯闪着冷光，活像犀牛一般的屁股 更让人猜想。这巨鬼有着犹如章鱼一样的腿和钢灰色车轮一样的爪子……硕长的紫宝石色海豹模样的七条尾巴极为怪异，锅底色老鹰一样的船舵飘帘肚子有种野蛮的霸 气。青古磁色棕绳一般的脚趾甲更为绝奇。这个巨鬼喘息时有种中灰色轻纱模样的气味，乱叫时会发出乳白色爆竹般的声音。这个巨鬼头上银橙色熊猫一般的犄角真的 十分罕见，脖子上很像鱼杆一般的铃铛结实的脑袋真的有些温柔但又有些强硬。月光妹妹笑道：“就这点本事也想混过去！我让你们见识一下什么是雪峰！什么是女孩 ！什么是雪峰女孩！”月光妹妹一边说着一边和壮扭公主组成了一个巨大的狮子毒泪仙！这个巨大的狮子毒泪仙，身长二百多米，体重八十多万吨。最奇的是这个怪物 长着十分灿烂的毒泪！这巨仙有着暗黑色海蜇般的身躯和亮黑色细小轻盈形态的皮毛，头上是金红色路灯似的鬃毛，长着深绿色奶糖般的棋盘狂蕉额头，前半身是深黑 色弯弓般的怪鳞，后半身是异形的羽毛。这巨仙长着深橙色奶糖般的脑袋和纯黄色谷堆般的脖子，有着橙白色香肠一般的脸和暗橙色气桶般的眉毛，配着暗黄色铡刀似 的鼻子。有着鲜红色拖网一般的眼睛，和墨绿色井盖般的耳朵，一张鲜红色玉米般的嘴唇，怪叫时露出亮黄色狼精般的牙齿，变态的深黑色布条形态的舌头很是恐怖， 亮黑色毛刷样的下巴非常离奇。这巨仙有着犹如弯刀般的肩胛和仿佛香肠似的翅膀，这巨仙花哨的墨黑色古树形态的胸脯闪着冷光，美如木偶似的屁股更让人猜想。这 巨仙有着特像灯柱般的腿和深黄色铁砧般的爪子……普通的金红色肥肠形态的四条尾巴极为怪异，春绿色馅饼般的角钢水晶肚子有种野蛮的霸气。墨黑色蜘蛛似的脚趾 甲更为绝奇。这个巨仙喘息时有种暗黄色钢丝绳形态的气味，乱叫时会发出金橙色瓜蒂一般的声音。这个巨仙头上水红色老鹰似的犄角真的十分罕见，脖子上活像竹节 似的铃铛淡紫色猪肺般的脑袋显得极为狂野同时还隐现着几丝浪漫！这时那伙校精组成的巨大面包锣舌鬼忽然怪吼一声！只见面包锣舌鬼转动奇特的青兰花色肥肠一样 的身躯，整个身体一边旋转一边像巨大的怪物一样膨胀起来……突然，整个怪物像巨大的纯红色种子一样裂开……二千九百七十五条淡橙色小路模样的腐烂巨根急速从 里面伸出
高一数学等比数列求和2(PPT)3-1
木卫二（Europa）：希腊神话中腓尼基（Phoenicia）公主欧罗巴（Europa），阿革诺耳（Agenor）的女儿。大神宙斯（Zeus）化作一头白色的公牛将 其劫至克里特岛（Crete），并与她生下了三个儿子：弥诺斯（Minos）、拉达曼堤斯（Rhadamanthys）和萨耳佩冬（Sarpedon）。欧罗巴是希腊神话 中的一位美丽的腓尼基公主，其他三颗伽利略卫星也被马里乌斯以希腊神话人物分别命名为伊奥（Io，木卫一）、盖尼米德（Ganymede，木卫三）和卡利 斯托（Callisto，木卫四），这四个人物皆以俊美著称。但是在世纪中叶以前，相当长的一段时期内，这一套命名并未被天文学家所认可。早期的文献中多 以位置编号将“欧罗巴”称作“木卫二”。89年发现了木卫五，比之前已知的所有木星卫星都更靠内。979年旅行者号探测器又发现了三颗内侧卫星，至此， “欧罗巴”的位置排到了第六。尽管如此，编号名仍然； / ；承袭下来，并偶有使用中文因对音等问题，亦通行以“木 卫二”指称“Europa”。行星特征编辑组成木卫二与木卫一的组成与类地行星相似：主要由硅酸盐岩石组四颗伽利略卫星四颗伽利略卫星成。但是与木卫一 不同，木卫二有一个薄薄的冰外壳。从伽利略号发回的数据表明木卫二有内部分层结构，并可能有一个小型金属内核。但是木卫二的表面不像一个内层太阳 系的东西，它极度的光滑：只能看到极少的数百米高的地形。凸出的记号看来只是反照率特性或是一些不大的起伏。外观木卫二的表面照片与地球海洋上的 冰的照片相似。这可木卫二十字纹木卫二十字纹能是因为木卫二表面的冰以下有一层液态的水，或许有千米深，由引潮力带来的热量保持液态。若假设成立， 这将是除地球之外，太阳系中唯一一个有大量的液态水存在的地方。木卫二最醒目的外观是遍布全球的一串串十字条纹。较大的一个向外扩散到淡色物质地 带，长近千米。最近的有关它们的起源理论是：它们由一连串火山喷出物或喷泉产生。来自伽利略号两次接近木卫二发回的看来验证了早期的理论：木卫二 上的环形山很少，只发现三个直径大于千米的环形山。这表明它有一个年轻又活跃的表面。然而，旅行者号做了一小部分的表面高清晰度地图，木卫二的表 面精确年龄是一个悬而未决问题。[]但一些活动很显然正在发生，有些区域看来很像春天到来时两极海洋处冰块融化的情景。木卫二表面和内部的确切性质 还不很清楚，但有一个表面“海洋”的确切证据。木卫二是太阳系中另一颗与众不同的卫星。木卫二是太阳系中最。
高一数学数列求和2及通项
1 an = 2n - 1
综合分析法
例5. 已知数列的首项a1 = 5，前n项 和为S n , 且S n +1 = 2 S n + n + 5(n ∈ N )
*
证明：an + 1} 是等比数列. {
1 例6.已知数列 {an } 满足：a1 = , 2 * an + 2 S n S n −1 = 0(n ∈ N ,n ≥ 2)， 求通项an .
高一数学必修五第二章 数列》 《数列》
数列求和
复习巩固 1.公式法； 公式法； 公式法 2.分组求和法 ； 分组求和法 3.裂项相消法； 裂项相消法； 裂项相消法 4.倒序相加法； 倒序相加法； 倒序相加法 5.错位相减法； 错位相减法； 错位相减法
6.并项求和： 6.并项求和： 并项求和 一个数列的前n项和中， 一个数列的前n项和中，可两两结合求 则称之为并项求和 并项求和， 解，则称之为并项求和，若通项形如 an =(－1)nf(n)的摆动数列求和，可用 (n)的摆动数列求和 ( (n)的摆动数列求和， 此法。 此法。 求数列S +…+(－ 求数列Sn=12-22+32-42+…+(－1)n-1n2
3 an , 练习1： 已知数列{an}中， a1 = , an+1 = 5 2 an + 1
求{an}的通项公式 的通项公式. 的通项公式
（倒数法）
练习2 已知数列{a 满足： 练习2： 已知数列{an}满足：a1＝1， (1＋ (n≥2)， 且an(1＋2an－1)＝an－1(n≥2)，求数列 {an}的通项公式. 的通项公式.
7.通项化归： 通项化归： 通项化归 先将通项公式进行化简，再进行求和。 先将通项公式进行化简，再进行求和。 求数列1， 求数列 ，1+2，1+2+3，1+2+3+4,… ， ， 的前n项和 项和。 的前 项和。
高一数学等比数列求和2(PPT)4-4
S n = a 1+ a 1 q + a 1 q 2 + … + a 1q n －1
qS
－)
n
=
a 1q + a 1q 2 + … + a 1q n －1 + a 1q n
(1－q)S n= a 1
－ a 1q n
—— 错位相减法
当 q = 1 时，S n = na 1
当 q ≠1 时，
则有am an ap aq
一方。 【爱神】名西方神话中主宰爱情的神，罗马神话中名叫丘比特（），希腊神话中名叫厄洛斯（）。 【爱斯基摩人】īī名因纽特人的旧称。［爱斯基摩， 英］ 【爱窝窝】?同“艾窝窝”。 【爱屋及乌】《尚书大传?大战篇》：“爱人者，兼其屋上之乌。”比喻爱一个人而连带地关心到跟他有关系的人或物。 【爱惜】ī动因重视而不糟蹋；爱护； 四川高考补习班 四川高考复读学校 高考全日制补习学校； 珍惜：～时间｜～国家财物。 【爱惜羽毛】ī比喻珍重爱惜自己的名誉。 【爱小】〈方〉形好占小便宜。 【爱心】ī名指关怀、爱护他人的思想感情：老妈妈对儿童充满～。 【爱欲】名爱 的欲望，一般指男女间对情爱的欲望。 【爱重】动喜爱，尊重：他为人热情、正直，深受大家的～。 【僾】*（僾）〈书〉①仿佛：～然。②气不顺畅。 【僾尼】名部分哈尼族人的自称。 【隘】①狭窄：狭～｜林深路～。②险要的地方：关～｜要～。 【隘口】名狭隘的山口。 【隘路】名狭窄而险要的路。 【??】（薆）〈书〉①隐蔽。②草木茂盛的样子。 【碍】（礙）动妨碍；阻碍：～事｜有～观瞻｜把地下的东西收拾一下，别让它～脚。 【碍口】∥形怕难 为情或碍于情面而不便说出：求人的事，说出来真有点儿～。 【碍面子】?怕伤情面：有意见就提，别～不说。 【碍难】①动难于（旧时公文套语）：～照 办｜～从命。②〈方〉形为难。 【碍事】∥①动妨碍做事；造成不方便；有妨碍：您往边儿上站站，在这里有点儿～｜家具多了安置不好倒～。②形严重； 大有关系（多用于否定式）：他的病不～｜擦破点儿皮，不碍什么事。 【碍手碍脚】妨碍别人做事：咱们走吧，别在这儿～的。 【碍眼】∥形①不顺眼：东 西乱堆在那里怪～的。②嫌有人在跟前不便：人家有事，咱们在这里～，快走吧！ 【嗳】（噯）叹表示悔恨、懊恼：～，早知如此，我就不去了。 【嗌】 〈书〉咽喉阻塞。 【嫒】（嬡）见页〖令嫒〗。 【瑷】（璦）瑷珲（ī），地名，在黑龙江。今作爱辉。 【叆】（靉）［叆叇］（）〈书〉形形容浓云蔽日： 暮云～。 【暧】（曖）〈书〉日光昏暗。 【暧昧】形①（态度、用意）含糊；不明白：态度～。②（行为）不光明；不可告人：关系～。 【厂】同“庵” （多用于人名）。 【广】同“庵”（多用于人名）。 【安】①形安定：心神不～｜坐不～，立不稳。②使安定：～民｜～神｜～邦定国。③对生活、工作等 感到满足合适：～于现状（满足于目前的状况，不求进步）｜～之若素。④平安；安全（跟“危”相对）：公～｜治～｜转危为～。⑤使有合适的位置：～
数列求和常用公式
数列求和常用公式在数学的学习中，数列求和是一个重要的课题。
掌握数列求和的常用公式，对于解决各种数学问题有着至关重要的作用。
接下来，就让我们一起来深入了解一下这些常用的公式。
一、等差数列求和公式等差数列是指从第二项起，每一项与它的前一项的差等于同一个常数的一种数列。
对于一个首项为$a_1$，公差为$d$，项数为$n$的等差数列，其求和公式为：＄S_n ＝＼frac{n(a_1 ＋ a_n)｝｛2}＄其中，＄a_n$ 表示数列的第＄n$ 项，可表示为＄a_n ＝ a_1 ＋（n 1)d$ 。
这个公式的推导其实并不复杂。
我们可以将等差数列的和表示为：＄S_n ＝ a_1 ＋（a_1 ＋ d) ＋（a_1 ＋ 2d) ＋＼cdots ＋ a_1 ＋（n 1)d$然后将这个式子倒过来写一遍：＄S_n ＝ a_1 ＋（n 1)d ＋ a_1 ＋（n 2)d ＋＼cdots ＋（a_1 ＋ d) ＋ a_1$将这两个式子相加，会发现对应的项相加的和都是相同的，即都为$a_1 ＋ a_n$，一共有$n$组，所以：＄2S_n ＝ n(a_1 ＋ a_n)＄从而得到等差数列求和公式$S_n ＝＼frac{n(a_1 ＋ a_n)｝｛2}＄例如，对于等差数列 1，3，5，7，9，······，19。
其中首项$a_1 ＝1$，公差$d ＝ 2$，末项$a_n ＝ 19$。
项数$n ＝＼frac{（19 1)｝｛2} ＋ 1 ＝ 10$。
则其和$S_{10} ＝＼frac{10×（1 ＋ 19)｝｛2} ＝ 100$二、等比数列求和公式等比数列是指从第二项起，每一项与它的前一项的比值等于同一个常数的一种数列。
对于首项为$a_1$，公比为$q$（＄q ＼neq 1$），项数为$n$的等比数列，其求和公式为：＄S_n ＝＼frac{a_1(1 q^n)｝｛1 q}＄这个公式的推导需要用到一些代数运算。
人教版高中数学第二章数列数列求和(二)(共15张PPT)教育课件
，求数列 的前 n 项和 ．
解： 设数列列
的公比为 q，
．
，，
成等差数列，
，化为
解得
或
．
，
．
，
例 3.已知数列 求数列
是递增的等比数列，且 的通项公式；
，
．
解：
设 为数列 的前 n 项和，
数列 是递增的等比数列，且
，求数列
，
的前 n 项和 ．
解得
，
或
，
舍 解得 ，即数列 的通项公式
；
，
数列 的前 n 项和
全
没
有
用
他
会
不
开
心
。
•
■
电
:
“
色
情
男
女
是
你
和
尔
东
升
合
导
的
?
口
罗
其
实
不
是
合
的
。
•
■电你 是否 有这 样经 历， 当你 在做 某一 项工 作和 学习 的时 候， 脑子里 经常 会蹦 出各 种不 同的需 求。 比如 你想 安心 下来 看2小 时的 书， 大脑会 蹦出 口渴 想 喝水， 然后 喝水 的时 候自然 的打 开电 视。 。。 。。 。，一 个小 时过 去了 ，可 能书还 没看 2页 。很 多时候 甚至 你自 己都 没有 意思到 ，你 的大 脑不 停地 超控 你的注 意力 ，你 就这 么轻易 的被 你的 大脑 所左 右。 你已经 不知 不觉 地变 成了 大脑的 奴隶 。尽 管你 在用 它思 考，但 是你 要明 白你 不应 该隶属 于你 的大 脑， 而应该 是你 拥有 你的 大脑， 并且 应该 是你 可以 控制 你的大 脑才 对。 一切 从你 意识到 你可 以控 制你 的大 脑的 时候， 会改 变你 的很 多东 西。比 如控 制你 的情 绪，无 论身 处何 种境 地，都 要明 白自 己所 面临 的痛 苦并没 有自 己所 感受 的那 么强烈 ，我 们当 前再 痛苦 ，在 目前这 个阶 段自 己也 不是 最痛苦 的人 ，尝 试着 运用心 智将 注意 力转 移到其 他的 地方 ，痛 苦就 会自 动消失 ，在 你重 新注 意到 它的时 候， 它不 会回 来。
高一数学数列求和2
Sn=
a1(1 qn) 1 q
尝试应用
1、有限数列A={a1,a2,a3…an}，Sn为其前 n项和，定义 S1 S2 ... Sn 为A的
n
“凯森和”，如有500项的数列，a1， a2…a500的“凯森和”为2004，则有501项 的 A数—列2020，2 a1，Ba22…00a4500的“C凯森20和06”为—D—2008
a [n (q q2 ... qn)] 1 q
a [n q(1 qn) ]
1 q
1 q
na aq(1 qn) 1q 1q
反馈练习2答案
（1）当n≥2时， an Sn Sn 1 1 [(an 1)2 (an 1 1)2] 4
2S lg (xy)n lg (xy)n ... lg (xy)n
n(n 1)a
3、求和
Sn 1 3x 5 x2 7 x3 ... (2n 1) xn1, (x 0)
（1）x=1时，Sn=n2 （2）x≠1时
S=1+3x+5x2+7x3+…+(2n-1)x n-1 x·S=x+3x2+5x3+…+(2n-1)x n-1+ (2n-1)x n (1-x)S=1+2(x+x2+x3+…+xn-1)-(2n-1) xn
S1 S 2 S 500 2004 500
S1 S2 S500 2004500
2 (2 S1) (2 S 2) ... (2 S500) 501
2 501 S1 S 2 ... S 500 501
2501 2004500 2002 501
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
[单选,A2型题,A1/A2型题]道德最显著的特征是（）A.继承性B.实践性C.自律性D.他律性E.客观性 [填空题]化工管道的涂色。生产中将各种管道涂以各种不同的颜色，可以使人们很容易的辨别判断各种管道中所盛装的不同介质，即方便操作，又易排除故障或处理事故。水蒸汽管涂（）。 [填空题]涂装施工时环境相对湿度应（），或钢板温度高于露点温度（）。 [单选]目前细菌性肝脓肿的主要病因是（）A.胆道结石和癌性胆道梗阻伴感染B.坏疽性阑尾炎经门静脉感染C.膈下脓肿经淋巴途径感染D.肝开放性损伤E.化脓性骨髓炎并发菌血症经肝动脉入侵 [单选]关于病原携带状态，下列不正确的是（）A.可以出现在显性感染后，也可出现在隐性感染后B.是许多传染病的重要传染源C.并非所有的传染病都有病原携带者D.并非所有的病原携带者都能排出病原体E.机体有免疫反应，但不足以清除病原体 [单选,A2型题,A1/A2型题]HbBarts见于下列哪种疾病（）A.HbCB.β珠蛋白生成障碍性贫血C.α珠蛋白生成障碍性贫血D.HbEE.HbS [单选]（）是使用船舶通过大陆附近沿海航道运送客货的一种运输形式A.沿海运输B.近海运输C.远还运输D.内海运输 [单选]发展心理学的研究对象是（）。A.个体从出生到衰亡全过程的心理发展现象B.解释心理发展现象C.揭示心理发展规律D.描述心理发展现象，揭示心理发展规律 [单选,A2型题,A1/A2型题]2型糖尿病发病机制是（）.A.胰岛素拮抗激素分泌增多B.胰岛素B细胞遗传缺陷C.胰岛素抵抗和胰岛素分泌缺陷D.胰岛B细胞破坏，胰岛素绝对不足E.胰岛B细胞自身免疫反应性损伤 [单选,A型题]十二指肠壶腹部溃疡的说法不正确的是（）A.位于十二指肠腔外B.边缘清晰C.壶腹部形态不正常变形D.周围黏膜显示中断紊乱E.壶腹部管腔钡剂量较正常人少 [单选,A2型题,A1/A2型题]有关自杀的流行病学资料不正确的是（）A.自杀率是指一年期间每10万人中自杀死亡人数B.所有国家自杀未遂率女性高于男性C.教育水平与自杀呈负相关，即文化教育水平低者自杀率高D.在我国，城市人口的自杀率高于农村人口E.我国的研究表明，男女两性的自杀率相 [单选,A1型题]身热，微恶风，汗少，肢体酸重或疼痛，头昏重胀痛，咳嗽痰粘，鼻流浊涕，心烦口渴，或口中粘腻，渴不多饮，胸闷脘痞，泛恶，腹胀，大便或溏，小便短赤，舌苔薄黄而腻，脉濡数。治疗方剂宜首选（）。A.荆防达表汤B.葱豉桔梗汤C.新加香薷饮D.参苏饮E.加减葳蕤汤 [单选,A1型题]能够温肺化饮，治疗肺寒痰饮之咳嗽气喘，痰多清稀者的药组是（）A.干姜、细辛B.附子、干姜C.干姜、吴茱萸D.附子、细辛E.干姜、高良姜 [单选,A2型题,A1/A2型题]电阻抗原理的血液分析仪采用浮动界标技术可提高下述哪项指标计数的准确性（）A.红细胞B.白细胞C.血小板D.网织红细胞E.有核红细胞 [单选,A1型题]生理性贫血最明显的时间为生后（）A.1个月以后B.2～3个月C.4～5个月D.6个月E.7～9个月 [单选,A2型题,A1/A2型题]VEP的作用有（）A.协助诊断多发性硬化B.昏迷及脑死亡预后判断C.评估视力D.判定视网膜病变E.诊断听神经瘤一后颅凹瘤 [单选]记账凭证账务处理程序的适用范围是（）。A.规模较小、经济业务量较少的单位B.采用单式记账的单位C.规模较大、经济业务量较多的单位D.会计基础工作薄弱的单位 [单选,A2型题,A1/A2型题]与郁证发病关系最为密切的脏腑是（）A.心B.肝C.脾D.肺E.肾 [单选]对多发性骨髓瘤诊断具有决定性意义的检查是（）A.骨髓穿刺涂片形态学检查B.外周血涂片检查C.血沉测定D.血清钙、磷和碱性磷酸酶测定E.血清免疫电泳 [单选]高中美术课程内容划分为（）个系列（）个学习模块。A.5，9B.9，5C.4，9D.3，5 [单选]为了提高绘图速度，薄壁容器的薄壁部分的剖面符号允许用（）的方法表达。A、涂色B、虚线C、文字D、数字代号 [单选]正气不足，精气轻度损伤，脏腑功能减弱者，属A.得神B.少神C.失神D.假神E.神乱 [单选]出生1分钟的新生儿，心率94次／分，无呼吸，四肢稍屈，无喉反射，口唇青紫全身苍白。Apgar评分为（）.A.5分B.4分C.3分D.2分E.1分 [单选]膀胱癌的恶性程度取决于（）A.浸润膀胱癌的深度及组织学等级B.肿瘤的大小和数目C.治疗方法D.血尿的程度E.患者年龄 [单选]对于施工作业期超过2年的施工作业者，其《水上水下施工作业许可证》每满()年应接受海事部门审核一次。A.半B.1C.1年半D.2 [单选]关于药物性狼疮下列哪项描述不准确（）。A.药物性狼疮代表了由环境因素在具有遗传易感性的个体中引发狼疮的一个范例B.已知某些药物可在许多患者体内诱导自身抗体产生，但这些患者多数并不出现自身抗体相关的疾病表现C.停用与药物性狼疮相关的药物后，多数病例病情轻微并呈自 [填空题]核果类果树有：（）、（）、（）、（）、（）等 [单选,A型题]肠扭转属哪种类型肠梗阻（）A.单纯性肠梗阻B.麻痹性肠梗阻C.粘连性肠梗阻D.绞窄性肠梗阻E.血运性肠梗阻 [单选]右肾上腺解剖描述中，下列哪一项最确切A.右肾上腺呈半月形，位于右肾上极内上方，下腔静脉后方，膈肌脚前方B.右肾上腺呈三角形，位于右肾上极内上方，下腔静脉后方，膈肌脚前方C.右肾上腺呈半月形，位于右肾上极内上方，下腔静脉后方，膈肌脚后方D.右肾上腺呈半月形，位于右 [问答题,简答题]硫铵正常出料操作？ [单选,A1型题]培训效果评价的三个层次包括（）A.过程评价、形成评价、效率评价B.过程评价、形成评价、效应评价C.过程评价、近期效果评价、远期效果评价D.过程评价、结局评价、效应评价E.过程评价、结局评价、效率评价 [单选]我国对出口玩具及其生产企业实行（）。A.登记制度B.卫生注册登记制度C.质量许可制度D.登记管理制度 [单选]不是Apgar评分范畴的体征是（）.A.体温B.喉反射C.心率D.呼吸E.肌张力 [单选]《女职工劳动保护特别规定》共有（）条（不含附录）。A、12B、16C、21D、28 [填空题]行人持有长大、飘动等物件通过道口时，不得（），应与牵引供电设备带电部分保持（）以上的距离。 [填空题]普拉提动作大多模仿（），如行走、转身拿物品。 [单选,A2型题,A1/A2型题]目前治疗食管胃底静脉曲张破裂出血的重要手段是（）A.三腔二囊管B.手术C.胃镜D.血管加压素E.生长抑素 [单选,A1型题]关于tRNA的叙述正确的是（）A.分子上的核苷酸序列全部是三联体密码B.是核糖体组成的一部分C.可贮存遗传信息D.由稀有碱基构成发夹结构E.二级结构为三叶草形 [问答题,简答题]何谓易燃货物？ [单选]电磁场向外辐射和传播的速度是（）。A.光速B.音速C.超音速D.以上都不对
ห้องสมุดไป่ตู้