3.3高斯光束的传播特性详解
高斯光束的特点
高斯光束的特点高斯光束是一种常见的光束形式，它具有一些独特的特征和性质。
在这篇文章中，我将详细介绍高斯光束的特点和应用。
高斯光束的产生首先，让我们了解高斯光束的产生机制。
高斯光束是由激光器产生的，其中的光源是一个能够将能量转换为光的物质。
在激光器内部，光被引导通过透镜并被聚焦在一个非常小的点上。
这个非常小的点就是所谓的高斯光束。
高斯光束的特性接下来是高斯光束的一些重要特性：1. 对称性：高斯光束在垂直和水平方向上具有相同的亮度分布，呈现完美的对称性。
2. 聚焦性：高斯光束能够通过透镜聚焦到一个非常小的点上，这使得它在许多领域都具有广泛的应用。
3. 窄束宽：高斯光束的光束宽度非常窄，这意味着它能够将光精确地聚焦在一个非常小的区域内。
这使其在制造领域中应用越来越广泛，比如在半导体微处理器和纳米加工中使用。
4. 相位一致性：高斯光束中的光波具有相位一致性。
这意味着高斯光束中的光波可以相互干涉，并且具有非常大的干涉强度，使其在干涉仪和光学器件中应用广泛。
5. 光束稳定性：高斯光束的光束是稳定的，它不会像其他类型的光束一样发生绕射或扩散。
这使得它在通信和传输领域中应用广泛。
应用领域高斯光束在许多领域中都得到了广泛应用，以下是其中一些领域：1. 通信和传输：在光纤通信和光学传输系统中使用高斯光束可以提供更好的性能和可靠性。
高斯光束产生的光束非常窄，可以提供更高的传输速率和更少的数据丢失。
2. 制造和加工：高斯光束的光束聚焦非常精确，因此它在制造和加工领域中使用越来越广泛。
例如，它可以用于微加工、纳米加工、刻蚀和切割。
3. 治疗和医学：高斯光束已被用于医学成像和激光治疗。
它可以用于照射和去除组织中的癌细胞。
4. 科学研究：高斯光束在科学研究领域中应用广泛。
它可以用于干涉仪、单光子实验、冷却原子、微分析和高分辨率成像等。
总结在本文中，我详细介绍了高斯光束的特点和应用领域。
高斯光束通过激光器产生，具有对称性、聚焦性、窄束宽、相位一致性和光束稳定性等特点，其应用领域包括通信和传输、制造和加工、治疗和医学和科学研究等。
光学谐振腔理论-第8节-高斯光束的传输
05 高斯光束的未来发展与应 用
高斯光束在光学通信中的应用
高速光通信
高斯光束在光学通信中具有较高的传输速度和较低的信号衰减，有助于实现高 速、大容量的光通信系统。
远程通信
高斯光束具有较好的光束质量和传输稳定性，适用于长距离的光纤通信，有助 于实现远程、稳定的通信连接。
高斯光束在光学传感中的应用
03 高斯光束的调制与控制
高斯光束的相位调制
01
相位调制是指通过改变高斯光束的相位分布来改变其波前的状 态。
02
常见的相位调制方法包括利用液晶空间光调制器、光栅或其他
光学元件对高斯光束进行相位调制。
相位调制在光学通信、光学传感和光学计算等领域有广泛应用，
03
可以实现光束的聚焦、散焦、波形转换等功能。
高斯光束的波前测量
波前测量概述
波前是描述光束相位变化的物理量，高斯光束的波前测量有助于 了解光束的传播特性和干涉、衍射等光学现象。
波前测量方法
常用的波前测量方法有干涉法、散斑法、剪切干涉法等，可以根据 高斯光束的特点和测量精度要求选择合适的方法。
测量误差来源
波前测量误差主要来源于光束的聚焦、光束截面分布、光学元件的 误差等因素。
高斯光束的聚焦特性
聚焦原理
高斯光束经过透镜聚焦后，其横截面 上的强度分布会发生变化，形成明暗 相间的干涉条纹。
干涉条纹
干涉条纹的形状取决于透镜的焦距和 光束的束腰半径。当透镜焦距一定时 ，束腰半径越小，干涉条纹越密集； 反之，则越稀疏。
02 高斯光束在光学谐振腔中 的应用
光学谐振腔对高斯光束的影响
偏振态调制是指通过改变高斯光 束的偏振状态来改变其电磁场分
布。
常见的偏振态调制方法包括利用 偏振片、电光晶体或液晶等对高
3.3 高斯光束的振幅和强度分布 激光原理及应用 电子课件
2z0
x2 y2 12Lz0
2
z z 0 x 2 2 R 0 y 2 R 01 x 2 R 0 2 y 2 R 0R 0 2 x 2 y 2 R 0
R 0 2 x 2 y 2 z z 0 R 0 2
上一页 回首页 下一页 回末页 回目录
3.3.4 高斯光束的高亮度
第 三 章
激 光 器 的 输 出 特 性
3
3 高 斯 光 束 传 面在其法线方向上单位立体角范围内输出去的辐射功率。 B I SΩ
Ω(R)2 R22
2.一般的激光器是向着数量级约为10－6 sr的立体角范围内输出激光光束的。而普 通光源发光(如电灯光)是朝向空间各个可能的方向的，它的发光立体角为4πsr。 相比之下，普通光源的发光立体角是激光的约百万倍。
三 章
激 光 器
2(z)lz im 021z(z)(z02)222
2 2 L 0
的
输 2.由波动光学知道，在单色平行光照明下，一个半径为 r 的圆孔夫琅和费衍射角
出 (主极大至第一极小值之间的夹角) 0.61r 。与上式相比较可知．高斯光束
特 性
半角远场发散角在数值上等于以腰斑 0 为半径的光束的衍射角，即它已达到了衍 射极限。
§.
3 3.共焦腔基模光束的理论发散角具有毫弧度的数量缀，它的方向性相当好。
3 高 斯
4.由于高阶模的发散角是随着模的阶次的增大而增大，所以多模振荡时，光束的 方向性要比单基模振荡差。
光
束
传
播
特
性
上一页 回首页 下一页 回末页 回目录
共焦腔反射镜面是共焦场中曲率最大的等相位面
§.
3 4.共焦场中等相位面的分布如图(3-9)所示。
3.3 高斯光束的振幅和强度分布 激光原理及应用 电子课件
第 1. 远场发散角2(全角) 定义为双曲线的两根渐近线之间的夹角（参见图(3-8)）
三 章
激 光 器
2(z)lz im 021z(z)(z02)222
2 2 L 0
的
输 2.由波动光学知道，在单色平行光照明下，一个半径为 r 的圆孔夫琅和费衍射角
出 (主极大至第一极小值之间的夹角) 0.61r 。与上式相比较可知．高斯光束
第 三 章
激 光 器
4.
0 (z ) 12 2 sL [1 12 (2 L z)2 L ] (z)0 1(z0 2 )2 0 2 2(z 0 2 2)21
的 输
5. 基模光斑半径随 z 按双曲线规律变化，如图(3-8)。
出
特
性
§.
3
3
高
斯 光
图(3-8) 基模光斑半径随z按双曲线规律的变化
2z0
x2 y2 12Lz0
2
z z 0 x 2 2 R 0 y 2 R 01 x 2 R 0 2 y 2 R 0R 0 2 x 2 y 2 R 0
R 0 2 x 2 y 2 z z 0 R 0 2
上一页 回首页 下一页 回末页 回目录
3.3.2 高斯光束的相位分布
第
2. R 0 2 x 2 y 2 z z 0 R 0 2 表明等位相面在近轴区域可看成半径为R0的球面
x2
Ly2](mn1)(2)
kL212Lz12L2zLz2
x2
Ly22zkL212Lz0
2z0
忽略由于z变化引起的 的微小变化，用 ( z0 )代替 (z)，则在腔轴附近有
2z
z z0
1
L 2z L
2
x2
y2 L
33高斯光束的传播特性详解
exp
1
4
2
x2 y2
s2
——基模截面是高斯函数
2、光斑尺寸振幅下降为最大值1/e时的光斑半径
(z) s
2
1 2 s
2
1
4z2 L2
3
(z) s 1 2 s
2
2
ωs xs2 ys2 L
4z2
1
L2
共焦谐振腔示意图
25
长半径球面腔
长半径球面谐振腔的性能介于共焦腔与球面腔之间，它的特点 如下： 1） 中等的衍射损耗；2）较易安装调整； 3）模体积很大； 4）腔内没有很高的光辐射聚焦现象；
3.3 高斯光束的传播特性
回顾 ——求解对称开腔中的自再现模积分方程, 了解输出激光的具体场的分布
前瞻 —— 研究高斯光束的传播特性
1
3.3.1 高斯光束的振幅和强度分布
一、共焦腔内或腔外的一点的行波场的解析式：
umn x, y, z CmnHm
2 1
2
2 ws
x Hn
17
数值例:
器件
辐射能量 脉冲时间
普通红宝石激光器
1J
10-4s
调Q红宝石激光器
1J
10-9s
调Q及锁模红宝石激光器 1J
10-12～10-13s
P 104W 109W 1012～1013 W
*结论:输出能量一定时, 激光器由于脉冲时间缩短可使△I很大; 而且因θ(或Ω)很小, 故亮度B很大。
18
s 20
2 2 0
20
小结：高斯光束的基本性质
1. 高斯光束在其轴线附近可看作是一种非均 匀高斯球面波，
高斯光束的传播讲义
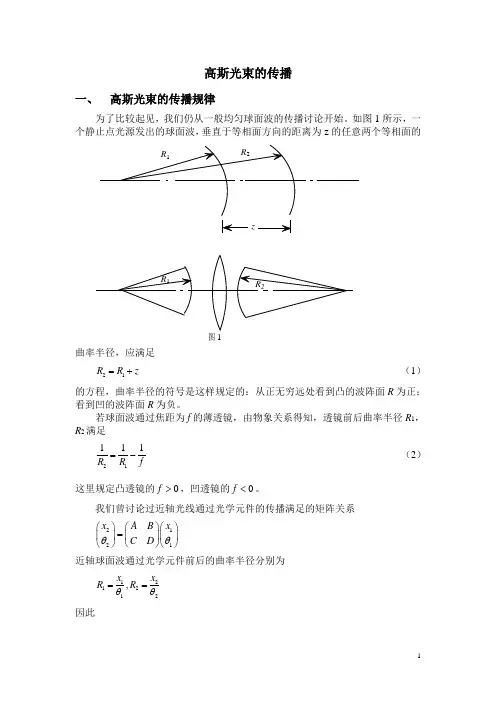
高斯光束的传播一、 高斯光束的传播规律为了比较起见，我们仍从一般均匀球面波的传播讨论开始。
如图1所示，一个静止点光源发出的球面波，垂直于等相面方向的距离为z 的任意两个等相面的z图1曲率半径，应满足21R R z =+（1）的方程，曲率半径的符号是这样规定的：从正无穷远处看到凸的波阵面R 为正；看到凹的波阵面R 为负。
若球面波通过焦距为f 的薄透镜，由物象关系得知，透镜前后曲率半径R 1，R 2满足21111R R f=- （2）这里规定凸透镜的0f >，凹透镜的0f <。
我们曾讨论过近轴光线通过光学元件的传播满足的矩阵关系2121x x AB CD θθ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭近轴球面波通过光学元件前后的曲率半径分别为121212,x x R R θθ==因此1211112121111x A Bx Ax B AR B R x C x D C R DCDθθθθθ+++====+++ （3）所以对于一般均匀球面波，只用一个参数——曲率半径R 就可完全描述其传播和变换的特性。
与普通球面波不同，高斯光束必须由两个量即R （z ）和w (z)来描写。
但下面将看到，对于高斯光束——非均匀的、曲率中心不断变化的球面波——也具有一个与一般球面波曲率半径R 的作用类似的复曲率半径q (z )，它可被用来描述高斯光束的传播行为。
在推导高斯光束表达式时，我们已经得出复曲率半径在均匀空间传播的表达式，具体过程可以参考伍长征编写的《激光原理》书中的（3.3-14）式，即21q q z=+ （4）这里21,q q 分别为传播方向上任意两点21,z z 处的复曲率半径，z 为两点间距离，21z z z =-，参见图2(a)。
再看高斯光束通过薄透镜的变换，如图2(b)。
令薄透镜焦距为f ，由于是近轴光线，波阵面是一球面，透镜前后曲率半径应满足21111R R f=-,000(,)q w R 111(,)q w R 222(,)qwR z 1z 2图2(a)f 20w 10w q 1q 2图2(b)又透镜足够薄，两侧光斑尺寸相等，即12w w =，与上式合并，可以变形为22222112121()i iR kwR kw f-=-- (5)由复曲率半径定义式2112()()()i q z R z kw z =-，可得21111q q f=-（6）比较（4）式和（6）式与（1）式和（2）式知道，利用复曲率半径q ，形式上完全可等价于球面波的曲率半径R 。
高斯光束的传播特性
在近轴情况下，等相位面是顶点位于z 旋转抛物面，抛物面的焦距为 在近轴情况下，等相位面是顶点位于z0的旋转抛物面，抛物面的焦距为：
z0 f2 f '= + 2 2 z0
可以证明，在近轴情况下，共焦场的在z0处的等相位面近 可以证明，在近轴情况下，共焦场的在z 似为球面，其曲率半径为： 似为球面，其曲率半径为：
2
位相因子， exp (− iφ ( x, y , z ))：位相因子，决定了共焦腔的位相分布
2 2 u mn ( x, y , z ) = C mn H m ⋅ 1+ ζ 2 w s
2 2 x H n ⋅ 1+ ζ 2 w s
2 x2 + y2 y ⋅ exp − 1 + ζ 2 ⋅ w 2 exp(− iφ ( x, y , z )) s
λz 2 1+ ( 2 ) πω 0
⇒ 2θ = 2
2λ 2λ = πL πω0
高阶模的发散角随阶次的增大而增大，方向性变差！ 高阶模的发散角随阶次的增大而增大，方向性变差！
2λ 2λ 2θ = 2 = πL πω0
不同的腰半径的激光光束的远场发散角对比图
例：某共焦腔氦氖激光器，L=30cm, λ = 0.638µm 某共焦腔氦氖激光器，
一、等相位面的分布
1、等相位面——行波场中相位相同的点连成的曲面 、等相位面 行波场中相位相同的点连成的曲面 2、与腔轴线相交于z0的等相位面的方程 、与腔轴线相交于
φ (x, y, z ) = φ (0,0, z0 )
L 2z 2z L x2 + y2 π φ ( x, y, z ) = k[ (1 + ) + ] − (m + n + 1)( − ϕ ) = φ (0,0, z0 ) 2 L 1 + ( 2 z L) 2 L 2
高斯光束光斑大小
高斯光束光斑大小
摘要：
一、高斯光束的基本概念
二、高斯光束的传输特性
三、高斯光束的光斑大小与能量分布
四、高斯光束在光学系统中的应用
五、测量高斯光束束腰宽度的方法
正文：
一、高斯光束的基本概念
高斯光束是一种常见的光学光束，它的形状呈高斯分布。
在高斯光束中，光斑大小、能量分布等参数都是重要的特性。
二、高斯光束的传输特性
高斯光束的传输特性表现为，在远离光源的地方，光束会沿着传播方向呈特定角度扩散。
这个特定角度即为我们所称的远场发散角。
远场发散角与光束的波长成正比，与光束的束腰半径成反比。
因此，束腰半径越小，远场发散角越大。
三、高斯光束的光斑大小与能量分布
高斯光束的光斑大小与能量分布紧密相关。
光斑大小决定了光束在空间中的覆盖范围，而能量分布则影响了光束的亮度。
高斯光束的光斑大小与其束腰半径有关，束腰半径越小，光斑大小越小。
四、高斯光束在光学系统中的应用
高斯光束在光学系统中有着广泛的应用，如激光加工、激光通信、光学成像等。
在光学系统设计中，我们需要根据高斯光束的特性来优化系统的性能。
五、测量高斯光束束腰宽度的方法
测量高斯光束的束腰宽度一般通过测量不同位置处光束的宽度，再进行双曲线拟合求解。
但需要注意的是，激光器的束腰半径意义不大，可以通过后续光束的准直聚焦改变其束腰半径。
高斯光束的传播特性课件
加精准，能够实现更高的光束质量和更稳定的传输。
动态调控
02
通过实时监测和反馈系统，实现对高斯光束的动态调控，以满
足不同应用场景的需求。
多光束控制
03
未来将实现多光束的独立控制和协同操作，提高光束的灵活性
和应用范围。
高斯光束在量子通信中的应用
1 2 3
安全性增强 高斯光束在量子通信中能够提供更强的安全性保 障，通过量子纠缠和量子密钥分发等技术，实现 更加安全的通信传输。
传输距离提升 随着量子通信技术的发展，高斯光束的应用将有 助于提高量子通信的传输距离和稳定性。
网络架构优化 高斯光束在量子通信网络架构中能够提供更灵活 和高效的光路设计，优化网络性能和扩展性。
高斯光束在其他领域的应用
生物医学成像
高斯光束在生物医学领域可用于光学显微镜、光谱仪等设备的成像 技术，提高成像质量和分辨率。
在生物医学成像中的应用
光学成像
高斯光束作为照明光源，能够提高光学成像的分辨率和对比度。
荧光成像
利用高斯光束激发荧光标记物，实现生物组织的荧光成像。
光声成像
结合高斯光束与光声效应，实现生物组织的高分辨率、高对比度 的光声成像。
05
高斯光束的未来展
高斯光束控制技术的发展
高精度控制
01
随着光学技术和计算机技术的发展，未来高斯光束的控制将更
高斯光束的强度分布和相位分 布都可以用高斯函数描述，这 使得高斯光束在许多领域都有 广泛的应用。
02
高斯光束的播特性
传播过程中的光强分布变化
01 02
光强分布变化规律
高斯光束在传播过程中，光强分布呈现中间高、两侧低的形态，类似于 钟形曲线。随着传播距离的增加，光强分布逐渐展宽，但中心峰值保持 不变。
《激光原理》3.3高斯光束的传播特性(新)
z = f, 即镜面处R最小,且等于镜面本身曲率半径
证 R(z) z f 2
z
dR
f2
dz 1 z2 0
zf
R( f ) ( f f 2 ) 2 f R f
z
-f 0
f
R02 x2 y2 z z0 R0 2
1.当 z0 0 时，R(z0 ) 2.当 z0 时，R(z0 ) 3.当 z0 f 时，R(z0 ) z0 4.当 z0 f 时，R(z0 ) L 2 f
束腰处的等相位面为平面， 曲 率中心在无穷远处
无穷远处等相位面为平 面，曲率中心在z=0处
光束可近似为一个 由z=0点发出的半径 为z的球面波。
由 0s 20 可知,镜面上的光斑尺寸,基模体积和远
V000
L
2 0
发散角等高斯光束的参数都可以通过
2 2 基模腰斑半径(“腰粗”)ω0来表征,故 0 “腰粗”是高斯光束的一个特征参数.
计算表明： 2 内含86.5%的光束总功率
Area
立体角的单位为sr，称为球面度。1sr是这样的 立体角：其顶点位于球心，它在球面上所截取 的面积等于以球半径为边长的正方形面积。
f ' z0 f 2 2 2z0
可以证明，在近轴情况下，共焦场的在z0处的等相位面近 似为球面，其曲率半径为：
R0
2
f
'
z0 [1
(
f z0
)2 ]
z0 [1
(L 2z0
)2 ]
(3 38)
则有：
z
z0
x2 y2 2R0
R0
x2 y2 1 R02 R0
高斯光束的传播特性课件
高斯光束的未来发展趋势
01 发展现状分析
前景广阔
02 未来趋势探讨
挑战与机遇并存
03 科学研究发展
跨学科交叉
高斯光束在工业应用中的创新
制造工艺
高效精准 节约成本
设备应用
智能控制 自动化生产
材料加工
高质量 快速加工
能源利用
节能环保 绿色生产
● 07
第7章 高斯光束的传播特性 课件
高斯光束的重要性
折射率与热效应
热效应
高斯光束在介质中 传播时会产生热效
应。
折射率变化
热效应会导致折射率 发生变化，影响高斯 光束的传播和聚焦效
果。
总结
高斯光束的传播特性受到折射率、衍射效应、非线性光学和热 效应等因素的影响。理解这些因素对于光学应用和光束传输具 有重要意义。
● 03
第3章 高斯光束的光学系统
高斯光束的聚焦系统
● 04
第四章 高斯光束的传播实验
高斯光束的干涉实验
迈克尔逊干涉仪观测
利用迈克尔逊干涉 仪观测高斯光束的
干涉条纹
分析干涉条纹
分析干涉条纹的形状 和对比度，验证高斯
光束的传播特性
高斯光束的衍射实验
在衍射光栅实验中，观测高斯光束的衍射效 应是探究光栅对高斯光束的光斑形状和光强 分布的影响。通过实验，可以进一步了解光 的衍射现象，验证高斯光束在衍射过程中的 特性。
衍射效应
光束传播中的衍射 现象
散射效应
光束在物质中传播时 的散射现象
折射效应
光束在介质中传播时 的折射规律
高斯光束的调制特性
高斯光束可以通过调制改变其传播特性，例 如调制频率、相位等参数可以实现对光束的 精准控制。调制技术在光通信和激光加工中 有着重要的应用价值。
第三章 高斯光束及其特性精选全文
R2 ( z )
AR1(z) CR1(z)
DB,
A C
B
D
1 1 /
f
0
1
反映了近轴球面波曲率半径的传输与光学系统矩阵元之间的关系
§3.1 基模高斯光束
球面波的传播规律可以统一写成
R2
AR1 CR1
B D
结论：具有固定曲率中心的普通傍轴球面波可以由其曲率半径R 来描述，传播规律由变换矩阵确定。
f
2 2
2 F
q
(1
l F
)q (l q (1
l l
)
ll F
)
F
F
0
(l
F F )2
f
2 0
§3.1 基模高斯光束
出射光束的束腰位置和尺寸 随入射光束的变化：
l
l(l F ) (l F )2
f f
2 2
F
0
(l
F F )2
f
2 0
§3.1 基模高斯光束
0
(l
§3.1 基模高斯光束
球面反射镜对高斯光束的自再现变换：
F 1 R(l) 2
F
1 2
R球面
R球面 R(l)
当入射在球面镜上的高斯光束波前曲率半径正好等于球面镜的曲率半径 时，在反射时高斯光束的参数将不发生变化，即像高斯光束与物高斯光 束完全重合。通常将这种情况称为反射镜与高斯光束的波前相匹配。
第三章 高斯光束及其特性
本章大纲
§3.1 基模高斯光束 掌握高斯光束q参数的表达 高斯光束在线性光学系统中的变换 高斯光束的自再现变换与稳定球面腔模式的关系
§3.2 高阶高斯光束 了解高阶高斯光束的特性。
高斯光束的传播特性新.ppt
x2
y2 L
2z0
x2 y2
1
L 2z0
2
R0
z 0 [1
(L 2z0
)2 ]
当 z0 0 时， R(z0 ) 当 z0 时， R(z0 )
当 z0 f
时，R(z ) L 0
腔中点或距腔中点无限 远处，等相面为平面
20为基模光束的发散角
由于高阶模的发散角是随着模的 阶次的增大而增大，所以多模振 荡时，光束的方向性要比单基模 振荡差。
由 0s 20 可知,镜面上的光斑尺寸,基模体积和远
V000
L
2 0
发散角等高斯光束的参数都可以通过
2 2 0
基模腰斑半径(“腰粗”)ω0来表征,故 “腰粗”是高斯光束的一个特征参数.
图3-7 计算腔内外光场分布的示意图
umnx, y, z CmnHm
2
1
2
2 ws
x Hn
2
1
2
2 ws
y
exp
2
1
2
x2 y2 ws2
exp
i x,
y,
z
( x,
y, z)
k
L 2
(1
)
1
2
x2
L
y
2
(m
n
1)(
2
)
arctg 1 arctg L 2z
1
L 2z
激光原理3.3高斯光束的传播特性(2014)_图文(精)
激光原理
高福斌
2013116
2013.11.6
/25 1
3.3 高斯光束的传播特性
回顾——求解对称开腔中的自再现模积分方程, 了解输出激光的具体场的分布——
前瞻研究高斯光束的传播特性
/22 2
一、等相位面的分布
等相位面 1、等相位面——行波场中相位相同的点连成的曲面(
, , x y z ϕx
z
z 0
(
00,0, z ϕ共焦场等相面的分布
/25
9
三 . 共焦场的等相位面的分布图
共焦场等相面的分布
可以证明:
如果在场的任意一个等相位面处放上一块具有相应曲率的反射镜片,则入射在该镜片上的场将准确地沿着原入射方向返 /25
16回,这样共焦场分布将不会受到扰动.这是非常重要的性质.
z 小结:高斯光束的基本性质
1. 高斯光束在其轴线附近可看作是一种非均匀高斯
球面波,
22. 在其传播过程中曲率中心不断改变
3. 其振幅在横截面内为一高斯光束
4. 强度集中在轴线及其附近
5. 等相位面保持球面/25 17
数值例 :
器件辐射能量脉冲时间 P
普通红宝石激光器 1J 10-4s 104W 1J 10910
调 Q 红宝石激光器 1J 10-9s 109W 调 Q 及锁模红宝石激光器 1J 10-12~10-13s 1012~1013W *输出能量一定时 , 激光器由于脉冲时间缩短可使△ I 很大 ; ,
而且因θ(或Ω 很小 , 故亮度 B 很大。
/25 23。
高斯光束的基本性质及特征参数r
综上所述，基模高斯光束在其传播轴线附近， 能够看作是一种非均匀旳球面波，其等相位面是曲 率中心不断变化旳球面，振幅和强度在模截面内保 持高斯分布。
photomultiplier
photodiode
Avalanche photodiode
高斯光束旳基本性质及特征参数
基模高斯光束 高斯光束在自由空间旳传播规律
高斯光束旳参数特征
4、高斯光束
由激光器产生旳激光束既不是上面讨论旳均匀平 面光波，也不是均匀球面光波，而是一种振幅和等 相位面在变化旳高斯球面光波，即高斯光束。
以基模TEM00高斯光束为例，体现式为：
E0
ωγ2 2zeik
z
γ2
2 z z2
02 f 2 1
如图1-7所示。
在Z=0处，ω（z）=ω0到达极小值，称为束 腰半径。
(2)基模高斯光束场旳相位因子
00 r, z
k z
2R
2
z
arctan
z f
决定了基模高斯光束旳空间相移特征。
其中，kz描述了高斯光束旳几何相移； arctan(z/f)描述了高斯光束在空间行进距离z处， 相对于几何相移旳附加相移；因子kr2/(2R(z))则表 达与横向坐标r有关旳相移，它表白高斯光束旳等 相位面是以R(z)为半径旳球面。
R(z)随Z变化规律为：
Rz
z 1
f2 z2
z
f2 z
结论：
a)当Z=0时，R(z)→∞，表白束腰所在处旳等 相位面为平面。
b) 当Z→±∞时，│R(z)│≈z→∞表白离束腰无 限远处旳等相位面亦为平面，且曲率中心就在束腰 处；
c)当z=±f时，│R(z)│=2f，到达极小值 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2、与腔轴线相交于z0的等相位面的方程
x, y, z 0,0, z0
L 2z 2z L x2 y 2 ( x, y, z ) k[ (1 ) ] ( m n 1 )( ) (0,0, z0 ) 2 L 1 ( 2 z L) 2 L 2
3.3 高斯光束的传播特性
回顾 ——求解对称开腔中的自再现模积分方程, 了解输出激光的具体场的分布 前瞻 —— 研究高斯光束的传播特性
1
3.3.1 高斯光束的振幅和强度分布
一、共焦腔内或腔外的一点的行波场的解析式：
2 2 umn x, y, z Cmn H m 1 2 w s 2 2 x H n 1 2 w s 2 x2 y 2 y exp 1 2 w2 exp i x, y, z s
s
s
①当 z=0 时， z 达到最小值 0 1 s 1
2
L zf 2
L 2
——高斯光束的基模腰斑半径(腰粗)
②当
时，即在镜面上时，有：
z 20 L
3、 ( z ) 在纵截面上的表达式
L 2z 2 ( z) [1 ( ) ] z 2 2 z2 2 L 1 ( z ) 0 1 ( 2 ) 2 2 2 0 0 (0 ) 1 1 L 0 s 2 2
位相弯曲因子
附加相移因子
L 2z 2z L x2 y 2 ( x, y, z ) k[ (1 ) ] (m n 1)( ) 2 2 L 1 ( 2 z L) L 2
传播因子
———决定了共焦场的位相分布
L 2z arctan L 2z
7
一、等相位面的分布
• ： exp i x, y, z 位相因子，决定了共焦腔的
位相分布。
2
2 2 umn x, y, z Cmn H m 1 2 w s
2 2 x H n 1 2 w s
2 x2 y 2 y exp 1 2 w2 exp i x, y, z s
2 mn
——基模截面是高斯函数
2、光斑尺寸振幅下降为最大值1/e时的光斑半径
4z 2 ( z) 1 1 2 L 2 2
2
s
s
3
2 4 z ( z) 1 2 1 2 L 2z 2 L ( z ) [ 1 ( ) ] 2 2 2 L 2 2 ωs xs ys L
6
3.3.2 高斯光束的相位分布
共焦腔内或腔外的一点的行波场的解析式：
2 2 2 2 umn x, y, z Cmn H m 1 2 w x H n 1 2 w y s s 相位因子 2 2 2 x y exp exp i x, y, z 2 2 ws 1
0 mn
图(3-8) 基模光斑半径随z按双曲线规律的变化
决定一个模式能否振荡，能 获得多大的输出功率，与其 它模式的竞争情况等。
V
0 00
1 L2 2 L0 s 2 2
1 L2 高阶模： V Lms ns （2m 1 ） （ 2n 1 ） 2 2 0 （2m 1 ） （ 2n 1 ） V00
若忽略由于z的变化而造成附加相移因子的微小变化，则在近 轴情况下，z处的等相位面方程为：
2z x2 y 2 L z z0 2 L 2z 1 L
2 z0 x2 y 2 x2 y 2 L 2 L L 2 2 z0 1 2 z0 1 L 2z 0
二、振幅分布和光斑尺寸 1、振幅分布 对基横模TEM00 基横模TEM00的光强
U 00 2 x2 y2 Cmn exp 1 2 2 s
2
I 00 U 00
4 x2 y 2 C exp 1 2 2 s
2z 2 2 L 2 z0 L 2 z x y L k 1 z k 1 z 0 2 2 2 L L 2 L 2 2z 1 L
1
2 2 Hm 1 2 w s
2 2 x H n 1 2 w s
2 x2 y2 y exp 1 2 w2 行波场横向振幅分布因子 s
—厄米—高斯函数 在横截面内的场振幅分布按高斯函数所描述的 规律从中心(即传输轴线)向外平滑地降落。 花样：沿x方向有m条节线，沿y方向有n条节线。
4
2 z2 1 2 2 2 0 (0 )
——光斑半径随z按照双曲线规律变化。
5
三、 模体积 1、定义：描述某一腔模在 腔内扩展的空间体积。 2、意义：模体积大，对 激活介质能量的提取就 大，对模式振荡作贡献 的粒子数越多，就有可 能获得大的输出功率。 3、对称共焦腔基模的模 体积：看成底半径为ω0， 高为L的圆柱体。