塑性本构关系PPT
合集下载
材料工程塑性理论(本构关系)

L
d
p i
用来描述硬化程度
i
H(
L
d
p i
)
对上式求导,有:
H
di
d
p i
d 3dip 3di 2i 2iH
等效塑性应变总量:沿应变路径累积
Levy-Mises方程:
d ij
d ij '
3d i 2 iH
ij
'
Levy-Mises硬化材料本构方程
d x
3d i 2 iH
x
dy 23diHi y
d z
3d i 2 iH
z
d ij
3d
2
i
iH
ij
4. 全量理论(形变理论)
Hencky 全量理论,1924 应力偏量分量与塑性应变偏量分量(不含弹性部分)应相似且同轴:
p x
p y
p z
p xy
p yz
p zx
' x
' y
' z
xy
yz
zx
或
ij
' ij
物理概念: 1)塑性应变全量与应力主轴重合 2)塑性应变全量的分量与应力偏量分量成比例
dij d ij
Note:(1)已知应变增量分量且对于特定材料,可以 求得应力偏量分量或正应力之差 ,但一般不能求出正 应力的数值 ,因为这时平均应力未知。 (2)已知应力分量,能求得应力偏量,但只能求得应 变增量的比值而不能求得应变增量的数值(对于理想 塑性材料)。理想塑性材料应变分量的增量与应力分 量之间无单值关系(很多解),dλ不是常数。 (3)若两正应力相等,则由于应力偏量分量相同,相 应的应变增量也相同,反之亦然。 (4)若某一方向的应变增量为零,则该方向的正应力 应等于平均应力。
塑性力学03-塑性本构关系

3-2 广义Hooke定律 • 在弹性范围内, 广义Hooke定律可以表达为 1 ij 1 ij ij kk E 1 2 1 • 也可以表示为: ii ii eij Sij E 2G 由应力和应变的分解式,即 ij Sij ij m , ij eij ij m 代入上面广义Hooke定律的公式,考虑到 G E / 2 1 1 eij ij m 1 S ij ij m ij kk E 1 1 1 2 1 S 3 S ij m ij ij m ij m ij E 2G E 所以可以写成两个相应分解张量之间的关系. 我们来证明一下:
因为应力强度和应变强度的公式为:
3 i Sij Sij 2 2 i eij eij 3
把 eij Sij 代入上面右式并考虑上面左式得到
(3)应力强度是应变强度的强度函数 i i 线假定的硬化条件.
3 i 2 i , 即按单一曲
综上所述, 全量型塑性本构方程为 3 i 1 2 eij Sij i i ii ii 2 i E 注意的是上式只是描述了加载过程中的弹塑性变形规律. 加 载的标志是应力强度 i 成单调增长. i 下降时为卸载过 程, 它时服从增量Hooke定律.
1. Levy-Mises流动法则 这个理论认为应变增量主轴和应力 主轴重合, 应变增量分量与相应的应力偏量分量成比例, 即
d ij d Sij
d 0
式中的比例系数决定于质点的位置和荷载的水平. 这一理论是 Levy和Mises分别在1871年和1931年独立提出的, 所以被称为 Levy-Mises流动法则. 这个关系式不包括弹性变形部分, 所以 只适用刚塑性体. 2. Prandtl-Reuss流动法则 这个理论考虑了塑性状态变形中 的弹性变形部分, 并认为弹性变形服从广义Hooke定律; 而对 于塑性变形部分, 被认为塑性应变增量的主轴和应力偏量的主 轴重合. 即 1 e e deij deij deij dSij d Sij 这就是 2G Prandtl1 2 又由塑性不可压缩性, Reuss流 d ii d ii 体积变化式弹性的,有 E 动法则
第三章 塑性状态下的本构关系
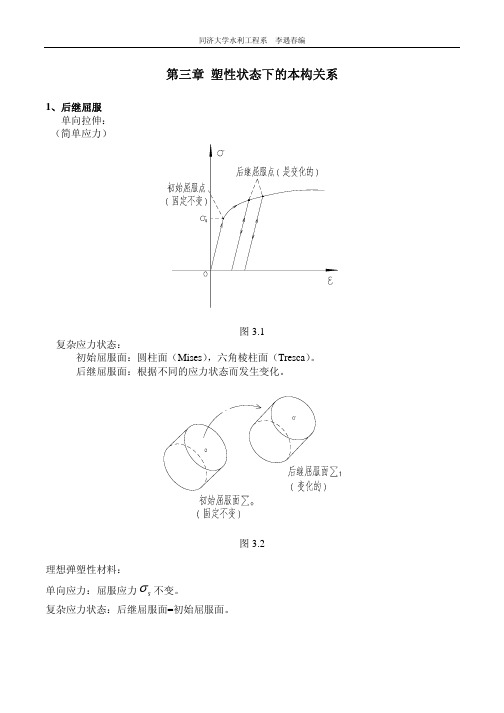
⎧d ε p1 = (σ 1 − σ m ) ⋅ d λ ⎪ p ⎨d ε 2 = (σ 2 − σ m ) ⋅ d λ ⎪ p ⎩d ε 3 = (σ 3 − σ m ) ⋅ d λ
(3.26)
同济大学水利工程系
李遇春编
由(3.26)式得:
( dε
p 1
2 2 2 − d ε p 2 ) + ( d ε p1 − d ε p 3 ) + ( d ε p 2 − d ε p 3 ) = ( d λ ) ⎡ ⎣(σ 1 − σ 2 ) + (σ 1 − σ 3 ) + (σ 2 − σ 3 ) ⎤ ⎦ 2 2 2 2
复杂应力状态
同济大学水利工程系
李遇春编
′+ + σ s′− = 2σ s 单向应力状态 σ s
复杂应力状态
f * (σ ij ) − c = 0
(初始屈服面)
m ) − c = 0 (后继屈服面) f * (σ ij + σ ij
m :应力位移 σ ij
, c 不变。见图 3.9,屈服面作平移,位置改变,大小与形状不变。
N
d ε p ij
(塑性应变)
2 产生塑性变形为 d ε 过程○
p ij
,其塑性功为: (σ ij + dσ ij − σ ij )d ε
o
p ij
o = (σ ij − σ ij )d ε p ij
若
塑性功满足下式:
同济大学水利工程系
李遇春编
o (σ ij − σ ij )d ε p ij = dσ ij d ε p ij ≥ 0
⇓
平均弹性正应变增量
dsij deeij
= 2G
(3.26)
同济大学水利工程系
李遇春编
由(3.26)式得:
( dε
p 1
2 2 2 − d ε p 2 ) + ( d ε p1 − d ε p 3 ) + ( d ε p 2 − d ε p 3 ) = ( d λ ) ⎡ ⎣(σ 1 − σ 2 ) + (σ 1 − σ 3 ) + (σ 2 − σ 3 ) ⎤ ⎦ 2 2 2 2
复杂应力状态
同济大学水利工程系
李遇春编
′+ + σ s′− = 2σ s 单向应力状态 σ s
复杂应力状态
f * (σ ij ) − c = 0
(初始屈服面)
m ) − c = 0 (后继屈服面) f * (σ ij + σ ij
m :应力位移 σ ij
, c 不变。见图 3.9,屈服面作平移,位置改变,大小与形状不变。
N
d ε p ij
(塑性应变)
2 产生塑性变形为 d ε 过程○
p ij
,其塑性功为: (σ ij + dσ ij − σ ij )d ε
o
p ij
o = (σ ij − σ ij )d ε p ij
若
塑性功满足下式:
同济大学水利工程系
李遇春编
o (σ ij − σ ij )d ε p ij = dσ ij d ε p ij ≥ 0
⇓
平均弹性正应变增量
dsij deeij
= 2G
弹塑性本构模型理论课件

。
材料屈服强度影响规律
屈服强度定义
材料开始发生明显塑性变形的最小应力值,反映了材料抵抗塑性变 形的能力。
屈服强度对弹塑性行为的影响
屈服强度越大,材料抵抗塑性变形的能力越强,进入塑性阶段所需 的应力水平越高,材料的塑性变形能力越差。
屈服强度的影响因素
材料的晶体结构、化学成分、温度、应变速率等都会影响屈服强度 的大小。
材料弹性模量影响规律
弹性模量定义
01
材料在弹性阶段内,应力与应变之比,反映了材料抵抗弹性变
形的能力。
弹性模量对弹塑性行为的影响
02
弹性模量越大,材料的刚度越大,相同应力作用下产生的弹性
变形越小,进入塑性阶段所需的应力水平越高。
弹性模量的影响因素
03
材料的晶体结构、化学成分、温度等都会影响弹性模量的大小
弹性阶段
材料在受力初期表现出弹性行为,应 力与应变呈线性关系,卸载后无残余 变形。
屈服阶段
当应力达到屈服强度时,材料进入塑 性阶段,应力不再增加但应变继续增 加,卸载后有残余变形。
强化阶段
材料在塑性阶段表现出应变硬化特性 ,随着塑性应变的增加,屈服强度逐 渐提高。
理想弹塑性模型
无强化阶段的弹塑性模型,屈服后应 力保持恒定,应变无限增加。
通过实验测定金属材料的弹性模量、屈服强度、硬化模量等参 数,为模拟提供准确数据。
利用有限元软件建立金属材料的弹塑性行为模型,进行加载、 卸载等模拟过程。
将模拟结果与实验结果进行对比,验证弹塑性本构模型在金属 材料行为模拟中的准确性和可靠性。
实例二:混凝土结构弹塑性损伤评估
损伤模型选择
针对混凝土结构的损伤特点,选择合适 的弹塑性损伤本构模型,如塑性损伤模
弹塑性力学第5章—塑性本构关系

3 2
sij
−
Cdε
p ij
sij −
Cdε
p ij
−σs = 0
C表征材料强化的大小,来自单向拉伸
5.3 后继屈服条件
1、等向强化模型
单向拉伸实验曲线中三个方向的塑性主应变为
ε1p
= ε p,
ε
p 2
=
ε
p 3
= − 1ε p
2
其中ε p为单向拉伸方向的塑性应变,由此得到等效塑性应变
( ) ( ) ( ) ε p =
4 3
J
′
2
=
2 9
⎡ ⎢⎣
ε1p
−
ε
p 2
2+
ε
p 2
−
ε
p 3
2+
ε
p 3
最大畸变能是材料屈服的原因
J2 = k2
J 2反映了材料的畸变能( U0d
=
J2 2G
)
( ) J2
=
1 2
sij sij
=
1 6
(σ1 − σ2 )2 + (σ2 − σ3 )2 + (σ3 − σ1)2
k 由实验确定,根据简单拉伸实验,在材料屈服时
[ ] J2
=1 6
(σ 0 − 0)2 + 0 + (0 −σ 0 )2
−0.8
屈服条件类似,主要区别是
−1.0
混凝土的抗压强度比抗拉强
−1.2
度高得多。
5.2 常用的屈服条件
5.2.3 混凝土的莫尔-库仑屈服条件
在实验基础上,提出线性化的莫尔-库仑屈服条件,σ
′
0
,
σ
塑性力学第四章(1)-塑性本构关系

第四章
塑性本构关系
加载与卸载关系 全量型本构关系 增量本构关系
加载与卸载关系
理想弹塑性材料的加卸载准则
r r ∂f =0 d σ ⋅ n = d σ ij ∂ σ ij
r r ∂f ∂f d σ ⋅ n = d σ ij <0 ∂ σ ij
加载 卸载
r dσ
r n
dσ
r
f (σ ij ) = 0
o
1 εx = σx − µ σ y +σz E 1 εy = σ y − µ (σ z + σ x ) E 1 εz = σz − µ σx +σ y E
[
(
)]
体积应变: 体积应变:
θ = εx +ε y +εz
[ [
(
] )]
体积应力: 体积应力:
Θ =σx +σ y +σz
µε = µσ
形变理论( 理论) 形变理论( Hencky — Iliushin 理论)
体积变化是弹性的,且与平均应力成正比。 1. 体积变化是弹性的,且与平均应力成正比。
E σm = εm (1 − 2 µ )
应变偏量与应力偏量成比例。 2. 应变偏量与应力偏量成比例。
弹性阶段: 弹性阶段: 塑性阶段: 塑性阶段:
∂ϕ ⋅ d σ ij = 0 ⇒ 中性变载 ∂ σ ij
r r dσ ⋅ n > 0 r r dσ ⋅ n < 0
加卸载准则
r r dσ ⋅ n = 0
中性变载: 中性变载:当应力增量沿加载 面切线方向变化, 面切线方向变化, 而加载面并不扩大 时,不产生新的塑 性变形。 性变形。
塑性本构关系
加载与卸载关系 全量型本构关系 增量本构关系
加载与卸载关系
理想弹塑性材料的加卸载准则
r r ∂f =0 d σ ⋅ n = d σ ij ∂ σ ij
r r ∂f ∂f d σ ⋅ n = d σ ij <0 ∂ σ ij
加载 卸载
r dσ
r n
dσ
r
f (σ ij ) = 0
o
1 εx = σx − µ σ y +σz E 1 εy = σ y − µ (σ z + σ x ) E 1 εz = σz − µ σx +σ y E
[
(
)]
体积应变: 体积应变:
θ = εx +ε y +εz
[ [
(
] )]
体积应力: 体积应力:
Θ =σx +σ y +σz
µε = µσ
形变理论( 理论) 形变理论( Hencky — Iliushin 理论)
体积变化是弹性的,且与平均应力成正比。 1. 体积变化是弹性的,且与平均应力成正比。
E σm = εm (1 − 2 µ )
应变偏量与应力偏量成比例。 2. 应变偏量与应力偏量成比例。
弹性阶段: 弹性阶段: 塑性阶段: 塑性阶段:
∂ϕ ⋅ d σ ij = 0 ⇒ 中性变载 ∂ σ ij
r r dσ ⋅ n > 0 r r dσ ⋅ n < 0
加卸载准则
r r dσ ⋅ n = 0
中性变载: 中性变载:当应力增量沿加载 面切线方向变化, 面切线方向变化, 而加载面并不扩大 时,不产生新的塑 性变形。 性变形。
本构方程(塑性应力-应变关系)

d ij
(3 2
d
p
)
' ij
1 2G
d
' ij
1 2
E
d mij
材料全量塑性本构关系
➢ 材料增量本构理论虽然比较严谨,与实际情况比较 接近。但是在实际应用时需要沿加载路径积分,从 工程应用的角度讲是不方便的
➢ 许多学者(例如Hencky、Nadai、伊留申)相继提 出了描述应力与全量应变之间的关系,称为全量理 论,也称为形变理论
➢适合于弹性变形不可忽
略,且塑性变形的硬化
率接近于不变的材料。
例如合金钢、铝合金等
O e
等效应力—等效应变简化模型
➢ 刚塑性线性硬化材料模
型
如果弹性变形可以忽略,
材料的硬化认为是线性
的。其数学表达式为
s
s k2
➢适合于经过较大的冷
变形量之后,并且其加
工硬化率几乎不变的金
属材料
O
材料弹性本构关系
d
e ij
其中塑性应变增量dijp由Levy—Mises理论
给出
d
p ij
d
' ij
3 2
d
p
' ij
材料增量塑性本构关系
➢ Prandtl-Reuss理论
其中弹性应变增量dije 由广义虎克定律的微
分形式给出
d
e ij
1 2G
d
' ij
1 2
E
d mij
可以得到Prandtl-Reuss本构方程为
➢ 增量本构理论又称为流动理论
材料增量塑性本构关系
➢ Levy—Mises理论
材料为理想刚塑性材料,即弹性应变增量为零, 塑性应变增量就是总应变增量;
塑性力学03-塑性本构关系ppt课件

dii
1 2
E
d ii
这就是
PrandtlReuss流 动法则
11
3-8 理想弹塑性材料的增量本构方程
• 对于理想弹塑性材料, 后继屈服面和初始屈服面是重合的. 若
采用Mises条件, 则应有
i
3 2
求微分有
Sij Sij s
SijdSij 0
又因为应变比能的增量为
dW ijdij mij Sij dmij deij
d Sij Sij
d
2 3
2 i
所以有
d
3dWd
2
2 i
12
• 理想弹塑性材料的增量型本构方程可以写为
dii
1 2
E
d ii
deij
1 2G
dSij
3dWd
2
2 s
Sij
3-9 理想刚塑性材料的增量型本构方程
• 理想刚塑性材料的Levy-Mises流动法则为 dij dSij
其中(1)和(3) 在第二章已经解决, 本章要解决第(2)点.
2
3-2 广义Hooke定律
• 在弹性范围内, 广义Hooke定律可以表达为
ij
1 E
1
ij
ij kk
• 也可以表示为:
ii
1 2
E
ii
eij
1 2G
Sij
我们来证明一下:
由应力和应变的分解式,即 ij Sij ij m , ij eij ijm
o
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
厦门大学土木工程系 张灿辉
PM-ch03.5-15
(3)塑性势理论
畸变能屈服函数就是塑性势
厦门大学土木工程系 张灿辉
流动法则
ij
U 0 ( ij ) ij
PM-ch03.5-16
1 U 0 ( ij ) Lijkl ij kl 2
塑性位势理论:Mises将弹性位势理论推广到塑性理论,提出 塑性流动方向(塑性应变增量矢量的方向)与塑性势函数的 梯度方向一致: g d ijp d ij 关联流动法则 非关联流动法则
又
3J 2
3d p d 2
当理想弹塑性材料 s ,强化材料 根据塑性变形历史 (实验)得到 ( p ) ,上述结果是在主轴方向。
厦门大学土木工程系 张灿辉
PM-ch03.5-9
Prandtl-Resuss理论
Prandtl (1924年)-Resuss(1930年)
Ludwig Prandtl
厦门大学土木工程系 张灿辉
PM-ch03.5-6
塑性应变增量与应力关系
为了确定塑性应变增量与应力的关系,需要以实验为基 础找出它们的关系。 Lode曾用受轴向拉伸和内压同时作用的金属薄壁管作实验, 所采用的参数为 和 d p
S 2 S3 2 3 1 2 1, 2 S1 S3 1 3
厦门大学土木工程系 张灿辉
PM-ch03.5-21
应力点在非交点上
f n n f
当应力点位于f1=0上
f1 p p p d d 1 ( d : d : d 1 2 3 ) = (0 d1 d1) ij
p ij
当应力点位于f2=0上
p d ij d 2
厦门大学土木工程系 张灿辉
PM-ch03.5-7
相同的比值
d 1p d 2p ( S1 S 2 )d
d 1p d 3p d 2p d 3p d 或 S1 S3 S 2 S3
d 2p d 3p ( S 2 S3 )d d 3p d 1p ( S3 S1 )d
厦门大学土木工程系 张灿辉
PM-ch03.5-3
弹性应变与塑性应变
弹塑性物体内任一点处应力状态进入塑性状态以后,相应的应 e 变 ij 总可以分解成为两部分:弹性应变部分 ij 和塑性应变 p e ij ij ijp 部 ij ,即: 当外载荷有微小增量时,总应变也要有微小增量 d ij ,同理可得
厦门大学土木工程系 张灿辉
PM-ch03.5-1
3.5 塑性本构关系
1 增量理论 2 全量理论
厦门大学土木工程系 张灿辉
1 增量理论
PM-ch03.5-2
前已阐明材料的塑性应力应变关系的重要特点是它的非线性 和不唯一性。所谓非线性是指应力应变关系不是线性比例关 系;所谓不唯一性是指应变不能由应力唯一确定。 因此,在塑性变形阶段,应变不仅和应力状态有关,而且还 和变形历史有关。如果不知道变形的历史,便不能只根据即时 应力状态唯一地确定塑性应变状态。而且只知道最终的应变状 态,也不能唯一地确定应力状态。 考虑应变历史,研究应力和应变增量之间的关系,以这种关 系为基础的理论称为增量理论(或流动理论)。
d
p
d 2p d 3p 2 p 1 p d 1 d 3
通过实验结果,得出大致结论为: d p 则认为 可写为 S2 S3 d 2p d 3p S1 S3 d 1p d 3p d 1p d 3p d 2p d 3p d S1 S3 S 2 S3
e d ijp d ij d ij
若认为球应力作用下物体只产生弹性的体变(即体积改变); 而偏应力作用下物体只产生畸变(即形状的改变),但畸变包 括有弹性畸变和塑性畸变两部分。这就是说塑性变形仅由应力 偏量所引起。且在塑性状态,若认为材料不可压缩,则体积变 形为零,即:
deij d ij ij d m
f g f , d d ij
p ij
g f
厦门大学土木工程系 张灿辉
Mises形式的塑性势能函数
g ( ij ) J 2 k 0
p d 由流动法则得: ij Sij d
PM-ch03.5-17
p d kk S kk d 0 不会产生塑性体积变化:
Prandtl-Reuss 增量理论 (理想弹塑性材料)
Levy-Mises增量理论 (理想刚塑性材料)
可以看出,增量理论的本构方程与广义虎克定律式在形式上十分 相似,除含应变增量外,所不同的是系数部分。这反映了塑性变 形过程的不可压缩性和塑性变形的非线性,及其对加载路径的依 赖性等。在此方程中,若应变增量为已知,则可唯一地求出应力 偏量。
这就是Prandtl-Reuss方程。
厦门大学土木工程系 张灿辉
Levy-Mises方程
d ij d ijp Sij d
PM-ch03.5-18
在大塑性流动中,忽略弹性变形,得到Levy-Mises方程:
相对弹性力学问题,增加了d未知数,也增加了一个方程 (屈服条件) 理想弹塑性问题,考虑平衡方程+几何方程+物理方程+ 屈服条件
p d ij deijp 塑性应变增量是一个偏量
p p p p d xp d y d zp d xy d yz d zx d Sx Sy Sz 2 xy 2 yz 2 zx
展开为
e deij deij deijp 考虑弹性应变,得到: dsij Sij d deij 2G
f 2 p p (d1p : d 2 : d3 ) = (d2 0 d2) ij
PM-ch03.5-8
比值的大小
d ijp d ijp Sij Sij (d ) 2 2 J 2 (d ) 2
2 eij eij 3
类比
d p
2 p p 2 p p d ij deij d ij d ij 3 3 3 Sij Sij 2
p 3 d d ijp Sij d Sij 2
3 2 s d ij d ij d ij , Sij 2 3 d ij d ij
d ij d ij 1 2 1 1 J 2 Sij Sij s , d 2 s 2 2(d ) 3
应变Lode参数
d
p
2d 2p d 1p d 3p d 1p d 3p
d 1p d 2p d 3p d S1 S2 S3
d 1p S1d
Hale Waihona Puke d 2p S 2 d d 3p S3 d
在变形的瞬间,主轴方向的塑性应变的增量与相应的应力偏量 分量的比值都是相同的,比值为d。 d ijp Sij d
厦门大学土木工程系 张灿辉
(2)Levy-Mises理论
理想刚塑性
e d ij 0, d ij d ijp
——理想刚塑性
1 , d m 0, de 0 2 1 3 d p deij dSij Sij 2G 2 1 1 d kk d kk where 3K 2
1 J2 2 3
而
3J 2
1 2 2 dW p dJ 2 2 J 2 d 2 J 2 d d 2G 3
3 dW p d 2 2
Prandtl-Resuss 理论的全部关系: 1 3 dW p deij dSij Sij 2 2G 2 1 1 d kk d kk where 3K 2
PM-ch03.5-5
(1)Prandtl-Resuss理论
——理想弹塑性
普朗特( L. Prandtl ) 1875 年生于 德国, 1953 年逝世。曾任哥廷根 大学力学教授, 是一位优秀的应 用力学专家,他的研究工作推动了 塑性力学的发展, 给出了一种有 效的塑性本构关系。此外, 他在 空气动力学方面也有重要贡献。
3 d d ij Sij 2 d m d kk 0 Levy-Mises 理论的全部关系
厦门大学土木工程系 张灿辉
PM-ch03.5-13
比较
p 3 d d ijp Sij d Sij 2 p d 1 p d x x ( y z ) 2 1 x x ( y z ) E
1 3 d p deij dSij sij 2G 2 1 1 d kk d kk where 3K 2
厦门大学土木工程系 张灿辉
PM-ch03.5-10
转换形式
1 deij dSij Sij d 令 2G 1 J 2 Sij Sij 又 2 1 dW p Sij deij Sij dSij Sij Sij d 2G dJ 2 Sij dSij 0
厦门大学土木工程系 张灿辉
PM-ch03.5-4
弹性应变增量
e d ij d ij d ijp
由广义 Hooke 定律,deij 与应力增量 dij 之间为:
(1 ) 3 d d ij d m ij E E
e ij
d ijp ?
厦门大学土木工程系 张灿辉
展开
广义胡克定律
厦门大学土木工程系 张灿辉
PM-ch03.5-14
说明
1 3 d p deij dSij Sij 2G 2 1 1 d ii d ii , ( ) 3K 2 3 d d ij Sij 2 d m 0
