工程塑性理论(本构关系)
合集下载
材料工程塑性理论(本构关系)

L
d
p i
用来描述硬化程度
i
H(
L
d
p i
)
对上式求导,有:
H
di
d
p i
d 3dip 3di 2i 2iH
等效塑性应变总量:沿应变路径累积
Levy-Mises方程:
d ij
d ij '
3d i 2 iH
ij
'
Levy-Mises硬化材料本构方程
d x
3d i 2 iH
x
dy 23diHi y
d z
3d i 2 iH
z
d ij
3d
2
i
iH
ij
4. 全量理论(形变理论)
Hencky 全量理论,1924 应力偏量分量与塑性应变偏量分量(不含弹性部分)应相似且同轴:
p x
p y
p z
p xy
p yz
p zx
' x
' y
' z
xy
yz
zx
或
ij
' ij
物理概念: 1)塑性应变全量与应力主轴重合 2)塑性应变全量的分量与应力偏量分量成比例
dij d ij
Note:(1)已知应变增量分量且对于特定材料,可以 求得应力偏量分量或正应力之差 ,但一般不能求出正 应力的数值 ,因为这时平均应力未知。 (2)已知应力分量,能求得应力偏量,但只能求得应 变增量的比值而不能求得应变增量的数值(对于理想 塑性材料)。理想塑性材料应变分量的增量与应力分 量之间无单值关系(很多解),dλ不是常数。 (3)若两正应力相等,则由于应力偏量分量相同,相 应的应变增量也相同,反之亦然。 (4)若某一方向的应变增量为零,则该方向的正应力 应等于平均应力。
第4章 塑性应力应变关系(本构方程)

强化材料卸载:
f ( ij ) 0,
f df d ij 0 ij
4.3 增量理论
在塑性变形时,全量应变和加载历史有关,要建立普遍的全量应变与应力 之间的关系是很困难的,所以主要研究应力和应变增量或应变速率之间的关系 。这种关系叫做增量理论,其中包括:密席斯方程、塑性流动方程和劳斯方程 。前两者适用于理想刚塑性材料,后者适用于弹塑性材料。
x
y 4G2 x y
2
2
2 2 6 xy 4G 2 xy 6
2 2 2 2 2 2 xy yz xz 等式左边为: x y y z z x 6
1 等效应力为:
1 i 2 1
2 2 2 yz xz x y y z z x 6 xy 2 2 2
则等效应变与弹性应变强度关系为: 当 =0.5 时
3 i = 2(1 )
i
弹性应力应变关系特点: 1.应力与应变成线性关系 2.弹性变形是可逆的,应力应变关系单值对 应 3.弹性变形时,应力球张量使物体产生体积 变化;物体形状的改变只是由应力偏张量引 起的。 4.应力主轴与应变2G
同理可得:
y m
1 - E 1 - E
x
z m z
m
1 y y 2G
1 z z 2G
m
x
1 x 2G
1 y y 2G 1 z z 2G
d
2 2 2 x d y d y d z d z d x 6 d xy d yz d xz 2 2 2
弹塑性_塑性力学基本方程和解法

在加载过程中物体各点处的偏应力分量 sij 保持比例不变。在工程允许精度下,也可推
广应用于稍为偏离简单加载的情况。
以上各种理论中涉及的一些假设,例如:塑性应变偏量的增在单一的函数关系等假设,都得到了常用金属材
料大量试验的验证。
z 强化规律 对于理想弹塑性材料,材料一旦屈服,其应力状态点在主应力空间中就落在屈服
变形, Hα 也不变,于是
∂f ∂σ ij
除等向强化外,有些强化材料表现为随动强化(图 7.7b),即,在强化过程中,屈
服面的大小和形状保持不变,只随塑性变形的发展而在应力空间中平移。还有些材料
在强化过程中随动强化与等向强化同时发生,称为混合强化。
由于在应力和强化参数空间中,表示应力状态的应力点只可能位于后继屈服面
(或加载面)上或其内,不可能位于曲面之外,若加载面是一个正则曲面,则有
⎯2⎯
研究生学位课弹塑性力学电子讲义
姚振汉
⎧ε = 0 ⎨⎩σ = σ s
当 σ <σs 当 ε >0
(2)
图 7.5 理想弹塑性和刚塑性
当考虑材料强化性质时,可在理想弹塑性模型的基础上加以改进,采用线性强化 弹塑性模型来近似:
⎧σ = Eε
⎨⎩σ = σ s +E1 (ε − εs )
当 ε ≤εs 当 ε >εs
(5)
⎯3⎯
第七章 塑性力学的基本方程与解法
其中 k 可由单向拉伸或其它材料试验测得的σ s 确定, k = σ s 2 。当不能确定主应力的 排序时,在以三个主应力为坐标轴的应力空间中,由特雷斯卡条件所包围的弹性状态 的应力空间为
σ1 −σ 2 ≤ 2k, σ 2 −σ 3 ≤ 2k, σ 3 −σ1 ≤ 2k
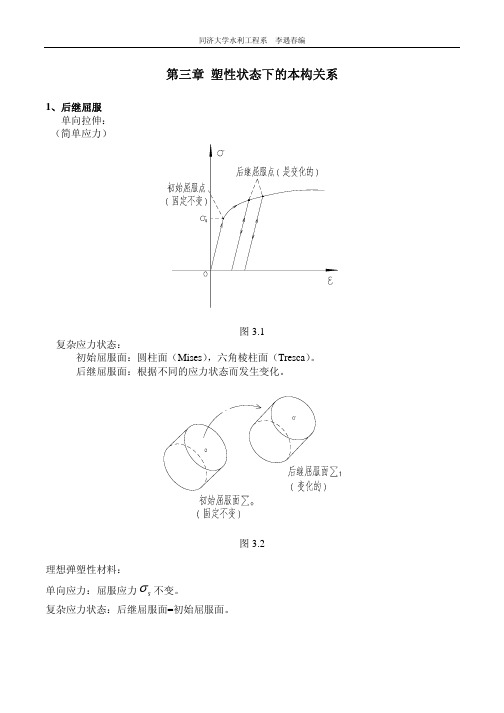
第三章 塑性状态下的本构关系
⎧d ε p1 = (σ 1 − σ m ) ⋅ d λ ⎪ p ⎨d ε 2 = (σ 2 − σ m ) ⋅ d λ ⎪ p ⎩d ε 3 = (σ 3 − σ m ) ⋅ d λ
(3.26)
同济大学水利工程系
李遇春编
由(3.26)式得:
( dε
p 1
2 2 2 − d ε p 2 ) + ( d ε p1 − d ε p 3 ) + ( d ε p 2 − d ε p 3 ) = ( d λ ) ⎡ ⎣(σ 1 − σ 2 ) + (σ 1 − σ 3 ) + (σ 2 − σ 3 ) ⎤ ⎦ 2 2 2 2
复杂应力状态
同济大学水利工程系
李遇春编
′+ + σ s′− = 2σ s 单向应力状态 σ s
复杂应力状态
f * (σ ij ) − c = 0
(初始屈服面)
m ) − c = 0 (后继屈服面) f * (σ ij + σ ij
m :应力位移 σ ij
, c 不变。见图 3.9,屈服面作平移,位置改变,大小与形状不变。
N
d ε p ij
(塑性应变)
2 产生塑性变形为 d ε 过程○
p ij
,其塑性功为: (σ ij + dσ ij − σ ij )d ε
o
p ij
o = (σ ij − σ ij )d ε p ij
若
塑性功满足下式:
同济大学水利工程系
李遇春编
o (σ ij − σ ij )d ε p ij = dσ ij d ε p ij ≥ 0
⇓
平均弹性正应变增量
dsij deeij
= 2G
(3.26)
同济大学水利工程系
李遇春编
由(3.26)式得:
( dε
p 1
2 2 2 − d ε p 2 ) + ( d ε p1 − d ε p 3 ) + ( d ε p 2 − d ε p 3 ) = ( d λ ) ⎡ ⎣(σ 1 − σ 2 ) + (σ 1 − σ 3 ) + (σ 2 − σ 3 ) ⎤ ⎦ 2 2 2 2
复杂应力状态
同济大学水利工程系
李遇春编
′+ + σ s′− = 2σ s 单向应力状态 σ s
复杂应力状态
f * (σ ij ) − c = 0
(初始屈服面)
m ) − c = 0 (后继屈服面) f * (σ ij + σ ij
m :应力位移 σ ij
, c 不变。见图 3.9,屈服面作平移,位置改变,大小与形状不变。
N
d ε p ij
(塑性应变)
2 产生塑性变形为 d ε 过程○
p ij
,其塑性功为: (σ ij + dσ ij − σ ij )d ε
o
p ij
o = (σ ij − σ ij )d ε p ij
若
塑性功满足下式:
同济大学水利工程系
李遇春编
o (σ ij − σ ij )d ε p ij = dσ ij d ε p ij ≥ 0
⇓
平均弹性正应变增量
dsij deeij
= 2G
塑性理论2

p
(20) (21)
2 d i (d 1p d 2p ) 2 (d 2p d 3p ) 2 +(d 3p d 1p ) 2 3
式(19)说明d 是由塑性变形过程中某瞬时 i 和 i 来确定。对于 理想刚塑性材料,式中的 i = s 将式(19)代入(17),得
一、Drucker公设
1. 稳定材料和不稳定材料. 材料的拉伸应力应变曲线可能有: , 0 应变都增 加 0 ,材料是硬化的。 在这一变形工程中, 附加应力在应变增量上作正功,这种特性的材料被称为稳定材 料或硬化材料。 b 、 c 所示,应力应变曲线在过D点以后, 应变增加,应力减 小,存在 0 ,此时应力增量作负功, 这种特性的材料 被称为材料不稳定或软化材料
f d ij 2[(2 1 2 3 ) d 1 (2 2 1 3 ) d 2 ij (2 3 2 1 ) d 3 ] 从
(0) ij
f , d ij = 8 104 MPa,为卸载; ij
塑性本构关系
塑性本构关系即塑性力学中应力与应变之间的关 系,即本构关系,建立的方程称为本构方程或物性方 程。由于塑性变形规律的复杂性, 到目前为止这个塑 性本构关系问题还没有得到满意的解决。经典塑性本 构关系的理论分为两大类: 增量理论:建立了应力偏量与应变偏量间的正比关系; 全量理论:也叫形变理论,它建立了应力与应变全量 间的关系。
1870年St-Venant就提出,在塑性应变时,应力主轴与 应变增量主轴相重合的见解,并发表了应力分量与 应变速率分量成正比的等式关系。1871年Levy提出 了应力与应变增量的比例关系。直到1913年Mises独 立提出了与Levy相同的塑性变形方程,才形成了著 名的Levy-Mises(莱维-米泽斯)增量理论的本构方程。
(20) (21)
2 d i (d 1p d 2p ) 2 (d 2p d 3p ) 2 +(d 3p d 1p ) 2 3
式(19)说明d 是由塑性变形过程中某瞬时 i 和 i 来确定。对于 理想刚塑性材料,式中的 i = s 将式(19)代入(17),得
一、Drucker公设
1. 稳定材料和不稳定材料. 材料的拉伸应力应变曲线可能有: , 0 应变都增 加 0 ,材料是硬化的。 在这一变形工程中, 附加应力在应变增量上作正功,这种特性的材料被称为稳定材 料或硬化材料。 b 、 c 所示,应力应变曲线在过D点以后, 应变增加,应力减 小,存在 0 ,此时应力增量作负功, 这种特性的材料 被称为材料不稳定或软化材料
f d ij 2[(2 1 2 3 ) d 1 (2 2 1 3 ) d 2 ij (2 3 2 1 ) d 3 ] 从
(0) ij
f , d ij = 8 104 MPa,为卸载; ij
塑性本构关系
塑性本构关系即塑性力学中应力与应变之间的关 系,即本构关系,建立的方程称为本构方程或物性方 程。由于塑性变形规律的复杂性, 到目前为止这个塑 性本构关系问题还没有得到满意的解决。经典塑性本 构关系的理论分为两大类: 增量理论:建立了应力偏量与应变偏量间的正比关系; 全量理论:也叫形变理论,它建立了应力与应变全量 间的关系。
1870年St-Venant就提出,在塑性应变时,应力主轴与 应变增量主轴相重合的见解,并发表了应力分量与 应变速率分量成正比的等式关系。1871年Levy提出 了应力与应变增量的比例关系。直到1913年Mises独 立提出了与Levy相同的塑性变形方程,才形成了著 名的Levy-Mises(莱维-米泽斯)增量理论的本构方程。
第十七章 塑性应力应变关系(本构关系)

• 广义胡克定律的比例式:
x y y z z x xy yz zx 1 x y y z z x xy yz zx 2G
弹性应力应变关系的特点
• 应力与应变完全呈线性关系,应力主轴与应变主 轴重合。 • 弹性变形是可逆的,应力与应变单值对应。 • 弹性变形时,应力球张量使物体产生体积变化, 泊松比υ<0.5
' y
z
' z
xy
xy
yz
yz
zx
zx
d
d 3 2
x y
z x d x y y z z x 1 2 2 3 3 1 d 1 2 2 3 3 1
• 流动理论是描述材料处于塑性状态时,应 力与应变增量或应变速率之间关系的理论。 该理论针对是加载过程的任一瞬间,认为 应力状态确定的不是全量应变,而是该瞬 时的应变增量,从而撇开了加载路线和加 载历史的影响。
Levy—Mises方程
' ' ij ij d
x
' x
y
第五节 塑性应力应变关系(本构关系)
• 一、弹性应力应变关系———Hooke’s Law 对于各向同性材料,有广义虎克定律:
1 1 x y z ; xy xy E 2G 1 1 y y x z ; yz yz E 2G 1 1 z z x y ; zx zx E 2G
• 弹塑性
塑性应变
塑性本构方程

这是七个方程
1 2 ii ii E
1 eij Sij 2G
第二个式子是六个方程,但因为有 Sii 0 , 所以有5个是独立的. 从第二式可以看到在弹性范围内应力主轴和应变主轴是一致 的. 应变偏量的分量和相应的应力偏量的分量成正比. 第二式也可以写成 Sij 2Geij ,把它代入等效应力的表达式 就可以得到下面的第二式, 然后有 G / 3 再代回上面第 一式得到下面的第二式. 3 • 所以也可写成如下形式 eij Sij 3G 2 • 当应力从加载面卸载, 也服从广义Hooke定律,写成增量形式 1 2 1 d ii d ii deij dSij E 2G
O
0 O 0
O
0
a 所示的材料,随加载应力,应变都增加,材料是硬化的. 在这
一变形工程中,附加应力在应变增量上作正功,这种特性的材料 被称为稳定材料或硬化材料. b 所示,应力应变曲线在过D点 以后, 应变增加,应力减小,此时应力增量作负功, 这种特性的材 料被称为材料不稳定或软化材料. c 所示,与能量守恒矛盾,所 以不可能.
d d p 0
ij
ij
ij
d ij d ijp 0
第二式中的等号适用于理想 塑性材料.
Drucker公设在塑性力学中有 重要意义.
3. 屈服面的外凸性和塑性应变增量的法向性 •我们如将塑性应变空间与应力空间重合起来,由Drucker公 设的第一式, 把它看成是两个矢量的点积. 0 p 0 p n d d ij ij ij ij ij ij cos 0 C d p ij 0 A0 A AC cos 0 图示即 ij ij
工程塑性理论应力应变关系

2
E
m
y
m
1 E
y
z
x
1 2
E
m
z
m
1 E
z
x y {}
1
2
E
m
x m , y m ,
x y
x m , y m ,
xy y z
xyzymmmm
,
z z m
z
z
m
Gz 2z1Em
x
1 2G
x
,
y
1 2G
y
,
z
1 2G
z
,
xy
yx
1 2G
xy
即应变增量张量就是应变增量偏张量。
在上述假设基础上,可假设应变增量与 应力偏张量成正比,即
d ij ij d
d x d y d z d xy d yz d zx d x m y m z m xy yz zx
式中:dλ—正的瞬时常数,在加载的不同 瞬时是变化的,在卸载时,dλ=0。
d ij ij d
d x x m d
x
x
y
3
z
d
2 3
d
x
1 2
y
z
d x
2 3
d
x
1 2
y
z
,
d y
2 3
d
y
1 2
z
x ,
d z
2 3
d
z
1 2
x
y
,
d xy
xy
d
d yz yzd
d zx zx d
将上式正应变两两相减,并写出切应变公式:
yz
2G
zx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
R0 R90 1 R0 1 R90
x h y k2 2
2 2 p xy
2
a 22
c 2a
h R0 1 R90 1 R0 R90
参数p隐函数,通过迭代方法(代数方程数值解)
r
2m sm x y
(a)
弹性应变增量
e ij
e ,服从虎克定律 d ij
1 1 2 d d ij d m ij 2G E
(b)
(a)+(b),及Prandtl-Reuss方程
1 1 2 d ij d ij d ij d m ij 2G E
d ij 或 d ij 1 d ij 2G
弹性变形时任意应力状态下等效应力与等效 应变关系
用应力差与应变差成比例的形式表示为:
1 2 2 3 3 1 E 2G 1 2 2 3 3 1 1
1 2 2 3 3 1 2 2 2 1 2 2 3 3 1
超塑性锻造
板料(管) 各向同性 成形 厚向各向异 性 各向异性 模具 线弹性 各向异性弹性 Prandtl方程 (弹塑性) Mises
刚粘塑性模型
(1)幂函数硬化 (2)拉伸数据
k,n K, n, r
K, n, r0, r45,r90
Hill
LS-dyna 37#
Barlet-Lian
LS-dyna 36#
1.44
1.51
1.50
1.47
1.43
1.42
2、各向异性材料(Barlat-Lian)本构关系 (LS-Dyna 36#材料模型)
ak1 k2 a(k1 k2 ) c(2k2 ) 2
m m m
对于面心立方材料:m=8, 体心立方材料, m=6
k1
m s
x h y
G
E 2(1 )
用主应力、主 3 E 1 2 2 3 1 E 1 3 3 1 2 E
弹性本构关系:本构方程 塑性本构关系:(1)本构方程;(2)屈服条 件;(3)硬化条件(应力-应变关系曲线)
本构关系是材料物理性质,取决于材料本身, 与应力状态无关
2、加载方式
简单加载:各应力分量按比例增大,应力主轴方向保持不变
ij
o ij
η—常数或单调增量函数
复杂加载:应力分量之间无一定关系,应力主轴方向变化
4、全量理论
1 1 2 3 2 i 1 2 2 3 1 i 2 i 1 3 3 1 2 i 2
1 i i
i A(B i )n
第三节、增量理论
1、Levy-Mises增量理论
(1)材料为理想刚塑性,服从Mesis 屈服准则 (2)应变增量主轴与应力主轴重合 (3) 应变增量与应力偏量成比例
d ij d ij '
塑性变形体积不变,只有形状的变化 塑性应变增量就是总的应变增量
(2)非线性
xy
D B P
A
C
σ
x
(3)依赖于加载路径(应力状态不仅与应力状态有关,而 且与加载路径或历史有关)
硬化材料的塑性变形量完全取决于第一 次到达加载曲面时的应力状态。必须以加载为 前提,立足于每一加载瞬间,来建立塑性变形 时的应力应变关系。换句话说,建立塑性变形 时的应力应变关系必须考虑加载历史。
3、加载准则(条件)
单向应力状态: d 0 加载,塑性应力应变关系 d 0 卸载,服从弹性规律 d 0 载荷不变,应变值不变 塑性变形功
dw p 0 dw p 0
复杂应力状态: id i 0 加载
id i 0
id i 0
卸载
i 不变) 中性变载(应力分量可能变化,
应力偏量与应变偏量关系
1 m 2G 1 m
2 m 2G 2 m 3 m 2G 3 m
ij ' 2G ij '
应力偏量与应变偏量成正比 形状的变化是由应力的偏张量引起的
1
定义迭代函数,用45度方向r值,求其数值解
g ( p)
2m s2 x y
1 r450
圆形件拉深(凸耳现象)
厚向各向异性(37#)
各向异性(36#)
3、可压缩材料(粉末材料)本构关系
2 2 F AJ BJ C 屈服准则(函数) 2 1 S 0 J 2 -应力偏量第二不变量
平面应力状态下(板料成形),Hill正交异性屈服准则:
1 2r i [ 2 1 2 ]2 s r 1 2 1 2
r 2r45 r90 r 0 4
B r t
Levy-Mises增量理论:
d1 d i
i
( 1
r 2) 1 r
r d 2 ( 2 1) i 1 r
E E1, E2, E3
3 1 2 4
B B
T
不锈钢和碳钢应力应变关系曲线
1Cr18Ni9Ti
600
SUS304
500
stress MPa
400
300
STKM13B(日本)碳钢
200
100
0 -0.05 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35
Strain
铝合金硬化曲线随温度变化
0.15 120
(2)双线性硬化模型
E tg
硬化模量: E1
tg
塑性:
i E i
E E1 100 0 i
i s E1( i s ) i
(3)幂函数硬化模型 多数金属材料,最常用
i K in
n值:板料成形重要参数,抗拉伸失稳能力 钢:n=0.22-0.24 不锈钢:n=0.3-0.4 (4)swift模型
4、硬化条件(单一曲线假设)
单向拉伸/压缩:应力-应变曲线
( )
加载点A:屈服应力 A ( A ) 含义:硬化材料 屈服应力随变形程度而提高, 且为瞬态应变函数。
复杂应力(二维、三维), i s 达到屈服,硬化后 等效应力 i 提高, i 与等效应变 i
1 2 d m d m E
由于考虑了弹性变形,引入了球张量,已知 d ij 求出 ij 对于硬化材料,变形过程每瞬时
d
为定值, d ij 与 ij
完全单值关系
3、硬化材料的增量理论
在复杂加载条件下,等效塑性应变总量
L
d i p
i H d i
L
p
d i H p 切线模量 d i
x
1
1 [ 1 ( 2 3 )] E 1 2 [ 2 ( 3 1 )] E
3
xy
1 XY G
. . . .
1 [ 3 ( 1 2 )] E
材料常数E, 钢:E 210GPa 铝:E 70GPa 0.3
Material: 5A02 Condition: Cold drawing Size: Φ65×1.5mm
镁合金硬化曲线随温度变化
Engineering Plasticity 工程塑性理论
塑性本构关系
苑世剑
2005年12月
2005级硕士研究生
第一节、弹性本构关系
第一节、弹性本构关系
1、单向应力
E
2、各向同性材料——虎克定律
1 [ x ( y z )] E 1 y [ y ( z x )] E 1 z [ z ( x y )] E
1)简单加载 2)小塑性变形(塑性变形数量 与弹性变形相当) n 3)硬化材料 i K i 或理想弹 塑性材料
1924年 Mesis提出增量理论 1943年 依留申提出全量理论
第四节
各向异性材料和可压缩材料增量理论
1、正交各向异性材料(LS-Dyna 37#材料模型)
板料/管材成形考虑各向异性(r值) 各向异性扎制加工过程成形
体积应变与平均应力(静水压、应力球张量) 关系 1 2 1 2 3 1 2 3 E
式中
1 2 3 3 m
1 2 m m E
——体积变化率
1 2 3 3 m——三倍的平均应力
所以,体积的变化率与平均应力成正比
J1
应力张量第一不变量
A、B、C-材料孔洞体积分数
F ij ij
本构方程:
3 1 1 ij ij kk ij 3 A 18B
B , A 1 不可压缩材料
第五节、材料模型选择
工艺 体积 成形 冷成形 等温成形 材料模型 本构方程 Levy-Mises 方程 (忽略弹性变形) 屈服条件 Mises 硬化条件 刚塑性(硬化) 理想刚塑性(硬化) 提供参数
3、弹性应力应变关系特点 1) 线性 2) 单值 3) 可逆 4) 应力主轴与应变主轴重合 5) 体积变化(平均应变)与静水应力成比例 6) 应变偏量与应力偏量成比例 7) 单向拉伸时的应力应变关系可以适应(推 广)任意应力状态
第二节、塑性本构关系特点与基本概念
1、塑性变形应力应变关系的特点
R0 R90 1 R0 1 R90
x h y k2 2
2 2 p xy
2
a 22
c 2a
h R0 1 R90 1 R0 R90
参数p隐函数,通过迭代方法(代数方程数值解)
r
2m sm x y
(a)
弹性应变增量
e ij
e ,服从虎克定律 d ij
1 1 2 d d ij d m ij 2G E
(b)
(a)+(b),及Prandtl-Reuss方程
1 1 2 d ij d ij d ij d m ij 2G E
d ij 或 d ij 1 d ij 2G
弹性变形时任意应力状态下等效应力与等效 应变关系
用应力差与应变差成比例的形式表示为:
1 2 2 3 3 1 E 2G 1 2 2 3 3 1 1
1 2 2 3 3 1 2 2 2 1 2 2 3 3 1
超塑性锻造
板料(管) 各向同性 成形 厚向各向异 性 各向异性 模具 线弹性 各向异性弹性 Prandtl方程 (弹塑性) Mises
刚粘塑性模型
(1)幂函数硬化 (2)拉伸数据
k,n K, n, r
K, n, r0, r45,r90
Hill
LS-dyna 37#
Barlet-Lian
LS-dyna 36#
1.44
1.51
1.50
1.47
1.43
1.42
2、各向异性材料(Barlat-Lian)本构关系 (LS-Dyna 36#材料模型)
ak1 k2 a(k1 k2 ) c(2k2 ) 2
m m m
对于面心立方材料:m=8, 体心立方材料, m=6
k1
m s
x h y
G
E 2(1 )
用主应力、主 3 E 1 2 2 3 1 E 1 3 3 1 2 E
弹性本构关系:本构方程 塑性本构关系:(1)本构方程;(2)屈服条 件;(3)硬化条件(应力-应变关系曲线)
本构关系是材料物理性质,取决于材料本身, 与应力状态无关
2、加载方式
简单加载:各应力分量按比例增大,应力主轴方向保持不变
ij
o ij
η—常数或单调增量函数
复杂加载:应力分量之间无一定关系,应力主轴方向变化
4、全量理论
1 1 2 3 2 i 1 2 2 3 1 i 2 i 1 3 3 1 2 i 2
1 i i
i A(B i )n
第三节、增量理论
1、Levy-Mises增量理论
(1)材料为理想刚塑性,服从Mesis 屈服准则 (2)应变增量主轴与应力主轴重合 (3) 应变增量与应力偏量成比例
d ij d ij '
塑性变形体积不变,只有形状的变化 塑性应变增量就是总的应变增量
(2)非线性
xy
D B P
A
C
σ
x
(3)依赖于加载路径(应力状态不仅与应力状态有关,而 且与加载路径或历史有关)
硬化材料的塑性变形量完全取决于第一 次到达加载曲面时的应力状态。必须以加载为 前提,立足于每一加载瞬间,来建立塑性变形 时的应力应变关系。换句话说,建立塑性变形 时的应力应变关系必须考虑加载历史。
3、加载准则(条件)
单向应力状态: d 0 加载,塑性应力应变关系 d 0 卸载,服从弹性规律 d 0 载荷不变,应变值不变 塑性变形功
dw p 0 dw p 0
复杂应力状态: id i 0 加载
id i 0
id i 0
卸载
i 不变) 中性变载(应力分量可能变化,
应力偏量与应变偏量关系
1 m 2G 1 m
2 m 2G 2 m 3 m 2G 3 m
ij ' 2G ij '
应力偏量与应变偏量成正比 形状的变化是由应力的偏张量引起的
1
定义迭代函数,用45度方向r值,求其数值解
g ( p)
2m s2 x y
1 r450
圆形件拉深(凸耳现象)
厚向各向异性(37#)
各向异性(36#)
3、可压缩材料(粉末材料)本构关系
2 2 F AJ BJ C 屈服准则(函数) 2 1 S 0 J 2 -应力偏量第二不变量
平面应力状态下(板料成形),Hill正交异性屈服准则:
1 2r i [ 2 1 2 ]2 s r 1 2 1 2
r 2r45 r90 r 0 4
B r t
Levy-Mises增量理论:
d1 d i
i
( 1
r 2) 1 r
r d 2 ( 2 1) i 1 r
E E1, E2, E3
3 1 2 4
B B
T
不锈钢和碳钢应力应变关系曲线
1Cr18Ni9Ti
600
SUS304
500
stress MPa
400
300
STKM13B(日本)碳钢
200
100
0 -0.05 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35
Strain
铝合金硬化曲线随温度变化
0.15 120
(2)双线性硬化模型
E tg
硬化模量: E1
tg
塑性:
i E i
E E1 100 0 i
i s E1( i s ) i
(3)幂函数硬化模型 多数金属材料,最常用
i K in
n值:板料成形重要参数,抗拉伸失稳能力 钢:n=0.22-0.24 不锈钢:n=0.3-0.4 (4)swift模型
4、硬化条件(单一曲线假设)
单向拉伸/压缩:应力-应变曲线
( )
加载点A:屈服应力 A ( A ) 含义:硬化材料 屈服应力随变形程度而提高, 且为瞬态应变函数。
复杂应力(二维、三维), i s 达到屈服,硬化后 等效应力 i 提高, i 与等效应变 i
1 2 d m d m E
由于考虑了弹性变形,引入了球张量,已知 d ij 求出 ij 对于硬化材料,变形过程每瞬时
d
为定值, d ij 与 ij
完全单值关系
3、硬化材料的增量理论
在复杂加载条件下,等效塑性应变总量
L
d i p
i H d i
L
p
d i H p 切线模量 d i
x
1
1 [ 1 ( 2 3 )] E 1 2 [ 2 ( 3 1 )] E
3
xy
1 XY G
. . . .
1 [ 3 ( 1 2 )] E
材料常数E, 钢:E 210GPa 铝:E 70GPa 0.3
Material: 5A02 Condition: Cold drawing Size: Φ65×1.5mm
镁合金硬化曲线随温度变化
Engineering Plasticity 工程塑性理论
塑性本构关系
苑世剑
2005年12月
2005级硕士研究生
第一节、弹性本构关系
第一节、弹性本构关系
1、单向应力
E
2、各向同性材料——虎克定律
1 [ x ( y z )] E 1 y [ y ( z x )] E 1 z [ z ( x y )] E
1)简单加载 2)小塑性变形(塑性变形数量 与弹性变形相当) n 3)硬化材料 i K i 或理想弹 塑性材料
1924年 Mesis提出增量理论 1943年 依留申提出全量理论
第四节
各向异性材料和可压缩材料增量理论
1、正交各向异性材料(LS-Dyna 37#材料模型)
板料/管材成形考虑各向异性(r值) 各向异性扎制加工过程成形
体积应变与平均应力(静水压、应力球张量) 关系 1 2 1 2 3 1 2 3 E
式中
1 2 3 3 m
1 2 m m E
——体积变化率
1 2 3 3 m——三倍的平均应力
所以,体积的变化率与平均应力成正比
J1
应力张量第一不变量
A、B、C-材料孔洞体积分数
F ij ij
本构方程:
3 1 1 ij ij kk ij 3 A 18B
B , A 1 不可压缩材料
第五节、材料模型选择
工艺 体积 成形 冷成形 等温成形 材料模型 本构方程 Levy-Mises 方程 (忽略弹性变形) 屈服条件 Mises 硬化条件 刚塑性(硬化) 理想刚塑性(硬化) 提供参数
3、弹性应力应变关系特点 1) 线性 2) 单值 3) 可逆 4) 应力主轴与应变主轴重合 5) 体积变化(平均应变)与静水应力成比例 6) 应变偏量与应力偏量成比例 7) 单向拉伸时的应力应变关系可以适应(推 广)任意应力状态
第二节、塑性本构关系特点与基本概念
1、塑性变形应力应变关系的特点
