高一数学人教a版必修1学业分层测评4_并集、交集_word版含解析
高中数学人教a版高一必修一_第一章_集合与函数概念_学业分层测评2_word版有答案

学业分层测评(二)集合的表示(建议用时:45分钟)[学业达标]一、选择题1.把集合{x|x2-3x+2=0}用列举法表示为()A.{x=1,x=2} B.{x|x=1,x=2}C.{x2-3x+2=0} D.{1,2}【解析】解方程x2-3x+2=0可得x=1或2,所以集合{x|x2-3x+2=0}用列举法可表示为{1,2}.【答案】 D2.(2016·石家庄高一检测)设集合A={1,2,4},集合B={x|x=a+b,a∈A,b∈A},则集合B中的元素个数为()A.4 B.5C.6 D.7【解析】由题意,B={2,3,4,5,6,8},共有6个元素,故选C.【答案】 C3.(2016·漳州高一检测)下列各组两个集合M和N表示同一集合的是()A.M={π},N={3.141 59}B.M={2,3},N={(2,3)}C.M={(x,y)|x+y=1},N={y|x+y=1}D.M={x|x2+1=0},N=∅【解析】对于A,∵π≠3.141 59,∴{π}≠{3.141 59}.对于B,前者包含2个元素,而后者只含一个元素,是个点.对于C,前者是直线x+y=1上点的集合,而后者是函数y=-x +1的值域.对于D,∵x2+1=0无解,∴{x|x2+1=0}=∅,故选D.【答案】 D4.(2016·贵阳高一检测)设集合A={-2,0,1,3},集合B={x|-x∈A,1-x∉A},则集合B中元素的个数为() 【导学号:97030008】A.1 B.2C.3 D.4【解析】若x∈B,则-x∈A,∴x的可能取值为:2,0,-1,-3,当2∈B时,则1-2=-1∉A,∴2∈B;当0∈B时,则1-0∈A,∴0∉B;当-1∈B时,则1-(-1)=2∉A,∴-1∈B;当-3∈B时,则1-(-3)=4∉A,∴-3∈B.综上,B={-3,-1,2},所以集合B含有的元素个数为3,故选C.【答案】 C5.已知P={x|2<x<k,x∈N},若集合P中恰有3个元素,则()A.5<x<6 B.5≤x<6C.5<x≤6 D.5≤x≤6【解析】因为P中恰有3个元素,所以P={3,4,5},可得5<k≤6,故选C.【答案】 C二、填空题6.已知集合A={-1,-2,0,1,2},B={x|x=y2,y∈A},则用列举法表示B应为________.【解析】(-1)2=12=1,(-2)2=22=4,02=0,所以B={0,1,4}.【答案】{0,1,4}7.已知集合A={x|x2+2x+a=0},若1∈A,则A=________.【解析】把x=1代入方程x2+2x+a=0可得a=-3,解方程x2+2x-3=0可得A={-3,1}.【答案】{-3,1}8.(2016·松原高一检测)若2∉{x|x-a<0},则实数a的取值集合是________.【解析】由题意,{x|x-a<0}={x|x<a},∵2∉{x|x-a<0},∴a≤2,∴实数a的取值集合是{a|a≤2}.【答案】{a|a≤2}三、解答题9.用适当的方法表示下列集合:(1)方程x2+y2-4x+6y+13=0的解集;(2)1 000以内被3除余2的正整数组成的集合;(3)平面直角坐标系中第二象限内的点组成的集合;(4)二次函数y=x2-10图象上的所有点组成的集合.【解】(1)方程x2+y2-4x+6y+13=0可化为(x-2)2+(y+3)2=0,解得x=2,y=-3,所以方程的解集为{(x,y)|x=2,y=-3}.(2)集合的代表元素是数,用描述法可表示为{x|x=3k+2,k∈N且x<1 000}.(3)集合的代表元素是点,用描述法可表示为{(x,y)|x<0,且y>0}.(4)“二次函数y=x2-10图象上的所有点”用描述法表示为{(x,y)|y=x2-10}.10.(2016·宁德高一检测)若-3∈{a-3,2a-1,a2+1},求实数a的值.【解】∵-3∈{a-3,2a-1,a2+1},又a2+1≥1,∴-3=a-3,或-3=2a-1,解得a=0,或a=-1,当a=0时,{a-3,2a-1,a2+1}={-3,-1,1},满足集合三要素;当a=-1时,{a-3,2a-1,a2+1}={-4,-3,2},满足集合三要素;∴a=0或-1.[能力提升]1.集合A={1,2,3,4,5},B={1,2,3},C={z|z=xy,x∈A且y∈B},则集合C中的元素个数为()A.3 B.4C.11 D.12【解析】C={1,2,3,4,5,6,8,9,10,12,15},故选C.【答案】 C2.已知集合A={2,0,1,4},B={k|k∈R,k2-2∈A,k-2∉A},则集合B中所有的元素之和为()A.2 B.-2C.0 D. 2【解析】若k2-2=2,得k=2或k=-2,当k=2时,k-2=0不满足条件,当k=-2时,k-2=-4,满足条件;若k2-2=0,得k=±2,显然满足条件;若k2-2=1,得k=±3,显然满足条件;若k2-2=4,得k=±6,显然满足条件.所以集合B中的元素为-2,±2,±3,±6,所以集合B中的元素之和为-2,则选B.【答案】 B3.已知集合M={a,2,3+a},集合N={3,2,a2},若M=N,则a=()A.1 B.3C.0 D.0或1【解析】 因为集合M 与集合N 相等.所以⎩⎨⎧ a =33+a =a 2或⎩⎨⎧a =a 23+a =3, 对于⎩⎨⎧ a =33+a =a 2,无解; 对于⎩⎨⎧a =a 23+a =3, 解得a =0,综上可知a =0.【答案】 C4.设集合B =⎩⎨⎧⎭⎬⎫x ∈N ⎪⎪⎪62+x ∈N , (1)试判断元素1和2与集合B 的关系;(2)用列举法表示集合B . 【导学号:97030009】【解】 (1)当x =1时,62+1=2∈N ;当x =2时,62+2=32∉N ,所以1∈B,2∉B . (2)令x =0,1,4代入62+x ∈N 检验,可得B ={0,1,4}.。
1.3 集合的基本运算——并集、交集 课件-2024-2025学年高一上学期数学人教A版必修1

0
1
2
3
注重数形结合:
若给定的集合是不等式的解集,用数轴求解(特别注意端点的虚实);
若给定的集合是抽象集合,可以用Venn图求解.
复习旧课
探究新知
新知讲解
典例分析
小试牛刀
课堂小结
变式(1)设集合A ={1,3,5,7}, 集合B ={0,2,3,4,6}, 求A∪B.
(2)设集合A={x|-1<x≤2}, 集合B={x|0<x≤3},求A∪B.
B={x|x是立德中学2020年9月在校的高一年级同学},
C={x|x是立德中学2020年9月在校的高一年级女同学}.
集合C是由所有既属于A又属于集合B的元素组成的.
作业布置
复习旧课
探究新知
新知讲解
典例分析
小试牛刀
课堂小结
作业布置
集合运算——交集
自然语言
一般地,由所有属于集合A且属于集合B的元素组成的集合,称为
集合
=B
(2)如何判断集合间关系?
关注集合中的元素特征
(3)我们知道,实数有加、减、乘、除等运算.集合是否也有类似的运算呢?
复习旧课
探究新知
新知讲解
典例分析
小试牛刀
课堂小结
作业布置
观察下面的集合,类比实数的加法运算,你能说出集合C与集合A、B
之间的关系吗?
(1) A={1,3,5}, B={2,4,6}, C={1,2,3,4,5,6};
(1)A∩A=A;(2的交集运算有哪些性质呢?
.
小试牛刀
课堂小结
作业布置
复习旧课
探究新知
新知讲解
典例分析
新教材高中数学课时素养评价四并集交集新人教A版必修第一册

新教材高中数学课时素养评价四并集交集新人教A版必修第一册并集、交集(25分钟·50分)一、选择题(每小题4分,共16分,多项选择题全选对的得4分,选对但不全的得2分,有选错的得0分)1.(2018·全国卷Ⅲ)已知集合A={x|x-1≥0},B={0,1,2},则A∩B= ( )A.{0}B.{1}C.{1,2}D.{0,1,2}【解析】选C.因为A={x|x-1≥0}={x|x≥1},B={0,1,2},所以A∩B={1,2}.2.已知集合A={x|2≤x<4},B={x|3x-7≥8-2x},则A∪B= ( )A.{x|3≤x<4}B.{x|x≥2}C.{x|2≤x<4}D.{x|2≤x≤3}【解析】选B.因为A={x|2≤x<4},B={x|x≥3},所以A∪B={x|x≥2}.3.(多选题)已知集合A={x|x2=x},集合B中有两个元素,且满足A∪B={0,1,2},则集合B可以是( )A.{0,1}B.{0,2}C.{0,3}D.{1,2}【解析】选B、D.因为A={0,1},集合B中有两个元素,且满足A∪B={0,1,2},所以集合B可以是{0,2}或{1,2}.【加练·固】设集合A={a,b},B={a+1,5},若A∩B={2},则A∪B等于 ( )A.{1,2,5}B.{1,2}C.{1,5}D.{2,5}【解析】选A.因为A∩B={2},所以2∈A,且2∈B,所以a+1=2, 所以a=1,所以b=2.所以A={1,2},B={2,5},所以A∪B={1,2,5}.4.已知集合A={x|-1≤x<2},B={x|x<a},若A∩B≠∅,则实数a的取值范围为( ) A.-1<a≤2 B.a>-1C.a>-2D.a≥2【解析】选B.因为A={x|-1≤x<2},B={x|x<a},A∩B≠∅,画出数轴表示两个集合如下:观察图形可知a>-1.【加练·固】已知A={x|x≥1},B=x≤x≤2a-1,若A∩B≠∅,则实数a的取值范围是( )A.{a|a≥1}B.C. D.{a|a>1}【解析】选A.A={x|x≥1},B=x≤x≤2a-1,且A∩B≠∅,所以2a-1≥1,所以a≥1.【误区警示】解答本题容易出现2a-1>1,解得a>1的错误.二、填空题(每小题4分,共8分)5.已知集合A={x|-3≤x≤3},B={x|x≥2},则A∩B=____,A∪B=____.【解析】A∩B={x|2≤x≤3},A∪B={x|x≥-3}.答案:{x|2≤x≤3} {x|x≥-3}6.(2017·江苏高考)已知集合A={1,2},B={a,a2+3},若A∩B={1},则实数a的值为________.【解析】由题意知1∈B,显然a2+3≥3,所以a=1,此时a2+3=4,满足题意,故答案为1.答案:1三、解答题(共26分)7.(12分)已知集合A={x|x2-px-2=0},B={x|x2+qx+r=0},若A∪B={-2,1,5},A∩B={-2},求p+q+r的值.【解析】因为A∩B={-2},所以-2∈A,代入x2-px-2=0.解得p=-1,所以A={-2,1},由A∪B={-2,1,5},A∩B={-2},得B={-2,5}.所以-2,5是方程x2+qx+r=0的两个根,由根与系数的关系可得-q=-2+5,r=(-2)×5.所以q=-3,r=-10,所以p+q+r =-14.8.(14分)已知A={x|x2-ax+a2-19=0},B={x|x2-5x+8=2},C={x|x2+2x-8=0},若∅ (A∩B),且A∩C=∅,求a的值.【解析】A={x|x2-ax+a2-19=0},B={2,3},C={-4,2}.因为∅ (A∩B),且A∩C=∅,那么3∈A,故9-3a+a2-19=0.即a2-3a-10=0.所以a=-2或a=5.当a=-2时A={x|x2+2x-15=0}={3,-5},符合题意.当a=5时A={x|x2-5x+6=0}={2,3},不符合A∩C=∅.综上知,a=-2.(15分钟·30分)1.(4分)已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},则集合A∩B中所有元素的和为( )A.14B.22C.32D.34【解析】选B.集合A中元素满足x=3n+2,n∈N,即被3除余2,而集合B中满足这一要求的元素只有8和14,即A∩B={8,14},8+14=22.2.(4分)若集合A={0,1,2,x},B={1,x2},A∪B=A,则满足条件的实数x有( )A.1个B.2个C.3个D.4个【解析】选B.因为A∪B=A,所以B⊆A.因为A={0,1,2,x},B={1,x2},所以x2=0或x2=2或x2=x,解得x=0或或-或1.经检验,当x=或-时满足题意.3.(4分)若集合M={x|-2<x<3},N={y|y=x2+1,x∈R},则集合M∩N=________.【解析】由y=x2+1≥1,化简集合B={y|y≥1},又因为M={x|-2<x<3},所以M∩N={x|1≤x<3}(或{y|1≤y<3}).答案:{x|1≤x<3}(或{y|1≤y<3})【加练·固】已知集合P={y|y=x+1,x≥0},Q={y|y=5-x2,x∈R},则P∪Q=________.【解析】因为P={y|y=x+1,x≥0}={y|y≥1},Q={y|y=5-x2,x∈R}={y|y≤5},所以P∪Q=R. 答案:R4.(4分)集合A={x|2k<x<2k+1,k∈Z},B={x|1<x<6},则A∩B =________.【解析】在数轴上表示集合A,B,如图所以A∩B={x|2<x<3或4<x<5}.答案:{x|2<x<3或4<x<5}5.(14分)若集合A={x|x2+5x-6=0},B={x|x2+2(m+1)x+m2-3=0}.(1)若m=0,写出A∪B的子集.(2)若A∩B=B,求实数m的取值范围.【解析】A={-6,1}.(1)根据题意,m=0时,B={1,-3},A∪B={-6,-3,1};所以A∪B的子集为:∅,{-6},{-3},{1},{-6,-3},{-6,1},{-3,1},{-6,-3,1}.(2)由已知得B⊆A,对于集合B,Δ=4(m+1)2-4(m2-3)=8m+16.当m<-2时,B=∅,成立.当m=-2时,B={1}⊆A,成立.当m>-2时,又B⊆A,所以B={-6,1};所以⇒m无解,综上所述:m的取值范围是m≤-2.1.设A={x|1≤x≤4},B={x|x>t},若A∩B只有一个子集,则t的取值范围是________.【解析】若A∩B只有一个子集,则必然为空集,即A∩B=∅.由A={x|1≤x≤4},B={x|x>t},则t≥4.答案:{t|t≥4}【加练·固】设集合A={2,3,4,5},B={4,5,6,7},则满足S⊆A且S∩B≠∅的集合的S个数为( )A.10B.11C.12D.13【解析】选C.集合A的子集有∅,{2},{3},{4},{5},{2,3},{2,4},{2,5},{3,4},{3,5},{4,5},{3,4,5},{2,4,5},{2,3,5},{2,3,4},{2,3,4,5},共16个;又S∩B≠∅, B={4,5,6,7},所以S只能为{4},{5},{2,4},{2,5},{3,4},{3,5},{4,5},{3,4,5},{2,4,5},{2,3,5},{2,3,4},{2,3,4,5},共12个.2.已知集合A={x|-2<x<8},B={x|2m-1<x<m+3}.(1)若A∪B=A,求实数m的取值范围.(2)若A∩B={x|a<x<b}且b-a=3,求实数m的取值范围.【解析】(1)因为A∪B=A,则B⊆A,集合B有两种情况:当B=∅时,则m满足2m-1≥m+3解得m≥4;当B≠∅时,则m满足解得-≤m<4.综上m的取值范围是m≥-.(2)因为A={x|-2<x<8},8-(-2)=10,所以若A∩B={x|a<x<b}且b-a=3,应有以下三种情况:①当A∩B=B时,则m满足,解得m=1,②当A∩B={x|2m-1<x<8}时,则m满足此时满足条件的m不存在.③当A∩B={x|-2<x<m+3}时,则m满足解得m=-2,综上,m的值为-2或1.。
高一数学人教A版必修1学业分层测评5 补集及综合应用 Word版含解析

学业分层测评(五) 补集及综合应用(建议用时:分钟)[学业达标]一、选择题.若全集={}且∁={},则集合的真子集共有( ).个.个.个.个【解析】={},真子集有-=.【答案】.已知全集=,={≤},={≥},则集合∁(∪)=( ).{≤}.{≥}.{≤≤}.{<<}【解析】由题意可知,∪={≤或≥},所以∁(∪)={<<}.【答案】.(·天津高考)已知全集={},集合={},集合={},则集合∩∁=( ).{}.{}.{}.{}【解析】由题意得∁={},∴∩∁={}∩{}={}.【答案】.(·中山高一检测)设全集={},集合={},={},则图--中的阴影部分表示的集合为( )图--.{}.{}.{}.{}【解析】全集={},集合={},={},由韦恩图可知阴影部分表示的集合为(∁)∩,∵∁={},∴(∁)∩={}.故选.【答案】.(·南阳高一检测)已知集合={<},={<<},且∪(∁)=,则实数的取值范围是( ) 【导学号:】.<.≤.>.≥【解析】∵集合={<},={<<},∴∁={≤或≥},因为∪∁=,所以≥,故选.【答案】二、填空题.(·杭州模拟)设集合={>-},={+-≤},则(∁)∪=.【解析】∵集合={>-},∴∁={≤-},由+-≤,得={-≤≤},故(∁)∪={≤}.【答案】(-∞,].已知集合、均为全集={}的子集,且∁(∪)={},={},则∩∁=.【解析】∵={},∁(∪)={},∴∪={},又∵={},∴{}⊆⊆{}.又∁={},∴∩∁={}.【答案】{}.设全集=,集合={≥},={≥},则∁与∁的包含关系是.【解析】∁={<},∁={<}={<}.∴∁⊆∁.【答案】∁⊆∁三、解答题。
高中数学人教A版必修一课后练习4 并集和交集

高中数学人教A版必修一课后练习4并集和交集题组1:夯实基础1.已知集合M={x|-3<x≤5},N={x|x<-5,或x>4},则M∪N=()A.{x|x<-5,或x>-3} B.{x|-5<x<4}C.{x|-3<x<4} D.{x|x<-3,或x>5}解析:在数轴上分别表示集合M和N,如图所示,则M∪N={x|x<-5,或x>-3}.答案:A2.(2019天津,文1)设集合A={-1,1,2,3,5},B={2,3,4},C={x∈R|1≤x<3},则(A∩C)∪B=() A.{2} B.{2,3}C.{-1,2,3} D.{1,2,3,4}解析:A∩C={1,2},(A∩C)∪B={1,2,3,4},故选D.答案:D3.已知集合A={x|x=2n-3,n∈N},B={-3,1,4,7,10},则集合A∩B中元素的个数为() A.5 B.4 C.3 D.2解析:由条件知,当n=0时,2n-3=-3;当n=2时,2n-3=1;当n=5时,2n-3=7.所以A∩B={-3,1,7}.故选C.答案:C4.若A={x∈N|1≤x≤10},B={x∈R|x2+x-6=0},则图中阴影部分表示的集合为()A.{2} B.{3}C.{-3,2} D.{-2,3}解析:A={1,2,3,4,5,6,7,8,9,10},B={-3,2},由题意可知,阴影部分即为A∩B,故A∩B={2}.答案:A5.已知集合S={直角三角形},集合P={等腰三角形},则S∩P=____________________.解析:S∩P表示集合S和集合P的公共元素组成的集合,故S∩P={等腰直角三角形}.答案:{等腰直角三角形}6.已知集合A={1,2,3},B={2,m,4},A∩B={2,3},则m=__________.解析:由于A∩B={2,3},则3∈B,又B={2,m,4},则m=3.答案:37.已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,则实数a的取值范围是__________.解析:用数轴表示集合A,B,如图所示,因为A∪B=R,则在数轴上实数a与1重合或在1的左边,所以a≤1.答案:a≤1},集合B={x|2x-1<3},求A∩B,A∪B.8.已知集合A={x|{3-x>0,3x+6>0解解不等式组{3-x>0,3x+6>0,得-2<x<3,即A={x|-2<x<3}.解不等式2x-1<3,得x<2,即B={x|x<2},在数轴上分别表示集合A,B,如图所示.则A∩B={x|-2<x<2},A∪B={x|x<3}.9.已知集合M={x|2x-4=0},集合N={x|x2-3x+m=0},(1)当m=2时,求M∩N,M∪N;(2)当M∩N=⌀时,求实数m的取值范围.解(1)由题意得,M={2},当m=2时,N={x|x2-3x+2=0}={1,2},则M∩N={2},M∪N={1,2}.(2)M={2}≠⌀,则2不是方程x2-3x+m=0的解,所以4-6+m≠0,即m≠2.所以实数m的取值范围为m≠2.题组2:难点突破1.设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=()A.{1,-3} B.{1,0}C.{1,3} D.{1,5}解析:∵A∩B={1},∴1∈B.∴1-4+m=0,即m=3.∴B={x|x2-4x+3=0}={1,3}.故选C.答案:C2.已知集合A={x|-3≤x≤8},B={x|x>a},若A∩B≠⌀,则a的取值范围是()A.a<8 B.a>8C.a>-3 D.-3<a≤8解析:A={x|-3≤x≤8},B={x|x>a},要使A∩B≠⌀,借助数轴可知a<8.答案:A3.设A,B是非空集合,定义A*B={x|x∈A∪B且x∉A∩B},已知A={x|0≤x≤3},B={x|x≥1},则A*B 等于()A.{x|1≤x<3}B.{x|1≤x≤3}C.{x|0≤x<1或x>3}D.{x|0≤x≤1或x≥3}解析:由题意知,A∪B={x|x≥0},A∩B={x|1≤x≤3},则A*B={x|0≤x<1或x>3}.答案:C4.已知集合M={(x,y)|x+y=2},N={(x,y)|x-y=4},那么集合M∩N=__________.解析:由{x+x=2,x-x=4,解得{x=3,x=-1.∴M∩N={(3,-1)}.答案:{(3,-1)}5.已知集合A={x|x<1,或x>5},B={x|a≤x≤b},且A∪B=R,A∩B={x|5<x≤6},则2a-b=__________.解析:如图所示,可知a =1,b =6,2a -b =-4.答案:-46.若集合A ={x |3ax -1=0},B ={x |x 2-5x +4=0},且A ∪B =B ,则a 的值是__________.解析:∵B ={1,4},A ∪B =B ,∴A ⊆B .当a =0时,A =⌀,符合题意;当a ≠0时,A ={13x },∴13x =1或13x =4,∴a =13或a =112.综上,a =0,13,112.答案:0,13,1127.设集合A ={x |-1≤x ≤2},B ={x |x 2-(2m +1)x +2m<0}.(1)当m<12时,化简集合B ;(2)若A ∪B =A ,求实数m 的取值范围.解由不等式x 2-(2m +1)x +2m<0,得(x -1)(x -2m )<0.(1)当m<12时,2m<1,∴集合B ={x |2m<x<1}.(2)若A ∪B =A ,则B ⊆A ,①当m<12时,B ={x |2m<x<1},此时-1≤2m<1,解得-12≤m<12;②当m =12时,B =⌀,有B ⊆A 成立;③当m>12时,B ={x |1<x<2m },此时1<2m ≤2,解得12<m ≤1.综上所述,所求m 的取值范围是{x |-12≤x ≤1}.8.某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有多少人?解设参加数学、物理、化学小组的人数构成的集合分别为A ,B ,C ,同时参加数学和化学小组的有x 人,由题意可得如图所示的Venn 图.由全班共36名同学参加课外探究小组可得(26-6-x)+6+(15-10)+4+(13-4-x)+x=36,解得x=8,即同时参加数学和化学小组的有8人.。
高一数学人教A版必修1练习第4课时 交集、并集 Word版含解析
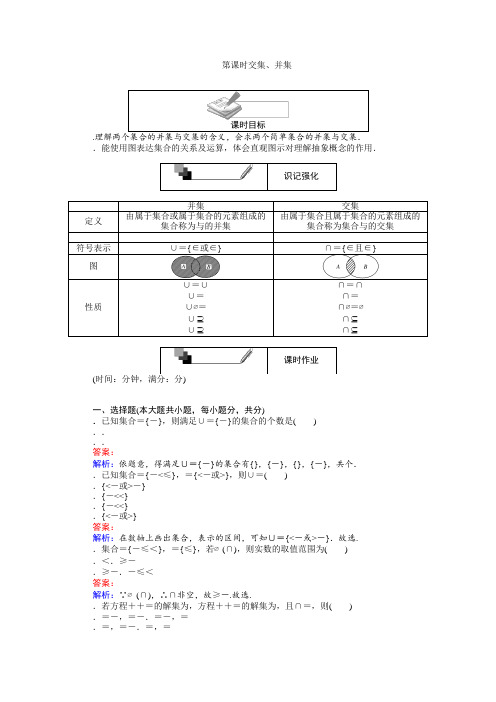
.{-<<}
.{-<<}
.{<-或>}
答案:
解析:在数轴上画出集合,表示的区间,可知∪={<-或>-}.故选.
.集合={-≤<},={≤},若∅(∩),则实数的取值范围为()
.<.≥-
.≥-.-≤<
答案:
解析:∵∅(∩),∴∩非空,故≥-.故选.
.若方程++=的解集为,方程++=的解集为,且∩=,则()
图
性质
∪=∪
∪=
∪∅=
∪⊇
∪⊇
∩=∩
∩=
∩∅=∅
∩⊆
∩⊆
课时作业
(时间:分钟,满分:分)
一、选择题(本大题共小题,每小题分,共分)
.已知集合={-},则满足∪={-}的集合的个数是()
..
..
答案:
解析:依题意,得满足∪={-}的集合有{},{-},{},{-},共个.
.已知集合={-<≤},={<-或>},则∪=()
结合二次函数=--的图象,可得>或<-.
所以实数的取值范围为{>或<-}.
()因为∩至多有一个元素,所以方程组无解或只有一组解,
即一元二次方程+(-)+=无实数根或有两个相等的实数根,
所以Δ=(-)-=--≤,
结合二次函数=--的图象,可得-≤≤.
所以实数的取值范围为{-≤≤}.
能力提升
.(分)对于集合,,我们把集合{∈,且∉}叫做集合与的差集,记作-.若={},={},则-=.
.已知集合={(,)=+},={=-},则∩=()
.{-}.{(-,-)}
.∅.{-}
最新高中数学人教版A版必修一学案:第一单元 1.1.3 第1课时 并集、交集 Word版含答案-

1.1.3集合的基本运算第1课时并集、交集学习目标 1.理解两个集合的并集与交集的含义,会求两个简单集合的并集和交集(重点).2.能使用Venn图表示集合的并集、交集运算结果(难点).3.掌握有关的术语和符号,并会用它们正确进行集合的并集与交集运算(重点).预习教材P8-P9,完成下面问题:知识点1并集(1)文字语言:由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B的并集.(2)符号语言:A∪B={x|x∈A或x∈B}.(3)图形语言:如图所示.【预习评价】(1)已知集合A={x|x>0},B={x|-1≤x≤2},则A∪B等于()A.{x|x≥-1}B.{x|x≤2}C.{x|0<x≤2}D.{x|-1≤x≤2}(2)已知集合A={1,2,3},B={2,4,5},则集合A∪B中元素的个数为________.解析(1)A∪B={x|x>0}∪{x|-1≤x≤2}={x|x≥-1}.(2)A∪B={1,2,3}∪{2,4,5}={1,2,3,4,5},共5个元素.答案(1)A(2)5知识点2交集(1)文字语言:由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集.(2)符号语言:A∩B={x|x∈A且x∈B}.(3)图形语言:如图所示.【预习评价】(1)若集合M={-1,1},N={-2,1,0},则M∩N=()A.{0,-1}B.{1} C.{0}D.{-1,1}(2)若P={x|x≥1},Q={x|-1<x<4},则P∩Q=________.解析(1)M∩N={-1,1}∩{-2,1,0}={1},故选B.(2)如图所示,P∩Q={x|1≤x<4}.答案(1)B(2){x|1≤x<4}题型一并集的概念及简单应用【例1】(1)设集合M={4,5,6,8},集合N={3,5,7,8},那么M∪N等于()A.{3,4,5,6,7,8}B.{5,8} C.{3,5,7,8}D.{4,5,6,8}(2)已知集合P={x|x<3},Q={x|-1≤x≤4},那么P∪Q等于()A.{x|-1≤x<3}B.{x|-1≤x≤4}C.{x|x≤4}D.{x|x≥-1}解析(1)由定义知M∪N={3,4,5,6,7,8}.(2)在数轴上表示两个集合,如图,可得P∪Q={x|x≤4}.答案(1)A(2)C规律方法求集合并集的两种方法(1)定义法:若集合是用列举法表示的,可以直接利用并集的定义求解;(2)数形结合法:若集合是用描述法表示的由实数组成的数集,则可以借助数轴分析法求解,此时要注意集合的端点能否取到.【训练1】已知集合M={0,1,3},N={x|x=3a,a∈M},则M∪N=()A.{0}B.{0,3}C.{1,3,9}D.{0,1,3,9}解析易知N={0,3,9},故M∪N={0,1,3,9}.答案 D题型二交集的概念及简单应用【例2】(1)A={x∈N|1≤x≤10},B={x∈R|x2+x-6=0},则图中阴影部分表示的集合为( )A .{2}B .{3}C .{-3,2}D .{-2,3}(2)设集合A ={x |-1≤x ≤2},B ={x |0≤x ≤4},则A ∩B =( )A .{x |0≤x ≤2}B .{x |1≤x ≤2}C .{x |0≤x ≤4}D .{x |1≤x ≤4}解析 (1)易知A ={1,2,3,4,5,6,7,8,9,10},B ={-3,2},图中阴影部分表示的集合为A ∩B ={2},故选A .(2)在数轴上表示出集合A 与B ,如图所示.则由交集的定义知,A ∩B ={x |0≤x ≤2}.答案 (1)A (2)A规律方法 求集合A ∩B 的常见类型(1)若A ,B 的代表元素是方程的根,则应先解方程求出方程的根后,再求两集合的交集.(2)若集合的代表元素是有序数对,则A ∩B 是指两个方程组成的方程组的解集,解集是点集.(3)若A ,B 是无限数集,可以利用数轴来求解,但要注意利用数轴表示不等式时,含有端点的值用实心点表示,不含有端点的值用空心圈表示.【训练2】 (1)已知集合A ={x |x =3n +2,n ∈N },B ={6,8,10,12,14},则集合A ∩B 中元素的个数为( )A .5B .4C .3D .2(2)已知M ={(x ,y )|x +y =2},N ={(x ,y )|x -y =4},则M ∩N =( )A .x =3,y =-1B .(3,-1)C .{3,-1}D .{(3,-1)}解析 (1)8=3×2+2,14=3×4+2,故A ∩B ={8,14},故选D .(2)由⎩⎪⎨⎪⎧ x +y =2,x -y =4,得⎩⎪⎨⎪⎧x =3,y =-1,故M ∩N ={(3,-1)}. 答案 (1)D (2)DA 与B 具有怎样的关系?解 A ∩B =A ⇔A ∪B =B ⇔A ⊆B ,即A ∩B =A ,A ∪B =B ,A ⊆B 三者为等价关系.【探究2】 若集合={x |x 2+2x -a =0}=∅,求a 的取值范围.解 由题意知方程x 2+2x -a =0无实根,故Δ=4+4a <0,解得a <-1.【探究3】 设集合A ={1,2},若B ⊆A ,求B .解 B =∅或{1}或{2}或{1,2}.【探究4】 设集合A ={x |x 2-3x +2=0},B ={x |x 2+2(a -1)x +(a 2-5)=0}.(1)若A ∩B ={2},求实数a 的值;(2)若A ∪B =A ,求实数a 的取值范围.解 (1)由题可知:A ={x |x 2-3x +2=0}={1,2},∵A ∩B ={2},∴2∈B ,将2带入集合B 中得:4+4(a -1)+(a 2-5)=0,解得:a =-5或a =1.当a =-5时,集合B ={2,10}符合题意;当a =1时,集合B ={2,-2},符合题意.综上所述:a =-5或a =1.(2)若A ∪B =A ,则B ⊆A ,∵A ={1,2},∴B =∅或B ={1}或{2}或{1,2}.若B =∅,则Δ=4(a -1)2-4(a 2-5)=24-8a <0,解得a >3;若B ={1},则⎩⎪⎨⎪⎧ Δ=24-8a =0,x =-2(a -1)2=1-a =1,即⎩⎪⎨⎪⎧ a =3,a =0,不成立; 若B ={2},则⎩⎪⎨⎪⎧ Δ=24-8a =0,x =-2(a -1)2=1-a =2,即⎩⎪⎨⎪⎧a =3,a =-1,不成立; 若B ={1,2},则⎩⎪⎨⎪⎧ Δ=24-8a >0,1+2=-2(a -1),1×2=a 2-5,即⎩⎪⎨⎪⎧ a <3,a =-12,a =±7,此时不成立,综上a >3.规律方法 利用集合交集、并集的性质解题的依据及关注点(1)依据:A ∩B =A ⇔A ⊆B ,A ∪B =A ⇔B ⊆A .(2)关注点:当集合A ⊆B 时,若集合A 不确定,运算时要考虑A =∅的情况,否则易漏解.【训练3】 已知集合A ={x |2a ≤x ≤a +3},B ={x |x <-1或x >5},若A ∩B =∅,求实数a 的取值范围.解 由A ∩B =∅,(1)若A =∅,有2a >a +3,∴a >3.(2)若A ≠∅,如下图:∴⎩⎪⎨⎪⎧ 2a ≥-1,a +3≤5,2a ≤a +3,解得-12≤a ≤2. 综上所述,a 的取值范围是{a |-12≤a ≤2或a >3}.课堂达标1.设集合A ={0,1,2,3},集合B ={2,3,4},则A ∩B =( )A .{2,3}B .{0,1}C .{0,1,4}D .{0,1,2,3,4}解析 因为集合A ={0,1,2,3},集合B ={2,3,4},所以A ∩B ={2,3},故选A .答案 A2.已知集合A ={x |-1≤x <3},B ={x |2<x ≤5},则A ∪B =( )A .{x |2<x <3}B .{x |-1≤x ≤5}C .{x |-1<x <5}D .{x |-1<x ≤5}解析 ∵集合A ={x |-1≤x <3},B ={x |2<x ≤5},∴A ∪B ={x |-1≤x ≤5},故选B . 答案 B3.已知集合M ={-1,0},则满足M ∪N ={-1,0,1}的集合N 的个数是( )A .2B .3C .4D .8解析 由M ∪N ={-1,0,1},得到集合M ⊆M ∪N ,且集合N ⊆M ∪N ,又M ={0,-1},所以元素1∈N ,则集合N 可以为{1}或{0,1}或{-1,1}或{0,-1,1},共4个.故选C .答案 C4.设集合A ={(x ,y )|y =ax +1},B ={(x ,y )|y =x +b },且A ∩B ={(2,5)},则( )A .a =3,b =2B .a =2,b =3C .a =-3,b =-2D .a =-2,b =-3解析 ∵A ∩B ={(2,5)},∴⎩⎪⎨⎪⎧5=2a +1,5=2+b ,解得a =2,b =3,故选B . 答案 B5.已知集合A ={x |3≤x <7},B ={x |2<x <10},C ={x |x <3或x ≥7},求:(1)A ∪B ;(2)C ∩B .解 (1)由集合A ={x |3≤x <7},B ={x |2<x <10},把两集合表示在数轴上如图所示:得到A ∪B ={x |2<x <10};(2)由集合B ={x |2<x <10},C ={x |x <3或x ≥7},把两集合表示在数轴上如图所示:则C ∩B ={x |2<x <3或7≤x <10}.课堂小结1.对并集、交集概念的理解(1)对于并集,要注意其中“或”的意义,“或”与通常所说的“非此即彼”有原则性的区别,它们是“相容”的.“x ∈A ,或x ∈B ”这一条件,包括下列三种情况:x ∈A 但x ∉B ;x ∈B 但x ∉A ;x ∈A 且x ∈B .因此,A ∪B 是由所有至少属于A ,B 两者之一的元素组成的集合.(2)A ∩B 中的元素是“所有”属于集合A 且属于集合B 的元素,而不是部分,特别地,当集合A 和集合B 没有公共元素时,不能说A 与B 没有交集,而是A ∩B =∅.2.集合的交、并运算中的注意事项(1)对于元素个数有限的集合,可直接根据集合的“交”、“并”定义求解,但要注意集合元素的互异性.(2)对于元素个数无限的集合,进行交、并运算时,可借助数轴,利用数轴分析法求解,但要注意端点值取到与否.。
高中数学人教a版高一必修一_学业分层测评(五)_word版有答案

学业分层测评(五)补集及综合应用(建议用时:45分钟)[学业达标]一、选择题1.若全集U={0,1,2,3}且∁U A={2},则集合A的真子集共有()A.3个B.5个C.7个D.8个【解析】A={0,1,3},真子集有23-1=7.【答案】 C2.已知全集U=R,A={x|x≤0},B={x|x≥1},则集合∁U(A∪B)=()A.{x|x≥0} B.{x|x≤1}C.{x|0≤x≤1} D.{x|0<x<1}【解析】由题意可知,A∪B={x|x≤0或x≥1},所以∁U(A∪B)={x|0<x<1}.【答案】 D3.(2015·天津高考)已知全集U={1,2,3,4,5,6,7,8},集合A={2,3,5,6},集合B={1,3,4,6,7},则集合A∩∁U B=()A.{2,5} B.{3,6}C.{2,5,6} D.{2,3,5,6,8}【解析】由题意得∁U B={2,5,8},∴A∩∁U B={2,3,5,6}∩{2,5,8}={2,5}.【答案】 A4.(2016·中山高一检测)设全集U={1,2,3,4,5,6,7,8},集合A={1,2,3,5},B={2,4,6},则图1-1-2中的阴影部分表示的集合为()图1-1-2A.{2} B.{4,6}C.{1,3,5} D.{4,6,7,8}【解析】全集U={1,2,3,4,5,6,7,8},集合A={1,2,3,5},B={2,4,6},由韦恩图可知阴影部分表示的集合为(∁U A)∩B,∵∁U A={4,6,7,8},∴(∁U A)∩B={4,6}.故选B.【答案】 B5.(2016·南阳高一检测)已知集合A={x|x<a},B={x|1<x<2},且A∪(∁R B)=R,则实数a的取值范围是() 【导学号:97030023】A.a≤2 B.a<1C.a≥2 D.a>2【解析】∵集合A={x|x<a},B={x|1<x<2},∴∁R B={x|x≤1或x≥2},因为A∪∁R B=R,所以a≥2,故选C.【答案】 C二、填空题6.(2016·杭州模拟)设集合S={x|x>-2},T={x|x2+3x-4≤0},则(∁R S)∪T=________.【解析】∵集合S={x|x>-2},∴∁R S={x|x≤-2},由x2+3x-4≤0,得T={x|-4≤x≤1},故(∁R S)∪T={x|x≤1}.【答案】(-∞,1]7.已知集合A、B均为全集U={1,2,3,4}的子集,且∁U(A∪B)={4},B={1,2},则A∩∁B=________.U【解析】∵U={1,2,3,4},∁U(A∪B)={4},∴A∪B={1,2,3},又∵B={1,2},∴{3}⊆A⊆{1,2,3}.又∁U B={3,4},∴A∩∁U B={3}.【答案】{3}8.设全集U=R,集合A={x|x≥0},B={y|y≥1},则∁U A与∁U B的包含关系是________.【解析】∁U A={x|x<0},∁U B={y|y<1}={x|x<1}.∴∁U A⊆∁U B.【答案】∁U A⊆∁U B三、解答题9.(2016·宁波高一检测)设A={x∈Z||x|<6},B={1,2,3},C={3,4,5},求:(1)A∪(B∩C);(2)A∩∁A(B∪C).【解】A={-5,-4,-3,-2,-1,0,1,2,3,4,5},(1)由B∩C={3},∴A∪(B∩C)=A={-5,-4,-3,-2,-1,0,1,2,3,4,5}.(2)由B∪C={1,2,3,4,5},∁A(B∪C)={-5,-4,-3,-2,-1,0},∴A∩∁A(B∪C)={-5,-4,-3,-2,-1,0}.10.设全集为R,A={x|3≤x<7},B={x|2<x<10},求:(1)A∩B;(2)∁R A;(3)∁R(A∪B).【解】(1)∵A={x|3≤x<7},B={x|2<x<10},∴A∩B={x|3≤x<7}.(2)又全集为R,A={x|3≤x<7},∴∁R A={x|x<3或x≥7}.(3)∵A∪B={x|2<x<10},∴∁R(A∪B)={x|x≤2或x≥10}.[能力提升]1.(2016·石家庄高一检测)若全集U={1,2,3,4,5,6},M={2,3},N={1,4},则集合{5,6}等于()A.M∪N B.M∩NC.(∁U M)∪(∁U N) D.(∁U M)∩(∁U N)【解析】∵全集U={1,2,3,4,5,6},M={2,3},N={1,4},∴M∪N={1,2,3,4},则(∁U M)∩(∁U N)=∁U(M∪N)={5,6}.故选D.【答案】 D2.已知全集U={1,2,3,4,5},集合A={x|x2-3x+2=0},B={x|x=2a,a∈A},则集合∁U(A ∪B)中元素个数为()A.1 B.2C.3 D.4【解析】∵A={1,2},∴B={2,4},∴A∪B={1,2,4},∴∁U(A∪B)={3,5}.【答案】 B3.已知全集U={2,3,a2-a-1},A={2,3},若∁U A={1},则实数a的值是________.【解析】 ∵U ={2,3,a 2-a -1},A ={2,3},∁U A ={1},∴a 2-a -1=1,即a 2-a -2=0,解得a =-1或a =2.【答案】 -1或24.(2016·哈尔滨师大附中高一检测)设全集U =R ,集合A ={x |x ≤-2或x ≥5},B ={x |x ≤2}.求(1)∁U (A ∪B );(2)记∁U (A ∪B )=D ,C ={x |2a -3≤x ≤-a },且C ∩D =C ,求a 的取值范围. 【导学号:97030024】【解】 (1)由题意知,A ={x |x ≤-2或x ≥5},B ={x |x ≤2},则A ∪B ={x |x ≤2或x ≥5}, 又全集U =R ,∁U (A ∪B )={x |2<x <5}.(2)由(1)得D ={x |2<x <5},由C ∩D =C 得C ⊆D ,①当C =∅时,有-a <2a -3,解得a >1;②当C ≠∅时,有⎩⎨⎧ 2a -3≤-a2a -3>2-a <5,解得a ∈∅. 综上,a 的取值范围为(1,+∞).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学人教a版必修1学业分层测评4_并集、交集_word
版含解析
学业分层测评(四)并集、交集
(建议用时:45分钟)
[学业达标]
一、选择题
1.(2016·湛江高一检测)设集合A={1,3},集合B={1,2,4,5},则集合A∪B=()
A.{1,3,1,2,4,5} B.{1}
C.{1,2,3,4,5} D.{2,3,4,5}
【解析】∵集合A={1,3},集合B={1,2,4,5},∴集合A∪B={1,2,3,4,5}.故选C.
【答案】 C
2.(2016·中山高一检测)已知集合A={x∈R|x≤5},B={x∈R|x>1},那么A∩B等于() A.{1,2,3,4,5} B.{2,3,4,5}
C.{2,3,4} D.{x∈R|1<x≤5}
【解析】∵A={x∈R|x≤5},B={x∈R|x>1},∴A∩B={x∈R|1<x≤5},故选D.
【答案】 D
3.设集合A={1,2},则满足A∪B={1,2,3}的集合B的个数是()
A.1 B.3
C.4 D.8
【解析】A={1,2},A∪B={1,2,3},则集合B中必含有元素3,即此题可转化为求集合A={1,2}的子集个数问题,所以满足题目条件的集合B共有22=4个.故选C.
【答案】 C
4.(2016·保定高一检测)设集合A={1,4,x},B={1,x2}且A∪B={1,4,x},则满足条件的实数x的个数是() 【导学号:97030016】
A.1个B.2个
C.3个D.4个
【解析】∵A={1,4,x},∴x≠1,x≠4且x2≠1,得x≠±1且x≠4,∵A∪B={1,4,x},
∴x2=x或x2=4,解之得x=0或x=±2,满足条件的实数x有0,2,-2,共3个,故选C.
【答案】 C
5.(2016·东城高一检测)已知集合M={0,x},N={1,2},若M∩N={2},则M∪N=() A.{0,x,1,2} B.{2,0,1,2}
C.{0,1,2} D.不能确定
【解析】∵M∩N={2},∴2∈M,而M={0,x},则x=2,∴M={0,2},
∴M∪N={0,1,2},故选C.
【答案】 C
二、填空题
6.某校高一某班共有45人,摸底测验数学20人得优,语文15人得优,两门都不得优20人,则两门都得优的人数为________人.
【解析】如图,设两门都得优的人数是x,则依题意得20-x+(15-x)+x+20=45,
整理,得-x+55=45,解得x=10,即两门都得优的人数是10人.
【答案】10
7.(2016·廊坊高一检测)若集合A={x|-1≤x<2},B={x|x≤a},若A∩B≠∅,则实数a 的取值范围是________.
【解析】A={x|-1≤x<2},B={x|x≤a},由A∩B≠∅,得a≥-1.
【答案】a≥-1
8.(2016·达州高一检测)已知A={1,2,3},B={x∈R|x2-ax+1=0,a∈A},若A∩B=B,则a的值为________.
【解析】由题意得,当a=1时,方程x2-ax+1=0即x2-x+1=0无解,集合B=∅,满足题意;
当a=2时,方程x2-ax+1=0即x2-2x+1=0有两个相等的实根1,集合B={1},满足题意;
当a =3时,方程x 2-ax +1=0即x 2
-3x +1=0有两个不相等的实根3+52,3-52,集合B =⎩⎨⎧⎭⎬⎫3+52
,3-52,不满足题意.综上可知,a 的值为1或2. 【答案】 1或2
三、解答题
9.(2016·滁州高一检测)设A ={x |x 2+ax +12=0},B ={x |x 2+3x +2b =0},A ∩B ={2},C ={2,-3},
(1)求a ,b 的值及A ,B ;
(2)求(A ∪B )∩C .
【解】 (1)∵A ∩B ={2},∴4+2a +12=0,即a =-8,4+6+2b =0,即b =-5, ∴A ={x |x 2-8x +12=0}={2,6},B ={x |x 2+3x -10=0}={2,-5}.
(2)∵A ∪B ={-5,2,6},C ={2,-3},∴(A ∪B )∩C ={2}.
10.已知集合A ={x |a -1<x <2a +1},B ={x |0<x <1}. 【导学号:97030017】
(1)若a =12,求A ∩B ;
(2)若A ∩B =∅,求实数a 的取值范围.
【解】 (1)当a =12时,A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪
-12<x <2,B ={x |0<x <1},∴A ∩B ={x |0<x <1}. (2)若A ∩B =∅,当A =∅时,有a -1≥2a +1,∴a ≤-2.
当A ≠∅时,有⎩⎪⎨⎪⎧
a -1<2a +1
2a +1≤0或a -1≥1,
∴-2<a ≤-12或a ≥2.
综上可得,a ≤-12或a ≥2.
[能力提升]
1.设A ={x |x 2-8x +15=0},B ={x |ax -1=0}.若A ∩B =B ,则实数a 组成的集合C 中元素的个数为( )
A .0
B .1
C .2
D .3
【解析】 当a =0时,由题意B =∅,又A ={3,5},B ⊆A ,当a ≠0
时,B =⎩⎨⎧⎭⎬⎫1a ,又A =
{3,5},B ⊆A ,此时1a =3或5,则有a =13或a =15,故C =⎩⎨⎧⎭⎬⎫0,13,15. 【答案】 D
2.设集合A =⎩⎪⎨⎪⎧⎭
⎪⎬⎪⎫x ⎪⎪⎪ ⎪⎪⎪⎪⎪⎪x -32=12,B ={t |t 2+2(a +1)t +(a 2-5)=0}.若A ∩B =B ,则实数a 的取值范围为( )
A .{a |a ≤-2}
B .{a |a ≤-3}
C .{a |a ≤-4}
D .{a |a ≤-1} 【解析】
∵A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ ⎪⎪⎪⎪⎪⎪x -32=12={1,2},B ={t |t 2+2(a +1)t +(a 2-5)=0}.由A ∩B =B , 得B ⊆A .
当4(a +1)2-4(a 2-5)<0,即a <-3时,B =∅,符合题意;
当4(a +1)2-4(a 2-5)=0,即a =-3时,B ={t |t 2-4t +4=0}={2},符合题意; 当4(a +1)2-4(a 2-5)>0,即a >-3时,要使B ⊆A ,则B =A ,
即⎩⎪⎨⎪⎧
1+2=-2(a +1)
1×2=a 2-5,
此方程组无解.∴实数a 的取值范围是{a |a ≤-3}. 【答案】 B
3.集合A ={0,2,a },B ={1,a 2},若A ∪B ={0,1,2,4,16},则a 的值为( ) 【导学号:97030018】
A .0
B .1
C .2
D .4 【解析】 ∵A ∪B ={0,1,2,a ,a 2},又A ∪B ={0,1,2,4,16},
∴{a ,a 2}={4,16},∴a =4.
【答案】 D
4.(2016·郑州高一检测)设集合A ={x |-1<x <4},B =⎩⎪⎨⎪⎧⎭
⎪⎬⎪⎫x ⎪⎪⎪ -5<x <32,C ={x |1-2a <x <
2a }.
(1)若C =∅,求实数a 的取值范围;
(2)若C ≠∅且C ⊆(A ∩B ),求实数a 的取值范围.
【解】 (1)∵C ={x |1-2a <x <2a }=∅,
∴1-2a ≥2a ,∴a ≤14,
即实数a 的取值范围是⎝ ⎛⎦
⎥⎤-∞,14. (2)∵C ={x |1-2a <x <2a }≠∅,∴1-2a <2a ,即a >14.
∵A ={x |-1<x <4},B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪
⎪⎪ -5<x <32, ∴A ∩B =⎩⎪⎨⎪⎧⎭
⎪⎬⎪⎫x ⎪⎪⎪ -1<x <32, ∵C ⊆(A ∩B ),∴⎩⎪⎨⎪⎧ 1-2a ≥-12a ≤32
a >14,
解得14<a ≤34,即实数a 的取值范围是⎝ ⎛⎦⎥⎤14,34.。
