河南省安阳市第六十三中学九年级数学下册 26.1 二次函数(第一课时)习题(无答案) 新人教版
新人教版九年级数学下册 26.1.1 二次函数同步练习(含答案)

26.1.1 二次函数
1. 下列五个函数关系式:①25y ax x =-+,②y =-x 2+1,③y =32
+2x ,④2325y x x =--,⑤2256
y x x =-+.其中是二次函数的有( ) A .1个 B .2个 C .3个 D .4个 2. 下列结论正确的是( )
A .关于x 的二次函数y =a (x +2)2中,自变量的取值范围是x ≠-2
B .二次函数自变量的取值范围是所有实数
C .在函数y =-x 22
中,自变量的取值范围是x ≠0 D .二次函数自变量的取值范围是非零实数
3. 如图,直角三角形AOB 中,AB ⊥OB ,且AB =OB =3,设直线x =t 截此三角形所得的阴影部
分的面积为S ,则S 与t 之间的函数关系式为( )
A .S=t
B .212S t =
C .S=t 2
D .2112
S t =- 4. 当m =_________时,2(2)m m y m x +=+是关于x 的二次函数.
5. 国家决定对某药品价格分两次降价,若设平均每次降价的百分率为x ,该药品原价为18
元,降价后的价格为y 元,则y 与x 之间的函数关系式为 .
参考答案
1.B
2.B
3.B
4.1
5.y=18(1-x)2。
九年级数学下册 26.1《二次函数》习题精选 新人教版

一、选择题1.(口答)下列函数中,哪些是二次函数?(1)y=5x +1 (2)y=4x2-1(3)y=2x3-3x2 (4)y=5x4-3x +12、二次函数c bx x y ++=2的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )A .x =4 B. x =3 C. x =-5 D. x =-1。
3、直角坐标平面上将二次函数y =-2(x -1)2-2的图象向左平移1个单位,再向上平移1个单位,则其顶点为( )A.(0,0) B.(1,-2) C.(0,-1) D.(-2,1)4、已知二次函数b x a y +-=2)1(有最小值 –1,则a 与b 之间的大小关系是 ( )A .a <bB .a=bC .a >bD .不能确定二、填空题1、抛物线y=(k+1)x 2+k 2-9开口向下,且经过原点,则k =—————————2、已知抛物线y=x 2+(n-3)x+n+1经过坐标原点O ,求这条抛物线的顶点P 的坐标3、、二次函数c bx x y ++=2的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )(A )1x =- (B )1x = (C )2x =(D )3x =4、顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为___________________.5、已知二次函数y =ax 2+bx +c ,当x =1时,y 有最大值为5,且它的图象经过点(2,3),求这个函数的关系式.三、计算题1、某水果批发商场经销一种水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现, 在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.(10分)(1)当每千克涨价为多少元时,每天的盈利最多?最多是多少?(2)若商场只要求保证每天的盈利为6000元,同时又可使顾客得到实惠,每千克应涨价为多少元?2、如图(1),在Rt ⊿ABC 中,∠C=90°,BC=4,AC=8,点D 在斜边AB 上,分别作DE ⊥AC ,DF ⊥BC ,垂足分别为E 、F ,得四边形DECF ,设DE=x ,DF=y .(1)用含y 的代数式表示AE ;(2)求y 与x 之间的函数关系式,并求出x 的取值范围;(3)设四边形DECF 的面积为S ,求S 与x 之间的函数关系,并求出S 的最大值.图(1) 图(2)参考答案选择题1.略 2、D 3、C 4、C填空题1.–3 2.(2,-4)3.A4.y=-(x+2)2 -55.y=-2x2+4x+3。
26.1二次函数(第1课时)

在上面的问题中, 在上面的问题中,函数都是用自变量的二次式表示的.
的函数,叫做二次函数.其中, 是自变量 是自变量, 的函数,叫做二次函数.其中,x是自变量, 二次函数 a,b,c分别是函数表达式的二次项系数、一次项系数 分别是函数表达式的二次项系数、 分别是函数表达式的二次项系数 和常数项.
y = ax2 + bx + c( a, b, c是 数 a ≠ 0) 常 ,
y = 20x + 40x + 20
2
思考: 思考: 这三个关系式中, ( )是不是x 这三个关系式中,y(d)是不是 (n)函数?为什么? )函数?为什么?
有什么共同点? 有什么共同点? y = 6x2 1 2 3 d= n − n 2 2
① ② ③
函
数
y = 20x2 + 40x + 20
一般地, 一般地,形如
M
N
即
1 d = n(n − 3) 2
1 2 3 d= n − n 2 2
②
问题3 某工厂一种产品现在的年产量是20件 问题 :某工厂一种产品现在的年产量是 件,计划今后两 年增加产量.如果每年都比上一年的产量增加x倍 年增加产量.如果每年都比上一年的产量增加 倍,那么两 年后这种产品的产量y将随计划所定的 的值而确定, 与 之 将随计划所定的x的值而确定 年后这种产品的产量 将随计划所定的 的值而确定,y与x之 间的关系应怎样表示? 间的关系应怎样表示?
{
a − b + c = 10 a+b+c = 4 4a + 2b + c = 7
待定系数法
解得,a = 2, b = −3, c = 5
∴ 所求的二次函数是y = 2 x 2 − 3 x + 5
(完整版)人教九年级数学下册同步练习题及答案
2
-
3,如果
y 随 x 的增大而减小,那么
x 的取值范围是 ______.
2.抛物线 y= (x-1) 2+2 的对称轴是直线 ____顶点坐标为 ____。
3 .抛物线 y 3(x 1)2 2 可由抛物线 y 3 x 2 先向 ____ 平移 ______ 单位,再向 _____ 平移
_______ 单位得到。
1
1.形如 _______ ________ 的函数叫做二次函数 .
2.扇形周长为 10,半径为 x,面积为 y,则 y 与 x 的函数关系式为 _______________ 。
3.下列函数中 , 不是二次函数的是 ( )
A.y=1- 2 x 2
B.y=2(x-1) 2+4 C.y= 1 (x-1)(x+4) D.y=(x-2)
式 :a____0,b____0,c_____0;a+b+c_____0,a-b+c_____0.
2.函数 y=(x+1)(x-2) 的图像的对称轴是 _____, 顶点为 ____.
2
3.若二次函数 y=x - 2x+c 图象的顶点在 x 轴上,则 c 等于 ( )
A. - 1 B.1 4.已知一次函数
3 . 如 果 二 次 函 数 y x2 2 x c 的 图 象 过 点 ( 1 , 2 ), 则 这 个 二 次 函 数 的 解 析 式 为
_____________ 。
4.抛物线 y=x2+1 的图象大致是(
)
y
y
y
y
O
-1
x
O
-1
x
1
O
x
1
九年级数学下第26章二次函数26.1二次函数及其图象2二次函数y=ax2的图象习题新人教

•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月27日星期日2022/3/272022/3/272022/3/27 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/272022/3/272022/3/273/27/2022 •3、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之失败。 2022/3/272022/3/27March 27, 2022
x> 0时 , y随 x的 增 大 而 增 大 , x< 0时 , y随 x的 增 大 而 减 小 .
2.a<0⇔开口向下⇔有最大值⇔
x> 0时 , y随 x的 增 大 而 减 小 , x< 0时 , y随 x的 增 大 而 增 大 .
知识点 2 求二次函数y=ax2的解析式
【例2】(2013·山西中考)如图是我省某地一座抛物线形拱桥,
(1)求此抛物线的解析式. (2)过点P作CB所在直线的垂线,垂足为点R, 求证:PF=PR.
【解析】(1)由题意可得:点A的坐标为(2,-1),
∵抛物线的顶点为坐标原点O,
∴可设抛物线的解析式为:y=ax2, 将点A(2,-1)代入可得:4a=-1,解得a=- 1 ,
4
∴抛物线的解析式为y=- 1 x2.
【例1】函数 ym2xm 2m 4 是关于x的二次函数,求:
(1)满足条件的m的值. (2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何 值时,y随x的增大而增大? (3)m为何值时,抛物线的开口方向向下?这时当x为何值时,y随x 的增大而减小?
【解题探究】(1)函数是二次函数的条件是自变量的最高次数
初中数学九年级下册第二十六章《二次函数》中考试题汇总

初中数学九年级下册第二十六章《二次函数》中考试题汇总新课标人教版初中数学九年级下册第二十第六章二次函数试题总结一.选择题2y??3倍?6x?5的图像的顶点坐标是(a)1(2022)二次函数a.(-1,8)b.(1,8)c.(-1,2)d.(1,-4)2.(2022兰州)抛物线y?十、bx?C.图像向右移动2个单位,向下移动3个单位。
获得的图像的解析公式是y?十、2倍?3,那么B和C的值是(B)a.b=2,c=2b.b=2,c=0c.b=-2,c=-1d.b=-3,c=23.(2022河北)如图所示,抛物线y?x2?bx?C的对称轴是x?2.点a和B在抛物线上,ab平行于x轴,其中点a的坐标为(0,3),那么点B的坐标为(d)a.(2,3)b.(3,2)c.(3,3)d.(4,3)4.(2022年陕西)将抛物线C:y=x2+3x-10和抛物线C转换为C/。
如果两条抛物线C,C/关于直线x=1对称,正确的平移方法是(C)a将抛物线C向右平移225个单位b将抛物线c向右平移3个单位2c将抛物线c向右平移5个单位d将抛物线c向右平移6个单位5.(2022遵义)如图所示,两条抛物线Y1??121x?1、 y2??x2?1和2分别通过点22??2,0?,? 2,0? 阴影部分被两条平行于Y轴的平行线包围的面积为(a)a.8b.6c.10d.4Yb.第二象限d.第四象限26.(2022年莱芜)二次函数y?斧头?bx?图中显示了C的图像,然后是一阶函数y?bx?a的图像不正确经过(b)a.第一象限c.第三象限公牛7.(2021丽水)如图,四边形abcd中,∠bad=∠acb=90°,ab=ad,ac=4bc,设cd的长为x,四边形abcd的面积为y,则y与x之间的函数关系式是(c)a、是吗?22x25b.y?422xc.y?x2255d.y?42x58.(2022年丽水)在以下四幅功能图中,当x>0时,y随x的增加而增加为(c)9.(2021成都)把抛物线y?x2向右平移1个单位,所得抛物线的函数表达式为(d)(a)y?x2?1(b)y?(x?1)2(c)y?x2?1(d)y?(x?1)222岁?斧头?bx?塞??bx?4ac?b10。
九年级数学下册 26.1 二次函数 二次函数y=ax2的图像与

二次函数y=ax²的图像与性质【导学】1.(1)画y=x²的图像;(2)在同一坐标系中画y=2x²、y=0.5x²、y=-x平方的图像2.抛物线y=ax²的性质3.抛物线y=ax²与y=-ax²关于y轴对称.【例题】例1.已知二次函数y=ax²(a≠0)的图像经过点A(1,-4)(1)求a的值,并写出这个二次函数的解析式;(2)说出这个二次函数图像的顶点坐标、对称轴、开口方向;(3)判断点B(-0.5,-2)是否在此抛物线上;(4)求出抛物线上纵坐标为﹣8的点的坐标.例2.已知y=(k+2)是关于x的二次函数,且当x>0时,y随x的增大而减小。
求k的值.【练习】1.函数y=3x²的图像是,对称轴是;开口向;顶点是;顶点是图像的最点.2.抛物线y=(a-2)x²经过点(1,3),则a= .3.二次函数y=ax²,当x=1时,y=4,则y=8时,x= .4.函数y=m时二次函数,当m=时,其图像开口向上;当m=时。
其图像开口向下.5.若点A(2,n)在抛物线y=-x²,则点A关于y轴对称点的坐标是6.对于函数y=x²,当-1≤x≤2时,y的取值范围是 .7.抛物线y=-2x²不具有的性质是()A.开口向下B.对称轴是y轴C.与y轴不相交D.最高点是原点8.下列关于抛物线y=x²和y=-x²的关系的说法错误的是()A.它们有共同的顶点和对称轴B.它们都关于y轴对称C.它们的形状相同,开口方向相反D.点A(-2,4)在抛物线y=x²上也在y=-x平方上9.下列抛物线中,开口向下且开口最大的是()A.y=-x²B.y=-x²C. y=x²D.y=x²10.已知函数y=ax²的图像过点(1,2)和点(4,m)(1)求a和m的值;(2)点(-1,2)在函数y=ax²的图像上吗?为什么?。
(完整版)人教九年级数学下册同步练习题及答案

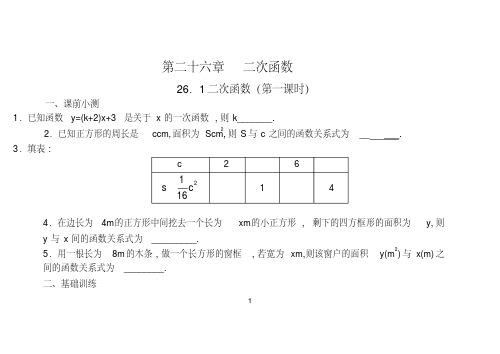
第二十六章二次函数26.1二次函数(第一课时)一、课前小测1.已知函数y=(k+2)x+3是关于x的一次函数,则k_______.2.已知正方形的周长是ccm,面积为Scm2,则S与c之间的函数关系式为__ ___. 3.填表:4.在边长为4m的正方形中间挖去一个长为xm的小正方形, 剩下的四方框形的面积为y,则y与x间的函数关系式为_________.5.用一根长为8m的木条,做一个长方形的窗框,若宽为xm,则该窗户的面积y(m2)与x(m)之间的函数关系式为________.二、基础训练121.形如_______ ________的函数叫做二次函数.2.扇形周长为10,半径为x ,面积为y ,则y 与x 的函数关系式为_______________。
3.下列函数中,不是二次函数的是( )x 2 B.y=2(x-1)2+4 C.y=12(x-1)(x+4) D.y=(x-2)2-x 2 4.在半径为4cm 的圆中, 挖去一个半径为xcm 的圆面, 剩下一个圆环的面积为ycm 2,则y与x 的函数关系式为( )A.y=πx 2-4 B.y=π(2-x)2; C.y=-(x 2+4) D.y=-πx 2+16π 5.若y=(2-m)22m x -是二次函数,则m 等于( )A.±2 B.2 C.-2 D.不能确定三、综合训练1.已知y 与x 2成正比例,并且当x=1时,y=2,求函数y 与x 的函数关系式,并求当x=-3时,y的值.当y=8时,求x 的值.2.已知函数y =(m 2-m )x 2+(m -1)x +m +1.(1)若这个函数是一次函数,求m 的值;(2)若这个函数是二次函数,则m 的值应怎样?326.1二次函数(第二课时)一、课前小测1.函数y =ax 2+bx +c (a ,b ,c 是常数)是二次函数的条件是( )A.a ≠0,b ≠0,c ≠0B.a <0,b ≠0,c ≠0C.a >0,b ≠0,c ≠0D.a ≠02.下列函数中:①y =-x 2;②y =2x ;③y =22+x 2-x 3;④m =3-t -t 2是二次函数的是__ __(其中x 、t 为自变量).3.当k=__ ___时,27(3)k y k x -=+是二次函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
26.1二次函数(第一课时)习题
1、已知圆的面积是Scm 2
,圆的半径是Rcm ,写出圆的面积S 与半径R 之间的函数关系式__________
2、已知一个矩形的周长是60m ,一边长是Lm ,写出这个矩形的面积S (m 2)与这个矩形的一
边长L 之间的函数关系式__________
3、农机厂第一个月水泵的产量为50台,第三个月的产量y (台)与月平均增长率x 之间的函数关系__________
4、下列函数中:①y =-x 2;②y =2x ;③y =22+x 2-x 3;④m =3-t -t 2是二次函数的是__ ____(其中x 、t 为自变量).
二、选择题
1、下列各关系式中,属于二次函数的是(x 为自变量) ( ) A.y =
8
1x 2 B.y =12 x C.y =21x D. y =a 2x 2、函数y =ax 2+bx +c (a ,b ,c 是常数)是二次函数的条件是( )
A.a ≠0,b ≠0,c ≠0
B.a <0, b ≠0,c ≠0
C.a >0,b ≠0,c ≠0
D.a ≠0
3、自由落体公式h =2
1gt 2(g 为常量),h 与t 之间的关系是( ) A.正比例函数 B.一次函数
C.二次函数
D.以上答案都不对
三、解答题
下列函数中,哪些是二次函数?哪些不是二次函数?若是二次函数,指出a ,b ,c ?
(1)y=2-3x 2; (2)y=x (x-4);
(3)y=7x (1-x )+4x 2; (4)y=(x-6)(6+x )。
◎综合应用拓展
1、已知函数y =(m 2-m )x 2+(m -1)x +m +1.
(1)若这个函数是一次函数,求m 的值;
(2)若这个函数是二次函数,则m 的值应怎样?
2、如图,一块草地是长80 m、宽60 m的矩形,欲在中间修筑两条互相垂直的宽为x m 的小路,这时草坪面积为y m2.求y与x的函数关系式,并写出自变量x的取值范围.。
