凹凸函数在求最值中的两例应用
凸(凹)函数的若干应用

凸函数(convex function) 是一类在某个域内单调递增的函数,即对于函数f(x),若存在常数a,使得对于任意x1≤x2,都有f(x1)≤a·f(x2)。
凹函数(concave function) 则是在某个域内单调递减的函数,即对于函数f(x),若存在常数a,使得对于任意x1≤x2,都有f(x1)≥a·f(x2)。
凸函数和凹函数在很多领域都有应用,例如:
1.数学优化:在优化理论中,凸函数的最小值往往是全局最小值,而凹函数的最大值往往
是全局最大值。
因此,凸函数和凹函数在数学优化中有重要作用。
2.计算机科学:在计算机科学中,凸函数和凹函数可用于评估算法的时间复杂度和空间复
杂度。
3.经济学:在经济学中,凸函数常用于表示边际成本(marginal cost) 和边际效用(marginal
utility) 等概念。
4.医学研究:在医学研究中,凸函数和凹函数可用于表示药物的剂量反应关系
(dose-response relationship) 等。
5.统计学:在统计学中,凸函数常用于表示统计模型的拟合情况。
凸函数 凹函数

凸函数凹函数凸函数与凹函数是微积分中常见的概念,一般用于描述函数的形态。
它们的定义都是在定义域上,凸函数是函数在定义域内的任意两点之间的连线所形成的线段上的所有函数值不超过该线段端点的函数值,凹函数则是函数在定义域内的任意两点之间的连线所形成的线段上的所有函数值都不少于该线段端点的函数值。
简单来说,凸函数就是“弯弯的”向上的函数,凹函数则是“弯弯的”向下的函数。
下面我们将详细介绍凸函数和凹函数的定义以及一些例子和应用。
一、凸函数1.1 定义:若函数 f(x) 的定义域 D 是一个凸集合,并且对于 D 中的任意两点 x1, x2 以及任意实数λ ∈ [0,1],都有:f(λx1 + (1-λ)x2) ≤ λf(x1) + (1-λ)f(x2)则函数 f(x) 称为凸函数。
其中,λx1 + (1-λ)x2 是点 x1 和 x2 之间的中点,λ表示分配参数,(1-λ)表示剩余参数。
1.2 示例:函数 f(x) = x2 + 2x + 1 在 (-∞,+∞) 上是一个凸函数。
这个二次函数开口向上,图形很像一个碗,我们可以根据凸函数定义来验证它是否是凸函数。
首先,函数的定义域为 (-∞,+∞),包含了所有的实数,是一个凸集合;其次,在该定义域内,任取两点 x1和x2,且λ∈[0,1],我们可以在两点间连接一条线段,然后将这条线段分割为λx1和(1-λ)x2两部分,其中λx1表示x1所占的比重,(1-λ)x2表示x2所占的比重。
因为 f(x) 是一个二次函数,所以它是圆形的,当λ=0.5 时,分割点正好在圆心上,所以分割点的函数值就等于函数的最小值,即:f(λx1 + (1-λ)x2) = f((x1+x2)/2) = (x1+x2)2/4 + 2(x1+x2)/2 + 1 = (x1+x2)2/4 + x1 + x2 + 1/2。
此时,我们将 f(x1) 和 f(x2) 带入定义式中计算:λf(x1) + (1-λ)f(x2) = λ(x1)2 + 2λx1 + λ + (1-λ)(x2)2 + 2(1-λ)x2 + 1-λ= λx1^2 + (1-λ)x2^2 + 2λx1 + 2(1-λ)x2 + λ + 1-λ= λx12 + (1-λ)x22 + 2λx1 + 2(1-λ)x2 + 1我们可以发现,当将上式中“+λ+1-λ”化简后,它们和上面的 f(x1) + f(x2) 等价,且还多了一些其他的正数。
函数凹凸的定义

02 函数凹凸的几何意义
凹函数的几何意义
凹函数图像呈下凹状,即对于函数图 像上的任意两点A和B,如果A、B两 点连线的中点始终位于A、B连线的下 方,则该函数为凹函数。
在几何意义上,凹函数具有一个明显 的特征,即函数图像上任意两点的连 线的斜率始终小于或等于该点处的函 数导数。
凸函数的几何意义
通过分析函数的凹凸性,我们可以确定函数的拐点,从而更好地理解函数 的性质,为求解最优化问题提供指导。
在求解无约束最优化问题时,可以利用函数凹凸性选择合适的算法,如梯 度下降法、牛顿法等,以提高求解效率。
在经济学中的应用
函数凹凸性在经济学中也有 广泛应用,它可以帮助我们 理解经济现象和预测经济行
为。
函数凹凸的定义
目录
• 函数凹凸的基本概念 • 函数凹凸的几何意义 • 函数凹凸的判定方法 • 函数凹凸的应用 • 函数凹凸的反例 • 函数凹凸的扩展知识
01 函数凹凸的基本概念
凹函数
01
凹函数是指函数图形在任意两点 之间总是位于这两点连线的下方, 即对于定义域内的任意x1和x2, 都有 f((x1+x2)/2)≥f(x1)+f(x2)/2。
03
在计算机科学中,函数凹凸性可以帮助我们设计更有效的算法和数据 结构,如动态规划、图算法等。
04
在生物学中,函数凹凸性可以帮助我们理解生物系统的复杂性和行为, 如生态学、生物化学反应等。
05 函数凹凸的反例
凹函数的反例
总结词
凹函数的反例是指函数图像呈现下凹形状的反例。
详细描述
凹函数的反例通常是指那些在一定区间内,函数值随着自变量的增加而减少的函数。例如,二次函数 $f(x) = x^2$在区间$(-infty, 0)$内是一个凹函数的反例,因为在这个区间内,函数值随着$x$的增加 而减少。
函数凹凸性判别法与应用讲解

函数凹凸性判别法与应用作者:祝红丽 指导老师:邢抱花摘要 函数的凹凸性是函数的重要性质之一.它反映在函数图象上就是曲线的弯曲方向,通过它可以较好地掌握函数对应曲线的性状.本文基于函数凹凸性概念的分析,着重探讨了函数凹凸性的判别方法以及在解题中的应用,如在不等式证明中的应用以及在求函数最值时的应用等.并结合相关例题做了较详细的论述.关键词 凹凸性 导数 不等式 应用1 引言函数的凹凸理论在高等数学中占有重要地位.函数的凹凸性揭示了函数的因变量随自变量变化而变化的快慢程度,如果结合函数的其它性质,可以使我们对函数的认识更加精确.以函数()y f x 在某区间I 上单调增加为例说明.我们不难理解,随着自变量x 的稳定增加,当函数y 的增量越来越大时,函数图形是凹的,当函数y 的增量越来越小时,函数图形是凸的,当函数y 的增量保持不变时,函数图象是直线,对于减函数我们可以作类似的分析.作为研究分析函数的工具和方法,它在许多学科里有着重要的应用.长期以来,很多学者致力于函数凹凸性的判别法及其应用的研究.近年来,关于函数凹凸性的判定与应用的研究取得了一些成果,使函数凹凸性的判别法与应用更加的广泛.本文先从两个具体的函数图象为出发点,直观上观察函数图象的弯曲方向,从而引出函数凹凸性的概念和拐点的定义.并在此基础上介绍了凹凸函数的几何特征,接着介绍函数凹凸性的几种判别方法,如:用定义去判别函数的凹凸性,利用二阶导函数判别函数的凹凸性,及利用函数凹凸性的判定定理判别函数的凹凸性.其中利用函数凹凸性的概念是最基本的判别方法,利用二阶导函数与函数凹凸性之间的关系是最常用的判别方法.最后举例介绍了函数凹凸性在证明不等式、求函数最值以及函数作图中的应用.虽然说并不是所有的不等式都能利用函数的凹凸性证明,但是利用函数的凹凸性去证明某些不等式,是其它方法不可替代的.利用函数凹凸性证明不等式丰富了不等式的证明方法,开阔了解题思路.利用导数分析函数的上升、下降,图形的凹凸性和极值.根据对这些的讨论可以帮助我们画出用公式表示的函数图形,了解函数的凹凸性能够使对函数图形的描绘更加精确化.2 凹凸函数及拐点的定义我们已经熟悉函数2y x =和lg y x =的图象.2x lg y =.凸性的分析定义形式较多,下面给出函数凹凸性定义的更一般的形式. 2.1函数凹凸性的定义定义 设函数()f x 在区间I 上连续,若对I 上的任意两点1x ,2x 和任意实数(0,1)λ∈,总有: 1212[)]()(1)()f x x f x f x λλλλ≤+-+(1-, 则称f 为I 上的凹函数. 反之,如果总有:1212[)]()(1)()f x x f x f x λλλλ≥+-+(1-,则称f 为I 上的凸函数. 特别地,当λ=12时,满足121211()()()222x x f f x f x +≤+的函数为凹函数,满足121211()()()222x x f f x f x +≥+的函数为凸函数. 如果定义中的不等式改为严格不等式,则相应的函数称为严格凹函数和严格凸函数.2.2 凹函数与凸函数的几何意义定义中凹函数与凸函数的图象如图1、图2.图1 图2 凹函数(凸函数)的几何意义:连接曲线()y f x =上任意两点的弦总位于对应曲线的上方(下方).2.3 拐点的定义设曲线()y f x =在点0,0(())x f x 处有穿过曲线的切线.且在切点近旁,曲线的切线的两侧分别是严格凹和严格凸的,这时称点0,0(())x f x 为曲线()y f x =的拐点.X由定义可见,对于具有凹凸性的函数而言,拐点正是函数的凹凸性发生改变的那一点,即拐点的两侧邻域有着互异的严格凹凸性.如下图中的M 点.严格地说,拐点都是平面光滑曲线(即切线连续变动的曲线)弯曲方向发生改变的转折点,拐点的几何特征是该点的切线不是在曲线的一侧“托着曲线”而是切线在切点处把曲线一分为二,分别在切线的两侧.易知,有正弦曲线的图象可知sin y x =有拐点(,0)k π ,k 为整数.2.4 拐点的判别法(1)若()f x 在0x 处连续,在0x 两侧()''f x 反号,则()()00,x f x 是曲线()y f x =的拐点.(2)若()''00f x =,()(3)00f x ≠,则()()00,x f x 是()y f x =的拐点.例题1 求下列函数的拐点 ()1()()2211xf x x =+-; ()2 ()3f x x =. 解 ()1()()()'3211x f x x -+=-,()()()''2421x f x x +=- , 当()()2,11,x ∈-⋃+∞时,()''0fx >; 当(),2x ∈-∞-时,()''0f x < ,又()529f -=, 所以点52,9⎛⎫- ⎪⎝⎭是函数的拐点. ()2()'23f x x =,()''6f x x =,()'''6f x =,()''00f =,()'''00f ≠,所以点()0,0是函数的拐点.注意:函数的拐点只是表示在该点的两侧函数具有不同的严格凹凸性,而不能只依靠判断二阶导数是否为零来确定函数的拐点.对于二阶导数不存在的点0x ,检查''()f x 在0x 左右两侧邻近的符号,那么当两侧邻近的符号相反时,点00(,())x f x 是曲线()y f x =的拐点,当两侧的符号相同时,点00(,())x f x 不是曲线()y f x =的拐点函数的拐点.因此函数的拐点与二次导数是否存在没有必然的联系.例如:1()f x x x=+在0x =时的情况.易知''32()f x x =,()f x 在0x =处的二阶导数不存在,但是当0x <时,''()0f x <,当0x >时,''()0f x >,所以0x =是()f x 的一个拐点.3 函数凹凸性的判别法观察函数图象,我们很容易得出结论:凹函数的一阶导数是不断变大的,而凸函数的一阶导数则恰恰相反.这是我们通过观察几何图形进行直观的感知得到的结论,但是人的观察不可避免的存在着一定的局限性,只有通过严密的证明得到的结论才能使人信服.迄今为止,判别函数的凹凸性已经有很多的方法.3.1 定义法判别函数的凹凸性用定义法去判别函数的凹凸性是最基本的判定方法,也是其它判定方法的基础.所以对定义的理解和掌握是至关重要的.例题2 f ,g 均为I 上的连续函数,证明:(1)若f ,g 均为凹函数,则g f +为凹函数;(2)若f ,g 均为递增非负凹函数,则g f ⋅为凹函数.证明 设任意的1x ,2x I ∈,(0,1)λ∈,(1)、因为f ,g 均为凹函数,所以由定义知:1212[)]()(1)()f x x f x f x λλλλ≤+-+(1-和1212[)]()(1)()g x x g x g x λλλλ≤+-+(1-.两式相加:12[)]f x x λλ+(1-+12[)]g x x λλ+(1-≤12()(1)()f x f x λλ+-+12()(1)()g x g x λλ+-, 即:1212()[)]()()(1)()()f g x x f g x f g x λλλλ+≤++-++(1-, 所以f g +为凹函数.(2)、由题题意得:121212()[)][)][)]f g x x f x x g x x λλλλλλ⋅=⋅+(1-+(1-+(1-1212[()(1)()][()(1)()]f x f x g x g x λλλλ≤+-⋅+-221122()()(1)()()f x g x f x g x λλ=+-1122(1)[()()()()]f x g x f x g x λλ+-+.下面只要证明:221122()()(1)()()f x g x f x g x λλ+-1122(1)[()()()()]f x g x f x g x λλ+-+12()()(1)()()f g x f g x λλ≤⋅+-⋅即可.采用做差法比较两者的大小:221122()()(1)()()f x g x f x g x λλ+-1122(1)[()()()()]f x g x f x g x λλ+-+-12()()(1)()()f g x f g x λλ⋅+-⋅=1212(1)[()()][()()]f x f x g x g x λλ----0≤. 综上所述,可得1212()[(1)]()()(1)()()f g x x f g x f g x λλλλ⋅+-≤⋅+-⋅.所以f g ⋅是凹函数.例3 ()f x 为区间I 上的可导函数,证明:若对于I 上的任意两点1x ,2x ,有'21121()()()()f x f x f x x x ≥+-, 则()f x 为I 上的凹函数.证明 设以1x ,2x 为I 上任意两点,12(1)x x x λλ=+- , 01λ<< .由'21121()()()()f x f x f x x x ≥+-, 并利用112(1)()x x x x λ-=--与221()x x x x λ-=-,''1112()()()()()(1)()()f x f x f x x x f x x x f x λ≥+-=+--.''2221()()()()()()()f x f x f x x x f x x x f x λ≥+-=+-.分别用λ与1λ-上列两式并相加,得到:1212()(1)()()[(1)]f x f x f x f x x λλλλ+-≥=+-.所以()f x 为I 上的凹函数.3.2 函数凹凸性的判定定理定理 ()f x 为I 上的函数,若对于I 上的任意三点123x x x <<,总有:32212132()()()()f x f x f x f x x x x x --≤-- , 则()f x 为I 上的凹函数. 证明 在I 上任取两点13,x x 13()x x <,在13[,]x x 上任取一点213(1),(0,1)x x x λλλ=+-∈,则,3231x x x x λ-=-,21311x x x x λ--=- , 因为 32212132()()()()f x f x f x f x x x x x --≤-- ,所以有: 322212321213()()()()()()()()x x f x x x f x x x f x x x f x -+-≤-+-.所以有,312321213()()()()()()x x f x x x f x x x f x -≤-+- ,因为 310x x ->,所以不等式两边同时除以31()x x -有:32212133131()()()x x x x f x f x f x x x x x --≤+--. 即213()()(1)()f x f x f x λλ≤+-又213()[(1)]f x f x x λλ=+-.所以1313[(1)]()(1)()f x x f x f x λλλλ+-≤+-.所以()f x 为I 上的凹函数.例题4 设()f x 为区间I 上的函数,若对于00,x I ∀∈∃实数a ,使得x I ∀∈,有00()()()f x a x x f x ≥-+, 证明:()f x 为区间I 上的凹函数.证明 设123x x x <<是区间I 上任意三点,由已知条件,对于2x ,存在实数a ,使得,22()()()f x a x x f x ≥-+, ()x I ∀∈.令1x x = , 有1122()()()f x a x x f x ≥-+,得到1212()()f x f x a x x -≤-. 再令3x x =, 有3322()()()f x a x x f x ≥-+ ,得到3232()()f x f x a x x -≥-. 综上所述,32123212()()()()f x f x f x f x a x x x x --≥≥-- ,所以()f x 为区间I 上的凹函数. 3.3 函数凹凸性的充要条件充要条件 设函数()y f x =在I 上连续,在I 内具有一阶和二阶导数,那么,(1)若在I 内恒有''()0f x ≥,则()f x 在I 上的图形是凹的;(2)若在I 内恒有''()0f x ≤,则()f x 在I 上的图形是凸的.注意:若在区间I 内的某一子区间上''()0f x ≡,则()y f x =在该子区间上的图形是一段直线,该子区间既非凹区间也非凸区间.证明 (1)充分性:因为''()0f x ≥,所以'f 为I 上的增函数,设任意的1x ,2x ∈I ,在以1x ,2x (不妨设12x x <)为端点的区间上,由拉格朗日中值定理和'f 为I 上的增函数,可得:''2121121()()()()()()f x f x f x x f x x x ξ-=-≥-,即对I 上的任意两点1x ,2x ,有:'21121()()()()f x f x f x x x ≥+-.令312(1)x x x λλ=+-,01λ<<,有,1312(1)()x x x x λ-=--;2321()x x x x λ-=-;所以,''133133123()()()()()(1)()()f x f x f x x x f x x x f x λ≥+-=+--.''233233213()()()()()()()f x f x f x x x f x x x f x λ≥+-=+-.以上两个不等式的两端分别乘以λ与(1)λ-并相加得:12312()(1)()()[(1)]f x f x f x f x x λλλλ+-≥=+-.即()f x 在I 是凹函数;必要性:任取I 上两点()1212,x x x x <及充分小的正数h .由于1122x h x x x h -<<<+,根据()f x 是凹函数及函数凹凸性的判定定理有:()()()()()()11212221f x f x h f x f x f x h f x h x x h---+-≤≤-. 由于()f x 是可导函数,令0h +→时可得()()()()21''1221f x f x f x f x x x -≤≤-. 所以()'f x 为I 上的增函数,所以在I 内恒有''()0f x ≥.(2)''()0f x ≤的情况类似的可以证明.例题5 求曲线3()(12ln 10)f x x x =-的凹凸区间及拐点.解 函数的定义域为(0,)+∞,又'22()36ln 18f x x x x =-,''()72ln f x x x =,令''()0f x =,即72ln 0x x =,得到1x =,点1x =把定义域分成两个部分即(0,1]与[1,)∞.在各部分区间内'()f x 与''()f x 的符号,相应曲段弧的升降及凹凸、拐点等,如下图表:可得:在(0,1]内,''()0f x ≤,因此是曲线的凸区间.在[1,)∞内,''()0f x ≥,因此是曲线的凹区间.所以:点(1,10)-是曲线的拐点.小结:求曲线凹凸区间及拐点的步骤:首先找出可能是拐点的横坐标(包括使二阶导数为零的点和二阶导数不存在的点),再利用二阶导数的符号判断该曲线的凹凸区间及拐点. 4 函数凹凸性的应用函数凹凸性的应用及其广泛,很多与函数、不等式交汇的综合问题都可以利用函数的凹凸性加以解决.利用函数的凹凸性去解决问题,往往能够使某些复杂的问题简单化.接下来,我们重点讨论函数凹凸性在不等式的证明、求函数最值以及函数作图等中的应用.4.1 函数凹凸性在证明不等式中的应用有些不等式的表达形式很简单,但如果通过常规的证明方法和技巧却很难达到预期的效果,这就需要我们另辟蹊径,寻找更有效的方法技巧,利用凹凸函数的性质不但可以减少计算量,使解题更加合理,而且借助凹凸函数的几何特征可以使解题思路更加清晰直观.4.1.1 利用函数的凹凸性证明一个重要的不等式定理 如果()f x 是凸函数⇔对12,,[0,1]n ∀∂∂⋅⋅⋅∂∈,满足121n ∂+∂+⋅⋅⋅+∂=,都有11221122()()()()n n n n f x x x f x f x f x ∂+∂+⋅⋅⋅+∂≥∂+∂+⋅⋅⋅+∂. 特别地,当121n n∂=∂=⋅⋅⋅=∂=时,上述不等式称为琴生(Jensen )不等式. 例题 6 任意n 个非负实数的调和平均值小于或等于它们的几何平均值小于或等于他们的算数平均值.即:0i x ∀≥,(1,2,,)i n =⋅⋅⋅, 恒有:1212111n n x x x nnx x x ++⋅⋅⋅+≤≤++⋅⋅⋅+. 当且仅当12n x x x ==⋅⋅⋅=时等号成立.证明 考虑函数ln y x =,很容易判断出其是凸函数,有琴生(Jensen )不等式得到:1212121111lnln ln ln ln()n n n x x x x x x x x x n n n n n++⋅⋅⋅+≥++⋅⋅⋅+=⋅⋅⋅=. 即:12ln n x x x n++⋅⋅⋅+≥ln y x =在定义域上是单调递增的.12n x x x n ++⋅⋅⋅+≤,当且仅当12n a a a ==⋅⋅⋅=时等号成立. 另一方面, ln 12111n nx x x ++⋅⋅⋅+=12111ln n x x x n ++⋅⋅⋅+-121111(ln ln ln )nn x x x ≤-++⋅⋅⋅+=即:12ln 111n nx x x ≤++⋅⋅⋅+又ln y x =在定义域上是单调递增的.所以有:12111nnx x x ≤++⋅⋅⋅+12n a a a ==⋅⋅⋅=时等号成立.综上所述有:1212111n n x x x n nx x x ++⋅⋅⋅+≤≤++⋅⋅⋅+. 当且仅当12n a a a ==⋅⋅⋅=时等号成立.注意:利用函数的凹凸性证明不等式时,一定要注意构造或者引进我们所需要的辅助函数,使条件和结论、已知与未知建立联系.4.1.2 凹凸函数不等式的积分形式定理 设()f x 是[,]a b 上的可积函数且()m f x M ≤≤,()t ϕ是[,]m M 上的连续凸函数,则:11(())[()]b b a af x dx f x dx b a b a ϕϕ≥--⎰⎰(如果()t ϕ是凹函数,则不等式反向). 例题7 设()f x 为[,]a b 上的正值连续函数, 证明:11ln ()ln ()b b a a f x dx f x dx b a b a≤--⎰⎰. 证明 令()ln t t ϕ=,由上述定理得:11(())ln ()b b a a f x dx f x dx b a b a ϕ=--⎰⎰ ≥1ln ()b af x dx b a -⎰.即得证. 例题8设()f x 在[0,1]上连续可导,'()0,()0f x f x ≥≤.若0()()xF x f t dt =⎰,证明: 10(1)()2(),(0,1)xF F x F t dt x ≤≤∈⎰. 证明 由0()()xF x f t dt =⎰,可得'()()F x f x =,进而得到'''()()F x f x =,所以''()0F x ≤.由函数凹凸性的充要条件知()F x 为凸函数.所以有:[1(1)0](1)(1)(0)F x x x F x F ⋅+-⋅≥⋅+-.又(0)0F =,所以()(1)F x x F ≥⋅.另一方面,由Hadamard 不等式:设函数()f x 是[,]a b 上连续的凸函数,对任意的12,[,],x x a b ∈12x x < ,有:21121221()()1()()22x x x x f x f x f f t dt x x ++≥≥-⎰,得101(0)(1)()102F F F t dt +≥-⎰. 即:10(1)()2F F t dt ≥⎰,又'()()0F x f x =≥,所以()F x 在[0,1]为单调增函数,所以有: (1)()22F F x ≥, 即102()()F t dt F x ≥⎰.综上所述, 即有: 10(1)()2(),(0,1)xF F x F t dt x ≤≤∈⎰. 小结:利用函数凹凸性证明不等式虽然有一定的局限性,但是它却能够避免一些繁杂的解题过程,大大的简化解题步骤,是其它方法不能达到的.利用函数凹凸性证明不等式的解题关键是构造合适的辅助函数,能够使问题和已知的条件联系起来,只有这样才能达到预期的效果.4.2 函数凹凸性在求函数最值中的应用通过观察不等式的证明,我们可以发现,如果不等式的一边是常数的话,那么不等式的证明就演变成了求函数的最值问题,我们就可以利用函数的凹凸性来求函数的最值,从而就可以避免繁杂的化简、转化、变形等过程.若能够灵活运用函数的凹凸性解题,可达到事半功倍的效果.例题9 设0(1,2,)k x k n >=⋅⋅⋅,试求 1212222()()n nx x x x x x ++⋅⋅⋅++⋅⋅⋅+的最小值. 解析 如果采用一般的解题方法,我们就会发现很难找到问题的突破口,但是如果我们采用函数的凹凸性去思考,再结合着题目的表达形式,就很容易联想到琴生(Jensen )不等式,问题就迎刃而解了.解 设2()f x x =,则'22()f x x =-,''44()0x f x x=>.所以()f x 为凹函数,由琴生(Jensen )不等式12121()[()()()]n n x x x f f x f x f x n n ++⋅⋅⋅≤++⋅⋅⋅+,得: 121221222()n nn x x x n x x x ≤++⋅⋅⋅+++⋅⋅⋅. 化简整理得:1212222()()n nx x x x x x ++⋅⋅⋅++⋅⋅⋅+22n ≥, 所以1212222()()n nx x x x x x ++⋅⋅⋅++⋅⋅⋅+的最小值为22n . 例题10 设函数()f x 为[,]a b 上的凸函数,则求()f x 在闭区间[,]a b 上的最值. 解 对于任意的[,]x a b ∈,取b x b aλ-=-,([0,1]λ∈),所以有(1)x a b λλ=+-. 进而有()[(1)]f x f a b λλ=+-,又()f x 为[,]a b 上的凸函数所以有:()[(1)]()(1)()min{(),()}f x f a b f a f b f a f b λλλλ=+-≥+-≥.所以()f x 的最小值为min{(),()}f a f b .记区间[,]a b 的中点为A ,且2a b A +=,设任意的[,]x a b ∈关于A 的对称点为'x 则有 '22x x a b ++=,又()f x 是[,]a b 上的凸函数,所以有: ''()()()()()2222a b x x f x f x f x m f f ++++=≥≥,即:()2()2a b f x f m +≤-).(其中min{(),()}m f a f b =).所以()f x 的最大值为 :2()2a b f m +-,(其中min{(),()}m f a f b =. 注意:此例题可以表述为若函数()f x 在[,]a b 为凸函数,则()f x 在闭区间[,]a b 上有界.例题11 若,,,a b c d R +∈,且16a b c d +++=,求2222a b c d +++的最小值.解 设2()f x x =,则'()2f x x =,''()20f x =>,所以()f x 为凹函数.所以有:1()[()()()()]44a b c d f f a f b f c f d +++≤+++. 即:22222()1()164a b c d a b c d +++≤+++. 化简整理得:222264a b c d +++≥,当且仅当4a b c d ====时等号成立.小结:求函数最值的常用方法是利用函数的单调性、求导和均值不等式等方法,但是求函数值域没有通用的方法和固定的模式,要靠在学习过程中不断积累,掌握规律.而利用函数的凹凸性求解,为求函数最值开辟了一条新的路径.从上面几个例题可以看出利用函数凹凸性去求函数最值的关键还是构造合适的辅助函数. 4.3 利用函数的凹凸性作函数图象图象是刻画函数变量之间关系的一个重要途径,是研究函数性质的一种常用方法,是数形结合的基础和依据.函数图象是函数的一种表达形式,它形象地显示了函数的性质,为研究数量关系提供了“形”的直观性,是探求解题途径、获得问题结果的重要工具.但是在实际的解题过程中,并不是所有的函数图形都能够很容易地作出.下面我们就利用函数的凹凸性去解决一些函数作图问题.例题12 作出函数2()[cos(2arccos )]f αα=的图形.解析 题目中的函数解析表达式不够直观,我们考虑将函数做恒等变换,之后再利用函数的凹凸性作出函数图象.解 因为2cos(2arccos )12sin cos arc αα=-,设sin cos x arc α=,[1,1]x ∈- ,所以所给函数的表达式可以写成22()(12)f x x =-,且函数的定义域为[1,1]x ∈-,该函数是偶函数,它的图形关于y 轴对称,因此只需讨论区间[1,0]-上的图形即可.'()8(1)(1)f x x =-,进而得到:''2()4881)f x x =-=-+,在区间[1,0]-上,'()0f x =的解为0x =或x =''()0f x =,的解为x =.用点2x =-和6x =-把区间[1,0]-划分为[1,2--,[,26--,[6-三个部分区间.在各部分区间内'()f x 及''()f x 的符号、相应曲线弧的升降、凹凸性、极值点因而在2x =-处,()f x 取极小值0,再由函数关于y 轴对称,所以在0x =处,()f x 取极大值1,在2x =处,()f x 取极小值0,曲线有两个拐点 4()69-和4)69. 函数的图象如下图所示:小结:利用函数凹凸性作图的步骤: (1)确定函数()f x 的定义域,讨论函数的一些基本性质,如奇偶性、对称性和周期性等,并求出函数的一阶导数'()f x 及二阶导数''()f x .(2)求出方程'()0f x =和''()0f x =在定义域内的全部实根及使'()f x 和''()f x 不存在的点,用以上两种点将函数()f x 的定义域划分成几个部分区间.(3)确定在这些部分区间内'()f x 及''()f x 的符号,并由此确定函数图形的升降和凹凸、极值点和拐点.(4)确定函数图形的水平铅直渐近线.(5)列表并作出函数图象.函数的凹凸性揭示了函数因变量随自变量变化而变化的快慢程度,如果结合函数其它性质,可使我们对函数图象的描绘更加的准确.4.4 利用函数的凹凸性判断函数单调性判断函数单调性的一般方法是利用导函数的正负来判断的,但是利用函数的凹凸性来判断函数的单调性,作为判断函数单调性方法的补充,是需要我们了解的.例题13 设()00f =,()f x 在[)0,+∞上为非负的严格凹函数,()()f x F x x=,()0x >.试证明:()(),f x F x 为严格递增的函数.证明 因为()f x 为严格凹函数,()00f =,所以()()()()00f x f x f F x x x -==-为严格递增的.因为()f x 是非负函数,所以对于 0x ∀>,有()()00f x f ≥=.若某点10x >,使得()10f x =,则在[]10,x 上有()0f x ≡ 与()f x 为严格凹函数矛盾. 所以0x ∀>,有()0f x >,最后设120x x <<,则:()()()()()21112111000f x f x f x f f x x x x x -->=>--,得()f x 为严格递增的()0x >.结 束 语本文从函数凹凸性的概念出发,通过具体的实例较系统地介绍了函数凹凸性的常规的判定方法及在证明不等式、求函数最值以及在作函数图象时的应用.把握函数凹凸性在数学中的应用,关键就是在把握函数凹凸性的基本概念、定理的基础上,同时加强此方面的训练和研究.函数凹凸性的应用,拓展了学习和研究的邻域.由于受到各种因素的限制,本文也有一定的不足之处.函数凹凸性的判别方法与应用还有很多,本文只介绍了其中的一部分,还有其它方法与应用可以补充.参考文献[1] 宣立新. 高等数学(上册)[M].高等教育出版社,1999.[2] 华东师范大学数学系[M].数学分析.高等教育出版社,2007.[3] 毛纲源.高等数学解题方法技巧归纳[M].华中理工大学出版社,2002.[4] 于淑兰.关于曲线拐点的判别法[J].数学的实践与认识,2003,33(1):98-100.[5] 刘玉琏,傅沛仁.数学分析讲义(第三版)[M].高等教育出版社,1995.[6] 沈家英,方永宏.高等数学(上册)[M].山东大学出版社,1995.[7] 裴礼文.数学分析中的典型问题与方法[M].高等教育出版社,2007.[8] 孙清华,郑小姣.高等数学内容、方法与技巧[M].华中科技大学出版社,2004.[9] Fred Brauer .Fundamentals of Advanced Mathematics[M] .Higher Education Press,2006.[10] 何卫力,缪克英.高等数学方法导引(上)[M].北京交通大学出版社,2004.[11] 盛祥耀.高等数学[M].高等教育出版社,2004.[12] 刘士强.数学分析[M].广西民族出版社,2000.The discrimination approach and application of concave and convex function Author: Zhu Hongli Supervisor: Xing BaohuaAbstract Concave and convex function is one of the important properties in function.It reflects curving direction of the curve on the function image, and it allows you to grasp the curve properties better about the corresponding function. This paper bases on analysis about the concept of convex and concave function, and focuses on exploring the discrimination approach and application of concave and convex function, such as the application in inequality proving and function max/min value, etc. It makes a detailed exposition with relevant examples.Keywords concave and convex derivative inequality application.。
函数凹凸性在高考数学中的命题分析

函数凹凸性在高考数学中的命题分析纪定春(四川师范大学数学科学学院㊀610068)摘㊀要:凹凸性是刻画连续函数性质的重要方法ꎬ在高等数学中具有广泛的应用价值ꎬ是高考数学试题的命题点.介绍了函数的凹凸性及等价命题ꎬ对近年高考数学中含有函数凹凸性的试题进行了命题分析和评注.关键词:高考数学ꎻ函数凹凸性ꎻ命题分析中图分类号:G632㊀㊀㊀㊀㊀㊀文献标识码:A㊀㊀㊀㊀㊀㊀文章编号:1008-0333(2020)28-0082-03收稿日期:2020-07-05作者简介:纪定春(1995-)ꎬ男ꎬ四川省资阳人ꎬ研究生ꎬ从事数学数学研究.㊀㊀一㊁函数凹凸性及等价命题简介定义㊀设f是定义在区间I上的函数ꎬ若对I上的任意两点x1ꎬx2和任意实数λɪ(0ꎬ1)总有f(λx1+(1-λ)x2)ɤλf(x1)+(1-λ)f(x2)ꎬ则称f为I上的凸函数.反之ꎬ如果总有f(λx1+(1-λ)x2)ȡλf(x1)+(1-λ)f(x2)ꎬ则称f为I上的凹函数.注意:为了便于识记ꎬ以下不妨将凸函数㊁凹函数分别称为下凸函数和上凸函数.定义的推广ꎬ即詹森不等式:若f是[aꎬb]上的凸函数ꎬ则对任意xiɪ[aꎬb]ꎬλi>0(i=1ꎬ2ꎬ ꎬn)ꎬðni=1λi=1ꎬ有f(ðni=1λixi)ɤðni=1λif(xi).函数凹凸性的几个等价命题:(1)当切线(一阶导数)在函数图象上方时ꎬ函数是上凸函数ꎬ反之为下凸函数ꎻ(2)当一阶导数单调递减时ꎬ函数是上凸函数ꎬ反之为下凸函数ꎻ(3)当二阶导数小于等于零时ꎬ函数为上凸函数ꎬ反之为下凸函数.这几种描述方式都是等价的ꎬ只是所站的角度不同ꎬ可参见文[2].㊀㊀二㊁函数凹凸性在高考数学试题中的命题分析函数的凹凸性作为描述连续函数局部性质的方法ꎬ不仅在高等数学中具有广泛而重要的应用价值ꎬ而且是高考数学的命题热点.在刻画函数的凹凸性时ꎬ可以利用一阶㊁二阶导数等ꎬ这就将函数的凹凸性与高中数学中的导数知识联系起来.近年来ꎬ为何以导数作为高考数学的压轴题呢?有三点猜测:其一是导数本身蕴含了丰富的数学思想ꎬ如分割思想㊁极限(逼近)思想㊁特殊与一般思想㊁局部与整体思想等ꎻ其二是导数是研究连续函数和离散变量的重要工具ꎬ如在连续函数中ꎬ求函数的最大值㊁最小值㊁极值㊁拐点等ꎬ在离散型变量中ꎬ如求数列通项㊁求和㊁求极限等.其三是高中导数与大学数学中的知识点交汇较多ꎬ可以为高考数学命题者提供更多的视角和切入点.例1㊀(2018年高考理科全国卷Ⅰ第16题)已知函数f(x)=2sinx+sin2xꎬ则f(x)的最小值是㊀㊀.分析㊀为了方便研究函数f(x)=2sinx+sin2x的最值ꎬ可以将函数的自变量范围限制在一个更小的区间上.注意到ꎬ在正弦函数中ꎬ有sinx=sin(π-x)成立.显然ꎬ在区间[0ꎬπ2]上ꎬ函数sinx和sin2x均为上凸函数ꎬ故可以考虑使用函数的凹凸性来求最值.解析㊀不妨假设0<x<π2ꎬ此时有sinx>0ꎬsin2x>0.f(x)=2sinx+sin2x=sin(π-x)+sin(π-x)+sin2xɤ3sinπ-x+π-x+2x3=3sin2π3=323.当且仅当 π-x=2x 时ꎬ即x=π3时ꎬ等号成立.因为函数f(x)是奇函数ꎬ所以函数f(x)的最小值为-323.评注㊀该试题在当年高考中的得分率比较低ꎬ看似简单的试题ꎬ实则具有很强的 杀伤力 ꎬ很多考生过后反映ꎬ该题的运算量太大了ꎬ在高考场上耽误了太多时间.28但这是高考数学中的一道优秀试题ꎬ值得细细地去品味.其实ꎬ该试题的思路有很多ꎬ如导数法㊁换元法㊁均值不等式法等ꎬ或者是凭借不等式的取等条件ꎬ用已有的经验去先猜后证 .例2㊀(2017年全国高考数学文科卷Ⅱ第21题)设函数f(x)=(1-x2)ex.图1(1)讨论f(x)的单调性ꎻ(2)当xȡ0时ꎬf(x)ɤax+1ꎬ求a的取值范围.解析㊀问题(1)解答略.对问题(2)ꎬ通过图1ꎬ不难发现ꎬ当xȡ0时ꎬ函数f(x)=(1-x2)ex是上凸函数.现在严格来说明ꎬ对f(x)求二阶导ꎬ可得fᵡ(x)=-ex(x2+4x+1)ꎬ显然当xȡ0时ꎬ有fᵡ(x)ɤ0ꎬ所以函数f(x)在xɪ[0ꎬ+ɕ)是上凸函数.显然ꎬ函数f(x)和直线y=ax+1过点(0ꎬ1).要使xȡ0时ꎬf(x)ɤax+1ꎬ则需直线y=ax+1在点(0ꎬ1)的斜率大于等于函数f(x)在点(0ꎬ1)处的斜率ꎬ即aȡlimxң0fᶄ(x)=ex(1-2x-x2)|x=0=1.所以ꎬa的取值范围为[1ꎬ+ɕ).评注㊀该方法是从函数的凹凸性来求解参数的范围ꎬ当然该试题的思路开阔ꎬ解决方法较多ꎬ如分类讨论法㊁参数分离法㊁构造导数定义法㊁洛必达法则㊁柯西中值定理㊁拉格朗日中值定理等.在高考数学考试中ꎬ可以借助导数为工具ꎬ画出函数的大致图象ꎬ然后再利用二阶导数来判断函数的凹凸性ꎬ这对求解切线的斜率问题是有帮助的.例3㊀(2014年新课标2理科第21题)设函数f(x)=ex-e-x-2x.(1)讨论f(x)的单调性ꎻ(2)设g(x)=f(2x)-4bf(x)ꎬ当x>0时ꎬg(x)>0ꎬ求b的最大值ꎻ(3)已知1.4142<2<1.4143ꎬ估计ln2的近似值(精确到0.001).解析㊀问题(1)和问题(3)解答略.对问题(2)ꎬ由题可知g(x)=e2x-e-2x-4x-4b(ex-e-x-2x)>0ꎬ即e2x-e-2x-4b(ex-e-x)>(4-8b)x.不妨设函数m(x)=e2x-e-2x-4b(ex-e-x)ꎬ则mᶄ(x)=2e2x+2e-2x-4b(ex+e-x).注意到mᶄ(0)=4-8bꎬ且m(x)过点(0ꎬ0)ꎬ所以直线y=(4-8b)x恰好是函数m(x)在x=0处的切线.当x>0时ꎬ要使得e2x-e-2x-4b(ex-e-x)>(4-8b)x成立ꎬ则需要过原点的直线y=(4-8b)x始终在函数m(x)图象的下方.如果能够说明函数m(x)在x>0时为下凸函数ꎬ则问题解决.对mᶄ(x)求导ꎬ可得mᵡ(x)=4e2x-4e-2x-4b(ex-e-x)=4(ex-e-x)(ex+e-x-b).令mᵡ(x)=0ꎬ则ex-e-x=0或ex+e-x-b=0.由ex-e-x=0ꎬ可得x=0.代入ex+e-x-b=0ꎬ可得b=2.此时ꎬ函数m(x)只有x=0这一个拐点ꎬ即函数凹凸性的连接点.则现在需要对b进行讨论ꎬ当bɤ2时ꎬ易得xɪ(-ɕꎬ0)时ꎬ有ex+e-x-b>0ꎬex-e-x<0ꎬ则mᵡ(x)<0ꎬ于是m(x)在xɪ(-ɕꎬ0)上是上凸函数.同理ꎬ可以判断函数m(x)在xɪ(0ꎬ+ɕ)上是下凸函数.对b>2ꎬ可判断不成立.故要使m(x)>(4-8b)xꎬ则需要bɤ2.评注㊀该方法主要是关注函数m(x)在x=0处的切线ꎬ恰好是直线y=(4-8b)x的斜率ꎬ进而想到使用函数的凹凸性来求参数的取值范围.可见ꎬ高考导数中求参数最值问题ꎬ常常利用函数的凹凸性来作为命题点.例4㊀(2010年福建高考文科第22题)已知函数f(x)=13x3-x2+ax+b的图象在点P(0ꎬf(0))处的切线方程为y=3x-2.(1)求实数aꎬb的值ꎻ(2)设g(x)=f(x)+mx-1是[2ꎬ+ɕ)上的增函数ꎬ①求实数m的最大值ꎻ②当m取最大值时ꎬ是否存在点Qꎬ使得过点Q的直线若能与曲线y=g(x)围成两个封闭图形ꎬ则这两个封闭图形的面积总相等?若存在ꎬ求出点Q的坐标ꎻ若不存在ꎬ说明理由.解析㊀由问题(1)和问题(2)的①ꎬ可知a=3ꎬb=-2ꎬm=3.所以g(x)=13x3-x2+3x-2+3x-1.要使得过点Q的直线能与曲线y=g(x)围成的两个封闭图形的面积相等ꎬ则需要函数具有高度的中心对称性.注意到g(x)中 y=3x-1 是反比例函数ꎬ点(1ꎬ0)是y=3x-1对称中心ꎬ且函数y=3x-1在xɪ(1ꎬ+ɕ)上是下凸函数ꎬ在xɪ(-ɕꎬ1)是上凸函数ꎬ则可以先 猜测 函数g(x)的对称中心为(1ꎬy)ꎬ现在需要说明 x=1 是否为对称中心的横坐标.从函数凹凸性的角度来看ꎬ就是要找函数g(x)的拐点ꎬ即凹凸函数的分界点.38对g(x)求二阶导数ꎬ可得gᵡ(x)=2x-2+6(x-1)3ꎬ令gᵡ(x)>0ꎬ可得xɪ(1ꎬ+ɕ).同理ꎬ令gᵡ(x)<0ꎬ可得xɪ(-ɕꎬ1).所以函数g(x)在xɪ(1ꎬ+ɕ)上为下凸函数ꎬ在xɪ(-ɕꎬ1)上是上凸函数.故中心对称的横坐标为1.又因为g(x)=13x3-x2+3x-2+3x-1=13(x-1)3+2(x-1)+3x-1+13ꎬ所以函数g(x)的对称中心为(1ꎬ13).所以存在点Q(1ꎬ13)ꎬ使得点Q的直线能与曲线y=g(x)围成的两个封闭图形的面积相等.评注㊀该方法ꎬ是通过题干中提供的信息 过点Q的直线若能与曲线y=g(x)围成两个封闭图形 并且 面积相等 ꎬ自然想到这样的函数需要高度的中心对称ꎬ在g(x)的解析式中含有项 3x-1 ꎬ这关于点(1ꎬ0)成中心对称ꎬ由此考虑用函数的凹凸性来判断.例5㊀(2005年全国高考理科卷Ⅰ第22题)(1)设函数f(x)=xlog2x+(1-x)log2(1-x)(0<x<1)ꎬ求函数f(x)的最小值ꎻ(2)设正数p1ꎬp2ꎬp3ꎬ ꎬp2ꎬ满足p1+p2+p3+ +p2=1ꎬ求证:p1log2p1+p2log2p2+p3log2p3+ +p2log2p2ȡ-n.解析㊀问题(1)解答略.问题(2)ꎬ可以用传统的数学归纳法ꎬ这是一个关于正整数n的命题ꎬ并且问题(1)的结论ꎬ可以为问题(2)作归纳奠基ꎬ则只需要说明归纳假设和归纳总结即可ꎬ但是解答过程比较繁琐ꎬ现在用高等数学的方法来证明.不妨设函数g(x)=xlog2xꎬ则gᶄ(x)=log2x+1ln2ꎬgᵡ(x)=1xln2.因为0<x<1ꎬ所以gᵡ(x)>0ꎬ所以函数g(x)在xɪ(0ꎬ1)是下凸函数.由詹森不等式ꎬ可知p1log2p1+p2log2p2+p3log2p3+ +p2log2p2ȡ2n(p1+p2+ +p22n)log2(p1+p2+ +p22n)=-n.即p1log2p1+p2log2p2+p3log2p3+ +p2log2p2ȡ-n.㊀评注㊀可见ꎬ从高等数学的视角出发ꎬ可以极大地简化运算量.只需要掌握函数凹凸性的两个核心步骤即:求导判断㊁放缩ꎬ然后就直接使用詹森不等式来证明ꎬ而詹森不等式ꎬ就是推广了的函数凹凸性的不等式性质.因此ꎬ从本质上讲ꎬ依然是用函数的凹凸性.㊀㊀三㊁对数学教学的启示要回归教材.高中数学教材是学生学习数学知识和形成数学素养的重要载体.然而ꎬ现行的高中数学课堂ꎬ已经脱离了数学教材ꎬ更多的是用导学案㊁辅导资料等来代替教材ꎬ通过短时间的知识讲解ꎬ就进入几乎 疯狂 的 刷题+评讲 模式ꎬ然后在不断的试错中积累数学经验.在这种教学模式下ꎬ学生体会不到数学学习的快乐ꎬ感觉数学就像是无尽的深渊.2012年ꎬ新浪微博曾做过一项调查ꎬ有将近70%的人想让数学 滚出高考 ꎬ可见大部分人曾经被数学伤害过.这可能是 题海战术 对他们的身心造成了伤害.其实ꎬ数学教学应该回归课本ꎬ将课本的知识点㊁习题㊁思考题等掌握好ꎬ然后再做适当的思维拓展题ꎬ这就足以应对高考试题了.同时ꎬ也可以留更多的时间来锻炼和提升学生的其它能力ꎬ如组织㊁管理㊁口才㊁演讲等能力ꎬ促进学生身心全面和谐的发展.要深度挖掘教材习题.数学教材是数学教学的范本ꎬ具有规范性㊁系统性㊁科学性等特点.教材习题ꎬ是学生巩固数学新知的重要素材ꎬ也是高考数学命题的素材来源.数学教师ꎬ在熟练掌握习题的基础上ꎬ还需要深入地挖掘教材中的 好题 .所谓好题ꎬ就是要蕴含丰富的数学思想㊁开阔的思路㊁广阔的切入点等ꎬ同时还要看是否具有高等数学的背景.在高考数学中ꎬ命题者对具有高等数学背景的教材习题比较重视ꎬ有时常通过这类习题改编ꎬ然后命制成高考数学试题.其实ꎬ函数的凹凸性出现在高考数学中ꎬ并不是没有依据的.在人教A版数学必修1第45页ꎬ有这样一道证明题.证明:(1)若f(x)=ax+bꎬ则f(x1+x22)=f(x1)+f(x2)2ꎻ(2)若g(x)=x2+ax+bꎬ则g(x1+x22)ɤg(x1)+g(x2)2.其实ꎬ这个试题中就已经蕴含了函数 凹凸性 ꎬ但是很多教师和学生并没有真正地重视教材的课后习题.因此ꎬ在数学教学活动中ꎬ应当重视数学教材习题的深度挖掘ꎬ挖掘其中的高等数学背景ꎬ剖析背后的数学本质ꎬ感悟试题设计所蕴含的数学思想等.㊀㊀参考文献:[1]华东师范大学数学系.数学分析上册(第三版)[M].北京:高等教育出版社ꎬ1999.[2]张海芳.函数凹凸性的等价定义及其证明[J].文山学院学报ꎬ2015ꎬ28(06):63-65+68.[3]中华人民共和国教育部.普通高中课程标准实验教课书 数学1(必修A版)[M].北京:人民教育出版社ꎬ2007.[责任编辑:李㊀璟]48。
凹函数与凸函数的性质及应用

凹函数与凸函数的性质及应用函数的凸性和凹性是用来描述函数图像弯曲方向的重要性质。
凸函数和凹函数在形状上有明显的区别,这些区别可以通过函数的导数,特别是二阶导数来刻画。
1.2.凹函数(Concave Function):o凹函数的图像呈现一种“向下凹”或“向上凸”的形状。
也就是说,如果我们在函数的图像上任意取两点并连接这两点形成一条线段,那么这条线段将始终位于函数图像的上方。
o从数学角度来说,如果一个函数在其定义域内的任意两点x1和x2之间,对于任意实数λ∈(0,1),都有f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2),则称该函数为凹函数。
o凹函数的二阶导数在其定义域内始终非正,即f''(x) ≤0。
如果二阶导数在某个区间内严格小于零,则称该函数在该区间内是严格凹的。
3.4.凸函数(Convex Function):o凸函数的图像呈现一种“向上凸”或“向下凹”的形状。
也就是说,如果我们在函数的图像上任意取两点并连接这两点形成一条线段,那么这条线段将始终位于函数图像的下方。
o从数学角度来说,如果一个函数在其定义域内的任意两点x1和x2之间,对于任意实数λ∈(0,1),都有f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2),则称该函数为凸函数。
o凸函数的二阶导数在其定义域内始终非负,即f''(x) ≥0。
如果二阶导数在某个区间内严格大于零,则称该函数在该区间内是严格凸的。
这些性质使得我们能够通过观察函数的二阶导数来判断函数的形状,从而更好地理解函数的性质和行为。
在优化问题、经济学、概率论和统计学等多个领域,凸性和凹性的概念都非常重要,因为它们可以帮助我们分析和解决各种问题。
例如,在优化问题中,凸函数通常比凹函数更容易处理,因为凸函数的最优解通常是全局最优解,而凹函数的最优解则可能是局部最优解。
函数的凹凸性,极值
f
( x0 )
lim
xx_
0
f ( x) f ( x0 ) lim
x x0
xx_
0
f ( x) 0 x x0
f ( x) 0 ( x x0 )
f
( x0 )
lim
x x
0
f ( x) f ( x0 ) lim
x x0
x x
0
f ( x) 0
x x0
f ( x)在x0两侧异号。
如 果 存 在 着 点x0的 一 个 邻 域, 对 于 这 邻 域 内 的 任何点x,除了点x0外, f ( x) f ( x0 )均成立,就称 f ( x0 )是函数f ( x)的一个极小值.
函数的极大值与极小值统称为极值,使函数取得 极值的点称为极值点.
21
y
极大值点 y 极小值点
y 不是极值点
但在(,0)内, y 0, 曲线在(,0]上是凹的; 在(0,)内, y 0, 曲线在[0,)上是凸的.
点(0,0)是曲线 y 3 x的拐点.
16
求曲线 y f ( x) 拐点的一般步骤 :
( 1 ) 求 f ( x) 的定义域 (或确定讨论区间) ; (2) 计算 f ( x) , f ( x) , (如需要可求出 f ( x)) ; (3) 求拐点可疑点 :
f ( x) 0 ( x x0 )
14
例5 求曲线 y sin x cos x ([0,2]内) 的拐点.
解 y cos x sin x , y sin x cos x ,
y cos x sin x .
令 y 0,
得
x1
3 4
,
x2
7 4
.
f (3) 2 0,
函数的凹凸性在高考中的应用

函数的凹凸性在高考中的应用教学目的: ①了解函数的凹凸性,掌握增量法解决凹凸曲线问题。
②培养学生探索创新能力,鼓励学生进行研究型学习。
教学重点:掌握增量法解决凹凸曲线问题教学难点:函数的凹凸性定义及图像特征教学过程:一、课题导入1.展示崇仁县第二中学20XX届高三第一次月考试题12得分统计表2.组织学生现场解答月考试题12并进行得分统计,以引出课题———题目:一高为H、满缸水量为V的鱼缸的截面如图1所示,其底部碰了一个小洞,满缸水从洞中流出.若鱼缸水深为h时水的体积为V,则函数V=f(h)的大致图象可能是图2中的().(选自《中学数学教学参考》20XX年第1~2合期)的《试题集绵》.函数凹凸性问题是近几年高考与平时训练中的一种新题型.这种题情景新颖、背景公平,能考查学生的创新能力和潜在的数学素质,体现“高考命题范围遵循教学大纲,又不拘泥于教学大纲”的改革精神.但由于函数曲线的凹凸性在中学教材中既没有明确的定义,又没有作专门的研究,因此,就多数学生而言,对这类凹凸性曲线问题往往束手无策;而教师的“导数”理解又不能被学生所接受.所以,对这类非常规性问题作一探索,并引导学生去得到一般性的解法,无疑对学生数学素质的提高和创新精神的培养以及在迅速准确解答高考中出现此类的试题都是十分重要的。
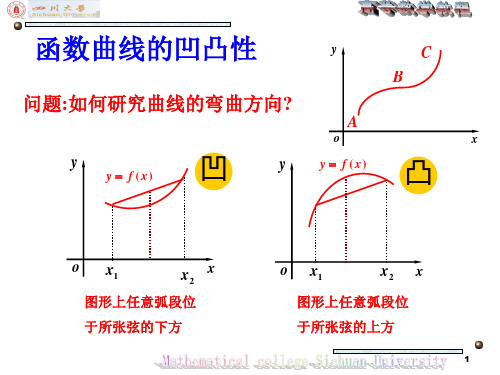
二、新课讲授1、凹凸函数定义及几何特征图1 图2⑴引出凹凸函数的定义:如图3根据单调函数的图像特征可知:函数)(1x f 与)(2x f 都是增函数。
但是)(1x f 与)(2x f 递增方式不同。
不同在哪儿?把形如)(1x f 的增长方式的函数称为凹函数,而形如)(2x f 的增长方式的函数称为凸函数。
⑵凹凸函数定义(根据同济大学数学教研室主编《高等数学》第201页):设函数f 为定义在区间I 上的函数,若对(a ,b )上任意两点1x 、2x ,恒有:(1)1212()()()22x x f x f x f ++<,则称f 为(a ,b )上的凹函数; (2)1212()()()22x x f x f x f ++>,则称f 为(a ,b )上的凸函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
凹凸函数在求最值中的两例应用
作者:刘丽娜
来源:《吉林省教育学院学报·上旬刊》2013年第10期
摘要:从凹凸函数的定义和几何特征出发,归纳了它在初等数学中的一些性质,结合实例总结了它在求最值中的应用。
关键词:凹函数;凸函数;最值
中图分类号:O13 文献标识码:A 文章编号:1671—1580(2013)02
一、凹凸函数定义及几何特征
为了行文方便,我们先来介绍一下凹凸函数定义和几何特征。
则分别称f(x)在区间I上是凸函数或凹函数。
以上两个不等式中当且仅当x1=x2时等式成立。
如图1所示,设A1,A2是凸函数y=f(x)曲线上两点,它们对应的横坐标满足x10,
q1+q2=1,使得x0=q1x1+q2x2,过点x0作ox轴的垂线交曲线y=f(x)于A,交A1A2于B,则(1.1)式左端即为A点纵坐标,右端即为B点纵坐标,因此,凸函数的几何意义就是,其函数曲线在任意两点A1与A2之间的部分位于弦A1A2的下方。
根据以上几何特征,我们可以直接推导一个关于凸函数的不等式,设函数y=f(x),
A1A2为f(x)图像上的任一弦,设A1[x1,f(x1)],A2[x2,f(x2)],x1
如果函数f(x)是凹函数,那么不等式(1.3)中的不等号方向相反。
二、凹凸函数的一些性质
根据凹凸函数的定义可以证明下面的定理:
定理1 若函数f(x)在区间I上为凸(凹)函数,区间I1I,则函数f(x)在区间I1上也为凸(凹)函数。
定理2 若f(x)和g(x)在区间I上都是凸(凹)函数,则f(x)+g(x)在区间I上也是凸(凹)函数。
定理3 若f(x)在区间I上是凸(凹)函数,则当a>0时,af(x)在区间I上也是凸(凹)函数,而当a
推论1 若f(x)在区间I上是凸(凹)函数,则-f(x)在区间I上为凹(凸)函数。
推论2 在区间I上,如果f(x)是凸(凹)函数,而且g(x)是凹(凸)函数,那么f (x)-g(x)为凸(凹)函数。
推论3 如果f(x)在区间I上是凸(凹)函数,a为常数,那么f(x)+a和f(x)+ax在区间I上都是凸(凹)函数。
定理4 设y=f[g(x)]是y=f(u)(u∈J)和u=g(x)(x∈J)的复合函数,而且g(x)在I上为凸(凹)函数,则
(1)当f(u)在区间J上为增的凸(凹)函数时,f[g(x)]在I上的凸(凹)函数。
(2)当f(u)在区间J上为减的凹(凸)函数时,f[g(x)]在I上的凹(凸)函数。
判断一个函数在给定区间上的凹凸性,可应用定义性质或图象。
利用定义性质可证明下列结论:
1)对数函数y=logax.(a>0,a≠1).在区间(0,+∞)上,当a>1时为凹函数,当a
2)指数函数y=ax.(a>0,a≠1).在区间(-∞,+∞)上为凸函数。
3)幂函数y=xa在(0,+∞)上,当a1时为凸函数,当0
4)y=sinx在[(2k-1)π,2kπ]上为凸函数。
5)y=cosx在2kπ-π2 ,2kπ+π2上为凹函数,在2kπ+π2 ,2kπ+3π2上为凸函数。
6)y=tgx在2kπ-π2,2kπ上为凹函数,在2kπ,2kπ+π2上为凸函数。
定理5 如果函数f(x)在区间I上凸(凹)函数,那么对任意的x0∈I,函数φ(x)=f (x)-f(x0)x-x0(x≠x0)在数集I0上是增(减)函数。
其中I0是由区间I去掉x0后所得之数集。
当函数是凹函数时,不等式(2.1)中的不等号改变方向。
从不等式(2.1)还可以得到一个非常重要的推论。
推论4 如果f(x)是D上的凸(凹)函数则对于x1,x2,…,xn∈D,n∈N,有
三、凹凸函数在求最值中的应用
我们注意到一些最值问题可以转化为不等式来求,因此凹凸性质解决最值问题有独到之处。
解由结论6)可知tgx在0,π2内为凸函数,再根据结论3)可知u5在(0,+∞)内为增的凸函数,所以tg5x在区间(0,π2)内也为凸函数,根据不等式(2.2),对于A2,B2,
C2∈ 0,π2.及A+B+C=π.故tg5A2+tg5B2+tg5C2的最小值为39.
本文是在初等数学范围内对凹凸函数的一些应用作了探讨,但凹凸函数的应用问题远不止于此,它在其他范围内的应用更为广泛,例如高等数学范围内的最优化﹑偏微分方程等问题。
[参考文献]
[1]刘玉琏.数学分析讲义[M].北京:高等教育出版社,1996.
[2]邓东皋,尹小玲.数学分析[M].北京:高等教育出版社,1999.
[3]程其襄.数学分析[M].北京:高等教育出版社,2001.
[4]徐利治,王心华.数学分析的方法及例题选讲[M].北京:高等教育出版社,1984.
[5]林源渠等编.北京大学数学分析习题集[M].北京:高等教育出版社,1986.。
