圆的方程
高中数学圆及其方程

圆及其方程一、公式及相关内容(1)圆的标准方程:222()()x a y b r -+-= (圆心及半径)(2)圆的一般方程:220x y Dx Ey F ++++= (无xy 项,22,x y 系数相等且不为零)(3)圆的参数方程:cos sin x a r y b r θθ=+⎧⎨=+⎩(θ为参数)上述方程中均有三个字母系数,因此确定一个圆需要三个独立的条件。
(4)过圆 222x y r +=上一点00(,)P x y 的切线方程为200xx yy r +=圆 222xy r +=的斜率为k 的切线方程为y kx =± (掌握推导方法)(5)经过两圆:221110x y D x E y F ++++=,222220x y D x E y F ++++=交点的圆的方程为2222111222()0x y D x E y F x y D x E y F λ+++++++++= 当1λ=-时,得到两圆公共弦所在直线方程121212()()()0D D x E E y F F -+-+-=(6)判断点与圆的位置关系:取决于点与圆心的距离与圆半径的比较结果 (7)直线与圆的位置关系:一:圆心到直线的距离与圆半径比较二:直线与圆方程组成的方程组的解的个数:∆法(8)圆与圆位置关系:圆心距d 与两圆半径,R r 的比较:d R r d R r R r d R r d R r d R r>+⎧⎪=+⎪⎪-<<+⎨⎪=-⎪<-⎪⎩(9)公切线求法:通过比例求得公切线与连心线的交 点A 的坐标,用点斜式设公切线的 方程,然后求得斜率k ,得到公切 线方程。
外离 外切 相交 内切 内含二 求圆的方程1. 求经过两点(1,4),(3,2)A B -,且圆心在y 轴上的圆的方程。
(标准方程法,垂径弦性质)2.(1)已知圆经过(2,3)A -和(2,5)B --两点,若圆心在直线230x y --=上,求圆的方程; (2)求过点(1,0),(3,0),(0,1)A B C -的圆的方程。
圆的方程

1圆的方程1. 标准方程:)0()()(222>=-+-r r b y a x 圆心),(b a C ,半径r 。
当0==b a 时,圆心在原点的圆的方程为:222r y x =+.2. 一般方程:022=++++F Ey Dx y x ,(0422>-+F E D )圆心为点,22D E ⎛⎫-- ⎪⎝⎭,半径r =例1. 圆心在原点,等于5的圆的方程,并判断点M 1(5,-7)M 2(-5,-1)是否在这个圆上。
例2. 满足下列各条件圆的方程:()1以)9,4(A ,)3,6(B 为直径的圆;(2) 圆心在原点,半径是3; (3) 经过点P(5,1),圆心在点C(8,-3);(4) 过)2,5(A ,)2,3(-B 两点,圆心在直线32=-y x 上的圆的方程;例3. 过三点O (0,0),M 1(1,1),M 2(4,2)的圆方程,并求这个圆的半径长和圆心坐标。
21. 以两点()3,1A --和()5,5B 为直径端点的圆的方程是.A 100)2()1(22=++-y x .B 100)2()1(22=-+-y x.C 25)2()1(22=-+-y x .D 25)2()1(22=+++y x2. 圆5)2(22=++y x 关于原点()0,0对称的圆的方程为.A ()2225x y -+= .B ()2225x y +-=.C 5)2()2(22=+++y x .D 5)2(22=++y x3 . 已知圆222440x y x y ++-+=关于直线2y x b =+成轴对称,则b = 4. 圆22220x y x y +-+=的周长是 ( )A.B .2πCD .4π5 . 已知两条直线12:330,:4610.l ax y l x y +-=+-=若12//l l ,则a = 6. 已知两条直线2y ax =-和(2)1y a x =++互相垂直,则a 等于( )A .2B .1C .0D .1-3. 直线与圆的位置关系4. 直线截圆所得弦长:AB =r 为半径,d 直线到圆心的距离).5. 圆与圆的位置关系:例3. 直线l :3x +y -6=0和圆心为C 的圆x 2+y 2-2y -4=0,判断直线l 与圆的位置关系,如果相交,求它们交点坐标3例4. M (-3,-3)的直线l 被圆x 2+y 2+4y -21=0所截得的弦长为45,b直线l 的方程。
圆的方程的知识点总结

圆的方程的知识点总结一、圆的标准方程圆的标准方程是圆心在原点(0,0)、半径为r的圆的方程。
它可以表示为:x^2 + y^2 = r^2其中,(x,y)是圆上的任意点,r是圆的半径。
这个方程可以用来描述一个圆的几何形状和位置。
当圆心不在原点时,我们可以通过平移坐标系的方式将圆心移到原点,然后再应用标准方程。
这样,任意圆的方程都可以被化简为标准方程的形式。
二、圆的一般方程圆的一般方程是一个更一般的表示方法,它可以描述任意圆的方程,即圆心不一定在原点,半径也不一定为正值。
一般方程的形式如下:(x - h)^2 + (y - k)^2 = r^2其中(h,k)是圆心的坐标,r是圆的半径。
通过这个方程,我们可以描述圆的任何位置和大小。
三、圆的参数方程圆的参数方程是用参数形式表示的圆的方程。
一个圆的参数方程可以表示为:x = r*cos(t)y = r*sin(t)其中,t是一个参数,取值范围一般是[0,2π]。
通过不同的参数取值,我们可以得到圆上的所有点。
参数方程的形式在一些数学和物理问题中有一定的应用价值。
四、圆的性质1.圆的直径和周长圆的直径是通过圆心的任意一条线段,它的长度是圆的半径的两倍。
而圆的周长则是圆周的长度,可以通过以下公式计算:C = 2πr其中,r是圆的半径,C是圆的周长。
2.圆的面积圆的面积是圆内部的所有点的集合,可以利用下面的公式来计算:A = πr^2其中,r是圆的半径,A是圆的面积。
这个公式也可以通过积分的方式来推导。
3.切线对于给定的圆和一点P在圆上,我们可以找到一条直线,它通过点P且与圆相切。
切线的斜率可以通过圆心和点P的连线来确定。
这个性质在解决与圆有关的问题时有很大的帮助。
五、圆的应用圆在日常生活和工程中有着广泛的应用,下面是一些例子:1. 圆的几何构造:利用圆的性质可以进行各种几何构造,例如正多边形的内切圆和外接圆、切线的构造等。
2. 圆的运动学:在物理学中,圆的运动学问题是一个常见的问题,如圆周运动、圆形轨道的运动等。
高中数学圆的标准方程
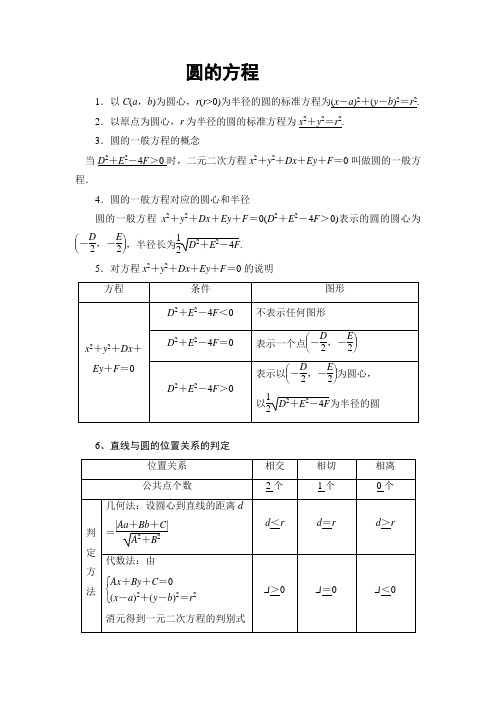
圆的方程1.以C (a ,b )为圆心,r (r >0)为半径的圆的标准方程为(x -a )2+(y -b )2=r 2. 2.以原点为圆心,r 为半径的圆的标准方程为x 2+y 2=r 2. 3.圆的一般方程的概念当D 2+E 2-4F >0时,二元二次方程x 2+y 2+Dx +Ey +F =0叫做圆的一般方程.4.圆的一般方程对应的圆心和半径圆的一般方程x 2+y 2+Dx +Ey +F =0(D 2+E 2-4F >0)表示的圆的圆心为⎝ ⎛⎭⎪⎫-D2,-E 2,半径长为12D 2+E 2-4F .5.对方程x 2+y 2+Dx +Ey +F =0的说明6、直线与圆的位置关系的判定例题讲解1、已知圆的方程是(x-2)2+(y-3)2=4,则点P(3,2)()A.是圆心B.在圆上C.在圆内D.在圆外2、已知一圆的圆心为点(2,-3),一条直径的两个端点分别在x轴和y轴上,则此圆的方程是()A.(x-2)2+(y+3)2=13B.(x+2)2+(y-3)2=13C.(x-2)2+(y+3)2=52D.(x+2)2+(y-3)2=523、以点A(-5,4)为圆心,且与x轴相切的圆的方程是()A.(x+5)2+(y-4)2=25B.(x-5)2+(y+4)2=16C.(x+5)2+(y-4)2=16D.(x-5)2+(y+4)2=25巩固练习1、求圆心在直线x-2y-3=0上,且过点A(2,-3),B(-2,-5)的圆的标准方程.2、求圆心在x轴上,且过点A(5,2)和B(3,-2)的圆的标准方程.3、若P(x,y)是圆C(x-3)2+y2=4上任意一点,请求出P(x,y)到直线x-y +1=0的距离的最大值和最小值.4、已知圆C:(x-3)2+(y-4)2=1,点A(0,-1),B(0,1),设P是圆C上的动点,令d=|P A|2+|PB|2,求d的最大值及最小值.图4-1-15、直线3x+4y+12=0与圆(x-1)2+(y+1)2=9的位置关系是()A.过圆心B.相切C.相离D.相交但不过圆心6、已知直线ax+by+c=0(ab≠0)与圆x2+y2=1相切,则三边长分别为|a|,|b|,|c|的三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.不存在7、已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y +3=0相切,则圆C的方程为____________________.8、过点P(-1,2)且与圆C:x2+y2=5相切的直线方程是________.课后练习1、圆x2+y2-4x+6y=0的圆心坐标是()A.(2,3) B.(-2,3)C.(-2,-3) D.(2,-3)2、已知方程x 2+y 2-2x +2k +3=0表示圆,则k 的取值范围是( ) A .(-∞,-1)B .(3,+∞)C .(-∞,-1)∪(3,+∞)D.⎝ ⎛⎭⎪⎫-32,+∞ 3、若方程x 2+y 2+Dx +Ey +F =0表示以(2,-4)为圆心,4为半径的圆,则F =________.4、设A 为圆(x -1)2+y 2=1上的动点,P A 是圆的切线且|P A |=1,则P 点的轨迹方程是__________.5、求经过三点A (1,-1),B (1,4),C (4,-2)的圆的一般方程.6、过点(-1,-2)的直线l 被圆x 2+y 2-2x -2y +1=0截得的弦长为2,求直线l 的方程.7、 已知动点M 到点(8,0)的距离等于点M 到点(2,0)的距离的2倍,你能求出点M 的轨迹方程吗?8、 已知直角△ABC 的斜边为AB ,且A (-1,0),B (3,0),请求出直角顶点C 的轨迹方程.9、已知圆心为C 的圆经过点A (1,1)和B (2,-2),且圆心C 在直线l :x -y+1=0上.(1)求圆C 的方程;(2)线段PQ 的端点P 的坐标是(5,0),端点Q 在圆C 上运动,求线段PQ 的中点M 的轨迹方程.。
圆的一般方程表达式

圆的表达式是:(x-a)²+(y-b)²=R²。
圆的一般方程:x²+y²+Dx+Ey+F=0(D²+E²-4F>0)。
圆半径的长度定出圆周的大小,圆心的位置确定圆在平面上的位置。
1、已知:圆半径长R;中心A的坐标(a,b),则圆的大小及其在平面上关于坐标轴的位置就已确定了。
根据图形的几何尺寸与坐标的可以得出圆的标准方程。
结论如下:(x-a)²+(y-b)²=R²当圆的中心A 与原点重合时,即原点为中心时,即a=b=0,圆的方程为:x²+y²=R²
2、圆的标准方程(x-a)²+(y-b)²=r²中,有三个参数a、b、r,即圆心坐标为(a,b),只要求出a、b、r,这时圆的方程就被确定,因此确定圆方程,须三个独立条件,其中圆心坐标是圆的定位条件,半径是圆的定形条件。
3、圆的相关信息:由Ax+By+C=0,可得y=(-C-Ax)/B,(其中B不等于0),代入x²+y²+Dx+Ey+F=0,即成为一个关于x的方程。
圆的方程

解:已知圆心C是(1,3),那么只要再求出圆的半径r, 就能写出圆的方程. 因为圆C和直线3x-4y-7=0相切,所以半径r等于圆 心C到这条直线的距离.根据点到直线的距离公式, 得: | 3 1 4 3 7 |
r
3 (4)
2
2
16 5
因此,所求的圆的方程是:(x-1)2+(y-3)2=.
256 25
例4
已知圆的方程是x2+y2=r2,求经过圆 上一点M(x0,y0)的切线方程.
y
P
M
分析(一):设切线斜率为k,OM 斜率为k1,则:
x0 1 k 即k k1 y0
所以切线方程为: x0x+y0y=r2 分析(二):设P为切线上任意一 点,则OM⊥MP,所以: OM MP 0 (x0,y0)· (x-x0,y-y0)=0 所以切线方程为:x0x+y0y=r2.
O
x
例5 如图是某圆拱桥的一孔圆拱示意图.该圆 拱跨度AB=20m,拱高OP=4m,在建造时每隔4 m需要用一个支柱支撑,求支柱A2P2 的长度 (精确到0.01m).
P2 y P x A O
A
1
A
2
A
3
A
4
B
P2
y
பைடு நூலகம்
P
x O A
3
A
A
1
A
2
A
4
B
例6
已知圆心在x轴上,且距原点距离3 个单位,半径为5的圆的方程.
2
(x-a)2+(y-b)2=r2
(1)方程中参数a、b、r的意义是什么?
(2)当圆心在原点时圆的方程的形式是什么?
圆方程的各种形式

圆方程的各种形式圆是一个平面上所有点到圆心的距离都相等的几何图形。
圆方程描述了圆的性质和特征。
在本文中,我们将讨论圆方程的各种形式。
1.标准方程:圆的标准方程是最基本的形式,它使用圆心的坐标和半径来定义圆。
如果圆的圆心是(h,k),半径为r,则圆的标准方程为:(x-h)²+(y-k)²=r²其中(x,y)是圆上的任意一点。
2.一般方程:圆的一般方程是另一种形式,它可以将圆的方程转换为一个二次方程。
一般方程的一般形式为:Ax²+Ay²+Dx+Ey+F=0其中A、D、E和F是常数。
要将标准方程转换为一般方程,你可以进行平方展开并将所有项相加。
3.参数方程:圆的参数方程使用参数t来表示圆上的点。
该方程的一般形式为:x = h + r * cos(t)y = k + r * sin(t)其中(h,k)是圆心的坐标,r是半径。
参数t的范围通常是[0,2π]。
4.极坐标方程:圆的极坐标方程使用极坐标来描述圆。
该方程的一般形式为:r = a + b * cos(θ)其中a和b是常数,θ是角度。
通常情况下,θ的范围是[0,2π]。
5.中心半径形式:中心半径形式是另一种表达圆的方式。
它使用圆心的坐标和半径来定义圆。
该形式的一般形式为:(h,k)±r其中(h,k)是圆心的坐标,±表示圆的内外部,r是半径。
该形式更加简洁,适用于描述圆的位置关系。
6.过三点圆方程:如果给出了圆上的三个点的坐标,我们可以使用过三点圆方程来定义圆。
给定三个不共线的点(x1,y1)、(x2,y2)和(x3,y3),过三点圆方程的一般形式为:(x-a)²+(y-b)²=r²其中a和b是圆心的坐标,r是半径。
7.方程组形式:方程组形式是将两个方程组合在一起来描述圆的方式。
一般形式为:f(x,y)=0g(x,y)=0其中f(x,y)和g(x,y)分别表示两个方程。
圆的方程

5.弦长与切线方程,切线长的求法
(1)弦长求法一般采用几何法:弦心距d,圆半径r, 2 弦长l,则 d 2 l r 2 2 (2)圆的切线方程: 若点 P( x0,y0 ) 在圆 x2 y 2 r 2 上,则过点P的切线 方程为 x0 x y0 y r 2 若点 P( x0,y0 ) 在圆 ( x a)2 ( y b)2 r 2 上,则过 点P的切线方程为 ( x a)(x0 a) ( y b) ( y0 b) r 2
二、学习方法指导
例1 当曲线 y 1 4 x 2 与直线y=k(x-2)+4有两个相异
交点时,实数k的取值范围是(
5 A. 0, 12 1 3 B. 3, 4
)
5 3 C. , 12 4
5 D. , 12
2 故所求圆的方程为 ( x 19 ) ( y
例5 求圆心在直线x-y-4=0上,并且经过两圆
2 2 2 2 C1 :x y 4 x 3 0 和 C2 : x y 4 y 3 0
的交点的圆的方程. 思路分析:求经过两圆交点的圆,可利用圆系方程求解. 解:设所求圆的方程为
解得a=2或a=4. 所求直线l的方程为x+2y-3=0或x+4y-3=0 说明:本题巧用根与系数的关系,列出 x1x2 y1 y2 0 进而求得方程,另外,在设方程时,设过(3,0)的的直线方程
x+ay-3=0可避免讨论。
例4 求过P(5,-3),Q(0,6)两点,且圆心在直线2x-3y-6=0 上的圆的方程. 思路分析:可依据不同的条件,选择恰当的形式,但是要注意 圆的有关几何性质的运用.
思路分析:可以先求出两圆交点坐标,利用两点间的距离 求之;亦可利用几何法求.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆
一.复习指导:
1. 节的主要基础知识是圆的标准方程和一般方程,求圆的方程、及用解析法研究与圆有 关的位置关系问题。
2. 于圆的几何性质在平面几何中已做了比较全面的研究,因此,在解析几何中解决有关 圆的问题时,应注意使用圆的几何性质,这是数形结合思想解决这类问题的主要特点。
3.主要问题:求圆的方程;求圆的切线方程;直线与圆的位置关系等等。
二.知识点举例:
例1. 求圆心在直线0y x 4=+上,且与直线01y x =-+切于点)2,3(P -的圆的方程。
例2. 若圆0m y x 2y x 22=+--+与直线04y 2x :l =-+的两个交点为N ,M ,且满
足ON OM ⊥(O 为原点),求m 的值。
例3. 已知圆8y x 22=+及定点)0,4(P ,问过P 的直线,倾斜角在什么范围取值时,该
直线与已知圆相交?相切?并求出切线的方程。
例4. 一条直线经过点)2
3
,3(P --,被圆25y x 22=+截得的弦长为8,求此弦所在的直 线方程。
例5. 自点)3,3(A -发出的光线l 射到x 轴上,被x 轴反射,其反射光线所在的直线与圆
07y 4x 4y x 22=+--+相切,求光线l 所在的直线方程。
例6. 已知直线l :0k 34y kx =-+-和曲线2x x 231y :C -++=)3x 1(≤≤-有两
个交点时,实数k 的取值范围是 。
例7. 已知圆M 的方程4)4y ()3x (2
2=-+-和两定点)0,1(B ),0,1(A -。
在圆上求一点P ,使22BP AP +取得最小值。
例8. 实数y ,x 满足方程012y 6x 6y x 22=+--+,求
x
y 的最大值和最小值
能力训练
1.0B ,0C A =≠=是方程0F Ey Dx Cy Bxy Ax 22=+++++表示圆的( )
A 、充分非必要条件
B 、必要非充分条件
C 、充要条件
D 、既非充分条件也非必要条件
2.方程01a a 2ay 2ax y x 222=-+++++表示圆,则a 的取值范围是( )
A 、2a -<或32a >
B 、2a 32<<-
C 、0a 2<<-
D 、3
2a 2<<- 3.两圆07y 4x 4y x :C 221=+-++,013y 10x 4y x :C 222=+--+的公切线有( )
A 、2条
B 、3条
C 、4条
D 、以上都不是
4.若直线l :k x y +=和曲线2x 1y :C -=)1x 1(≤≤-有两个不同的交点,则实数k 的取值范围是( )
A 、2k >或2k -<
B 、2k 2<<-
C 、2k 1<<
D 、2k 1<≤
5.圆09y 6x 2y x :C 221=+--+关于直线01y x =--对称的曲线方程为( )
A 、09y 6x 2y x 22=++++
B 、09y 2x 6y x 22=+--+
C 、 015x 8y x 22=+-+
D 、015x 8y x 22=--+
6.直线a y 3x =+与圆1y x 22=+在第一象限内有两个不同的交点,则实数a 的取值范围是( )
A 、2a 1<<
B 、2a 2<<-
C 、3a 1<
< D 、2a 3<< 7.直线0c by ax =++与圆1y x 22=+有两个交点,则实数c ,b ,a 应满足的关系是( )
A 、222c b a ≤+
B 、222c b a <+
C 、222c b a ≥+
D 、2
22c b a >+
8.圆06y 4x 4y x 22=++-+截直线05y x =--所得的弦长为( ) A 、6 B 、
225 C 、1 D 、5 9.和x 轴相切并和圆1y x 22=+外切的圆心轨迹方程为( )
A 、1y 2x 2+=
B 、y 21x 2-=
C 、1y 2x 2+=
D 、1y 2x 2-=5
10.在圆4y x 22=+上,与直线012y 3x 4=-+距离最近的点的坐标是( )
A 、)56
,58( B 、)5
6,58(- C 、)56,58(- D 、)56,58(--
11.圆9)3y ()3x (22=-+-上到直线011y 4x 3=-+的距离等于1的点的个数为 。
12.直线2kx y +=与圆2y x 22=+有两个不同的交点,则k 的取值范围是 。
13.一圆C 过圆0x 2y x 22=-+与直线03y 2x =-+的交点,且圆心C 在x 轴上,求
该圆C 的方程
14.已知ABC ∆中,5BC ,4AC ,3AB ===,ABC ∆内切圆上一动点P ,试求
222PC PB PA ++的取值范围。
15.已知圆的方程1y )1x (22=+-,过原点O 作圆的任意弦,求这些弦的中点M 的轨
迹方程。
