2-6-矩阵的秩_生产经营管理_经管营销_专业资料.ppt
合集下载
2.6-矩阵的秩
001
1 0 5 1 0 5 1 0 5 1 0 0
E(1, 3(5)) = 0 1 0 , 0 1 0 0 1 0 = 0 1 0 .
00 1 001 00 1 001
第二章 矩阵
§2.6 方阵的逆矩阵
2. 可逆矩阵的分解
***
(1) * * *
** * ***
***
= ***
10 0
010.
000 *** 000 001
第二章 矩阵
2 0 4 1
0 1 3 2 的3阶子式有14个:
4 0 8 2
§2.5矩阵的秩
2 0 4 2 0 1 2 4 1 0 4 1
0 1 3 = 0 1 2 = 0 3 2 = 1 3 2 = 0. 4 0 8 4 0 2 4 8 2 0 8 2
第二章 矩阵
§2.5矩阵的秩
问题: 假若一个56的矩阵中所有3阶子式都等
1 0
0 1
3/2 1
3 1
5/2 1
1 3 2 故A1 = 3/2 3 5/2 .
1 1 1
第二章 矩阵
§2.6 方阵的逆矩阵
三. 用初等变换解矩阵方程
设A可逆, 则A可以经过有限次初等行变换化为 行最简形——单位矩阵E.
下面用初等变换解矩阵方程AX = B. 注意到X = A1B.
(A B) … (E ?)
第二章 矩阵
§2.5 矩阵的秩
定理2. 设A是满秩方阵,则存在初等方阵
P1, P2, , Ps. 使得 Ps Ps1 , P2P1A E
第二章 矩阵
§2.5 矩阵的秩
定理3. mn矩阵A, m阶初等矩阵
P1, P2, …, Ps 及m阶初等矩阵
1 0 5 1 0 5 1 0 5 1 0 0
E(1, 3(5)) = 0 1 0 , 0 1 0 0 1 0 = 0 1 0 .
00 1 001 00 1 001
第二章 矩阵
§2.6 方阵的逆矩阵
2. 可逆矩阵的分解
***
(1) * * *
** * ***
***
= ***
10 0
010.
000 *** 000 001
第二章 矩阵
2 0 4 1
0 1 3 2 的3阶子式有14个:
4 0 8 2
§2.5矩阵的秩
2 0 4 2 0 1 2 4 1 0 4 1
0 1 3 = 0 1 2 = 0 3 2 = 1 3 2 = 0. 4 0 8 4 0 2 4 8 2 0 8 2
第二章 矩阵
§2.5矩阵的秩
问题: 假若一个56的矩阵中所有3阶子式都等
1 0
0 1
3/2 1
3 1
5/2 1
1 3 2 故A1 = 3/2 3 5/2 .
1 1 1
第二章 矩阵
§2.6 方阵的逆矩阵
三. 用初等变换解矩阵方程
设A可逆, 则A可以经过有限次初等行变换化为 行最简形——单位矩阵E.
下面用初等变换解矩阵方程AX = B. 注意到X = A1B.
(A B) … (E ?)
第二章 矩阵
§2.5 矩阵的秩
定理2. 设A是满秩方阵,则存在初等方阵
P1, P2, , Ps. 使得 Ps Ps1 , P2P1A E
第二章 矩阵
§2.5 矩阵的秩
定理3. mn矩阵A, m阶初等矩阵
P1, P2, …, Ps 及m阶初等矩阵
2.6 矩阵的秩

§2.6 矩阵的秩 第 §2.6 矩阵的秩 二 章 一、矩阵秩的基本概念与性质 矩 阵
二、利用初等变换求矩阵的秩 三、矩阵秩的不等式
1
§2.6 矩阵的秩 第 一、矩阵秩的基本概念与性质 二 对于线性方程组的求解问题,除了需要研究其求解方法 章 之外,更重要的是要弄清楚一个给定的线性方程组中到底有 矩 阵
r ( A) r ( I A) r ( A ( I A)) n r ( A A2 ) n n , r ( A) r ( I A) n .
20
§2.6 矩阵的秩 第 二 章 矩 阵
轻松一下吧 ……
21
§2.6 矩阵的秩 第 三、矩阵秩的不等式 二 1. 关于矩阵乘积的秩的不等式 章 2. 关于矩阵求和的秩的不等式 矩 *证明 阵
定理3 r ( A B) r ( A) r ( B) . (略)
18
§2.6 矩阵的秩 第 小结 二 1. 矩阵秩的概念 章 矩 阵
2. 求矩阵秩的方法
(1) 利用定义; (2) 初等变换法。 3. 矩阵秩的不等式
故 r ( A) 2, r ( B) 3 .
11
§2.6 矩阵的秩 第 三、矩阵秩的不等式 二 1. 关于矩阵乘积的秩的不等式 章 定理1 r ( A B) min(r ( A) , r ( B)) . 矩 阵
证明 (1) 设 A 的秩为 r(A) = s, 则存在可逆矩阵 P,使得
A1 } s 行 1 A1 P A , A P , 0 0 1 A1 B 1 A1 AB P B P , 0 0
A 的秩,记作 r ( A )。
换句话说,矩阵 A 的秩 r ( A ) 是 A 中不等于零的 子式的最高阶数。 注 (1) 规定零矩阵的秩等于零。
二、利用初等变换求矩阵的秩 三、矩阵秩的不等式
1
§2.6 矩阵的秩 第 一、矩阵秩的基本概念与性质 二 对于线性方程组的求解问题,除了需要研究其求解方法 章 之外,更重要的是要弄清楚一个给定的线性方程组中到底有 矩 阵
r ( A) r ( I A) r ( A ( I A)) n r ( A A2 ) n n , r ( A) r ( I A) n .
20
§2.6 矩阵的秩 第 二 章 矩 阵
轻松一下吧 ……
21
§2.6 矩阵的秩 第 三、矩阵秩的不等式 二 1. 关于矩阵乘积的秩的不等式 章 2. 关于矩阵求和的秩的不等式 矩 *证明 阵
定理3 r ( A B) r ( A) r ( B) . (略)
18
§2.6 矩阵的秩 第 小结 二 1. 矩阵秩的概念 章 矩 阵
2. 求矩阵秩的方法
(1) 利用定义; (2) 初等变换法。 3. 矩阵秩的不等式
故 r ( A) 2, r ( B) 3 .
11
§2.6 矩阵的秩 第 三、矩阵秩的不等式 二 1. 关于矩阵乘积的秩的不等式 章 定理1 r ( A B) min(r ( A) , r ( B)) . 矩 阵
证明 (1) 设 A 的秩为 r(A) = s, 则存在可逆矩阵 P,使得
A1 } s 行 1 A1 P A , A P , 0 0 1 A1 B 1 A1 AB P B P , 0 0
A 的秩,记作 r ( A )。
换句话说,矩阵 A 的秩 r ( A ) 是 A 中不等于零的 子式的最高阶数。 注 (1) 规定零矩阵的秩等于零。
矩阵的秩及其求法ppt课件

2,求,
5 3 6
1 A 3
1
1 1
2 1 2 0
1
3
1 4
2 4
5 3 6 0 8 5 4
1 1 1 2 R( A) 2,
0 3 4 4 0 5 1 0
设
1 A 4
2 6
3 5
1
4
,共有C
2 3
C
2 4
18
Байду номын сангаас1 0 1 1
个二阶子式,有
C
3 4
C 33
4 个三阶子式。
12 3 而 D3 4 6 5 为 A 的一个三阶子式。
1 0 1
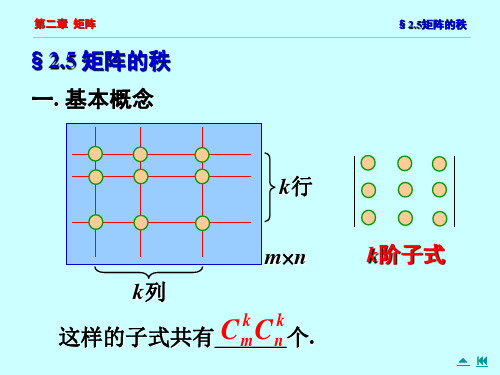
显然, m n 矩阵 A 共有 cmk cnk 个 k 阶子式。
ppt课件
3
2. 矩阵的秩
定义2 设 A
aij
,有r
mn
阶子式不为0,任何r+1阶
子式(如果存在的话)全为0 , 称r为矩阵A的秩,
记作R(A)或秩(A)。
二、矩阵秩的求法
1、子式判别法(定义)。
例1
B
1 0
12 为阶梯形矩阵,求R(B)。
解 由于 1 2 0 ,二阶子式不为0,所以 R(B) = 2. 01
ppt课件
4
例2
1 A 0
2 1
3 0
0 1
求R(A)。
0 0 1 0
解: 1 2 3 0 1 0 1 0 存在一个三阶子式不为0,
001
5
A没有4阶子式,所以 R(A) = 3.
ppt课件
2.6.1----矩阵秩的定义-§2.6-----矩阵的秩

PAQ
Er O
O O
,
将矩阵分块为
Q1B
B1 B2
其中,B1是r ×p 矩阵,B2是(n-r) ×p 矩阵。
由于
PAB
(
PAQ)(Q
1B)
Er O
所以
O
O
B1
B2
B1
O
,
R(AB)
R(PAB)
R
B1 O
R(B1
).
注意B1是Q-1B去掉n-r行得到的矩阵,而矩阵每去掉一行 其秩减 1 或不变,因此
R(B1) ≥R(Q-1B)- (n- r) =R(B) - (n- r) .
从而
R(AB)≥ r +R(B)-n。
即 R(AB)≥ R(A)+R(B)-n。
显然,在上式中当AB=O时,有公式
R(A)+R(B) n.
例5 设A为n阶方阵( n ≥2),A*是A的伴随矩阵,试证
1)当R(A)=n时,R(A*)=n; 2)当R(A)=n-1时,R(A*)=1; 3)当R(A)<n-1时,R(A*)=0。 证明 1)当R(A)=n时,即A为满秩矩阵,所以| A*|=| A|n-1
≠0,从而R(A*)=n。 2)当R(A)=n-1时,|A|=0,所以A A*= |A|E=O。由 R(A)+R(A*) n,
得R(A*) 1。又由R(A)=n-1知, A中至少有一个元素的 代数余子式不等于零,即A*是非零矩阵,从而R(A*) ≥ 1, 故R(A*)=1。
3)当R(A)<n-1时, A的每一个n-1阶子式都为零,因 而A的所有元素的代数余子式均为零,即A*是零矩阵,故 R(A*)=0。
若A为n阶方阵,且R(A)= n,则称A为满秩矩阵。它既 是行满秩矩阵,又是列满秩矩阵。显然,方阵A可逆的充 分必要条件是A为满秩矩阵。
2_6矩阵的秩PPT课件

如 1 2 1 3 0 0 2 2 0 0 0 0
0 1 2 2 3 0 0 1 2 1 0 0 0 0 1
《线性代数》
返回
下页
结束
定理2 任何一个秩为r 的矩阵A=(aij) m╳n都可以通过初等 行变换化为行阶梯形矩阵Br,且Br的非零行数为r. 即
b1 *
0
b2
A 初等行变换 Br
23 1
解法2: 用初等行变换将A化成行阶梯形矩阵,得
1
0
1 2
2
1
1
r3 2r1
0
1 2
2 1
r3 12r2
1 0
1 2
2
1
2 3 1
0 1 3
0 0 5 2
所以r(A)=3,A满秩,故A可逆.
《线性代数》
返回
下页
结束
为方便学习与回顾本课程,请在下
载后进行查阅和编辑,疑问之处请
若|A| = 0,则r(A)<n ,称A为降秩矩阵.
结论:n阶方阵A可逆的充分必要条件是A满秩.
《线性代数》
返回
下页
结束
例1. 求下列矩阵的秩.
1 2 3 2 C 2 4 6 4
3 0 9 6 解: C的最高阶子式三阶子式全部都等于零,即
123 122 132 232 2 4 6 2 4 4 2 6 4 4 6 4 0
规定零矩阵的秩为零. 易见:
(1)若A是m╳n矩阵,则r(A) ≤min{m,n}.
(2)若m╳n矩阵A中有一个r阶子式不等于零 ,则r(A) ≥r; 若所有r+1阶子式全等于零,则r(A) ≤ r.
(3) r(A) = r(AT) . (4) r(kA) = r(A),k≠0 . (5) 对n阶方阵A,若|A|≠0,则r(A)=n ,称A为满秩矩阵 ;
线代课件-矩阵的秩

6
4 1
4 0
0
0
0
0
行階梯形矩陣有 3 個非零行,故R(A) = 3 .
第二步求 A 的最高階非零子式.選取行階梯形矩陣中非零行
的第一個非零元,所與在之的對列應的是選取矩陣 A 的第一、
二、四列. 3 2 5 1 6 1
A0
3 2
2 0
6
r
~
0
4
5 0 0
1 4
B0
1
6
1
§2.6 矩陣的秩
一、矩陣的秩的概念
定義:在 m×n 矩陣 A 中,任取 k 行 k 列( k ≤ m,k≤n), 位於這些行列交叉處的 k2 個元素,不改變它們在 A中所處 的位置次序而得的 k 階行列式,稱為矩陣 A 的 k 階子式.
顯然,m×n 矩陣
A的
k
階子式共有
C
k m
C
k n
個.
概念辨析: k 階子式、矩陣的子塊、餘子式、代數餘子式
1 2 2 1 1
例:設
A
2
4
8
0
,
b
2
,求矩陣
A
及矩陣
2 4 2 3 3
3
6
0
6
4
B = (A, b) 的秩.
分析:對 B 作初等行變換變為行階梯形矩陣,設 B 的行階梯 形矩陣為B ( A, b),則 A 就是 A 的行階梯形矩陣,因此可從 中同時看出R(A)及 R(B) .
1 2 2 1 1 1 2 2 1 1
解:B
2
4
பைடு நூலகம்
8
0
2
r
~
0
0
2
矩阵的秩教学课件

当A=O时,规定R(A)=0 即:若矩阵 A 中有一个 s 阶子式不为 0,则 R(A) s;若 A 中所有 t 阶子式全为 0,则R(A) < t.
练习:P55 29、30
例 1 求矩阵 A 的秩 R(A) ,其中 3 2 1 1
A = 1 2 3 2 4 4 2 3
解: 按定义,存在不为零的二阶子式:
123
例如,已知A= 0 1 0 1 ,因为 0 1 0 =10,
0010
001
所以R(A)=3.
12 又如 B= 0 1
00
110 R(B)=2; C= 0 1 0
001
R(C)=3.
矩阵的秩: 定义2 设A为mn矩阵,如果A中不为零的子式最高
阶数为r,即存在r阶子式不为零,而任何r+1阶子式皆为 零,则=r
从例 1 可知, 对于一般的矩阵, 当行数与列数 较高时, 按定义求秩的计算量很大.
然而对于行阶梯形矩阵, 它的秩就等于非零行 的行数.
并且每个矩阵都能用行初等变换化为行阶梯
形矩阵. 问题是,初等变换是否改变矩阵的秩呢?
于是我们有下面的定理:
定理 1 矩阵 A 经初等变换后,其秩不变.
证明: 设R(A) = r,对其实施有限次的初等
1 0
3 2
一、矩阵的秩
k 阶子式: 定义1 设A是mn矩阵,从A中任取k行k列(kmin(m, n)),
位于这些行和列的相交处的元素,保持它们原来的相对位置 所构成的k阶行列式,称为矩阵A的一个k阶子式.
2123 例如,已知矩阵 A= 4 1 3 5 .
2012 223
选定第1、2、3行及第1、3、4列,得3阶子式 4 3 5 . 212
3 2 0
练习:P55 29、30
例 1 求矩阵 A 的秩 R(A) ,其中 3 2 1 1
A = 1 2 3 2 4 4 2 3
解: 按定义,存在不为零的二阶子式:
123
例如,已知A= 0 1 0 1 ,因为 0 1 0 =10,
0010
001
所以R(A)=3.
12 又如 B= 0 1
00
110 R(B)=2; C= 0 1 0
001
R(C)=3.
矩阵的秩: 定义2 设A为mn矩阵,如果A中不为零的子式最高
阶数为r,即存在r阶子式不为零,而任何r+1阶子式皆为 零,则=r
从例 1 可知, 对于一般的矩阵, 当行数与列数 较高时, 按定义求秩的计算量很大.
然而对于行阶梯形矩阵, 它的秩就等于非零行 的行数.
并且每个矩阵都能用行初等变换化为行阶梯
形矩阵. 问题是,初等变换是否改变矩阵的秩呢?
于是我们有下面的定理:
定理 1 矩阵 A 经初等变换后,其秩不变.
证明: 设R(A) = r,对其实施有限次的初等
1 0
3 2
一、矩阵的秩
k 阶子式: 定义1 设A是mn矩阵,从A中任取k行k列(kmin(m, n)),
位于这些行和列的相交处的元素,保持它们原来的相对位置 所构成的k阶行列式,称为矩阵A的一个k阶子式.
2123 例如,已知矩阵 A= 4 1 3 5 .
2012 223
选定第1、2、3行及第1、3、4列,得3阶子式 4 3 5 . 212
3 2 0
线性代数课件--06 矩阵的秩 -PPT精选文档

由于 n阶矩阵 的 n阶子式只有一个 ,当
时,R(A)n.所以可逆矩阵的秩等于矩阵
的阶数,可逆矩阵又称满秩矩阵,不可逆矩阵又 称降秩矩阵.
8
A 0
四、矩阵的秩的计算
定理3 若 A~B,则 R(A)R(B).
即两个等价矩阵的秩相等. 证明 说明 根据此定理,为求矩阵的秩,只要把矩阵用 初等行变换变成行阶梯形矩阵,行阶梯形矩 阵中非零行的行数即是矩阵的秩.
用初等变换把矩阵
A
2 3
4 6
5 4
3 2
化为标准形.
4 8 17 11
矩 阵
解 2
A3 4
4 6 8
5 3
1
4 17
2 11
r1 2 r1 r2
3 4
2 6 8
6 4 17
4 2 11
的 秩
r2 3r1 1
当矩阵A中有某个 s阶子式不为0,则 R(A)s; 当矩阵A中所有 t阶子式都为0,则 R(A)t;
7
A
A
矩阵的秩等于行阶梯形矩阵的非零行数,这也 可以作为矩阵的秩定义,但是这样定义矩阵的秩 不能清楚表明矩阵的特征.
对于 n阶矩阵 A,当R(A)n时, A称为满秩
矩阵;否则称为降秩矩阵.
r3
4r1
0 0
2 0 0
6 14 7
4 10 5
r2 (114) r3 7r2
1 0 0
2 0 0
6 1 0
4
5 7
0
r1 6r2
1 0
0
2 0 0
0 1 0
2 7
时,R(A)n.所以可逆矩阵的秩等于矩阵
的阶数,可逆矩阵又称满秩矩阵,不可逆矩阵又 称降秩矩阵.
8
A 0
四、矩阵的秩的计算
定理3 若 A~B,则 R(A)R(B).
即两个等价矩阵的秩相等. 证明 说明 根据此定理,为求矩阵的秩,只要把矩阵用 初等行变换变成行阶梯形矩阵,行阶梯形矩 阵中非零行的行数即是矩阵的秩.
用初等变换把矩阵
A
2 3
4 6
5 4
3 2
化为标准形.
4 8 17 11
矩 阵
解 2
A3 4
4 6 8
5 3
1
4 17
2 11
r1 2 r1 r2
3 4
2 6 8
6 4 17
4 2 11
的 秩
r2 3r1 1
当矩阵A中有某个 s阶子式不为0,则 R(A)s; 当矩阵A中所有 t阶子式都为0,则 R(A)t;
7
A
A
矩阵的秩等于行阶梯形矩阵的非零行数,这也 可以作为矩阵的秩定义,但是这样定义矩阵的秩 不能清楚表明矩阵的特征.
对于 n阶矩阵 A,当R(A)n时, A称为满秩
矩阵;否则称为降秩矩阵.
r3
4r1
0 0
2 0 0
6 14 7
4 10 5
r2 (114) r3 7r2
1 0 0
2 0 0
6 1 0
4
5 7
0
r1 6r2
1 0
0
2 0 0
0 1 0
2 7
