2019年数学中考真题知识点汇编21 几何图形初步(含解析).docx
2019最新山西中考数学考试试题及知识点解析

2019年山西省初中学业水平考试数学(满分120分,考试时间120分钟)一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个均计零分1.(2019山西,1题,3分) -3的绝对值是( )A.-3B.3C.13D.13【答案】B【解析】负数的绝对值是它的相反数,∴|-3|=3,故选B.【知识点】绝对值2.(2019山西,2题,3分)下列运算正确的是( )A.2a+3a=5a2B.(a+2b)2=a2+4b2C.a2·a3=a6D.(-ab2)3=-a3b6【答案】D【解析】A.2a+3a=5a,故A错误;B.(a+2b)2=a2+2ab+4b2,故B错误;C.a2·a3=a5,故C错误;D.(-ab2)3=-a3b6,正确,故选D.【知识点】合并同类项,同底数幂的乘法,积的乘方,幂的乘方,完全平方公式3.(2019山西,3题,3分)某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与"点"字所在面相对的面上的汉字是( )A.青B.春C.梦D.想第3题图【答案】B【解析】根据正方体的展开与折叠中面的关系,可知与"点"字所在面相对的面上的汉字是春,故选B.【知识点】展开与折叠4.(2019山西,4题,3分)下列二次根式是最简二次根式的是( )【答案】D【解析】最简二次根式的根号内不能含有分母,不能含有可开的尽方的因数,故选D.【知识点】最简二次根式5.(2019山西,5题,3分) 如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )A.30°B.35°C.40°D.45°第5题图【答案】C【解析】△ABC中,AB=AC,∠A=30°,∴∠B=75°,∵∠1=145°,∴∠FDB=35°过点B作BG∥a∥b,∴∠FDB=∠DBG,∠2=∠CBG,∵∠B=∠ABG+∠CBG,∴∠2=40°,故选C第5题答图【知识点】等腰三角形,三角形内角和,平行线的性质6.(2019山西,6题,3分)不等式组13224xx->⎧⎨-<⎩的解集是( )A.x>4B.x>-1C.-1<x<4D.x<-1【答案】A【解析】解不等式①得x>4,解不等式②得x>-1,∴原不等式组的解集是x>4,故选A.【知识点】解不等式组7.(2019山西,7题,3分)五台山景区空气清爽,景色宜人."五一"小长假期间购票进山游客12万人次,再创历史新高.五台山景区门票价格旺季168元/人.以此计算,"五一"小长假期间五台山景区进山门票总收入用科学记数法表示为( )A.2.016×108元B.0.2016×107元C.2.016×107元D.2016×104元【答案】C【解析】120000×168=20160000=2.016×107,故选C【知识点】科学记数法8.(2019山西,8题,3分)一元二次方程x2-4x-1=0配方后可化为( )A.(x+2)2=3B.(x+2)2=5C.(x-2)2=3D.(x-2)2=5【答案】D【解析】原方程可化为:x2-4x=1,x2-4x+4=1+4,(x-2)2=5,故选D.【知识点】配方法9.(2019山西,9题,3分)北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊杆,拉索与主梁相连.最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象——抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米,(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系,则次抛物线型钢拱的函数表达式为( )A.y =26675x 2 B.y =26675-x 2 C.y =131350x 2 D.y =131350-x 2第9题图 【答案】B【解析】设二次函数表达式为y =ax 2,由题可知,点A 坐标为(-45,-78),代入表达式可得:-78=a(-45)2,解得a =26675-,∴二次函数表达式为y =26675-x 2,故选B. 【知识点】二次函数的应用10.(2019山西,10题,3分)如图,在Rt △ABC 中,∠ABC =90°,AB ==2,以AB 的中点O 为圆心,OA 的长为半径作半圆交AC 于点D,则图中阴影部分的面积为( )2π- 2πC.πD.2π第10题图【答案】A【思路分析】根据三角形的边的关系求出角度,在圆中求出扇形圆心角,阴影部分就是△ABC 的面积减去△AOD的面积和扇形BOD 的面积,分别算出各图形的面积,即可得到结果.【解题过程】在Rt △ABC 中,连接OD,∠ABC =90°,AB ==2,∴∠A =30°,∠DOB =60°,过点D 作DE⊥AB 于点E,∵AB =∴AO =OD ∴DE =32,∴S 阴影=S △ABC -S △AOD -S扇形BOD =-2π=2π-,故选A.第10题答图【知识点】三角函数,三角形面积,扇形面积二、填空题:本大题共5小题,满分15分,只填写最后结果,每小题填对得3分.11.(2019山西,11题,3分)化简211x xx x---的结果是________.【答案】31 x x-【解析】2231111 x x x x x x x x x+-==----【知识点】分式化简12.(2019山西,12题,3分)要表示一个家庭一年用于"教育","服装","食品","其他"这四项的支出各占家庭本年总支出的百分比,从"扇形统计图","条形统计图","折线统计图"中选择一种统计图,最适合的统计图是________.【答案】扇形统计图【解析】∵要表示四项支出各占家庭本年总支出的百分比,∴用扇形统计图最适合.【知识点】统计图的选择13.(2019山西,13题,3分)如图,在一块长12m,宽8m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,且栽种花草的面积为77m2,设道路的宽为x m,则根据题意,可列方程为________.第13题图【答案】(12-x)(8-x)=77【解析】栽种花草的部分可以看成一个矩形,长为(12-x)m,宽为(8-x)m,根据面积等量关系可列方程(12-x)(8-x)=77.【知识点】一元二次方程的应用14.(2019山西,14题,3分)如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A的坐标为(-4,0),点D的坐标为(-1,4),反比例函数y=kx(x>0)的图象恰好经过点C,则k的值为________.第14题图【答案】16【解析】分别过点D,C作x轴的垂线,垂足为E,F,则AD=5,∴AB=CB=5,∴B(1,0),由△DAE≌△CBF,可得BF=AE=3,CF=DE=4,∴C(4,4),∴k=xy=16.第14题答图【知识点】菱形性质,勾股定理,反比例函数15.(2019山西,15题,3分)如图,在△ABC 中,∠BAC =90°,AB =AC =10cm,点D 为△ABC 内一点,∠BAD =15°,AD =6cm,连接BD,将△ABD 绕点A 按逆时针方向旋转,使AB 与AC 重合,点D 的对应点为点E,连接DE,DE 交AC 于点F,则CF 的长为________cm.第15题图 【答案】10-26【思路分析】由旋转得到对应边相等,在△ADF 中,构造直角三角形,利用三角函数,求得AF 的长度,进而求得FC. 【解题过程】∵∠BAC =90°,∠BAD =15°,∴∠DAF =75°由旋转可知,∠ADF =45°,过点A 作AM ⊥DF 于点M,∴AM =22AD =32,∴AF =233AM =26,∵AC =AB =10,∴FC =AC -AF =10-26第15题答图【知识点】图形的旋转,三角函数三、解答题:本大题共8小题,满分75分,要写出必要的文字说明、证明过程或演算步骤.16.(2019山西,16题,5分)(1)计算:()201273tan 6022π-⎛⎫+--+- ⎪⎝⎭(2)解方程组:32820x y x y -=-⎧⎨+=⎩【思路分析】(1)按照实数的运算法则进行计算;(2)运用加减消元法或代入消元法进行解方程. 【解题过程】(1)原式=334331=5+-+; (2)32820x y x y -=-⎧⎨+=⎩①②,①+②,得:3x+x =-8+0,∴4x =-8,x =-2,把x =-2代入②,得-2+2y =0,∴y =1,∴,原M方程组的解为:21 xy=-⎧⎨=⎩.【知识点】二次根式的化简,负指数幂,特殊角的三角函数值,零指数幂,加减消元法解二元一次方程组17.(2019山西,17题,5分)已知,如图,点B,D在线段AE上,AD=BE,AC∥EF,∠C=∠F,求证:BC=DF.第17题图【思路分析】由平行得到角相等,再处理条件AD=BE,得到全等三角形,进而得到BC=DF.【解题过程】∵AD=BE,∴AD-BD=BE-BD,∴AB=DE,∵AC∥EF,∴∠A=∠E,在△ABC和△EDF中,∠C=∠F,∠A=∠E,AB=ED,∴△ABC≌△EDF,∴BC=DF.【知识点】平行线的性质,三角形全等18.(2019山西,18题,8分)中华人民共和国第二届青年运动会(简称二青会)将于2019年8月在山西举行.太原市作为主赛区,将承担多项赛事.现正从某高校的甲,乙两班分别招募10人作为颁奖礼仪志愿者,同学们勇跃报名,甲,乙两班各报了20人,现已对他们进行了基本素质测评,满分10分,各班按测评成绩从高分到低分的顺序各录用10人.对这次基本素质测评中甲,乙两班学生的成绩绘制了如图所示的统计图.请解答下列问题:(1)甲班的小华和乙班的小丽基本素质测评成绩都为7分,请你分别判断小华,小丽能否被用(只写判断结果,不必写理由).(2)请你对甲,乙两班各被录用的10名志愿者的成票作出评价(从"众数","中位数"或"平均数"中的一个方面评价即可).(3)甲乙两班被录用的每一位志愿者都将通过抽取卡片的方式决定去以下四个场馆中的两个场馆进行频奖礼仪服务,四个场馆分别为:太原学院足球场,太原市沙滩排球场,山西省射击射箭训练基地,太原水上运动中心,这四个场馆分别用字母A,B,C,D表示.现把分别印有A,B,C,D的四张卡片(除字母外,其余都相同)背面朝上,洗匀放好,志愿者小玲从中随机抽取一张(不放回),再从中随机抽取一张.请你用列表或画树状图的方法求小玲抽到的两张卡片恰好是"A"和"B"的概率.第18题图【思路分析】(1)观察统计图,可判断两人是否在前10名,即可做出判断;(2)根据"众数","中位数"和"平均数"的特点,进行评价;(3)列表列举出所有的结果,计算概率即可.【解题过程】(1)小华:不能被录用,小丽:能被录用.(2)从众数来看:甲,乙两班各被录用的10名志愿者成绩的众数分别为8分,10分,说明甲班被录用的10名志愿者中8分最多,乙班被录用的10名志愿者中10分最多.从中位数来看:甲,乙两班各被录用的10名志愿者成绩的中位数分别为9分,8.5分,说明甲班被录用的10名志愿者成绩的中位数大于乙班被录用的10名志愿者成绩的中位数.从平均数来看:甲,乙两班各被录用的10名志愿者成绩的平均数分别为8.9分,8.7分,说明甲班被录用的10名志愿者成绩的平均数大于乙班被录用的10名志愿者成绩的平均数.由列表可知,一共有12种可能出现的结果,且每种结果出现的可能性相同,其中,抽到"A"和"B"的结果有2种,∴,P(抽到"A"和"B")=21= 126【知识点】众数,中位数,平均数,列表法,求概率19.(2019山西,19题,8分)某游泳馆推出了两种收费方式.方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年使用,凭卡游泳,每次游泳再付费30元.方式二:顾客不购买会员卡,每次游泳付费40元.设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).(1)请分别写出y1,y2与x之间的函数表达式.(2)小亮一年内在此游泳馆游泳的次数x在什么范围时,选择方式一比方式二省钱.【思路分析】(1)根据两种方式的描述即可得到表达式;(2)令y1<y2,即可解得x的范围.【解题过程】(1)y1=30x+200,y2=40x(2)由y1<y2,得30x+300<40x,解之,得x>20,当x>20时,选择方式一比方式二省钱.【知识点】一次函数的应用20.(2019山西,20题,8分)某"综合与实践"小组开展了测量本校旗杆高度的实践活动.他们制定了测量方案,并利用课余时间完成了实地测量.他们在该旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取他们的平均值作为测量结果,测量数据如下表(不完整).任务一:两次测量A,B之间的距离的平均值是______m.任务二:根据以上测量结果,请你帮助该"综合与实践"小组求出学校旗杆GH的高度.(参考数据:sin25.7°≈0.43,cos25.7°≈0.90,tan25.7°≈0.48,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)任务三:该"综合与实践"小组在制定方案时,讨论过"利用物体在阳光下的影子测量旗杆的高度"的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可)【思路分析】任务一:根据平均数的计算方法求值即可;任务二:设出旗杆高度,表示出CE,DE的长度,得到方程,即可解得;任务三:根据实际情况分析原因.【解题过程】任务一:平均值=(5.4+5.6)÷2=5.5m任务二:由题意可得,四边形ACDB,ACEH都是矩形,∴EH=AC=1.5,CD=AB=5.5,设EG=xm,在Rt△DEG中,∠DEG=90°,∠GDE=31°,∵tan31°=EGDE,∴DE=tan31x,在Rt△CEG中,∠CEG=90°,∠GCE=25.7°,∵tan25.7°=EGCE,∴CE=tan25.7x,∵CD=CE-DE,∴tan25.7x-tan31x=5.5,∴x=13.2,∴GH=GE+EH=13.2+1.5=14.7.答:旗杆GH的高度为14.7m.任务三:答案不唯一:没有太阳光,旗杆底部不可到达,测量旗杆影子的长度遇到困难等.【知识点】三角函数的应用21.(2019山西,21题,10分)阅读以下材料,并按要求完成相应的任务:莱昂哈德·欧拉(Leonhard Euler )是瑞士数学家,在数学上经常见到以他的名字命名的重要常数,公式和定理,下面就是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则22=2OI R Rr.如图1, O和 I分别是△ABC的外接圆和内切圆, I与AB相切于点F,设 O的半径为R, I的半径为r,外心O(三角形三边垂直平分线的交点)与内心I(三角形三条角平分线的交点)之间的距离OI=d,则有22=2d R Rr.下面是该定理的证明过程(部分):延长AI交 O于点D,过点I作 O的直径MN,连接DM,AN.∵∠D=∠N,∠DMI=∠NAI(同弧所对的圆周角相等),∴△MDI ∽△ANI.∴IM IDIA IN.∴IA ID IM IN . ① 如图2,在图1(隐去MD,AN )的基础上作 O 的直径DE,连接BE,BD,BI,IF.∵DE 是 O 的直径,∴∠DBE =90°.∵ I 与AB 相切于点F,∴∠AFI =90°,∴∠DBE =∠IFA. ∵∠BAD =∠E (同弧所对的圆周角相等),∴△AIF ∽△EDB. ∴IA IFDE BD.∴IA BD DE IF . ② …… 任务:(1)观察发现:IM =R+r,IN =_____(用含R,d 的代数式表示); (2)请判断BD 和ID 的数量关系,并说明理由;(3)请观察式子①和式子②,并利用任务(1),(2)的结论,按照上面的证明思路,完成该定理证明的剩余部分; (4)应用:若△ABC 的外接圆的半径为5cm,内切圆的半径为2cm,则△ABC 的外心与内心之间的距离为___cm第21题图【思路分析】(1)MN 是直径,根据内切圆与外接圆半径与它的关系得到IN 的代数式(2)由内切圆是三角形三条角平分线的交点,转化相等的角,再利用同弧所对的圆周角相等转化角,最后得到∠BID =∠DBI,利用等角对等边得证(3)由材料得到的结论及任务(1)(2)等量代换得线段等积式,从而得证结论(4)根据结论直接应用求解. 【解题过程】(1)IN =R -d;(2)BD =ID.理由如下:∵点I 是△ABC 的内心,∴∠BAD =∠CAD,∠CBI =∠ABI,∵∠DBC =∠CAD,∠BID =∠BAD+∠ABI,∠DBI =∠DBC+∠CBI,∴∠BID =∠DBI,∴BD =ID; (3)由(2)知:BD =ID,∴IA IDDE IF ,又∵IA ID IM IN ,∴DE IFIM IN ,∴2R r R d R d ,∴222R d Rr ,∴222d R Rr ;(4)由222d R Rr 得222252525d R Rr ,∵d>0,∴5d .【知识点】三角形的内心,圆的对称性,等角对等边22.(2019山西,22题,8分)综合与实践 动手操作:第一步:如图1,正方形纸片ABCD 沿对角线AC 所在的直线折叠,展开铺平,再沿过点C 的直线折叠,使点B,点D 都落在对角线AC 上.此时,点B 与点D 重合,记为点N,且点E,点N,点F 三点在同一条直线上,折痕分别为CE,CF.如图2.第二步:再沿AC 所在的直线折叠,△ACE 与△ACF 重合,得到图3.第三步:在图3的基础上继续折叠,使点C 与点F 重合,得到图4,展开铺平,连接EF,FG,GM,ME,如图5.图中的虚线为折痕.第22题图 问题解决:(1)在图5中,∠BEC 的度数是_____,AEBE的值是_____; (2)在图5中,请判断四边形EMGF 的形状,并说明理由;(3)在不增加字母的条件下,请你以图5中的字母表示的点为顶点,动手画出....一个菱形(正方形除外),并写出这个菱形:_______.【思路分析】(1)通过折叠转化角相等,进而利用内角和求∠BEC 的度数,再利用45°三角函数解决线段的比值问题(2)根据第1问的提示,可以通过折叠求角的度数,进而得到四边形各内角的度数为90°,利用三个内角为90°的四边形是矩形进而可以判定四边形的形状是矩形(3)利用多次折叠可以得到很多相等的线段以及互相垂直的线段,可以利用四边相等的四边形是菱形或对角线互相垂直平分的四边形是菱形来得到符合条件的菱形.【解题过程】(1)∵正方形ABCD,∴∠ACB =45°,由折叠知:∠1=∠2=22.5°,∠BEC =∠CEN,BE =EN,∴∠BEC =90°-∠1=67.5°,∴∠AEN =180°-∠BEC -∠CEN =45°,∴cos45°=2EN AE ,2AE EN,2AE AE BE EN;(2)四边形EMGF 是矩形.理由如下:∵四边形ABCD 是正方形,∴∠B =∠BCD =∠D =90°,由折叠可知:∠1=∠2=∠3=∠4,CM =CG,∠BEC =∠NEC =∠NFC =∠DFC,∴∠1=∠2=∠3=∠4=°904=22.5°,∴∠BEC =∠NEC =∠NFC =∠DFC =67.5°,由折叠知:MH,GH 分别垂直平分EC,FC,∴MC =ME,GC =GF.∴∠5=∠1=22.5°,∠6=∠4=22.5°,∴∠MEF =∠GFE =90°.∵∠MCG =90°,CM =CG,∴∠CMG =45°,又∵∠BME =∠1+∠5=45°,∴∠EMG =180°-∠CMG -∠BME =90°,∴四边形EMGF 是矩形; (3)答案不唯一,画出正确的图形(一个即可).菱形FGCH (或菱形EMCH )第22题答图【知识点】折叠,三角形内角和,三角函数,矩形,菱形23.(2019山西,23题,8分)综合与探究如图,抛物线y =ax 2+bx+6经过点A (-2,0),B(4,0)两点,与y 轴交于点C.点D 是抛物线上一个动点,设点D 的横坐标为m(1<m<4).连接AC,BC,DB,DC. (1)求抛物线的函数表达式;(2)当△BCD 的面积等于△AOC 的面积的34时,求m 的值; (3)在(2)的条件下,若点M 是x 轴上一动点,点N 是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N 为顶点的四边形是平行四边形.若存在,请直接写出点M 的坐标;若不存在,请说明理由.第23题图【思路分析】(1)将点A,B 的坐标代入表达式可得;(2)计算△AOC 的面积,用含m 的代数式表示出△BCD 的面积,得到方程,解得m 的值;(3)以BD 为边或对角线,通过解方程得到点M 的坐标.【解题过程】(1)∵抛物线y =ax 2+bx+6经过点A (-2,0),B(4,0)两点,∴426016460a b a b -+=⎧⎨++=⎩,解之,得:3432a b ⎧=-⎪⎪⎨⎪=⎪⎩,∴抛物线的函数表达式为:233642y x x =-++; (2)作直线DE ⊥x 轴于点E,交BC 于点G,作CF ⊥DE,垂足为点F,∵点A 的坐标为(-2,0),∴OA =2,由x =0,得y =6,∴点C 的坐标为(0,6),∴OC =6,∴S △AOC =12OA ·OC =6,∴S △BCD =34S △AOC =92.设直线BC 的函数表达式为y =kx+n,由B,C 两点的坐标得:406k n n +=⎧⎨=⎩,解之,得:326k n ⎧=-⎪⎨⎪=⎩,∴直线BC 的函数表达式为:y =-32x+6.∴点G 的坐标为(m,-32m+6),∴DG =233642m m -++-(-32m +6)=2334m m -+.∵点B 的坐标为(4,0),∴OB =4,∴S △BCD =S △CDG +S △BDG =2364m m -+.∴2364m m -+=92,解之,得m 1=3,m 2=1,∴m 的值为3.第23题答图(3)存在点M,其坐标为:M 1(8,0),M 2(0,0),M 34(【知识点】二次函数表达式,三角形面积,坐标运算,平行四边形的存在性。
2019中考数学知识点总结

考点一、实数的概念及分类 (3 分)1、实数的分类2、无理数在理解无理数时,要抓住“无限不循环”这一时之,归纳起来有四类:1)开方开不尽的数,如 7,32 等;( 2)有特定意义的数,如圆周率 π,或化简后含有 π的数,如 π+8 等;3( 3)有特定结构的数,如 0.1010010001 ⋯等;( 4)某些三角函数,如 sin60o等 考点二、实数的倒数、相反数和绝对值 (3 分)1、相反数实数与它的相反数时一对数(只有符号不同的两个数叫做互为相反数,零的相反数是零) ,从数轴上看,互为相反数的两个数所对应的点关于原点对称,如 果 a 与 b 互为相反数,则有 a+b=0, a=— b ,反之亦成立。
2、绝对值一个数的绝对值就是表示这个数的点与原点的距离, |a|≥0。
零的绝对值时它本身,也可看成它的相反数,若 |a|=a ,则 a ≥0;若 |a|=-a ,则 a ≤0。
正数大于零,负数小于零,正数大于一切负数,两个负数,绝对值大的反而小。
3、倒数如果 a 与 b 互为倒数,则有 ab=1,反之亦成立。
倒数等于本身的数是 1 和-1。
零没有倒数。
考点三、平方根、算数平方根和立方根 (3—10 分)1、平方根如果一个数的平方等于 a ,那么这个数就叫做 a 的平方根(或二次方跟) 。
第 1 页 共 68 页 1第一章 实数实数 有理数零负有理数正无理数无理数负无理数正有理数有限小数和无限循环小数无限不循环小数一个数有两个平方根,他们互为相反数;零的平方根是零;负数没有平方根。
正数a的平方根记做“ a ”。
2、算术平方根正数a的正的平方根叫做a的算术平方根,记作“ a ”。
正数和零的算术平方根都只有一个,零的算术平方根是零。
a(a 0) a 0a2 a;注意a 的双重非负性:-a(a<0) a 03、立方根如果一个数的立方等于a,那么这个数就叫做a 的立方根(或a 的三次方根)。
一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零。
第一部分基础考过关-专题13几何图形初步-备战2024年中考数学真题解密(全国通用)(含解析)

专题13几何图形初步目录一览知识目标(新课程标准提炼)中考解密(分析考察方向,精准把握重难点)重点考向(以真题为例,探究中考命题方向)►考向一认识立体图形►考向二几何体的展开与折叠►考向三有关角的计算问题►考向四余角、补角与对顶角、邻补角►考向五平行线的性质与判定最新真题荟萃(精选最新典型真题,强化知识运用,优化解题技巧)1. 掌握五个基本事实;2. 会比较线段的长短,理解线段的和、差,以及线段中点的意义;3. 理解角的概念,能比较角的大小.认识度、分、秒,会对度、分、秒进行简单的换算,并会计算角的和、差;4. 理解对顶角、余角、补角等概念,探索并掌握对顶角相等、同角(等角)的余角相等、同角(等角)的补角相等的性质;识别同位角、内错角、同旁内角;5. 理解垂线、垂线段的概念,能用三角尺或量角器过一点画已知直线的垂线;6. 理解平行线的概念;掌握平行线的性质定理;探索并证明平行线的判定定理和性质定理;7. 了解平行于同一条直线的两条直线平行;8. 通过具体实例,了解定义、命题、定理、推论的意义.结合具体实例,会区分命题的条件和结论,了解原命题及其逆命题的概念.会识别两个互逆的命题,知道原命题成立其逆命题不一定成立;9. 了解反例的作用,知道利用反例可以判断一个命题是错误的.通过实例体会反证法的含义.该版块内容是初中几何的基础,是非常基础也是非常重要的,年年都会考查,分值为8分左右,预计2023年各地中考还将出现,大部分地区在选填题中考察可能性较大,主要考察平行线的性质和判定、方位角、角度的大小等知识,这些知识点考查较容易,另外平行线的性质可能在综合题中出现,考查学生能力,比如:作平行的辅助线,构造特殊四边形,此类题目有一定难度,需要学生灵活掌握.►考向一 认识立体图形(2023•乐山)1.下面几何体中,是圆柱的是( )A .B .C .D . (2023•娄底)2.一个长方体物体的一顶点所在A 、B 、C 三个面的面积比是3:2:1,如果分别按A 、B 、C 面朝上将此物体放在水平地面上,地面所受的压力产生的压强分别为A P 、B P 、C P (压强的计算公式为F P S =),则::A B C P P P =( )A .2:3:6B .6:3:2C .1:2:3D .3:2:1(2023•巴中)3.下列图形中为圆柱的是( )A . B . C . D .►考向二 几何体的展开与折叠(2023•达州)4.下列图形中,是长方体表面展开图的是()A.B.C.D.(2023•威海)5.如图是一正方体的表面展开图.将其折叠成正方体后,与顶点K距离最远的顶点是( )A.A点B.B点C.C点D.D点(2023•青岛)6.一个不透明小立方块的六个面上分别标有数字1,2,3,4,5,6,其展开图如图①所示.在一张不透明的桌子上,按图②方式将三个这样的小立方块搭成一个几何体,则该几何体能看得到的面上数字之和最小是( )A.31B.32C.33D.34►考向三有关角的计算问题(2022•烟台)7.如图,某海域中有A ,B ,C 三个小岛,其中A 在B 的南偏西40°方向,C 在B 的南偏东35°方向,且B ,C 到A 的距离相等,则小岛C 相对于小岛A 的方向是( )A .北偏东70°B .北偏东75°C .南偏西70°D .南偏西20°(2022•湘潭)8.如图,一束光沿CD 方向,先后经过平面镜OB 、OA 反射后,沿EF 方向射出,已知120AOB ∠=︒,20CDB ∠=︒,则∠=AEF .(2019•烟台)9.小明将一张正方形纸片按如图所示顺序折叠成纸飞机,当机翼展开在同一平面时(机翼间无缝隙),AOB ∠的度数是 .►考向四 余角、补角与对顶角、邻补角解题技巧/易错易混1.识别对顶角时,要抓住两个关键要素:一是顶点,二是边.先看两个角是否有公共顶点,再看两个角的两边是否分别互为反向延长线.两条直线相交形成两对对顶角.2.互为邻补角的两个角一定互补,但互补的两个角不一定是邻补角;一个角的邻补角有两个,但一个角的补角可以有很多个(2023•北京)10.如图,90AOC BOD ∠=∠=︒,126AOD ∠=︒,则BOC ∠的大小为( )A .36︒B .44︒C .54︒D .63︒(2023•河南)11.如图,直线AB ,CD 相交于点O ,若180∠=︒,230∠=︒,则AOE ∠的度数为( )A .30︒B .50︒C .60︒D .80︒(2022•桂林)12.如图,直线l 1,l 2相交于点O ,∠1=70°,则∠2= °.►考向五 平行线的性质与判定(2023•绵阳)13.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,1122,2∠=︒∠的度数为( )A .32︒B .58︒C .68︒D .78︒(2023•重庆)14.如图,,⊥∥AB CD AD AC ,若155∠=︒,则2∠的度数为( )A .35︒B .45︒C .50︒D .55︒(2023•金华)15.如图,已知12350∠=∠=∠=︒,则4∠的度数是( )A .120︒B .125︒C .130︒D .135︒(2022•自贡)16.如图,直线,AB CD 相交于点O ,若130∠= ,则2∠的度数是( )A .30°B .40°C .60°D .150°(2022•河北)17.①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )A .①③B .②③C .③④D .①④(2023•临沂)18.下图中用量角器测得ABC ∠的度数是( )A .50︒B .80︒C .130︒D .150︒(2023•河北)19.淇淇一家要到革命圣地西柏坡参观.如图,西柏坡位于淇淇家南偏西70︒的方向,则淇淇家位于西柏坡的( )A .南偏西70︒方向B .南偏东20︒方向C .北偏西20︒方向D .北偏东70︒方向(2022•甘肃)20.若40A ∠=︒,则A ∠的余角的大小是( )A .50°B .60°C .140°D .160°(2023•金昌)21.如图1,汉代初期的《淮南万毕术》是中国古代有关物理、化学的重要文献,书中记载了我国古代学者在科学领域做过的一些探索及成就.其中所记载的“取大镜高悬,置水盆于其下,则见四邻矣”,是古人利用光的反射定律改变光路的方法,即“反射光线与入射光线、法线在同一平面上;反射光线和入射光线位于法线的两侧;反射角等于入射角”.为了探清一口深井的底部情况,运用此原理,如图在井口放置一面平面镜可改变光路,当太阳光线AB 与地面CD 所成夹角50ABC ∠=︒时,要使太阳光线经反射后刚好垂直于地面射入深井底部,则需要调整平面镜EF 与地面的夹角EBC ∠=( )A .60︒B .70︒C .80︒D .85︒(2023•临沂)22.在同一平面内,过直线l 外一点P 作l 的垂线m ,再过P 作m 的垂线n ,则直线l 与n 的位置关系是( )A .相交B .相交且垂直C .平行D .不能确定(2022•泸州)23.如图,直线a b ,直线c 分别交a ,b 于点A ,C ,点B 在直线b 上,AB AC ⊥,若1130∠=︒,则2∠的度数是( )A .30︒B .40︒C .50︒D .70︒(2022•贺州)24.如图,直线a ,b 被直线c 所截,下列各组角是同位角的是( )A .1∠与2∠B .1∠与3∠C .2∠与3∠D .3∠与4∠(2022•台州)25.如图,已知190∠=︒,为保证两条铁轨平行,添加的下列条件中,正确的是( )A .290∠=︒B .390∠=︒C .490∠=︒D .590∠=︒(2022•吉林)26.如图,如果12∠=∠,那么AB CD ∥,其依据可以简单说成( )A .两直线平行,内错角相等B .内错角相等,两直线平行C .两直线平行,同位角相等D .同位角相等,两直线平行(2021•铜仁市)27.直线AB 、BC 、CD 、EG 如图所示,1280∠=∠=︒,340∠=︒,则下列结论错误的是( )A .//AB CDB .40EBF ∠=︒C .32FCG ∠+∠=∠D .EF BE>(2023•内蒙古)28.将一副直角三角板按如图所示的方式摆放,点C 在FD 的延长线上,且AB FC ,则CBD ∠的度数为( )A .10︒B .15︒C .20︒D .25︒(2023•荆州)29.如图所示的“箭头”图形中,AB CD ∥,80B D ∠=∠= ,47E F ∠=∠= ,则图中G ∠的度数是( )A .80B .76C .66D .56(2023•常州)30.若圆柱的底面半径和高均为a ,则它的体积是 (用含a 的代数式表示).(2023•无锡)31.若直三棱柱的上下底面为正三角形,侧面展开图是边长为6的正方形,则该直三棱柱的表面积为 .(2022•百色)32.如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么∠BAC 的大小为(2022•玉林)33.已知∠α=60°,则∠α的余角等于 度.(2022•连云港)34.已知∠A 的补角是60°,则A ∠= ︒.(2022•西藏)35.如图,依下列步骤尺规作图,并保留作图痕迹:(1)分别以点A,B为圆心,大于12AB的长为半径作弧,两弧相交于E,F两点,作直线EF;(2)以点A为圆心,适当长为半径画弧,分别交AB,AC于点G,H,再分别以点G,H为圆心,大于12GH的长为半径画弧,两弧在∠BAC的内部相交于点O,画射线AO,交直线EF于点M.已知线段AB=6,∠BAC=60°,则点M到射线AC的距离为.(2023•镇江)36.如图,一条公路经两次转弯后,方向未变.第一次的拐角ABC∠是140︒,第二次的拐角BCD∠是°.(2021•兰州)37.将一副三角板如图摆放,则∥,理由是.(2023•台州)38.用一张等宽的纸条折成如图所示的图案,若120∠=︒,则∠2的度数为.(2023•武汉)39.如图,在四边形ABCD 中,,AD BC B D ∠=∠∥,点E 在BA 的延长线上,连接CE .(1)求证:E ECD ∠=∠;(2)若60,∠=︒E CE 平分BCD ∠,直接写出BCE 的形状.(2022•武汉)40.如图,在四边形ABCD 中,AD BC ∥,80B ∠=︒.(1)求BAD ∠的度数;(2)AE 平分BAD ∠交BC 于点E ,50BCD ∠=︒.求证:AE DC ∥.参考答案:1.B【分析】根据圆柱的特征,即可解答.【详解】解:A.是正方体,故不符合题意;B.是圆柱,故符合题意;C.是圆锥,故不符合题意;D.是球体,故不符合题意,故选:B.【点睛】本题考查了认识立体图形,熟练掌握每个几何体的特征是解题的关键.2.A【分析】首先根据长方体的性质,得出相对面的面积相等,再根据物体的压力不变,结合反比例函数的性质进行分析,即可得出答案.【详解】解:∵长方体物体的一顶点所在A、B、C三个面的面积比是3:2:1,∴长方体物体的A、B、C三面所对的与水平地面接触的面积比也为3:2:1,∵FPS=,0F>,且F一定,∴P随S的增大而减小,∴111::::2:3:6321A B CP P P==.故选:A.【点睛】本题考查了反比例函数的性质,解本题的关键在熟练掌握反比例函数的性质.3.B【分析】圆柱是由上下两个平行且大小一样的圆面和一个侧面(曲面)组成的立体图形,直接根据圆柱体的几何特点解答即可.【详解】根据圆柱的特点可知选项B中的图形是圆柱.故选:B.【点睛】此题考查认识立体图形,熟记常见的立体图形的几何特点是解题的关键.4.C【分析】根据长方体有六个面,以及Z字型进行判断即可.【详解】解:A中展开图有7个面,不符合要求;B中展开图无法还原成长方体,不符合要求;C正确,故符合要求;D中展开图有5个面,不符合要求,故选:C.【点睛】本题考查了长方体的展开图.解题的关键在于对知识的熟练掌握.5.D【分析】根据题意画出立体图形,即可求解.【详解】解:折叠之后如图所示,则K与点D的距离最远,故选D.【点睛】本题考查了正方体的展开与折叠,学生需要有一定的空间想象能力.6.B【分析】根据正方体展开图的特征,得出相对面上的数字,再结合正方体摆放方式,得出使该几何体能看得到的面上数字之和最小,则看不见的面数字之和要最大,即可解答.【详解】解:由图①可知:1的相对面是3,2的相对面是4,5的相对面是6,由图2可知:要使该几何体能看得到的面上数字之和最小,则看不见的面数字之和要最大,上面的正方体有一个面被遮住,则这个面数字为6,++++=;能看见的面数字之和为:1234515左下的正方体有3个面被遮住,其中两个为相对面,则这三个面数字分别为4,5,6,++=;能看见的面数字之和为:1236右下的正方体有2个面被遮住,这两个面不是相对面,则这两个面数字为4,6,+++=;能看见的面数字之和为:123511++=,∴能看得到的面上数字之和最小为:1561132故选:B.【点睛】本题主要考查了正方体的相对面,掌握正方体展开图中“相间一行是相对面”,是解题的关键.7.A【分析】根据题意可得∠ABC =75°,AD ∥BE ,AB =AC ,再根据等腰三角形的性质可得∠ABC =∠C =75°,从而求出∠BAC 的度数,然后利用平行线的性质可得∠DAB =∠ABE =40°,从而求出∠DAC 的度数,即可解答.【详解】解:如图:由题意得:∠ABC =∠ABE +∠CBE =40°+35°=75°,AD ∥BE ,AB =AC ,∴∠ABC =∠C =75°,∴∠BAC =180°﹣∠ABC ﹣∠C =30°,∵AD ∥BE ,∴∠DAB =∠ABE =40°,∴∠DAC =∠DAB +∠BAC =40°+30°=70°,∴小岛C 相对于小岛A 的方向是北偏东70°,故选:A ..【点睛】本题考查了方向角,等腰三角形的性质,熟练掌握等腰三角形的性质是解题的关键.8.40°##40度【分析】根据入射角等于反射角,可得,CDB EDO DEO AEF ∠=∠∠=∠,根据三角形内角和定理求得40OED ∠=︒,进而即可求解.【详解】解:依题意,,CDB EDO DEO AEF ∠=∠∠=∠,∵120AOB ∠=︒,20CDB ∠=︒,20CDB EDO ∴∠=∠=︒,∴18040OED ODE AOB ∠=-∠-∠=︒,∴40AEF DEO ∠=∠=︒.故答案为:40°.【点睛】本题考查了轴对称的性质,三角形内角和定理的应用,掌握轴对称的性质是解题的关键.9.45°【分析】根据折叠过程可知,在折叠过程中角一直是轴对称的折叠.【详解】在折叠过程中角一直是轴对称的折叠,22.5245AOB ︒︒∠=⨯=故答案为45°【点睛】考核知识点:轴对称.理解折叠的本质是关键.10.C【分析】由90AOC BOD ∠=∠=︒,126AOD ∠︒=,可求出COD ∠的度数,再根据角与角之间的关系求解.【详解】∵=90AOC ∠︒,126AOD ∠︒=,∴36COD AOD AOC ∠=∠-∠=︒,∵90BOD ∠=︒,∴903654BOC BOD COD ∠=∠-∠=︒-︒=︒.故选:C .【点睛】本题考查的知识点是角的计算,注意此题的解题技巧:两个直角相加和AOD ∠相比,多加了BOC ∠.11.B【分析】根据对顶角相等可得180AOD ∠=∠=︒,再根据角的和差关系可得答案.【详解】解:∵180∠=︒,∴180AOD ∠=∠=︒,∵230∠=︒,∴2803050AOE AOD ∠=∠-∠=︒-︒=︒,故选:B【点睛】本题主要考查了对顶角的性质,解题的关键是掌握对顶角相等.12.70【分析】根据对顶角的性质解答即可.【详解】解:∵∠1和∠2是对顶角,∴∠2=∠1=70°,故答案为:70.【点睛】本题主要考查了对顶角,熟练掌握对顶角相等是解答本题的关键.13.B【分析】本题主要考查了平行线的性质.根据平行线的性质解答,即可求解.【详解】解:如图,根据题意得:a b ,c d ∥,∴13180∠+∠=︒,32∠=∠,∵1122∠=︒,∴258∠=︒.故选:B .14.A【分析】根据两直线平行,同旁内角互补可得CAB ∠的度数,根据垂直的定义可得90CAD ∠=︒,然后根据2CAB CAD Ð=Ð-Ð即可得出答案.【详解】解:∵AB CD ∥,155∠=︒,∴18055125CAB Ð=°-°=°,∵AD AC ⊥,∴90CAD ∠=︒,∴21259035CAB CAD Ð=Ð-Ð=°-°=°,故选:A .【点睛】本题考查了平行线的性质以及垂线的定义,熟知两直线平行同旁内角互补是解本题的关键.15.C【分析】由1350∠=∠=︒可得a b ∥,可得2550∠=∠=︒,再利用邻补角的含义可得答案.【详解】解:如图,标记角,∵1350∠=∠=︒,∴a b ∥,而250∠=︒,∴2550∠=∠=︒,∴41805130∠=︒-∠=︒;故选C【点睛】本题考查的是平行线的判定与性质,邻补角的含义,熟记平行线的判定与性质是解本题的关键.16.A【分析】根据对顶角相等可得2=1=30∠∠︒.【详解】解:∵130∠= ,1∠与2∠是对顶角,∴2=1=30∠∠︒.故选:A .【点睛】本题考查了对顶角,解题的关键是熟练掌握对顶角的性质:对顶角相等.17.D【分析】观察图形可知,①~④的小正方体的个数分别为4,3,3,2,其中②③组合不能 构成长方体,①④组合符合题意【详解】解:观察图形可知,①~④的小正方体的个数分别为4,3,3,2,其中②③组合不能构成长方体,①④组合符合题意故选D【点睛】本题考查了立体图形,应用空间想象能力是解题的关键.18.C【分析】由图形可直接得出.【详解】解:由题意,可得130ABC ∠=︒,故选:C .【点睛】本题考查角的度量,量角器的使用方法,正确使用量角器是解题的关键.19.D【分析】根据方向角的定义可得答案.【详解】解:如图:∵西柏坡位于淇淇家南偏西70︒的方向,∴淇淇家位于西柏坡的北偏东70︒方向.故选D .【点睛】本题主要考查方向角,理解方向角的定义是正确解答的关键.20.A【分析】用90°减去40°即可求解.【详解】解:∵40A ∠=︒,∴A ∠的余角=904050︒-︒=︒,故选A【点睛】本题考查了求一个角的余角,掌握和为90° 的两角互为余角是解题的关键.21.B【分析】如图,过B 作BQ ⊥平面镜EF ,可得90QBE QBF ∠=∠=︒,ABC CBQ ABQ MBQ ∠+∠=∠=∠,而90CBQ QBM CBM ∠+∠=∠=︒,再建立方程5090CBQ CBQ ︒+∠=︒-∠,可得20CBQ ∠=︒,从而可得答案.【详解】解:如图,过B 作BQ ⊥平面镜EF ,∴90QBE QBF ∠=∠=︒,ABC CBQ ABQ MBQ ∠+∠=∠=∠,而90CBQ QBM CBM ∠+∠=∠=︒,∴5090CBQ CBQ ︒+∠=︒-∠,∴20CBQ ∠=︒,∴902070EBC ∠=︒-︒=︒,故选B .【点睛】本题考查的是垂直的定义,角的和差运算,角平分线的含义,属于跨学科题,熟记基础概念是解本题的关键.22.C【分析】本题考查了垂线和平行线,熟练掌握同一平面内,垂直于同一条直线的两条直线平行是关键.根据同一平面内,垂直于同一条直线的两条直线平行,即可得出答案.【详解】解:∵l m ⊥,n m ⊥,∴l n ∥.故选:C .23.B【分析】本题考查平行线的性质,解答本题的关键是明确平行线的性质.首先利用平行线的性质得到1DAC ∠∠=,然后利用AB AC ⊥得到90BAC ∠=︒,最后利用角的和差关系求解.【详解】解:如图所示,∵直线a b ,∴1DAC ∠∠=,∵1130∠=︒,∴130DAC ∠=︒,又∵AB AC ⊥,∴90BAC ∠=︒,∴21309040DAC BAC ∠∠∠=-=︒-︒=︒.故选:B .24.B【分析】两条线a 、b 被第三条直线c 所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角,据此作答即可.【详解】解:∠1与∠2是对顶角,选项A 不符合题意;∠1与∠3是同位角,选项B 符合题意;∠2与∠3是内错角,选项C 不符合题意;∠3与∠4是邻补角,选项D 不符合题意;故选:B .【点睛】此题考查了同位角、内错角、同旁内角,熟记同位角、内错角、同旁内角的定义是解题的关键.25.C【分析】根据平行线的判定方法进行判断即可.【详解】解:A.∠1与∠2是邻补角,无法判断两条铁轨平行,故此选项不符合题意;B. ∠1与∠3与两条铁轨平行没有关系,故此选项不符合题意;C. ∠1与∠4是同位角,且∠1=∠4=90°,故两条铁轨平行,所以该选项正确;D. ∠1与∠5与两条铁轨平行没有关系,故此选项不符合题意;故选:C .【点睛】本题主要考查了平行线的判定,熟练掌握平行线的判定是解答本题的关键.26.D【分析】根据“同位角相等,两直线平行”即可得.【详解】解:因为1∠与2∠是一对相等的同位角,得出结论是AB CD ,所以其依据可以简单说成同位角相等,两直线平行,故选:D .【点睛】本题考查了平行线的判定,熟练掌握平行线的判定方法是解题关键.27.D【分析】根据平行线的判定定理、三角形的外角定理以及等腰三角形的等角对等边的性质依次判断.【详解】解:∵1280∠=∠=︒,∴//AB CD ,故A 选项正确;∵180∠=︒,∴80EBF EFB ∠+∠=︒,∵340EFB ∠=∠=︒,∴40EBF ∠=︒,故B 选项正确;32FCG ∠+∠=∠,故C 选项正确;∵40EFB EBF ∠=∠=︒,∴EF=BE ,故D 选项错误,故选:D .【点睛】此题考查平行线的判定定理、三角形的外角定理以及等腰三角形的等角对等边的性质,熟记各定理是解题的关键.28.B【分析】平行线的性质,得到ABD FDE ∠=∠,再利用CBD ABD ABC ∠=∠-∠,进行求解即可.【详解】解:由题意,得:4530EDF ABC ∠=︒∠=︒,,∵AB FC ,∴45ABD FDE ∠=∠=︒,∴15CBD ABD ABC ∠=∠-∠=︒;故选B .【点睛】本题考查平行线的性质,三角板中角度的计算.正确的识图,掌握平行线的性质,是解题的关键.29.C【分析】延长AB 交EG 于点M ,延长CD 交GF 于点N ,过点G 作AB 的平行线GH ,根据平行线的性质即可解答.【详解】解:如图,延长AB 交EG 于点M ,延长CD 交GF 于点N ,过点G 作AB 的平行线GH ,4780,E F EBA FDC ∠=∠=∠=∠= ,33EMA EBA E ∴∠=∠-∠=︒,33FNC FDC F ∠=∠-∠=︒,,AB CD AB HG ∥∥ ,HG CD ∴∥,33MGH EMA ∴∠=∠=︒,33NGH FND ∠=∠=︒,333366EGF ∴∠=︒+︒=︒,故选:C .【点睛】本题考查了平行线的判定及性质,三角形外角的定义和性质,作出正确的辅助线是解题的关键.30.3πa 【详解】根据圆柱的体积=圆柱的底面积⨯圆柱的高,可得23ππV a a a == .故答案为:3πa .【点睛】本题主要考查代数式和整式的乘法运算,牢记整式乘法的运算性质是解题的关键.31.36+##36+【分析】根据题意得出正三角形的边长为2,进而根据表面积等于两个底面积加上侧面正方形的面积即可求解.【详解】解:∵侧面展开图是边长为6的正方形,∴底面周长为6,∵底面为正三角形,∴正三角形的边长为2作CD AB ⊥,ABC 是等边三角形,2AB BC AC ===,1AD ∴=,∴在直角ADC ∆中,CD ==,122ABC S ∴=⨯=∴该直三棱柱的表面积为6636⨯+=+故答案为:36+.【点睛】本题考查了三棱柱的侧面展开图的面积,等边三角形的性质,正方形的性质,熟练掌握以上知识是解题的关键.32.135°##135度【分析】根据三角板及其摆放位置可得180,45BAO BAC OAC OAC ∠=︒=∠+∠∠=︒,求解即可.【详解】180,45BAO BAC OAC OAC ∠=︒=∠+∠∠=︒ ,18045135BAC ∴∠=︒-︒=︒,故答案为:135°.【点睛】本题考查了求一个角的补角,即两个角的和为180度时,这两个角互为补角,熟练掌握知识点是解题的关键.33.30【详解】∵互余两角的和等于90°,∴α的余角为:90°-60°=30°.故答案为:3034.120【分析】如果两个角的和等于180°,就说这两个角互为补角.由此定义即可求解.【详解】解:∵∠A 的补角是60°,∴∠A =180°-60°=120°,故答案为:120.【点睛】本题考查补角的定义,熟练掌握两个角互为补角的定义是解题的关键.35【分析】根据线段的垂直平分线和角平分线的作法可知:EF 是线段AB 的垂直平分线,AO 是∠AOB 的平分线,利用线段的垂直平分线的性质和角平分线的性质的求解即可.【详解】解:如图所示:根据题意可知:EF 是线段AB 的垂直平分线,AO 是∠BAC 的平分线,∵AB =6,∠BAC =60°,∴∠BAO =∠CAO =12∠BAC =30°,AD =12AB =3,∴AM =2MD ,在Rt △ADM 中,222(2)MD MD AD =+,即22243MD MD =+,∴MD ∵AM 是∠AOB 的平分线,MD ⊥AB ,∴点M 到射线AC【点睛】本题考查作图-基本作图,线段的垂直平分线的性质,角平分线的性质等知识,解题的关键是理解题意灵活运用基本作图的知识解决问题.36.140【分析】根据两次转弯后方向不变得到AB CD ,即可得到140BCD ABC ∠=∠=︒.【详解】解:∵一条公路经两次转弯后,方向未变,∴转弯前后两条道路平行,即AB CD ,∴140BCD ABC ∠=∠=︒.故答案为:140.【点睛】此题考查了平行线的性质,由题意得到AB CD 是解题的关键.37. BC DE 内错角相等,两直线平行【分析】根据三角板的角度可知90BCA DEF ∠=∠=︒,根据内错角相等,两直线平行判断即可.【详解】解:一副三角板如图摆放,∴90BCA DEF ∠=∠=︒,∴//BC DE (内错角相等,两直线平行),故答案为:BC ;DE ;内错角相等,两直线平行.【点睛】本题考查了平行线的判定,熟知平行线的判定定理是解本题的关键.38.140︒##140度【分析】如图,先标注点与角,由对折可得:1420∠=∠=︒,求解3180220140∠=︒-⨯︒=︒,利用AB CD ∥,从而可得答案.【详解】解:如图,先标注点与角,由对折可得:1420∠=∠=︒,∴3180220140∠=︒-⨯︒=︒,∵AB CD ∥,∴23140∠=∠=︒;故答案为:140︒【点睛】本题考查的是折叠的性质,平行线的性质,熟记两直线平行,同位角相等是解本题的关键.39.(1)见解析(2)等边三角形【分析】(1)由平行线的性质得到EAD B ∠=∠,已知,B D ∠=∠则EAD D ∠=∠,可判定,BE CD ∥即可得到E ECD ∠=∠;(2)由60E ∠=︒,E ECD ∠=∠得到60ECD E ∠=∠=︒,由CE 平分BCD ∠,得到60BCE ECD ∠=∠=︒,进一步可得BCE E BEC ∠=∠=∠,即可证明BCE 是等边三角形.【详解】(1)证明:AD BC ,∴EAD B ∠=∠,,B D ∠=∠ EAD D ∴∠=∠,,BE CD ∴∥E ECD ∴∠=∠.(2)∵60E ∠=︒,E ECD ∠=∠,∴60ECD E ∠=∠=︒,∵CE 平分BCD ∠,∴60BCE ECD ∠=∠=︒,∴60BCE E ∠=∠=︒,∴18060B BCE E ∠=︒-∠-∠=︒,∴BCE E B ∠=∠=∠,∴BCE 是等边三角形【点睛】此题考查了平行线的判定和性质、等边三角形的判定、三角形内角和定理、角平分线的定义等知识,熟练掌握平行线的判定和性质是解题的关键.40.(1)100BAD ∠=︒(2)证明见解析【分析】本题主要考查了平行线的判定和性质.(1)根据两直线平行,同旁内角互补,即可求解;(2)根据AE 平分BAD ∠,可得50DAE ∠=︒.再由AD BC ∥,可得50AEB DAE ∠=∠=︒.即可求证.【详解】(1)解:∵AD BC ∥,∴180B BAD ∠+∠=°,∵80B ∠=︒,∴100BAD ∠=︒.(2)证明:∵AE 平分BAD ∠,∴1502DAE BAD ∠=∠=︒.∵AD BC ∥,∴50AEB DAE ∠=∠=︒.∵50BCD ∠=︒,∴BCD AEB ∠=∠.∴AE DC ∥.。
2019年数学中考真题知识点汇编42 尺规作图(含解析).docx

【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
】一、选择题9.(2019·长沙)如图,Rt △ABC 中,∠C=90°,∠B=30°,分别以点A 和点B 为圆心,大于12AB 的长为半径作弧,两弧相交于M 、N 两点,作直线MN ,交BC 于点D ,连接AD ,则∠CAD 的度数是【 】A .20°B .30°C .45°D .60°【答案】B【解析】在△ABC 中,∵∠B=30°,∠C=90°,∴∠BAC=180°-∠B-∠C=60°,由作图可知MN 为AB 的中垂线,∴DA=DB ,∴∠DAB=∠B=30°,∴∠CAD=∠BAC-∠DAB=30°,故本题选:B .8. (2019·烟台)已知60AOB ∠=︒,以O 为圆心,以任意长为半径作弧,交OA ,OB 于点M ,N ,分别以M ,N 为圆心,以大于12MN 的长度为半径作弧,两弧在AOB ∠内交于点P ,以OP 为边作15POC ∠=︒,则BOC ∠的度数为( ).A .15︒B .45︒C .15︒或30︒D .15︒或45︒ 【答案】D【解析】由题目可以得出OP 为AOB ∠的平分线,所以1302AOP BOP AOB ∠=∠=∠=︒,又因为15POC ∠=︒,考虑到点C 有可能在AOP ∠内也有可能在BOP ∠内,所以当点C 在AOP ∠内时BOC ∠45BOP POC =∠+∠=︒,当点C 在BOP ∠内时BOC ∠15BOP POC =∠-∠=︒. 2. 3. 4. 39.二、填空题 1. 2. 3. 4. 5. 6. 2 39.三、解答题22.(2019山东省德州市,22,12)如图,∠BPD=120°,点A、C分别在射线PB、PD上,∠P AC=30°,AC =2.(1)用尺规在图中作一段劣弧,使得它在A、C两点分别与射线PB和PD相切.要求:写出作法,并保留作图痕迹;(2)根据(1)的作法,结合已有条件,请写出已知和求证,并证明;(3)求所得的劣弧与线段P A、PC围成的封闭图形的面积.【解题过程】(1)如图,(2)已知:如图,∠BPD=120°,点A、C分别在射线PB、PD上,∠P AC=30°,AC=2,过A、C分别作PB、PD的垂线,它们相交于O,以OA为半径作⊙O,OA⊥PB,求证:PB、PC为⊙O的切线;证明:∵∠BPD=120°,P AC=30°,∴∠PCA=30°,∴P A=PC,连接OP,∵OA⊥P A,PC⊥OC,∴∠P AO=∠PCO=90°,∵OP=OP,∴Rt△P AO≌Rt△PCO(HL)∴OA=OC,∴PB、PC为⊙O的切线;(3)∵∠OAP=∠OCP=90°﹣30°=60°,∴△OAC为等边三角形,∴OA=AC=2,∠AOC=60°,∵OP平分∠APC,∴∠APO=60°,∴AP=×2=2,∴劣弧AC与线段P A、PC围成的封闭图形的面积=S四边形APCO﹣S扇形AOC=2××2×2﹣=4﹣2π.20.(2019·泰州)如图,△ABC中,∠C=90º, AC=4, BC=8.(1)用直尺和圆规作AB的垂直平分线; (保留作图痕迹,不要求写作法)(2)若(1)中所作的垂直平分线交BC于点D,求BD的长.第20题图【解题过程】(1)如图所示,直线DE为所求的AB的垂直平分线;(2)连接AD,因为DE垂直平分AB,所以AD=BD,设AD=BD=x,则CD=8-x,在Rt△ACD中,AC2+CD2=AD2,即42+(8-x)2=x2,解之得,x=5,所以BD的长为5.20.(2019浙江省温州市,20,8分)(本题满分8分)如图,在7×5的方格纸ABCD 中,请按要求画图,且所画格点三角形与格点四边形的顶点均不与点A ,B ,C ,D 重合.(1)在图1中画一个格点△EFG ,使点E ,F ,G 分别落在边AB ,BC ,CD 上,且∠EFG=90°;(2)在图2中画一个格点四边形MNPQ ,使点M ,N ,P ,Q 分别落在边AB ,BC ,CD ,DA 上,且MP=NQ . 注:图1,图2在答题纸上.【解题过程】(1)画法不唯一,如图1或如图2等;(2)画法不唯一,如图3或如图4等.图1 图2 图3 图420.(2019·嘉兴)在6×6的方格纸中,点A ,B ,C 都在格点上,按要求画图: (1)在图1中找一个格点D ,使以点A ,B ,C ,D 为顶点的四边形是平行四边形. (2)在图2中仅用无刻度的直尺,把线段AB 三等分(保留画图痕迹,不写画法).【解题过程】解:(1)由勾股定理得: CD =AB =CD'=,BD =AC =BD''=,AD'=BC =AD''=;画出图形如图1所示; (2)如图2所示.第20题图DCBA E FG A BCD G F EA BCD QP NM A B CD MNP QA B CD21.(2019江苏盐城卷,21,8如图,AD是△ABC的角平分线.(1)作线段AD的垂直平分线EF,分别交AB、AC于点E、F;(2)(用直尺和圆规作图,标明字母,保留作图痕迹,不写作法.)(3)连接DE、DF,四边形AEDF是_________形.(直接写出答案)【解题过程】(1)如图所示:直线EF就是线段AD的垂直平分线.(2)菱形.证明:连结DE、DF∵EF垂直平分AD∴EA=ED,FA=FD∴∠EAD=∠EDA, ∠FAD=∠FDA∵AD是∠BAC的平分线∴∠EAD=∠FAD∴∠EAD=∠EDA=∠FAD=∠FDA∴AE∥DF,AF∥ED∴四边形AEDF为平行四边形∵EA=ED∴四边形AEDF为菱形.15.(2019·青岛)已知:∠α,直线l及l上两点A, B.求作:Rt△ABC,使点C在直线l的上方,且∠ABC= 90° , ∠BAC=∠α.【解题过程】如国所示:则Rt△ABC即为所求.15.(2019江西省,15,6分)在△ABC中,AB=AC,点A在以BC为直径的半圆内,请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).(1)在图1中作弦EF,使EF∥BC;(2)在图2中以BC为边作一个45°的圆周角.【解题过程】解:(1)如图所示∴DE即为所求.(2)如图所示∴∠MBC即为所求.21.(2019·陇南)已知:在△ABC中,AB=AC.(1)求作:△ABC的外接圆.(要求:尺规作图,保留作图痕迹,不写作法)(2)若△ABC的外接圆的圆心O到BC边的距离为4,BC=6,则S⊙O=.解:(1)如图⊙O即为所求.(2)设线段BC的垂直平分线交BC于点E.由题意可知,OE=4,BE=EC=3,在Rt△OBE中,OB==5,∴S圆O=π•52=25π.故答案为25π.1.(2019·济宁)如图,点M和点N在∠AOB内部.(1)请你作出点P,使点P到点M和点N的距离相等,且到∠AOB两边的距离也相等(保留作图痕迹,不写作法);(2)请说明作图理由.解:(1)画出∠AOB的角平分线,画出线段MN的垂直平分线,两者的交点就得到P点.(2)作图的理由:点P在∠AOB的角平分线上,又在线段MN的垂直平分线上,∠AOB的角平分线和线段MN 的垂直平分线的交点即为所求.2(2019·无锡)按要求作图,不要求写作法,但要保留作图痕迹(1)如图1,A为圆O上一点,请用直尺(不带刻度)和圆规作出得内接正方形;EA(2)我们知道,三角形具有性质,三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高交于同一点,请运用上述性质,只用直尺(不带刻度)作图:②如图2,在□ABCD中,E为CD的中点,作BC的中点F;②图3,在由小正方形组成的网格中,的顶点都在小正方形的顶点上,作△ABC的高AH.解:(1) 连结AE 并延长交圆E 于点C ,作AC 的中垂线交圆于点B ,D ,四边形ABCD 即为所求.(2)①连结AC ,BD 交于点O ,连结EB 交AC 于点G ,连结DG 并延长交CB 于点F , F 即为所求.②CBB。
2019年各地中考解析版数学试卷汇编:图形的展开与叠折(Word版)
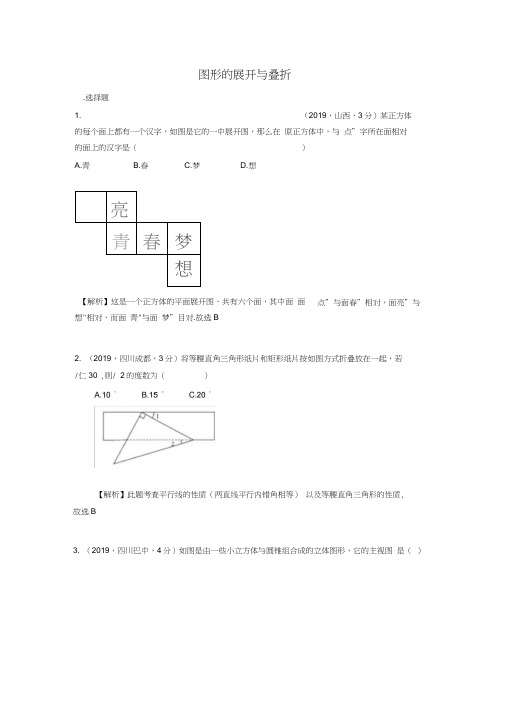
图形的展开与叠折.选择题1. (2019,山西,3分)某正方体的每个面上都有一个汉字,如图是它的一中展开图,那么在原正方体中,与点”字所在面相对的面上的汉字是()A.青B.春C.梦D.想亮青春梦想【解析】这是一个正方体的平面展开图,共有六个面,其中面面想"相对,而面青"与面梦”目对.故选B2. (2019,四川成都,3分)将等腰直角三角形纸片和矩形纸片按如图方式折叠放在一起,若/仁30°,则/ 2的度数为()【解析】此题考查平行线的性质(两直线平行内错角相等)以及等腰直角三角形的性质,故选B3. (2019,四川巴中,4分)如图是由一些小立方体与圆锥组合成的立体图形,它的主视图是()点”与面春”相对,面亮”与---------- ---- . 故选:C .【点评】本题考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出 来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.4. (2019?贵州毕节?3分)由下面正方体的平面展开图可知,原正方体“中”字所在面的对【分析】正方体的展开图有 11种情况,分析平面展开图的各种情况后再认真确定哪两个 面的对面.【解答】解:根据正方体相对的面的特点, “中”字所在的面的对面的汉字是“的” 故选:B .【点评】本题考查了正方体侧面展开图,熟记正方体侧面展开图对面和相邻的面是解题 的关键.5 (2019?江苏连云港?3分)一个几何体的侧面展开图如图所示, 则该几何体的底面是()C .中D .梦 面的汉字是(A .B .【分析】根据几何体的侧面展开图可知该几何体为四棱锥,所以它的底面是四边形. 【解答】解:由题意可知,该几何体为四棱锥,所以它的底面是四边 形.故选:B .【点评】本题主要考查了几何体的展开图,熟练掌握棱锥的展开图是解答本题的关键.6 (2019?湖南邵阳?3 分)如图,在 Rt △ ABC 中,/ BAC = 90°,/ B = 36°, AD 是斜边 BC 上的中线,将△ ACD 沿AD 对折,使点C 落在点F 处,线段DF 与AB 相交于点E ,则 / BED 等于()A . 120°B . 108°C . 72°D . 36°【分析】根据三角形内角和定理求出/ C = 90°-/ B = 54° .由直角三角形斜边上的中线的性质得出 AD = BD = CD ,利用等腰三角形的性质求出/ BAD = / B = 36°,/ DAC=/ C = 54°,利用三角形内角和定理求出/ADC = 180° -/ DAC -/ C = 72° .再根据折叠的性质得出/ ADF =/ ADC = 72 °,然后根据三角形外角的性质得出/ BED = /BAD+ / ADF = 108 ° .【解答】解:•••在 Rt A ABC 中,/ BAC = 90°,/ B = 36°, •••/ C = 90°-/ B = 54 ° .T AD 是斜边BC 上的中线,AD = BD = CD ,• / BAD = / B = 36°,/ DAC = / C = 54° , • / ADC = 180°-/ DAC -/ C = 72°.•••将△ ACD 沿AD 对折,使点C 落在点F处,•••/ ADF = Z ADC = 72°,•••/ BED = Z BAD + Z ADF = 36°+72° =108 ° .故选:B.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了直角三角形斜边上的中线的性质、等腰三角形的性质、三角形内角和定理以及三角形外角的性质.7. (2019?浙江金华?3分)如图物体由两个圆锥组成,其主视图中, 若上面圆锥的侧面积为1,则下面圆锥的侧面积为()故答案为:D.Z A=90; Z ABC=105°A. 2B.【答案】D【考点】圆锥的计算【解析】【解答】解:设BD=2r ,•••Z A=90°,• AB=AD= . 2 r, Z ABD=45 ,C.-D. 2上面圆锥的侧面积S=丄2 nrJ2 r=1 ,2• Z ABC=105 ,•Z CBD=60 ,又• CB=CD ,•△ CBD是边长为2r的等边三角形,F面圆锥的侧面积S=丄2 n 2r=2 n 2=2 nX2A'2.【分析】设 BD=2r ,根据勾股定理得 AB=AD= J2 r , / ABD=45 ,由圆锥侧面积公式得 2n • 2 r=1,求得r 2=1,结合已知条件得 / CBD=60,根据等边三角形判定得△ CBD 是边长为2r 的等边三角形,由圆锥侧面积公式得下面圆锥的侧面积即可求得答案 8( 2019?广东深圳?3分)下列哪个图形是正方体的展开图()【答案】B【考点】立体图形的展开9(2019?广西贵港? 3分)将一条宽度为2cm 的彩带按如图所示的方法折叠,折痕为 AB ,重 叠部分ABC (图中阴影部分),若/ ACB = 45°,则重叠部分的面积为()【分析】过B 作BD 丄AC 于D ,则/ BDC = 90°,依据勾股定理即可得出BC 的长,进而得到重叠部分的面积.【解答】解:如图,过 B 作BD 丄AC 于D ,则/ BDC = 90°, •••/ ACB = 45 ° , •••/ CBD = 45°, BD = CD = 2cm , • Rt △ BCD 中,BC = . 2222 = 2 ~2 ( cm ),•重叠部分的面积为 1 x 2-、2 x 2 = 2、、2 ( cm ),2故选:A .B . 2 3 cm 2 2C . 4cm 2cmA . 2 ■- 2cm 2【点评】本题主要考查了折叠问题,折叠是一种对称变换,它属于轴对称,折叠前后图 形的形状和大小不变,位置变化,对应边和对应角相等.10 ( 2019?浙江金华?3分)将一张正方形纸片按如图步骤,通过折叠得到图 去一个角,展开铺平后得到图 ⑤,其中FM , GN 是折痕,【答案】 A 【考点】剪纸问题点0,如图,④,再沿虚线剪若正方形EFGH 与五边形MCNGF的面积相等,则的值是()5 _ 一 2 A.21 C.22 D.2【解析】【解答】解:设大正方形边长为 a ,小正方形边长为 x ,连结NM ,作GO 丄NM 于依题可得:2NM= 一 2a -42xa , FM=GN= 一2/B. 2•••正方形EFGH 与五边形 MCNGF 的面积相等, • 2_(2x+V2a)(T2a-2x) 1 2 •• x = + — a16 8• a= 5 x ,• FM _ a - T5x_血x 亦"FG 一 2x = 2x = 2.故答案为:A.【分析】设大正方形边长为 a ,小正方形边长为x ,连结NM ,作GO 丄NM 于点O ,根据题意可得,NM=迈 a , FM=GN= a _ 2x , NO = 2=、习心,2 4(2x . 2a)(、,2a -2x)+ a1611. (2019?山东省济宁市 ?3分)如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是()AAAUB .••• NO=手-x 2-2X• GO= , GN2_N02=2a -2x 42 2根据勾股定理得V2a -2x2G0=,由题意建立方程x =4解之可得 a= ,5x ,由FMFG2x,将a= .5x 代入即可得出答案【分析】由平面图形的折叠及几何体的展开图解题,注意带图案的一个面不是底面.【解答】解:选项 A 和C 带图案的一个面是底面,不能折叠成原几何体的形式; 选项B 能折叠成原几何体的形式;选项D 折叠后下面带三角形的面与原几何体中的位置不 同.故选:B .【点评】本题主要考查了几何体的展开图.解题时勿忘记正四棱柱的特征及正方体展开 图的各种情形.注意做题时可亲自动手操作一下,增强空间想象能力.二.填空题1 (2019?甘肃? 3分)如图,在矩形 ABCD 中,AB = 10, AD = 6, E 为BC 上一点,把厶CDE10沿DE 折叠,使点C 落在AB 边上的F 处,贝U CE 的长为 一.3【分析】设 CE = x ,贝U BE = 6- x 由折叠性质可知,EF = CE = x , DF = CD = AB = 10,所2 2 2 2 2以 AF = 8, BF = AB — AF = 10- 8 = 2,在 Rt A BEF 中,BE +BF = EF ,即(6 - x ) +2 =x 2,解得 x = 一 .3【解答】解:设CE = x ,贝U BE = 6- x 由折叠性质可知,EF = CE = x , DF = CD = AB = 10, 在 Rt △ DAF 中,AD = 6, DF = 10, ••• AF = 8,••• BF = AB - AF = 10- 8= 2,2 2 2在 Rt △ BEF 中,BE 2+BF 2= EF 2,【考点】网版权所几何体的展开图即(6_ x ) 2+22 = x 2,10解得x =—【点评】本题考查了矩形,熟练掌握矩形的性质以及勾股定理是解题的关键.2. (2019?广西贵港? 3分)如图,在扇形 OAB 中,半径OA 与OB 的夹角为120°,点A 与 点B的距离为2、_3,若扇形OAB 恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为2 3 —【分析】利用弧长=圆锥的周长这一等量关系可求解. 【解答】解:连接 AB ,过O 作OM 丄AB 于M ,•••/ AOB = 120°, OA = OB , •••/ BAO = 30°, AM =、., 3 , ••• OA = 2,120二 2 180 • r = 232故答案是:一3【点评】本题运用了弧长公式和圆的周长公式,建立准确的等量关系是解题的关键.三.解答题1 (2019?湖南岳阳? 10分)操作体验:如图,在矩形ABCD 中,点E.F 分别在边AD.BC 上,故答案为10 3将矩形ABCD 沿直线EF 折叠,使点D 恰好与点B 重合,点C 落在点C '处.点P 为直 线EF 上一动点(不与 E.F 重合),过点P 分别作直线BE.BF 的垂线,垂足分别为点 M 和N ,以PM 、PN 为邻边构造平行四边形 PMQN .(1) 如图1,求证:BE = BF ;(2) 特例感知:如图 2,若DE = 5, CF = 2,当点P 在线段EF 上运动时,求平行四边形PMQN 的周长;(3) 类比探究:若DE = a , CF = b .①如图3,当点P 在线段EF 的延长线上运动时, 试用含A.b 的式子表示QM 与QN 之间 的数量关系,并证明②如图4,当点P 在线段FE 的延长线上运动时,请直接用含【分析】(1)证明/ BEF = Z BFE 即可解决问题(也可以利用全等三角形的性质解决问题即可).(2)如图2中,连接BP ,作EH 丄BC 于H ,则四边形 ABHE 是矩形.利用面积法证明PM + PN = EH ,利用勾股定理求出 AB 即可解决问题.(3) ①如图3中,连接 BP ,作 EHL BC 于H .由S A EBP- S A BFA S A EBF ,可得 丄2BE?PM -?BF?PN= - ?BF?EH 由 BE = BF ,推出 PM- PN= EH=、. a 2 — b ? 由此即可解决 2 2 ' 问题.②如图4,当点 P 在线段 FE 的延长线上运动时,同法可证: QM - QN = PN - PM = a 2 -b 2 .【解答】(1)证明:如图1中, A.b 的式子表示 QM 与QN 之间的数量关系.(不要求写证明过程)•••四边形ABCD是矩形,••• AD // BC,•••/ DEF = Z EFB , 由翻折可知:/ DEF = Z BEF,•••/ BEF =Z EFB ,• BE= BF .(2)解:如图2中,连接BP,作EH丄BC于H,则四边形ABHE是矩形,EH= AB.•/ DE = EB= BF = 5, CF = 2,AD = BC= 7, AE= 2,在Rt△ ABE 中,•••/ A= 90°, BE= 5, AE= 2,• AB= •, 52匚22=21 ,T S^BEF = S PBE+S A PBF, PM _L BE, PN丄BF ,1 1 1•— ?BF?EH = - ?BE?PM+ —?BF?PN ,2 2 2•/ BE= BF ,PM+PN = EH =、、21 ,•••四边形PMQN是平行四边形,•四边形PMQN 的周长=2 ( PM + PN)= 2 •. 21 .(3)①证明:如图3中,连接BP,作EH丄BC于H .C P\竝\••• ED = EB = BF = a, CF = b,AD = BC= a+b,••• AE= AD - DE = b,••• EH = AB = -, a2 -b2,T S^EBP - S BFP = S EBF ,1 1 1•——BE?PM - ?BF?PN = ?BF?EH ,2 2 2•/ BE= BF ,PM - PN= EH =、.、a2 _b2,•••四边形PMQN是平行四边形,• QN - QM =( PM - PN) = .. a2_ b2.②如图4,当点P在线段FE的延长线上运动时,同法可证:QM - QN = PN - PM =【点评】本题属于四边形综合题,考查了矩形的性质和判定,翻折变换,等腰三角形的性质,平行四边形的性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,学会利用面积法证明线段之间的关系,属于中考压轴题.2 (2019?湖南衡阳?12分)如图,在等边厶ABC中,AB = 6cm,动点P从点A出发以lcm/s 的速度沿AB匀速运动.动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动,当点P到达点B时,点P、Q同时停止运动.设运动时间为以t (s).过点P作PE丄AC于E,连接PQ交AC边于D .以CQ、CE为边作平行四边形CQFE .(1 )当t为何值时,△ BPQ为直角三角形;(2)是否存在某一时刻t,使点F在/ ABC的平分线上?若存在,求出t的值,若不存在,请说明理由;(3 )求DE的长;(4)取线段BC的中点M,连接PM,将△ BPM沿直线PM翻折,得厶B' PM,连接AB 当t为何值时,AB'的值最小?并求出最小值.【分析】(1 )当BQ = 2BP时,/ BPQ = 90°,由此构建方程即可解决问题.(2)如图1中,连接BF交AC于M .证明EF = 2EM,由此构建方程即可解决问题.1(3)证明DE = AC即可解决问题.2(4)如图3中,连接AM , AB '.根据AB ' > AM-MB '求解即可解决问题.【解答】解:(1)v^ ABC是等边三角形,•••/ B= 60°,•••当BQ= 2BP 时,/ BPQ= 90°,• 6+t= 2 (6 - t),• -1= 3,• t= 3时,△ BPQ是直角三角形.(2)存在.理由:如图1中,连接BF交AC于M .•/ BF 平分/ ABC, BA = BC,• BF 丄AC, AM = CM = 3cm,•/ EF // BQ ,•••/ EFM =Z FBC = - / ABC = 30°,12• EF = 2EM ,1• t = 2?( 3 - t ),2解得t = 3.(3)如图2中,作PK // BC 交AC 于K .@2 .•••△ ABC 是等边三角形,•-Z B =Z A = 60°,•/ PK // BC ,• / APK =Z B = 60°,• / A =Z APK =Z AKP = 60°,• △ APK 是等边三角形,• PA = PK ,•/ PE 丄 AK ,• AE = EK ,•/ AP = CQ = PK ,/ PKD = Z DCQ ,/ PDK = Z QDC ,• △ PKD ◎△ QCD (AAS ),• DK = DC ,1 1 • DE = EK+DK = - (AK+CK )= — AC = 3 (cm ).2 2(4) 如图3中,连接AM ,ABBM = CM = 3, AB = AC,••• AM 丄BC,••• AM = , AB?匚BM 2= 3.3 ,•/ AB'> AM - MB ',• AB,》3、.3 - 3,• AB'的最小值为3 ...3 - 3.【点评】本题属于四边形综合题,考查了等边三角形的性质,平行四边形的判定和性质, 翻折变换,全等三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.。
2019中考数学知识点:中考数学几何知识点精品教育.doc

中考数学知识点:中考数学几何知识点从某种意义上来说中考数学中几何做的如何直接决定了中考数学是否能够拿到高分,是否能够拉开差距。
由此看来,数学中几何对于中考数学来说非常重要。
得几何者得中考数学天下。
通常情况下,几何在中考中呈现方式为:选择题中小题计算相应的角度、线段,填空题中也以相应的计算为基础。
选择填空每题各四分。
接下来在解答题中,通常会考查简单的全等三角形、圆中的切线证明以及圆中计算和证明、第22题动手操作或者几何变通思维能力题目、24题代几综合题目、25题几何综合压轴题。
其中,第22、24、25通常被称为中考数学压轴题,这三道题目做的好与坏直接关系到中考数学分数的高与低。
在23题中一般考查几何辅助线思维能力锻炼,考查学生空间想象能力以及动手操作能力;24一般考查二次函数与四边形、三角形乃至于圆的综合,题目难度系数较大,是每一届中考考生的绊脚石之一(2019年24题考查几何综合思维能力,主题考查旋转变换思想)。
25题一般考查几何综合变换,常常和几何中的几何变换之旋转、平移、轴对称。
这三大变换足以让很多学生扣分,如2019年北京中考25题考查几何轴对称导致当年满分和高分分数剧降!那么面对几何的重要性,在刚进入初三的孩子们来说,我们需要注意如下几点:1、重视新课中的基础。
在学校学习新课的时候就一定要打扎实基础,把每一个基础的知识点弄清楚。
把每一个定理和定理的证明方法弄明白,从而联想到相关的知识点。
上课勤做笔记,记住每一个闪光的思路。
2、注重归纳。
把自己在课本辅导书上做到的相关的题型总结在一起,经常回顾,同时标记重要题型。
3、保持四边形、三角形中辅助线添加熟练。
特别是几何三大变换,旋转、平移、轴对称要熟练,多练习这类型的题目。
4、多练习题目。
5、熟练掌握初中阶段数学模型。
掌握模型,熟练运用阶梯技巧。
2019年中考初中数学几何题知识点详细介绍

2019年中考初中数学几何题知识点详细介绍各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢
初中数学几何题学习对学生们来说非常重要,下面,教育初中频道小编为学生们详细介绍!
一、计算图形面积
二、用面积法求线段长或证明线段间的数量关系,角相等及比例式
1. 用面积法证线段相等
【例1】已知:如图1,AD是△ABC 的中线,CF⊥AD于F,BE⊥AD交AD 的延长线于E。
求证:CF=BE。
2. 用面积法证两角相等
【例2】如图2,C是线段AB上的
一点,△ACD、△BCE都是等边三角形,AE、BD相交于O。
求证:∠AOC=∠BOC。
3. 用面积法证线段不等
【例3】如图3,在△ABC中,已知AB>AC,∠A的平分线交BC于D。
求证:BD>CD。
4. 用面积法证线段的和差
【例4】已知:如图4,设等边△ABC 一边上的高为h,P为等边△ABC内的任意一点,PD⊥BC于D,PE⊥AC于E,PF⊥AB于F。
求证:PE+PF+PD=h。
5. 用面积法证比例式或等积式
还没有用过面积法的可以行动起来了~~涨分势在必得!
以上就是初中数学几何题的详细内容,更多精彩内容尽请关注教育初中频道!
各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢。
2019吉林中考数学试题及知识点解析

2019吉林省数学中考解析2分)如图,数轴上蝴蝶所在点表示的数可能为(A) 3 (B) 2 (C) 1 (D) -1【答案】D【解析】从图中可以看出蝴蝶在原点的左侧,所以可能是-1,故选择D 【知识点】数轴2.(2019吉林省,2, 2分)如图,由6个相同的小正方体组合成一个立方体,它的俯视图为Q rffb m mzn(A> <»> 3)【答案】D【解析】从上面看是一行四个小正方形,故选D【知识点】三视图3.(2019吉林省,3, 2分)若a为实数,则下列格式的运算结果比a小的是(A) a+1 (B) a-1 (C) axl (D) a4-1【答案】B【解析】选项A比a大1;选项C,选项D和a相等,只有选项B比a小,故选B【知识点】实数的大小4.(2019吉林省,4, 2分)把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为(A) 30°(B) 90°(C) 120°(D) 180°【答案】C【解析】这个交通标志图案是由3个基本图案组成的,所以旋转角至少为120。
,故选C【知识点】图形的旋转5.(2019吉林省,5,2分)如图,在O0中,弧AB所对的圆周角NACB=50°,若P为弧AB上一点,NA0P=55°, 则NP0B的度数为一、单项选择题1. (2019 吉林省,1,(A) 30° (B) 45° (C) 55°(D) 60°【答案】B 【解析】根据同弧所对的圆周角是圆心角的一半可知,ZA0B=2ZACB=U0° ,因为NAOP=55° ,所以NPOB 的度 数为45° ,故选B【知识点】同弧所对的圆周角与圆心角的关系6. (2019吉林省,6, 2分)曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游 人更好的观赏风光,如图,A 、B 两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是(A )两点之间,线段最短 (B )平行于同一条直线的两条直线平行(C )垂线段最短 (D )两点确定一条直线【答案】A【解析】这里主要体现了长度问题,所以蕴含的数学道理是两点之间,线段最短,选择A【知识点】生活中的数学应用二、填空题7. (2019吉林省,7, 3分)分解因式;a 3-l=【答案】Q+l ) Q-1)【解析】平方差公式:两数和与这两数的差的积【知识点】公式法因式分解8. (2019吉林省,8, 3分)不等式3x-2>l 的解集是【答案】A1【解析】移项,得3x>2+l,即3x>3,【知识点】解不等式9. (2019吉林省,9, 3分)计算工•土 = _________________________2厂y【答案】?【解析】单项式乘以单项式,分子分母分别相乘,能约分的要约分【知识点】整式的乘法,约分10. (2019吉林省,10, 3分)若关于X 的一元二次方程(x+3) Jc 有实数根,则c 的值可以为出一个即可)【答案】答案不唯一,例如5, (c20时方程都有实数根)【解析】c ,0时方程都有实数根【知识点】一元二次方程根的情况11. (2019吉林省,11, 3分)如图,E 为AABC 边CA 延长线上一点,过点E 作ED 〃BC,若ZBAC=70°, Z (写CED=50° ,则NB=【答案】60°【解析】因为ED 〃BC,所以NCED=NC=50° ,因为NBAC=70° ,三角形内角和为80° ,所以NB=60°【知识点】平行线的性质,三角形内角和定理12. (2019吉林省,12, 3分)如图,在四边形ABCD 中,AB=10, BD±AD,若将4BCD 沿BD 折叠,点C 与边AB 的中点E 恰好重合,则四边形BCDE 的周长为5+5+5+5=20【知识点】直角三角形斜边的中线等于斜边的一半,折叠的性质13. (2019吉林省,13, 3分)在某一时刻,侧的一根高为1. 8m 的竹竿的影长为3m,同时同地测得一栋楼的影 长为90m,则这栋楼的高度为 m【答案】54 【解析】由同一时刻阳光下的影子与物高之间的关系可曙嗤,喷得•••可求得这栋楼的高度为54米.【知识点】由同一时刻阳光下的影子与物高之间的关系,图形的相似的实际应用14. (2019吉林省,14, 3分)如图,在扇形0AB 中,ZA0B=90° , D 、E 分别是半径0A, 0B 上的点,以OD,OE 为邻边的0DCE 的顶点C 在弧AB 上,若0D=8, 0E=6,则阴影部分图形的面积是 (结 果保留八)【答案】25力-48【解析】如图,连接DE,OCV0ODCE, ZA0B=90° ,,回ODCE 是矩形,,DE=OC, TtZkDOE 中,0D=8, 0E=6, ADE=10=0C,,S 护S 扇-S 矩=-AB【解析】••,BDJLAD, E 为AB 的中点,•••BE=DE= 2=5, •.•折叠,•••BC=BE=5,CD=DE=5, •••四边形 BCDE 的周长为—nxlO2-6x8=25n-484【知识点】矩形的性质,扇形的面积三、解答题15.(2019吉林省,15, 5分)先化简,再求值:(a-D'+a(a+2),其中a二、历【思路分析】将原代数式化简求值即可【解题过程】解:原式寸-2a+l+J+2a=21+1,当航及时,原式二 2 x(V2)2 +1 = 2x2 + 1 =5 【知识点】整式的运算16.(2019吉林省,16, 5分)甲口袋中装有红色、绿色两把扇子,这两把扇子出颜色外无其他差别;乙口袋中装有红色、绿色两条手绢,这两条手绢除颜色外无其他差别,从甲口袋中随机取出一把扇子,从乙口袋中随机取出一条手绢,用树状图或列表的方法,求取出的扇子和手绢都是红色的概率.【思路分析】根据题意画出树状图或者列出表格,即可求出概率共有4种等可能结果,其中取出的擅自和手绢都是红色的有1种可能,1•p -4•(以的的擅自和手用都是红色)一【知识点】概率17.(2019吉林省,17, 5分)已知y是x的反比例函数,并且当x=2时,尸6,(1)求y关于X的函数解析式;(2)当x=4时,求y的值【思路分析】(1)将x=2时,y=6代入解析式即可求出待定系数,即可求出解析式;(2)当x=4时,代入(1)中的解析式,可求出y的值【解题过程】解:(1)•・3是x的反比例函数,工设y=' (kWO), x丁当 x=2 时,y=6,Ak=xy=12,.」2••y——X⑵当x=4时,12代入y二上得,X12勺y=— = 34【知识点】反比例函数18.(2019吉林省,18, 5分)如图,在0ABCD中,点E在边AD上,以C为圆心,AE长为半径画弧,交边BC于点F,连接BE, DF求证:ZiABE丝 ZkCDF【思路分析】由作图可知,AE=CF,有平行四边形的性质可知对边相等,对角相等,由SAS可以证明两个三角形全等.【解题过程】解:由题意得AE二FCV0ABCD,AAB=DC, ZA=ZC 在aABE和aCDF中, AE=CF, ZA=ZC, AB=DC,/.△ABE^ACDF【知识点】平行四边形的性质,三角形的全等四、解答题19.(2019吉林省,19, 1分)图①,图②均为4x4的正方形网格,每个小正方形的顶点称为格点,在图①中已画出线段AB,在图②中已画出线段CD,其中A,B,C,D均为格点,按下列要求画图:(1)在图①中,以AB为对角线画一个菱形AEBF,且&F为格点;(2)在图②中,以CD为对角线画一个对边不相等的四边形CGDH,且G,H为格点,ZCGD=ZCHD=90°【思路分析】(1)AB为对角线长为4,则另一条对角线在AB的中垂线上,如图所示;(2)根据勾股定理,画出格点三角形,如图所示【解题过程】【知识点】菱形,勾股定理20. (2019 吉林省,20, 7 分)问题解决糖甜芦一般是用竹签串上山楂,再蘸以冰糖而成,现将一些山楂分别串在若干跟竹签上,如果每根竹签串5 个山楂,还剩余4个山楂;如果每根竹签串8个山楂,还剩余7根竹签,这些竹签有多少根?山楂有多少个?反思归纳现有a 根竹签,b 个山楂,若每根竹签串c 个山楂,还剩余d 个山楂,则下列等式成立的是 (填写序号)(1) bc+d=a; (2)ac+d=b; (3)ac-d=b【思路分析】(1)根据题意表示出山楂的个数,列出二元一次方程组即可解决 (2)表示出山楂的总个数,即竹签串的山楂与剩余的山楂的和就是总山楂的个数 【解题过程】问题解决 解:设竹签x 根,山楂y个,根据座意得产中/解霄片端答:竹签有20根,山植104个反思归纳(2) 【知识点】二元一次方程组的应用,代数式21. (2019吉林省,21, 7分)墙壁及淋浴花洒截面如图所示,已知花酒底座A 与地面的距离AB 为170cm,花 洒AC 的长为30的,与墙壁的夹角NCAD 为43。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
】
一、选择题
5.(2019·绍兴 )如图,墙上钉着三根木条a,b,c ,量得∠1=70°,∠2=100°,那么木条a,b 所在直线所夹的锐角是 ( )
A.5°
B.10°
C.30°
D.70°
【答案】B
【解析】将木条a 和b 延长交于一点P ,构造一个三角形,由三角形的内角和定理可知∠P =180°-100°-70°=10°.
1. (2019·怀化) 与30°的角互为余角的角的度数是( ) A.30° B.60° C.70° D.90° 【答案】B. 【解析】∵30°+60°=90°, ∴30°的余角为60°. 故选B.
2. (2019·湖州)已知∠α=60°32′,则∠α的余角是( )
A .29°28′
B .29°68′
C .119°28′
D .119°68′ 【答案】A
【解析】∵∠α=60°32′, 60°32′+29°28′=90°,∴∠α的余角是29°28′.故选A .
二、填空题 13.(2019·威海)
把一块含有45°角的直角三角板与两条长边平行的直尺如图放置 (直角顶点在直尺的一条长边上). 若∠1=23°,则∠2= °.
【答案】68°
【解析】根据平行线的性质求出∠2的同位角度数,由三角形外角性质可得∠1+45°=68°.
三、解答题 20.(2019·武汉)如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形ABCD
的顶点
在格点上,点E 是边DC 与网格线的交点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由
(1) 如图1,过点A 画线段AF ,使AF ∥DC ,且AF =DC (2) 如图1,在边AB 上画一点G ,使∠AGD =∠BGC (3) 如图2,过点E 画线段EM ,使EM ∥AB ,且EM =AB
图1 图2 【解题过程】(1)画图如图1;(2)画图如图1;(3)画图如图2.
中考数学知识点代数式 一、 重要概念
分类:
1.代数式与有理式
用运算符号把数或表示数的字母连结而成的式子,叫做代数式。
单独
的一个数或字母也是代数式。
整式和分式统称为有理式。
2.整式和分式
含有加、减、乘、除、乘方运算的代数式叫做有理式。
没有除法运算或虽有除法运算但除式中不含有字母的有理式叫做整式。
有除法运算并且除式中含有字母的有理式叫做分式。
3.单项式与多项式
没有加减运算的整式叫做单项式。
(数字与字母的积—包括单独的一个数或字母)
几个单项式的和,叫做多项式。
说明:①根据除式中有否字母,将整式和分式区别开;根据整式中有否加减运算,把单项式、多项式区分开。
②进行代数式分类时,是以所给的代数式为对象,而非以变形后的代数式为对象。
划分代数式类别时,是从外形来看。
如,
=x, =│x│等。
4.系数与指数
区别与联系:①从位置上看;②从表示的意义上看
5.同类项及其合并
条件:①字母相同;②相同字母的指数相同
合并依据:乘法分配律
6.根式
表示方根的代数式叫做根式。
含有关于字母开方运算的代数式叫做无理式。
注意:①从外形上判断;②区别:、是根式,但不是无理式(是无理数)。
7.算术平方根
⑴正数a的正的平方根( [a≥0—与“平方根”的区别]);
⑵算术平方根与绝对值
①联系:都是非负数,=│a│
②区别:│a│中,a为一切实数; 中,a为非负数。
8.同类二次根式、最简二次根式、分母有理化
化为最简二次根式以后,被开方数相同的二次根式叫做同类二次根式。
满足条件:①被开方数的因数是整数,因式是整式;②被开方数中不含有开得尽方的因数或因式。
把分母中的根号划去叫做分母有理化。
9.指数
⑴( —幂,乘方运算)
①a>0时,>0;②a0(n是偶数),⑵零指数:=1(a≠0)
负整指数:=1/ (a≠0,p是正整数)
二、运算定律、性质、法则
1.分式的加、减、乘、除、乘方、开方法则
2.分式的性质
⑴基本性质:= (m≠0)
⑵符号法则:
⑶繁分式:①定义;②化简方法(两种)
3.整式运算法则(去括号、添括号法则)
4.幂的运算性质:①· = ;②÷ = ;③= ;④= ;⑤
技巧:
5.乘法法则:⑴单×单;⑵单×多;⑶多×多。
6.乘法公式:(正、逆用)
(a+b)(a-b)=
(a±b) =
7.除法法则:⑴单÷单;⑵多÷单。
8.因式分解:⑴定义;⑵方法:a.提公因式法;b.公式法;c.十字相乘法;d.分组分解法;e.求根公式法。
9.算术根的性质:= ; ; (a≥0,b≥0); (a≥0,b>0)(正用、逆用)
10.根式运算法则:⑴加法法则(合并同类二次根式);⑵乘、除法法则;⑶分母有理化:a. ;b. ;c. .
11.科学记数法:(1≤a<10,n是整数。
