建模与仿真实验
控制工程实训课程学习总结基于MATLAB的系统建模与仿真实验报告
控制工程实训课程学习总结基于MATLAB 的系统建模与仿真实验报告摘要：本报告以控制工程实训课程学习为背景，基于MATLAB软件进行系统建模与仿真实验。
通过对实验过程的总结，详细阐述了系统建模与仿真的步骤及关键技巧，并结合实际案例进行了实验验证。
本次实训课程的学习使我深入理解了控制工程的基础理论，并掌握了利用MATLAB进行系统建模与仿真的方法。
1. 引言控制工程是一门应用广泛的学科，具有重要的理论和实践意义。
在控制工程实训课程中，学生通过实验来加深对控制系统的理解，并运用所学知识进行系统建模与仿真。
本次实训课程主要基于MATLAB软件进行，本文将对实验过程进行总结与报告。
2. 系统建模与仿真步骤2.1 确定系统模型在进行系统建模与仿真实验之前，首先需要确定系统的数学模型。
根据实际问题，可以选择线性或非线性模型，并利用控制理论进行建模。
在这个步骤中，需要深入理解系统的特性与工作原理，并将其用数学方程表示出来。
2.2 参数识别与估计参数识别与估计是系统建模的关键，它的准确性直接影响到后续仿真结果的可靠性。
通过实际实验数据，利用系统辨识方法对系统的未知参数进行估计。
在MATLAB中，可以使用系统辨识工具包来进行参数辨识。
2.3 选择仿真方法系统建模与仿真中，需要选择合适的仿真方法。
在部分情况下，可以使用传统的数值积分方法进行仿真；而在其他复杂的系统中，可以采用基于物理原理的仿真方法，如基于有限元法或多体动力学仿真等。
2.4 仿真结果分析仿真结果的分析能够直观地反映系统的动态响应特性。
在仿真过程中，需对系统的稳态误差、动态响应、鲁棒性等进行综合分析与评价。
通过与理论期望值的比较，可以对系统的性能进行评估，并进行进一步的优化设计。
3. 实验案例及仿真验证以PID控制器为例，说明系统建模与仿真的步骤。
首先，根据PID控制器的原理以及被控对象的特性，建立数学模型。
然后，通过实际实验数据对PID参数进行辨识和估计。
建模与仿真实验报告
建模与仿真实验报告建模与仿真实验报告引言建模与仿真是一种常用的方法，用于研究和分析复杂系统的行为。
通过建立数学模型并进行仿真实验，我们可以更好地理解系统的运行机制，预测其未来的发展趋势，并为决策提供依据。
本实验报告将介绍我所进行的建模与仿真实验，以及所得到的结果和结论。
1. 实验目标本次实验的目标是研究一个电动汽车的充电过程，并通过建模与仿真来模拟和分析其充电时间和电池寿命。
2. 实验步骤2.1 建立数学模型首先，我们需要建立一个数学模型来描述电动汽车充电过程。
根据电动汽车的充电特性和电池的充电曲线，我们选择了一个二阶指数函数来表示充电速度和电池容量之间的关系。
通过对历史充电数据的分析，我们确定了模型的参数，并进行了合理的调整和验证。
2.2 仿真实验基于建立的数学模型，我们使用MATLAB软件进行了仿真实验。
通过输入不同的充电时间和初始电池容量，我们可以获得充电过程中电池容量的变化情况，并进一步分析充电时间与电池寿命之间的关系。
3. 实验结果通过多次仿真实验，我们得到了一系列充电时间和电池寿命的数据。
根据这些数据，我们可以绘制出充电时间与电池寿命的关系曲线。
实验结果表明，充电时间与电池寿命呈现出一种非线性的关系，即充电时间的增加并不总是能够延长电池的使用寿命。
4. 结果分析通过对实验结果的分析，我们可以得出以下结论：4.1 充电时间的增加并不总是能够延长电池的使用寿命。
虽然在一定范围内增加充电时间可以提高电池的容量，但过长的充电时间会导致电池内部产生过多的热量，从而缩短电池的寿命。
4.2 充电速度对电池寿命的影响较大。
较快的充电速度会增加电池的热量产生，从而缩短电池的寿命；而较慢的充电速度则可以减少电池的热量产生，延长电池的寿命。
4.3 充电时间和电池寿命之间的关系受到电池类型和充电方式等因素的影响。
不同类型的电池在充电过程中表现出不同的特性，因此在实际应用中需要根据具体情况进行充电策略的选择。
系统建模与仿真实验
系统仿真与建模分析实验实验一生态平衡建模实验系统描述：在一个封闭的海岛上，设有两个群体：1. 狐狸（FOXES）;2.啮齿动物（RODENTS情况是：1）狐狸出生后，需要八个月成长为成年狐狸，幼年狐狸每只（每月）要吃10 只啮齿动物，若没有吃的就饿死，幼年狐狸的出生率为4，成年狐狸死亡因素有两个，一是每只狐狸每月要吃60 只啮齿动物，若没有吃的就要饿死，二是从仿真时间算起，十年之后，每月要被猎人打死4 只。
2）啮齿动物RODY出生后，三个月即可长成为成年啮齿动物，啮齿动物的出生率为0.8 ，如果幼年啮齿动物的父母死亡，则以短缺扶养和保护而死亡。
成年啮齿动物每月的死亡率有两个原因决定：一个是被狐狸吃掉，一个原因是总数超过100000（十万）只，则以水草不足而饿死。
一、实验目的：通过此实验了解系统动力学的仿真方法，学会用所学的建模理论来对实际问题进行建模，并对实际问题进行分析。
对此生态平衡系统进行仿真实验，改变不同的控制参数，分析实验的结果，得出系统保持生态平衡的条件，为决策者决策提供理论分析基础。
二．实验原理系统动力学（System Dynamics）是美国麻省理工学院J.W福雷斯特（JayW Forrester教授创立的一门新兴学科。
它按照自身独特的方法论建立系统的动态模型，并借助于计算机进行仿真，以处理行为随时间变化的系统的问题。
系统动力学首先强调系统性的观点，以及联系、发展、运动的观点，是研究复杂系统，诸如:社会、经济、环境、人口、生态平衡、产业发展等的有效工具。
系统动力学的研究对象主要是社会经济系统。
社会经济系统的范围十分广泛，凡是涉及到人类的社会活动和经济活动的系统都属于社会系统。
诸如本文要研究的人口系统、资源系统、环境系统、经济系统、科技系统、能源系统，都属于社会经济系统。
系统动力学的基础是通过实验方法认识系统的行为，为管理决策者提供决策的依据。
系统动力学仿真的基本步骤是：（1）明确建模目的一般来说，系统动力学对社会系统进行仿真实验的主要目的是认识和预测系统的结构和设计最佳参数，为制定合理的政策提供依据。
ATRU建模与仿真分析 实验报告模板仿真操作说明 (1)
实验一、ATRU正常工况供电特性仿真实验一、实验目的1．测量ATRU空载时的变压器输出及直流输出电压，观测电压波形，分析验证移相原理。
2.带载状态下，测量ATRU负载时的供电特性曲线，分析滤波前后波形THD大小及区别，并分析原因。
二、预习要点1．ATRU工作原理是什么？在空载实验时应该如何测量电压移相波形？2．做负载供电特性实验时，THD及直流畸变系数的定义是什么？如何测量？三、实验项目1．空载实验自耦变压器移相原理分析。
2．负载供电特性。
3．变压变频输入实验。
四、实验内容及步骤1．空载实验和变压器移相原理仿真分析1）参考仿真操作说明书建立仿真模型，将输入电压幅值设定为115V，频率为400Hz，将幅值和频率固定，电源设置完成，设置仿真时间1s，启动开始仿真。
2）测试并记录变压器输出线电压、整流器输出电压、负载端电压，记录其波形并进行分析。
3）记录整流器并联输出端和输出滤波后的电压波形，改变输出滤波电感和电容值，分析滤波效果。
5）根据自耦变压器变压器输出线电压向量图，选择两个线电压，记录两个线电压波形的时间差，计算出两波形的相位差，验证变压器的移相原理。
图1变压器输出线电压向量图2．负载特性测试1）将输出接上负载，由空载到负载状态，ATRU进入正常工作状态，仿真时间1S；2）选择输出负载，加入5kW、10kW、3kW负载，观察不同负载情况下，输出电压和电流的变化。
记录于表1.表1ATRU负载实验序号1234负载(kW)空载负载电压(V)负载电流(I)3．变压变频实验1）分别将输人电压幅值调整为108V和118V，频率为额定频率400Hz，观察改变输入电压幅值对ATRU输出性能的影响。
2）调节变频电源的幅值固定为额定115V，将输入电压频率调整为350Hz至450HZ观察改变输入电压频率对ATRU输出性能的影响。
五、实验报告1.分析ATRU空载仿真实验电压及电流波形数据，给出自耦变压器输出电压移相波形及电流波形分析。
simulink仿真实验报告
Simulink仿真实验报告1. 引言本报告旨在对Simulink仿真实验进行全面、详细、完整且深入地探讨。
Simulink 是一种基于模型的设计和仿真环境，广泛应用于工程领域。
本实验通过使用Simulink进行系统建模和仿真，以验证系统的性能和可行性。
2. 实验目的本实验的主要目的是熟悉Simulink的基本操作和功能，并通过实际案例来了解系统建模和仿真的过程。
具体目标如下： 1. 掌握Simulink的界面和基本操作； 2. 学习如何建立系统模型； 3. 了解如何进行仿真和分析。
3. 实验步骤3.1 Simulink介绍Simulink是一种图形化的建模和仿真环境，可以用于设计和分析各种系统。
它提供了丰富的工具箱和模块，使得系统建模变得更加简单和直观。
3.2 Simulink界面Simulink的界面由多个窗口组成，包括模型窗口、库浏览器、信号浏览器等。
模型窗口是主要的工作区域，用于建立和编辑系统模型。
3.3 系统建模在Simulink中，系统模型由各种模块和连接线组成。
模块可以是数学运算、信号源、控制器等。
通过拖拽和连接这些模块，可以建立系统的结构。
3.4 仿真设置在进行仿真前，需要设置仿真参数，如仿真时间、步长等。
这些参数会影响仿真的准确性和效率。
3.5 仿真分析仿真完成后，可以对系统的性能进行分析。
Simulink提供了丰富的工具和图表，可以用于绘制系统的输出响应、频谱分析等。
4. 实验案例本实验选取了一个简单的控制系统作为案例，用于说明Simulink的应用过程。
4.1 系统描述控制系统包括一个输入信号、一个控制器和一个输出信号。
输入信号经过控制器后，通过输出信号进行输出。
4.2 模型建立在Simulink的模型窗口中，通过拖拽和连接模块，可以建立控制系统的模型。
首先添加输入信号模块，然后添加控制器模块，最后添加输出信号模块。
4.3 仿真设置设置仿真参数，如仿真时间为10秒，步长为0.01秒。
实验5_SIMULINK建模与仿真实验
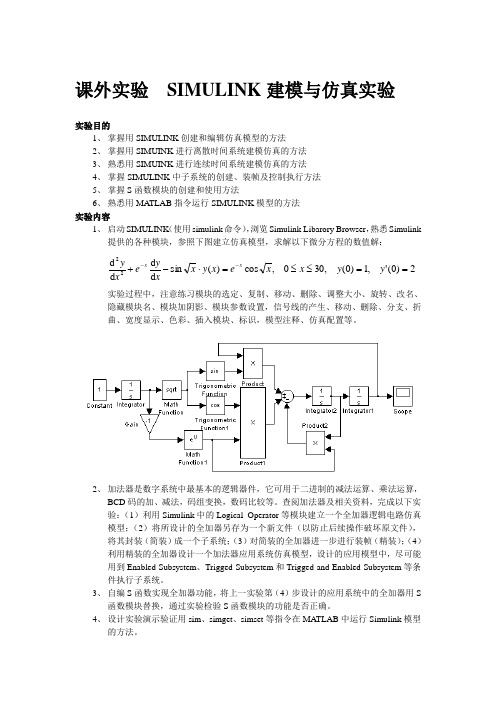
课外实验 SIMULINK 建模与仿真实验 实验目的1、 掌握用SIMULINK 创建和编辑仿真模型的方法2、 掌握用SIMUINK 进行离散时间系统建模仿真的方法3、 熟悉用SIMUINK 进行连续时间系统建模仿真的方法4、 掌握SIMULINK 中子系统的创建、装帧及控制执行方法5、 掌握S 函数模块的创建和使用方法6、 熟悉用MA TLAB 指令运行SIMULINK 模型的方法实验内容1、 启动SIMULINK （使用simulink 命令），浏览Simulink Libarory Browser ，熟悉Simulink 提供的各种模块，参照下图建立仿真模型，求解以下微分方程的数值解： 2)0(',1)0(,300,cos )(sin d d d d 22==≤≤=⋅-+--y y x x e x y x x y e x y x x 实验过程中，注意练习模块的选定、复制、移动、删除、调整大小、旋转、改名、隐藏模块名、模块加阴影、模块参数设置，信号线的产生、移动、删除、分支、折曲、宽度显示、色彩、插入模块、标识，模型注释、仿真配置等。
2、 加法器是数字系统中最基本的逻辑器件，它可用于二进制的减法运算、乘法运算，BCD 码的加、减法，码组变换，数码比较等。
查阅加法器及相关资料，完成以下实验：（1）利用Simulink 中的Logical Operator 等模块建立一个全加器逻辑电路仿真模型；（2）将所设计的全加器另存为一个新文件（以防止后续操作破坏原文件），将其封装（简装）成一个子系统；（3）对简装的全加器进一步进行装帧（精装）；（4）利用精装的全加器设计一个加法器应用系统仿真模型，设计的应用模型中，尽可能用到Enabled Subsystem 、Trigged Subsystem 和Trigged and Enabled Subsystem 等条件执行子系统。
3、 自编S 函数实现全加器功能，将上一实验第（4）步设计的应用系统中的全加器用S 函数模块替换，通过实验检验S 函数模块的功能是否正确。
simulink仿真实验报告
simulink仿真实验报告Simulink 仿真实验报告引言：Simulink 是一种常用的建模和仿真工具，它可以帮助工程师们在设计和开发过程中进行系统级建模和仿真。
本文将通过一个实际的仿真实验来展示 Simulink 的应用。
一、实验背景在现代工程领域中，系统的建模和仿真是非常重要的一步。
通过仿真实验，我们可以在实际制造之前对系统进行测试和优化，节省了时间和成本。
本实验的目标是使用 Simulink 对一个电机驱动系统进行建模和仿真，以验证其性能和稳定性。
二、实验步骤1. 系统建模在 Simulink 中，我们首先需要将电机驱动系统进行建模。
我们可以使用Simulink 提供的各种组件来构建系统模型，例如传感器、控制器、电机等。
在本实验中，我们将使用 PID 控制器来控制电机的转速。
2. 参数设置在建模过程中，我们需要设置各个组件的参数。
例如，我们需要设置 PID 控制器的比例、积分和微分系数，以及电机的转动惯量和阻尼系数等。
这些参数的设置将直接影响系统的性能。
3. 仿真运行在模型建立和参数设置完成后，我们可以进行仿真运行。
通过设置仿真时间和输入信号，我们可以观察系统在不同条件下的响应情况。
例如，我们可以通过改变输入信号的频率和幅度来测试系统的稳定性和鲁棒性。
4. 结果分析仿真运行完成后，我们可以分析仿真结果。
通过观察输出信号的波形和频谱，我们可以评估系统的性能和稳定性。
例如，我们可以计算系统的响应时间、超调量和稳态误差等指标，以评估系统的控制效果。
三、实验结果在本实验中，我们成功建立了一个电机驱动系统的 Simulink 模型，并进行了仿真运行。
通过观察仿真结果，我们发现系统在不同输入信号条件下的响应情况。
在一些情况下，系统的响应时间较短，稳态误差较小，表现出良好的控制效果。
然而，在一些极端情况下，系统可能出现超调或不稳定的现象，需要进一步优化参数和控制策略。
四、实验总结通过本次仿真实验，我们深入了解了 Simulink 的应用和优势。
simulink建模及动态仿真的一些实验步骤
simulink建模及动态仿真的一些实验步骤Simulink是MATLAB中的一种可视化仿真工具，可以用于动态系统建模、仿真和分析。
以下是一些Simulink建模及动态仿真的实验步骤：启动Simulink：首先，需要打开MATLAB，然后在MATLAB 的命令窗口中输入“simulink”命令，或者点击工具栏中的Simulink 图标来启动Simulink。
新建模型：在Simulink的启动界面中，可以选择“Blank Model”来新建一个空白的模型。
也可以选择其他预设的模型模板来开始建模。
构建系统模型：在新建的模型窗口中，可以通过从Simulink 的模块库中拖拽模块到模型窗口中来构建系统模型。
模块库中包含了各种类型的模块，如源模块、接收模块、处理模块等。
将这些模块按照系统的结构和功能连接起来，形成一个完整的系统模型。
设置模块参数：对于模型中的每个模块，都可以双击打开其参数设置对话框，设置其参数和初始条件。
这些参数和初始条件将决定模块在仿真中的行为。
设置仿真参数：在模型窗口的工具栏中，可以点击“Simulation”->“Model Configuration Parameters”来打开仿真参数设置对话框。
在这个对话框中，可以设置仿真的起始和结束时间、仿真步长、求解器类型等参数。
开始仿真：完成以上步骤后，可以点击模型窗口工具栏中的“Run”按钮来开始仿真。
在仿真过程中，可以实时观察模型中各个模块的状态和输出。
分析结果：仿真结束后，可以使用Simulink提供的各种分析工具来分析仿真结果。
例如，可以使用示波器模块来显示仿真过程中某个模块的输出波形，也可以使用MATLAB的工作空间来查看和处理仿真数据。
以上步骤是一个基本的Simulink建模和动态仿真的过程。
在实际使用中，可能还需要根据具体的需求和系统特点进行一些额外的设置和调整。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课程名称电力电子建模与仿真学生姓名学号专业班级电气专业指导教师2012年5月31日PWM, bipolar-voltage-switching, 1-phase(1PHBSINV)The experiment circuit diagram as above.Problems1. Obtain the following waveforms using 1Phbsinv: (a) o v and o i .Figure 1-1Output voltage （o v ） and current （o i ） waveform(b) o v and d i .Electronics Modeling Simplified using PSpice (Release 9)," . Time0s5ms 10ms 15ms 20ms 25ms 30ms 35ms 40ms 45ms 50msI(V5)-20A0A20AV1(L1) - V2(V5)-400V0V400VSEL>>Time0s5ms 10ms 15ms 20ms 25ms 30ms 35ms 40ms 45ms 50msI(V1)-20A0A20AV1(L1) - V2(V5)-400V0V400VSEL>>Figure 1-2Output voltage （o v ） and the input current （i d ） waveform(c) o v , o i and o p .Figure 1-3 Output voltage （o v ）,current （o i ）,and power （o p ） of the waveform2. Obtain v01 by means of Fourier analysis of the o v waveform. Compare 1o v with its precalculated nominal value.Output voltage to Fourier analysis.FOURIER COMPONENTS OF TRANSIENT RESPONSE V(N00396,N00826)DC COMPONENT = -1.364900E+00HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZEDNO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG)1 4.000E+01 2.152E+02 1.000E+00 7.240E+01 0.000E+00 2 8.000E+01 8.215E-01 3.817E-03 -1.373E+02 -2.821E+02 3 1.200E+02 1.087E+00 5.052E-03 -8.038E+01 -2.976E+024 1.600E+02 6.943E-01 3.226E-03 -8.213E+01 -3.717E+025 2.000E+02 5.693E-01 2.645E-03 -9.786E+01 -4.599E+026 2.400E+02 6.443E-01 2.993E-03 8.586E+01 -3.485E+027 2.800E+02 9.711E-01 4.512E-03 3.420E+01 -4.726E+028 3.200E+02 1.027E+00 4.772E-03 9.653E+01 -4.827E+029 3.600E+02 1.231E+00 5.722E-03 1.556E+02 -4.960E+02 10 4.000E+02 1.534E+00 7.125E-03 3.867E+01 -6.853E+02 11 4.400E+02 6.245E-01 2.902E-03 1.273E+02 -6.690E+02 12 4.800E+02 3.197E-01 1.485E-03 -3.498E+01 -9.037E+02Time0s5ms10ms 15ms 20ms 25ms 30ms 35ms 40ms 45ms 50msI(V5) * (V1(L1)-V2(V5))-5.0KW0W 5.0KW I(V5)-20A0A 20A V1(L1) - V2(V5)-400V0V 400V SEL>>13 5.200E+02 1.613E+00 7.495E-03 -1.635E+02 -1.105E+03 14 5.600E+02 1.071E+00 4.974E-03 -1.276E+01 -1.026E+03 15 6.000E+02 2.202E-01 1.023E-03 7.034E+01 -1.016E+03 16 6.400E+02 1.064E+00 4.943E-03 -4.897E+01 -1.207E+03 17 6.800E+02 6.628E-01 3.079E-03 -1.572E+02 -1.388E+03 18 7.200E+02 1.169E+00 5.433E-03 -8.197E+01 -1.385E+03 19 7.600E+02 8.240E-01 3.828E-03 -8.104E+01 -1.457E+03 20 8.000E+02 1.059E+00 4.919E-03 1.142E+02 -1.334E+03TOTAL HARMONIC DISTORTION = 1.969687E+00 PERCENTV 01.peak =215.2VV o1=01.peak2=2=152.17VV o 1（rms ）=153.33VThrough the comparison we found Fourier analysis get V o1 and its precalculated nominal value V o 1（rms ） approximately equal .3. Using the results of Problem 2, obtain the ripple component ripple v waveform in the output voltage.Figure 1-4the ripple component V ripple waveform in the output voltage.4. Obtain 1o i by means of Fourier analysis of the o i waveform. Compare 1o i with itsprecalculated nominal value.For the output current of Fourier analysis as follows.FOURIER COMPONENTS OF TRANSIENT RESPONSE I(V_V5)DC COMPONENT = -4.719698E-01HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZEDTime0s5ms 10ms15ms 20ms 25ms 30msV1(L1) - V2(V5) -215.2 * SIN(2*pi*40*Time+72.4)-500V0V500VNO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG)1 4.000E+01 1.354E+01 1.000E+00 4.403E+01 0.000E+002 8.000E+01 3.947E-02 2.916E-03 -1.560E+02 -2.441E+02 3 1.200E+02 7.786E-02 5.752E-03 -1.118E+02 -2.439E+024 1.600E+02 2.435E-02 1.799E-03 -1.555E+02 -3.317E+025 2.000E+02 2.570E-02 1.899E-03 -1.064E+02 -3.265E+026 2.400E+02 1.252E-02 9.249E-04 1.561E+02 -1.081E+027 2.800E+02 2.285E-03 1.688E-04 1.474E+02 -1.609E+028 3.200E+02 4.269E-03 3.154E-04 1.430E+02 -2.092E+029 3.600E+02 4.284E-03 3.165E-04 1.701E+02 -2.262E+02 10 4.000E+02 9.197E-03 6.794E-04 -1.136E+02 -5.539E+02 11 4.400E+02 1.157E-02 8.546E-04 1.496E+02 -3.348E+02 12 4.800E+02 6.981E-03 5.157E-04 1.585E+02 -3.699E+02 13 5.200E+02 1.201E-02 8.870E-04 1.259E+02 -4.466E+02 14 5.600E+02 8.194E-03 6.053E-04 -1.427E+02 -7.591E+02 15 6.000E+02 5.535E-03 4.089E-04 -1.350E+02 -7.956E+02 16 6.400E+02 4.930E-03 3.642E-04 -1.476E+02 -8.522E+02 17 6.800E+02 4.122E-03 3.045E-04 1.635E+02 -5.851E+02 18 7.200E+02 7.549E-03 5.577E-04 1.583E+02 -6.343E+02 19 7.600E+02 4.627E-03 3.418E-04 -1.707E+02 -1.007E+03 20 8.000E+02 1.062E-03 7.843E-05 1.569E+02 -7.238E+02TOTAL HARMONIC DISTORTION = 7.276557E-01 PERCENTI o 1=2=9.574AI o 1(rms )=10AThrough the comparison I didn't find that by Fourier analysis get I o 1 and itsprecalculated nominal value I o 1(rms ) approximately equal.5. Using the results of Problem 4, obtain the ripple component ripple i in the output current.Time0s5ms10ms 15ms 20ms 25ms 30msI(V5) -13.54 * SIN(2*pi*40*Time+44.03)-20A0A20AFigure 1-5the ripple componenti in the output current.ripple6. Obtain ()I avg and 2d i(the component at the 2nd harmonicdfrequency) by means of the Fourier analysis of the id waveform. Compare them with their precalculated nominal values.Below is the input current to id Fourier analysis results.FOURIER COMPONENTS OF TRANSIENT RESPONSE I(V_V1)DC COMPONENT = -4.893025E+00HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZEDNO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG)1 4.000E+01 4.692E-01 1.000E+00 6.937E+01 0.000E+002 8.000E+01 5.423E+00 1.156E+01 -1.554E+02 -2.942E+023 1.200E+02 6.118E-02 1.304E-01 3.030E+01 -1.778E+024 1.600E+02 8.395E-02 1.789E-01 5.346E+01 -2.240E+025 2.000E+02 4.896E-02 1.043E-01 -9.629E+00 -3.565E+026 2.400E+02 3.820E-02 8.141E-02 -5.784E+00 -4.220E+027 2.800E+02 4.377E-02 9.328E-02 -1.139E+02 -5.995E+028 3.200E+02 5.191E-02 1.106E-01 7.187E+01 -4.831E+029 3.600E+02 3.148E-02 6.709E-02 -1.697E+02 -7.940E+0210 4.000E+02 5.119E-02 1.091E-01 -7.545E+01 -7.691E+0211 4.400E+02 3.731E-02 7.952E-02 -1.656E+02 -9.287E+0212 4.800E+02 1.236E-02 2.634E-02 6.434E+01 -7.681E+0213 5.200E+02 4.233E-02 9.020E-02 -1.740E+02 -1.076E+0314 5.600E+02 2.151E-02 4.585E-02 -9.854E+01 -1.070E+0315 6.000E+02 3.325E-02 7.085E-02 1.731E+02 -8.674E+0216 6.400E+02 4.631E-02 9.869E-02 3.875E+01 -1.071E+0317 6.800E+02 4.390E-02 9.355E-02 1.430E+02 -1.036E+0318 7.200E+02 5.532E-02 1.179E-01 -8.981E+01 -1.338E+0319 7.600E+02 3.294E-02 7.020E-02 3.511E+01 -1.283E+0320 8.000E+02 1.153E-01 2.458E-01 7.638E+00 -1.380E+03TOTAL HARMONIC DISTORTION = 1.156687E+03 PERCENTI d AVG=4.893Ai d2=5.423sin(2π×80t−155.4)I d2‘=2=3.83ABy their precalculated nominal values calculated the following parameters.V o=153.33VI o=10AV d=271VI d=V o I oV d cosφ=153.33×10271×cos44.03=5.08AI d2=2o oV=2271=4ABy above calculation and comparison found that I d AVG and I d value is very close, I d2‘and I d2also approximately equal.7. Using the results of Problem 6, obtain the high frequency ripple componentdi, ripple in the input dc current. Calculate its rms value.I d1=2=0.332A%THD=1156.687I s=I d1(THD)=0.332×11.56687=3.838APWM Inverter, 3-phase (PWMINV3)The experiment circuit diagram as above.Problems1. Obtain the following waveforms using : (a)V AN and A i .Figure 2-1Node A and the voltage between N(V AN ) and through the inductance of L1current(A i ) waveform(b) an v and A i .PWM_TRI_3PH_SUBCKT1f s = 1kHzGB1GB2GC1GC2v cA v cB v cC GA1GA2V13V15GA1Electronics Modeling Simplified using PSpice (Release 9)," .V14GB1GC1GB2GC2GA2Time0s5ms 10ms 15ms 20ms 25ms 30ms 35ms 40ms 45ms 50msI(L1)-20A0A20AV1(L1)-400V0V400VSEL>> Time0s5ms 10ms 15ms 20ms 25ms 30ms 35ms 40ms 45ms 50msI(L1)-20A0A20AV1(L1) - V2(V5)-400V0V400VSEL>>Figure 2-2 Node A and the voltage between n(V An ) and through the inductance of L1current(A i ) waveform(c) AN v and d i .Figure 2-3Node A and the voltage between N(V An ) and input current d i waveform2. Obtain 1An v by means of Fourier analysis of the An v waveform. Compare 1An v withits precalculated nominal value.For the output current of Fourier analysis as followsFOURIER COMPONENTS OF TRANSIENT RESPONSE V(VA,VNEUTRAL)DC COMPONENT = -2.239930E-02HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZEDNO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG)1 4.762E+01 1.491E+02 1.000E+00 1.372E+02 0.000E+00 2 9.524E+01 4.832E-01 3.240E-03 -8.232E+01 -3.568E+02 3 1.429E+02 4.600E-02 3.085E-04 -1.106E+02 -5.222E+02 4 1.905E+02 4.246E-01 2.848E-03 1.929E+01 -5.296E+025 2.381E+02 6.052E-01 4.059E-03 3.124E+00 -6.830E+026 2.857E+02 4.407E-02 2.955E-04 -1.323E+02 -9.557E+027 3.333E+02 7.786E-01 5.222E-03 1.476E+02 -8.130E+028 3.810E+02 6.795E-01 4.557E-03 1.786E+02 -9.192E+029 4.286E+02 4.730E-02 3.172E-04 -1.491E+02 -1.384E+03 10 4.762E+02 9.098E-01 6.101E-03 1.662E+02 -1.206E+03 11 5.238E+02 1.551E-01 1.040E-03 -7.099E+01 -1.580E+03 12 5.714E+02 4.816E-02 3.230E-04 -1.729E+02 -1.820E+03 13 6.190E+02 1.455E+00 9.758E-03 1.256E+02 -1.658E+03Time0s0.5ms 1.0ms 1.5ms 2.0ms 2.5ms 3.0ms 3.5ms 4.0ms 4.5ms 5.0msI(V1)-20A-10A0AV1(L1)-400V0V400VSEL>>14 6.667E+02 8.385E-01 5.623E-03 -9.956E+01 -2.021E+03 15 7.143E+02 4.384E-02 2.940E-04 1.718E+02 -1.887E+03 16 7.619E+02 2.030E-01 1.361E-03 -9.822E+01 -2.294E+03 17 8.095E+02 1.799E+00 1.207E-02 -9.840E+01 -2.431E+03 18 8.571E+02 4.842E-02 3.247E-04 1.518E+02 -2.318E+03 19 9.048E+02 4.585E+01 3.075E-01 1.751E+02 -2.432E+03 20 9.524E+02 7.544E-01 5.059E-03 7.145E+01 -2.673E+03TOTAL HARMONIC DISTORTION = 3.081436E+01 PERCENTV An 1=2=105.43VV An 1(rms )=105.39VHave above comparison, through the Fourier analysis, the calculated V An 1 and its precalculated nominal value V An 1(rms ) approximately equal, the error is very small3. Using the results of Problem 2, obtain the ripple component ripple v waveform in theoutput voltage.Figure 2-4 the ripple component ripple v waveform in theoutput voltage4. Obtain 1A i by means of Fourier analysis of A i waveform. Compare1A i with itsprecalculated nominal value.For the output current of Fourier analysis as followsFOURIER COMPONENTS OF TRANSIENT RESPONSE I(L_L1)DC COMPONENT = -1.633990E-02HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZEDTime0s5ms 10ms 15ms20ms 25ms 30ms 35ms 40ms 45ms 50msV1(L1) - V2(V5) -149.1 * SIN(2*pi*47.619*Time+137.2)-400V0V400VNO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG)1 4.762E+01 1.417E+01 1.000E+00 1.076E+02 0.000E+00 2 9.524E+01 1.690E-02 1.193E-03 -1.546E+02 -3.698E+02 3 1.429E+02 8.724E-03 6.157E-04 1.718E+02 -1.510E+02 4 1.905E+02 7.686E-03 5.424E-04 1.213E+02 -3.090E+025 2.381E+02 1.073E-02 7.575E-04 -1.011E+02 -6.390E+026 2.857E+02 3.529E-03 2.491E-04 1.441E+02 -5.014E+027 3.333E+02 4.672E-03 3.297E-04 3.532E+01 -7.177E+028 3.810E+02 5.291E-03 3.734E-04 1.213E+02 -7.393E+029 4.286E+02 2.874E-03 2.028E-04 1.227E+02 -8.455E+02 10 4.762E+02 6.673E-03 4.709E-04 1.030E+02 -9.728E+02 11 5.238E+02 7.769E-03 5.483E-04 9.967E+01 -1.084E+03 12 5.714E+02 1.698E-03 1.198E-04 1.012E+02 -1.190E+03 13 6.190E+02 6.125E-03 4.322E-04 7.720E+01 -1.321E+03 14 6.667E+02 1.612E-03 1.137E-04 1.249E+02 -1.381E+03 15 7.143E+02 1.685E-03 1.189E-04 8.254E+01 -1.531E+03 16 7.619E+02 2.819E-03 1.990E-04 1.944E+00 -1.719E+03 17 8.095E+02 4.433E-02 3.129E-03 1.731E+02 -1.656E+03 18 8.571E+02 1.128E-03 7.959E-05 6.326E+01 -1.873E+03 19 9.048E+02 8.088E-01 5.708E-02 8.755E+01 -1.957E+03 20 9.524E+02 9.749E-03 6.880E-04 -3.756E+01 -2.189E+03TOTAL HARMONIC DISTORTION = 5.720013E+00 PERCENTI A 1=2=10.02AI A 1(rms )=10AHave above comparison, through the Fourier analysis, the calculated I A 1 and its precalculated nominal value I A 1(rms ) approximately equal, the error is very small5. Using the results of Problem 4, obtain the ripple component ripple i in the output current.Time0s5ms 10ms 15ms20ms 25ms 30ms 35ms 40ms 45ms 50msI(L1) -14.17 * SIN(2*pi*47.619*Time+107.6)-20A0A20AFigure 2-5the ripple component ripple i in the output current.6. Obtain ()d I avg by means of Fourier analysis and obtain the high frequency ripple ,d ripple i = d i - ()d I avg in the input current.For the output current of Fourier analysis as followsFOURIER COMPONENTS OF TRANSIENT RESPONSE I(V_V1)DC COMPONENT = -8.787830E+00HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZEDNO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG)1 4.762E+01 1.441E-02 1.000E+00 1.634E+02 0.000E+00 2 9.524E+01 1.172E-02 8.135E-01 2.644E+01 -3.004E+023 1.429E+02 5.315E-02 3.689E+00 1.406E+02 -3.497E+024 1.905E+02 6.418E-03 4.454E-01 7.955E+01 -5.742E+025 2.381E+02 7.029E-03 4.879E-01 -1.301E+01 -8.302E+026 2.857E+02 4.560E-02 3.165E+00 -1.116E+02 -1.092E+037 3.333E+02 5.715E-03 3.967E-01 7.054E+01 -1.073E+038 3.810E+02 6.181E-03 4.290E-01 -2.357E+01 -1.331E+039 4.286E+02 9.775E-02 6.784E+00 -1.723E+01 -1.488E+03 10 4.762E+02 5.177E-03 3.593E-01 5.656E+01 -1.578E+03 11 5.238E+02 5.693E-03 3.951E-01 -4.294E+01 -1.841E+03 12 5.714E+02 9.631E-02 6.684E+00 -7.650E+01 -2.038E+03 13 6.190E+02 5.416E-03 3.759E-01 3.786E+01 -2.087E+03 14 6.667E+02 5.940E-03 4.123E-01 -6.016E+01 -2.348E+03 15 7.143E+02 6.415E-02 4.452E+00 8.983E+01 -2.362E+03 16 7.619E+02 5.151E-03 3.575E-01 1.546E+01 -2.599E+03 17 8.095E+02 5.751E-03 3.992E-01 -9.197E+01 -2.870E+03 18 8.571E+02 2.787E+00 1.934E+02 -3.141E+01 -2.973E+03 19 9.048E+02 2.586E-03 1.794E-01 -7.696E+01 -3.182E+03 20 9.524E+02 2.128E-03 1.477E-01 -9.392E+01 -3.363E+03TOTAL HARMONIC DISTORTION = 1.937989E+04 PERCENTI d （AVG ）=8.78783AFigure 2-6the high frequency ripple ,d ripple i = d i - ()d I avg in the input current7. Obtain the load neutral voltage with respect to the mid-point of the dc input voltage.As mentioned in the circuit diagram, dc power supply side split into two power supply, and their voltage values are the same.Figure 2-7 the load neutral voltage with respect to the mid-point of the dc input voltage.Time0s1ms2ms 3ms 4ms 5ms 6ms 7ms 8ms 9ms 10ms-I(V1) -8.78783-10A0A10AGB2GA2V14V13Electronics Modeling Simplified using PSpice (Release 9)," .GC1PWM_TRI_3PH_SUBCKT1f s = 1kHzGB1GB2GC1GC2v cA v cB v cC GA1GA2GB1GA1GC2V15Time0s1ms2ms 3ms 4ms 5ms 6ms 7ms 8ms 9ms 10msV(V5:-) - V(V111:+)-200V0V200V。