2015数学模拟试卷(3) 打 (2)

合集下载

2015届中考数学模拟训练题(三)参考答案

2015届中考数学模拟训练题（三）参考答案一、选择题（共10小题，每小题3分，共30分） DBBCA ABDCC二、填空题(共6小题，每小题3分，共18分） 11. -2 ， 12. 52.510⨯， 13.12， 14. 960， 15.30y x =， 16.152. 三、解答题（共8小题，共72分）17.(1)y 21x =- (2)3x ≤ 18.(1)略（2）1319. (1)略（2）212010P == 20. (1)略(2)略（3）(2,0)P 21.（1）连接BE 、CD 、OD 、OE 、OB 、OC ，易证12ADE ABC ∠=∠,12AED ACB ∠=∠,∴60ADE AED ∠+∠=︒,0120ADE ∠= 120DOE BOC ∠=∠=︒, ∴ BC =DE.(2)过点A 作AM ⊥AD 于M .，过点A 作AN ⊥AD 于N .∵tan ∠ADE ＝12，0120BAC ∠=∴可令AM=1，AC=2，DM=DA=，1122DA CM CD AN ⋅=⋅∴5AN =∴sin 10AED ∠=.22.（1）设该公司生产每件商品的成本为m 元，则1+40%0.7(2040)m =⨯+（）解得30m =即该公司生产每件商品的成本为30元；（2）设销售该商品第x 天时，当天的利润为w 元，则 2(2002)(4030)2(45)6050w x x x =-+-=--+ 所以当45x =，w 有最大值，且最大值6050w =.即销售该商品第45天时，每天的利润最大，最大利润6050元；B（3）10502000a ≤≤23.（1）∵∠EPF=∠CPH =∠HAC =45︒,∴∠BFH =45︒.(2) 过点B 作BG ∥CD 交FH 的延长线于G.∵30G GDC HAC ABC ∠=∠=∠=∠=︒,2221tan 3CHAC ABC BH AB ==∠= 又CD CH BG BH=，1tan BG BF G==∠ ∴BF =；(3)tan CDαBF=. 25.（1）（1，4）；（2）如图过P 作x 轴的垂线再过A 、B 作y 轴的垂线构造两个直角三角形△PBE 、△APF ，要使△CPD 为直角三角形，只能是∠CPD ＝900，所以易证△PBE ∽△APF ，∴PE AFBE PF= 设A （1x ，21124ax ax a -++）、B （2x ，22224ax ax a -++）∴211221224(24)114(24)ax ax a x x ax ax a --++-=---++ 即212(1)(1)1a x x --=- ∴21212[()1]1a x x x x -++=-①联立224y ax ax a y kx k ⎧=-++⎨=-⎩得：2(2)40ax a k x a k -++++= ∴122k x x a +=+ 1241k x x a a=++②把②代入①解得14a =-。

2015年初中数学中考升学模拟试卷(三)

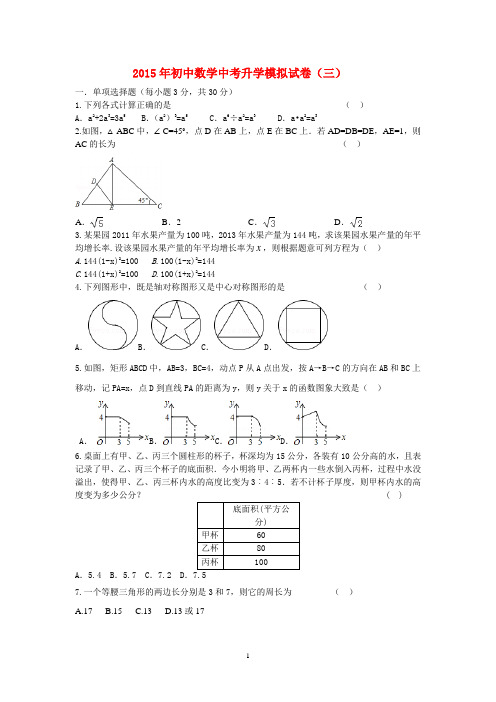
2015年初中数学中考升学模拟试卷（三）一．单项选择题（每小题3分，共30分）1.下列各式计算正确的是（）A．a2+2a3=3a5 B．（a2）3=a5 C．a6÷a2=a3 D．a•a2=a32.如图，△ABC中，∠C=45°，点D在AB上，点E在BC上．若AD=DB=DE，AE=1，则AC的长为（）B均增长率.设该果园水果产量的年平均增长率为x，则根据题意可列方程为（）A.144(1-x)2=100B.100(1-x)2=144C.144(1+x)2=100D.100(1+x)2=1444.下列图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．5.如图，矩形ABCD中，AB=3，BC=4，动点P从A点出发，按A→B→C的方向在AB和BC上移动，记PA=x，点D到直线PA的距离为y，则y关于x的函数图象大致是（）A．B．C．D．6.桌面上有甲、乙、丙三个圆柱形的杯子，杯深均为15公分，各装有10公分高的水，且表记录了甲、乙、丙三个杯子的底面积．今小明将甲、乙两杯内一些水倒入丙杯，过程中水没溢出，使得甲、乙、丙三杯内水的高度比变为3︰4︰5．若不计杯子厚度，则甲杯内水的高度变为多少公分？A．5.4 B．5.7 C．7.2 D．7.57.一个等腰三角形的两边长分别是3和7，则它的周长为（）A.17B.15C.13D.13或178.不等式组的解集是（）A.﹣1≤x ＜2B.x ≥﹣1C.x ＜2D.﹣1＜x ≤29.如图，△ABC 与△DEF 关于y 轴对称，已知A （﹣4，6），B （﹣6，2），E （2，1），则点D 的坐标为（）A.（﹣4，6）B.（4，6）C.（﹣2，1）D.（6，2）10．如图，四边形ABCD 是矩形，AB=6cm ，BC=8cm ，把矩形沿直线BD 折叠，点C 落在点E 处，BE 与AD 相交于点F ，连接AE ，下列结论：①△FED 是等腰三角形；②四边形ABDE 是等腰梯形；③图中共有6对全等三角形；④四边形BCDF 的周长为cm ；⑤AE 的长为cm ．其中结论正确的个数为（）A.2个B.3个C.4个D.5个二．填空题（共10道小题，每小题3分，共30分）11.已知地球的表面积约为510000000km 2，数510000000用科学记数法可表示为 . 12.在函数中，自变量x 的取值范围是 .13.过点（﹣1，7）的一条直线与x 轴，y 轴分别相交于点A ，B ，且与直线平行．则在线段AB 上，横、纵坐标都是整数的点的坐标是．14题图 18题图 19题图 20题图15.不等式组的解集是．16.若a ＜＜b ，且a ，b 为连续正整数，则b 2﹣a 2= ．17.某校举办“成语听写大赛”，15名学生进入决赛，他们所得分数互不相同，比赛共设8个获奖名额，某学生知道自己的分数后，要判断自己能否获奖，他应该关注的统计量是（填“平均数”或“中位数”）18.如图，矩形ABCD 的面积为（用含x 的代数式表示）．19.如图，直线a 、b 与直线c 相交，且a ∥b ，∠α=55°，则∠β= ．20.如图，正比例函数y=kx 与反比例函数y =x1 的图象相交于A ，B 两点，过B 作X 轴的垂线交X 轴于点C ，连接AC ，则△ABC 的面积是三．解答题（21题5分、22题6分、23题5分、24题8分、25题6分、26题8分、27题8分、28题14分，共60分）21.先化简，再求值：（+）•（x 2﹣1），其中x =．22．甲，乙两辆汽车分别从A ，B 两地同时出发，沿同一条公路相向而行，乙车出发2h 后休息，与甲车相遇后，继续行驶．设甲，乙两车与B 地的路程分别为y 甲（km ），y 乙（km ），甲车行驶的时间为x （h ），y 甲，y 乙与x 之间的函数图象如图所示，结合图象解答下列问题：（注：横轴的3应该为5）（1）乙车休息了 h ；（2）求乙车与甲车相遇后y 乙与x 的函数解析式，并写出自变量x 的取值范围；（3）当两车相距40km 时，直接写出x 的值．23.为了提高学生书写汉字的能力，增强保护汉字的意识，我市举办了首届“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每正确听写出一个汉字得1（1）求表中a 的值；（2）请把频数分布直方图补充完整；（3）若测试成绩不低于40分为优秀，则本次测试的优秀率是多少？（4）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小宇与小强两名男同学能分在同一组的概率．24.某企业新增了一个化工项目，为了节约资源，保护环境，该企业决定购买A、B两种型号（1）该企业有几种购买方案？（2）哪种方案更省钱，说明理由．25.两个长为2cm，宽为1cm的长方形，摆放在直线l上（如图①），CE=2cm，将长方形ABCD 绕着点C顺时针旋转α角，将长方形EFGH绕着点E逆时针旋转相同的角度．（1）当旋转到顶点D、H重合时，连接AE、CG，求证：△AED≌△GCD（如图②）．（2）当α=45°时（如图③），求证：四边形MHND为正方形．26.如图，四边形OABC是平行四边形，以O为圆心，OA为半径的圆交AB于D，延长AO 交⊙O于E，连接CD，CE，若CE是⊙O的切线，解答下列问题：（1）求证：CD是⊙O的切线；（2）若BC=3，CD=4，求平行四边形OABC的面积．27．平面直角坐标系xOy中，点A、B分别在函数y1=（x＞0）与y2=﹣（x＜0）的图象上，A、B的横坐标分别为a、b．（1）若AB∥x轴，求△OAB的面积；（2）若△OAB是以AB为底边的等腰三角形，且a+b≠0，求ab的值；（3）作边长为3的正方形ACDE，使AC∥x轴，点D在点A的左上方，那么，对大于或等于4的任意实数a，CD边与函数y1=（x＞0）的图象都有交点，请说明理由．28.如图矩形OABC，AB=2OA=2n，分别以OA和OC为x、y轴建立平面直角坐标系，连接OB，沿OB折叠，使点A落在P处。

2015年高三数学理科模拟试卷及参考答案

2015年高三数学理科模拟试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分150分。

考试时间120分钟。

第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1．若复数221z i i=++，其中i 是虚数单位，则复数z 的模为( )A.22B. 2C. 3D. 2 2．设a ∈R ，则“4a =”是“直线1:230l ax y +-=与直线2:20l x y a +-=平行”的( )条件A. 充分不必要B. 必要不充分C. 充要D. 既不充分也不必要3．设函数()2xf x =，则下列结论中正确的是( ) A. (1)(2)(2)f f f -<<- B. (2)(1)(2)f f f -<-<C. (2)(2)(1)f f f <-<-D. (1)(2)(2)f f f -<-<4．设等差数列{n a 的前n 项和是n S ，若11m m a a a +-<<-(m ∈N *,且2m ≥)，则必定有( )A. 0m S >，且10m S +<B. 0m S <，且10m S +>C. 0m S >，且10m S +>D. 0m S <，且10m S +<5．已知实数x ∈[1，9]，执行如图所示的流程图，则输出的x 不小于55的概率为( ) A.14B.23C.28D.386．某几何体的立体图如图所示，该几何体的三视图不可能是（）A ．B ．C ．D ．7．设函数()log (01)a f x x a =<<的定义域为[,](m n m <)n ,值域为[0,1],若n m -的最小值为13,则实数a 的值为( )A. 14B.14或23C.23D.23或348．设双曲线22143x y-=的左,右焦点分别为12,F F,过1F的直线l交双曲线左支于,A B两点,则22BF AF+的最小值为( )A.192B. 11C. 12D. 169．已知集合{}(,)(1)(1)A x y x x y y r=-+-≤，集合{}222(,)B x y x y r=+≤，若BA⊂，则实数r可以取的一个值是( )A. 21+ B. 3 C. 2 D.212+10．设函数11,(,2)()1(2),[2,)2x xf xf x x⎧--∈-∞⎪=⎨-∈+∞⎪⎩，则函数()()1F x xf x=-的零点的个数为( )A. 4B. 5C. 6D. 711．设等差数列{}na满足：22222233363645sin cos cos cos sin sin1sin()a a a a a aa a-+-=+，公差(1,0)d∈-.若当且仅当9n=时，数列{}n a的前n项和n S取得最大值，则首项1a的取值范围是( )A.74,63ππ⎛⎫⎪⎝⎭B.43,32ππ⎛⎫⎪⎝⎭C.74,63ππ⎡⎤⎢⎥⎣⎦D.43,32ππ⎡⎤⎢⎥⎣⎦12．已知椭圆，过椭圆右焦点F的直线L交椭圆于A、B两点，交y轴于P点．设，则λ1+λ2等于（）A．B．C．D．第Ⅱ卷(非选择题共90分)二、填空题：本大题共4小题，每小题5分，共20分.把答案填在答题卡的相应位置.13．从3,2,1,0中任取三个数字，组成无重复数字的三位数中，偶数的个数是(用数字回答)．14．若整数．．,x y满足不等式组70y xx yx-≥⎧⎪+-≤⎨⎪≥⎩,则2x y+的最大值为15．已知正三棱锥P﹣ABC中，E、F分别是AC，PC的中点，若EF⊥BF，AB=2，则三棱锥P﹣ABC的外接球的表面积为．16．设P（x，y）为函数y=x2﹣1图象上一动点，记，则当m最小时，点P的坐标为．三．解答题。

2015年高考数学模拟试题及答案

2 2
（1）求数列 a n 的通项公式；（2）设 bn
1 ,数列 bn 的前 n 项和为 Tn ,求证: Tn 2 . 2 an
20．（本小题共 13 分）若双曲线 E :
x2 y 2 1(a 0, b 0) 的离心率等于 2 ，焦点到渐近线的距离为 1，直线 y kx 1 与双 a 2 b2
D C
A．
3 10 10
B．
10 10
C．
5 10
D．
5 15
E
B A 7．已知正四棱柱 ABCD A1B1C1D1 中，AB 2, CC1 2 2 ，E 为 CC1 的中点，则直线 AC1 与平面 BED
的距离为 A．2 B．
3
C． 2
D．1
8．将甲、乙、丙等六人分配到高中三个年级，每个年级 2 人，要求甲必须在高一年级，乙和丙均不能在高三年级，则不同的安排种数为
(2)由（1）可知 bn 20．（本小题共 13 分）
c a 2 1 2 解：（1）由 a 得 b2 1 b 1
设 A x1 , y1 , B x2 , y2 ，由
故双曲线 E 的方程为 x y 1
2 2
y kx 1 得 1 k 2 x 2 2kx 2 0 2 2 x y 1

x 1 0 ，则 A B x 3
2 3
D． (, 1)
A． (3, )
B． (1, )
2 3
C． ( ,3)
2
2. 设 x R ， i 是虚数单位，则“ x 3 ”是“复数 z ( x 2 x 3) ( x 1)i 为纯虚数” 的 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 3．某几何体的正视图和侧视图均如图 1 所示，则该几何体的俯视图不可能是

南京市2015届高三年级第三次模拟考试数学WORD版与答案.doc

市 2015 届高三年级第三次模拟考试数学2015.05注意事项：1．本试卷共 4 页，包括填空题（第 1 题 ~第 14 题）、解答题（第15 题 ~第 20 题）两部分．本试卷满分为160 分，考试时间为120 分钟．2．答题前，请务必将自己的、班级、学校写在答题纸上．试题的答案写在答题纸．．．上对应题目的答案空格．考试结束后，交回答题纸．参考公式样本数据 x1， x2，， x n的方差 s2＝1 n －－ 1 nn ∑ (x i－ x )2，其中 x ＝n∑ x i．i ＝ 1 i ＝ 1锥体的体积公式：1h 为锥体的高．V＝ Sh，其中 S 为锥体的底面积，3一、填空题：本大题共14 小题，每小题 5 分，共70 分．请把答案填写在答题纸相应位置上．．．．．．．．2i－ 1，其中 i 为虚数单位，则z 的模为▲．1．已知复数 z＝1－i2．经统计，在银行一个营业窗口每天上午9 点钟排队等候的人数及相应概率如下：排队人数0 1 2 3 4 ≥ 5 概率0.1 0.16 0.3 0.3 0.1 0.04 则该营业窗口上午9 点钟时，至少有 2 人排队的概率是▲．x＋y≤ 2，3．若变量 x， y 满足约束条件 x≥1，则 z＝2x＋ y 的最大值是▲．y≥ 0，4．右图是一个算法流程图，则输出k 的值是▲．5．如图是甲、乙两位射击运动员的 5 次训练成绩（单位：环）的茎叶图，则成绩较为稳定（方差较小）的运动员是▲．开始k← 1S←40k←k＋ 1S←S－ 2k乙S≤ 0甲N 7 8Y输出 k 9 7 8 8 93 1 0 9 6 9 结束（第 4 题图）（第 5 题图）6．记不等式 x2＋ x－ 6＜ 0 的解集为集合A，函数 y＝ lg(x－ a)的定义域为集合 B．若“ x∈ A”是“ x∈ B”的充分条件，则实数 a 的取值围为▲．27．在平面直角坐标系xOy 中，过双曲线C： x2－y ＝ 1 的右焦点 F 作 x 轴的垂线 l，则 l 与双曲线 C3的两条渐近线所围成的三角形的面积是▲．8．已知正六棱锥P－ ABCDEF 的底面边长为2，侧棱长为 4，则此六棱锥的体积为▲．9．在△ ABC 中，ABC＝ 120 ， BA＝2， BC＝ 3，D ， E 是线段 AC 的三等分点，则 BD · BE 的值为▲．10．记等差数列 { a } 的前 n 项和为 S ．若 S－1 ＝8，S ＝ 0，S1＝－ 10，则正整数 k＝▲．n n k k k＋11．若将函数 f(x)＝∣ sin( x－6) ∣( ＞0)的图象向左平移9个单位后，所得图象对应的函数为偶函数，则实数的最小值是▲．4x ＋y的最大值为▲．12．已知 x，y 为正实数，则4x＋y x＋ y13．在平面直角坐标系xOy 中，圆 C 的方程为 (x－ 1)2＋ (y－ 1)2＝ 9，直线 l：y＝ kx＋ 3 与圆 C 相交于 A，B 两点， M 为弦 AB 上一动点，以 M 为圆心， 2 为半径的圆与圆C 总有公共点，则实数k 的取值围为▲．14．已知 a， t 为正实数，函数f(x)＝ x2－ 2x＋a，且对任意的x∈ [0， t] ，都有 f(x)∈ [ － a， a]．若对每一个正实数 a，记 t 的最大值为 g(a)，则函数 g(a)的值域为▲．二、解答题：本大题共 6 小题，共计90 分．请在答题纸指定区域作答，解答时应写出文字说明、证．．．．．．．明过程或演算步骤．15．（本小题满分14 分）在△ ABC 中，角 A， B，C 所对的边分别为a， b，c．已知 acosC＋ ccosA＝ 2bcosA．（1）求角 A 的值；（2）求 sinB＋ sinC 的取值围．16．（本小题满分14 分）在四棱锥 P－ABCD 中， BC∥ AD ， PA⊥ PD ， AD＝ 2BC， AB＝ PB， E 为 PA 的中点．（ 1）求证：BE∥平面 PCD ；P（ 2）求证：平面 PAB⊥平面 PCD．EA DB C（第 16 题图）17．（本小题满分14 分）如图，摩天轮的半径 OA 为 50m，它的最低点 A 距地面的高度忽略不计．地面上有一长度为 240m 的景观带 MN ，它与摩天轮在同一竖直平面，且AM ＝ 60m．点 P 从最低点 A 处按逆时针方向转动到最高点 B 处，记AOP＝，∈ (0，π)．（ 1）当2＝3时，求点 P 距地面的高度PQ；（ 2）试确定的值，使得MPN 取得最大值．BPOA Q M N（第 17 题图）18．（本小题满分16 分）在平面直角坐标系xOy 中，设中心在坐标原点的椭圆 C 的左、右焦点分别为F1、 F 2，右准线l： x＝m＋ 1 与 x 轴的交点为B， BF 2＝m．（1）已知点 ( 6， 1)在椭圆 C 上，数 m 的值；2（2）已知定点 A(－ 2， 0)．①若椭圆 C 上存在点T，使得TA＝2，求椭圆 C 的离心率的取值围；TF 1②当 m＝1 时，记 M 为椭圆 C 上的动点，直线AM ， BM 分别与椭圆 C 交于另一点P，Q，→→→→若 AM ＝λAP ， BM＝BQ ，求证：λ＋为定值．yM lPQBAF1 OF2 x（第 18 题图）19． (本小题满分16 分 )已知函数f(x)＝ x2－ x＋ t， t≥ 0， g(x)＝ lnx．（ 1）令 h( x)＝ f(x)＋ g(x)，求证： h(x)是增函数；（ 2）直线 l 与函数f(x)， g(x)的图象都相切．对于确定的正实数t，讨论直线l 的条数，并说明理由．20．（本小题满分16 分）已知数列 { a n} 的各项均为正数，其前n 项的和为S n，且对任意的m，n∈ N* ，都有 (S m＋n＋ S1)2＝ 4a2m a2n．（1）求a2的值； a1（2）求证： { a n} 为等比数列；（ 3）已知数列 { c n } ， { d n } 满足 |c n |＝ |d n|＝ a n， p(p≥ 3)是给定的正整数，数列{ c n} ， { d n} 的前 p 项的和分别为T p，R p，且 T p＝R p，求证：对任意正整数k(1≤ k≤ p)， c k＝ d k．市 2015 届高三年级第三次模拟考试数学附加题2015.05 注意事项：1．附加题供选修物理的考生使用．2．本试卷共 40 分，考试时间 30 分钟．3．答题前，考生务必将自己的、班级、学校写在答题纸上．试题的答案写在答题纸上对应题目．．．的答案空格．考试结束后，交回答题纸．21．【选做题】在 A 、 B、 C、 D 四小题中只要选做 2 题，每小题10 分，共计卷纸指定20 分．请在答．．．．．区域作答．解答应写出文字说明、证明过程或演算步骤．．．A ．选修 4— 1：几何证明选讲如图， AB，AC 是⊙ O 的切线， ADE 是⊙ O 的割线，求证：BE· CD ＝ BD · CE．BEDA OC（第 21A 题图）B．选修 4－ 2：矩阵与变换已知矩阵 A ＝a1，直线l：x－y＋4＝0在矩阵A对应的变换作用下变为1 a直线 l ： x－ y＋ 2a＝ 0．（ 1）数 a 的值；（2）求 A2．C．选修 4－ 4：坐标系与参数方程在极坐标系中，设圆 C：＝ 4 cos 与直线 l：＝( ∈ R)交于 A，B 两点，求以 AB 为直径的圆4的极坐标方程．D．选修 4－ 5：不等式选讲1已知实数x， y 满足 x＞ y，求证： 2x＋x2－2xy＋y2≥ 2y＋ 3．【必做题】第22 题、第 23 题，每题 10 分，共计 20 分．请在答卷纸指定区域作答．解答应写出文字．．．．．．．说明、证明过程或演算步骤．22．（本小题满分10 分）如图，四棱锥P－ ABCD 中， PA 平面 ABCD ， AD ∥ BC，AB AD ， BC＝2 3，AB＝1， BD ＝PAP3＝2．（1）求异面直线 BD 与 PC 所成角的余弦值；（2）求二面角 A－PD－ C 的余弦值．ADB C23．（本小题满分10 分）已知集合 A 是集合 P n＝ {1 ，2，3，，n} ( n≥3，n∈ N *) 的子集，且 A 中恰有 3 个元素，同时这3 个元素的和是 3 的倍数．记符合上述条件的集合 A 的个数为f(n)．（1）求 f(3)， f(4) ；（2）求 f(n)（用含 n 的式子表示）．市 2015 届高三第三次模拟考试数学参考答案及评分标准2015.05说明：1．本解答给出的解法供参考．如果考生的解法与本解答不同，可根据试题的主要考查容比照评分标准制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数，填空题不给中间分数．一、填空题：本大题共14 小题，每小题 5 分，共 70 分．1． 52． 0.743． 4 4． 6 5．甲 6． (－∞，－ 3] 7． 4 38． 129． 11 10． 9911．312． 413． [－ 3，＋∞ )14． (0， 1)∪{2}234二、解答题：本大题共6 小题，共 90 分．15．解：（ 1）因为 acosC ＋ ccosA ＝ 2bcosA ，所以 sinAcosC ＋ sinCcosA ＝2sinBcosA ，即 sin(A ＋ C)＝2sinBcosA ．因为 A ＋ B ＋C ＝ π，所以 sin(A ＋ C)＝ sinB ．从而 sinB ＝2sinBcosA ．4 分因为 sinB ≠0，所以 cosA ＝ 1．2π7 分因为 0＜ A ＜ π，所以 A ＝．32π2π 2π（2） sinB ＋ sinC ＝ sinB ＋ sin( 3 －B)＝ sinB ＋ sin 3 cosB －cos 3 sinB3 sinB ＋ 3π 11 分＝ 2 cosB ＝ 3sin( B ＋ )． 2 6因为 0＜ B ＜ 2π π π 5π，所以＜B ＋＜．3 6 6 6所以 sinB ＋sinC 的取值围为 (3， 3]．14 分216．明：（ 1）取 PD 的中点 F ，接 EF ， CF．因 E PA 的中点，所以1 EF∥ AD ，EF ＝ AD ．2 1因 BC∥ AD， BC＝ AD ，2所以 EF∥ BC，EF＝BC ．所以四形 BCFE 平行四形．所以 BE∥ CF ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分PE FA DB C（第 16 题图）因 BE 平面 PCD， CF 平面 PCD，所以 BE∥平面 PCD ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分（2）因 AB ＝ PB，EPA 的中点，所以 PA⊥BE．因 BE∥ CF ，所以 PA⊥ CF．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9 分因 PA⊥PD ，PD 平面 PCD ，CF 平面 PCD，PD∩CF＝F，所以 PA⊥平面 PCD．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分因 PA 平面 PAB，所以平面 PAB 平面 PCD．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯14 分17．解：（ 1）由意，得 PQ＝ 50－ 50cos ．从而，当＝2 2＝75．3， PQ＝ 50－50cos 3即点 P 距地面的高度 75m．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分（2）（方法一）由意，得 AQ＝ 50sin ，从而 MQ ＝ 60－ 50sin ， NQ＝ 300－ 50sin ．又 PQ＝ 50－50cos ，所以 tan NPQ＝NQ＝ 6－ sin，tan MQ ＝ 6－ 5sin．PQ 1－ cos MPQ ＝PQ 5－5cos⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯从而 tan MPN ＝ tan( NPQ－ MPQ)6－ sin－6－ 5sin＝ tan NPQ－ tan MPQ ＝ 1－cos 5－ 5cos 1＋ tan NPQ tan MPQ 6－ sin 6－ 5sin1＋1－ cos ×5－ 5cos12(1－ cos )．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯＝18sin － 5cos23－令 g( )＝12(1－ cos )，∈ (0，π)，23－18sin －5cos6分9分g ( )＝ 12× 18(sin＋ cos － 1)∈(0 ，π)．(23－ 18sin － 5cos )2，由 g ( )＝ 0，得 sin＋ cos － 1＝ 0，解得＝ 2．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 11 分当 ∈ (0， ) ， g () ＞0， g() 增函数；当∈ ( ， ) ， g ( )＜ 0，g() 减函数，22所以，当＝， g()有极大，也最大．2因 0＜MPQ ＜ NPQ ＜ 2，所以 0＜ MPN ＜2，从而当 g( )＝ tanMPN 取得最大，MPN 取得最大．即当＝2 ，MPN 取得最大．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯14 分（方法二）以点 A 坐原点， AM x 建立平面直角坐系，O 的方程 x 2＋ (y －50)2＝502，即 x 2＋ y 2－ 100y ＝ 0，点 M(60，0)， N(300， 0)．点 P 的坐(x 0， y 0)，所以 Q (x 0 ， 0)，且 x 02＋ y 0 2－ 100y 0＝ 0．NQ 300－x 0MQ 60－ x从而 tan NPQ ＝ PQ ＝， tan MPQ ＝PQ ＝y 0y 0．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6 分从而 tan MPN ＝ tan( NPQ － MPQ)300－ x 060－ x 0＝ tanNPQ － tan MPQy 0 － y 0＝300－ x 060－x 01＋ tan NPQ tan MPQ1＋y 0 × y24y 0＝10y 0－ 36x 0＋ 1800．由意知， x 0＝ 50sin ， y 0＝ 50－50cos ，所以 tan 12(1 － cos )⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9 分MPN ＝＝．23－18sin －5cos（下同方法一）2218．解：（ 1） C 的方程x2＋ y2＝ 1(a ＞ b ＞ 0)．aba 2a 2＝ m ＋ 1，＝ m ＋ 1，解得 b 2＝ m ，由意，得 c(m ＋ 1)－c ＝m ，c ＝ 1．所以方程x 2＋y 2＝ 1．m ＋ 1 m因 C 点 (6， 1)，所以 3 ＋1＝1，2 2(m＋ 1) m1解得 m＝ 2 或 m＝－2 (舍去）．所以 m＝ 2．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分（2）① 点 T(x， y)．由TA＝2，得 (x＋ 2)2＋ y2＝ 2[( x＋ 1)2＋y2 ]，即 x2＋y2＝ 2．⋯⋯⋯⋯⋯⋯⋯ 6 分TF 1x2＋ y2＝ 2，由 x2＋ y2＝1，得 y2＝ m2－ m．m＋ 1 m因此 0≤ m2－ m≤ m，解得 1≤ m≤ 2．所以 C 的离心率 e＝ 1 ∈ [ 3， 2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10 分m＋ 1 3 2 ] ．②（方法一）M(x0， y0)，P(x1，y1) ，Q(x2， y2)．AM ＝ (x0＋ 2， y0)， AP ＝ (x1＋2， y1)．由AM＝ AP ，得x0＋ 2＝ (x1＋ 2)，0 1y ＝y ．从而x0＝ x1＋ 2( －1)，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分0 1y ＝y ．因 x02 ＋ y02＝ 1，所以[x1＋ 2( －1)]2 ＋ ( y1)2＝ 1．2 2x12即2(2＋y12)＋2 (－1)x1＋2(－1)2－1＝0．因x212＋y12＝1，代入得 2 (－1)x1＋32－4＋1＝0．由意知，≠1，故 x1＝－3－1，所以 x0 －3．2 ＝2同理可得 x0＝－＋3．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯14 分2因此－3＝－＋ 3，2 2所以＋＝6．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯16 分（方法二）M(x0， y0)， P(x1， y1)，Q(x2， y2)．直 AM 的方程 y＝y0 (x＋ 2)．x ＋ 2将 y＝y0(x＋2) 代入x2 1 2 2 2＋ y2＝ 1，得( (x0＋ 2)2＋ y0 )x2＋4y0 x＋ 4y0－ (x0＋2) 2＝ 0(*) ．0 2 2x ＋ 2因 x 02 2 2＝ 0．2＋ y 02＝ 1，所以（ * ）可化 (2x 0＋ 3)x 2＋ 4y 0x － 3x 0－ 4x 020＋ 4．因 x 013x 0＋4x 0，所以 x 13xx＝－2x 0 ＋3＝－2x 0＋ 3同理 x 2 ＝ 3x 0－4．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯14 分2x 0－3→→因 AM ＝ AP ， BM ＝BQ ，所以＋＝ x 0＋ 2＋x 0 － 2＝x 0＋ 2＋x 0－ 2x 1＋ 2 x 1 － 2 － 3x 0＋ 4＋ 2 3x 0－ 4－ 22x ＋ 32x － 3＝(x 0＋ 2)(2x 0＋ 3)＋ (x 0 －2)(2 x 0－ 3)＝ 6．－x 0＋ 2x 0＋2即 λ＋定 6．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯16 分19．解：（ 1）由 h(x)＝ f(x)＋ g(x)＝ x 2－ x ＋ t ＋ lnx ，得 h' (x)＝ 2x － 1＋ 1， x ＞ 0．x1 ≥2 12，所以 h' (x)＞ 0，因 2x ＋2x ·＝ 2xx从而函数 h(x)是增函数．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分（ 2）直 l 分切 f(x)， g( x)的象于点 (x 1， x 12－ x 1＋ t) ， (x 2， lnx 2)，由 f'(x)＝ 2x － 1，得 l 的方程 y － (x 12 －x 1 ＋t)＝ (2x 1－ 1)(x － x 1)，即 y ＝ (2x 1－ 1)x －x 1 2＋ t ．由 g'(x) ＝1，得 l 的方程y － lnx 2＝ 1 (x － x 2)，即 y ＝ 1 ·x ＋ lnx 2 －1．xx 2 x 2 2x 1－ 1＝ 1，所以x 2 (*) － x 12＋t ＝ lnx 2－ 1．消去 x 1 得 ln x 2＋ (1＋ x 2)2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分4x 2 － (t ＋ 1)＝ 0 (**) ．2令 F(x)＝ lnx ＋ (1＋ x)2 － (t ＋1)， F' (x)＝ 1－ 1＋ x 2x 2－ x － 1 (2x ＋1)( x －1)， x ＞ 0． 2 2x 3 ＝ 3＝ 34x x 2x 2x由 F' (x)＝ 0，解得 x ＝ 1．当 0＜x ＜ 1 ， F' (x)＜ 0，当 x ＞ 1 ， F' ( x)＞ 0，所以 F(x)在 (0，1) 上减，在 (1，＋∞ )上增，从而 F(x)min ＝ F(1) ＝－ t ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 9 分当 t ＝ 0 ，方程 (**) 只有唯一正数解，从而方程 (*) 有唯一一解，即存在唯一一条足意的直；⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯11 分当 t ＞ 0， F(1)＜ 0，由于 F(e t ＋1 )＞ ln(e t ＋ 1)－ (t ＋ 1)＝ 0，故方程 (**) 在 (1，＋∞ )上存在唯一解；⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 13 分令 k(x)＝ lnx ＋ 1－ 1(x ≤ 1)，由于 k' (x)＝ 1－ 12＝x －2 1≤0，故 k (x)在 (0， 1]上减，xx xx故当 0＜ x ＜ 1 ， k (x)＞ k (1)＝ 0，即 lnx ＞ 1－1，x 从而 lnx ＋ (1 ＋x)21－ 1 22－ (t ＋ 1)＞ (2x 2 ) － t ．4x所以 F(1 )＞ ( t ＋ 1)2－ t ＝ t ＋ 1＞ 0，又 0＜ 1＜ 1， 2( t ＋ 1)2 4 2( t ＋ 1) 故方程 (**) 在 (0， 1)上存在唯一解．所以当 t ＞ 0 ，方程 (**) 有两个不同的正数解，方程 (*) 有两解．即存在两条足意的直．上，当 t ＝ 0 ，与两个函数象同相切的直的条数1；当 t ＞ 0 ，与两个函数象同相切的直的条数2．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯16 分m ＋n12＝4a 2n 2m 2 1 2＝4a 22 21 2＝ 4a 2220．解：（ 1）由 (S＋ S ) a ，得(S ＋S) ，即 (a ＋ 2a ) ．因 a 1＞ 0， a 2＞ 0，所以 a 2＋ 2a 1＝ a 2，即a 2＝ 2．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分a 1明：（2）（方法一）令 m ＝ 1， n ＝2，得 (S 312＝ 4a 2 4 ，即 (2a 1 23 2＝ 4a 2 4，＋ S ) a ＋ a ＋ a ) a 令 m ＝ n ＝2，得 S 4＋ S 1＝ 2a 4，即 2a 1＋ a 2＋ a 3＝a 4．所以 a 4 ＝4a 2＝ 8a 1．又因a 2＝ 2，所以 a 31．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6 分＝ 4aa 1由 (S m ＋ n ＋ S 1)2＝ 4a 2n a 2m ，得 (S n ＋1＋ S 1)2＝ 4a 2n a 2， (S n ＋ 2＋S 1)2＝ 4a 2n a 4．两式相除，得 (S ＋ S ) ＝ a 4，所以 S ＋ S ＝a 4＝2． n ＋ 2 1 2 a 2 n ＋2 1a 2 n ＋11 2 n ＋11(S ＋ S ) S ＋ S即 S n ＋2 ＋S 1＝ 2(S n ＋ 1＋ S 1)，从而 S n ＋3＋ S 1＝ 2(S n ＋2 ＋S 1)．所以 a n ＋3＝ 2a n ＋ 2，故当 n ≥ 3 ， { a n } 是公比 2 的等比数列．又因 a 3 ＝2a 2＝ 4a 1，从而 a n ＝ a 1· 2 n －1， n ∈ N* ．然， a n1n －1足，＝a · 2因此 { a n } 是首 a 1，公比2 的等比数列．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10 分（方法二）在 (S＋n ＋ S 1)2＝ 4a2n a 2m 中，m令 m ＝ n ，得 S 2n ＋ S 1＝ 2a 2n ．① 令 m ＝ n ＋ 1，得 S 2n ＋ 1＋ S 1＝ 2 a 2n a 2n ＋ 2 ，②在①中，用 n ＋1 代 n 得， S 2n ＋2＋ S 1＝ 2a 2n ＋2．③ ②－①，得 a 2n ＋ 1 ＝ 2 a 2n a 2n ＋2 － 2a 2n ＝ 2 a 2n ( a 2n ＋ 2－ a 2n )， ④ ③－②，得 a 2n ＋ 2＝ 2a 2n ＋2－ 2 a 2n a 2n ＋2 ＝2 a 2n ＋2( a 2n ＋2－ a 2n )， ⑤ 由④⑤得 a 2n ＋ 1 a 2n 2 n ＋ 2．⑥＝ a⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分⑥代入④，得a 2n ＋1 ＝2a 2n ；⑥代入⑤得a 2n ＋ 2＝ 2a 2 n ＋ 1，所以 a 2n＋2＝ a 2n ＋1＝ 2．又 a 2＝ 2，2n ＋ 1a 2na 1a从而 a · 2 n － 1， n ∈ N* ．n ＝ a 1然， a 2 n －1 足，n ＝a 1·因此 { a n } 是首 a 1，公比 2的等比数列．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10 分（3）由（ 2）知， a n ＝ a 1·2 n －1．因 |c p p 1 p －1，所以 c p p p p|＝ |d |＝ a · 2＝ d 或 c ＝－ d ．若 c p ＝－ d p ，不妨 c p ＞ 0，d p ＜0，T p ≥ a 1· 2p －1－ (a 1· 2p － 2＋ a 1 ·2p －3＋⋯＋ a 1)＝a 1· 2p －1 － a 1 · (2p －1－ 1)＝ a 1＞ 0． R p ≤－ a 1 ·2p － 1＋ (a 1· 2p － 2＋ a 1· 2p － 3＋⋯＋ a 1)＝－ a 1· 2p －1＋ a 1· (2p －1－ 1)＝－ a 1＜ 0．与 T p ＝R p 矛盾，所以c p ＝d p ．从而 T p －1＝ R p － 1．由上明，同理可得c p －1＝d p － 1．如此下去，可得 c p － 2＝d p － 2， c p － 3＝d p － 3．⋯， c 1 ＝d 1．即任意正整数 k(1 ≤k ≤ p)， c k ＝d k ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯16 分市 2015 届高三第三次模拟考试数学附加题参考答案及评分标准2015.05 21．【做】在 A 、B 、C、 D 四小中只能做 2 ，每小 10 分，共 20 分．A ．修 4— 1：几何明明：因 AB 是⊙ O 的切，所以 ABD ＝ AEB．又因BAD ＝ EAB，所以△ BAD ∽△ EAB．所以BD＝AB．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分BE AECD AC同理，CE＝AE.．因 AB， AC 是⊙ O 的切，所以AB＝ AC．因此BD＝CD，即 BE· CD＝ BD·CE．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10 分BE CEB．修 4— 2：矩与解：（ 1）直l 上一点 M 0(x0， y0) 在矩 A 的作用下l 上点 M(x， y)，x a 1 x ax ＋ y ，0 0 0y 1 a y0 0＋ ay 0x所以 x＝ ax0＋ y0，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分y＝ x0＋ ay0．代入 l 方程得 (ax0＋y0)－ (x0＋ ay0)＋ 2a＝0，即 (a－ 1)x0－ (a－ 1)y0＋ 2a＝ 0．因 (x0， y0)足 x0－ y0＋ 4＝ 0，所以2a＝ 4，解得 a＝ 2．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分a－ 1（2）由 A＝ 2 1，得A2＝ 2 1 2 1 ＝ 54 ．⋯⋯⋯⋯⋯⋯⋯10 分1 2 1 2 1 2 4 5C．修 4— 4：坐系与参数方程解：以极点坐原点，极x 的正半，建立直角坐系，由意，得C 的直角坐方程x2＋y2－4x＝ 0，直 l 的直角坐方程y＝ x．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分由x2＋ y2－ 4x＝0，x＝ 0，或x＝2，y＝x，解得y＝ 0，y＝ 2．所以 A(0， 0)， B(2， 2)．从而以 AB 直径的的直角坐方程( x－ 1) 2＋ (y－ 1)2＝ 2，即 x2＋ y2＝ 2x＋ 2y．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分将其化极坐方程：2－ 2 (cos ＋ sin )＝0，即＝ 2(cos ＋sin )．⋯⋯⋯⋯⋯⋯⋯⋯10 分D．修 4— 5：不等式明：因 x＞ y，所以 x－ y＞ 0，从而1左＝ (x－ y)＋ (x－ y)＋(x－y)2＋2y3 1 ＋2y≥ 3( x－y) (x－y)(x－ y)2＝ 2y＋ 3＝右．即原不等式成立．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10 分【必做】第 22 、第23 ，每10 分，共 20 分．22．解：（ 1）因 PA 平面 ABCD ， AB 平面 ABCD ，AD 平面 ABCD ，所以 PA AB，PA AD ．又 AD AB，故分以 AB， AD， AP 所在直 x ， y ， z 建立空直角坐系．根据条件得 AD ＝ 3．z所以 B(1， 0，0)，D (0，3， 0)， C(1，23，0)，P(0，0，2)．3从而 BD＝(－1，3， 0)， PC ＝ (1， 23，－ 2)．3⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分异面直 BD ， PC 所成角，PAD yB Cxcos→→BD PC＝ |cos＜ BD ， PC ＞ |＝ | |∣BD∣ ∣PC∣2 3＝ |(－ 1， 3， 0)·(1， 3 ，－2)|＝ 57．19382×3即异面直 BD 与 PC 所成角的余弦57． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分38（2）因 AB 平面 PAD ，所以平面 PAD 的一个法向量AB ＝(1，0， 0)．平面 PCD 的一个法向量n ＝ (x ， y ， z)，由 n PC ， n PD ， PC ＝ (1，2 3，－ 2)， PD ＝(0 ，3，－ 2)，32 2 3x ＝ 3z ，得 x ＋ 3 y － 2z ＝0，解得2 33y － 2z ＝ 0，y ＝ 3 z ．不妨取 z ＝3，得 n ＝ (2， 2 3， 3)． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分二面角 A －PD － C 的大小，cos ＝ cos ＜ AB ， n ＞＝AB·n＝(1， 0，0)·(2， 2 3， 3)＝ 2．∣ AB ∣×∣ n ∣1× 55即二面角 A －PD － C 的余弦 2．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10 分523．解：（ 1）f(3)＝ 1， f(4)＝ 2；⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分n（ 2） A 0＝ { m ∣ m ＝ 3p ，p ∈ N* ， p ≤ 3} ，n ＋ 1A 1＝ { m ∣ m ＝ 3p －1， p ∈ N* ， p ≤3} ，n ＋ 2A 2＝ { m ∣ m ＝ 3p －2， p ∈ N* ， p ≤3 } ，它所含元素的个数分 ∣A 0∣，∣ A 1∣，∣ A 2∣．⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分①当 n ＝ 3k ， ∣ A 0∣＝∣ A 1∣＝∣ A 2∣＝ k ．1k ＝ 1， 2 ， f(n)＝ (C k )3＝ k 3；k ≥ 33 13 3， f(n)＝ 3C k ＋(C k )3＝ k 3－ k 2＋ k ．22从而 f(n)＝ 111 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6 分18 n3－n 2＋ n ， n ＝ 3k ，k ∈ N* ．63②当 n ＝ 3k － 1 ， ∣ A 0∣＝ k － 1，∣ A 1∣＝∣ A 2∣＝ k ．k ＝ 2， f(n)＝ f(5) ＝2× 2× 1＝ 4；k ＝ 3 ， f(n)＝ f(8) ＝1＋ 1＋ 3× 3× 2＝20；k ＞ 33 311 2 3 32 5 ， f(n)＝ C k－1＋2C k ＋ C k －1(C k ) ＝ k － 3k＋ k － 1；22从而 f(n)＝ 131 2 1 4 ， n ＝ 3k － 1， k ∈N* ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分18 n －n＋ n －639③当 n ＝ 3k － 2 ，∣ A 0∣＝ k － 1，∣ A 1∣＝ k － 1，∣ A 2∣＝ k ．k ＝ 2 ， f(n)＝ f(4) ＝2× 1× 1＝ 2；k ＝ 3 ， f(n)＝ f(7) ＝1＋ 3× 2× 2＝ 13；3 31213 3 9 2k ＞ 3 ， f(n)＝ 2C k －1 ＋ C k ＋ (C k －1)C k ＝k－ k ＋ 5k － 2；22从而 f(n)＝ 1 3 1 2 1 2 ， n ＝ 3k － 2， k ∈N* ．18 n － 6 n ＋ n －3 91 3 12 118 n － n ＋ n ， n ＝ 3k ，k ∈ N* ，63所以 f(n)＝1 3 12 14， n ＝ 3k － 1， k ∈ N* ， ⋯⋯⋯⋯⋯⋯⋯⋯ 10 分18 n － n ＋ n －6 3 91 n 3－1n 2＋ 1n － 2， n ＝ 3k － 2， k ∈ N* ．18639。

2015年中考模拟数学试题(三)及答案

2015年中考数学模拟测试卷(三)时间120分钟满分120分 2015.4.11一、选择题（每小题3分共36分）1．对于任意实数x ，代数式53212+-x x 的值是一个（ ▲ ）A ．非负数B ．正数C ．负数D ．整数2．如图，C 、D 是线段AB 上两点，若CB ＝4cm ，DB=7cm ，且D 是AC 的中点，则AC 的长等于（）A ．3cmB ．6cmC ．10cmD ．14cm3．某地，今年1月1日至4日每天的最高气温与最低气温如下表：其中温差最大的是（） A ．1月1日B ．1月2日C ．1月3日D ．1月4日4．在同一时刻，身高1.6米的小强在阳光下的影长为0.8米，一棵大树的影长为4.8米，则树的高度为（） A ．4.8米B ．6.4米C ．9.6米D ．10米5．下列运算正确的是A ．a 3•a 2=a 6B ．2a （3a ﹣1）=6a 3﹣1C ．（3a 2）2=6a 4D ．2a+3a=5a6．下列运算正确的是（） A.x 4·x 3=x 12 B.（x 3）4＝x 7 C.x 4÷x 3=x(x ≠0) D.x 4+x 4=x 87．关于函数y= 3x ＋1，下列结论正确的是A ．图象必经过点(－2，5)B ．y 随x 的增大而减小C ．当x ＞—12时，y ＞0 D ．图象经过第一、二、三象限 8．若a为有理数，则说法正确是( )[A ．－a 一定是负数B ．| a |一定是正数C ．| a |一定不是负数D ．－a 2一定是负数9．将y=2x 2的函数图象向左平移2个单位长度后，得到的函数解析式是（） A. y=2x 2+2 B. y=2（x+2）2 C. y=（x －2）2 D. y=2x 2－2 10．不等式组⎩⎨⎧><-01x x 的解集在数轴可表示为（ ▲ ）11．下列计算正确的是（）A ．133-=-B ．236a a a ⋅=C ．22(1)1x x +=+D ．=12．某品牌商品，按标价九折出售，仍可获得20%的利润.若该商品标价为28元，则商品的进价为：A. 21元B. 19.8元C. 22.4元D. 25.2元二、填空题（每小题3分共24分）13．观察下面一列数，根据规律写出横线上的数。

长沙市2015年数学模拟试卷3

第6题图2015年长沙市初中毕业学业水平考试模拟试卷数学（三）注意事项：1、答题前，请考生先将自己的姓名、准考证号填写清楚，并认真核对条形码上的姓名、准考证号、考室和座位号；2、必须在答题卡上答题，在草稿纸、试题卷上答题无效；3、答题时，请考生注意各大题题号后面的答题提示；4、请勿折叠答题卡，保持字体工整、笔迹清晰、卡面清洁；5、答题卡上不得使用涂改液、涂改胶和贴纸；6、本学科试卷共26个小题，考试时量120分钟，满分120分。

一、选择题（在下列各题的四个选项中，只有一项是符合题意的。

请在答题卡中填涂符合题意的选项。

本题共12个小题，每小题3分，共36分）1．2-的相反数是A ．12-B ．2C ．2-D ．122．下列运算正确的是A ．22223a a a -+=B ．223(2)6a a a ⨯-=-C ．842a a a ÷=D ．224(2)4a a =3．一个正方形的面积为20，那它的边长应在A ．2到3之间B ．3到4之间C ．4到5之间D ．5到6之间4．用配方法解一元二次方程x 2＋4x ＝5时，此方程可变形为A ．(x +2)2＝1B ．(x -2)2＝1C ．(x +2)2＝9D ．(x -2)2＝95．二次函数21(3)52y x =--+的开口、对称轴、顶点坐标分别是 A ．向下，直线3x =，(35)-， B ．向上，直线3x =，(35)，C ．向下，直线3x =，(35)，D ．向上，直线3x =-，(35)，6．如图，AB 为⊙O 的直径，CD 为弦，AB ⊥CD ，如果∠BOC ＝70°，那么∠A 的度数为A ．70°B ．35°C ．30°D ．20°7．已知圆锥的底面半径为4 cm ，母线长为5 cm ，则这个圆锥的侧面积是A ．20π cm 2B ．20 cm 2C ．40π cm 2D ．40 cm 2第8题图8．如图是某市某月1日至10日的空气质量指数趋势图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染，某人随机选择7月1日至7月8日中的某一天到达该市，并连续停留3天．则此人在该市停留期间有且仅有1天空气质量重度污染的概率是A ．14B ．18C ．12D ．34 9．下列图形，既是中心对称图形，又是轴对称图形的是A ．等边三角形B ．平行四边形C ．正五边形D ．正六边形10．一次函数1y kx =+的图象如下图，则反比例函数(0)k y x x=<的图象只能是A B C D11．今年我市有7万名学生参加中考，为了了解这些考生的数学成绩，从中抽取2 000名考生的数学成绩进行统计分析．在这个问题中，有下列说法：①这7万名考生的数学中考成绩的全体是总体；②每个考生是个体；③2 000名考生是总体的一个样本；④样本容量是2 000．其中说法正确的有A ．4个B ．3个C ．2个D ．1个12．如图，△AOB 为等腰三角形，顶点A 的坐标为(2，5)，底边OB 在x 轴上．将△AOB绕点B 按顺时针方向旋转一定角度后得△A 'O 'B ，点A 的对应点A '在x 轴上，则点O '的坐标是A ．(203，103)B ．(163，453)C ．(203，453)D ．(163，43)二、填空题（本题共6个小题，每小题3分，共18分）13．如图，在四边形ABCD 中，AB ∥CD ，要使得四边形ABCD 是平行四边形，应添加的条件是（只填写一个条件，不使用图形以外的字母和线段）．14．一组数据按从小到大的顺序排列为1，2，3，3，4，5，则这组数据的方差是．第13题图第15题图第16题图15．拱桥截面是一条抛物线，如图所示，现测得水面宽AB =16 m ，拱顶O 到水面的距离为8 m ，在图中的直角坐标系内，拱桥所在抛物线的解析式是______________.16．如图，小明在打网球时，使球恰好能打过网，而且落在离网4米的位置上，则球拍击球的高度h 为．17．已知关于x 的方程21x m x +=-的解是正数，则m 的取值范围是_____________. 18．一艘轮船从A 地匀速驶往B 地，到达后用了半小时卸货，随即匀速返回，已知轮船返回的速度是它从A 地驶往B地的速度的1.5倍．轮船离A 地的距离y （千米）关于时间x （小时）的函数图象如图所示．则a = （小时）.三、解答题（本题共8个小题，第19、20小题每小题6分，第21、22小题每小题8分，第23、24小题每小题9分，第25、26小题每小题10分，共66分）19．201()20153222sin 452--+÷-︒.20．已知12x y ==-，.求221()x y x y xy y-÷--的值.21．在长沙市初三年级学生考查科目中，对物理实验操作、化学实验操作成绩进行抽样调查，成绩评定为A 、B 、C 、D 四个等级．现抽取这两种成绩共1 000份进行统计分析，其中A 、B 、C 、D 分别表示优秀、良好、合格、不合格四个等级．相关数据统计如下表及图所示．（1）请将上表补充完整（直接填数据，不写解答过程）；（2）长沙市共有66 000名学生参加测试，试估计该市初三年级学生化学实验操作优秀的大约有多少人；（3）在这66 000名学生中，物理实验操作不合格的大约有多少人？22．如图所示，AC 为⊙O 的直径且P A ⊥AC ，BC 是⊙O 的一条弦，直线PB 交直线AC 于点D ，且PB =P A .（1）求证：直线PB 是⊙O 的切线；（2）已知：2DB BP=，求cos BCA ∠的值. A BC D 物理实验操作 18045 15 化学实验操作 225250 50 等级人数科目23．某学校计划用180 000元从厂家那里购买A 型、B 型、C 型三种型号的电脑，其中A 型出厂价为5 400元，B 型出厂价为3 600元，C 型出厂价为1 800元.（1）若学校同时购进其中两种不同型号的电脑共40部，并将180 000元恰好用完.请你帮助学校计算一下如何购买；（2）若学校同时购进三种不同型号的电脑共40部，并将180 000元恰好用完，并且要求C 型电脑的购买数量不少于6部且不多于8部，请你设计几种不同购买方案供学校选择，并说明理由.24．如图，过平行四边形ABCD 的对角线BD 的中点O 作两条互相垂直的直线，且交AB 、CD 的延长线于点E G 、，交BC AD 、于点 F H 、，连接EF FG GH EH 、、、.（1）求证：△BEO ≌△DGO ；（2）试判断四边形EFGH 的形状，并说明理由.25．设() 123 i x i n =⋅⋅⋅，，，，为任意代数式，我们规定：{}12max n y x x x = ，，，表示x 1，x 2，…，x n 中的最大值，如{}max 122y ==，．（1）求{}max 3y x =，；（2）借助函数图象，解不等式1max 12x x ⎧⎫+≥⎨⎬⎩⎭，；（3）若21max 1432y x x a x x ⎧⎫=-+-+⎨⎬⎩⎭，，的最小值为1，求实数a 的值.26．如图，二次函数22123x y x m m=--+（其中m 是常数，且0m >）的图象与x 轴分别交于点A 、B （点A 位于点B 的左侧），与y 轴交于点C ，作CD ∥AB ，点D 在二次函数的图象上，连接BD ．过点B 作射线BE 交二次函数的图象于点E ，使得AB 平分∠DBE ．（1）求点C 的坐标；（2）求证：BD BE为定值；（3）二次函数22123x y x m m=--+的顶点为F ，过点C F 、作直线与x 轴交于点G ．试说明：以 GF 、BD 、BE 的长度为三边长的三角形是什么三角形？请说明理由.。

2015年山西中考数学试卷(模拟三)

2015年山西中考数学试题（模拟三）第Ⅰ卷选择题（共30分）一. 选择题（本大题共10个小题，每小题3分，共30分.在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑） 1、计算33)4(7-+之值为（）A ．9B ． 27C ． 279D ． 4072、近年来，随着交通网络的不断完善，我省近郊游持续升温。

据统计，在今年“五一”期间，某风景区接待游览的人数约为20.3万人，这一数据用科学记数法表示为 (A)4103.20⨯人 (B)51003.2⨯人 (C) 41003.2⨯人 (D)31003.2⨯人 3、如图，正比例函数y 1与反比例函数y 2相交于点E （-1，2），若y 1＞y 2＞0，则x 的取值范围在数轴上表示正确的是（）A ．B ．C ．D ．4、下列说法正确的是（）A ．一个游戏中奖的概率是 1100，则做100次这样的游戏一定会中奖B ．为了了解全国中学生的心理健康状况，应采用普查的方式C ．一组数据0，1，2，1，1的众数和中位数都是1D ．若甲组数据的方差2S 甲＝0.2，乙组数据的方差2S 乙＝0.5，则乙组数据比甲组数据稳定 5、一副三角板,如图所示叠放在一起,则图中∠α的度数是（）A ．75B ．60C ．65D ． 556、连接一个几何图形上任意两点间的线段中，最长的线段称为这个几何图形的直径，根据此定义，图（扇形、菱形、直角梯形、红十字图标）中“直径”最小的是（）A ．B ．C ．D ．A ．200π米B ．100π米C ．400π米D ．300π米8、如图，正方形ABCD 中，AB ＝6，点E 在边CD 上，且CD ＝3DE ．将△ADE 沿AE 对折至△AFE ，延长EF 交边BC 于点G ，连结AG 、CF ．下列结论：①△ABG ≌△AFG ；②BG ＝GC ；③AG ∥CF ；④S △FGC ＝3．其中正确结论的个数是( )A ．4B ．3C ．2D ．19.如图是一个长方体，AB =3，BC =5，AF =6，要在长方体上系一根绳子连结绳子与DE 交于点P ，当所用绳子的长最短时，AP 的长为 A ．10 B C ．8 D ．25410、如图，在Rt ABC △中，∠C =90°，AB =5cm ，BC =3cm ，动点P 从点A以每秒1cm 的速度，沿A →B →C 的方向运动，到达点C 时停止.设y 运动时间为t 秒，则能反映y 与t 之间函数关系的大致图象是CABD第Ⅱ卷非选择题（90分）二填空题（本大题共6小题，每小题3分，共18分，把答案写在题中的横线上）11、方程组x 2y 57x 2y 13+=-⎧⎨-=⎩的解是 ▲ .12、有四张正面分别标有数字－3，0，1，5的不透明卡片，它们除数字不同外其余相同．现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为a ，则使关于x 的分式方程1－ax x －2＋2＝ 12－x 有正整数解的概率为．13、如图，在ABC Rt ∆中，已知90ACB ∠=︒，1AC =,3BC =,将ABC ∆绕着点A 按逆时针方向旋转30︒,使得点B 与点'B 重合，点C 与点 'C 重合，则图中阴影部分的面积为___________.14、Rt △ABC 中，已知∠C ＝90°，∠B ＝50°，点D 在边BC 上，BD ＝2CD ．把△ABC 绕着点D 逆时针旋转m （0＜m ＜180）度后，如果点B 恰好落在初始Rt △ABC 的边上，那么m ＝_________．15、如图，△ABC 中，∠ACB ＝90°，∠A ＝30°，将△ABC 绕C 点按逆时针方向旋转α角（0°＜α＜90°）得到△DEC ，设CD 交AB 于F ，连接AD ，当旋转角α度数为_______，△ADF 是等腰三角形。

2015年中考数学模拟试卷(3)

2015年中考数学模拟试卷(3)数学一、选择题（本大题满分36分，每小题3分. 在下列各题的四个备选答案中，只有一个是正确的，请在答题卷上把你认为正确的答案的字母代号按要求用2B 铅笔涂黑） 1. 2 sin 60°的值等于 A. 1B.23C. 2D. 32. 下列的几何图形中，一定是轴对称图形的有A. 5个B. 4个C. 3个D. 2个3. 据2013年1月24日《桂林日报》报道，临桂县2012年财政收入突破18亿元，在广西各县中排名第二. 将18亿用科学记数法表示为A. 1.8×10B. 1.8×108C. 1.8×109D. 1.8×10104. 估计8-1的值在A. 0到1之间B. 1到2之间C. 2到3之间D. 3至4之间 5. 将下列图形绕其对角线的交点顺时针旋转90°，所得图形一定与原图形重合的是 A. 平行四边形 B. 矩形 C. 正方形 D. 菱形 6. 如图，由5个完全相同的小正方体组合成一个立体图形，它的左视图是7. 为调查某校1500名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机抽取部分学生进行调查，并结合调查数据作出如图所示的扇形统计图. 根据统计图提供的信息，可估算出该校喜爱体育节目的学生共有 A. 1200名 B. 450名C. 400名D. 300名8. 用配方法解一元二次方程x 2+ 4x – 5 = 0，此方程可变形为 A. （x + 2）2= 9 B. （x - 2）2 = 9C. （x + 2）2 = 1D. （x - 2）2=19. 如图，在△ABC 中，AD ，BE 是两条中线，则S △EDC ∶S △ABC = A. 1∶2B. 1∶4C. 1∶3D. 2∶310. 下列各因式分解正确的是A. x 2 + 2x-1=（x - 1）2B. - x 2+（-2）2=（x - 2）（x + 2） C. x 3- 4x = x （x + 2）（x - 2）D. （x + 1）2= x 2 + 2x + 111. 如图，AB 是⊙O 的直径，点E 为BC 的中点，AB = 4，圆弧角扇形菱形等腰梯形A. B. C. D.（第9题图）（第7题图）∠BED = 120°，则图中阴影部分的面积之和为 A. 3 B. 23 C.23D. 112. 如图，△ABC 中，∠C = 90°，M 是AB 的中点，动点P 从点A出发，沿AC 方向匀速运动到终点C ，动点Q 从点C 出发，沿 CB 方向匀速运动到终点B. 已知P ，Q 两点同时出发，并同时到达终点，连接MP ，MQ ，PQ . 在整个运动过程中，△MPQ 的面积大小变化情况是 A. 一直增大B. 一直减小C. 先减小后增大D. 先增大后减小二、填空题（本大题满分18分，每小题3分，请将答案填在答题卷上，在试卷上答题无效） 13. 计算：│-31│= . 14. 已知一次函数y = kx + 3的图象经过第一、二、四象限，则k 的取值范围是 . 15. 在10个外观相同的产品中，有2个不合格产品，现从中任意抽取1个进行检测，抽到合格产品的概率是 .16. 在临桂新区建设中，需要修一段全长2400m 的道路，为了尽量减少施工对县城交通所造成的影响，实际工作效率比原计划提高了20%，结果提前8天完成任务，求原计划每天修路的长度. 若设原计划每天修路x m ，则根据题意可得方程 . 17. 在平面直角坐标系中，规定把一个三角形先沿着x 轴翻折，再向右平移2个单位称为1次变换. 如图，已知等边三角形 ABC 的顶点B ，C 的坐标分别是（-1，-1），（-3，-1），把 △ABC 经过连续9次这样的变换得到△A ′B ′C ′，则点A 的对应点A ′ 的坐标是 .18. 如图，已知等腰Rt △ABC 的直角边长为1，以Rt △ABC 的斜边AC 为直角边，画第二个等腰Rt △ACD ，再以Rt △ACD 的斜边AD 为直角边，画第三个等腰Rt △ADE ……依此类推直到第五个等腰Rt △AFG ，则由这五个等腰直角三角形所构成的图形的面积为 . 三、解答题（本大题8题，共66分，解答需写出必要的步骤和过程. 请将答案写在答题卷上，在试卷上答题无效）19. （本小题满分8分，每题4分）（1）计算：4 cos45°-8+(π-3) +(-1)3；（2）化简：（1 - n m n+）÷22n m m -.20. （本小题满分6分）（第12题图）（第17题图）（第18题图）°21. （本小题满分6分）如图，在△ABC 中，AB = AC ，∠ABC = 72°. （1）用直尺和圆规作∠ABC 的平分线BD 交AC 于点D （保留作图痕迹，不要求写作法）；（2）在（1）中作出∠ABC 的平分线BD 后，求∠BDC 的度数.22. （本小题满分8分）在开展“学雷锋社会实践”活动中，某校为了解全校1200名学生参加活动的情况，随机调查了50名学生每人参加活动的次数，并根据数据绘成条形统计图如下：（1）求这50个样本数据的平均数、众数和中位数；（2）根据样本数据，估算该校1200名学生共参加了多少次活动. 23. （本小题满分8分）如图，山坡上有一棵树AB ，树底部B 点到山脚C 点的距离BC 为63米，山坡的坡角为30°. 小宁在山脚的平地F 处测量这棵树的高，点 C 到测角仪EF 的水平距离CF = 1米，从E 处测得树顶部A 的仰角为45°，树底部B 的仰角为20°，求树 AB 的高度.（参考数值：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）24. （本小题满分8分）如图，PA ，PB 分别与⊙O 相切于点A ，B ，点M 在PB 上，且OM ∥AP ，MN ⊥AP ，垂足为N. （1）求证：OM = AN ；（2）若⊙O 的半径R = 3，PA = 9，求OM 的长.25. （本小题满分10分）某中学计划购买A 型和B 型课桌凳共200套. 经招标，购买一套A 型课桌凳比购买一套B 型课桌凳少用40元，且购买4套A 型和5套B 型课桌凳共需1820元.3121--+x x ≤1， ……① 解不等式组：3（x - 1）＜2 x + 1.……②（第21题图）（第23题图）（第24题图）（1）求购买一套A 型课桌凳和一套B 型课桌凳各需多少元？（2）学校根据实际情况，要求购买这两种课桌凳总费用不能超过40880元，并且购买A 型课桌凳的数量不能超过B 型课桌凳数量的32，求该校本次购买A 型和B 型课桌凳共有几种方案？哪种方案的总费用最低？26. （本小题满分12分）在平面直角坐标系中，现将一块等腰直角三角板ABC 放在第二象限，斜靠在两坐标轴上，点C 为（-1，0）. 如图所示，B 点在抛物线y =21x 2 -21x – 2图象上，过点B 作BD ⊥x 轴，垂足为D ，且B 点横坐标为-3. （1）求证：△BDC ≌ △COA ；（2）求BC 所在直线的函数关系式；（3）抛物线的对称轴上是否存在点P ，使△ACP 是以AC 为直角边的直角三角形？若存在，求出所有点P 的坐标；若不存在，请说明理由.2015年初三适应性检测参考答案与评分意见一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12 答案DACBCBDABCAC说明：第12题是一道几何开放题，学生可从几个特殊的点着手，计算几个特殊三角形面积从而降低难度，得出答案. 当点P ，Q 分别位于A 、C 两点时，S △MPQ =21S △ABC ；当点P 、Q 分别运动到AC ，BC 的中点时，此时，S △MPQ =21×21AC. 21BC =41S △ABC ；当点P 、Q 继续运动到点C ，B 时，S △MPQ =21S△ABC，故在整个运动变化中，△MPQ 的面积是先减小后增大，应选C.二、填空题 13.31； 14. k ＜0； 15. 54（若为108扣1分）； 16. x 2400-x%)201(2400= 8； 17. （16，1+3）； 18. 15.5（或231）. 三、解答题19. （1）解：原式 = 4×22-22+1-1……2分（每错1个扣1分，错2个以上不给分） = 0 …………………………………4分（第26题图）（2）解：原式 =（n m n m ++-n m n +）·m n m 22- …………2分= nm m +·m n m n m ))((-+ …………3分= m – n …………4分 20. 解：由①得3（1 + x ）- 2（x -1）≤6， …………1分化简得x ≤1. …………3分由②得3x – 3 ＜ 2x + 1， …………4分化简得x ＜4. …………5分 ∴原不等式组的解是x ≤1. …………6分21. 解（1）如图所示（作图正确得3分）（2）∵BD 平分∠ABC ，∠ABC = 72°， ∴∠ABD =21∠ABC = 36°， …………4分 ∵AB = AC ，∴∠C =∠ABC = 72°， …………5分 ∴∠A= 36°，∴∠BDC =∠A+∠ABD = 36° + 36° = 72°. …………6分 22. 解：（1）观察条形统计图，可知这组样本数据的平均数是 _x =50551841737231⨯+⨯+⨯+⨯+⨯　=3.3， …………1分∴这组样本数据的平均数是3.3. …………2分∵在这组样本数据中，4出现了18次，出现的次数最多， ∴这组数据的众数是4. …………4分∵将这组样本数据按从小到大的顺序排列，其中处在中间的两个数都是3，有233+ = 3. ∴这组数据的中位数是3. ………………6分（2）∵这组数据的平均数是3.3，∴估计全校1200人参加活动次数的总体平均数是3.3，有3.3×1200 = 3900. ∴该校学生共参加活动约3960次. ………………8分 23. 解：在Rt △BDC 中，∠BDC = 90°，BC = 63米，∠BCD = 30°， ∴DC = BC ·cos30° ……………………1分 = 63×23= 9， ……………………2分 ∴DF = DC + CF = 9 + 1 = 10，…………………3分 ∴GE = DF = 10. …………………4分在Rt △BGE 中，∠BEG = 20°， ∴BG = CG ·tan20° …………………5分 =10×0.36=3.6， …………………6分在Rt △AGE 中，∠AEG = 45°，∴AG = GE = 10， ……………………7分 ∴AB = AG – BG = 10 - 3.6 = 6.4.答：树AB 的高度约为6.4米. ……………8分24. 解（1）如图，连接OA ，则OA ⊥AP. ………………1分∵MN ⊥AP ，∴MN ∥OA. ………………2分 ∵OM ∥AP ，∴四边形ANMO 是矩形.∴OM = AN. ………………3分（2）连接OB ，则OB ⊥AP ，∵OA = MN ，OA = OB ，OM ∥BP ， ∴OB = MN ，∠OMB =∠NPM.∴Rt △OBM ≌Rt △MNP. ………………5分 ∴OM = MP.设OM = x ，则NP = 9- x . ………………6分在Rt △MNP 中，有x 2 = 32+（9- x ）2.∴x = 5. 即OM = 5 …………… 8分25. 解：（1）设A 型每套x 元，则B 型每套（x + 40）元. …………… 1分 ∴4x + 5（x + 40）=1820. ……………………………………… 2分∴x = 180，x + 40 = 220.即购买一套A 型课桌凳和一套B 型课桌凳各需180元、220元. ……………3分（2）设购买A 型课桌凳a 套，则购买B 型课桌凳（200 - a ）套.a ≤32（200 - a ）， ∴ …………… 4分 180 a + 220（200- a ）≤40880.解得78≤a ≤80. …………… 5分∵a 为整数，∴a = 78，79，80∴共有3种方案. ………………6分设购买课桌凳总费用为y 元，则y = 180a + 220（200 - a ）=-40a + 44000. …………… 7分 ∵-40＜0，y 随a 的增大而减小，∴当a = 80时，总费用最低，此时200- a =120. …………9分即总费用最低的方案是：购买A型80套，购买B型120套. ………………10分。

2015模拟数学模拟3

绝密★启用前2015年初三年级学业水平考试数学试题注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分120分．共8页．考试时间120分钟．2．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用2B铅笔涂写在答题卡上，并同时将考点、姓名、准考证号、座号填写在试卷规定的地方．3．选择题选出答案后，用2B铅笔把答题卡上对应题目的正确答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案，答案写在试卷上无效．4．数学考试不允许使用计算器，考试结束后，应将本试卷和答题卡一并交回．第I卷（选择题共45分）一、选择题（本大题共15个小题，每小题3分，共45分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．下列运算正确的是（）A. B. C. D.2．浙江省森林面积约为87663000亩，森林覆盖率60.5％．下列用科学记数法表示87663000正确的是（）。

A．8766.3×103 B．876.63×104 C．8.7663×106 D．8.7663×1073．的值等于（）A．4 B． C．2 D．24．如图，直线AB∥CD，直线EF分别交直线AB、CD于点E、 F，过点F作FG⊥FE，交直线AB于点G，若∠1=42°，则∠2的大小是（）A．56° B．48° C．46° D．40°5．在下列四个图案中，既是轴对称图形，又是中心对称图形的是（）A． B． C． D．6．将一张正方形纸片，按如图步骤①，②，沿虚线对着两次，然后沿③中的虚线剪去一个角，展开铺平后的图形是（）A．B．C．D．7．分式的计算结果是（）A． B． C． D．8．已知四边形ABCD和对角线AC、BD，顺次连接各边中点得四边形MNPQ，给出以下6个命题：①若所得四边形MNPQ为矩形，则原四边形ABCD为菱形；②若所得四边形MNPQ为菱形，则原四边形ABCD为矩形；③若所得四边形MNPQ为矩形，则AC⊥BD；④若所得四边形MNPQ为菱形，则AC=BD；⑤若所得四边形MNPQ为矩形，则∠BAD=90°；⑥若所得四边形MNPQ为菱形，则AB=AD.以上命题中，正确的是( ) A．①② B．③④ C．③④⑤⑥ D．①②③④9．已知函数y=（x﹣m）（x﹣n）（其中m＜n）的图象如图所示，则一次函数y=mx+n与反比例函数y=的图象可能是（）10．如图DE是△ABC的中位线，延长DE至F使EF＝DE，连接CF，则S△CEF∶S四边形BCED的值为（）A．1∶3 B．2∶3 C．1∶4 D．2∶5第10题图第11题图第12题图11．如图，在平面直角坐标系中，点A1，A2在x轴上，点B1，B2在y轴上，其坐标分别为A1（1，0），A2（2，0），B1（0，1），B2（0，2），分别以A1、A2、B1、B2其中的任意两点与点O为顶点作三角形，所作三角形是等腰三角形的概率是（）A．B．C．D．12．如图，O为矩形ABCD的中心，将直角三角板的直角顶点与O点重合，转动三角板使两直角边始终与BC，AB相交，交点分别为M，N．如果AB=4，AD=6，OM=x，ON=y．则y与x的关系是（）A． B． C．y=x D．13．如图，PA、PB切⊙O于A、B两点，CD切⊙O于点E，交PA，PB于C、D，若⊙O的半径为r，△PCD的周长等于3r，则tan∠APB的值是（）A． B． C． D．14．如图，下列图形都是由面积为1的正方形按一定的规律组成，其中，第（1）个图形中面积为1的正方形有2个，第（2）个图形中面积为1的正方形有5个，第（3）个图形中面积为1的正方形有9个，…，按此规律，则第（6）个图形中面积为1的正方形的个数为（）（1）（2）（3）（4）A.20B.27C.35D.4015．如图，已知边长为4的正方形ABCD， E是BC边上一动点(与B、C不重合)，连结AE，作EF⊥AE交∠BCD的外角平分线于F，设BE＝x，△ECF的面积为y，下列图象中，能表示y与x的函数关系的图象大致是（）A． B．C． D．第II卷（非选择题共75分）二、填空题（本大题共6个小题，每小题3分，共18分．把答案填在题中的横线上．）16．若 .17．分解因式：2a2－8b2=18．在平面直角坐标系中横、纵坐标均是整数的点称为整点，例如点（－1，4）是一个整点．直线y=－x+4与两坐标轴围成△AOB，点P是△AOB的边及其内部的整点，则点P落在以O为圆心，3为半径的圆内的概率为 .19．若分式方程：无解,则k=_________．20．如图，在直角坐标系中，点P0的坐标为（），将线段OP0绕点O按逆时针方向旋转45°，再将其长度伸长为OP0的2倍，得到线段OP1；又将线段OP1绕点O按逆时针方向旋转45°，长度伸长为OP1的2倍，得到线段OP2；如此下去，得到线段OP3，OP4，…，OP n（n为正整数），则点P2014的坐标是．第20题图第21题图21．如图，平行于x轴的直线AC分别交抛物线y1=x2（x≥0）与（x≥0）于B、C两点，过点C作y轴的平行线交y1于点D，直线DE∥AC,交y2于点E，则= .三、解答题（本大题共7个小题，共57分．解答应写出文字说明、证明过程或演算步骤．）22．(本小题满分7分)（1）计算.（2）解不等式组：；并将解集在数轴上表示出来．23．（本小题满分7分）（1）如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．已知AB＝8，CD＝2．（1）求⊙O的半径；（2）求sin∠BCE的值．（2）如图，矩形ABCD中，E是AD上的一点，F是AB上的一点，EF⊥EC，且EF=EC，DE=4cm，矩形ABCD的周长为32cm，求AE的长．24．（本小题满分8分）“六一”儿童节前，某玩具商店根据市场调查，用2500元购进一批儿童玩具，上市后很快脱销，接着又用4500元购进第二批这种玩具，所购数量是第一批数量的1.5倍，但每套进价多了10元．（1）求第一批玩具每套的进价是多少元？（2）如果这两批玩具每套售价相同，且全部售完后总利润不低于25%，那么每套售价至少是多少元？25. （本小题满分8分）每年3月12日，是中国的植树节。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2015小学数学毕业模拟试卷（三）20150618
姓名成绩
一、活用概念，对号入座。

（每空1分，共33分）
1、小明在小学上课，每节课的时间是40分钟，合（）小时；每天在校需要喝3瓶250毫升的矿泉水，合（）升；每瓶矿泉水售价2元4角，三瓶共（）元。

2、你知道全国小学生的人数吗？这个数是由1个亿、2个千万、8个百万和9个十万组成的，这个数写作（），改写成以“亿”作单位的数是（）亿。

3、（）12 ＝12÷（）＝0.25＝3 ︰（）＝（）％=（）折
4、6
13的分数单位是（），再添上（）个这样的分数单位就是最小的合数。

5、根据bc=a （a 、b 、c 是不为0的自然数），可知a 和b 的最大公因数是（）。

6、将一个周长是20分米的平行四边形框架拉成一个长方形，这个长方形的周长是（）分米，面积最大会是（）平方分米。

7、右面的立体图形是由棱长1厘米的小正方体组成的，它的表面积是（）平方厘米，至少
还需要（）个这样的小正方体才能拼一个正方体。

8.陈明今年上半年每个月的零花钱如下表：
他平均每个季度的零花钱是（）元；三月份比四月份多用（）％。

9、某公司发行10000张对奖券，其中一等奖10名，二等奖300名，三等奖1000名。

小张买了一张，问他获奖的可能性是（），获一等奖的可能性是（）。

10、用橡皮泥做一个圆柱形学具，做出的圆柱底面直径4厘米，高6厘米。

如果再做一个长方体纸盒，使橡皮泥圆柱正好能装进去，至少需要（）平方厘米硬纸。

11、直角三角形的一个锐角是46°，另一个锐角是（）°；等腰三角形的一个底角是40°，顶角是（）°；三角形三个角度数的比是2︰4︰3，最大的角是（）
12、一个圆锥形的稻谷堆，量得它的底面周长为12.56米，高为1.5米，已知每立方米稻谷重750千克，这堆稻谷共重（）千克。

13、大货车的载重量是小货车的2倍，用2辆大货车和6辆小货车一趟正好运完，员工要运50吨大米。

大货车的载重量是（）吨。

小货车载重量是（）吨。

14、、在股票交易中，买进必须按成交额的0.3％交纳印花税、0.15
1000股科技股，需要交纳印花税（）元、佣金（）元。

15、右图中甲、乙、丙三根木棒直插在水池中，三根木棒的长度之和是360厘米，
甲木棒的
43露出水面，乙木棒的74露出水面，丙木棒的5
2
露出水面，则水深（）厘米。

16、一根长1米，横截面直径是20厘米的木头浮在水面上，小明发现它正好
是一半露出水面，请你求出这根木头与水接触的面的面积是（）平方厘米。

二、反复比较，精挑细选。

（选择正确序号填入括号中，10分）
1、飞飞乘火车回老家东台，下午2时出发，12小时后到家，到达时看到的景象可能是（） A 、旭日东升 B 、残阳如血 C 、星光灿烂 D 、骄阳似火
2、右图是一个无盖正方体的展开图，A 面的对面应该是（）
A 、
B 面 B 、
C 面 C 、
D 面 D 、
E 面 3、下面的几句话中，正确的有（）句。

①一个平行四边形和一个三角形的底和面积分别相等，如果平行四边形的高是1.6分米，那三角形的高是0.8分米。

②能同时被2、3、5整除的最小三位数是120。

③6个人合吃一个西瓜，每人吃这个西瓜的6
1。

④正方形的面积与边长成正比例。

⑤用一根10cm 长的小棒和两根5cm 长的小棒可以围一个等腰三角形。

⑥要把病人一昼夜的体温变化情况用统计图表示出来，选用扇形统计图比较合适。

A 、 1
B 、 2
C 、 3
D 、 4 4、一个考场有30名考生，男女生人数的比可能是（）
A 、3﹕2
B 、4︰5
C 、1︰3
D 、3︰4 5、学校体育室里篮球个数比足球多40％，足球个数占两种球总数的（）。

A 、57 B 、 25 C 、 512 D 、712
三、注意审题，细心计算。

（共22分）
1、下面各题怎样算简便就怎样算。

（12分） 48×0.99 0.25×3.2×12.5 75×23－2÷5
7 38 ×[89 ÷(56 －3
4 )]
2、求x 的值：（6分）
32：6
5＝X ：18 5.5x ＋x ＝13 56 +1
6 x= 2
A
B C D
E
四、操作与应用。

（共5分）
（2）将图形B 先向右平移7格，再向上平移2格。

（3）将图形C 绕D 点顺时针旋转90°，画出图形C 按2︰1放大后的图形E 。

（4）以点O 为圆心，画一个直径是4厘米的半圆。

（一小格为1厘米）
五、探索与发现。

（共3分）
用一根长96厘米的绳子在地上摆正方形。

……
当这根绳子摆出48个正方形时，正方形的边长是（）厘米。

当这根绳子摆出n 个正方形时，顶点数是（）个。

六、走进生活，解决问题。

（1—3题每题4分，4-6题每题5分共27分）
1、学校用方砖铺会议室的地面。

原来打算用面积0.25平方米的方砖，需要540块。

现在改用面积0.36平方米的方砖，需要多少块？
2、一个三角形和一个平行四边形等底等高，三角形的面积是120平方厘米，底是15厘米。

平行四边形的高是多少厘米？（用方程解答）
3、下表是《道路安全法实施条例》规定：
王叔叔以50千米/时的速度在高速公路上行驶，前方出现限速40千米的标示。

如果李叔叔保持这个速度继续行驶，他将受到扣几分的处罚？（写出判断方法）
4、张老师在科学课上做实验，将一根140厘米长的铁丝剪成三段。

第二段铁丝比第一段长16厘米，第三段铁丝比第二段长24厘米。

第三段铁丝长多少厘米？（先把下图补充完整，再解答）第一段：
第二段：｝140厘米第三段：
5、妈妈的茶杯中部有一圈装饰带，那是怕烫伤妈妈的手特意贴上去的。

经过测量，这条装饰带正好宽5厘米，算一算，装饰带的面积至少是多少平方厘米？如果把0.5升的水倒入茶杯，能正好装满吗？
6、一根铁丝，第一次用去全长的1
5 ，第二次用去15米，这时用去的与剩下的长度比正好是4 ：1 。

这根
铁丝长多少米？
单位：厘米
15 5。