2015-2016年四川省成都市金牛区八年级上学期期中数学试卷及参考答案
2015-2016学年八年级数学上册期中检测试卷参考答案及评分标准201510

12015—2016学年度第一学期期中检测八 年 级 数 学 试 题(友情提醒:全卷满分100分,考试时间90分钟,请你掌握好时间.)一、选择题(每小题3分,共30分)(请将正确答案序号填入以下表格相应的题号下,否则不得分)1. 下列图形分别是桂林、湖南、甘肃、佛山电视台的台徽,其中为轴对称图形的是( ☆ )A .B .C .D .2. 以下列各组线段为边,能组成三角形的是( ☆ )A . 2cm ,3cm ,5cmB . 5cm ,6cm ,10cmC . 1cm ,1cm ,3cmD . 3cm ,4cm ,9cm3. 已知点M (a ,3),点N (2,b )关于y 轴对称,则(a+b )2015的值( ☆ )A .-3B . -1C .1D . 34. 如图1,∠B=∠D=90°,CB=CD ,∠1=30°,则∠2=( ☆ )A . 30°B . 40°C . 50°D . 60°5. 十二边形的外角和是( ☆ )A. 180°B. 360°C.1800 ° D2160°6. 已知等腰三角形一边长为4,一边的长为6,则等腰三角形的周长为( ☆)A .14 B . 16 C . 10 D . 14或16 7. 如图2,△ABC 中,AB=AC ,D 为BC 的中点,以下结论:(1)△ABD ≌△ACD ; (2)AD ⊥BC ;(3)∠B=∠C ; (4)AD 是△ABC 的角平分线.其中正确的有( ☆ ) A . 1个 B . 2个 C . 3个 D . 4个8. 已知△DEF ≌△ABC ,AB=AC ,且△ABC 的周长是23cm ,BC=4cm ,则△DEF 的边长中必有一边等于( ☆ )A . 9.5cmB . 9.5cm 或9cmC . 4cm 或9.5cmD . 9cm 9. 下列条件中,能判定△ABC ≌△DEF 的是( ☆ ) AC=,∠10. 如图3,BE 、CF 是△ABC 的角平分线,∠ABC=80°,∠ACB=60°,BE 、CF 相交于D ,则∠CDE 的度数是( ☆ )(图1)(图2)(图3)2A 、110°B 、70°C 、80°D 、75°二、填空题(每小题3分,共30分)11. 三角形的三边长分别为5,x ,8,则x 的取值范围是 .12. 已知如图4,△ABC ≌△FED ,且BC=DE ,∠A=30°,∠B=80°,则∠FDE= . 13. 如图5,则∠A+∠B+∠C+∠D+∠E+∠F 的度数为 .(图6)(图5)(图4)14. 如图6,已知AD 平分∠BAC ,要使△ABD ≌△ACD ,根据“AAS ”需要添加条件 _________ . 15. 如图7,在生活中,我们经常会看见在电线杆上拉两条钢线,来加固电线杆,这是利用了三角形的 .16. 如果一个多边形的每个内角都相等,且内角和为1800°,那么该多边形的一个外角 度. 17. 在直角坐标系中,如果点A 沿x 轴翻折后能够与点B (-1,4)重合,那么A ,B 两点之间的距离等于 .18. 如图8,在△ABC 中,AB =AC ,AF 是BC 边上的高,点E 、D 是AF 的三等分点,若△ABC 的面积为12cm 2,则图中全部阴影部分的面积是 ___cm 2.19. 如图9,已知∠ABD=40°,∠ACD=35°,∠A=55°,则∠BDC= .20. 如图10,△ABC 和△FED 中,BD=EC ,∠B=∠E .当添加条件 时,就可得到△ABC ≌△FED ,依据是 (只需填写一个你认为正确的条件).三、解答题(共40分)21. (7分) 完成下列证明过程.如图11,已知AB ∥DE ,AB=DE ,D ,C 在AF 上,且AD =CF ,求证:△ABC ≌△DEF .证明: ∵ AB ∥DE∴∠_________=∠_________( )∵ AD=CF ∴AD+DC=CF+DC 即_____________ 在△ABC 和△DEF 中AB DCEF( 图11 )( 图10 )( 图9 )A( 图8 )E3AB=DE__________________________∴△ABC ≌△DEF ()22.(8分)如图12,四边形ABCD 中,E 点在AD 上,其中∠BAE =∠BCE =∠ACD =90°, 且BC =CE .请完整说明为何△ABC 与△DEC 全等的理由.23.(5分)如图13,已知△ABC 的三个顶点分别为A (2,3)、B (3,1)、C (-2,-2)。
2015-2016学年八年级上学期期中考试数学试卷

2015.11
7 D 8 C
三.解答题(共 56 分) 1 3 19. (共 8 分) (1)原式=4+ + ……(3 分) 2 2 =6 ……(4 分) (2)原式=3+ 2-1-1……(3 分) = 2+1……………(4 分) 27 (2) (x+1)3= ……………(1 分) 64 3 x+1= …………………(2 分) 4 1 x=- ………………(4 分) 4
B.
C.
D.
5.等腰三角形的两边长分别为 3cm 和 7cm,则周长为………………………………………… B.17 cm C.13 cm 或 17 cm D.11 cm 或 17 cm
6. 如图, 已知 AB=AD, 那么添加下列一个条件后, 仍无法判定△ABC ≌ △ADC 的是……… ) B.∠BAC=∠DAC A
C
A.CB=CD
D
C.∠BCA=∠DCA
பைடு நூலகம்
D.∠B=∠D=
F B C
G E H D
(第 8 题)
(第 7 题)
7.如图,已知△ABC 与△CDE 都是等边三角形,点 B、C、D 在同一条直线上,AD 与 BE 相交于点 G, BE 与 AC 相交于点 F, AD 与 CE 相交于点 H, 则下列结论①△ACD≌△BCE ② ∠AGB=60° ③BF=AH ④△CFH 是等边三角形 ⑤连 CG,则∠BGC=∠DGC.其中正 确的个数是…( A.2 上; △A1B1A2、 △A2B2A3、 △A3B3A4…均为等边三角形. 若 OA1=1, 则△A2015B2015A2016 的边长为… ) B.3 C.4 D.5
2.平方根等于它本身的数是………………………………………………………………………
2015--2016学年度第一学期期中考试八年级数学试题详解

∴ -k+b=-5 2k+b=1
∴ k=2 b=-3
∴y=2x-3
(3) y=2x-3取y=0,得x=1.5
∴
1 2
×1.5×1=0.75
∴这两个函数图象与x轴所围成三角形面积为0.75.
21.(10分)如图△ABC中,BO,CO分别平分∠ABC和∠ACB. (1)若∠ABC=500,∠ACB=700,求∠BOC的度数; (2)若∠A=500,求∠BOC度数; (3)若∠A=α,试探究∠BOC与α的关系.(写出推理过程)
解:(2)∵∠A=500,
∴∠ABC+∠ACB=1800-∠A=1300
∵BO,CO分别平分∠ABC和∠ACB
∴∠OBC=
1 2
∠ABC
∠OCB=
1 2
∠ACB
∴∠OBC+∠OCB=
1 2
(∠ABC+∠ACB)
∴∠BOC=1800-(∠=×OB1213C0+0=∠6O50CB)
=1800- 650=1150
k(2-1)=3 ∴k=3 ∴y=3(x-1)=3x-3 ∴y与x的函数关系式为y=3x-3
19.(8分)函数,方程,不等式都是刻画量与量之间变化规 律的重要模型,它们之间存在密切联系.在学习了一次函 数与一次不等式的关系之后,运用所学的解题思想方法, 探究下列问题:已知两个函数y1,y2,它们的图象如图所示, 其中y1是一条直线,y2是一条曲线,请你根据图象回答: (1)当x取何值时,y2=0; (2)当x取何值时,y1= y2 ; (3)当x取何值时,y1>y2.
第13题
第14题
16.如图是甲乙两同学运动的路程s(米)与时间t(秒) 的一次函数图象,已知甲的速度比乙快,观察图象得 到如下信息: ①甲的速度比乙快1.5米/秒,②甲让乙先跑12米,③AB表 示甲的路程与时间的关系函数图象,④8秒后, 甲超过了 乙. 其中正确的信息有___①__②__④________.
2015-2016学年八年级上学期期中考试数学试卷

2015—2016学年度第一学期期中考试试卷初二数学(试题卷)(考试时间100分钟,满分100分)一.选择题(本大题共10小题,每题3分,共30分.)1.下列美丽的车标中是轴对称图形的个数有……………………………………………………………( ▲ )A .1个B .2个C .3个D .4个2.如图,在边长为1个单位长度的小正方形组成的网格中, A 、B 都是格点,则线段AB 的长度为………………………………………………………………………………………………( ▲ ) A. 5 B. 6 C.7 D. 83.一个等腰三角形的两边长分别是4和9,则它的周长是……………………………………( ▲ ) A .13 B .17 C .22 D .17或224. 下列结论错误的是…………………………………………………………………………………………………( ▲ )A .全等三角形对应边上的中线相等B .两个直角三角形中,两个锐角相等,则这两个三角形全等C .全等三角形对应边上的高相等D .两个直角三角形中,若有两组边对应相等,则这两个直角三角形全等5.如图,请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等有关的 知识,说明画出∠A'O'B'=∠AOB的依据是…………………………………………………………( ▲ ) A .SAS B .ASA C .AAS D .SSS6.已知△ABC 中,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,下列条件不能判断△ABC 是 直角三角形的是………………………………………………………………………………………………………( ▲ )(第2题图)A .∠A :∠B :∠C=3:4:5 B . a :b :c =5:12:13C . a 2=b 2-c 2D .∠A =∠C -∠B 7.在联欢会上,有A 、B 、C 三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置 是在△ABC的 ………………………………………………………………………………………………………( ▲ )A. 三边中线的交点 B .三边中垂线的交点 C .三条角平分线的交点 D .三边上高的交点8.如图,BD 是∠ABC 平分线,DE AB 于E ,AB =36cm,BC =24cm,S △ABC =144cm 2,则DE 的长是………( ▲ )A .4.8cmB .4.5cmC .4 cmD .2.4cm9.在如图的正方形网格上画有两条线段.现在要再画一条,使图中的三条线段组成一个轴对称图形, 能满足条件的线段有……………………………………………………………………………………………………………………( ▲ )A .2条B .3条C .4条D .5条10.如下图,已知∠AOB =α,在射线OA 、OB 上分别取点OA 1=OB 1,连结A 1B 1,在B 1A 1、(第8题图)B(第5题图)(第9题图)(第14题图)(第10题图)B 1B 上分别取点A 2、B 2,使B 1B 2= B 1A 2,连结A 2 B 2……按此规律下去,记∠A 2B 1 B 2=θ1,∠A 3B 2B 3=θ2,…, ∠A n +1B n B n +1=θn,则θ2016-θ2015的值为………………………………………………………………………………………………( ▲ )A .20151802α+ B . 20151802α- C .20161802α+ D .20161802α-二.填空题(本大题共8小题,每空3分,共24分.) 11.正方形是一个轴对称图形,它有 ▲ 条对称轴. 12.△ABC 是等腰三角形,若∠A =80°,则∠B = ▲.13.某直角三角形的两直角边长分别为6cm ,8 cm ,则此三角形斜边上的高的长是 ▲ cm .14.如图,∠1=∠2,要使△ABE ≌ △ACE ,则还需添加一个条件是 ▲ .15. 如图,长方体的底面边长分别为1cm 和3cm ,高为6cm .如果用一根细线从点A 开始经过4个侧面缠绕一圈到达点B ,那么所用细线最短需要 ▲ cm . 16.如图,△OAD ≌△OBC ,且∠O =70°,∠AEB =100°,则∠C = ▲ °.17.如图,AE ⊥AB ,且AE =AB ,BC ⊥CD ,且BC =CD ,请按照图中所标注的数据计算图中实线所围成的图形的面积S = ▲ .18.已知:如图,AD 、BE 分别是△ABC 的中线和角平分线, AD ⊥BE ,AD =8,BF =5,则AC 的长等于 ▲ .(第15题图)FBACDE (第18题图)CABED(第16题图) O(第17题图)(图1)(图2)三.解答题(本大题共6小题,共46分. 解答需写出必要的文字说明或演算步骤) 19.作图题:(6分)(1)如图,在图1所给方格纸中,每个小正方形边长都是1,标号为①②③的三个三角形均为格点三角形(顶点在方格顶点处),请按要求将图2中的指定图形分割成三个三角形,使它们与标号为①②③的三个三角形分别对应全等.(分割线画成实线.) (2)如图3,在长度为1个单位长度的小正方形组成的正方形网格中,点A 、B 、C 在小正方形的顶点上.①在图中画出与△ABC 关于直线L 成轴对称的△A′B′C′; ②请直线L 上找到一点P ,使得PC + PB 的距离之和最小..20.(6分)如图,四边形ABCD 中,AB ∥CD ,AB =CD ,A ∠ABE =∠CDF .(1)试说明:△ABE ≌△CDF ;(2)试说明:AF =CE .21.(6分)中菲黄岩岛争端持续,我海监船加大黄岩岛附近海域的巡航维权力度.如图,OA ⊥OB ,OA =36海里,OB =12海里,黄岩岛位于O 点,我国海监船在点B 处发现有一不明国籍的渔船,自A 点出发沿着AO 方向匀速驶向黄岩岛所在地点O ,我国海监船立即从B 处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C 处截住了渔船. (1)请用直尺和圆规作出C 处的位置; (2)求我国海监船行驶的航程BC 的长.22.(7分)如图,△ACB 与△ECD 都是等腰直角三角形,∠ACB =∠ECD =90º,点D 为AB 边上的一点,(1)试说明:∠EAC =∠B ;(2)若AD =10,BD =24,求DE 的长.O(图3)23.(6分)如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,且DC=BF,DE⊥CF于E,问E是CF的中点吗?试说明理由24.(6分)探索研究.请解决下列问题:(1)已知△ABC中,∠A=90°,∠B=67.5°,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,并把所有不同的分割方法都画出来,图不够可以自己画.只需画图,不必说明理由,但要在图中标出相等两角的度数).(2)已知等腰△ABC中,AB=AC,D为BC上一点,连接AD,若△ABD和△ACD都是等腰三角形,则∠B的度数为(请画出示意图,并标明必要的角度).25.(9分)如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.(1)试说明:AD∥BC;(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和G点的移动距离.2015—2016学年第一学期期中考试试卷初二数学参考答案 2015.11一、选择题(每题3分,共30分)二、填空题(每题3分,共24分)11.__ 4 ____; 12. 80°或50°或20°; 13.__ 4.8_ ;14.∠B =∠C 等; 15.__ 10 ; 16. 15° _; 17._ 50 _;18._ 13 ___.三、解答题: (第12题有一个答案给1分,多答,答错不得分) 19.(1) 图略---------2分 (2)① 图略--------2分 ②图略--------2分 20.(1)解:∵AB ∥CD∴∠BAE =∠DAF ---------1分又∵AB =CD ,∠ABE =∠CDF ---------2分∴△ABC ≌△DEF ---------3分 (2) ∵ △ABC ≌△DEF∴ AE=CF ---------4分 ∴ AE —EF=CF —EF ---------5分 ∴ AF=CE ---------6分21.(1)∴点C 就是所求点 ---------2分(2)解:连接BC ,由作图可得:CD 为AB 的中垂线∴CB =CA ---------3分 由题意可得:OC=36—CA=36—CB ---------4分 ∵OA ⊥OB∴在Rt △BOC 中,222BO CO BC +=∴22212(36)BC BC +-= ---------5分 ∴BC =20 ---------6分22.(1)∵∠ACB=∠E CD=90°∴∠ACB—∠ACD =∠E CD—∠ACD∴∠ECA=∠DCB ------------1分∵△ACB和△ECD都是等腰三角形∴EC=DC,AC=BC ------------2分∴△ACE≌△BCD ------------ 3分∴∠EAC=∠B ---------- 4分(2)∵△ACE≌△BCD∴AE=BD=24 -----------5分∵∠EAC=∠B=45 °∴∠EAD=∠EAC+∠CAD=90°------------6分∴在Rt△ADE中,222DE EA AD=+∴2221024DE=+∴DE=26 ------------7分23.解:E是CF的中点------------1分连结DF ------------2分∵AD⊥BC,F是AB边上的中点,∴DF就是Rt△ADB斜边AB上的中线------------3分∴DF =FB= 12AB------------4分∵DC=BF∴DC = DF ------------5分∵DE⊥CF∴DE平分CF,即E是CF的中点------------6分24.(1)------------2分(2)45°或36°------------4分------------6分25(1)证明:在△ABD和△CDB中AD=BCAB=CDBD=DB∴△ABD≌△CDB--------------1分∴∠ADB=∠CBD----------------2分∴AD∥BC----------------3分(2)解:设G点的移动距离为y,由(1)得∠EDG=∠FBG若△DEG与△BFG全等则有△DEG≌△BFG或△DGE≌△BFG可得:DE=BF,DG=BG;或DE=BG,DG=BF,----------------4分①当E由D到A,即0<t≤3时,有4t=12-t,解得t=2.4y=15-y y=7.5 ---------5分或4t = y,解得t= 112-t =15-y= 4 ----------------6分②当F由A返回到D,即3<t≤6时,有24-4t=12-t,解得t=4y=15-y y=7.5 ----7分或24-4t=y,解得t=4.212-t=15-y y=7.2 ----------------8分综上可知共有三次,移动的时间分别为1秒、2.4秒、4秒、4.2秒,移动的距离分别为4、7.5、7.5、7.2.----------------9分1、本试卷学生预计均分72分2、考点分布情况(按知识点)(1)全等三角形36分(2)轴对称图形38分(3)勾股定理26分。
2015—2016学年度第一学期期中质量测试八年级数学试题附答案
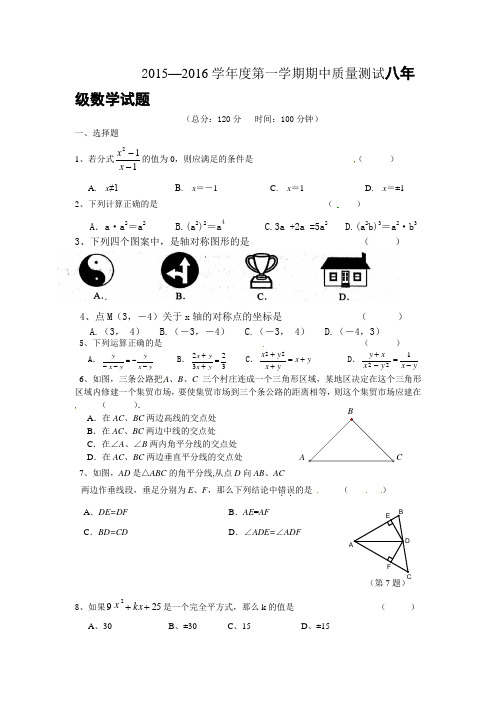
2015—2016学年度第一学期期中质量测试八年级数学试题(总分:120分时间:100分钟)一、选择题1、若分式112--xx的值为0,则应满足的条件是()A. x≠1B. x=-1C. x=1D. x=±12、下列计算正确的是()A.a·a2=a2 B.(a2)2=a4 C.3a+2a=5a2 D.(a2b)3=a2·b3 3、下列四个图案中,是轴对称图形的是()4、点M(3,-4)关于x轴的对称点的坐标是()A.(3, 4)B.(-3,-4)C.(-3, 4)D.(-4,3)5、下列运算正确的是()A.yxyyxy--=--B.3232=++yxyx C.yxyxyx+=++22D.yxyxxy-=-+1226、如图,三条公路把A、B、C三个村庄连成一个三角形区域,某地区决定在这个三角形区域内修建一个集贸市场,要使集贸市场到三个条公路的距离相等,则这个集贸市场应建在().A.在AC、BC两边高线的交点处B.在AC、BC两边中线的交点处C.在∠A、∠B两内角平分线的交点处D.在AC、BC两边垂直平分线的交点处7、如图,AD是△ABC的角平分线,从点D向AB、AC两边作垂线段,垂足分别为E、F,那么下列结论中错误..的是()A.DE=DF B.AE=AFC.BD=CD D.∠ADE=∠ADF8、如果2592++kxx是一个完全平方式,那么k的值是()A、30B、±30C、15D、±15BC(第7题)FEADB9、若把分式xyyx +中的x 和y 都扩大2倍,那么分式的值 ( ) A 、扩大2倍 B 、不变 C 、缩小2倍 D 、缩小4倍二、填空题10、一种细菌半径是0.000 012 1米, 将0.000 012 1用科学记数法表示为 . 11.计算: ()a a a 2262÷-= .12、如图,△ABC 中,∠C =90°,∠A =30°,AB 的垂 直平分线交AC 于D ,交AB 于E ,CD =2,则AC = .三、解答题13、分解因式:(4分) x 3﹣4x 2+4x14、先化简再求值:(6分))52)(52()1(42-+-+m m m ,其中3-=m15、解方程:(6分) .16、(6分)如图,点B ,E ,F ,C 在一条直线上,AB =DC ,BE =CF ,∠B =∠C . 求证:∠A =∠D .DECB12题(第16题)F E DCBA图8ABCDE17(8分)如图,∆ABC 中BD 、CD 平分∠ABC 、∠ACB ,过D 作直线平行于BC ,交AB 、AC 于E 、F ,求证:EF=BE+CF.18、如图8,在ABC ∆中,090=∠ACB ,CE BE BC AC ⊥=,于E ,AD CE ⊥于D . (1)求证:△ADC ≌△CEB .(5分)(2),5cm AD =cm DE 3=,求BE 的长度.(4分)第17题答案一、B B C A D C C BC二、1.21×10-5 , 3a-1 ,6 三、13、解:原式=x(x-2)214、解:原式=4m 2+8m+4-4m 2+25=8m+29当m=-3时,原式= -24+29=5 15、解:去分母得:x(x+2)-(x 2-4)=8整理 得:2x=4 解得:x=2经检验得x=2是原方程的增根 ∴原分式方程无解16、证明:∵BE =CF∴BF=CE在△ABE和△DCF中∵AB =DC ,∠B =∠C ,BF=CE∴△ABE≌△DCF∴∠A =∠D17、证明:∵BD平分∠ABC ∴∠EBD=∠DBC∵EF∥BC ∴∠EDB=∠DBC∴∠DBC=∠EBD ∴BE=DE 。
2015—2016学年八年级上学期数学期中试卷(5套)

2015—2016学年八年级上学期数学期中试
卷(5套)
2015年八年级上册数学期中考试题整理
八年级上册数学期中考试试卷:附答案
最新:初中二年级上册数学期中考试模拟试卷
2015—2016学年初二上学期数学期中试卷
八年级数学期中卷2015
一个学期一次的期中考试马上就要开始了,同学们正在进行紧张的复习。
这就是我们为大家准备的八年级上学期数学期中试卷,希望能够及时的帮助到大家。
为大家策划了八年级上册期中复习专题,为大家提供了八年级期中考试复习知识点、八年级期中考试复习要点、八年级期中考试模拟题、八年级期中考试试卷、八年级语文期中复习要点、八年级数学期中模拟题、八年级英语期中模拟题等相关内容,供大家复习参考。
四川省成都市八年级上学期期中数学试卷

四川省成都市八年级上学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分) (2019八上·融安期中) 如图,△ABC与△A′B′C′关于直线DE对称,且∠C=78°,∠B′=48°,则∠A的度数为()A . 48°B . 54°C . 74°D . 78°2. (2分) (2017七下·龙华期末) 如果一个三角形的两边长分别为5,12,则第三边的长可以是()A . 18B . 13C . 7D . 53. (2分) (2016八上·杭州月考) 下列各组数可能是一个三角形的边长的是()A . 1,2,4B . 4,5,9C . 4,6,8D . 5,5,114. (2分) (2016八上·江宁期中) 若等腰三角形的两边长分别为3cm和6cm,则该等腰三角形的周长是()A . 9cmB . 12cmC . 12cm或15cmD . 15cm5. (2分)如图,四个图形中,是轴对称图形的有()A . 4个B . 3个C . 2个D . 1个.6. (2分) (2019八上·嘉荫期末) 如图,D是BC的中点,E是AC的中点,△ADE的面积为2,则△ABC的面积为()A . 4B . 8C . 10D . 127. (2分)使两个直角三角形全等的条件()A . 一锐角对应相等B . 两锐角对应相等C . 一条边对应相等D . 两条边对应相等8. (2分)(2018·鄂尔多斯模拟) 如图.在△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心、适当长为半径作圆弧,分别交边AC,AB于点M、N;②分别以点M和点N为圆心、大于MN一半的长为半径作圆弧,在∠BAC 内,两弧交于点P;③作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是()A . 15B . 30C . 45D . 609. (2分)如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠EDF的度数为()A . 50°B . 40°C . 80°D . 60°10. (2分) (2017八上·南涧期中) 如图,△ABC中,AC=AD=BD,∠DAC=80º,则∠B的度数是()A . 40ºB . 35ºC . 25ºD . 20º二、填空题 (共6题;共6分)11. (1分) (2016八上·庆云期中) 一辆汽车车牌在水中的倒影为如图,该车牌的牌照号码是________.12. (1分)一个八边形的内角和是________13. (1分)如果点P1(﹣2,3)和P2(﹣2,b)关于x轴对称,则b= ________.14. (1分)如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论:①△EBF≌△DFC;(请②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是________ .写出正确结论的序号).15. (1分) (2017八上·马山期中) 如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是________.16. (1分) (2019七上·大东期末) 观察如图所示图形的构成规律,依照此规律,第个图形中共有________个“ ”.三、解答题 (共9题;共84分)17. (5分) (2015八上·宜昌期中) 如图,在△ABD和△ACD中,已知AB=AC,∠B=∠C,求证:AD是∠BAC 的平分线.18. (10分) (2017七下·南昌期中) 如图,在正方形网格中的每个小正方形边长都为1个单位长度,我们把每个小正方形的顶点称为格点,请分别仅用一把无刻度的直尺画图:(1)过点A画一条AB的垂线;(2)过点C画一条AB的平行线.19. (6分)(2017·柳江模拟) 已知:四边形ABCD如图所示.(1)填空∠A+∠B+∠C+∠D=________;(2)请用两种方法证明你的结论.20. (15分) (2017七下·荔湾期末) 如图所示,小方格边长为1个单位,(1)请写出△A BC各点的坐标.(2)求出S△ABC.(3)若把△ABC向上平移2个单位,再向右平移2个单位△A′B′C′,在图中画出△A′B′C′.21. (11分) (2017八上·武汉期中) 如图,△ABC和△ADE中,AB=AD,AC=AE,∠BAC=∠DAE,BC交DE于点O,∠BAD=a.(1)求证:∠BOD=a.(2)若AO平分∠DAC,求证:AC=AD.(3)若∠C=30°,OE交AC于F,且△AOF为等腰三角形,则a= ________22. (15分)(2017·濉溪模拟) 如图,在等腰直角△ABC中,∠ACB=90°,点D为三角形内一点,且∠ACD=∠DAB=∠DBC.(1)求∠CDB的度数;(2)求证:△DCA∽△DAB;(3)若CD的长为1,求AB的长.23. (5分) (2017八下·宝坻期中) 如图,在▱ABCD中,已知点E、F分别在边BC和AD上,且BE=DF.求证:AE=CF.24. (10分)(2020·西安模拟) 如图,△ABC为等边三角形,O为BC的中点,作⊙O与AC相切于点D.(1)求证:AB与⊙O相切;(2)延长AC到E,使得CE=AC,连接BE交⊙O与点F、M,若AB=4,求FM的长.25. (7分) (2018九上·南召期末) 如图1,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.(1)请直接写出PM与PN的数量关系及位置关系________;(2)现将图1中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图2,AE与MP、BD分别交于点G、H.请直接写出PM与PN的数量关系及位置关系________;(3)若图2中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图3,写出PM与PN的数量关系,并加以证明.参考答案一、选择题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共6题;共6分)11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共9题;共84分)17-1、18-1、18-2、19-1、19-2、20-1、20-2、20-3、21-1、21-2、21-3、22-1、22-2、22-3、23-1、24-1、24-2、25-1、25-2、25-3、。
2015-2016学年第一学期期中考试初二数学试卷附答案

2015-2016学年第一学期期中考试初二数学试卷(满分:100分,考试时间:120分钟)一、选择题:(本大题共10小题,每题3分,共30分)1.下列图案中是轴对称图形的有( )A.1个B.2个C.3个D.4个2.16的平方根是()A.4 B.±4 C.4D.±43.下列式子中,属于最简二次根式的是()A.9.0B.13C.20D.74.下列运算中错误的是()A.2×3= 6 B.12=22C.22+33=5 5 D.(-4)2=45.下列说法正确的是()A.平方根等于本身的数是0;B.36表示6的算术平方根;C.无限小数都是无理数;D.数轴上的每一个点都表示一个有理数.6.一个正方形的面积是20,估计它的边长大小在()A.2与3之间B.3与4之间C.4与5之间 D.5与6之间7. 在△ABC中,∠A、∠B、∠C的对应边分别是a、b、c,若∠A+∠C=90°,则下列等式中成立的是()A.c2-a2=b2B.a2+b2=c2C.b2+c2=a2D.a2+c2=b28.已知等腰三角形的两边长分别是3与6,那么它的周长等于()A.12 B.12或15 C.15 D.15或189. 如图,点D在AB上,点E在AC上,且∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是()A.AD=AE B.∠AEB=∠ADC C.BE=CD D.AB=AC10.如图是一张足够长的矩形纸条ABCD,以点A所在直线为折痕,折叠纸条,使点B(第17题图)(第18题图)(第9题图)(第10题图)落在边AD 上,折痕与边BC 交于点E ;然后将其展平,再以点E 所在直线为折痕, 使点A 落在边BC 上,折痕EF 交边AD 于点F .则∠AFE 的大小是 ( ) A .67.5° B . 60° C .45° D .22.5°二、填空题(本大题共8小题,每空2分,共16分) 11. 21-的相反数是 .12. 若2)3(-x =3﹣x ,则x 的取值范围是 .13. 2015年我市参加中考的学生人数大约为6.60×104人,对于这个用科学记数法表示的近似数,它精确到了 位.14. 已知实数错误!未找到引用源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015-2016学年四川省成都市金牛区八年级(上)期中数学试卷一.选择题(3×10=30分)1.(3分)9的平方根是()A.81 B.3 C.±3 D.±2.(3分)在3.14、﹣、、π、2.01001000100001这五个数中.无理数的个数是()A.1 B.2 C.3 D.43.(3分)下列各式中,错误的是()A.B.C.D.4.(3分)下列各组数据中,不能构成直角三角形的三边的是()A.3,4,5 B.9,41,40 C.6,3,5 D.13,12,55.(3分)若P的坐标为(a2+1,﹣a2﹣1),则P点在平面直角坐标系中的位置是()A.第一象限B.第二象限C.第三象限D.第四象限6.(3分)在平面直角坐标系中,已知一次函数y=kx+b的图象大致如图所示,则下列结论正确的是()A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<07.(3分)下列函数关系不是一次函数的是()A.汽车以120Km/h的速度匀速行驶,行驶路程y(Km)与时间t(h)之间的关系B.等腰三角形顶角y与底角x间的关系C.高为4cm的圆锥体积y (cm3)与底面半径x (cm)的关系D.一棵树现在高50cm,每月长高3cm,x个月后这棵树的高度y (cm)与生长月数x(月)之间的关系8.(3分)下列说法不正确的是()A.9的平方根是3B.无理数都是无限小数C.(3﹣π)2的算术平方根是π﹣3D.实数与数轴上的点是一一对应的9.(3分)已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是()A.24cm2B.36cm2C.48cm2D.60cm210.(3分)如图,将平面直角坐标系中的△AOB绕点O顺时针旋转90°得△A′OB′.已知∠AOB=60°,∠B=90°,AB=,则点B′的坐标是()A.B.C.D.二.填空题(3×5=15分)11.(3分)若式子有意义,则x的取值范围是.12.(3分)点P(2,﹣4)到x轴的距离为个单位,它关于原点的对称点的坐标为.13.(3分)当x=时,最简二次根式﹣5与2是同类二次根式.14.(3分)已知点P1(﹣1,y1),P2(﹣2,y2)是一次函数y=3x﹣2图象上的两点,则y1y2.(填“>”、“<”或“=”)15.(3分)如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离5cm,一只蚂蚁如果沿着长方体的表面从A点爬到B点,需要爬行的最短距离是.三.解答题(共55分)16.(10分)计算(1)﹣|﹣2|+(+1)0+(2)﹣+(﹣)﹣2.17.(10分)解方程(1)(4x+1)2=(2)(x﹣1)3+9=0.18.(5分)已知点A(3﹣a,7+a)在平面直角坐标系第一象限的角平分线上,求OA的值.19.(10分)已知:一次函数y=kx+b的图象经过M(0,2),N(1,3)两点.(1)求k、b的值;(2)若一次函数y=kx+b的图象与x轴交点为A(a,0),求a的值.20.(10分)如图,在四边形ABCD中,∠BAD=∠ACB=∠AED=90°,AB=AD.(1)求证:AC=DE;(2)若AC=4BC,CD=5,求四边形ABCD的面积.21.(10分)如图,已知直线y=x+1与x轴交于点A,与y轴交于点B,将△AOB 绕点O顺时针旋转90°后得到△COD.(1)求点C的坐标与线段AD的长;(2)点M在CD上,且CM=OM,求直线OM的解析式;(3)把OM向左平移,使之经过点A,求平移后的OM的解析式.四.填空题(5×4=20分)22.(4分)已知y=+5,则的值为.23.(4分)已知一次函数y=2x+a与y=﹣x+b的图象都经过A(2,0),且与y轴分别交于B,C,则△ABC的面积为.24.(4分)如图,在△ABC中,∠B=90°,AB=,将AC沿AE折叠,使点C与点D重合,且DE⊥BC,则AE=.25.(4分)若ab>0,a+b<0.那么下面各式:①=•;②•=1;③÷=﹣b;④•=a,其中正确的是(填序号)26.(4分)如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3);B1(4,0),B2(8,0),B3(16,0).(1)观察每次变换前后的三角形有何变化,找出规律,按次变化规律再将△OA3B3变换成△OA4B4,则A4的坐标是,B4的坐标是.(2)若按第(1)题找到的规律将△OAB进行了n次变换,得到△OA n B n,比较每次变换中三角形顶点坐标有何变化,找出规律,推测A n的坐标是.B n 的坐标是.五.解答题(26题8分,27题10分,28题12分,共30分)27.(8分)已知x=,y=(1)求x2﹣3xy+y2的值;(2)若x的整数部分是a,y的小数部分是b,求a2+b2的值.28.(10分)利用图形整体面积等于部分面积之和可以证明勾股定理.①如图(1)所示可以证明勾股定理,因为大正方形面积表示为(a+b)2,又可表示为c2+4×ab,所以(a+b)2=c2+4×ab,所以a2+b2+2ab=c2+2ab,所以a2+b2=c2,即直角三角形两直角边的平方和等于斜边的平方.②美国第20届总统伽菲尔德利用图(2)证明了勾股定理,请你用①的方法证明勾股定理;③如图(3)请你用①的方法证明勾股定理;④如图(4)请你用①的方法证明勾股定理.29.(12分)如图,已知直线l1的解析式为y=3x+6,直线l1与x轴,y轴分别相交于A,B两点,直线l2经过B,C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q在直线l2从点C向点B移动.点P,Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(1<t<10).(1)求直线l2的解析式;(2)设△PCQ的面积为S,请求出S关于t的函数关系式;(3)试探究:当t为何值时,△PCQ为等腰三角形?2015-2016学年四川省成都市金牛区八年级(上)期中数学试卷参考答案与试题解析一.选择题(3×10=30分)1.(3分)9的平方根是()A.81 B.3 C.±3 D.±【解答】解:∵(±3)2=9,∴9的平方根是±3,故选:C.2.(3分)在3.14、﹣、、π、2.01001000100001这五个数中.无理数的个数是()A.1 B.2 C.3 D.4【解答】解:π是无理数,故选:A.3.(3分)下列各式中,错误的是()A.B.C.D.【解答】解:A、=2,故选项错误;B、正确;C、正确;D、正确.故选:A.4.(3分)下列各组数据中,不能构成直角三角形的三边的是()A.3,4,5 B.9,41,40 C.6,3,5 D.13,12,5【解答】解:A、32+42=52,能构成直角三角形;B、92+402=412,能构成直角三角形;C、52+32≠62,不能构成直角三角形;D、52+122=132,能构成直角三角形.故选:C.5.(3分)若P的坐标为(a2+1,﹣a2﹣1),则P点在平面直角坐标系中的位置是()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:∵a2≥0,∴a2+1≥1,﹣a2﹣1≤﹣1,∴点P(a2+1,﹣a2﹣1)在第四象限.故选:D.6.(3分)在平面直角坐标系中,已知一次函数y=kx+b的图象大致如图所示,则下列结论正确的是()A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0【解答】解:∵一次函数y=kx+b的图象经过二、三、四象限,∴k<0,b<0.故选:D.7.(3分)下列函数关系不是一次函数的是()A.汽车以120Km/h的速度匀速行驶,行驶路程y(Km)与时间t(h)之间的关系B.等腰三角形顶角y与底角x间的关系C.高为4cm的圆锥体积y (cm3)与底面半径x (cm)的关系D.一棵树现在高50cm,每月长高3cm,x个月后这棵树的高度y (cm)与生长月数x(月)之间的关系【解答】解:高为4cm的圆锥体积y (cm3)与底面半径x (cm)的关系是二次函数,故C错误;故选:C.8.(3分)下列说法不正确的是()A.9的平方根是3B.无理数都是无限小数C.(3﹣π)2的算术平方根是π﹣3D.实数与数轴上的点是一一对应的【解答】解:9的平方根是±3故选:A.9.(3分)已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是()A.24cm2B.36cm2C.48cm2D.60cm2【解答】解:∵a+b=14∴(a+b)2=196∴2ab=196﹣(a2+b2)=96∴ab=24.故选:A.10.(3分)如图,将平面直角坐标系中的△AOB绕点O顺时针旋转90°得△A′OB′.已知∠AOB=60°,∠B=90°,AB=,则点B′的坐标是()A.B.C.D.【解答】解:如图,过点B′作B′C⊥x轴于点C,∵△AOB绕O点顺时针旋转90°得△A′OB′,∴OB′=OB,∠BOB′=90°,∵∠AOB=60°,OB=1,∴OB′=1,∠B′OC=180°﹣∠AOB﹣∠BOB′=180°﹣60°﹣90°=30°,∴OC=OB′cos30°=1×=,B′C=OB′sin30°=1×=,∴B′的坐标为(),故选:A.二.填空题(3×5=15分)11.(3分)若式子有意义,则x的取值范围是x>3.【解答】解:x﹣3>0,解得x>3.12.(3分)点P(2,﹣4)到x轴的距离为4个单位,它关于原点的对称点的坐标为(﹣2,4).【解答】解:点P(2,﹣4)到x轴的距离为4个单位,它关于原点的对称点的坐标为(﹣2,4).故答案为:4;(﹣2,4).13.(3分)当x=时,最简二次根式﹣5与2是同类二次根式.【解答】解:∵最简二次根式﹣5与2是同类二次根式,∴2x﹣3=5﹣x解得:x=.故答案为:.14.(3分)已知点P1(﹣1,y1),P2(﹣2,y2)是一次函数y=3x﹣2图象上的两点,则y1>y2.(填“>”、“<”或“=”)【解答】解:∵一次函数y=3x﹣2中,k=3>0,∴y随x的增大而增大.∵﹣1>﹣2,∴y1>y2.故答案为:>.15.(3分)如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离5cm,一只蚂蚁如果沿着长方体的表面从A点爬到B点,需要爬行的最短距离是25.【解答】解:如图:(1)AB===25;(2)AB===5 ;(3)AB===5.所以需要爬行的最短距离是25.故答案为:25.三.解答题(共55分)16.(10分)计算(1)﹣|﹣2|+(+1)0+(2)﹣+(﹣)﹣2.【解答】解:(1)原式=3﹣2+1+2=4;(2)原式=3﹣+4=7﹣.17.(10分)解方程(1)(4x+1)2=(2)(x﹣1)3+9=0.【解答】解:(1)(4x+1)2=,∴4x+1=±,解得x=或x=﹣.(2)(x﹣1)3+9=0.(x﹣1)3=﹣27,∴x﹣1=﹣3,解得x=﹣2.18.(5分)已知点A(3﹣a,7+a)在平面直角坐标系第一象限的角平分线上,求OA的值.【解答】解:由题意可知:点A在直线y=x上,∴7+a=3﹣a∴a=﹣2∴点A(5,5)∴OA==519.(10分)已知:一次函数y=kx+b的图象经过M(0,2),N(1,3)两点.(1)求k、b的值;(2)若一次函数y=kx+b的图象与x轴交点为A(a,0),求a的值.【解答】解:(1)由题意得,解得.∴k,b的值分别是1和2;(2)将k=1,b=2代入y=kx+b中得y=x+2.∵点A(a,0)在y=x+2的图象上,∴0=a+2,即a=﹣2.20.(10分)如图,在四边形ABCD中,∠BAD=∠ACB=∠AED=90°,AB=AD.(1)求证:AC=DE;(2)若AC=4BC,CD=5,求四边形ABCD的面积.【解答】(1)证明:∵∠BAD=∠ACB=∠AED=90°,∴∠B+∠BAC=∠BAC+∠DAE=90°,∴∠B=∠DAE,在△ABC与△ADE中,,∴△ABC≌△ADE,∴AC=DE;(2)解:∵△ABC≌△ADE,∴BC=AE,∵AC=4BC,∴CE=3BC,∵DE2+CE2=CD2,即(4BC)2+(3BC)2=52,∴BC=1,CE=3,AC=DE=4,∴四边形ABCD的面积=S△ABC +S△ADE+S△CDE=×1×4+×1×4+×3×4=10.21.(10分)如图,已知直线y=x+1与x轴交于点A,与y轴交于点B,将△AOB 绕点O顺时针旋转90°后得到△COD.(1)求点C的坐标与线段AD的长;(2)点M在CD上,且CM=OM,求直线OM的解析式;(3)把OM向左平移,使之经过点A,求平移后的OM的解析式.【解答】解:(1)在y=x+1中,令y=0可得x+1=0,解得x=﹣3,令x=0可得y=1,∴A(﹣3,0),B(0,1),∵将△AOB绕点O顺时针旋转90°后得到△COD,∴OC=OA=3,OD=OB=1,∴C(0,3),AD=OA+OD=3+1=4;(2)∵CM=OM,∴∠OCM=∠MOC,∵∠OCM+∠MDO=90°=∠COM+∠MOD,∴∠MOD=∠MDO,∴MD=OM,∴M为CD中点,∴M(,),设直线OM解析式为y=kx,∴=k,解得k=3,∴直线OM解析式为y=3x;(3)可设平移后的OM的解析式为y=3x+b,∵OM向左平移后经过点A,∴0=﹣9+b,解得b=9,∴平移后的OM的解析式为y=3x+9.四.填空题(5×4=20分)22.(4分)已知y=+5,则的值为2.【解答】解:∵y=+5,∴x=3,y=5.∴==2.故答案为:2.23.(4分)已知一次函数y=2x+a与y=﹣x+b的图象都经过A(2,0),且与y轴分别交于B,C,则△ABC的面积为6.【解答】解:∵把点A(2,0)代入y=2x+a,得:a=﹣4,∴点B(0,﹣4).∵把点A(2,0)代入y=﹣x+b,得b=2,∴点C(0,2).∴BC=|﹣4﹣2|=6,∴S=×2×6=6.△ABC故答案为:6.24.(4分)如图,在△ABC中,∠B=90°,AB=,将AC沿AE折叠,使点C与点D重合,且DE⊥BC,则AE=.【解答】解:∵将AC沿AE折叠,使点C与点D重合,∴∠AEC=∠AED,∵DE⊥BC,∴∠BED=90°,∴∠AEC=90°+∠AEB,∵∠AEC+∠AEB=180°,∴∠AEB+90°+∠AEB=180°,∴∠AEB=45°,∵∠B=90°,∴△ABE是等腰直角三角形,∴AE=AB=,故答案为:.25.(4分)若ab>0,a+b<0.那么下面各式:①=•;②•=1;③÷=﹣b;④•=a,其中正确的是②③(填序号)【解答】解:因为若ab>0,a+b<0,所以a<0,b<0.由于a<0,b<0,与无意义,所以①的变形错误;∵•==1,故②正确;∵÷===|b|,由于b<0,∴原式=﹣b,故③正确;∵•===|a|,由于a<0,∴原式=﹣a,故④计算错误.故答案为②③26.(4分)如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3);B1(4,0),B2(8,0),B3(16,0).(1)观察每次变换前后的三角形有何变化,找出规律,按次变化规律再将△OA3B3变换成△OA4B4,则A4的坐标是(16,3),B4的坐标是(32,0).(2)若按第(1)题找到的规律将△OAB进行了n次变换,得到△OA n B n,比较每次变换中三角形顶点坐标有何变化,找出规律,推测A n的坐标是(2n,3).B n 的坐标是(2n+1,0).【解答】解:(1)因为A(1,3),A1(2,3),A2(4,3),A3(8,3)…纵坐标不变为3,同时横坐标都和2有关,为2n,那么A4(16,3);因为B(2,0),B1(4,0),B2(8,0),B3(16,0)…纵坐标不变,为0,同时横坐标都和2有关为2n+1,那么B的坐标为B4(32,0);(2)由上题第一问规律可知A n的纵坐标总为3,横坐标为2n,B n的纵坐标总为0,横坐标为2n+1,∴A的坐标是(2n,3),B的坐标是(2n+1,0).故答案为(1)(16,3),(32,0),(2)(2n,3),(2n+1,0).五.解答题(26题8分,27题10分,28题12分,共30分)27.(8分)已知x=,y=(1)求x2﹣3xy+y2的值;(2)若x的整数部分是a,y的小数部分是b,求a2+b2的值.【解答】解:x==2﹣,y==2+,(1)x2﹣3xy+y2==7﹣4﹣3+7+4=11.(2)∵x=2﹣,y=2+,1<<2,∴0<2﹣<1,3<2+<4,∴x的整数部分是a=0,y的小数部分是b=2+﹣3=﹣1,∴=4﹣2.28.(10分)利用图形整体面积等于部分面积之和可以证明勾股定理.①如图(1)所示可以证明勾股定理,因为大正方形面积表示为(a+b)2,又可表示为c2+4×ab,所以(a+b)2=c2+4×ab,所以a2+b2+2ab=c2+2ab,所以a2+b2=c2,即直角三角形两直角边的平方和等于斜边的平方.②美国第20届总统伽菲尔德利用图(2)证明了勾股定理,请你用①的方法证明勾股定理;③如图(3)请你用①的方法证明勾股定理;④如图(4)请你用①的方法证明勾股定理.【解答】解:②梯形的面积为(a+b)(a+b)=a2+ab+b2,也可利用表示为ab+c2+ab,∴a2+ab+b2=ab+c2+ab,即a2+b2=c2②连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a=S△ACD+S△ABC=b2+ab.∵S四边形ADCB=S△ADB+S△DCB=c2+a(b﹣a)又∵S四边形ADCB∴b2+ab=c2+a(b﹣a),∴a2+b2=c2;④根据题意,中间小正方形的面积c2=(a+b)2﹣4××ab=a2+b2;即在直角三角形中斜边的平方等于两直角边的平方和.29.(12分)如图,已知直线l1的解析式为y=3x+6,直线l1与x轴,y轴分别相交于A,B两点,直线l2经过B,C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q在直线l2从点C向点B移动.点P,Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(1<t<10).(1)求直线l2的解析式;(2)设△PCQ的面积为S,请求出S关于t的函数关系式;(3)试探究:当t为何值时,△PCQ为等腰三角形?【解答】解:(1)由题意,知B(0,6),C(8,0),设直线l2的解析式为y=kx+b(k≠0),则,解得k=﹣,b=6,则l2的解析式为y=﹣x+6;(2)解法一:如图,过P作PD⊥l2于D,∵∠PDC=∠BOC=90°,∠DCP=∠OCB∴△PDC∽△BOC∴由题意,知OA=2,OB=6,OC=8∴BC==10,PC=10﹣t∴=,∴PD=(10﹣t)=CQ•PD=t•(10﹣t)=﹣t2+3t;∴S△PCQ解法二:如图,过Q作QD⊥x轴于D,∵∠QDC=∠BOC=90°,∠QCD=∠BCO∴△CQD∽△CBO∴由题意,知OA=2,OB=6,OC=8∴BC==10∴∴QD=t=PC•QD=(10﹣t)•t=﹣t2+3t;∴S△PCQ(3)∵PC=10﹣t,CQ=t,要想使△PCQ为等腰三角形,需满足CP=CQ,或QC=QP,或PC=PQ,∴当CP=CQ时,由题10﹣t=t,得t=5(秒);当QC=QP时,=,即=解得t=(秒);当PC=PQ时,=,即=,解得t=(秒);即t=5或或.赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.O DAB CEAOD CB2.如图,已知四边形ABCD 内接于⊙O ,对角线AC ⊥BD 于P ,设⊙O 的半径是2。
