2019高中数学人教a版必修4:课时跟踪检测(十) 正弦函数、余弦函数的单调性与最值 含解析
【高中教育】高中数学 1.4.1正弦函数、余弦函数的图象课时跟踪检测 新人教A版必修4.doc

高中数学 1.4.1正弦函数、余弦函数的图象课时跟踪检测新人教A版必修41.正弦函数y=sin x,x∈R的图象的一条对称轴是( )A.x轴B.y轴C.直线x=π2D.直线x=π解析:由y=sin x,x∈R的图象知,直线x=π2为其一条对称轴.答案:C2.在同一坐标系中,函数y=sin x,x∈[0,2π]与y=sin x,x∈[2π,4π]的图象( )A.重合B.形状相同,位置不同C.关于y轴对称D.形状不同,位置不同解析:由诱导公式一:sin(α+2kπ)=sin α(k∈Z),可知y=sin x在[0,2π]与[2π,4π]上图象形状完全相同,故选B.答案:B3.y=1+sin x,x∈[0,2π]的图象与直线y=2交点的个数是( )A.0 B.1C.2 D.3解析:作出y =1+sin x 在[0,2π]上的图象,可知只有一个交点.答案:B4.要得到y =cos x ,x ∈[-2π,0]的图象,只需将y =cos x ,x ∈[0,2π]的图象向________平移________个单位长度.解析:向左平移2π个单位长度即可. 答案:左 2π5.下列函数:①y =sin x -1;②y =|sin x |;③y =-cos x ;④y =cos 2 x ;⑤y =1-cos 2 x .其中与函数y =sin x 形状完全相同的是________.(填序号)解析:y =sin x -1是将y =sin x 向下平移1个单位,没改变形状,y =-cos x 是作了对称变换,没改变形状,与y =sin x 形状相同,∴①③完全相同.而②y =|sin x |,④y =cos 2 x =|cos x |和⑤y =1-cos 2 x =|sin x |与y =sinx 的形状不相同.答案:①③6.函数y =2cos x +1的定义域是____________.解析:2cos x +1≥0,cos x ≥-12,结合图象知x ∈⎣⎢⎡⎦⎥⎤2k π-23π,2k π+23π,k ∈Z .答案:⎣⎢⎡⎦⎥⎤2k π-23π,2k π+23π,k ∈Z 7.根据函数图象解不等式sin x >cos x ,x ∈[0,2π].解:在同一坐标系中画出函数y =sin x 和y =cos x 在x ∈[0,2π]上的图象,如图所示.可知,当π4<x <5π4时sin x >cos x , 即不等式的解集是⎝ ⎛⎭⎪⎫π4,5π4.8.函数y =cos x ·|tan x |⎝ ⎛⎭⎪⎫-π2<x <π2的大致图象是( )解析:y =cos x ·|tan x |=|sin x |,结合正弦函数的图象可知C 正确. 答案:C9.下列选项中是函数y =-cos x ,x ∈⎣⎢⎡⎦⎥⎤π2,5π2的图象上最高点的坐标的是( )A.⎝ ⎛⎭⎪⎫π2,0 B .(π,1) C .(2π,1)D.⎝ ⎛⎭⎪⎫5π2,1 解析:作出函数y =-cos x ,x ∈⎣⎢⎡⎦⎥⎤π2,5π2的图象如图所示:答案:B10.方程x 2=cos x 的实根个数是________.解析:在同一直角坐标系中画出y =x 2和y =cos x 的图象,观察交点个数为2.答案:211.求函数f (x )=lg(1+2cos x )的定义域.解:由1+2cos x >0得cos x >-12,画出y =cos x 图象的简图,可得定义域为⎝ ⎛⎭⎪⎫-2π3+2k π,2π3+2k π(k ∈Z ). 12.用“五点法”画函数y =2sin ⎝ ⎛⎭⎪⎫13x -π6在[0,6π]上的图象.解:列表如下:13.若函数y =2cos x (0≤x ≤2π)的图象和直线y =2围成一个封闭的平面图形,求这个封闭图形的面积.解:作图可知:图形S 1与S 2,S 3与S 4都是两个对称图形,有S 1=S 2,S 3=S 4,因此函数y =2cos x 的图象与直线y =2所围成的图形面积,可以等价转化为求矩形OABC的面积.∵OA=2,OC=2π,∴S矩形OABC=2×2π=4π.∴所求封闭图形的面积为4π.本节内容是在已知三角函数定义的基础上,运用学过的画图象的方法画出正、余弦函数的图象.1.正、余弦曲线在研究正、余弦函数的性质中有着非常重要的应用,是运用数形结合思想解决三角函数问题的基础.2.五点法是画三角函数图象的基本方法,要熟练掌握,与五点法作图有关的问题是高考常考知识点之一.。
2018-2019学年高中数学人教A版必修四检测:课时跟踪检测(九) 正弦函数、余弦函数的周期性与

姓名,年级:时间:课时跟踪检测(九) 正弦函数、余弦函数的周期性与奇偶性层级一学业水平达标1.函数f(x)=sin(-x)的奇偶性是( )A.奇函数B.偶函数C.既是奇函数又是偶函数 D.非奇非偶函数解析:选A 由于x∈R,且f(-x)=sin x=-sin(-x)=-f(x),所以f(x)为奇函数.2.函数y=-x cos x的部分图象是下图中的( )解析:选D 因为函数y=-x cos x是奇函数,图象关于原点对称,所以排除A、C;当x ∈错误!时,y=-x cos x<0,故排除B,选D.3.已知函数f(x)=sin错误!-1,则下列命题正确的是( )A.f(x)是周期为1的奇函数B.f(x)是周期为2的偶函数C.f(x)是周期为1的非奇非偶函数D.f(x)是周期为2的非奇非偶函数解析:选B f(x)=sin错误!-1=-cos πx-1,从而函数为偶函数,且T=错误!=2。
4.函数y=4sin(2x-π)的图象关于( )A.x轴对称B.原点对称C.y轴对称D.直线x=π2对称解析:选B y=4sin(2x-π)=-4sin 2x是奇函数,其图象关于原点对称.5.函数y=sin错误!的奇偶性是()A.奇函数B.偶函数C.非奇非偶函数D.既是奇函数也是偶函数解析:选B y=sin错误!=sin错误!=cos错误!,故为偶函数.6.函数y=cos错误!的最小正周期为________.解析:T=错误!=4π。
答案:4π7.函数ƒ(x)是以2为周期的函数,且ƒ(2)=3,则ƒ(6)=________。
解析:∵函数ƒ(x)是以2为周期的函数,且ƒ(2)=3,∴ƒ(6)=ƒ(2×2+2)=ƒ(2)=3。
答案:38.函数ƒ(x)=3cos错误!(ω>0)的最小正周期为错误!,则ƒ(π)=________。
解析:由已知错误!=错误!得ω=3,∴ƒ(x)=3cos错误!,∴ƒ(π)=3cos错误!=3cos错误!=-3cos错误!=-错误!。
【2019-2020高一数学试题】人教A版必修4《正弦函数、余弦函数的性质(1)》试题 答案解析

正弦函数、余弦函数的性质(1)——基础巩固类——一、选择题1.下列函数中,最小正周期为π的是( ) A .y =sin x B .y =cos x C .y =sin x2D .y =cos2x2.函数f (x )=x +sin x ,x ∈R ( )A .是奇函数,但不是偶函数B .是偶函数,但不是奇函数C .既是奇函数又是偶函数D .既不是奇函数又不是偶函数3.定义在R 上的函数f (x )周期为π,且是奇函数,f ⎝ ⎛⎭⎪⎫π4=1,则f ⎝ ⎛⎭⎪⎫3π4的值为( )A .1B .-1C .0D .24.函数y =sin ⎝ ⎛⎭⎪⎫2x +π3图象的对称轴方程可能是( ) A .x =-π6 B .x =-π12 C .x =π6 D .x =π12 5.下列四个函数中,是以π为周期的偶函数的是( )A .y =|sin x |B .y =|sin2x |C .y =|cos2x |D .y =cos3x6.如果函数f (x )=cos ⎝ ⎛⎭⎪⎫ωx +π4(ω>0)的相邻两个零点之间的距离为π6,则ω的值为( )A .3B .6C .12D .24二、填空题7.函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx +π4(ω>0)的周期为π4,则ω= .8.已知函数f (x )=ax +b sin x +1,若f (2 015)=7,则f (-2 015)= . 9.已知函数f (x )是以2为周期的函数,且当x ∈[1,3)时,f (x )=x -2,则f (-1)= .三、解答题10.判断函数f (x )=lg(sin x +1+sin 2x )的奇偶性.11.已知函数y =12sin x +12|sin x |. (1)画出函数的简图;(2)这个函数是周期函数吗?如果是,求出它的最小正周期.——能力提升类——12.已知函数y =2sin ⎝⎛⎭⎪⎫x +π4+φ是奇函数,则φ的值可以是( )A .0B .-π4 C.π2 D .π13.设函数f (x )(x ∈R )满足f (-x )=f (x ),f (x +2)=f (x ),则函数y =f (x )的图象是( )14.设函数f (x )=3sin ⎝ ⎛⎭⎪⎫ωx +π6,ω>0,x ∈(-∞,+∞),且以π2为最小正周期.若f ⎝ ⎛⎭⎪⎫α4+π12=95,则sin α的值为 .15.已知函数f (x )=cos ⎝⎛⎭⎪⎫2x +π3,若函数g (x )的最小正周期是π,且当x ∈⎣⎢⎡⎦⎥⎤-π2,π2时,g (x )=f ⎝ ⎛⎭⎪⎫x 2,求关于x 的方程g (x )=32的解集.正弦函数、余弦函数的性质(1)(答案解析)——基础巩固类——一、选择题1.下列函数中,最小正周期为π的是( D ) A .y =sin x B .y =cos x C .y =sin x2D .y =cos2x解析:A 项,y =sin x 的最小正周期为2π,故A 项不符合题意;B 项,y =cos x 的最小正周期为2π,故B 项不符合题意;C 项,y =sin x2的最小正周期为T =2πω=4π,故C 项不符合题意;D 项,y =cos2x 的最小正周期为T =2πω=π,故D 项符合题意.故选D.2.函数f (x )=x +sin x ,x ∈R ( A ) A .是奇函数,但不是偶函数 B .是偶函数,但不是奇函数 C .既是奇函数又是偶函数 D .既不是奇函数又不是偶函数解析:函数f (x )=x +sin x 的定义域为R ,f (-x )=-x +sin(-x )=-x -sin x =-f (x ),则f (x )为奇函数.故选A.3.定义在R 上的函数f (x )周期为π,且是奇函数,f ⎝ ⎛⎭⎪⎫π4=1,则f ⎝ ⎛⎭⎪⎫3π4的值为( B )A .1B .-1C .0D .2解析:∵T =π,且为奇函数.∴f ⎝ ⎛⎭⎪⎫34π=f ⎝ ⎛⎭⎪⎫34π-π=f ⎝ ⎛⎭⎪⎫-π4=-f ⎝ ⎛⎭⎪⎫π4=-1. 4.函数y =sin ⎝⎛⎭⎪⎫2x +π3图象的对称轴方程可能是( D )A .x =-π6 B .x =-π12 C .x =π6D .x =π12解析:令2x +π3=k π+π2(k ∈Z ),得x =k π2+π12(k ∈Z ).故选D. 5.下列四个函数中,是以π为周期的偶函数的是( A ) A .y =|sin x | B .y =|sin2x | C .y =|cos2x |D .y =cos3x解析:A 中的函数周期为π.B 中的函数周期为π2.C 中的函数周期为π2.D 中的函数周期为23π.故选A.6.如果函数f (x )=cos ⎝⎛⎭⎪⎫ωx +π4(ω>0)的相邻两个零点之间的距离为π6,则ω的值为( B )A .3B .6C .12D .24解析:函数f (x )=cos ⎝ ⎛⎭⎪⎫ωx +π4(ω>0)的相邻两个零点之间的距离为π6,∴T =2×π6=π3,又2πω=π3,∴ω=6.选B.二、填空题7.函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx +π4(ω>0)的周期为π4,则ω=8. 解析:π4=2πω,∴ω=8.8.已知函数f (x )=ax +b sin x +1,若f (2 015)=7,则f (-2 015)=-5. 解析:由f (2 015)=2 015a +b sin2 015+1=7, 得2 015a +b sin2 015=6,∴f (-2 015)=-2 015a -b sin2 015+1=-(2 015a +b sin2 015)+1=-6+1=-5.9.已知函数f (x )是以2为周期的函数,且当x ∈[1,3)时,f (x )=x -2,则f (-1)=-1.解析:因为T =2,则f (x )=f (x +2).又f (-1)=f (-1+2)=f (1),且x ∈[1,3)时,f (x )=x -2,所以f (-1)=f (1)=1-2=-1.三、解答题10.判断函数f (x )=lg(sin x +1+sin 2x )的奇偶性. 解:由题意知函数定义域为R .f (-x )=lg(-sin x +1+sin 2x )=lg 1sin x +1+sin 2x=-lg(sin x +1+sin 2x )=-f (x ),∴函数f (x )=lg(sin x +1+sin 2x )为奇函数. 11.已知函数y =12sin x +12|sin x |. (1)画出函数的简图;(2)这个函数是周期函数吗?如果是,求出它的最小正周期. 解:(1)y =12sin x +12|sin x |=⎩⎪⎨⎪⎧sin x ,x ∈[2k π,2k π+π](k ∈Z ),0,x ∈[2k π-π,2k π)(k ∈Z ).函数图象如图所示.(2)由图象知该函数是周期函数,其图象每隔2π重复一次,则函数的最小正周期是2π.——能力提升类——12.已知函数y =2sin ⎝ ⎛⎭⎪⎫x +π4+φ是奇函数,则φ的值可以是( B ) A .0 B .-π4 C.π2D .π解析:y =2sin ⎝⎛⎭⎪⎫x +π4+φ为奇函数,则只需π4+φ=k π,k ∈Z ,从而φ=k π-π4,k ∈Z .显然当k =0时,φ=-π4满足题意.13.设函数f (x )(x ∈R )满足f (-x )=f (x ),f (x +2)=f (x ),则函数y =f (x )的图象是( B )解析:A 项,由f (-x )=f (x )知函数f (x )为偶函数,故A 错.B 项,由函数f (x )为偶函数,周期为2,故B 正确.C 项,由函数f (x )为偶函数,故C 错.D 项,由函数f (x )周期为2.故D 错.14.设函数f (x )=3sin ⎝⎛⎭⎪⎫ωx +π6,ω>0,x ∈(-∞,+∞),且以π2为最小正周期.若f ⎝ ⎛⎭⎪⎫α4+π12=95,则sin α的值为±45. 解析:由题意得2πω=π2, ∴ω=4,∴f (x )=3sin ⎝ ⎛⎭⎪⎫4x +π6∴f ⎝ ⎛⎭⎪⎫α4+π12=3sin ⎝ ⎛⎭⎪⎫α+π2=3cos α=95. ∴cos α=35,∴sin α=±1-⎝ ⎛⎭⎪⎫352=±45. 15.已知函数f (x )=cos ⎝ ⎛⎭⎪⎫2x +π3,若函数g (x )的最小正周期是π,且当x ∈⎣⎢⎡⎦⎥⎤-π2,π2时,g (x )=f ⎝ ⎛⎭⎪⎫x 2,求关于x 的方程g (x )=32的解集.解:当x ∈⎣⎢⎡⎦⎥⎤-π2,π2时,g (x )=f ⎝ ⎛⎭⎪⎫x 2=cos ⎝⎛⎭⎪⎫x +π3.因为x +π3∈⎣⎢⎡⎦⎥⎤-π6,5π6,所以由g (x )=32 解得x +π3=-π6或π6, 即x =-π2或-π6.又因为g (x )的最小正周期为π.所以g (x )=32的解集为 ⎩⎨⎧⎭⎬⎫x|x =k π-π2或x =k π-π6,k ∈Z .。
人教a版必修4学案:1.4.1正弦函数、余弦函数的图象(含答案)
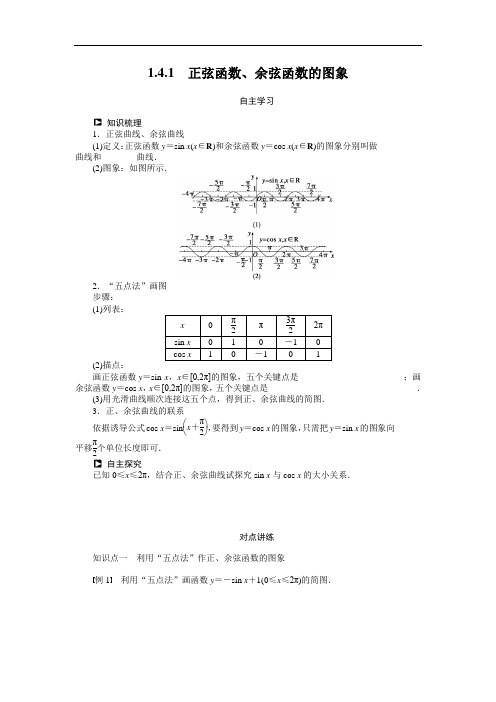
1.4.1 正弦函数、余弦函数的图象自主学习知识梳理1.正弦曲线、余弦曲线 (1)定义:正弦函数y =sin x (x ∈R )和余弦函数y =cos x (x ∈R )的图象分别叫做__________曲线和________曲线.(2)图象:如图所示.2.“五点法”画图 步骤: (1)列表:x 0 π2 π 3π2 2π sin x 0 1 0 -1 0 cos x1-11(2)描点:画正弦函数y =sin x ,x ∈[0,2π]的图象,五个关键点是________________________;画余弦函数y =cos x ,x ∈[0,2π]的图象,五个关键点是__________________________________.(3)用光滑曲线顺次连接这五个点,得到正、余弦曲线的简图. 3.正、余弦曲线的联系依据诱导公式cos x =sin ⎝⎛⎭⎫x +π2,要得到y =cos x 的图象,只需把y =sin x 的图象向______平移π2个单位长度即可.自主探究已知0≤x ≤2π,结合正、余弦曲线试探究sin x 与cos x 的大小关系.对点讲练知识点一 利用“五点法”作正、余弦函数的图象例1 利用“五点法”画函数y =-sin x +1(0≤x ≤2π)的简图.回顾归纳作正弦、余弦曲线要理解几何法作图,掌握五点法作图.“五点”即y=sin x或y=cos x的图象在一个最小正周期内的最高点、最低点和与x轴的交点.“五点法”是作简图的常用方法.变式训练1利用“五点法”画函数y=-1-cos x,x∈[0,2π]的简图.知识点二利用三角函数图象求定义域例2求函数f(x)=lg sin x+16-x2的定义域.回顾归纳一些三角函数的定义域可以借助函数图象直观地观察得到,同时要注意区间端点的取舍.变式训练2求函数f(x)=cos x+lg(8x-x2)的定义域.知识点三利用三角函数的图象判断方程解的个数例3在同一坐标系中,作函数y=sin x和y=lg x的图象,根据图象判断出方程sin x =lg x的解的个数.回顾归纳三角函数的图象是研究函数的重要工具,通过图象可较简便的解决问题,这正是数形结合思想方法的应用.变式训练3求方程x2=cos x的实数解的个数.1.正、余弦曲线在研究正、余弦函数的性质中有着非常重要的应用,是运用数形结合思想解决三角函数问题的基础.2.五点法是画三角函数图象的基本方法,要熟练掌握,与五点法作图有关的问题是高考常考知识点之一.课时作业一、选择题1.函数y =sin x (x ∈R )图象的一条对称轴是( ) A .x 轴 B .y 轴C .直线y =xD .直线x =π22.函数y =-cos x 的图象与余弦函数y =cos x 的图象( ) A .只关于x 轴对称 B .关于原点对称 C .关于原点、x 轴对称 D .关于原点、坐标轴对称 3.如果x ∈[0,2π],则函数y =sin x +-cos x 的定义域为( )A .[0,π] B.⎣⎡⎦⎤π2,3π2C.⎣⎡⎦⎤π2,πD.⎣⎡⎦⎤3π2,2π 4.在(0,2π)内使sin x >|cos x |的x 的取值范围是( ) A.⎝⎛⎭⎫π4,3π4 B.⎝⎛⎦⎤π4,π2∪⎝⎛⎦⎤5π4,3π2 C.⎝⎛⎭⎫π4,π2 D.⎝⎛⎭⎫5π4,7π4 5.已知函数y =2sin x ⎝⎛⎭⎫π2≤x ≤5π2的图象与直线y =2围成一个封闭的平面图形,那么此封闭图形的面积( )A .4B .8C .4πD .2π二、填空题6.函数y =cos x1+sin x的定义域为____________.7.函数y =2cos x +1的定义域是______________.8.设0≤x ≤2π,且|cos x -sin x |=sin x -cos x ,则x 的取值范围为________.三、解答题9.利用“五点法”作出下列函数的简图:(1)y =-sin x (0≤x ≤2π);(2)y =1+cos x (0≤x ≤2π).10.分别作出下列函数的图象.(1)y =|sin x |,x ∈R ;(2)y =sin|x |,x ∈R .§1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象答案知识梳理1.(1)正弦 余弦2.(2)(0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫3π2,-1,(2π,0) (0,1),⎝⎛⎭⎫π2,0,(π,-1),⎝⎛⎭⎫3π2,0,(2π,1) 3.左 自主探究解 正、余弦曲线如图所示.由图象可知①当x =π4或x =5π4时,sin x =cos x ,②当π4<x <5π4时,sin x >cos x .③当0≤x <π4或5π4<x ≤2π时,sin x <cos x .对点讲练例1 解 利用“五点法”作图 取值列表:x 0 π2π3π2 2π sin x 0 1 0 -1 0 1-sin x 1 0 121变式训练1 x0 π2 π 3π2 2π cos x 1 0 -1 0 1 -1-cos x-2-1-1-2例2 解 由题意,x 满足不等式组⎩⎨⎧sin x >016-x 2≥0, 即⎩⎨⎧-4≤x ≤4sin x >0,作出y =sin x 的图象,如图所示.结合图象可得:x ∈[-4,-π)∪(0,π).变式训练2 解 由⎩⎪⎨⎪⎧8x -x 2>0cos x ≥0,得⎩⎨⎧0<x <8cos x ≥0.画出y =cos x ,x ∈[0,3π]的图象,如图所示.结合图象可得:x ∈⎝⎛⎦⎤0,π2∪⎣⎡3π2,5π2.例3 解 建立坐标系xOy ,先用五点法画出函数y =sin x ,x ∈[0,2π]的图象,再依次向左、右连续平移2π个单位,得到y =sin x 的图象.描出点⎝⎛⎭⎫1101,(1,0),(10,1)并用光滑曲线连接得到y =lg x 的图象,如图所示.由图象可知方程sin x =lg x 的解有3个.变式训练3 解 作函数y =cos x 与y =x 2的图象,如图所示, 由图象,可知原方程有两个实数解.课时作业 1.D2.C [结合图象易知.]3.C [∵sin x ≥0且-cos x ≥0,∴x ∈⎣⎡⎦⎤π2π.] 4.A[∵sin x >|cos x |,∴sin x >0,∴x ∈(0,π),在同一坐标系中画出y =sin x ,x ∈(0,π)与y =|cos x |,x ∈(0,π)的图象,观察图象易得x ∈⎝⎛⎭⎫π4,3π4.]5.C [数形结合,如图所示.y =2sin x ,x ∈⎣⎡⎦⎤π2,5π2的图象与直线y =2围成的封闭平面图形面积相当于由x =π2,x =5π2, y =0,y =2围成的矩形面积,即S =⎝⎛⎭⎫5π2-π2×2=4π.]6.⎝⎛⎦⎤-π22k π,π2+2k π (k ∈Z ) 解析 x 应满足:⎩⎪⎨⎪⎧1+sin x ≠0⇒sin x ≠-1,cos x ≥0,综合正、余弦函数图象可知:-π2+2k π<x ≤π2+2k π. 7.⎣⎡⎦⎤2k π-2π3,2k π+2π3 ,(k ∈Z ) 解析 由2cos x +1≥0,得cos x ≥-12,∴2k π-2π3x ≤2k π+2π3,k ∈Z .8.⎣⎡⎦⎤π4,5π4 解析 由题意知sin x -cos x ≥0,即cos x ≤sin x ,在同一坐标系画出y =sin x ,x ∈[0,2π] 与y =cos x ,x ∈[0,2π]的图象,如图所示:观察图象得:π4≤x ≤5π4.9.解 利用“五点法”作图. (1)列表:(2)列表:10.解 (1)y =|sin x |=⎩⎪⎨⎪⎧sin x (2k π≤x ≤2k π+π)-sin x (2k π+π<x ≤2k π+2π)(k ∈Z ).其图象如图所示,(2)y =sin|x |=⎩⎪⎨⎪⎧sin x (x ≥0)-sin x (x <0),其图象如图所示,。
(浙江专版)高中数学课时跟踪检测(十)正弦函数、余弦函数的单调性与最值新人教A版必修4

课时跟踪检测(十) 正弦函数、余弦函数的单调性与最值层级一学业水平达标3 n3 n C. n,D. —, 2 n解析:选 C 由y = |sin x |的图象,易得函数 y = |sin x |的单调递增区间为n 3 nk n, k n + — , k €乙当k = 1时,得n, 为函数y = |sin x |的一个单调递增区间.3. 下列函数中,既为偶函数又在(0 ,n )上单调递增的是()A. y = |cos x |B . y = cos| — x |nxC. y = sin x — —D. y =— sinqn解析:选C y = |cos x |在0, "2上是减函数,排除 A ;nny = cos| — x | = cos| x | 在(0 , n )上是减函数. 排除 B; y = sin x —-^ = — sin — — x =x—cos x 是偶函数,且在(0 ,n )上单调递增,符合题意; y =— sin?在(0 ,n )上是单调递减的.n4.函数 y = sin x + ■— , x € R 在()n nA. — 2,"2上是增函数 B . [0 ,n ]上是减函数 C. [ — n, 0]上是减函数D. [ — n,n ]上是减函数n解析:选B y = sin x + 3 = cos x ,所以在区间[—n, 0]上是增函数,在[0 ,n ]上 是减函数,故1 .函数 f (x ) = — 2sin x + 1, x €n—2, n 的值域是(A. [1,3] C. [ — 3,1]n解析:选 B T x € —~, nB . [ —1,3] D. [ — 1,1] ,二 sin x € [ — 1,1],•••— 2sin x + 1€ [ — 1,3].2.函数y = |sin x |的一个单调递增区间是( ) A.B .n 3 n 4,~4选B.n n5. 函数f(x) = sin 2x ——在区间0,迈上的最小值为()A.—1D. 0一、,亠兀n n 3 n , n n ,解析:选B •- x€ 0,㊁,•••—- W2X— - ,「当2x —习一刁时,f(x)=sin 2x ——有最小值一 -^.6. ________________________________________ 已知函数y= 3cos(n—x),则当x = 时,函数取得最大值.解析:y = 3cos( n—x) =—3cos x,当cos x=—1,即x = 2k n + n, k € Z 时,y 有最大值3.答案:2k n + n, k€ Zn 2 n ,十7. y = sin x, x€ =, =—,贝U y 的范围是6 32解析:由正弦函数图象,对于x€,才,当x=^时,y max= 1,当x = -6时,y min1 1=2,从而y€ 2,1 .1答案:2,1%&函数y= sin( x+n )在一y, n上的单调递增区间为___________________ .nx,所以要求y= sin( x+n )在一~^,n上的单调递n n增区间,即求y = sin x在一~,n上的单调递减区间,易知为—,nn答案:~,n9.求下列函数的最大值和最小值.(1) y= 1 - ;sinc n x; (2) y = 3 + 2cos 2x + —3B.C.解析:因为sin( x +n ) =—sin解:⑴•••11 —尹n x > 0,—1 wsinx w 1,•- —1 wsinx w 1.•••当sin x = —1 时,y max= —;当sin x= 1时,ymin=#n(2) —1 < cos 2x + 3 < 1,n•••当cos 2x + — = 1 时,y max= 5 ;n当cos 2x+ "3 =一 1 时,y min = 1.10.比较下列各组数的大小.1.函数y= |sin x| + sin x的值域为()[—2,2] A. [ —1,1]B.C.[—2,0] D.[0,2]解析:选D■/y = |sin x| + sin x2sin x,sin x>0,0, sin x V 0.又,—1 wsinx< 1 ,•y€ [0,2],即函数的值域为[0,2]. 层级二(1)sin竽与11 nsin 帀;(2)cos5 n 16 n丁与COS亍sin解:(1) I函数11 ny= sin x 在-2,n 10 n 11 nn 上单调递减,且—V 17 V 17 Vn,10n• sin >175 n (2)cos一n=cos 2 n—二-=cos —, 3 3316 n 2 nCOS—= cos 2 n ——2n=co k •••函数y = cos x 在[0 ,n ]上单调递减,LT 2 n n 且0 V 厂V "3Vn,n 2 n•cos s<co话,•cos3 5 n 16 n<cos亍应试能力达标2. 函数y= 2sin w x+ :( w> 0)的周期为n,则其单调递增区间为(, 3 冗,nA. k n —~4-, k n —4 ( k € Z)3 n nB. 2k n —丁,2k n + 丁(k€ Z)4 43 n nC. k n —, k n^ —( k € Z)8 83 n nD. 2k n —三,2k n + y (k€ Z)2 n n n解析:选 C 周期T=n, J. =n, •••3= 2, J. y= 2sin 2x+ .由一;+ 2k n<2 xco 4 2 n n 十 3 n n+ 〒W2k n+h,k € Z, 得k n — W X W k n + 石,k € Z.4 2 8 83. 下列关系式中正确的是()A. sin 11 °v cos 10 °v sin 168 °B. sin 168 °v sin 11 °v cos 10 °C. sin 11 °v sin 168 °v cos 10 °D. sin 168 °v cos 10 °v sin 11 °解析:选 C sin 168 ° = sin(180 ° —12° ) = sin 12 ° , cos 10 ° = cos(90 ° —80°) =sin 80° .因为正弦函数y= sin x在区间[0,90 ° ]上为增函数,所以sin 11 °v sin 12 v sin 80 °,即卩sin 11 °v sin 168 °v cos 10 ° .n n4. 函数y= 2sin ——x —cos — + x (x € R)的最小值等于()A. —3 B . —2 C.—1 D. —, 5, t n n n解析:选 C •/—x + + x =3 6 2•y= 2sin7tn=2cos x+ —cos x +6 6n=cos x +• y min =—1.n 3 n 4 n 9 n n解析:T < 二-V 示"Vn ,又函数 y = sin x 在 ,n 上单调递减,2551025.函数值sin3n ~5~, sin9 nsin 10从大到小的顺序为_______ (用“〉”连接).sin3n 54 n 9 n > s r > sin70答案:3 n 4 n 9 n sin5 >sin5 >sin106.函数y= cos x在区间[—n, a]上为增函数,则a的取值范围是 _____________ 解析:••• y = cos x在[—n, 0]上是增函数,在[0 ,n ]上是减函数,只有一nV a W0时满足条件,故a€ ( —n, 0].答案:(一n, 0]7.设函数f(x) = :'2sin 2x—寸,x € R.(1)求函数f(x)的最小正周期和单调递增区间;n 3 n⑵ 求函数f (x)在区间y,-厂上的最小值和最大值,并求出取最值时x的值. 解:⑴最小正周期T= 22L=n,, n n n由2k n—— W2x—4 W2k n + ~( k € Z),“口n 3 n得k n — gW x W k n + _( k € Z),o o•函数f(x)的单调递增区间是k n — -, k n+寻(k € Z).o o7tn n⑵令t = 2x —,则由4 o x w芋可得45 n 3 n•••当t =〒,即x =〒时,, n 3 n ,•••当t =—,即X=-^时,y max= 2 X 1 = : 2&已知函数f (x) = 2a sinn n2x+石+ a+ b的定义域是0,三,值域是[—5,1],求a,b的值.n解:•••0W x w 2,n•・=W2x +6n2x+7 W1.b =— 5,a = 2,当 a >0 时,解得3a + b = 1,b =— 5.a =— 2,解得 b = 1. — 2, b = 1.当 a <0 时,因此 a = 2, b = 1,3a +b =— 5,b =— 5 或 a =。
人教版高中数学 高一人教A版必修4课时检测(八)正弦函数、余弦函数的图象

课时达标检测(八)正弦函数、余弦函数的图象一、选择题1.下列函数图象相同的是( ) A .f (x )=sin x 与g (x )=sin(π+x ) B .f (x )=sin ⎝⎛⎭⎫x -π2与g (x )=sin ⎝⎛⎭⎫π2-x C .f (x )=sin x 与g (x )=sin(-x ) D .f (x )=sin(2π+x )与g (x )=sin x 答案:D2.对余弦函数y =cos x 的图象,有以下描述:①向左向右无限延伸;②与y =sin x 的图象形状完全一样,只是位置不同;③与x 轴有无数多个交点;④关于y 轴对称.其中正确的描述有( ) A .1个 B .2个 C .3个 D .4个答案:D3.函数y =cos ⎝⎛⎭⎫x +π2的图象是( )答案:B4.不等式cos x <0,x ∈[0,2π]的解集为( ) A.⎝⎛⎭⎫π2,3π2 B.⎣⎡⎦⎤π2,3π2 C.⎝⎛⎭⎫0,π2 D.⎝⎛⎭⎫π2,2π 答案:A5.要得到正弦曲线,只要将余弦曲线( ) A .向右平移π2个单位长度B .向左平移π2个单位长度C .向右平移3π2个单位长度D .向左平移π个单位长度 答案:A 二、填空题6.当x ∈[-π,π]时,y =12x 与y =sin x 的图象交点的个数为________.答案:37.函数y =2cos x ,x ∈[0,2π]的图象和直线y =2围成的一个封闭的平面图形的面积是________.答案:4π8.方程sin x =lg x 的解有________个. 答案:3 三、解答题9.利用“五点法”作出y =sin ⎝⎛⎭⎫x -π2⎝⎛⎭⎫x ∈⎣⎡⎦⎤π2,5π2的图象. 解:列表如下.x π2 π 3π2 2π 5π2 sin ⎝⎛⎭⎫x -π2 01-1描点连线如图.10.作出函数y =-sin x ,x ∈[-π,π]的简图,并回答下列问题: (1)观察函数图象,写出满足下列条件的x 的区间: ①sin x >0,②sin x <0.(2)直线y =12与y =-sin x 的图象有几个交点?解:利用五点法作图.(1)根据图象,可知图象在x 轴上方时,-sin x >0, 在x 轴下方时,-sin x <0,所以当x ∈(-π,0)时,-sin x >0,sin x <0; 当x ∈(0,π)时,-sin x <0,sin x >0. (2)画出直线y =12,由图象可知有两个交点.11.方程sin x =1-a 2在x ∈⎣⎡⎦⎤π3,π上有两个实数根,求a 的取值范围. 解:首先作出y =sin x ,x ∈⎣⎡⎦⎤π3,π的图象,然后再作出y =1-a 2的图象,如果y =sin x ,x ∈⎣⎡⎦⎤π3,π与y =1-a 2的图象有两个交点,方程sin x =1-a 2,x ∈⎣⎡⎦⎤π3,π就有两个实数根. 设y 1=sin x ,x ∈⎣⎡⎦⎤π3,π,y 2=1-a 2.y 1=sin x ,x ∈⎣⎡⎦⎤π3,π的图象如图.由图象可知,当32≤1-a 2<1,即-1<a ≤1-3时,y =sin x ,x ∈⎣⎡⎦⎤π3,π的图象与y =1-a 2的图象有两个交点,即方程sin x =1-a 2在x ∈⎣⎡⎦⎤π3,π上有两个实根.。
2019_2020学年高中数学课时跟踪训练10正弦函数、余弦函数的性质(第二课时)新人教A版必修4

课时跟踪训练(十)(时间45分钟) 题型对点练(时间20分钟)题组一 正、余弦函数的单调性1.函数y =2sin ⎝ ⎛⎭⎪⎫2x -π4的一个单调递减区间是( ) A.⎣⎢⎡⎦⎥⎤3π8,7π8B.⎣⎢⎡⎦⎥⎤-π8,3π8C.⎣⎢⎡⎦⎥⎤3π4,5π4 D.⎣⎢⎡⎦⎥⎤-π4,π4[解析] 令z =2x -π4,函数y =sin z 的单调递减区间是⎣⎢⎡⎦⎥⎤π2+2k π,3π2+2k π(k ∈Z ).由π2+2k π≤2x -π4≤3π2+2k π,k ∈Z ,得3π8+k π≤x ≤7π8+k π,k ∈Z .令k =0,得3π8≤x ≤7π8. [答案] A 2.函数y =2-cos x的单调递增区间是( )A .[2k π+π,2k π+2π](k ∈Z )B .[k π+π,k π+2π](k ∈Z ) C.⎣⎢⎡⎦⎥⎤2k π,2k π+π2(k ∈Z )D .[2k π,2k π+π](k ∈Z )[解析] 令u =-cos x ,则y =2u.∵y =2u在u ∈(-∞,+∞)时是增函数,∴y =2-cos x的增区间即u =-cos x 的增区间,又u =cos x 的减区间是[2k π,2k π+π](k ∈Z ).故原函数的增区间为[2k π,2k π+π](k ∈Z ),选D.[答案] D3.函数y =cos x 在区间[-π,a ]上为增函数,则a 的取值范围是________. [解析] ∵y =cos x 在[-π,0]上是增函数,在[0,π]上是减函数,∴只有-π<a ≤0时,满足条件.故a 的取值范围是(-π,0].[答案] (-π,0]题组二 三角函数值的大小比较4.sin ⎝ ⎛⎭⎪⎫-376π________sin ⎝ ⎛⎭⎪⎫493π(填“>”或“<”).[解析] ∵sin ⎝ ⎛⎭⎪⎫-37π6=sin ⎝⎛⎭⎪⎫-6π-π6=sin ⎝ ⎛⎭⎪⎫-π6=-sin π6<0,sin ⎝ ⎛⎭⎪⎫493π=sin ⎝⎛⎭⎪⎫16π+π3=sin π3>0, ∴sin ⎝ ⎛⎭⎪⎫493π>sin ⎝ ⎛⎭⎪⎫-376π.[答案] <5.cos770°________sin980°(填“>”或“<”).[解析] ∵cos770°=cos(720°+50°)=cos50°=sin40°, sin980°=sin(720°+250°)=sin250°=sin(180°+70°) =sin70°>sin40°. ∴cos770°<sin980°. [答案] <6.sin1,sin2,sin3按从小到大排列的顺序为________________________. [解析] ∵1<π2<2<3<π,sin(π-2)=sin2,sin(π-3)=sin3.y =sin x 在⎝ ⎛⎭⎪⎫0,π2上递增,且0<π-3<1<π-2<π2, ∴sin(π-3)<sin1<sin(π-2), 即sin3<sin1<sin2. [答案] sin3<sin1<sin2 题组三 正、余弦函数的最值7.函数y =1-2cos π2x 的最小值,最大值分别是( )A .-1,3B .-1,1C .0,3D .0,1[解析] ∵x ∈R ,∴π2x ∈R ,∴y =cos π2x 的值域[-1,1].∴y =1-2cos π2x 的最大值为3,最小值-1.[答案] A8.若f (x )=2sin ωx (0<ω<1)在区间⎣⎢⎡⎦⎥⎤0,π3上的最大值是2,则ω=________.[解析] ∵x ∈⎣⎢⎡⎦⎥⎤0,π3,即0≤x ≤π3,且0<ω<1,∴0≤ωx ≤ωπ3<π3. ∵f (x )max =2sin ωπ3=2,∴sinωπ3=22,ωπ3=π4,即ω=34. [答案] 349.函数y =sin x 的定义域为[a ,b ],值域为⎣⎢⎡⎦⎥⎤-1,12,则b -a 的最大值与最小值之和为________.[解析] 由下图知:b -a 的最大值为13π6-5π6=4π3, b -a 的最小值为3π2-5π6=2π3. ∴最大值与最小值之和为4π3+2π3=2π.[答案] 2π综合提升练(时间25分钟)一、选择题1.下列函数中,既为偶函数又在(0,π)上单调递增的是( ) A .y =cos|x |B .y =cos|-x |C .y =sin ⎝⎛⎭⎪⎫x -π2D .y =-sin x2[解析] y =cos|x |在⎝⎛⎭⎪⎫0,π2上是减函数,排除A ;y =cos|-x |=cos|x |,排除B ;y=sin ⎝ ⎛⎭⎪⎫x -π2=-sin ⎝ ⎛⎭⎪⎫π2-x =-cos x 是偶函数,且在(0,π)上单调递增,符合题意;y=-sin x2,在(0,π)上是单调递减的. [答案] C2.函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π4在区间⎣⎢⎡⎦⎥⎤0,π2上的最小值为( ) A .-1 B .-22C.22D .0[解析] ∵x ∈⎣⎢⎡⎦⎥⎤0,π2,∴-π4≤2x -π4≤34π,∴当2x -π4=-π4时,f (x )=sin ⎝⎛⎭⎪⎫2x -π4有最小值-22. [答案] B3.函数y =4cos 2x +4cos x -2的值域是( ) A .[-2,6] B .[-3,6] C .[-2,4]D .[-3,8][解析] 令cos x =t ,则t ∈[-1,1],∴y =4t 2+4t -2=(2t +1)2-3,∴y ∈[-3,6]. [答案] B 二、填空题4.函数f (x )=sin ⎝⎛⎭⎪⎫x +π4图象的一条对称轴方程为________.[解析] 对于函数f (x )=sin ⎝ ⎛⎭⎪⎫x +π4,令x +π4=k π+π2,k ∈Z ,得x =k π+π4,k∈Z ,可得函数f (x )=sin ⎝⎛⎭⎪⎫x +π4的图象的一条对称轴方程为x =π4.[答案] x =π45.设函数f (x )=A +B sin x ,当B <0时,f (x )的最大值是32,最小值是-12,则A =________,B =________.[解析] 根据题意,得⎩⎪⎨⎪⎧A -B =32,A +B =-12.解得A =12,B =-1.[答案] 12 -1三、解答题6.求函数y =1+sin ⎝ ⎛⎭⎪⎫-12x +π4,x ∈[-4π,4π]的单调减区间.[解] y =1+sin ⎝ ⎛⎭⎪⎫-12x +π4 =-sin ⎝ ⎛⎭⎪⎫12x -π4+1.由2k π-π2≤12x -π4≤2k π+π2(k ∈Z ).解得4k π-π2≤x ≤4k π+32π(k ∈Z ).∴k =0时 ,x ∈⎣⎢⎡⎦⎥⎤-π2,3π2,k =1时,x ∈⎣⎢⎡⎦⎥⎤7π2,11π2, k =-1时,x ∈⎣⎢⎡⎦⎥⎤-9π2,-5π2.又∵x ∈[-4π,4π],∴函数y =1+sin ⎝ ⎛⎭⎪⎫-12x +π4的单调减区间为⎣⎢⎡⎦⎥⎤-4π,-5π2,⎣⎢⎡⎦⎥⎤-π2,3π2,⎣⎢⎡⎦⎥⎤7π2,4π.7.求下列函数的最大值和最小值. (1)f (x )=sin ⎝ ⎛⎭⎪⎫2x -π6,x ∈⎣⎢⎡⎦⎥⎤0,π2;(2)y =-2cos 2x +2sin x +3,x ∈⎣⎢⎡⎦⎥⎤π6,5π6.[解] (1)当x ∈⎣⎢⎡⎦⎥⎤0,π2时,2x -π6∈⎣⎢⎡⎦⎥⎤-π6,5π6,由函数图象知,f (x )=sin ⎝⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤sin ⎝ ⎛⎭⎪⎫-π6,sin π2=⎣⎢⎡⎦⎥⎤-12,1. 所以,f (x )在⎣⎢⎡⎦⎥⎤0,π2上的最大值和最小值分别为1,-12.(2)y =-2(1-sin 2x )+2sin x +3 =2sin 2x +2sin x +1 =2⎝⎛⎭⎪⎫sin x +122+12.∵x ∈⎣⎢⎡⎦⎥⎤π6,5π6,∴12≤sin x ≤1. 当sin x =1时,y max =5; 当sin x =12时,y min =52.。
【同步练习】2019年人教A版 高中数学必修4 课时跟踪检测 正弦函数、余弦函数的图象 Word版含解析

课时跟踪检测 正弦函数、余弦函数的图象层级一 学业水平达标1.用“五点法”画函数y=2-3sin x 的图象时,首先应描出五点的横坐标是( )A.0,π4,π2,3π4,πB.0,π2,π,3π2,2πC.0,π,2π,3π,4πD.0,π6,π3,π2,2π32.下列函数图象相同的是( )A.f(x)=sin x 与g(x)=sin(π+x)B.f(x)=sin ⎝ ⎛⎭⎪⎫x -π2与g(x)=sin ⎝ ⎛⎭⎪⎫π2-xC.f(x)=sin x 与g(x)=sin(-x)D.f(x)=sin(2π+x)与g(x)=sin x3.以下对正弦函数y=sin x 的图象描述不正确的是( )A.在x ∈[2k π,2k π+2π](k ∈Z)上的图象形状相同,只是位置不同B.介于直线y=1与直线y=-1之间C.关于x 轴对称D.与y 轴仅有一个交点4.不等式cos x<0,x ∈[0,2π]的解集为( ) A.⎝ ⎛⎭⎪⎫π2,3π2 B.⎣⎢⎡⎦⎥⎤π2,3π2 C.⎝ ⎛⎭⎪⎫0,π2 D.⎝ ⎛⎭⎪⎫π2,2π5.函数y=ln cos x ⎝ ⎛⎭⎪⎫-π2<x <π2的图象是( )6.方程sin x=lg x 的根的个数为________.7.函数y=2cos x -2的定义域是____________________________________.8.y=1+sin x ,x ∈[0,2π]的图象与y=32的交点的个数是________.9.用“五点法”作出函数y=1+2sin x ,x ∈[0,2π]的图象.10.求函数y= log 21sin x-1的定义域.层级二 应试能力达标1.用“五点法”作y=2sin 2x 的图象时,首先描出的五个点的横坐标是( )A.0,π2,π,3π2,2πB.0,π4,π2,3π4,πC.0,π,2π,3π,4πD.0,π6,π3,π2,2π32.在同一平面直角坐标系内,函数y=sin x ,x ∈[0,2π]与y=sin x ,x ∈[2π,4π]的图象( ) A.重合 B.形状相同,位置不同 C.关于y 轴对称 D.形状不同,位置不同3.在[0,2π]内,不等式sin x<-32的解集是( )A.(0,π)B.⎝ ⎛⎭⎪⎫π3,4π3C.⎝ ⎛⎭⎪⎫4π3,5π3D.⎝ ⎛⎭⎪⎫5π3,2π4.方程|x|=cos x 在(-∞,+∞)内( ) A.没有根 B.有且仅有一个根 C.有且仅有两个根 D.有无穷多个根5.函数y=2cos x ,x ∈[0,2π]的图象和直线y=2围成的一个封闭的平面图形的面积是________.6.当x ∈[-π,π]时,y=12x 与y=sin x 的图象交点的个数为________.7.利用“五点法”作出函数y=sin ⎝⎛⎭⎪⎫x -π2错误!未找到引用源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时跟踪检测(十) 正弦函数、余弦函数的单调性与最值
层级一 学业水平达标
1.函数f(x)=-2sin x +1,x ∈⎣⎢⎡⎦
⎥⎤-π2,π的值域是( ) A .[1,3]
B .[-1,3]
C .[-3,1]
D .[-1,1]
解析:选B ∵x ∈⎣⎢⎡⎦
⎥⎤-π2,π,∴sin x ∈[-1,1], ∴-2sin x +1∈[-1,3].
2.函数y =|sin x|的一个单调递增区间是( )
A .⎝ ⎛⎭
⎪⎫-π4,π4 B .⎝ ⎛⎭⎪⎫π4,3π4 C .⎝ ⎛⎭⎪⎫π,3π2 D .⎝ ⎛⎭
⎪⎫3π2,2π 解析:选C 由y =|sin x|的图象,易得函数y =|sin x|的单调递增区间
为⎝ ⎛⎭⎪⎫k π,k π+π2,k ∈Z ,当k =1时,得⎝
⎛⎭⎪⎫π,3π2为函数y =|sin x|的一个单调递增区间.
3.下列函数中,既为偶函数又在(0,π)上单调递增的是( )
A .y =|cos x|
B .y =cos|-x|
C .y =sin ⎝ ⎛⎭⎪⎫x -π2
D .y =-sin x 2
解析:选C y =|cos x|在⎝ ⎛⎭
⎪⎫0,π2上是减函数,排除A ; y =cos|-x|=cos|x|在(0,π)上是减函数.排除B ;y =sin ⎝ ⎛⎭
⎪⎫x -π2=-sin ⎝ ⎛⎭
⎪⎫π2-x =-cos x 是偶函数,且在(0,π)上单调递增,符合题意;y =-sin x 2在(0,π)上是单调递减的.
4.函数y =sin ⎝ ⎛⎭
⎪⎫x +π2,x ∈R 在( ) A .⎣⎢⎡⎦⎥⎤-π2,π2上是增函数 B .[0,π]上是减函数
C .[-π,0]上是减函数
D .[-π,π]上是减函数
解析:选B y =sin ⎝ ⎛⎭
⎪⎫x +π2=cos x ,所以在区间[-π,0]上是增函数,在[0,π]上是减函数,故选B.
5.函数f(x)=sin ⎝ ⎛⎭⎪⎫2x -π4在区间⎣⎢⎡⎦
⎥⎤0,π2上的最小值为( ) A .-1
B .-22
C .22
D .0 解析:选B ∵x ∈⎣
⎢⎡⎦⎥⎤0,π2,∴-π4≤2x -π4≤3π4,∴当2x -π4=-π4时,f(x)=sin ⎝ ⎛⎭
⎪⎫2x -π4有最小值-22. 6.已知函数y =3cos(π-x),则当x =________时,函数取得最大值. 解析:y =3cos(π-x)=-3cos x ,当cos x =-1,即x =2k π+π,k ∈Z 时,y 有最大值3.
答案:2k π+π,k ∈Z
7.y =sin x ,x ∈⎣⎢⎡⎦
⎥⎤π6,2π3,则y 的范围是________. 解析:由正弦函数图象,对于x ∈⎣⎢⎡⎦
⎥⎤π6,2π3,当x =π2时,y max =1,当x =π6时,y min =12,从而y ∈⎣⎢⎡⎦
⎥⎤12,1. 答案:⎣⎢⎡⎦
⎥⎤12,1 8.函数y =sin(x +π)在⎣⎢⎡⎦
⎥⎤-π2,π上的单调递增区间为________. 解析:因为sin(x +π)=-sin x ,所以要求y =sin(x +π)在⎣⎢⎡⎦
⎥⎤-π2,π上的单调递增区间,即求y =sin x 在⎣⎢⎡⎦⎥⎤-π2,π上的单调递减区间,易知为⎣⎢⎡⎦
⎥⎤π2,π. 答案:⎣⎢⎡⎦
⎥⎤π2,π
9.求下列函数的最大值和最小值.
(1)y = 1-12sin x ;(2)y =3+2cos ⎝ ⎛⎭
⎪⎫2x +π3. 解:(1)∵⎩⎨⎧ 1-12sin x ≥0,-1≤sin x ≤1,
∴-1≤sin x ≤1.
∴当sin x =-1时,y max =
62
; 当sin x =1时,y min =22. (2)∵-1≤cos ⎝ ⎛⎭
⎪⎫2x +π3≤1, ∴当cos ⎝ ⎛⎭
⎪⎫2x +π3=1时,y max =5; 当cos ⎝ ⎛⎭
⎪⎫2x +π3=-1时,y min =1. 10.比较下列各组数的大小.
(1)sin 10π17与sin 11π17;(2)cos 5π3与cos 16π9
. 解:(1)∵函数y =sin x 在⎣⎢⎡⎦
⎥⎤π2,π上单调递减,且π2<10π17<11π17<π,∴sin 10π17>sin 11π17. (2)cos 5π3=cos ⎝
⎛⎭⎪⎫2π-π3=cos π3, cos 16π9=cos ⎝
⎛⎭⎪⎫2π-2π9=cos 2π9. ∵函数y =cos x 在[0,π]上单调递减,
且0<2π9<π3
<π, ∴cos π3<cos 2π9,∴cos 5π3<cos 16π9
. 层级二 应试能力达标。
