必修二线面垂直经典例题
线面垂直题型20道

线面垂直题型20道
1. 两条直线的夹角为90度,则它们一定垂直。
2. 如果一条直线垂直于另一条直线,那么任意一条过这两条直线的线段,这条线段上的点就分别与这两条直线的交点连成的线段垂直。
3. 两条直线分别垂直于第三条直线,则这两条直线平行。
4. 一条线段的中垂线与线段垂直。
5. 任意一个点到平面上一直线的垂足所在的直线与这条直线垂直。
6. 如果一个三角形的两条边互相垂直,则这个三角形是直角三角形。
7. 如果一条直线与一个平面垂直,则这条直线称为这个平面的法线。
8. 一个正方体的某个面与它所在的平面垂直。
9. 一个矩形的对角线互相垂直。
10. 一个正方形的对角线互相垂直。
11. 如果两个面互相垂直,则它们的法线互相平行。
12. 如果平面P垂直于直线L1,且L1垂直于直线L2,则平面P和直线L2互相平行。
13. 如果两条直线互相垂直,则它们的斜率的乘积为-1。
14. 如果一条直线过一个圆的圆心,则这条直线与圆的切线垂直。
15. 如果一条直线垂直于直径所在的直线,则它和圆的切线互相平行。
16. 直角梯形的两条腰互相垂直。
17. 如果两个向量垂直,则它们的点积为0。
18. 如果直线L1垂直于平面P,那么L1上任意一点到P的距离均相等。
19. 一个正六面体的某个面与它所在的平面垂直。
20. 如果两个三维空间中的直线垂直,则它们的方向向量的点积为0。
线面垂直经典例题及练习题-完整可编辑版

页脚下载后可删除,如有侵权请告知删除!立体几何1.P 点在那么ABC ∆所在的平面外,O 点是P 点在平面ABC 内的射影 ,PA 、PB 、PC两两垂直,那么D 点是那么ABC ∆ 〔 B 〕(A)重心 (B) 垂心 (C)内心 (D)外心2.与两个相交平面的交线平行的直线和这两个平面的位置关系是 〔 A 〕(A)都平行 (B) 都相交 (C) 在两个平面内 (D)至少与其中一个平行3.假设两个平面内分别有一条直线,这两条直线互相平行,那么这两平面的位置关系是〔 A 〕(A)平行 (B) 相交 (C)平行或相交 (D)垂直 4.在空间,下述命题正确的选项是 〔 B 〕(A)假设直线//a 平面M ,直线b a ⊥,那么直线⊥b 平面M (B)假设平面M //平面N ,那么平面M 内任意直线a //平面N(C)假设平面M 与N 的交线为a ,平面M 内的直线a b ⊥,那么N b ⊥ (D)假设平面N 的两条直线都平行平面M ,那么平面N //平面M5.a 、b 表示两条直线,α、β、γ表示三个平面,以下命题中错误的选项是 〔A 〕 (A),,αα⊂⊂b a 且ββ//,//b a ,那么βα// (B)a 、b 是异面直线,那么存在唯一的平面与a 、b 等距 (C) ,,,b a b a ⊥⊂⊥βα那么βα// (D),,,//,βαβγγα⊥⊥⊥b a 那么b a ⊥6.直线l //平面α,αβ⊥,那么l 与平面β的位置关系是 〔 D 〕 (A) l β⊂ (B) //l β (C) l β与相交 (D ) 以上三种情况均有可能 7.直线l ⊥平面α,直线m ⊂平面β,有以下四个命题:①//l m αβ⇒⊥②//l m αβ⊥⇒③//l m αβ⇒⊥④//l m αβ⊥⇒,其中正确的选项是〔D 〕(A) ①② (B) ②④ (C) ③④ (D) ①③8.αβγδ,,,是四个不同的平面,且αγβγαδβδ⊥⊥⊥⊥,,,,那么〔 B 〕 (A)////αβγδ或 (B) ////αβγδ且(C) 四个平面中可能任意两个都不平行 (D) 四个平面中至多有一对平面平行 9.平面α和平面β相交,a 是α内的一条直线,那么〔 D 〕(A) 在β内一定存在与a 平行的直线 (B) 在β内一定存在与a 垂直的直线 (C) 在β内一定不存在与a 平行的直线 (D) 在β内一定不存在与a 垂直的直线页脚下载后可删除,如有侵权请告知删除!10.PA ⊥正方形ABCD 所在平面,垂足为A ,连PB PC PD AC BD ,,、,,那么互相垂直的平面有〔 C 〕(A) 5对 (B) 6对 (C) 7对 (D) 8对12. 如图9-29,P A ⊥平面ABCD ,ABCD 是矩形,M 、N 分别是AB 、PC 的中点. 求证:MN ⊥AB .13. :如图,AS ⊥平面SBC ,SO ⊥平面ABC 于O , 求证:AO ⊥BC .15. 如图,P ∉平面ABC ,PA=PB=PC ,∠APB=∠APC=60°,∠BPC=90 °求证:平面ABC ⊥平面PBC16. 如图:在斜边为AB 的R t △ABC 中,过点A 作PA ⊥平面ABC ,AE ⊥PB 于E ,AF ⊥PC 于F ,〔1〕求证:BC ⊥平面PAC ;〔2〕求证:PB ⊥平面AEF.17. 如图:PA ⊥平面PBC ,AB =AC ,M 是BC 的中点,求证:BC ⊥PM.CFEPBAC BAM P页脚下载后可删除,如有侵权请告知删除!如图,在正三棱柱111C B A ABC -.中,底面ABC 为正三角形,M 、N 、G 分别是棱CC 1、AB 、BC的中点.且AC CC 21=.〔Ⅰ〕求证:CN //平面 AMB 1; 〔Ⅱ〕求证:平面AMG .【本文档内容可以自由复制内容或自由编辑修改内容期待你的好评和关注,我们将会做得更好】。
线线垂直、线面垂直、面面垂直的习题及答案解析

线线垂直、线面垂直、面面垂直部分习及答案1.在四面体ABCD 中,△ABC 与△DBC 都是边长为4的正三角形.(1)求证:BC ⊥AD ;2如图,在三棱锥S —ABC 中,SA ⊥平面ABC ,平面SAB ⊥平面SBC . (1)求证:AB ⊥BC ;3.如图,四棱锥P —ABCD 的底面是边长为a 的正方形,PA ⊥底面ABCD ,E 为AB 的中点,且PA=AB .(1)求证:平面PCE ⊥平面PCD ;(2)求点A 到平面PCE 的距离.4. 如图2-4-2所示,三棱锥S —ABC 中,SB=AB ,SC=AC ,作AD ⊥BC 于D ,SH ⊥AD 于H , 求证:SH ⊥平面ABC.(第1题)5. 如图所示,已知Rt△ABC所在平面外一点S,且SA=SB=SC,点D 为斜边AC的中点.(1)求证:SD⊥平面ABC;(2)若AB=BC,求证:BD⊥平面SAC.6. 证明:在正方体ABCD-A1B1C1D1中,A1C⊥平面BC1DAC7. 如图所示,直三棱柱中,∠ACB=90°,AC=1,,侧棱,侧面的两条对角线交点为D,的中点为M.求证:CD⊥平面BDM.8.在三棱锥A-BCD中,BC=AC,AD=BD,作BE⊥CD,E为垂足,作AH⊥BE于H.求证:AH⊥平面BCD.9. 如图,过S引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC⊥平面BSC.10.如图,在长方体ABCD—A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.(1)求证:平面EDB⊥平面EBC;(2)求二面角E-DB-C的正切值.11:已知直线PA垂直于圆O所在的平面,A为垂足,AB为圆O的直径,C是圆周上异于A、B的一点。
求证:平面PAC 平面PBC。
12.. 如图1-10-3所示,过点S 引三条不共面的直线,使∠BSC=90°,∠ASB=∠ASC=60°,若截取SA=SB=SC. 求证:平面ABC ⊥平面BSC13. 如图1-10-5所示,在四面体ABCD 中,BD= a, AB=AD=BC=CD=AC=a.求证:平面ABD ⊥平面BCD .214.如图所示,△ABC 为正三角形,CE ⊥平面ABC ,BD ∥CE ,且CE=AC=2BD ,M 是AE 的中点,求证:(1)DE=DA ;(2)平面BDM ⊥平面ECA ;(3)平面DEA ⊥平面ECA .15.如图所示,已知PA ⊥矩形ABCD 所在平面,M 、N 分别是AB 、PC 的中点.(1)求证:MN ∥平面PAD ;(2)求证:MN ⊥CD ;(3)若∠PDA=45°,求证:MN ⊥平面PCD .16. 如图1,在正方体1111ABCD A B C D -中,M 为1CC 的中点,AC 交BD 于点O ,求证:1A O ⊥平面MBD答案与提示:1. 证明:(1)取BC 中点O ,连结AO ,DO .∵△ABC ,△BCD 都是边长为4的正三角形, ∴AO ⊥BC ,DO ⊥BC ,且AO ∩DO =O , ∴BC ⊥平面AOD .又AD ⊂平面AOD , ∴BC ⊥AD .2. 【证明】作AH ⊥SB 于H ,∵平面SAB ⊥平面SBC .平面SAB ∩平面SBC=SB ,∴AH ⊥平面SBC ,又SA ⊥平面ABC ,∴SA ⊥BC ,而SA 在平面SBC 上的射影为SB ,∴BC ⊥SB ,又SA ∩SB=S ,∴BC ⊥平面SAB .∴BC ⊥AB .3. 【证明】PA ⊥平面ABCD ,AD 是PD 在底面上的射影,又∵四边形ABCD 为矩形,∴CD ⊥AD ,∴CD ⊥PD ,∵AD ∩PD=D ∴CD ⊥面PAD ,∴∠PDA 为二面角P —CD —B 的平面角,∵PA=PB=AD ,PA ⊥AD ∴∠PDA=45°,取Rt △PAD 斜边PD 的中点F ,则AF ⊥PD ,∵AF ⊂面PAD ∴CD ⊥AF ,又PD ∩CD=D ∴AF ⊥平面PCD ,取PC 的中点G ,连GF 、AG 、EG ,则GF21CD 又AE 21CD ,∴GF AE ∴四边形AGEF 为平行四边形∴AF ∥EG ,∴EG ⊥平面PDC 又EG ⊂平面PEC ,∴平面PEC ⊥平面PCD .(2)【解】由(1)知AF ∥平面PEC ,平面PCD ⊥平面PEC ,过F 作FH ⊥PC 于H ,则FH ⊥平面PEC∴FH 为F 到平面PEC 的距离,即为A 到平面PEC 的距离.在△PFH 与 △PCD 中,∠P 为公共角,而∠FHP=∠CDP=90°,∴△PFH ∽△PCD .∴PC PFCD FH =,设AD=2,∴PF=2,PC=324822=+=+CD PD , ∴FH=362322=⋅∴A 到平面PEC 的距离为36. 4.【证明】取SA的中点E,连接EC ,EB. ∵SB=AB,SC=AC, ∴SA ⊥BE,SA ⊥CE. 又∵CE ∩BE=E, ∴SA ⊥平面BCE.∵BCBCE5. 证明:(1)因为SA=SC ,D 为AC 的中点, 所以SD ⊥AC.连接BD. 在Rt △ABC 中,有AD=DC=DB ,所以△SDB ≌△SDA , 所以∠SDB=∠SDA , 所以SD ⊥BD.又AC ∩BD=D , 所以SD ⊥平面ABC. (2)因为AB=BC ,D 是AC 的中点, 所以BD ⊥AC. 又由(1)知SD ⊥BD , 所以BD 垂直于平面SAC 内的两条相交直线,所以BD⊥平面SAC.6.证明:连结ACBD AC⊥AC为A1C在平面AC上的射影∴⊥⊥⎫⎬⎭⇒⊥BD A CA C BC A C BC D11111同理可证平面7.证明:如右图,连接、、,则.∵,∴为等腰三角形.又知D 为其底边的中点,∴.∵,,∴.又,∴. ∵为直角三角形,D为的中点,∴,.又,,∴..即CD⊥DM.∵、为平面BDM内两条相交直线,∴ CD⊥平面BDM.8.证明:取AB的中点F,连结CF,DF.∵AC BC=,∴CF AB⊥.∵AD BD⊥.=,∴DF AB又CF DF F=,∴AB⊥平面CDF.∵CD⊂平面CDF,∴⊥.C D又CD BE⊥,BE AB B=,∴CD⊥平面ABE,CD AH⊥.∵AH CD⊥,AH BE=,⊥,CD BE E∴AH⊥平面BCD.9.证明:如图,已知PA=PB=PC=a,由∠APB=∠APC=60°,△PAC,△PAB为正三角形,则有:PA=PB=PC=AB=AC=a,取BC中点为E直角△BPC中,,,由AB=AC ,AE ⊥BC ,直角△ABE 中,,,, 在△PEA 中,,,∴,平面ABC ⊥平面BPC.10. 证明:(1)在长方体ABCD -A 1B 1C 1D 1中,AB =2,BB 1=BC =1,E 为D 1C 1的中点.∴△DD 1E 为等腰直角三角形,∠D 1ED =45°.同理∠C 1EC=45°.∴︒=∠90DEC ,即DE ⊥EC .在长方体ABCD -1111D C B A 中,BC ⊥平面11DCC D ,又DE ⊂平面11DCC D , ∴BC ⊥DE .又C BC EC = ,∴DE ⊥平面EBC .∵平面DEB 过DE ,∴平面DEB ⊥平面EBC .(2)解:如图,过E 在平面11DCC D 中作EO ⊥DC 于O .在长方体ABCD -1111D C B A 中,∵面ABCD⊥面11DCC D ,∴EO ⊥面ABCD .过O 在平面DBC 中作OF ⊥DB 于F ,连结EF ,∴EF ⊥BD .∠EFO 为二面角E -DB -C 的平面角.利用平面几何知识1, (第10题)可得OF=5又OE=1,所以,tan∠EFO=5.11.(1)【证明】∵C是AB为直径的圆O的圆周上一点,AB是圆O 的直径∴BC⊥AC;又PA⊥平面ABC,BC⊂平面ABC,∴BC⊥PA,从而BC⊥平面PAC.∵BC ⊂平面PBC,∴平面PAC⊥平面PBC..12.证明:如图1-10-4所示,取BC的中点D,连接AD,SD.由题意知△ASB与△ASC是等边三角形,则AB=AC,∴AD⊥BC,SD⊥BC.令SA=a,在△SBC中,SD= a,又AD= = a,∴AD2+SD2=SA2,即AD⊥SD.又∵AD⊥BC,∴AD⊥平面SBC.∵AD ABC,∴平面ABC⊥平面SBC.13.证明:取BD的中点E,连接AE,CE.则AE⊥BD,BD⊥CE.在△ABD中,AB=a,BE= BD= ,∴AE= ,同理,CE= .在△AEC中,AE=EC= ,AC=a,∴AC2=AE2+EC2,即AE⊥EC.∵BD∩EC=E,∴AE⊥平面BCD.又∵AE ABD,∴平面ABD⊥平面BCD14.证明: ((1)取EC的中点F,连接DF.∵ CE⊥平面ABC,∴ CE⊥BC.易知DF∥BC,CE⊥DF.∵ BD∥CE,∴ BD⊥平面ABC.在Rt△EFD和Rt△DBA中,∵,,∴ Rt△EFD≌Rt△DBA.故DE=AD.(2)取AC的中点N,连接MN、BN,MN CF.∵ BD CF,∴ MN BD.N平面BDM.∵ EC⊥平面ABC,∴ EC⊥BN.又∵ AC⊥BN,∴ BN⊥平面ECA.又∵ BN平面MNBD,∴平面BDM⊥平面ECA.(3)∵ DM∥BN,BN⊥平面ECA,∴ DM⊥平面ECA.又∵ DM平面DEA,∴平面DEA⊥平面ECA.15.证明:(1)取PD的中点E,连接AE、EN,则,故AMNE为平行四边形,∴ MN∥AE.∵ AE平面PAD,MN平面PAD,∴ MN∥平面PAD.(2)要证MN⊥CD,可证MN⊥AB.由(1)知,需证AE⊥AB.∵ PA⊥平面ABCD,∴ PA⊥AB.又AD⊥AB,∴ AB⊥平面PAD.∴ AB⊥AE.即AB⊥MN.又CD∥AB,∴ MN⊥CD.(3)由(2)知,MN⊥CD,即AE⊥CD,再证AE⊥PD即可.∵ PA⊥平面ABCD,∴ PA⊥AD.又∠PDA=45°,E为PD的中点.∴ AE⊥PD,即MN⊥PD.又MN ⊥CD ,∴ MN ⊥平面PCD .16.证明:连结MO ,1A M ,∵DB ⊥1A A ,DB ⊥AC ,1A A AC A =,∴DB ⊥平面11A ACC ,而1AO ⊂平面11A ACC ∴DB ⊥1A O .设正方体棱长为a ,则22132A O a =,2234MO a =.在Rt △11A C M 中,22194A M a =.∵22211A O MO A M +=,∴1A O O M ⊥. ∵OM ∩DB =O ,∴ 1A O ⊥平面MBD .。
线面垂直判定经典证明题

线面垂直判定经典证明题1.已知:在三角形ABC中,PA垂直于AB和AC。
证明PA垂直于平面ABC。
2.已知:在三角形ABC中,PA垂直于AB,BC垂直于平面PAC。
证明PA垂直于BC。
3.已知:在三棱锥V-ABC中,VA=VC,AB=BC。
证明VB垂直于AC。
4.已知:在正方体ABCD-EFGH中,O为底面ABCD的中心。
证明BD垂直于平面AEGC。
5.已知:在圆O中,AB是直径,PA垂直于AC和AB。
证明BC垂直于平面PAC。
6.已知:在三角形ABC中,AD垂直于BD和DC,AD=BD=CD,∠BAC=60°。
证明BD垂直于平面ADC。
7.已知:在矩形ABCD中,PA垂直于平面ABCD,M和N分别是AB和PC的中点。
1) 证明MN平行于平面PAD。
2) 证明XXX垂直于CD。
3) 若∠PDA=45°,证明MN垂直于平面PCD。
8.已知:在棱形ABCD所在平面外,P满足PA=PC。
证明AC垂直于平面PBD。
9.已知四面体ABCD中,AB=AC,BD=CD,平面ABC垂直于平面BCD,E是棱BC的中点。
1) 证明AE垂直于平面BCD。
2) 证明AD垂直于BC。
10.在三棱锥ABCD中,AB=1,BC=2,BD=AC=3,AD=2.证明AB垂直于平面BCD。
11.在四棱锥S-ABCD中,SD垂直于平面ABCD,底面ABCD是正方形。
证明AC垂直于平面SBD。
12.已知:正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE垂直于平面CDE。
证明AB垂直于平面ADE。
13.在三棱锥P-ABC中,PA、PB、PC两两垂直,H是△XXX的垂心。
证明PH垂直于底面ABC。
14.在正方体ABCD-A1B1C1D1中,证明A1C垂直于平面BC1D1.15.在△ABC所在平面外一点S,SA垂直于平面ABC,平面SAB垂直于平面SBC。
证明AB垂直于BC。
16.在直三棱柱ABC-A1B1C1中,AC=BC=1,∠ACB=90°,AA1=2,D是A1B1的中点。
必修二线面垂直经典例题

又∵AB⊥AD 且 PA∩AD=A, ∴AB⊥平面 PAD,而 PD⊂平面 PAD, ∴AB⊥PD.又∵AB∩AE=A, ∴PD⊥平面 ABE.
解题小结:
破解此类问题的关键在于熟练把握空间垂直关系的判定与性质, 注意平面图形中的一些线线垂直关系的灵活利用,这是证明空间 垂直关系的基础.由于“线线垂直”、“线面垂直”、“面面垂 直”之间可以相互转化,因此整个证明过程围绕着线面垂直这个 核心而展开,这是化解空间垂直关系难点的技巧所在.
证明 (1)由四棱锥 P—ABCD 中, ∵PA⊥底面 ABCD,CD⊂平面 ABCD, ∴PA⊥CD.∵AC⊥CD,PA∩AC=A, ∴CD⊥平面 PAC. 而 AE⊂平面 PAC,∴CD⊥AE. (2)由 PA=AB=BC,∠ABC=60°, 可得 AC=PA. ∵E 是 PC 的中点,∴AE⊥PC. 由(1),知 AE⊥CD,且 PC∩CD=C, ∴AE⊥平面 PCD.
(2)求证:VB ⊥AC
小结:
A
K
C
1、问题(1)的线线垂直是通过平面几何知识解决的。 B
体现了空间向平面的转化。
2.问题(2)的线线垂直是异面垂直,又转化为新的线面 垂直解决;
即:欲证线面垂直,需证线线垂直,
欲证线线垂直,又需证新的线面垂直。
体现了空间关系的相互转化。
变题一:
空间四边形ABCD中,AB=AD,CB=CD, 求证: AC⊥BD.
知识背景:
1、线面垂直的定义; 2、线面垂直的最基本性质 ; 3.线面垂直的判定定理。
例1.三棱锥V-ABC中,VA=VC,AB=BC,K是AC的中点。
(1)求证:AC ⊥平面VKB (2)求证:VB ⊥AC
人教课标版高中数学必修2典型例题:直线与平面垂直的判定
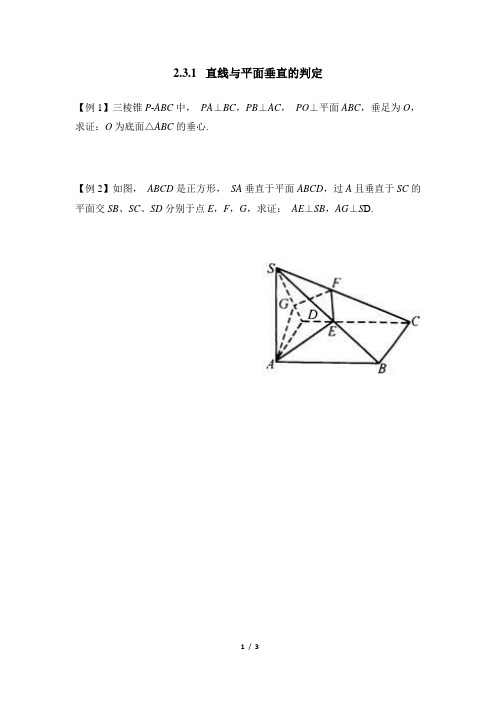
2.3.1 直线与平面垂直的判定
【例1】三棱锥P-ABC中,PA⊥BC,PB⊥AC,PO⊥平面ABC,垂足为O,求证:O为底面△ABC的垂心.
【例2】如图,ABCD是正方形,SA垂直于平面ABCD,过A且垂直于SC的平面交SB、SC、SD分别于点E,F,G,求证:AE⊥SB,AG⊥S D.
参考答案
例1
【分析】可证O为三角形ABC的两条高线的交点.
【证明】连接OA、OB、OC,∵PO⊥平面ABC,
∴.
又∵,
∴,得
,
∴O为底面△ABC的垂心.
【点拨】此例可以变式为“已知,求证”,其思路是接着利用射影是垂心的结论得到后进行证明. 三条侧棱两两垂直时,也可按同样的思路证出.
例2:
【分析】本题考查线面垂直的判定与性质定理,
以及线线垂直和线面垂直相互转化的思想.由于
图形的对称性,所以两个结论只需证一个即可.
欲证,可证平面,为此须
证,,进而转化证明平面,平面.
【证明】∵SA⊥平面ABCD,平面ABCD,
∴.
又∵ABCD为正方形,
∴.
∴平面.
∵平面,
∴.
又∵平面,
∴.
∴平面.
又∵平面,
∴,同理可证.
【点拨】(1)证明线线垂直,常用的方法有:同一平面内线线垂直、线面垂直的性质定理,三垂线定理与它的逆定理,以及与两条平行线中一条垂直就与另一条垂直.(2)本题的证明过程中反复交替使用“线线垂直”与“线面垂直”的相互联系,充分体现了数学化思想的优越性.。
第29讲 线面垂直证线线平行和垂直2种题型(解析版) 高一数学同步题型讲义(新人教2019)必修二

第29讲线面垂直证线线平行和垂直2种题型【题型目录】题型一:线面垂直的证线线平行题型二:线面垂直的证线线垂直【典型例题】题型一:线面垂直的证线线平行【例1】在正方体1111ABCD A B C D -中,直线l (与直线1BB 不重合)⊥平面ABCD ,则有()A .1BB l⊥B .1BB l ∥C .1BB 与l 异面D .1BB 与l 相交【答案】B【分析】根据线面垂直的性质即可得出答案.【详解】解:因为l ⊥平面ABCD ,且1BB ⊥平面ABCD ,直线l 与直线1BB 不重合,所以1BB l ∥.故选:B.【例2】在空间中,下列说法正确的是()A .垂直于同一直线的两条直线平行B .垂直于同一直线的两条直线垂直C .平行于同一平面的两条直线平行D .垂直于同一平面的两条直线平行【答案】D【分析】根据空间中线、面的位置关系理解判断A 、B 、C ,根据线面垂直的性质判断D .【详解】垂直于同一直线的两条直线的位置关系有:平行、相交和异面,A 、B 不正确;平行于同一平面的两条直线的位置关系有:平行、相交和异面,C 不正确;根据线面垂直的性质可知:D 正确;故选:D .【例3】圆柱OP 如图所示,AC 为下底面圆的直径,DE 为上底面圆的直径,BD ⊥底面ABC ,证明://BP 面AEC【答案】证明见解析【分析】连接BO ,OE ,OP ,可证明四边形PEOB 为平行四边形,得到//PB OE ,再通过线面平行的判定定理即可证明【详解】证明:连接BO ,OE ,OP ,可得OP ⊥平面ABC ,∵BD ⊥平面ABC ,∴//OP BD ,∵OP BD =,∴四边形OPDB 为平行四边形,∴//DP OB ,∴//PE OB 且PE OB =,∴四边形PEOB 为平行四边形,∴//PB OE ,∵OE ⊂平面AEC ,BP ⊄平面AEC ,∴//BP 平面AEC【例4】如图,已知多面体ABCDE ,⊥AE 平面,⊥ABC DC 平面ABC ,且2AE DC ==,证明://AC 平面BED .【答案】证明见解析.【分析】利用线面垂直的性质证得//AE DC ,进而得//AC ED ,再利用线面平行的判定推理作答.【详解】因为⊥AE 平面,⊥ABC DC 平面ABC ,则//AE DC ,又AE DC =,即四边形ACDE 为平行四边形,因此//AC ED ,而AC ⊄平面,⊂BED ED 平面BED ,所以//AC 平面BED .【题型专练】1.若a 、b 是空间中两条不同的直线,则a b ∥的充分条件是()A .直线a 、b 都垂直于直线lB .直线a 、b 都垂直于平面αC .直线a 、b 都与直线l 成30︒角D .直线a 、b 都与平面α成60︒角【答案】B【分析】根据线线平行、线线角等知识对选项进行分析,从而确定正确选项.【详解】A 选项,,a b 都与l 垂直,可能a b ⊥r r ,A 选项错误.B 选项,,a b 都垂直于平面α,则a b ∥,B 选项正确.C 选项,,a b 都与l 成30︒角,可能,a b 相交,C 选项错误.D 选项,,a b 都与平面α成60︒角,可能,a b 异面,D 选项错误.故选:B2.(多选题)已知α,β是两个不同的平面,m ,n ,l 是三条不同的直线,则下列命题中正确的是()A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若m α⊥,n α⊥,则m n ∥C .若l αβ= ,m α∥,m β∥,则m l ∥D .若l αβ= ,m α⊂,m l ⊥,则m β⊥【答案】BC【分析】利用面面垂直的性质判断选项A ;利用线面垂直的性质判断选项B ;利用线面平行的性质判断选项C ;利用线面垂直判定定理判断选项D.【详解】选项A :若αβ⊥,m α⊂,n β⊂,则m n ∥或m n 、相交或m n 、互为异面直线.判断错误;选项B :若m α⊥,n α⊥,则m n ∥.判断正确;选项C :设平面a αδ= ,m δ⊂,又m α∥,则m a∥设平面b βγ= ,m γ⊂,又m β∥,则m b ∥,则a b ∥,又b β⊂,a β⊄,则a β∥,又a α⊂,l αβ= ,则a l ∥,则m l ∥.判断正确;选项D :若l αβ= ,m α⊂,m l ⊥,则m β、的位置关系为相交,当且仅当αβ⊥时m β⊥.判断错误.故选:BC3.在梯形ABCD 中,AB CD ,2AB =,4CD =,3AD BC ==,BD 与AE 交于点G .如图所示沿梯形的两条高AE ,BF 所在直线翻折,使得90DEF CFE ∠=∠=︒.(1)求证:AD BC ∥;(2)求三棱锥C BDG -的体积.4.已知空间几何体ABCDE 中,ABC ,ECD 是全等的正三角形,平面ABC ⊥平面BCD ,平面ECD ⊥平面BCD .(1)若BD ==BC ED ⊥;(2)证明://AE BD .所以//AE MN ,又//MN BD ,所以//AE BD .题型二:线面垂直的证线线垂直【例1】如图,在三棱柱111ABC A B C -中,1AC BC ⊥,1AC CC =.(1)记平面1A BC 与平面111A B C 的交线为l ,求证://l 平面11BCC B ;(2)求证:11A C AB ⊥.【答案】(1)证明见解析;(2)证明见解析【分析】(1)由棱柱的性质得11//BC B C ,从而//BC 平面111A B C ,推导出//BC l ,由此能证明//l 平面11BCC B ;(2)连接1AC ,利用菱形的对角线相互垂直和已知条件得到线线垂直,再利用线面垂直的判定定理得到1A C ⊥平面11AB C ,进而利用线面垂直的性质证明11A C BC ⊥.【详解】(1)由棱柱的性质得11//BC B C ,因为BC ⊄平面111A B C ,11B C ⊂平面111A B C ,所以//BC 平面111A B C ,因为BC ⊂平面1A BC ,平面1A BC 与平面111A B C 的交线为l ,所以//BC l ,因为l ⊄平面11BCC B ,BC ⊂平面11BCC B ,∴//l 平面11BCC B .(2)连接1AC ,。
数学必修二直线与平面垂直的性质练习题含答案.docx

数学必修二直线与平面垂直的性质学校:班级:姓名:考号:1.是o。
的直径,点C是。
上的动点(点C不与4, B重合),过动点C的直线m垂直于O。
所在的平面,D,£分别是",VC的中点,则下列结论错误的是()A.直线DE //平面ABCB.直线DE 1平面UBCC.DE 1 VBD.DE 1 AB2,垂直于同一平面的两条直线()A.平行B.垂直C.相交D.异面3.设1, m, n均为直线,其中zn, 1在平面a内,贝lj'7 1 a"是“I 1 m且Z 1 n”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4. A ABC所在平面外一点F,分别连接P4、PB、PC,则这四个三角形中直角三角形最多有()A.4个B.3个C.2个D.1个5,下列命题中,真命题是()A.若一条直线平行于一个平面内的一条直线,则这条直线与这个平面平行B.若一条直线垂直于一个平面内的两条直线,则这条直线与这个平面垂直C.若一条直线与一个平面平行,则这条直线与这个平面内的任何一条直线平行D.若一条直线垂直于一个平面,则这条直线与这个平面内的任何一条直线垂直6,如图,在中,^ABC = 90°, P为&ABC所在平面外一点,P4 _L平面4BC, 则四面体P-ABC中共有()个直角三角形.A.4B.3C.2D.17.如图:已知AABC是直角三角形,履以=90。
,M为AB的中点,PM ABC所在的平面,那么PA、PB、PC的大小关系是()A.PA > PB > PCB.PB > PA > PCC.PC > PA > PBD.PA = PB = PC8.如图,已知四边形ABCD为正方形,PD 1平面0BCD且P D = AD,则下列命题中错误的是()PA.过BD且与PC平行的平面交P4于M点,则M为PA的中点B.过4C且与PB垂直的平面交PB于N点,则N为PB的中点C.HAD且与PC垂直的平面交PC于H点,则H为PC的中点D.过P、B、C的平面与平面PAD的交线为直线Z,贝U//AD9.过△ABC内一点M任作一条直线Z,再分别过顶点4, B, C作的垂线,垂足分别为D,E,F,若AD + BE + CF = 0恒成立,则点M是△ ABC的()A.垂心B.重心C.外心D.内心10,已知四棱柱ABCD - AWm底面为平行四边形,对角线4G与平面务BD相交于点P,贝叩是"BD 的()A.重心B.内心C.外心D.中心11.若0P垂直于正方形ABCD所在平面,且= 4P = 2,贝IJPC =.12,如果直线Z 1平面a,①若m//Z,则m 1 a;②若m 1 a,则m//Z;③若m/ / a, 则mil-,上述判断正确的是.13.如图,在正方体ABCD - AiBgiDi中,点F在侧面BCC1B1及其边界上运动,并且总是保持4P 与BD]垂直,则动点P的轨迹为.14,设a///?, AEa, Cea, Be/?, D G /?,直线AB 与CD 交于0,若AO = 8, B0 = 9, CD = 34,贝UC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
P
备选题: 如图所示,在四棱锥 P—ABCD 中,PA⊥底面 ABCD, AB⊥AD,AC⊥CD,∠ABC=60° ,PA=AB=BC,E 是 PC 的中 点. 证明:(1)CD⊥AE; (2)PD⊥平面 ABE.
解题分析:
第(1)问通过 DC⊥平面 PAC 证明; 也可通过 AE⊥平面 PCD 得到 结论; 第(2)问利用线面垂直的判定定理证明直线 PD 与平面 ABE 内的两条相交直线垂直.
证明 (1)由四棱锥 P—ABCD 中, ∵PA⊥底面 ABCD,CD⊂平面 ABCD, ∴PA⊥CD.∵AC⊥CD,PA∩AC=A, ∴CD⊥平面 PAC.
而 AE⊂平面 PAC,∴CD⊥AE.
(2)由 PA=AB=BC,∠ABC=60° , 可得 AC=PA.
∵E 是 PC 的中点,∴AE⊥PC. 由(1),知 AE⊥CD,且 PC∩CD=C, ∴AE⊥平面 PCD.
小结:线面垂直证明的难点突破
由于线面垂直的证明往往需要通过线线、线面垂直的
不断转化,所以我们一定要了解给出几何体中的已有 的垂直关系,进而寻找目标平面内与已知直线垂直的 直线。
特别是异面线线垂直的证明有一定难度,常常要转化
为先证一条直线和另一直线所在某个平面垂直。这个 平面的发现至关重要。
变题二: 判断:四边相等的四边形,对角线互相垂直
练习1:
(2011北京高考理科)如图,在四棱锥 P-ABCD中,PA⊥平面ABCD, BAD=600, 底面ABCD是菱形,AB=2, (1)求证:BD⊥平面PAC; (2)略; P (3)略。
D A B C
例2.如图,圆O所在一平面为 , AB是圆O 的直径,C 在圆周上, 且PA AC, PA AB, 求证:(1)PA BC (2)BC 平面PAC
思考:三棱锥中最多有几个直角三角形?
思考:三棱锥P-ABC中最多有几个直角三角形?
P
A C
O
B
例3、已知直角△ABC所在平面外有一点P,且 PA=PB=PC,D是斜边AB的中点,
求证:PD⊥平面ABC.
证明: ∵PA=PB,D为AB中点 ∴ PD⊥AB,连接CD, ∵D为Rt△ABC斜边的中点 ∴ CD=AD, 又PA=PC,PD=PD ∴ △PAD≌△PCD 而PD⊥AB ∴ PD⊥CD, CD∩AB = D ∴PD ⊥平面ABC P
C B
A
D
证明线线垂直的常用方法:
如果两条直线共面或能转化为共面,则转化为在平面
内证明垂直关系,用平面几何知识证明垂直的主要办 法有:勾股定理,等腰三角形三线合一,相似三角形 等; 如果两条直线异面,又不便平移到一个平面内证明垂 直,通常就再转化为证明平面内的直线与已知直线所 在的某个平面垂直。 即:通过另一组线面垂直证明线线垂直。
而 PD⊂平面 PCD,∴AE⊥PD. ∵PA⊥底面 ABCD,∴PA⊥AB.
又∵AB⊥AD 且 PA∩AD=A, ∴AB⊥平面 PAD,而 PD⊂平面 PAD, ∴AB⊥PD.又∵AB∩AE=A, ∴PD⊥平面 ABE.
解题小结:
破解此类问题的关键在于熟练把握空间垂直关系的判定与性质, 注意平面图形中的一些线线垂直关系的灵活利用, 这是证明空间 垂直关系的基础.由于“线线垂直”、“线面垂直”、“面面垂 直”之间可以相互转化, 因此整个证明过程围绕着线面垂直这个 核心而展开,这是化解空间垂直关系难点的技巧所在.
知识背景:
1、线面垂直的定义;
2、线面垂直的最基本性质;
3、线面垂直的判定定理。
例1、三棱锥V-ABC中,VA=VC,AB=BC,K是AC的中点。
(1)求证:AC ⊥平面VKB (2)求证:VB ⊥AC
V
K
A C
B
例1、三棱锥V-ABC中,VA=VC,AB=BC,K是AC的中点。 (1)求证:AC ⊥平面VKB (2)求证:VB ⊥AC
A K V
C
小结:
1、问题(1)的线线垂直是通过平面几何知识解决的。 体现了空间向平面的转化。 2、问题(2)的线线垂直是异面垂直,又转化为新的线面 垂直解决; 即:欲证线面垂直,需证线线垂直, 欲证线线垂直,又需证新的线面垂直。 体现了空间关系的相互转化。
B
变题一:
空间四边形ABCD中,AB=AD,CB=CD, 求证:AC⊥BD.
练习2. 如图,已知点M是菱形ABCD所在平面外一点,且MA=MC 求证:AC⊥平面BDM
M
D
O A B
C
练习3 如图 平面α、β相交于PQ,线段OA、OB分别垂直平面α、 β, 求证:PQ⊥AB 证明: ∵OA⊥α PQ α ∴ OA⊥PQ OB⊥β, PQ β ∴ OB⊥PQ 又OA∩OB=0 ∴PQ⊥平面OAB 而AB平面OAB ∴ PQ⊥AB O Q A
解:(1) AB , AC , 且AB AC A PA AC , PA AB PA 又 BC PA BC
A
P
O
C
B
(2) C为 圆 O上 一 点 ,AB 为 直 径 BC AC 1得BC PA, 由 又 PA AC A BC 面PAC
