线面垂直经典例题及练习题-(精.选)
立体几何线面垂直-题型全归纳(解析版)

立体几何线面垂直-题型全归纳题型一利用等腰三角形“三线合一”例题1、如图,在正三棱锥P-ABC中,E,F,G分别为线段PA,PB,BC的中点,证明:BC⊥平面PAG。
证明:在正三棱锥P-ABC中,AB=AC,G是BC的中点,∴AG⊥BC,又 PB=PC,G是BC的中点,∴PG⊥BC,PG⋂AG=G,PG,AG⊂平面PAG,∴BC⊥平面PAG,解题步骤(1)根据线段的中点,找出相应的等腰三角形;(2)格式“因为D是BC的中点,且AB=AC,所以AD⊥BC”;(3)依据“三线合一”得到线线垂直。
变式训练1、已知四面体ABCD中,AB=AC,BD=CD,E为棱BC的中点,求证:AD⊥BC证明:连接DE,AB=AC,E是BC的中点,∴AE⊥BC,又 BD=CD,E是BC的中点,∴DE⊥BC,AE⋂DE=E,AE,DE⊂平面ADE,∴BC⊥平面ADE,AD⊂平面ADE,∴AD⊥BC变式训练2、在三棱锥P ABC -中,2AC BC ==,90ACB ∠=,AP BP AB ==,PC AC ⊥.求证:PC AB ⊥证明:取AB的中点O,连接OP,OC, AP=BP,O是AB的中点,∴PE⊥AB,又 AC=BC,O是AB的中点,∴OC⊥AB,PO⋂CO=O,PO,CO⊂平面POC,∴AB⊥平面POC,PC⊂平面POC,∴AB⊥PC。
变式训练3、如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,E为CD的中点,060=∠ABC ,求证:AB⊥平面PAE。
证明: 底面ABCD是菱形,060=∠ABC ,∴AE⊥CD,又 AB//CD,∴AB⊥AE,又PA⊥平面ABCD,AB⊂平面ABCD,∴AB⊥PA,AP⋂AE=A,AP,AE⊂平面PAE,∴AB⊥平面PAE。
A CB P题型二利用勾股定理逆定理例题2、如图,在正方体1111D C B A ABCD -中,M 为棱1CC 的中点,AC 交BD 于点O ,求证:BDM1平面⊥O A 证明:连接OM,M A 1,11C A ,设正方体的棱长为2,则6222222121=+=+=AO A A O A 32122222=+=+=OC CM OM 91)22(222121121=+=+=M C C A M A 21221M A OM O A =+∴即:OM⊥OA 1又 在正方体1111D CB A ABCD -中,∴BD⊥OA 1 OM,BD⊂平面BDM,∴BDM1平面⊥O A 解题步骤(1)根据题干给出的线段长度(没有长度的可以假设),标示在图形上,找出相应的三角形;(2)把线段的长度分别求平方,判断能否构成“222c b a =+”;(3)根据平方关系得到线线垂直。
线面垂直经典例题及练习题-完整可编辑版

页脚下载后可删除,如有侵权请告知删除!立体几何1.P 点在那么ABC ∆所在的平面外,O 点是P 点在平面ABC 内的射影 ,PA 、PB 、PC两两垂直,那么D 点是那么ABC ∆ 〔 B 〕(A)重心 (B) 垂心 (C)内心 (D)外心2.与两个相交平面的交线平行的直线和这两个平面的位置关系是 〔 A 〕(A)都平行 (B) 都相交 (C) 在两个平面内 (D)至少与其中一个平行3.假设两个平面内分别有一条直线,这两条直线互相平行,那么这两平面的位置关系是〔 A 〕(A)平行 (B) 相交 (C)平行或相交 (D)垂直 4.在空间,下述命题正确的选项是 〔 B 〕(A)假设直线//a 平面M ,直线b a ⊥,那么直线⊥b 平面M (B)假设平面M //平面N ,那么平面M 内任意直线a //平面N(C)假设平面M 与N 的交线为a ,平面M 内的直线a b ⊥,那么N b ⊥ (D)假设平面N 的两条直线都平行平面M ,那么平面N //平面M5.a 、b 表示两条直线,α、β、γ表示三个平面,以下命题中错误的选项是 〔A 〕 (A),,αα⊂⊂b a 且ββ//,//b a ,那么βα// (B)a 、b 是异面直线,那么存在唯一的平面与a 、b 等距 (C) ,,,b a b a ⊥⊂⊥βα那么βα// (D),,,//,βαβγγα⊥⊥⊥b a 那么b a ⊥6.直线l //平面α,αβ⊥,那么l 与平面β的位置关系是 〔 D 〕 (A) l β⊂ (B) //l β (C) l β与相交 (D ) 以上三种情况均有可能 7.直线l ⊥平面α,直线m ⊂平面β,有以下四个命题:①//l m αβ⇒⊥②//l m αβ⊥⇒③//l m αβ⇒⊥④//l m αβ⊥⇒,其中正确的选项是〔D 〕(A) ①② (B) ②④ (C) ③④ (D) ①③8.αβγδ,,,是四个不同的平面,且αγβγαδβδ⊥⊥⊥⊥,,,,那么〔 B 〕 (A)////αβγδ或 (B) ////αβγδ且(C) 四个平面中可能任意两个都不平行 (D) 四个平面中至多有一对平面平行 9.平面α和平面β相交,a 是α内的一条直线,那么〔 D 〕(A) 在β内一定存在与a 平行的直线 (B) 在β内一定存在与a 垂直的直线 (C) 在β内一定不存在与a 平行的直线 (D) 在β内一定不存在与a 垂直的直线页脚下载后可删除,如有侵权请告知删除!10.PA ⊥正方形ABCD 所在平面,垂足为A ,连PB PC PD AC BD ,,、,,那么互相垂直的平面有〔 C 〕(A) 5对 (B) 6对 (C) 7对 (D) 8对12. 如图9-29,P A ⊥平面ABCD ,ABCD 是矩形,M 、N 分别是AB 、PC 的中点. 求证:MN ⊥AB .13. :如图,AS ⊥平面SBC ,SO ⊥平面ABC 于O , 求证:AO ⊥BC .15. 如图,P ∉平面ABC ,PA=PB=PC ,∠APB=∠APC=60°,∠BPC=90 °求证:平面ABC ⊥平面PBC16. 如图:在斜边为AB 的R t △ABC 中,过点A 作PA ⊥平面ABC ,AE ⊥PB 于E ,AF ⊥PC 于F ,〔1〕求证:BC ⊥平面PAC ;〔2〕求证:PB ⊥平面AEF.17. 如图:PA ⊥平面PBC ,AB =AC ,M 是BC 的中点,求证:BC ⊥PM.CFEPBAC BAM P页脚下载后可删除,如有侵权请告知删除!如图,在正三棱柱111C B A ABC -.中,底面ABC 为正三角形,M 、N 、G 分别是棱CC 1、AB 、BC的中点.且AC CC 21=.〔Ⅰ〕求证:CN //平面 AMB 1; 〔Ⅱ〕求证:平面AMG .【本文档内容可以自由复制内容或自由编辑修改内容期待你的好评和关注,我们将会做得更好】。
专题线面垂直
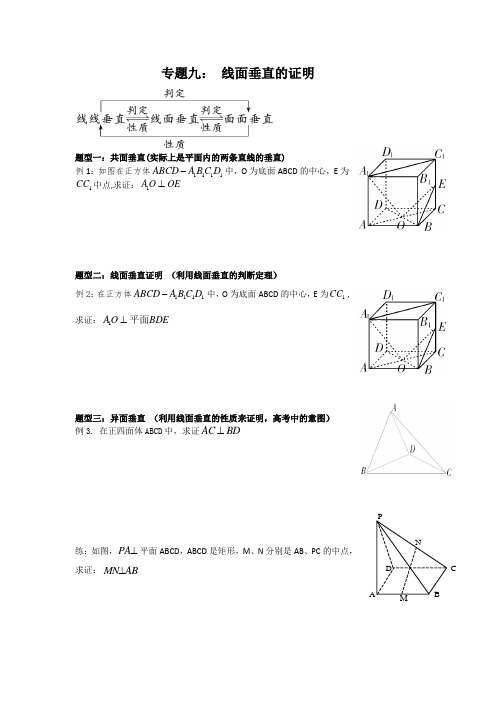
专题九: 线面垂直的证明
题型一:共面垂直(实际上是平面内的两条直线的垂直)
例1:如图在正方体1111ABCD A BC D -中,O 为底面ABCD 的中心,E 为
1CC 中点,求证:1
AO OE ⊥
题型二:线面垂直证明 (利用线面垂直的判断定理) 例2:在正方体中,
O 为底面ABCD 的中心,E 为,求证:
题型三:异面垂直 (利用线面垂直的性质来证明,高考中的意图)
例3. 在正四面体ABCD 中,求证
练:如图,平面ABCD ,ABCD 是矩形,M 、
N 分别是AB 、PC 的中点,求证:
1111ABCD A BC D -1CC 1
AO BDE ⊥平面AC BD ⊥PA ⊥MN AB ⊥
C
题型四:面面垂直的证明(本质上是证明线面垂直)
例4.已知PA 垂直于正方形A BCD 所在平面,连接PB 、PC 、PD 、AC 、BD,则下列垂直关系中正确的序号
是 .
①平面平面PBC ②平面平面PAD ③平面平面PCD
例5.如图,AB 是圆O的直径,C是圆周上一点,PA ⊥平面ABC .若AE ⊥PC ,E为垂足,F是PB 上任意一点,求证:平面AEF ⊥平面PBC .
PAB
⊥PAB ⊥PAB ⊥。
线面垂直练习题

线面垂直练习题一、选择题1. 若直线a与平面α内的直线b垂直,且b⊂α,那么直线a与平面α的关系是()。
A. 平行B. 垂直B. 相交D. 无法确定2. 在空间几何中,若直线m与平面α垂直,直线n在平面α内,且m与n相交,那么直线m与直线n的关系是()。
A. 垂直B. 平行C. 异面D. 相交3. 已知直线l垂直于平面α,点P在平面α外,若要确定过点P且垂直于平面α的直线,需要()。
A. 一条直线B. 两条直线C. 至少两条直线D. 无数条直线4. 若直线a与直线b相交,且a垂直于平面α,b在平面α内,则直线b与平面α的关系是()。
A. 垂直B. 平行C. 相交D. 无法确定5. 已知直线m垂直于直线n,直线m在平面β内,直线n在平面α内,若平面α与平面β垂直,则直线m与平面α的关系是()。
A. 垂直B. 平行C. 相交D. 异面二、填空题6. 若直线a与平面α垂直,直线a上的点A到平面α的距离为d,则直线a上任意一点到平面α的距离都是________。
7. 在空间几何中,若直线l1与直线l2垂直,且l1在平面α内,l2在平面β内,若平面α与平面β垂直,则直线l1与直线l2的位置关系是________。
8. 已知直线m垂直于平面α,若平面β与平面α垂直,且直线m在平面β内,则直线m与平面α的位置关系是________。
9. 若直线a与直线b垂直,直线a在平面α内,直线b在平面β内,且平面α与平面β垂直,则直线a与平面β的位置关系是________。
10. 若直线l垂直于平面α,点P在平面α上,直线l'过点P且与直线l垂直,则直线l'与平面α的位置关系是________。
三、解答题11. 已知直线a与平面α垂直,直线b在平面α内,直线a与直线b 相交于点A。
求证:点A是直线b在平面α上的垂足。
12. 已知平面α与平面β垂直,直线m垂直于平面α且在平面β内,直线n在平面α内。
求证:直线m与直线n垂直。
线面垂直与面面垂直垂直练习题精编版

线面垂直和而而垂直线面垂直专题练习一、定理填空:1.直线和平面垂直如果一条直线和_______________________________ ,就说这条直线和这个平面垂直.2.线面垂直判定定理和性质定理线面垂直判定定理:如果一条直线和一个平面内的两条相交宜线都垂直,那么这条直线垂直于这个平面.判定定理1:如果两条平行线中的一条垂直于一个平面,那么 ________________________ 判定定理2:如果一条直线垂宜于两个平行平面中的一个平面,那么___________________ 线面垂直性质定理:垂直于同一个平面的两条直线互相平行.性质定理1:垂直于同一条直线的两个平面互相平行。
二、精选习题:1•设"表示平面,b表示直线,给出下列四个命题:其中正确的命题是()A.①②B. ③C.②®®D.①②④2 •如图所示,在正方形初G?中,E、F分别是/识腮的中点•现在沿加、DF反EF吧HADE、△妙和△财折起,使小B、C三点重合,重合后的点记为*那么,在四面体—妙中, 必有()丄平面P£F 丄平面PEF丄平面妙丄平面财3•设日、6是异面直线,下列命題正确的是()A.过不在爪6上的一点"一定可以作一条直线和臼、b都相交B.过不在业b上的一点P—定可以作一个平面和日、b都垂直a IIba丄MUM"丄M"丄〃b//Ma//Ma丄b=> b 丄J/ 1二>〃丄M=> 6/ // hC.过日一定可以作一个平面与方垂直D.过日一定可以作一个平面与方平行4•如果克线人刃与平面a t P , Y满足:7=0 A Y . 7/7 a ,/^c a和刃丄Y ■那么必有 ( )A. a丄Y且1— B・a丄Y且m// P 〃卩且I— D.a〃B且a丄Y5.有三个命题:①垂直于同一个平面的两条直线平行;②过平面a的一条斜线/有且仅有一个平面与a垂直;③异面直线日、b不垂克,那么过臼的任一个平面与b都不垂直其中正确命题的个数为() .1 C6.设人刃为直线,a为平面,且/丄a ,给出下列命题① 若田丄a .则m// 7;②若刃丄7,则m// a ;③若m// a ,则刃丄7;④若m// /,则〃/丄a ,其中真命题的序号是 ()• • •A.①②③B.①②④C.②③④D. ®@®7•如图所示■三棱锥IT%中M〃丄侧面仏c且〃是△阴c的垂心,处是心边上的高.求证:VCLABx8•如图所示,丹丄矩形個Q?所在平面,M、N分别是泅、PC的(1)求证:MN//平面丹〃(2)求证:J側丄6Z2(3)若Z™=45°,求证:#V±平面尸仞・9•已知克三棱柱ABC-A^Cx中,ZJ€^90°亿^30°•於1, JJ I=A/6,J/是%的中点,求证:AB\LA\M.10•如图所示,正方体ABCD-A f B f C 〃的棱长为z "是旳9的中点,川是別/上一点, 且〃艸:NB=\: 2,必与加交于*(1)求证:AP丄平面ABCD.(2)求平面”忆与平面力D f〃所成的角.11.如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直二解:已知3〃乩a丄a •求证:b丄a •12.已知点P为平面ABC外一点,PA丄BC, PC丄AB,求证:PB丄AC.13.在正方体ABCD—AiBiCiDi中,求直线A)B和平面ARCD所成的角.14•如图,四面体A—BCD的棱长都相等,Q是AD的中点,求CQ与平面DBC所成的角的正弦15•如图11(1),在直四棱柱ABCD—ADGD冲, 已知DC二DD L2AD二2AB, AD丄DC, AB〃DC・(1)求证:DiCXACi;(2)设E是DC上一点,试确定E的位置,使BE〃平面ABD,并说明理由.16•如图12,在正方体ABCD—A I B.C I D B G为CG的中点, 0为底面ABCD的中心.求证:儿0丄平面GBD.4G17 •如图,已知a. b是两条相互垂直的异面直线,线段AB与两异面直线a. b垂直且相交,线段AB的长为定值叫定长为n (n>m)的线段PQ的两个端点分别在纭b上移动,N分别是AB、PQ的中点.求证:(1) AB丄M7;(2) MN的长是定值.18.如图,已知在侧棱垂直于底面三棱柱ABC-AiBiCi中.AC=3, AB=5> BC=4,AA F4.点 D 是AB 的中点.(1)求证:AC丄BG;(2)求证:AG〃平面CDBh面面垂直专题练习一.定理填空面面垂直的判定定理: _________________________________________________________面面垂直的性质定理: _________________________________________________________二、精选习题1、正方形ABCD沿对角线AC折成直二面角后,AB与CD所成的角等于 ____________2、三棱锥P-ABC的三条侧棱相等,则点P在平面ABC上的射影是AABC的一一心.3、一条直线与两个平面所成角相等,那么这两个平面的位置关系为■4、在正三棱锥中,相邻两面所成二面角的取值范围为 ____________________5、已知a-l-0是直二面角,,设直线AB与&成30角,AB二2, B到A在/上的射影7的距离为则AB与0所成角为6、在直二面角a-AB-0棱AB上取一点P,过P分别在z/7平面内作与棱成45°角的斜线PC、PD,则ZCPD的大小是 ________________7、正四面体中相邻两侧面所成的二面角的余弦值为 ____________________ •8、如图,在正方体ABCD-AiBiCiDi中.求证:平面ACD】丄平面BBDD10、如图,三棱锥P-ABC 中,PA 丄平面ABC, AC 丄BC,求证:平面PAC 丄平面PBC.11、如图,三棱锥P-ABC 中,PA 丄平面ABC,平面PAC 丄平面PBC •问ZkABC 是否为直角 三角形,若是,请给出证明;若不是,请举出反例.B。
线面垂直判定经典证明题

线面垂直判定经典证明题1.已知:在三角形ABC中,PA垂直于AB和AC。
证明PA垂直于平面ABC。
2.已知:在三角形ABC中,PA垂直于AB,BC垂直于平面PAC。
证明PA垂直于BC。
3.已知:在三棱锥V-ABC中,VA=VC,AB=BC。
证明VB垂直于AC。
4.已知:在正方体ABCD-EFGH中,O为底面ABCD的中心。
证明BD垂直于平面AEGC。
5.已知:在圆O中,AB是直径,PA垂直于AC和AB。
证明BC垂直于平面PAC。
6.已知:在三角形ABC中,AD垂直于BD和DC,AD=BD=CD,∠BAC=60°。
证明BD垂直于平面ADC。
7.已知:在矩形ABCD中,PA垂直于平面ABCD,M和N分别是AB和PC的中点。
1) 证明MN平行于平面PAD。
2) 证明XXX垂直于CD。
3) 若∠PDA=45°,证明MN垂直于平面PCD。
8.已知:在棱形ABCD所在平面外,P满足PA=PC。
证明AC垂直于平面PBD。
9.已知四面体ABCD中,AB=AC,BD=CD,平面ABC垂直于平面BCD,E是棱BC的中点。
1) 证明AE垂直于平面BCD。
2) 证明AD垂直于BC。
10.在三棱锥ABCD中,AB=1,BC=2,BD=AC=3,AD=2.证明AB垂直于平面BCD。
11.在四棱锥S-ABCD中,SD垂直于平面ABCD,底面ABCD是正方形。
证明AC垂直于平面SBD。
12.已知:正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE垂直于平面CDE。
证明AB垂直于平面ADE。
13.在三棱锥P-ABC中,PA、PB、PC两两垂直,H是△XXX的垂心。
证明PH垂直于底面ABC。
14.在正方体ABCD-A1B1C1D1中,证明A1C垂直于平面BC1D1.15.在△ABC所在平面外一点S,SA垂直于平面ABC,平面SAB垂直于平面SBC。
证明AB垂直于BC。
16.在直三棱柱ABC-A1B1C1中,AC=BC=1,∠ACB=90°,AA1=2,D是A1B1的中点。
线面垂直经典例题及练习题-

坐体几许之阳早格格创做1二笔曲,是内的射影,PA( B )(A)沉心 (B) 垂心 (C)内心 (D)中心2.取二个相接仄里的接线仄止的曲线战那二个仄里的位子闭系是( A )(A)皆仄止 (B) 皆相接(C) 正在二个仄里内 (D)起码取其中一个仄止3.若二个仄里内分别有一条曲线,那二条曲线互相仄止,那么那二仄里的位子闭系是( A )(A)仄止 (B) 相接 (C)仄止或者相接 (D)笔曲4.正在空间,下述命题精确的是( B )(A)(B)(C)(D)5中过失的是(A)存留唯一的仄里距仄里,,则取仄里的位子闭系是(D )D ) 以上三种情况均有大概7精确的是(D )(A)①②(B)②④ (C)③④(D)①③8.是四个分歧的仄里,且B )(C) 四个仄里中大概任性二个皆没有服止 (D) 四个仄里中至多有一对于仄里仄止9( D )(A) (B)(C) (D)10.已知正圆形地圆仄里,垂脚为,连C )(A)5对于 (B)6对于 (C)7对于(D) 8对于12.如图9-29,PA ⊥仄里ABCD ,ABCD 是矩形,M 、N 分别是AB 、PC 的中面.供证:MN ⊥AB .13. 已知:如图,AS ⊥仄里SBC ,SO⊥仄里ABC 于O ,供证:AO ⊥BC .15.已知如图,P ∉仄里ABC ,PA=PB=PC ,∠APB=∠APC=60°,∠BPC=90°供证:仄里ABC ⊥仄里PBC16. 如图:正在斜边为AB 的R t △ABC 中,过面A 做PA ⊥仄里ABC ,AE ⊥PB 于E ,AF⊥PC 于F ,(1)供证:BC ⊥仄里PAC ;(2)供证:PB ⊥仄里AEF. 17. 如图:PA ⊥仄里PBC ,AB =AC ,M 是BC 的中面,供证:BC ⊥PM.如图,正在正三棱柱111C B A ABC -.中,底里ABC 为正三角形,M 、N 、G 分别是棱CC 1、C F E PBAC B A M PAB、BC的中面.且ACCC2.1(Ⅰ)供证:CN//仄里AMB1;(Ⅱ)供证:仄里AMG.。
线面垂直练习题及答案

线面垂直练习题及答案线面垂直是几何学中的一项基本概念,用于描述线段、射线、直线和平面之间的垂直关系。
理解线面垂直的概念对于解决几何问题至关重要。
本文将为读者提供一些线面垂直练习题及答案,帮助读者巩固对该概念的理解。
练习题一:1. AB为一条线段,m是一平面。
如果AB与m垂直,判断下列命题的真假:a) 线段AB垂直于平面mb) 平面m垂直于线段ABc) 线段AB平行于平面m2. P是平面XYZ的内点,AP的延长线与平面XYZ有几个交点?练习题二:1. 给出下列命题的定义:a) 垂线b) 垂直平分线c) 垂直平面2. 在平面上画一条线段AB和一条直线l,求证:若线段AB与直线l垂直,则直线l过点A和点B的垂直平分线。
1. 已知直线l与平面P垂直,直线m过l上一点,那么直线m与平面P的关系是什么?2. 在长方形ABCD中,线段AC和线段BD相交于点O。
求证:线段AC与平面ABCD垂直。
答案及解析:练习题一:1. a) 假,线段AB无法垂直于平面m,因为线段只有两个端点而不是无限延伸。
b) 真,平面m可以垂直于线段AB。
c) 假,线段和平面不可能平行。
2. AP的延长线与平面XYZ有且只有一个交点。
练习题二:1. a) 垂线是与给定线段或直线垂直的线段或直线。
b) 垂直平分线是将给定线段或直线垂直平分的线段或直线。
c) 垂直平面是与给定平面垂直的平面。
2. 假设直线l过点A和点B的垂直平分线交线段AB于点M,则根据垂直平分线的定义,我们可以得出线段AM和线段BM的长度相等,且直线l与线段AM和线段BM都垂直。
1. 直线m与平面P平行。
2. 连接线段AC的中点和线段BD的中点,设为点O'。
根据长方形的性质,线段OO'相等且垂直于两个平行线段AC和BD。
因此,线段OO'垂直于平面ABCD,而线段OO'与线段AC相等,所以线段AC与平面ABCD垂直。
通过以上练习题及答案,我们可以加深对线面垂直概念的理解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何
1.P 点在则ABC ∆所在的平面外,O 点是P 点在平面ABC 内的射影 ,PA 、PB 、PC 两
两垂直,则D 点是则ABC ∆ ( B )
(A)重心 (B) 垂心 (C)内心 (D)外心
2.与两个相交平面的交线平行的直线和这两个平面的位置关系是 ( A )
(A)都平行 (B) 都相交
(C) 在两个平面内 (D)至少与其中一个平行
3.若两个平面内分别有一条直线,这两条直线互相平行,那么这两平面的位置关系是( A )
(A)平行 (B) 相交 (C)平行或相交 (D)垂直
4.在空间,下述命题正确的是 ( B )
(A)若直线//a 平面M ,直线b a ⊥,则直线⊥b 平面M
(B)若平面M //平面N ,则平面M 内任意直线a //平面N
(C)若平面M 与N 的交线为a ,平面M 内的直线a b ⊥,则N b ⊥
(D)若平面N 的两条直线都平行平面M ,则平面N //平面M
5.a 、b 表示两条直线,α、β、γ表示三个平面,下列命题中错误的是 (A )
(A),,αα⊂⊂b a 且ββ//,//b a ,则βα// (B)a 、b 是异面直线,则存在唯一的平面与a 、
b 等距 (C) ,,,b a b a ⊥⊂⊥βα则βα// (D),,,//,βαβγγα⊥⊥⊥b a 则b a ⊥
6.直线l //平面α,αβ⊥,则l 与平面β的位置关系是 ( D )
(A) l β⊂ (B) //l β (C) l β与相交 (D ) 以上三种情况均有可能
7.已知直线l ⊥平面α,直线m ⊂平面β,有以下四个命题:①//l m αβ⇒⊥②
//l m αβ⊥⇒③//l m αβ⇒⊥④//l m αβ⊥⇒,其中正确的是(D )
(A) ①② (B) ②④ (C) ③④ (D) ①③
8.αβγδ,,,是四个不同的平面,且αγβγαδβδ⊥⊥⊥⊥,,,,则( B )
(A) ////αβγδ或 (B) ////αβγδ且
(C) 四个平面中可能任意两个都不平行 (D) 四个平面中至多有一对平面平行
9.已知平面α和平面β相交,a 是α内的一条直线,则( D )
(A) 在β内一定存在与a 平行的直线 (B) 在β内一定存在与a 垂直的直线
(C) 在β内一定不存在与a 平行的直线 (D) 在β内一定不存在与a 垂直的直线
10.已知PA ⊥正方形ABCD 所在平面,垂足为A ,连PB PC PD AC BD ,,、,,则互
相垂直的平面有( C )
(A) 5对 (B) 6对 (C) 7对 (D) 8对
12. 如图9-29,P A ⊥平面ABCD ,ABCD 是矩形,M 、N 分别是AB 、PC 的中点. 求证:MN ⊥AB .
13. 已知:如图,AS ⊥平面SBC ,SO ⊥平面ABC 于O ,
求证:AO ⊥BC .
15. 已知如图,P 平面ABC ,PA=PB=PC ,∠APB=∠APC=60°,∠BPC=90 °求证:平面ABC ⊥平面PBC
16. 如图:在斜边为AB 的R t △ABC 中,过点A 作PA ⊥平面ABC ,AE ⊥PB 于E ,AF ⊥PC 于F ,(1)求证:BC ⊥平面PAC ;(2)求证:PB ⊥平面AEF.
17. 如图:PA ⊥平面PBC ,AB =AC ,M 是BC 的中点,求证:BC ⊥PM.
C
F E P
B A
C B A M
P
如图,在正三棱柱111C B A ABC -.中,底面ABC 为正三角形,M 、N 、G 分别是棱CC 1、AB 、BC 的中点.且AC CC 21=.
(Ⅰ)求证:CN //平面 AMB 1; (Ⅱ)求证:平面AMG .
最新文件
仅供参考 已改成word 文本 。
方便更改。
