采样控制系统2

合集下载

计算机控制系统第2章(第3次课最少拍)

2 1 1 T z (1 z ) 2 2 1 2 2 3 2 4 2 5 (2 z z ) T z 3.5 T z 7 T z 11.5 T z 1 3 2(1 z )
各个采样时刻的输出序列为：
y(0) 0, y(T ) 0, y(2T ) T 2 , y(3T ) 3.5T 2 , y(4T ) 7T 2 ,
2.3.2 最少拍(dead-beat)控制系统设计
需求与问题
• 经历最少的采样周期（最短的时间），使输出达到参考值。
解决的基本思路
• 使E(z)有限项（以z-1多次幂的多项式为有限项），且项数越少越好。 • D(z)满足物理可实现性 • 闭环系统稳定性
2.3.2 最少拍控制系统设计
最少拍（有限拍）控制是一种时间最优控制方式。设计目标：设计一个数字控制器D(z)，使系统在典型输入信号r(t)作用下，经过最少的采样周期，消除输出和输入之间的偏差，达到平衡。通常把一个采样周期称为一拍。设计准则：1）单位阶跃输入
1 z
各采样时刻输出序列为：
2 z 1 z 2 z 3 z 4
y(0) 0, y(T ) 2, y(2T ) 1, y(3T ) 1,
系统的输出响应曲线如图2-16(a)所示。
（2）单位加速度输入
Y ( z) Gc ( z) R( z )
而输入序列 y(0) 0, y(T ) 0.5T 2 , y(2T ) 2T 2 , y(3T ) 4.5T 2 , y(4T ) 8T 2 , 系统的输入和输出响应曲线如图2-16(b)所示。
最少拍控制器中的最少拍是针对某一典型输入设计的，对于其它典型输入则不一定为最少拍，甚至引起大的超调和静差。

现代控制技术基础习题集和答案解析

《现代控制技术基础》一、单选题1. 自动控制系统按输入量变化与否来分类，可分为（ A ）A 、随动系统与自动调整系统B 、线性系统与非线性系统C 、连续系统与离散系统D 、单输入－单输出系统与多输入－多输出系统2. 自动控制系统按系统中信号的特点来分类，可分为（ C ）A 、随动系统与自动调整系统B 、线性系统与非线性系统C 、连续系统与离散系统D 、单输入－单输出系统与多输入－多输出系统3. 普通机床的自动加工过程是（ C ）A 、闭环控制B 、伺服控制C 、开环控制D 、离散控制4. 形成反馈的测量元器件的精度对闭环控制系统的精度影响（ B）A 、等于零B 、很大C 、很小D 、可以忽略5. 自动控制系统需要分析的问题主要有（ A ）A 、稳定性、稳态响应、暂态响应B 、很大C 、很小D 、可以忽略6. 对积分环节进行比例负反馈，则变为（ D ）A 、比例环节B 、微分环节C 、比例积分环节D 、惯性环节7. 惯性环节的传递函数是（ A ）A 、1)(+=Ts Ks G B 、K s G =)(C 、Ts s G 1)(= D 、Ts s G =)(8. 比例环节的传递函数是（ B ）A 、1)(+=Ts Ks G B 、K s G =)(C 、Ts s G 1)(= D 、Ts s G =)(9. 微分环节的传递函数是（ D ）A 、1)(+=Ts Ks G B 、K s G =)(C 、Ts s G 1)(=D 、Ts s G =)(10. 积分环节的传递函数是（ C ）A 、1)(+=Ts K s G B 、K s G =)( C 、Ts s G 1)(= D 、Ts s G =)(11. 对于物理可实现系统，传递函数分子最高阶次m 与分母最高阶次n 应保持（ C ）A 、n m <B 、n m >C 、n m ≤D 、n m ≥12. f （t ）=0.5t +1，则L [f （t ）]=（ B ）A 、s s 15.02+ B 、s s 1212+C 、25.0sD 、s s +22113. f （t ）=2t +1，则L [f （t ）]=（ B ）A 、s s 122+B 、s s 122+C 、22sD 、s s +22114. 通常把反馈信号与偏差信号的拉普拉斯变换式之比，定义为（ C ）A 、闭环传递函数B 、前向通道传递函数C 、开环传递函数D 、误差传递函数15. 在闭环控制中，把从系统输入到系统输出的传递函数称为（ A ）A 、闭环传递函数B 、前向通道传递函数C 、开环传递函数D 、误差传递函数16. 单位脉冲信号的拉氏变换为（ B ）A 、L [1(t )]=1/sB 、L [δ(t )]=1C 、L [t •1(t )]=1/s 2D 、L [t 2/2]=1/s 317. 单位阶跃信号的拉氏变换为（ A ）A 、L [1(t )]=1/sB 、L [δ(t )]=1C 、L [t •1(t )]=1/s 2D 、L [t 2/2]=1/s 318. 单位斜坡信号的拉氏变换为（ C ）A 、L [1(t )]=1/sB 、L [δ(t )]=1C 、L [t •1(t )]=1/s 2D 、L [t 2/2]=1/s 319. 对于稳定的系统，时间响应中的暂态分量随时间增长趋于（ D ）A 、1B 、无穷大C 、稳态值D 、零20. 当稳定系统达到稳态后，稳态响应的期望值与实际值之间的误差，称为（B ）A 、扰动误差B 、稳态误差C 、暂态误差D 、给定偏差21. 对一阶系统的单位阶跃响应，当误差范围取2％时，调整时间为（ A ）A 、t s =4τB 、t s =3τC 、t s =2τD 、t s =τ22. 对一阶系统的单位阶跃响应，当误差范围取5％时，调整时间为（ B ）A 、t s =4τB 、t s =3τC 、t s =2τD 、t s =τ23. 根据线性定常系统稳定的充要条件，必须全部位于s 平面左半部的为系统全部的（ C ）A 、零点B 、临界点C 、极点D 、零点和极点24. 对二阶系统当10<<ξ时，其为（ B ）A 、过阻尼系统B 、欠阻尼系统C 、零阻尼系统D 、临界阻尼系统25. 根据劳斯稳定判据，系统具有正实部极点的个数应等于劳斯表中第1列元素（A ） A 、符号改变的次数B 、为负值的个数C 、为正值的个数D 、为零的次数26. 根据劳斯稳定判据，系统具有正实部极点的个数应等于劳斯表中第1列元素（B ） A 、符号改变的次数 B 、为负值的个数C 、为正值的个数D 、为零的次数27. 典型二阶系统的开环传递函数为（ C ）A 、阻尼振荡角频率B 、阻尼特性C 、时间常数D 、无阻尼固有频率28. 时间常数T 的大小反映了一阶系统的（ A ）A 、惯性的大小B 、输入量的大小C 、输出量的大小D 、准确性29. 典型二阶系统的特征方程为（ C ）A 、022=+s s n ξωB 、0222=++n n s ωξωC 、0222=++n n s s ωξωD 、022=++n n s s ωξω30. 调整时间t s 表示系统暂态响应持续的时间，从总体上反映系统的（ C ）A 、稳态误差B 、瞬态过程的平稳性C 、快速性D 、阻尼特性31. 伯德图低频段渐近线是34dB 的水平直线，传递函数是（ A ）A 、1250+sB 、5500+sC 、s 50D 、225s32. 过40=c ω且斜率为-20dB/dec 的频率特性是（ C ）A 、4040+ωj B 、)40(40+ωωj jC 、)101.0(40+ωωj jD 、)101.0(402+-ωωj33. 在ω＝10 rad/s 处，相角滞后90° 的传递函数是（ D ）A 、1020+s B 、20500+sC 、11010502++s sD 、11.001.0502++s s34. 放大器的对数增益为14dB ，其增益K 为（ B ）A 、2B 、5C 、10D 、5035. 过40=c ω且斜率为-40dB/dec 的频率特性是（ D ）A 、4040+ωj B 、)40(40+ωωj jC 、)101.0(40+ωωj jD 、)101.0(16002+-ωωj36. 下列传递函数中不是．．最小相位系统的是（ C ）A 、1020+s B 、20500+-sC 、156502--s sD 、451502+++s s s37. 伯德图低频段渐近线是20dB 的水平直线，传递函数是（ D）A 、12100+sB 、5500+sC 、250+s D 、110+s38. 在ω＝20 rad/s 处，相角滞后45° 的传递函数是（ B ）A 、1220+sB 、20500+sC 、12050+s D 、110+s39. 系统的截止频率愈大，则（ B ）A 、对高频噪声滤除性能愈好B 、上升时间愈小C 、快速性愈差D 、稳态误差愈小40. 进行频率特性分析时，对系统的输入信号为（ B ）A 、阶跃信号B 、正弦信号C 、脉冲信号D 、速度信号41. 积分环节的相角为（ A ）A 、-90ºB 、90ºC 、-180ºD 、180º42. 系统开环奈氏曲线与负实轴相交时的频率称为（ B ）A 、幅值交界频率B 、相位交界频率C 、幅值裕量D 、相位裕量43. 在具有相同幅频特性的情况下，相角变化范围最小的是（ C ）A 、快速响应系统B 、非最小相位系统C 、最小相位系统D 、高精度控制系统44. 微分环节的相角为（ B ）A 、-90ºB 、90ºC 、-180ºD 、180º45. 系统开环奈氏曲线与单位圆相交时的频率称为（ A ）A 、幅值交界频率B 、相位交界频率C 、幅值裕量D 、相位裕量46. 串联校正装置11)(21++=sT s T s G c ，若其为滞后校正，则应该（ B ）A 、T 1>T 2B 、T 1<T 2C 、T 1=T 2D 、T 1≠T 247. 若在系统的前向通路上串联比例－微分（PD ）校正装置，可使（ A） A 、相位超前 B 、相位滞后C 、相位不变D 、快速性变差48. 硬反馈指的是反馈校正装置的主体是（ C ）A 、积分环节B 、惯性环节C 、比例环节D 、微分环节49. 串联校正装置11)(21++=s T s T s G c ，若其为超前校正，则应该（ B ）A 、T 1>T 2B 、T 1<T 2C 、T 1=T 2D 、T 1≠T 250. 若在系统的前向通路上串联比例－积分（PI ）校正装置，可使（ B ）A 、相位超前B 、相位滞后C 、相位不变D 、快速性变好51. 软反馈指的是反馈校正装置的主体是（ D ）A 、积分环节B 、惯性环节C 、比例环节D 、微分环节52. 校正装置的传递函数是101.011.0++s s ，该校正是（ A ） A 、比例微分校正 B 、近似比例积分校正C 、比例积分校正D 、比例积分微分校正53. 比例－积分（PI ）校正能够改善系统的（ C ）A 、快速性B 、动态性能C 、稳态性能D 、相对稳定性54. 硬反馈在系统的动态和稳态过程中都起（ D ）A 、超前校正作用B 、滞后校正作用C 、滞后－超前校正作用D 、反馈校正作用55. PD 校正器又称为（ B ）A 、比例－积分校正B 、比例－微分校正C 、微分－积分校正D 、比例－微分－积分校正56. 闭环采样系统的稳定的充分必要条件为：系统特征方程的所有根均在Z 平面的（ D ）A 、左半平面B 、右半平面C 、单位圆外D 、单位圆内57. 采样控制系统中增加的特殊部件是（ A ）A 、采样开关和采样信号保持器B 、采样开关和模数转换器C 、采样信号保持器和数模转换器D 、采样开关和信号发生器58. 采样系统的闭环脉冲传递函数的极点位于单位圆内的正实轴上，则其暂态分量（ B ）A 、为衰减振荡函数B 、按指数规律衰减C 、是发散的D 、衰减越慢59. 单位阶跃函数的Z 变换是（ C ）A 、1B 、z 1C 、1-z zD 、zz 1- 60. 采样信号保持器的作用是将采样信号恢复为（ A ）A 、连续信号B 、离散信号C 、输出信号D 、偏差信号61. 采样系统的闭环脉冲传递函数的极点位于单位圆内的负实轴上，则其暂态分量（ A ）A 、为衰减振荡函数B 、按指数规律衰减C 、是发散的D 、衰减越慢62. 单位脉冲函数的Z 变换是（ A ）A 、1B 、z 1C 、1-z zD 、zz 1- 63. 采样控制系统的闭环脉冲传递函数的极点距z 平面坐标原点越近，则衰减速度（ B ）A 、越慢B 、越快C 、变化越慢D 、变化越快64. 为了使采样控制系统具有比较满意的暂态响应性能，闭环极点最好分布在（ D ）A 、单位圆外的左半部B 、单位圆外的右半部C 、单位圆内的左半部D 、单位圆内的右半部65. 在工程实际中，为了保证采样过程有足够的精确度，常取ωs 为（ C ）A 、2～4ωmaxB 、3～5ωmaxC 、5～10ωmaxD 、8～12ωmax66. 状态变量描述法不仅能反映系统输入和输出的关系，而且还能提供系统（ D ）A 、全部变量的信息B 、外部各个变量的信息C 、线性关系D 、内部各个变量的信息67. 能观标准型的系统矩阵是能控标准型系统矩阵的（ C ）A 、对称矩阵B 、逆阵C 、转置D 、单位阵68. 约当标准型的系统矩阵是对角线阵，对角线元素依次为（ C ）A 、零点B 、开环极点C 、系统特征根D 、各部分分式的系数69. 在现代控制理论中采用的状态变量描述法，又称为（ D ）A 、全部变量描述法B 、外部描述法C 、线性描述法D 、内部描述法70. 能观标准型的控制矩阵是能控标准型输出矩阵的（ C ）A 、对称矩阵B 、逆阵C 、转置D 、单位阵71. 线性定常系统状态能控的充分必要条件是，其能控性矩阵的（ B ）A 、行数为nB 、秩为nC 、列数为nD 、行列式值为n72. 系统状态变量的个数等于系统（ C ）A 、全部变量的个数B 、外部变量的个数C 、独立变量的个数D 、内部变量的个数73. 能观标准型的输出矩阵是能控标准型控制矩阵的（ C ）A 、对称矩阵B 、逆阵C 、转置D 、单位阵74. 线性定常系统状态完全能观的充分和必要条件是，其能观性矩阵的（ B ）A 、行数为nB 、秩为nC 、列数为nD 、行列式值为n75. 一个状态变量为n 维的单输入，单输出系统，下面说法正确的是（ A ）A 、系数阵A 为n ×n 维B 、控制阵B 为1×n 维C 、输出阵C 为n ×1维D 、A ，B ，C 三个阵均为n ×n 维二、计算题76. 求如图所示系统的微分方程，图中x(t)为输入位移，y(t)为输出位移。

计算机控制技术复习资料

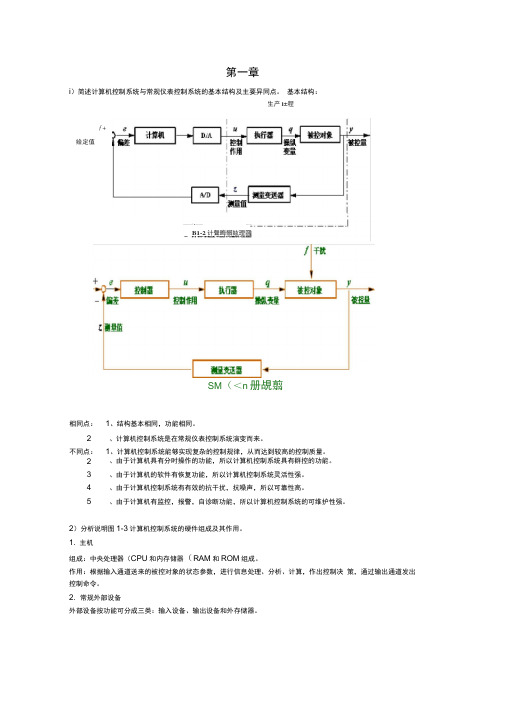
第一章i ）简述计算机控制系统与常规仪表控制系统的基本结构及主要异同点。

基本结构：SM （＜n 册覘翦相同点： 1、结构基本相同，功能相同。

2不同点：、计算机控制系统是在常规仪表控制系统演变而来。

1、计算机控制系统能够实现复杂的控制规律，从而达到较高的控制质量。

23 45、由于计算机具有分时操作的功能，所以计算机控制系统具有群控的功能。

、由于计算机的软件有恢复功能，所以计算机控制系统灵活性强。

、由于计算机控制系统有有效的抗干扰，抗噪声，所以可靠性高。

、由于计算机有监控，报警，自诊断功能，所以计算机控制系统的可维护性强。

2）分析说明图1-3计算机控制系统的硬件组成及其作用。

1. 主机组成：中央处理器（CPU 和内存储器（RAM 和ROM 组成。

作用：根据输入通道送来的被控对象的状态参数，进行信息处理、分析、计算，作出控制决策，通过输出通道发出控制命令。

2. 常规外部设备外部设备按功能可分成三类：输入设备、输出设备和外存储器。

生产i±程f +给定值———-—1 ■ -——— -—-—B1-2计聲晦髒絃理區输入设备有键盘、光电输入机、扫描仪等，用来输入程序、数据和操作命令。

输出设备有打印机、绘图机、显示器等，用来把各种信息和数据提供给操作者。

外存储器有磁盘装置、磁带装置、光驱装置，兼有输入、输出两种功能，用来存储系统程序和数据。

3. 过程输入/输出通道过程输入通道又分为模拟量输入通道和数字量输入通道两种；过程输出通道又分为模拟量输出通道和数字量输出通道两种。

作用：主机和被控对象实现信息传送与交换的通道。

4. 操作台操作台是操作员与计算机控制系统之间进行联系的纽带，可以完成向计算机输入程序、修改数据、显示参数以及发出各种操作命令等功能。

5. 通信设备在不同地理位置、不同功能的计算机之间通过通信设备连接成网络，以进行信息交换。

第二章1）课本14页的图2-2 以4位D/A 转换器为例说明其工作原理R--2R 电阻网络假设D3 D2、Di 、D0全为1,贝U B 图33-2BS 公转S1器原S0全部与“ 1 ”端相连。

控制工程基础-计算机采样控制系统(2)

11
脉冲传递函数（10）
1.有采样开关分隔的两个环节串联时，其脉冲传递函数等于各环节的脉冲传递函数之积。
X (z) G1(z) R(z)
C(z) G2 (z) X (z)
将X(z)代入C(z) C(z) G2 (z)G1zRz
Cz Rz
G1
z
G2
z
2.没有采样开关分隔的两环节串联时，其脉冲传递函数为各个
2021/2/20
第九章计算机采样控制系统
15
脉冲传递函数（14）
令
G' p s Gp ss
并根据前面介绍的环节串、并联脉冲传递函数求取方法，参照上图
，则带保持器的广义控制对象脉冲传递函数
Gz
C1
z C2 U z
z
G1z
G2
z
G1z
C1 z U z
Z
Gp' s
Z
g p' t
G2z
1 G1H (z)
闭环传递函数 (z) 的推导步骤：
1) 在主通道上建立输出 C(z)与中间变量 E(z)的关系；
2) 在闭环回路中建立中间变量 E(z) 与输入 R(z) 的关系；
3) 消去中间变量 E(z)，建立C(z) 和 R(z) 的关系。
2021/2/20
第九章计算机采样控制系统
21
脉冲传递函数（20）
Gz ZGs
即符号 ZGs、ZL1Gs 和 Z g*(t) 、 ZgkT 是等价的。
Gz Zg*(t) ZgkT ZL1Gs ZGS
2021/2/20
第九章计算机采样控制系统
7
脉冲传递函数（6）
如果系统的输入为任意函数的采样脉冲序列 r(kT) ，其Z变换

6_离散控制系统(2)

19
Z变换
解： E * ( s ) = ∑ e( kT )e − kTs = 1 + e −Ts + e − 2Ts +
k =0 ∞
E * ( s ) = ∑ e( kT )e − kTs
k =0
∞
例1：设e(t)=1(t)，试求e*(t)的拉氏变换。
= 1 , − Ts 1− e e −Ts < 1
给定值 + 反馈信号
扰动
-
A/D
数字计算机控制器
D/A
执行元件
对象
测量元件
2
线性定常连续控制系统：微分方程、传递函数； r(t) e(t)
控制器
u(t)
执行元件被控对象
c(t)
b(t)
检测元件
采样控制系统：差分方程、脉冲传递函数；连续信号
r(t) b(t) 测量元件
3
离散信号
采样开关 e*(t)
k =0
∞ k =0
20
∞
x*(t)的z变换记为Z[x*(t)]， Z (x* ( t )) = X ( z ) = ∑ x( kT ) z − k
Z变换
1、定义法(级数求和法)
知道连续函数x(t)在各采样时刻的离散值x*(t)，按定义求。例2：求 x1 ( t ) = u( t ) 和 x 2 ( t ) = ∑ δ ( t − kT ) 的z变换表达式。解： X ( z ) = x ( kT ) z − k = 1 + z −1 + z − 2 + ∑ 1
零阶保持器的频率特征
eh ( s ) 1 − e − Ts = = Gh ( s ) * e ( s) s

自动控制原理(二)

离散系统闭环脉冲传递函数的极点，则动态响应为（已知，则有的拉氏变换为，则判断题图中系统是否稳定非线性系统的及的轨迹如下图所示，试问）已知非线性系统的微分方程是,两输入，两输出的系统，其模拟结构图如图所示，其状态空间表达式为：（）B.C.已知系统传递函数,则系统的约旦标准型的实现为∙B.∙C.D.∙A.∙B.∙C.∙D.正确答案：B19已知系统：已知，下列有关该系统稳定性说法正确的是（）闭环脉冲传递函数分别为，输出为已知计算机控制系统如下图所示，采用数字比例控制，其中，,系统的闭环脉冲传递函数为的取值范围是系统的开环脉冲传递函数为的取值范围是已知，，。

符合系统描述的系统稳定系统稳定系统的闭环脉冲传递函数设离散系统如图所示，设，时，若要求其稳态误差,，该系统的闭环脉冲传递函数为该系统的开环脉冲传递函数为对于响应斜坡输入信号统（取F(z)=1），下列选项正确的是（）变换为数字控制器的脉冲传递函数为变换为变换为非线性系统的及的轨迹如下图所示，以下说法正确的是求下图中以电压为输入量，以电感中的电流和电容上的电压作为状态变量的状态方程为___，以电阻上的电压作为输出量的输出方程为___。

（）∙A.∙B.∙C.D.现用进行状态变换B.C.D.已知系统的传递函数为B. C.对线性系统作状态反馈 , A.某离散控制系统（单位反馈该系统稳态误差为代表时域中的延迟算子系统状态空间表达式中，若离散控制系统（单位反馈，则动态响应为的拉氏变换为，A.C.下图所示为某一闭环离散系统，则该系统的脉冲传递函数为（）离散系统闭环脉冲传递函数的极点,的的拉氏变换为，则。

新版自动控制理论实验课程教学大纲.答案

《自动控制理论》实验教学大纲课程名称：自动控制理论课程性质：非独立设课使用教材：自编课程编号：面向专业：自动化课程学分：考核方法：成绩是考核学习效果的重要手段，实验成绩按学生的实验态度，独立动手能力和实验报告综合评定，以20%的比例计入本门课程的总成绩。

实验课总成绩由平时成绩（20%）、实验理论考试成绩（40%）、实验操作考试成绩（40%）三部分组成，满分为100分。

实验理论考试内容包含实验原理、实验操作方法、实验现象解析、实验结果评价、实验方案设计等。

考试题型以填空、判断、选择、问答为主，同时可结合课程特点设计其他题型。

实验操作考试根据课程特点设计若干个考试内容，由学生抽签定题。

平时成绩考核满分为20分，平时成绩= 平时各次实验得分总和÷实验次数（≤20分）。

每次实验得分计算办法为：实验报告满分10分（其中未交实验报告或不合格者0分，合格6分，良好8分，优秀10分）；实验操作满分10分（其中旷课或不合格者0分，合格6分，良好8分，优秀10分）。

撰写人：任鸟飞审核人：胡皓课程简介：自动控制理论是电气工程及其自动化专业最主要的专业基础必修课。

通过本课程的各个教学环节的实践，要求学生能熟练利用模拟电路搭建需要的控制系统、熟练使用虚拟示波器测试系统的各项性能指标，并能根据性能指标的变化分析参数对系统的影响。

实验过程中要求学生熟悉自动控制理论中相关的知识点，可以在教师预设的实验前提下自己设计实验方案，完成实验任务。

教学大纲要求总学时80，其中理论教学68学时、实验12学时，实验个数6个。

9采样控制系统的分析√4选做10采样控制系统的动态校正√4选做合计实验一典型环节的电路模拟一、实验类型：综合性实验二、实验目的：1.熟悉THBCC-1型实验平台及“THBCC-1”软件的使用；2.熟悉各典型环节的阶跃响应特性及其电路模拟；3.测量各典型环节的阶跃响应曲线，并了解参数变化对其动态特性的影响。

三、实验内容与要求：1.设计并组建各典型环节的模拟电路；2.测量各典型环节的阶跃响应，并研究参数变化对其输出响应的影响；3.画出各典型环节的实验电路图，并注明参数。

计算机控制系统复习要点

计算机控制系统复习要点计算机控制系统复习要点第一章自动控制系统：被控对象检测传感装置控制器控制器：模拟控制器数字控制器（计算机实现）计算机控制系统：采用了数字控制器的自动控制系统包括计算机（硬件软件和网络）和生产过程（被控对象检测传感器执行机构）文档收集自网络，仅用于个人学习计算机控制系统执行控制程序过程：实时数据采集实时计算实时控制实时管理计算机控制系统存在两种信号：模拟信号和数字信号需要用离散控制理论对计算机控制系统进行分析和设计计算机控制系统硬件：主机外部设备过程通道生产过程。

1操作指导控制系统（odc）2直接数字控制系统（ddc）：为闭环控制3计算机监督系统（scc）：被控对象给定值可变4集散控制系统(dcs):草果管理功能的集中和控制功能的分散。

5现场总线控制系统（fcs）：1,系统内各设备的信号传输实现了全数字化，提高了信号传输的速度，精度和距离，是系统的可靠性提高；2.实现了控制功能的彻底分散，把控制功能分散到各现场设备和仪表中，使现场设备和仪表成为具有综合功能的只能设备和仪表。

文档收集自网络，仅用于个人学习6工业过程计算机集成制造系统1.2.计算机控制系统性能系统稳定性，能空性，能观性，动态特性及稳态特性。

G（s）：控制通道Km：放大系数Tm：惯性时间常数T:滞后时间常数Gn（s）：扰动通道Kn:放大系数Tn 惯性时间常数T：滞后时间常数控制系统性能采用超调量阿尔法（a%）调节时间ts 稳态误差ess来表示Kn越小，ess越小，控制精度越高Km对性能无影响Tn加大超调量减小Tm越小系统反应越灵敏性能越好Tn对性能无影响。

T使超调量增大ts延长T越大控制性能越差第二章2.1输入输出过程通道概述过程通道起到了cpu和被控对象之间的信息传送和变换的桥梁作用。

过程通道包括：模拟量输入通道模拟量输出通道数字量输入通道数字量输出通道2.2模拟量输入通道（将模拟信号转换为数字信号）普遍采用共用程控放大器和A/D转换器的结构形式主要由：传感器信号调理单元多路转换开关程控放大器采样保持器A/D转换器和I/O 接口电路。

trc控制原理(二)

trc控制原理(二)TRC控制原理什么是TRC控制原理？TRC指的是“Time-Resolved Control”，即时间分辨控制。

它是一种基于时间分辨的控制原理，用于实现精确、快速的控制系统。

TRC 广泛应用于光电子学、物理学、生物医学等领域，是一种重要的技术手段。

TRC控制原理的基本原理TRC控制原理基于时间分辨的观测和控制手段，通过精确测量和控制系统中各个组件的时间响应，从而实现精确的控制效果。

TRC控制原理的基本原理包括以下几个方面：1. 时间参考信号的产生在TRC控制系统中，需要产生一个精确、可靠的时间参考信号作为系统的基准。

这通常通过使用稳定的时钟源和频率计时器实现，以确保系统的时间参考信号具有良好的稳定性和准确性。

2. 信号的时间采样和延迟TRC控制系统需要对所控制的信号进行时间采样和延迟处理。

通过使用高速的采样设备和精确的延迟线路，可以实现对信号的准确采样和精确延迟，从而对系统进行快速响应和精确控制。

3. 信号的时间分析和传输TRC控制系统需要对采样和延迟后的信号进行时间分析和传输。

通过使用高速的信号处理器和可编程逻辑器件，可以对信号进行实时分析和传输，从而实现对系统的实时监测和控制。

4. 控制策略的优化和实现TRC控制系统需要设计和优化合适的控制策略，并通过实验验证和数字仿真等手段进行实现和调试。

通过不断优化控制策略，可以提高系统的控制精度和响应速度，从而满足实际应用的需求。

TRC控制原理的应用领域TRC控制原理具有广泛的应用领域，包括但不限于以下几个方面：1. 光电子学领域TRC控制原理在光电子学领域中被广泛应用于激光器的自适应控制、光学通信系统的优化和调节等方面。

通过精确测量和控制光信号的时间分辨特性，可以实现光信号的精确调节和优化。

2. 物理学研究领域TRC控制原理在物理学研究领域中被广泛应用于粒子加速器的控制、原子核碰撞实验的观测和分析等方面。

通过精确控制和测量粒子的时间分辨特性，可以实现粒子的精确操控和实验数据的准确分析。

自动控制原理第二章课后习题答案(免费)

自动控制原理第二章课后习题答案（免费）离散系统作业注明：*为选做题2-1 试求下列函数的Z 变换（1）()E z L =();n e t a = 解：01()[()]1k k k z E z L e t a z z z aa∞-=====--∑ （2） ();at e t e -= 解：12211()[()][]1...1atakT k aT aT aTaT k z E z L e t L ee z e z e z z e e z∞----------=====+++==--∑2-2 试求下列函数的终值：（1）112();(1)Tz E z z --=-解： 11111()(1)()1lim lim lim t z z Tz f t z E z z---→∞→→=-==∞- （2）2()(0.8)(0.1)z E z z z =--。

解：211(1)()(1)()0(0.8)(0.1)lim lim limt z z z z f t z E z z z →∞→→-=-==-- 2-3* 已知()(())E z L e t =,试证明下列关系成立：（1）[()][];n z L a e t E a =证明：0()()nn E z e nT z∞-==∑00()()()()[()]n n n n n n z z E e nT e nT a z L a e t a a ∞∞--=====∑∑ （2）()[()];dE z L te t TzT dz=-为采样周期。

证明：11100[()]()()()()()()()()()nn n n n n n n n n L te t nT e nT zTz ne nT z dE z de nT z dz dz e nT n zne nT z ∞∞---==∞-=∞∞----======-=-∑∑∑∑∑所以：()[()]dE z L te t Tzdz=- 2-4 试求下图闭环离散系统的脉冲传递函数()z Φ或输出z 变换()C z 。

离散控制系统的基本概念

自动控制原理
注：在理想采样及忽略量化误差情况下，数字控制系统近似于采样控制系统，将它们统称为离散系统。这使得采样控制系统与数字控制系统的分析与校正在理论上统一。
1.1 采样控制系统
一般来说，采样控制系统是对传感器所采集的连续信号在某些规定的时间上取值，然后通过对这些值的比较、计算和输出，来达到控制目标的系统。采样控制系统结构构成：主要由采样器、为连续信号的过程称为信号复现。实
现复现过程的装置称为保持器。
最简单的保持器是零阶保持器，它将脉冲序列 e(t) 复现为阶梯信号 eh (t) 如图1-3所示。
图1-3 信号复现过程
1.2 数字控制系统
数字控制系统是一种以数字计算机为控制器去控制具有连续工作状态的被控对象的闭环控制系统。其原理方框图如图1-4所示。
图1-4 数字控制系统方框图
过程分析：A/D转换器将连续信号转换成数字序列，经数字控制器处理后生成离散控制信号，再通过D/A转换器转换成连续控制信号作用于被控对象。
1.A/D转换器
A/D转换器是把连续的模拟信号转换为离散数字信号的装置。A/D转换包括采样过程和量化过程。
采样过程是每隔 T秒对连续信号 e(t) 进行一次采样，得到采样信号e(t)。
自动控制原理
离散控制系统的基本概念
1.连续系统：如果控制系统中的所有信号都是时间变量的连续函数，也就是说，这些信号在全部时间上都是已知的，则这样的系统称为连续时间系统，简称连续系统。
2.离散系统：如果控制系统中有一处或几处信号是脉冲序列或数码，则这样的系统称为离散时间系统，简称离散系统。
➢ 包括采样控制系统：系统中的离散信号是脉冲序列形式的离散系统，称为采样控制系统或脉冲控制系统。 ➢ 数字控制系统：把数字序列形式的离散系统，称为数字控制系统或计算机控制系统。

自动控制原理第七部分采样系统

稳定性判据
用于判断采样系统的稳定性，如 Nyquist稳定判据和Bode图分析方法。
稳定性分析方法
通过分析采样系统的极点和零点分布、频率响应特性等，评估系统的稳定性。
03
采样系统的性能分析
采样系统的频率响应
频率响应
描述了系统对不同频率输入信号的响应特性，通常用频率特性函数表示。
带宽
指系统能够处理的最高频率，决定了系统处理信号的能力。
只有稳定的系统才能在实际应用中得到有效控制。来自采样系统的动态性能分析
阶跃响应和脉冲响应
描述了系统对阶跃信号和脉冲信号的响应特性。
动态性能的定义
系统对输入信号的响应速度和超调量等动态特性。
动态性能的优化
通过调整系统参数，改善系统的动态性能，以满足实际应用需求。
04
采样系统的设计
采样系统的设计原则
在航空航天控制中的应用
导航与定位
采样系统能够实时采集航空航天器的位置、速度、姿态等数据，通过导航与定位算法，实现航空航天器的精确导航和定位。
姿态控制
采样系统能够实时采集航空航天器的姿态数据，通过姿态控制算法，实现航空航天器的稳定飞行和精确机动。
自主决策
采样系统能够实时采集航空航天器周围的环境信息，通过自主决策算法，实现航空航天器的自主避障、路径规划等任务。
采样系统的基本原理
采样系统基于时间离散化原理，通过在等间隔时间点上获取输入和输出信号的样本值，再根据这些样本值进行计算和控制，以实现对连续时间系统的近似或重构。
采样系统的组成
采样器
采样器是采样系统的核心部件，负责在等间隔时间点上采集输入和输出信号的样本值。
保持器
保持器用于在两次采样间隔期间保持输出信号不变，以实现连续时间系统的近似或重构。

自动控制系统的分类

加。
1-4 自动控制系统的基本要求
自动控制系统是否能很好地工作,是否能精确地保持被控量按照预定的要求规律变化这取决于被控对象和控制器及各功能元器件的特性参数是否设计得当。在理想情况下 , 控制系统的输出量和输入量 , 在任何时候均相等 , 系统完全无误差 , 且不受干扰的影响。实际系统中 , 由于各种各样原因 , 系统在受到输入信号(也包括扰动信号)的激励时,被控量将偏离输入信号作用前的初始值 ,经历一段动态过程(过渡过程)，则系统控制性能的优劣,可以从动态过程中较充分地表现出来。
1-3 自动控制系统的分类
1.按信号流向划分
（1）开环控制系统
信号流动由输入端到输出端单向流动。
（2）闭环控制系统若控制系统中信号除从输入端到输出端外, 还有输出到输入的反馈信号,则构成闭环控制系统,也称反馈控制系统,如图所示。
2.按系统输入信号划分（1）恒值调节系统(自动调节系统) 这种系统的特征是输入量为一恒值,通常称为系统的给定值。控制系统的任务是尽量排除各种干扰因素的影响,使输出量维持在给定值(期望值)。如工业过程中恒温、恒压、恒速等控制系统。
MATLAB分析与设计
1-6 本课程的内容和特点
一、自动控制理论的内容自动控制理论的内容与自动控制系统需要研究的问题密切相关。要研究的问题有两个方面，即控制系统的分析；控制系统设计与综合。（－）自动控制系统的分析控制系统分析主要包括三个方面内容：①稳定性分析；②稳态特性分析（准确性，精度）；③动态特性分析（暂态特性或瞬态特性）。（稳、准、快） 1．系统的稳定性分析 1、稳定性分析；给出判断系统稳定性的基本方法，并阐述系统的稳定性与系统结构（或称控制规律）及系统参数间的关系。 2、稳态特性分析：系统稳态特性表征了系统实际稳态值与希望稳态值之间的差值，即稳态误差，表征了控制系统的控制精度。给出计算系统稳态误差的方法，指出系统结构和参数对稳态特性的影响。

自动采样器操作规程

自动采样器操作规程
《自动采样器操作规程》
一、操作前的准备
1. 检查自动采样器的机械部件是否完好，有无松动、损坏等现象。

2. 确保采样器的供电正常，电源插头接触良好。

3. 检查采样器的样品瓶、管路等部件是否清洁并无异物。

4. 察看采样器的程序设置是否正确，包括时间、体积、速度等参数。

二、操作步骤
1. 将待采样的样品放置在采样器指定位置，并按照程序设置好采样的时间、体积等参数。

2. 打开采样器的电源开关，等待采样器初始化完成。

3. 在电脑终端上启动采样器的控制程序，并按照程序中的提示进行操作。

4. 在采样过程中，监视采样器的运行状态，及时处理异常情况。

5. 采样完成后，关闭电脑终端上的控制程序，并关闭采样器的电源开关。

三、注意事项
1. 在操作过程中，严格遵守操作规程，不得擅自更改采样器的程序设置。

2. 注意采样器的安全使用，避免触电、碰撞等危险操作。

3. 对于采样器的维护和保养，按照规定的周期进行清洁、润滑等工作。

4. 定期对采样器进行检查和维修，确保采样器的正常运行和安全使用。

通过遵守《自动采样器操作规程》，可保证采样器的安全运行，提高采样的准确性和稳定性。

同时，也能延长采样器的使用寿命，节省维护成本。

天津大学812自动控制理论2007-2011真题

天津大学招收2011年硕士学位研究生入学考试试题考试科目名称：自动控制理论考试科目代码：812所有答案必须写在试卷纸上，并写清楚题号，答案写在试题上无效。

提示：本套考卷的部分试题对于学术型硕士研究生考生和全日制专业学位硕士研究生考生有所区别，前面未标注的试题为所有考生必答题，前面有标注的试题请考生务必选择相应类型试题作答，选错不得分。

一、(25分)某直流电机电枢电压输入uα与转角输出θm间满足的微分方程为（１）给出从电枢电压uα到电机转速间的传递函数，给出从电枢电压uα到电机转角θm间的传递函数，求时电机转速的稳态值。

（２）引入反馈控制式中为θr转角的给定值，求系统的闭环传递函数。

（３）为使闭环系统的超调量为16%，试确定K的取值，问此时系统的调节时间？二．（25分）已知被控对象由下列三个传递函数顺序串联而成(1)试将G1（S）、G2（S）、G3（S）的输出依次取状态变量X1、X2、X3，列写被控对象的状态方程描述。

(2)设计状态反馈矩阵K T=[k1,k2,k3],使系统的闭环极点为-3，-2±j2。

三．（25分）某单位反馈系统被控对象的传递函数为调节器的传递函数为（1）试绘制系统kp 从0到＋∞、Ti从0到4两参数变化的根轨迹簇（具体绘图时取T=0.25、0.5、1、2、4）。

（2）根据根轨迹图，分别讨论kp 变化时、Ti变化时对系统闭环极点阻尼比和自然振荡频率的影响。

（3）谈论kp Ti=1、Ti变化时闭环系统的动态响应特性。

四．（25分）某单位反馈系统校正前的开环传递函数为要求校正后系统的加速度误差系数K a=31.6，系统开环传递函数中频段的斜率为-20dB /dec,函数穿越频率10rad/s，高频段的斜率为-40db/dec，且对频率为100rad/s的测量噪声扰动信号有-30dB的衰减。

（1）绘制希望的对数幅频特性曲线。

（2）给出校正装置的传递函数，它是一种什么校正装置？（3）计算校正前和校正后的系统相角裕度，定性说明系统的静态特性、稳定性和快速性的变化。

数字控制(徐丽娜)第2章

f (t )
*
k
f (kT ) (t kT )
k

f ( t ) ( t kT )
f ( t ) T ( t )
加权函数式中
T (t )
k
(t kT )

为理想采样开关产生的脉冲序列理想采样开关相当于个列。理想采样开关相当于一个理想脉冲发生器。
at j t
F ( j )
( f ( t ) 0，当t 0时) F ( j ) e
0
e
1 dt a j
0

采样信号f*(t) 的Fourier变换F*(j)—即采样过程的频域描述求法求法一：
根据 Fourier 变换的频率卷积定理，有下式成立 1 F [ f ( t ) g ( t )] F ( j ) * G ( j ) 2 式中 * 代表卷积： f ( t ) g ( t )
0
0.2 1.8 2.2 3.8

2.3 采样定理
f (t ) f * (t )
F ( j ) F * ( j )
F ( j )
g( t )
G ( j )
f (t )
F ( j )
2m时，采用如下低通滤波器可无失真地再现原信号。
0 T
T ( j )
t
jn s )
n
( j

s
Байду номын сангаас
s

(1) s 2 m
此时，高低频率之间不发生混频 (混叠)现象。现象
1 F * ( j ) T
n
F ( j

实验二控制系统的阶跃响应及稳定性分析

实验二控制系统的阶跃响应及稳定性分析一、实验目的及要求：1.掌握控制系统数学模型的基本描述方法；2.了解控制系统的稳定性分析方法；3.掌握控制时域分析基本方法。

二、实验内容：1.系统数学模型的几种表示方法（1）传递函数模型G(s)=tf()（2）零极点模型G(s)=zpk(z,p,k)其中，G(s)=将零点、极点及K值输入即可建立零极点模型。

z=[-z1,-z …,-z m]p=[-p1,-p …,-p]k=k(3)多项式求根的函数：roots ( )调用格式： z=roots(a)其中：z — 各个根所构成的向量 a — 多项式系数向量(4)两种模型之间的转换函数：[z ,p ,k]=tf2zp(num , den) %传递函数模型向零极点传递函数的转换[num , den ]=zp2tf(z ,p ,k) %零极点传递函数向传递函数模型的转换（5）feedback()函数：系统反馈连接调用格式：sys=feedback(s1,s2,sign)其中，s1为前向通道传递函数，s2为反馈通道传递函数，sign=-1时，表示系统为单位负反馈；sign=1时，表示系统为单位正反馈。

2.控制系统的稳定性分析方法（1）求闭环特征方程的根(用roots函数)；判断以为系统前向通道传递函数而构成的单位负反馈系统的稳定性，指出系统的闭环特征根的值：可编程如下：numg=1; deng=[1 1 2 23];numf=1; denf=1;[num,den]= feedback(numg,deng,numf,denf,-1);roots(den)（2）化为零极点模型，看极点是否在s右半平面（用pzmap）；3.控制系统根轨迹绘制rlocus() 函数：功能为求系统根轨迹rlocfind():计算给定根的根轨迹增益sgrid()函数：绘制连续时间系统根轨迹和零极点图中的阻尼系数和自然频率栅格线4.线性系统时间响应分析step( )函数---求系统阶跃响应impulse( )函数：求取系统的脉冲响应lsim( )函数：求系统的任意输入下的仿真三、实验报告要求：编出程序并运行，完成下面的练习题：1．写出表示下列传递函数模型的MATLAB程序，并运行实现：（1）（2） (3)>>num=4*conv([1,2],conv([1, 6, 6],[1, 6, 6]));>>den=conv([1,0],conv([1,1],conv([1,1],conv([1,1],[1,3,2,5]))));2．判断以为系统前向通道传递函数而构成的单位负反馈系统的稳定性，指出系统的闭环特征根的值。

二、选择性控制系统

过程控制与自动化仪表P222三、选择性控制系统选择性控制系统（超驰控制系统，override control system）也有人称其为自保护系统或软保护系统。

选择性控制是把生产过程中对某些工业参数的限制条件所构成的逻辑关系迭加到正常的自动控制系统上去的组合控制方案。

（一）控制原理选择性控制系统由正常控制部分和取代控制部分组成。

正常情况下正常控制部分工作，取代控制部分不工作；当生产过程某个参数趋于危险极限时但还未进人危险区域时，取代控制部分工作，而正常控制部分不工作，直到生产重新恢复正常，然后正常控制部分又重新工作。

从而，使控制系统能在正常和异常情况下自动切换工作，起到软保护的作用。

选择性控制系统的特点是选用了选择器，设有两个调节器(或两个以上的变送器)，通过具有选择功能的自动选择器（高值或低值选择器）或自动切换装置，选出能适应生产安全状况的控制信号实现对生产过程的自动控制。

根据选择器在整个系统的位置可分为两种类型。

其一是选择器安装在两个调节器的输出端，对调节器输出信号进行选择，两个调节器公用一个调节阀，如图1所示。

这类系统正常生产时，取代调节器处于待命备用状态，不正常工况出现时，由选择器选出能适应工况的控制信号，用取代调节器工作，结构简单，应用比较广泛。

其二是选择器安装在调节器之前，对变送器输出信号进行选择，这种系统至少有两个以上的变送器，由选择器选择符合工艺要求的输出信号送至调节器。

图2 类型二根据处理方法不同，选择性控制系统又可以分为三类：开关型选择性控制系统，由限位信号切断控制器输出；连续型选择性控制系统，由限位信号切换为另一个控制器输出给执行器；混合型选择性控制系统，采用两个限制信号，同时进行上述两种控制。

（二）工程设计应考虑的问题选择性控制系统的设计包括调节阀气开、气关形式选择，调节器正、反作用选择，选择器的选型及系统参数整定等内容。

1.调节阀气开、气关形式可按照单回路控制系统的方法确定，根据生产工艺安全原则来选择。